A Degradation Warning Method for Ultra-High Voltage Energy Devices Based on Time-Frequency Feature Prediction
Abstract
1. Introduction
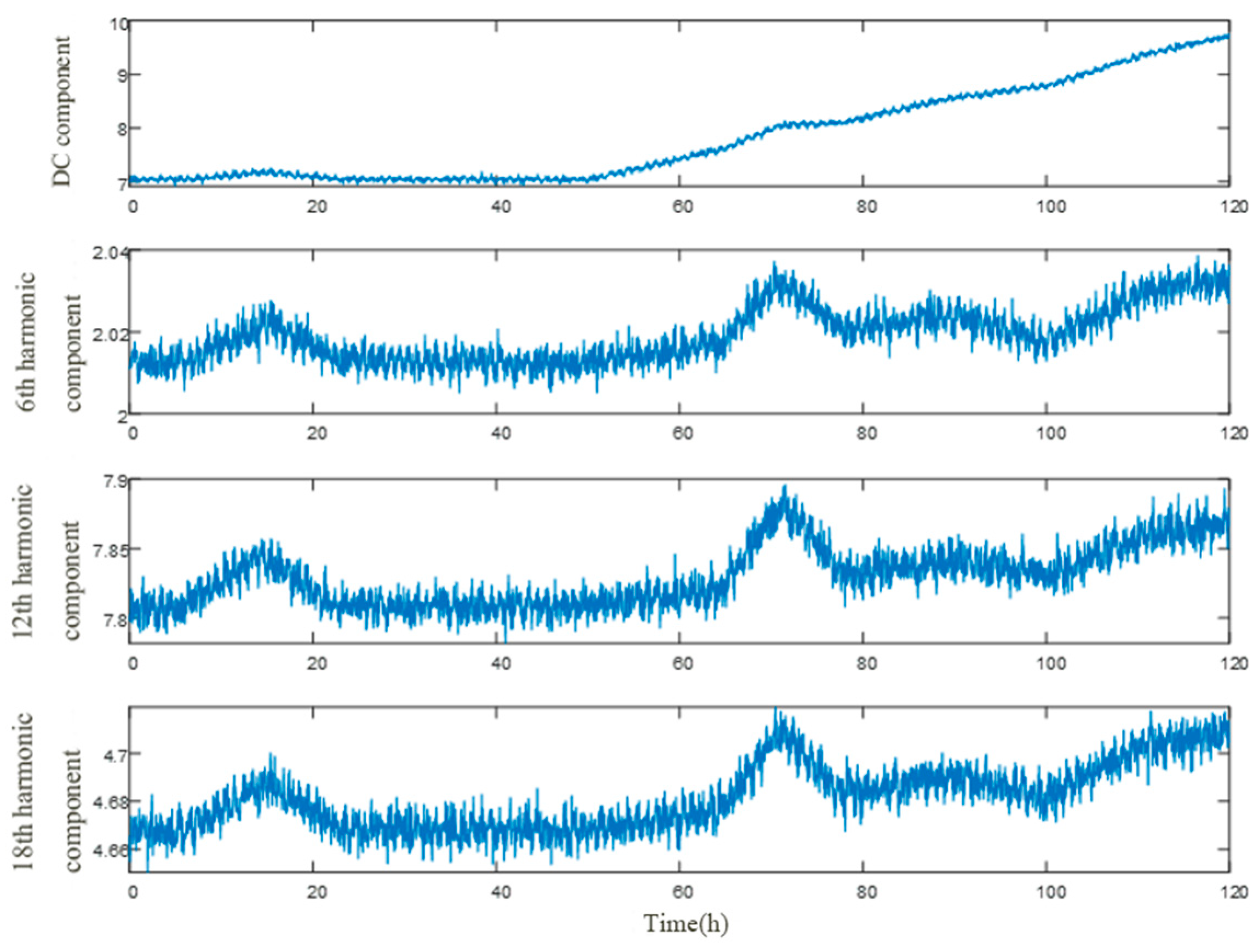
2. Leakage Current Harmonic Separation Algorithm
- The chosen embedding dimension significantly affects results during phase space reconstruction. However, current methods for determining this dimension lack precision.
- A sizeable embedding dimension may result in processing many ineffective components, leading to time consumption.
- The methods for initial single-component recombination and the criteria for iteration termination in symplectic geometry are unclear.
- The algorithm’s ability to suppress noise is insufficient when faced with strong noise signals.
2.1. Symplectic Geometric Matrix Transformation
2.2. Reconstruction of Symplectic Geometric Components
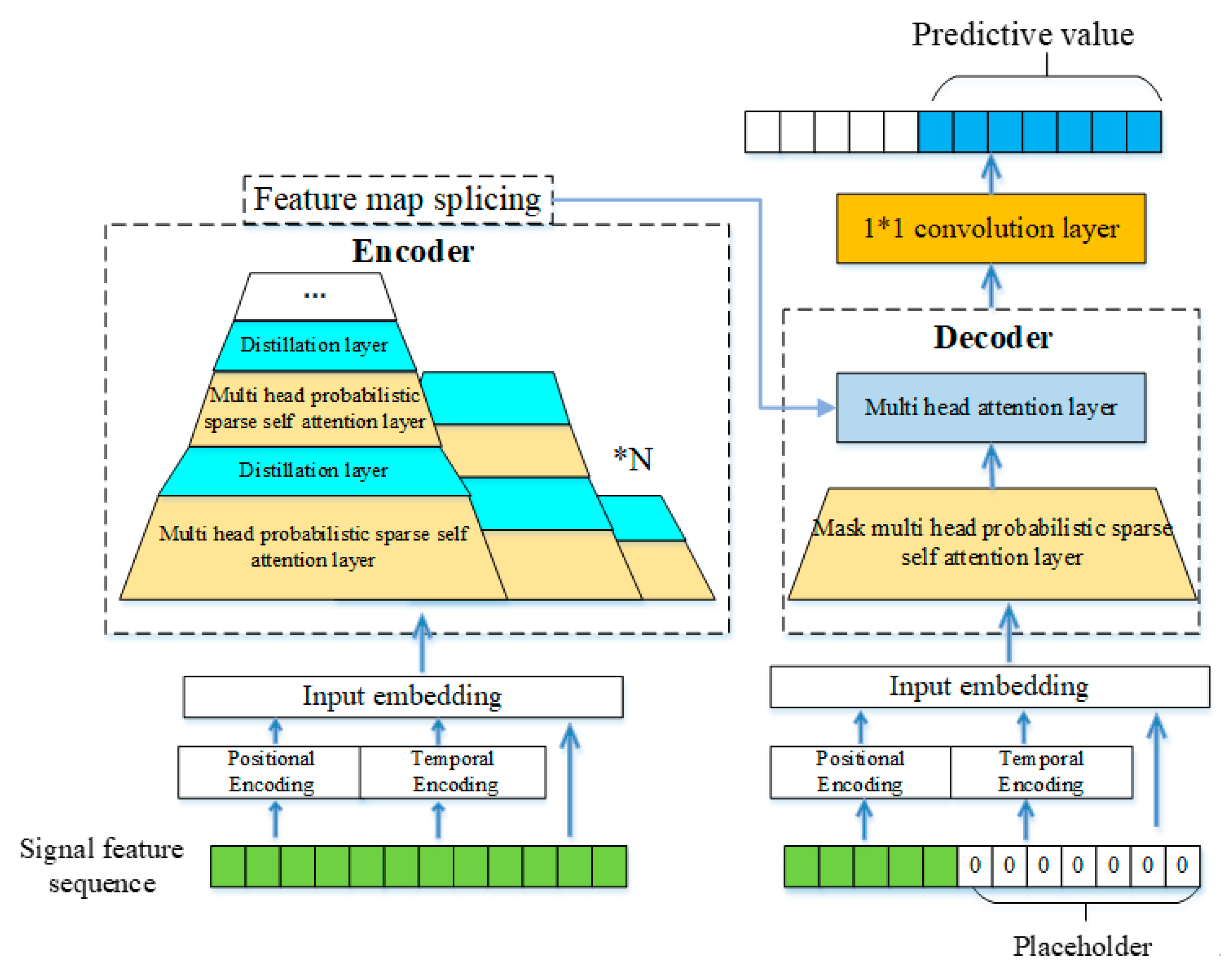
3. Prediction of the Time-Frequency Characteristics of Leakage Current Based on I-Informer
3.1. Model Input
3.2. Encoder
3.3. Decoder
4. Experiments
4.1. Evaluation Effect of the Comprehensive Indicator
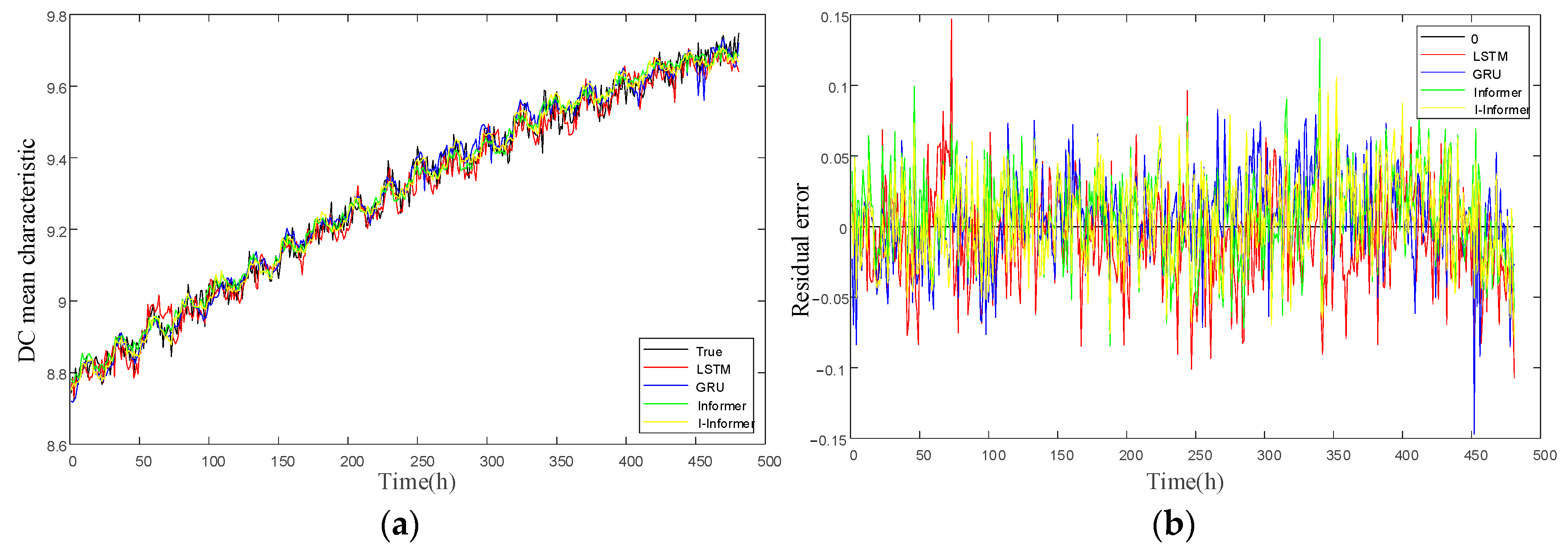
4.2. Leakage Current Characteristic Prediction Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, X.; Tang, Y.; Bu, G.; Shen, C.; Song, G.; Wang, Z.; Gan, D.; Hou, J.; Wang, B.; Zhao, B.; et al. Confronting Problem and Challenge of Large Scale AC-DC Hybrid Power Grid Operation. Proc. CSEE 2019, 39, 3107–3119. [Google Scholar]
- Liu, Z.; Wang, S.; Chong, Z.; Huang, Y.; Guo, X.; Xiao, K.; Liu, S.; Li, T.; Zhao, W. Controllable and Adaptive Energy Absorption Device for Hybrid Cascaded UHVDC Transmission System. Proc. CSEE 2021, 41, 514–523. [Google Scholar]
- Tao, J.; Zheng, Y.; Zhang, K. Electric field simulation and experimental verification of controllable energy dissipation device for ±800kV converter station. Electr. Eng. 2022, 3, 46–49. [Google Scholar]
- Madaschi, A.; Brunero, M.; Ferrario, M.; Marteli, P.; Boffi, P.; Martinelli, M. Experimental evaluation of the birefringence effect on faraday-based fiber-optic current sensors. IEEE Sens. Lett. 2022, 6, 5000404. [Google Scholar] [CrossRef]
- Zhong, J.; Che, C.; Wang, Q.; Zhao, L.; Wang, L.; Zhao, J.; Feng, R. Simulation analysis of internal electric field and voltage distribution of 500 kV metal oxide lightning arrester under different pollution states. Inn. Mong. Electr. Power Technol. 2023, 41, 52–58. [Google Scholar]
- Srividhya, J.P.; Sivakumar, D.; Shanmathi, T. A Review on causes, effects, and detection techniques of harmonics in the power system. In Proceedings of the 2016 International Conference on Computation of Power, Energy Information and Commuincation (ICCPEIC), Melmaruvathur, India, 20–21 April 2016; pp. 680–686. [Google Scholar]
- Cai, H.; Jia, L.; Liao, M.; Xu, D.; Guo, J. Study on the degradation characteristics of lightning impulse of lightning arresters. Electr. Porcelain Light. Arresters 2018, 4, 133–137. [Google Scholar]
- Wong, K.L. Electromagnetic emission based monitoring technique for polymer ZnO surge arresters. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 181–190. [Google Scholar] [CrossRef]
- Hu, T.; Liu, H.; Liu, G.; Mei, Q.; Ma, Y.; Liu, M. Lightning arrester infrared image fault detection method based on improved YOOv3. Infrared Technol. 2023, 45, 1256–1261. [Google Scholar]
- Cao, H.; Wang, L.; Zhu, Q.; Xu, X. Design and Implementation of MOA Full Current Online Monitoring Experimental Platform. Electr. Porcelain Arrester 2012, 4, 69–73. [Google Scholar]
- Xing, C.; Zhao, J.; Liu, T.; Yang, H.; Yang, S.; Wang, H. On site detection method for resistive current of metal oxide lightning arrester based on capacitive equipment grounding current. Electr. Porcelain Light. Arrester 2022, 1, 113–117. [Google Scholar]
- Khodsuz, M.; Mirzaie, M. A Modified Time-Delay Addition Method to Extract Resistive Leakage Current of MOSA. J. Inst. Eng. Ser. B 2016, 97, 445–451. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, L.; Ding, N.; Wei, J. Non-Intrusive Power Load Monitoring Based on Multi-scale Convolution and Layer-wise Residual Graph Convolution. Measurement 2025, 246, 116593. [Google Scholar] [CrossRef]
- Huang, H.; Jin, C.; Hao, H.; Liu, X. Full phase FFT analysis of leakage current in zinc oxide lightning arresters. J. Electron. Meas. Instrum. 2021, 35, 210–216. [Google Scholar]
- Pang, F.; Liu, Y.; Yuan, Y.; Gao, L. Influencing factors analysis on the detector output signal of fiber optic current transformer with sine modulation. Measurement 2020, 151, 107151. [Google Scholar] [CrossRef]
- Thanh, P.N.; Cho, M.Y. Online leakage current classification using convolutional neural network long short-term memory for high voltage insulators on web-based service. Electr. Power Syst. Res. 2023, 216, 109065. [Google Scholar] [CrossRef]
- Da, T.N.; Thanh, P.N.; Cho, M.Y. A cloud 15kV-HDPE insulator leakage current classification based improved particle swarm optimization and LSTM-CNN deep learning approach. Swarm Evol. Comput. 2024, 91, 101755. [Google Scholar]
- Klaar, A.C.R.; Stefenon, S.F.; Seman, L.O.; Mariani, V.C.; Coelho, L.D.S. Optimized EWT-Seq2Seq-LSTM with attention mechanism to insulators fault prediction. Sensors 2023, 23, 3202. [Google Scholar] [CrossRef]
- Pan, H.; Yang, Y.; Li, X.; Zheng, J.; Cheng, J. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 189–211. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Zhang, S.H.; Peng, J.Q.; Zhang, S. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Li, T.; Sun, J.; Wu, M.; Yang, S.; Song, K.; Li, J. Study on failure mechanism of arrester on roof of high-speed electric multiple units under high-order harmonics. China Saf. Sci. J. 2019, 29 (Suppl. S1), 88. [Google Scholar]
- Sun, J.; Ding, F.; Lv, Y.; Ren, J.; Song, S.; Li, T.; Zhi, Q.; Guo, C. Leakage current characteristics and ageing assessment technology of roof arrester under ultra harmonics overvoltage. High Volt. 2022, 7, 346–356. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, L.; Yang, J.; Liu, C.; Wang, D.; Yuan, S.; Ma, Y.; Zhao, H. An impulse aging assessment method for arrester under multiple strokes based on frequency domain dielectric spectroscopy. IEEE Trans. Power Deliv. 2023, 38, 2933–2943. [Google Scholar] [CrossRef]

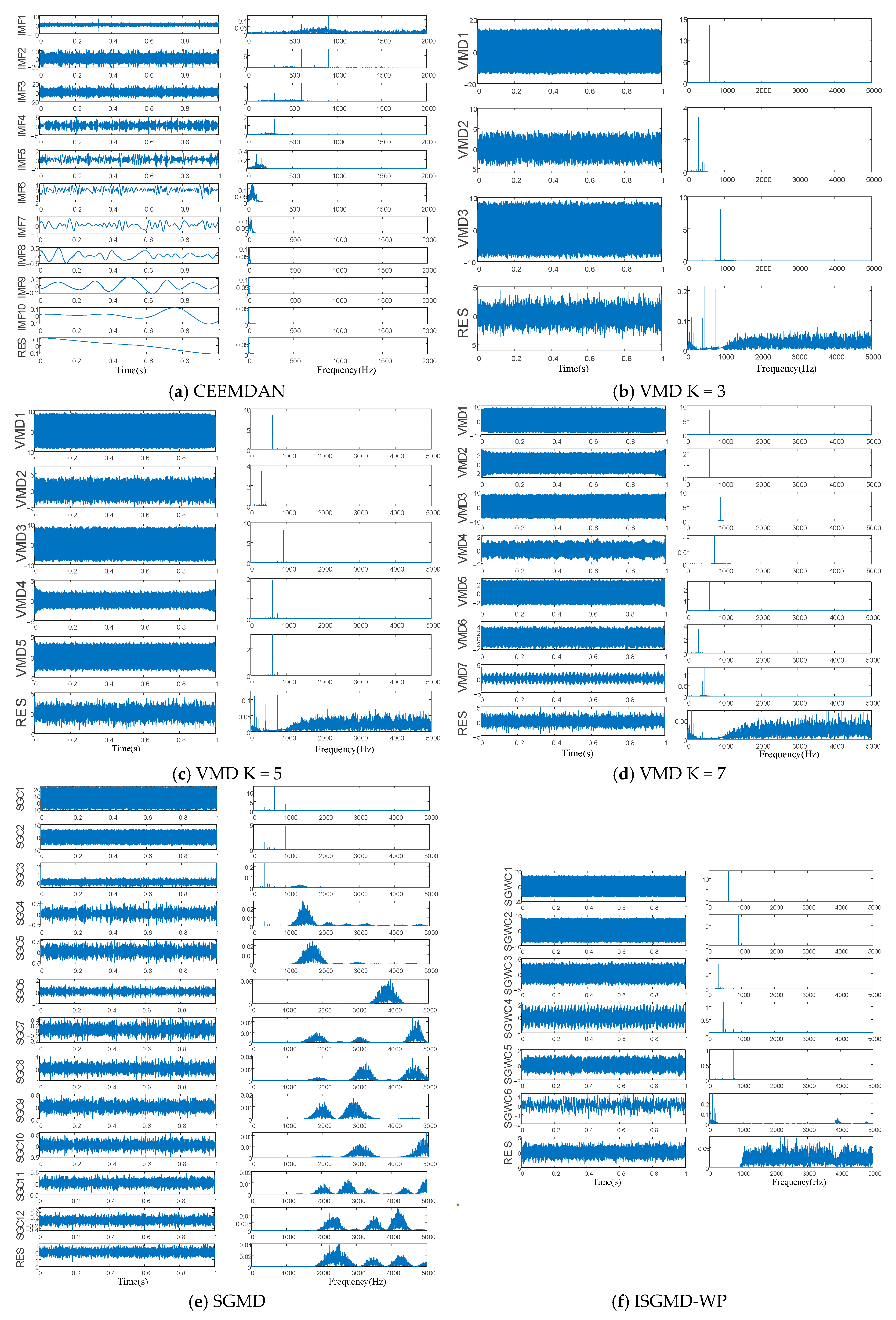
| SNR | VMD | SGMD | ISGMD-WP |
|---|---|---|---|
| −5 dB | 2.97597 | 3.26770 | 1.95689 |
| 5 dB | 0.29769 | 0.67891 | 0.24502 |
| 15 dB | 0.02907 | 0.44365 | 0.02264 |
| 25 dB | 0.00511 | 0.42125 | 0.00203 |
| Input Feature Count | Indicator Name | LSTM | GRU | Informer | I-Informer |
|---|---|---|---|---|---|
| 1 | MAE | 0.0387477 | 0.0358729 | 0.0337567 | 0.0319757 |
| RMSE | 0.0498476 | 0.0454695 | 0.0437456 | 0.0402823 | |
| 4 | MAE | 0.0302019 | 0.0280184 | 0.0266243 | 0.0253844 |
| RMSE | 0.0388004 | 0.0352935 | 0.0333787 | 0.0317544 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Wang, L.; Wei, J.; Wang, Y.; Wu, H. A Degradation Warning Method for Ultra-High Voltage Energy Devices Based on Time-Frequency Feature Prediction. Sensors 2025, 25, 3478. https://doi.org/10.3390/s25113478
Zhao P, Wang L, Wei J, Wang Y, Wu H. A Degradation Warning Method for Ultra-High Voltage Energy Devices Based on Time-Frequency Feature Prediction. Sensors. 2025; 25(11):3478. https://doi.org/10.3390/s25113478
Chicago/Turabian StyleZhao, Pinzhang, Lihui Wang, Jian Wei, Yifan Wang, and Haifeng Wu. 2025. "A Degradation Warning Method for Ultra-High Voltage Energy Devices Based on Time-Frequency Feature Prediction" Sensors 25, no. 11: 3478. https://doi.org/10.3390/s25113478
APA StyleZhao, P., Wang, L., Wei, J., Wang, Y., & Wu, H. (2025). A Degradation Warning Method for Ultra-High Voltage Energy Devices Based on Time-Frequency Feature Prediction. Sensors, 25(11), 3478. https://doi.org/10.3390/s25113478







