Asymmetric Double-Sideband Composite Signal and Dual-Carrier Cooperative Tracking-Based High-Precision Communication–Navigation Convergence Positioning Method
Abstract
1. Introduction
2. Asymmetric Double-Sideband Composite Location Signal and Reception
2.1. Asymmetric Double-Sideband Composite Location Signal
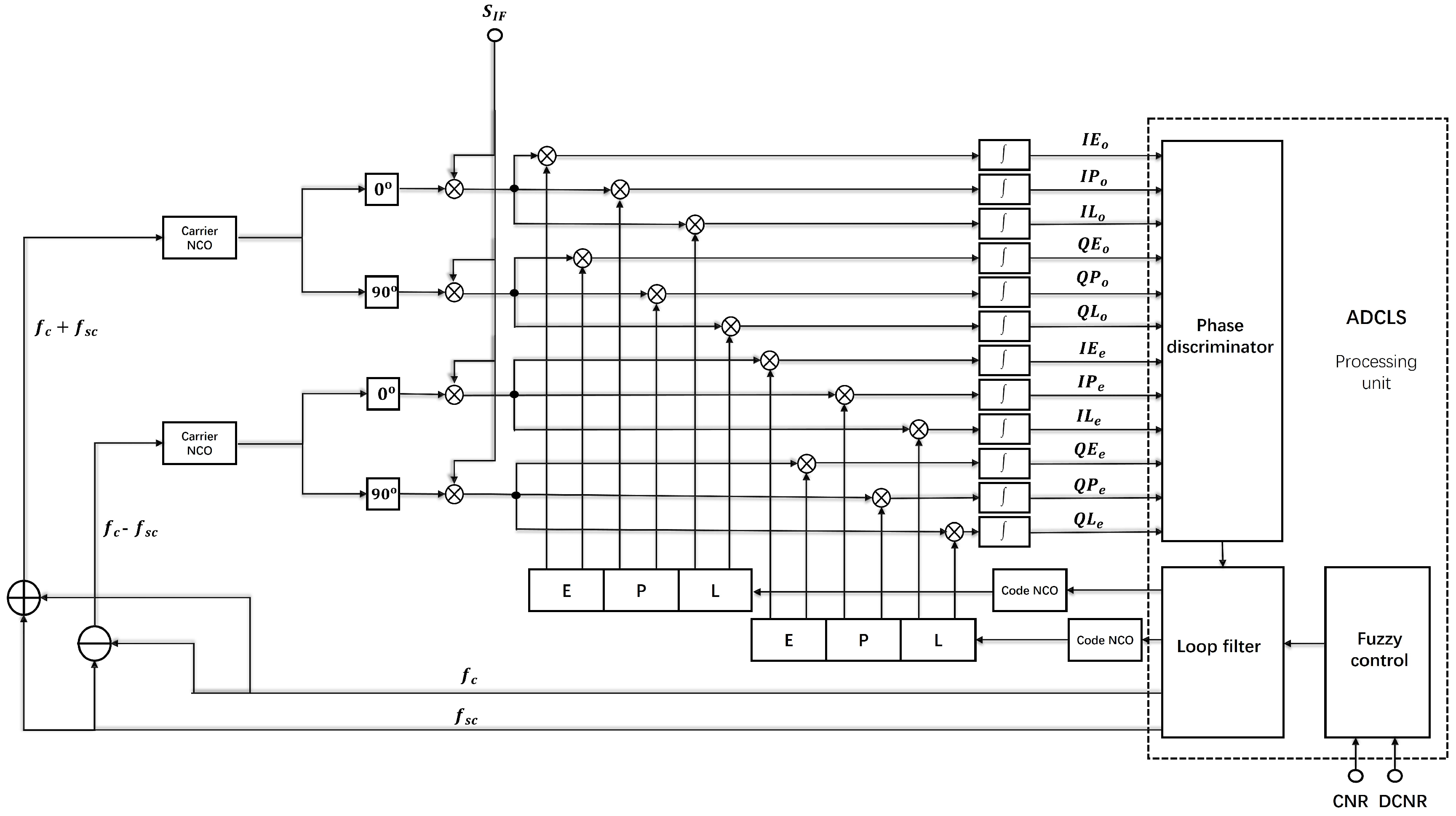
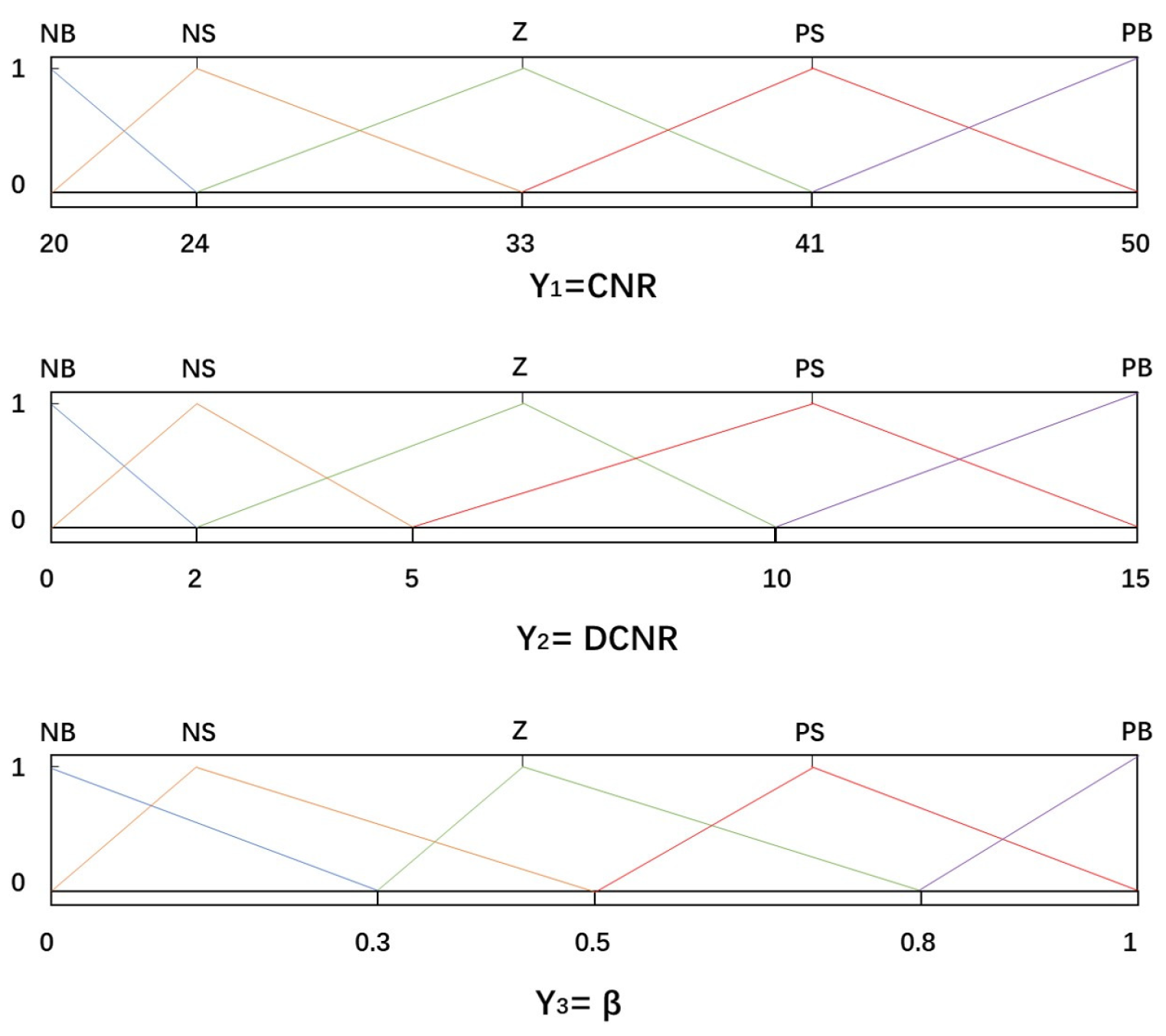
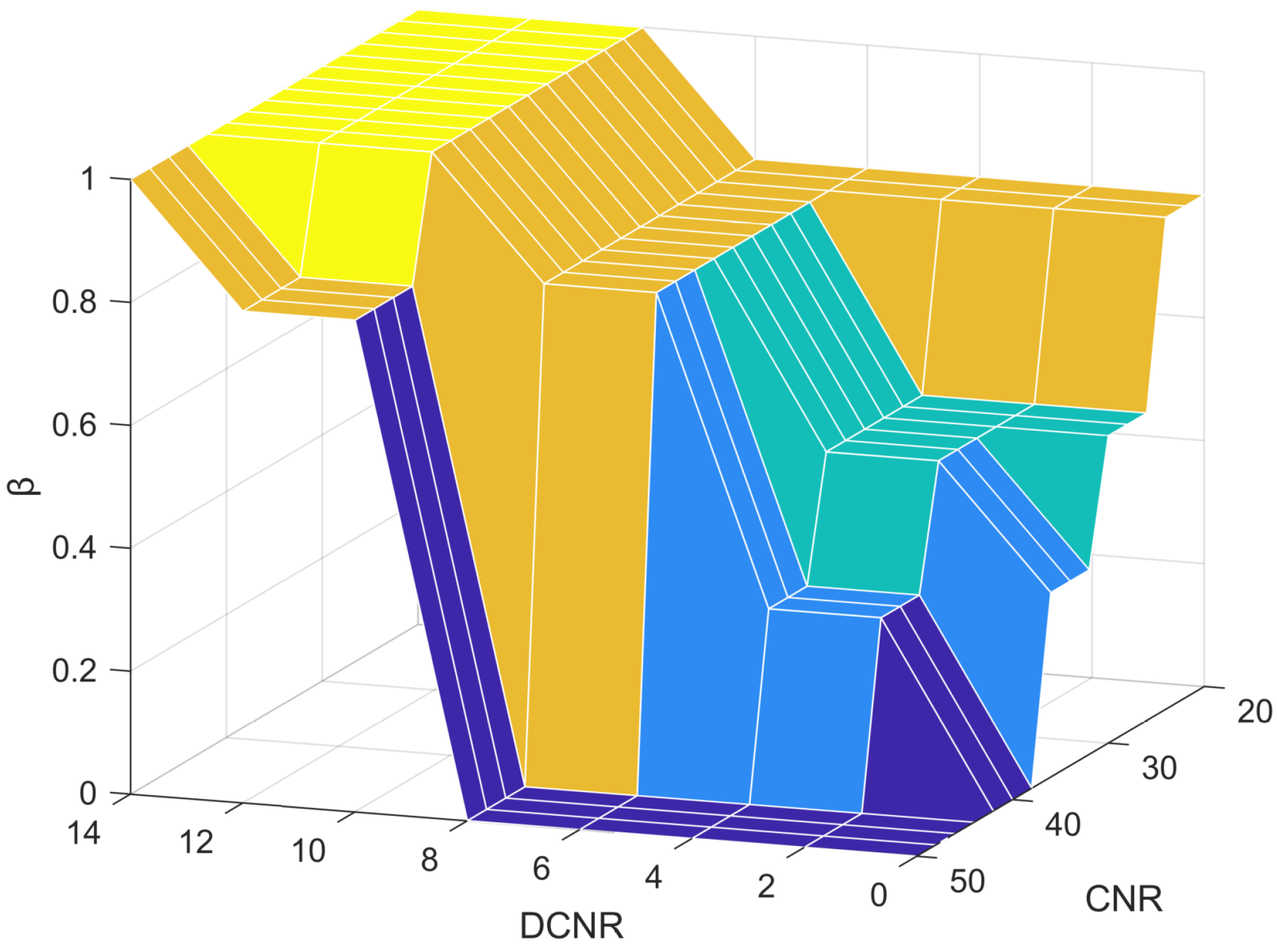
2.2. Asymmetric Double-Carrier Double-Code Loop Combined Tracking Loop Based on Fuzzy Control
2.3. Error Analysis
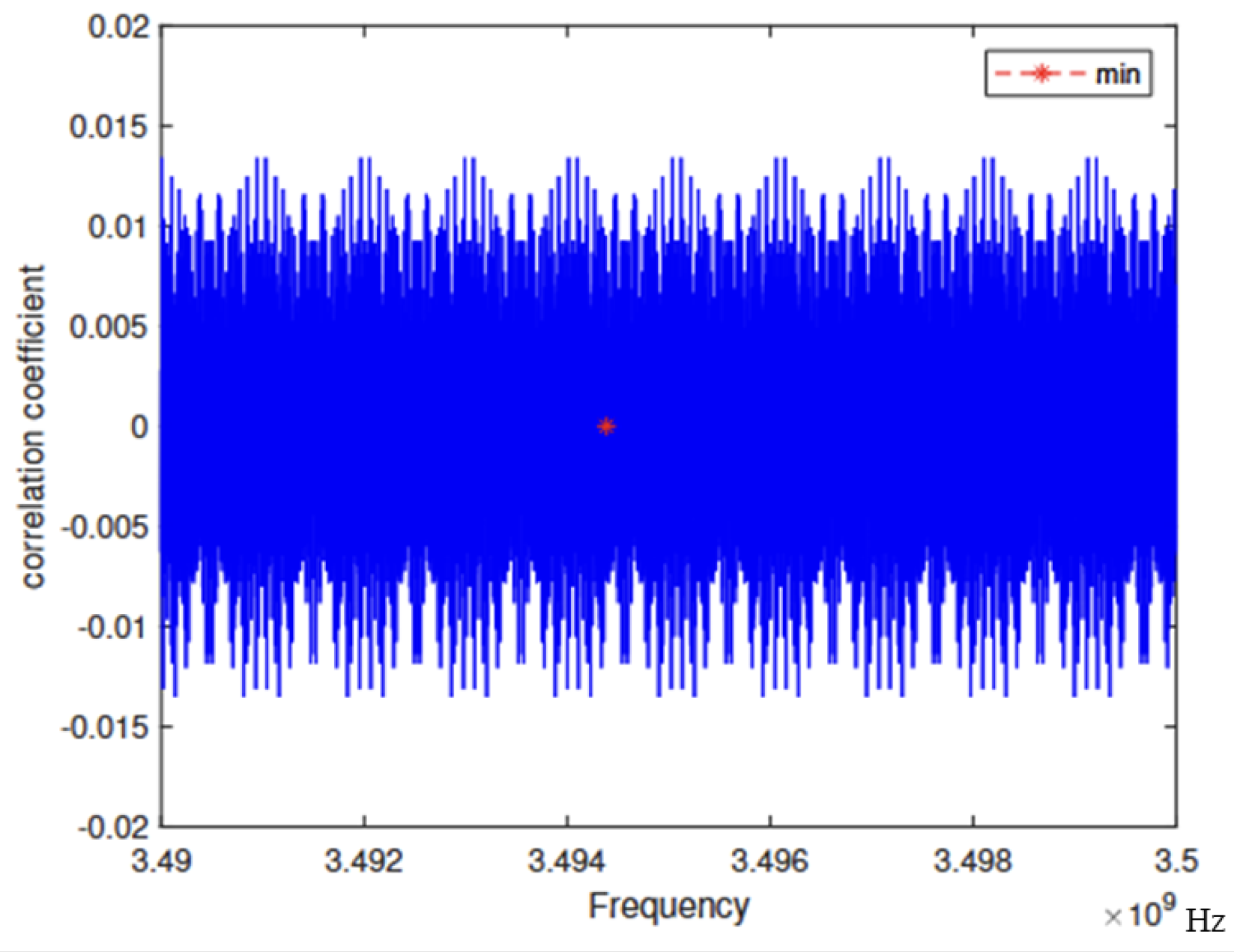
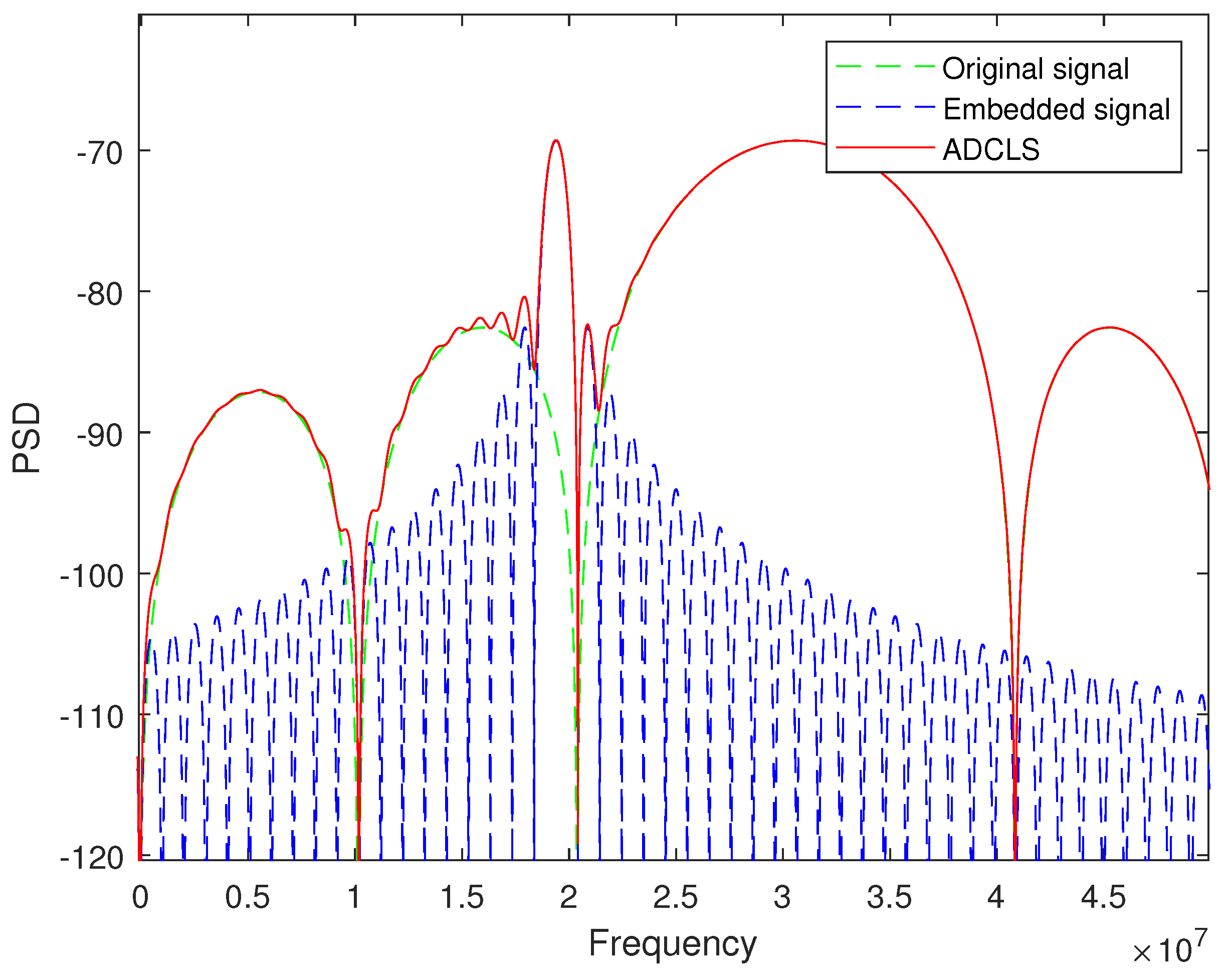
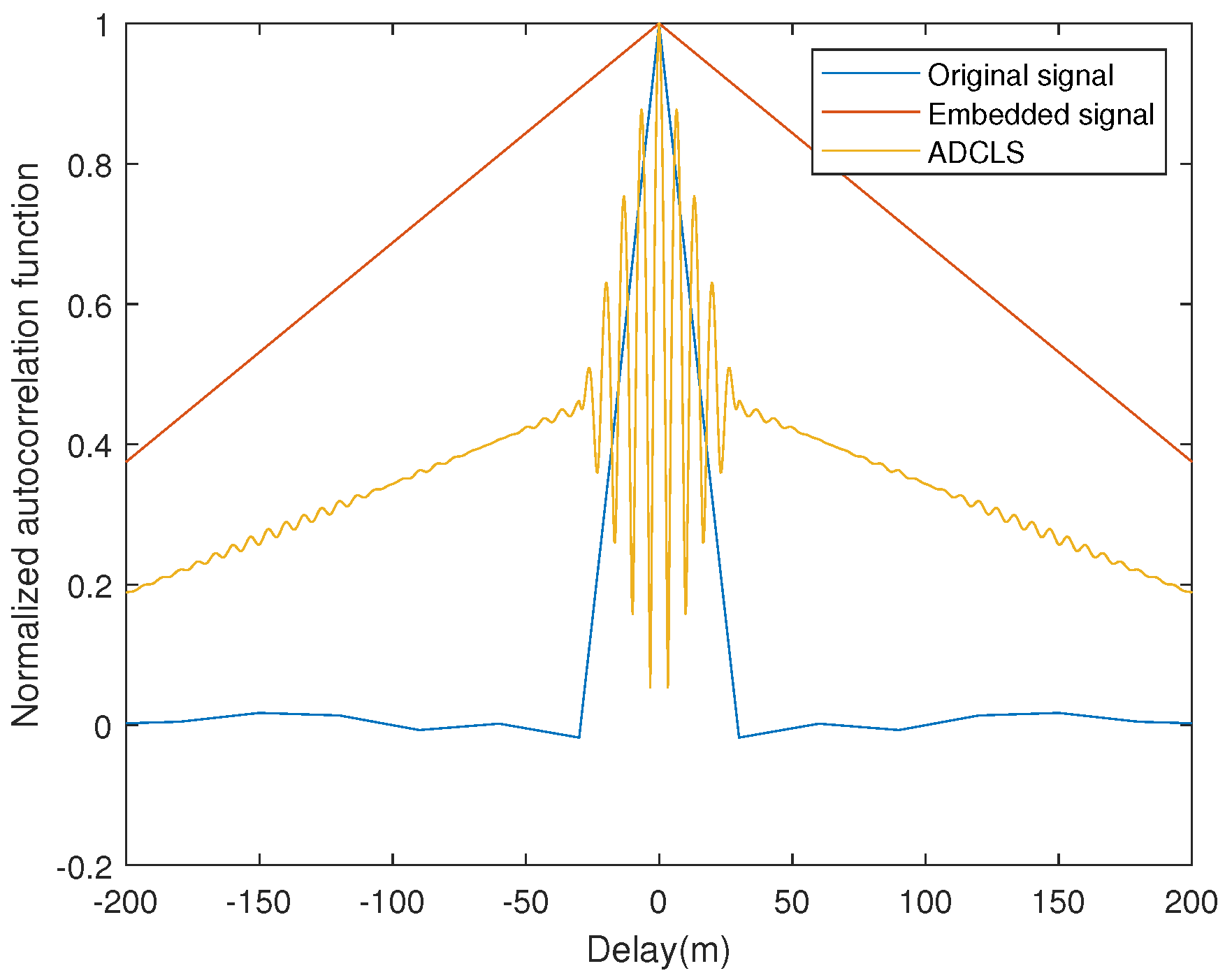
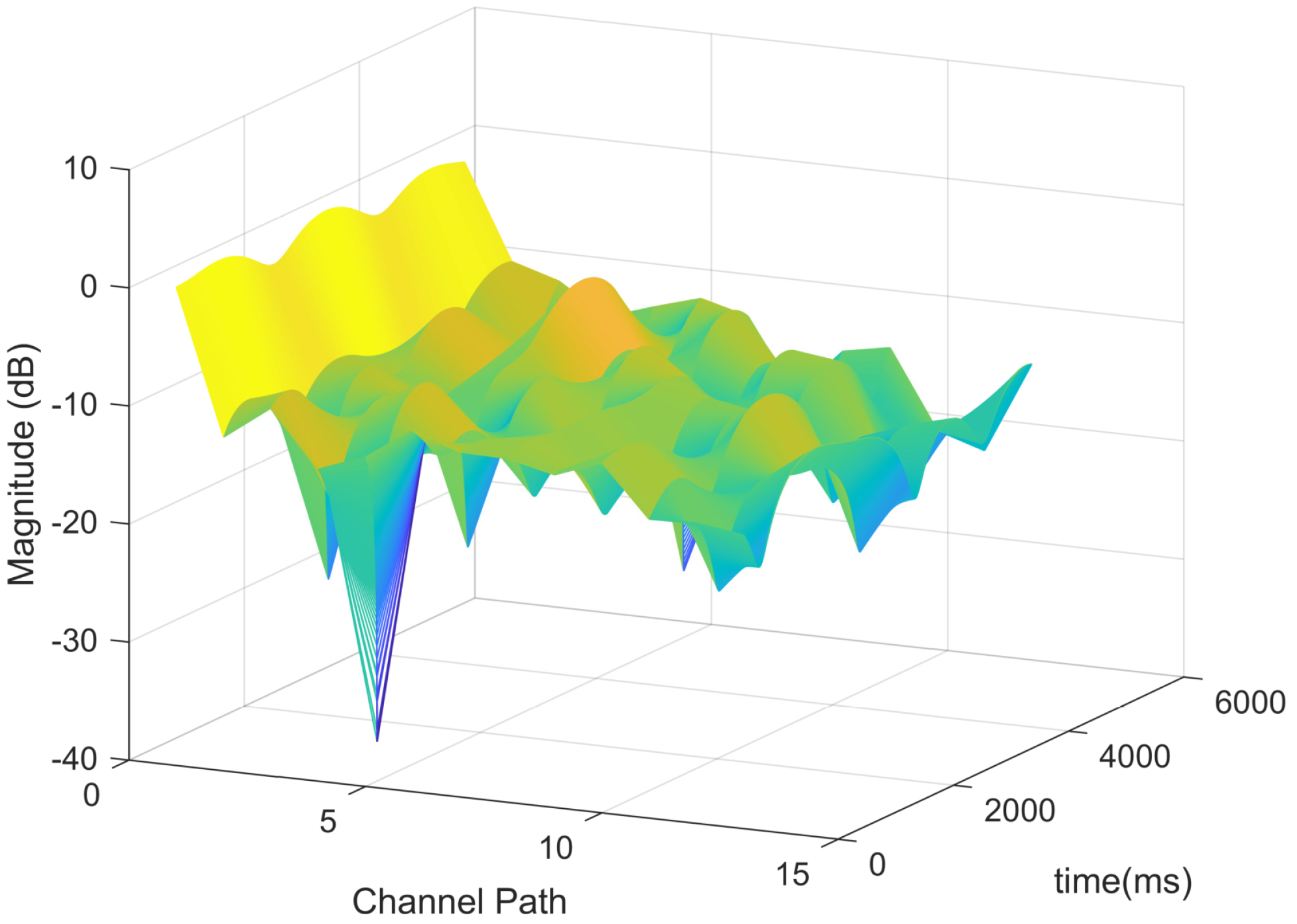
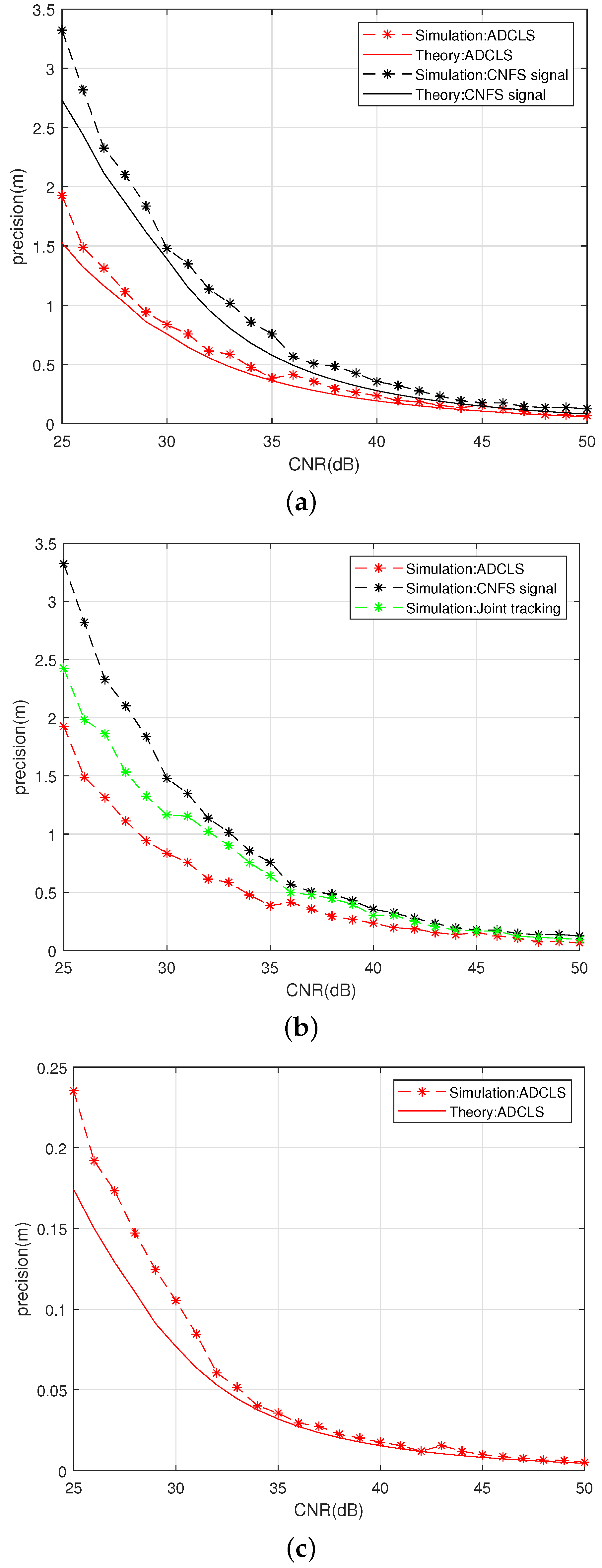
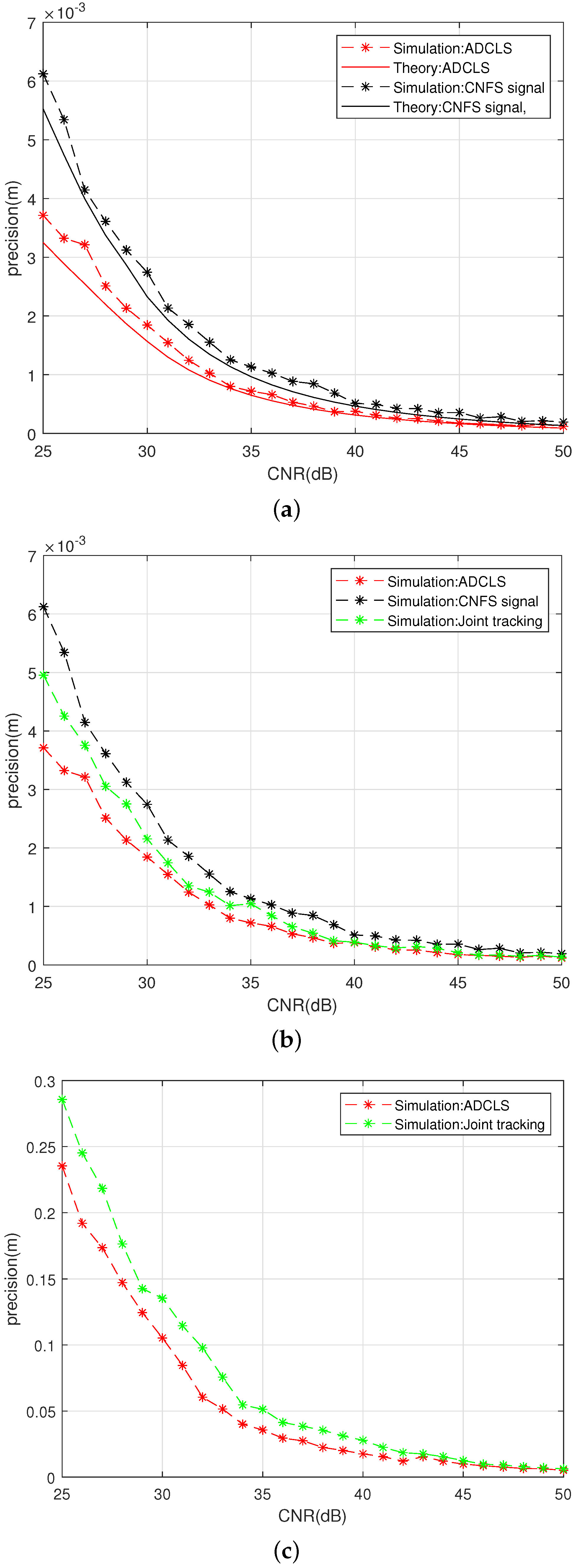
3. Simulation Results
Experimental Conditions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Lin, X.; Lee, J.; Toskala, A.; Sun, S.; Chiasserini, C.F.; Liu, L. 5g-advanced toward 6g: Past, present, and future. IEEE J. Sel. Areas Commun. 2023, 41, 1592–1619. [Google Scholar] [CrossRef]
- Abuyaghi, M.; Si-Mohammed, S.; Shaker, G.; Rosenberg, C. Positioning in 5g networks: Emerging techniques, use cases, and challenges. IEEE Internet Things J. 2025, 12, 1408–1427. [Google Scholar] [CrossRef]
- Wigren, T. Adaptive enhanced cell-id fingerprinting localization by clustering of precise position measurements. IEEE Trans. Veh. Technol. 2007, 56, 3199–3209. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, Y.; Ma, L.; Yang, S.; Feng, Z.; Pan, C.; Zhang, Q.; Wang, Y.; Wu, H.; Zhang, P. 5g prs-based sensing: A sensing reference signal approach for joint sensing and communication system. IEEE Trans. Veh. Technol. 2023, 72, 3250–3263. [Google Scholar] [CrossRef]
- Bednarz, M.; Zielinski, T.P. Remote radio frequency sensing based on 5g new radio positioning reference signals. Sensors 2025, 25, 337. [Google Scholar] [CrossRef]
- Gonzalez-Garrido, A.; Querol, J.; Wymeersch, H.; Chatzinotas, S. Interference analysis and modeling of positioning reference signals in 5g ntn. IEEE Open J. Commun. Soc. 2024, 5, 7567–7581. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, R.; Liu, Q.; Han, L.; Thompson, J.S. Feasibility study of uav-assisted anti-jamming positioning. IEEE Trans. Veh. Technol. 2021, 70, 7718–7733. [Google Scholar] [CrossRef]
- Martalò, M.; Perri, S.; Verdano, G.; Mola, F.D.; Monica, F.; Ferrari, G. Improved uwb tdoa-based positioning using a single hotspot for industrial iot applications. IEEE Trans. Ind. Informatics 2022, 18, 3915–3925. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Chen, X.; Cao, H.; Wang, C.; Li, J.; Shen, C.; Tang, J. Information monitoring and adaptive information fusion of multisource fusion navigation systems in complex environments. IEEE Internet Things J. 2024, 11, 25047–25056. [Google Scholar] [CrossRef]
- Chae, K.; Park, J.; Kim, Y. Rethinking autocorrelation for deep spectrum sensing in cognitive radio networks. IEEE Internet Things J. 2023, 10, 31–41. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, L.; Zhou, X.; Jiao, Z.; Guo, G.; Chen, R. Machine learning for time-of-arrival estimation with 5g signals in indoor positioning. IEEE Internet Things J. 2023, 10, 9782–9795. [Google Scholar] [CrossRef]
- Benrhaiem, W.; Hafid, A.; Sahu, P.K. Reliable emergency message dissemination scheme for urban vehicular networks. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1154–1166. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, C.; Kuang, L. Turbo iterative dsss acquisition in satellite high-mobility communications. IEEE Trans. Veh. Technol. 2021, 70, 12998–13009. [Google Scholar] [CrossRef]
- Xu, Y.; Xiong, H.; Yang, G.; Zhou, H. Carrier frequency synchronization of ldpc coded transmissions in high dynamic environments. IEEE Trans. Veh. Technol. 2024, 73, 10451–10463. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Xu, B.; Jia, J.; Sun, H.; Chen, C.; Duan, Z.; Bo, Y.; Hyyppä, J. Vector tracking based on factor graph optimization for gnss nlos bias estimation and correction. IEEE Internet Things J. 2022, 9, 16209–16221. [Google Scholar] [CrossRef]
- Gómez, M.; Solera-Rico, A.; Valero, E.; Lázaro, J.; Fernández-Prades, C. Enhancing gnss receiver performance with software-defined vector carrier tracking for rocket launching. Results Eng. 2023, 19, 101310. Available online: https://www.sciencedirect.com/science/article/pii/S2590123023004371 (accessed on 30 April 2025). [CrossRef]
- Zhao, H.; Diaz, J.C.G.; Hoyos, S. Multi-channel receiver nonlinearity cancellation using channel speculation passing algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 599–603. [Google Scholar] [CrossRef]
- Heragu, A.; Ruffieux, D.; Enz, C.C. A 2.4-ghz mems-based pll-free multi-channel receiver with channel filtering at rf. IEEE J.-Solid-State Circuits 2013, 48, 1689–1700. [Google Scholar] [CrossRef]
- Curran, J.T.; Navarro, M.; Anghileri, M.; Closas, P.; Pfletschinger, S. Coding aspects of secure gnss receivers. Proc. IEEE 2016, 104, 1271–1287. [Google Scholar] [CrossRef]
- Zhang, K.; Larsson, E.G.; Papadimitratos, P. Protecting gnss open service navigation message authentication against distance-decreasing attacks. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1224–1240. [Google Scholar] [CrossRef]
- Deng, Z.; Jia, B.; Tang, S.; Fu, X. A fine fast acquisition scheme for a communication and navigation fusion system. Appl. Sci. 2020, 10, 3434. [Google Scholar] [CrossRef]
- Borio, D.; Mongredien, C.; Lachapelle, G. Collaborative code tracking of composite gnss signals. IEEE J. Sel. Top. Signal Process. 2009, 3, 613–626. [Google Scholar] [CrossRef]
- Ortega, L.; Medina, D.; Vilà-Valls, J.; Vincent, F.; Chaumette, E. Positioning performance limits of gnss meta-signals and ho-boc signals. Sensors 2020, 20, 3586. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N.; Mosaad, M.I.; Colak, I.; Djilali, A.B.; Gasmi, H. Enhancement of the power quality of dfig-based dual-rotor wind turbine systems using fractional order fuzzy controller. Expert Syst. Appl. 2024, 238, 121695. Available online: https://www.sciencedirect.com/science/article/pii/S0957417423021978 (accessed on 30 April 2025). [CrossRef]
- Pan, Y.; Wu, Y.; Lam, H.-K. Security-based fuzzy control for nonlinear networked control systems with dos attacks via a resilient event-triggered scheme. IEEE Trans. Fuzzy Syst. 2022, 30, 4359–4368. [Google Scholar] [CrossRef]
- Wang, Q.; Cao, J.; Liu, H. Adaptive fuzzy control of nonlinear systems with predefined time and accuracy. IEEE Trans. Fuzzy Syst. 2022, 30, 5152–5165. [Google Scholar] [CrossRef]
- Shilpi; Kumar, A. Fuzzy distance jaya algorithm based node localization in anisotropic wireless sensor networks. IEEE Trans. Netw. Sci. Eng. 2024, 11, 6345–6355. [Google Scholar] [CrossRef]
- Kacimi, M.A.; Guenounou, O.; Brikh, L.; Yahiaoui, F.; Hadid, N. New mixed-coding pso algorithm for a self-adaptive and automatic learning of mamdani fuzzy rules. Eng. Appl. Artif. Intell. 2020, 89, 103417. Available online: https://www.sciencedirect.com/science/article/pii/S0952197619303240 (accessed on 30 April 2025). [CrossRef]
- Naimi, M.; Tahayori, H.; Sadeghian, A. A fast and accurate method for calculating the center of gravity of polygonal interval type-2 fuzzy sets. IEEE Trans. Fuzzy Syst. 2021, 29, 1472–1483. [Google Scholar] [CrossRef]
- Wang, X.; Kennedy, M.P. Enhanced jitter analysis and minimization for digital plls with mid-rise tdcs and its impact on output phase noise. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 5124–5137. [Google Scholar] [CrossRef]
- Tian, Z.; Cui, X.; Zhu, Y.; Lu, M. Dual high-resolution correlators for multipath mitigation in boc signals. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5012–5026. [Google Scholar] [CrossRef]
- Gao, X.; He, D.; Wang, P.; Yu, W. Signal parameter estimation based on esprit with state space model for 5g nr signals in indoor and urban environments. IEEE Trans. Veh. Technol. 2025, 74, 2276–2291. [Google Scholar] [CrossRef]
- Shamaei, K.; Kassas, Z.M. Receiver design and time of arrival estimation for opportunistic localization with 5g signals. IEEE Trans. Wirel. Commun. 2021, 20, 4716–4731. [Google Scholar] [CrossRef]

| Parameter | Parameter Settings |
|---|---|
| Coherent integration time | 1 ms |
| Sampling frequency | 50 MHz |
| Code ring noise bandwidth | 1 Hz |
| Main carrier noise bandwidth | 10 Hz |
| Subcarrier noise bandwidth | 0.8 Hz |
| Incoherent integration time | 1 ms |
| Correlator spacing | 0.5 |
| Sampling bit | 8 bit |
| Damping coefficient | 0.707 |
| Traction time | 350 ms |
| PMF-FFT numbers | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Ding, Z.; Gao, X.; Liu, P. Asymmetric Double-Sideband Composite Signal and Dual-Carrier Cooperative Tracking-Based High-Precision Communication–Navigation Convergence Positioning Method. Sensors 2025, 25, 3405. https://doi.org/10.3390/s25113405
Deng Z, Ding Z, Gao X, Liu P. Asymmetric Double-Sideband Composite Signal and Dual-Carrier Cooperative Tracking-Based High-Precision Communication–Navigation Convergence Positioning Method. Sensors. 2025; 25(11):3405. https://doi.org/10.3390/s25113405
Chicago/Turabian StyleDeng, Zhongliang, Zhenke Ding, Xiangchuan Gao, and Peijia Liu. 2025. "Asymmetric Double-Sideband Composite Signal and Dual-Carrier Cooperative Tracking-Based High-Precision Communication–Navigation Convergence Positioning Method" Sensors 25, no. 11: 3405. https://doi.org/10.3390/s25113405
APA StyleDeng, Z., Ding, Z., Gao, X., & Liu, P. (2025). Asymmetric Double-Sideband Composite Signal and Dual-Carrier Cooperative Tracking-Based High-Precision Communication–Navigation Convergence Positioning Method. Sensors, 25(11), 3405. https://doi.org/10.3390/s25113405






