Rapid Detection of Deployment Errors for Segmented Space Telescopes Based on Long-Range, High-Precision Edge Sensors
Abstract
1. Introduction
2. Method
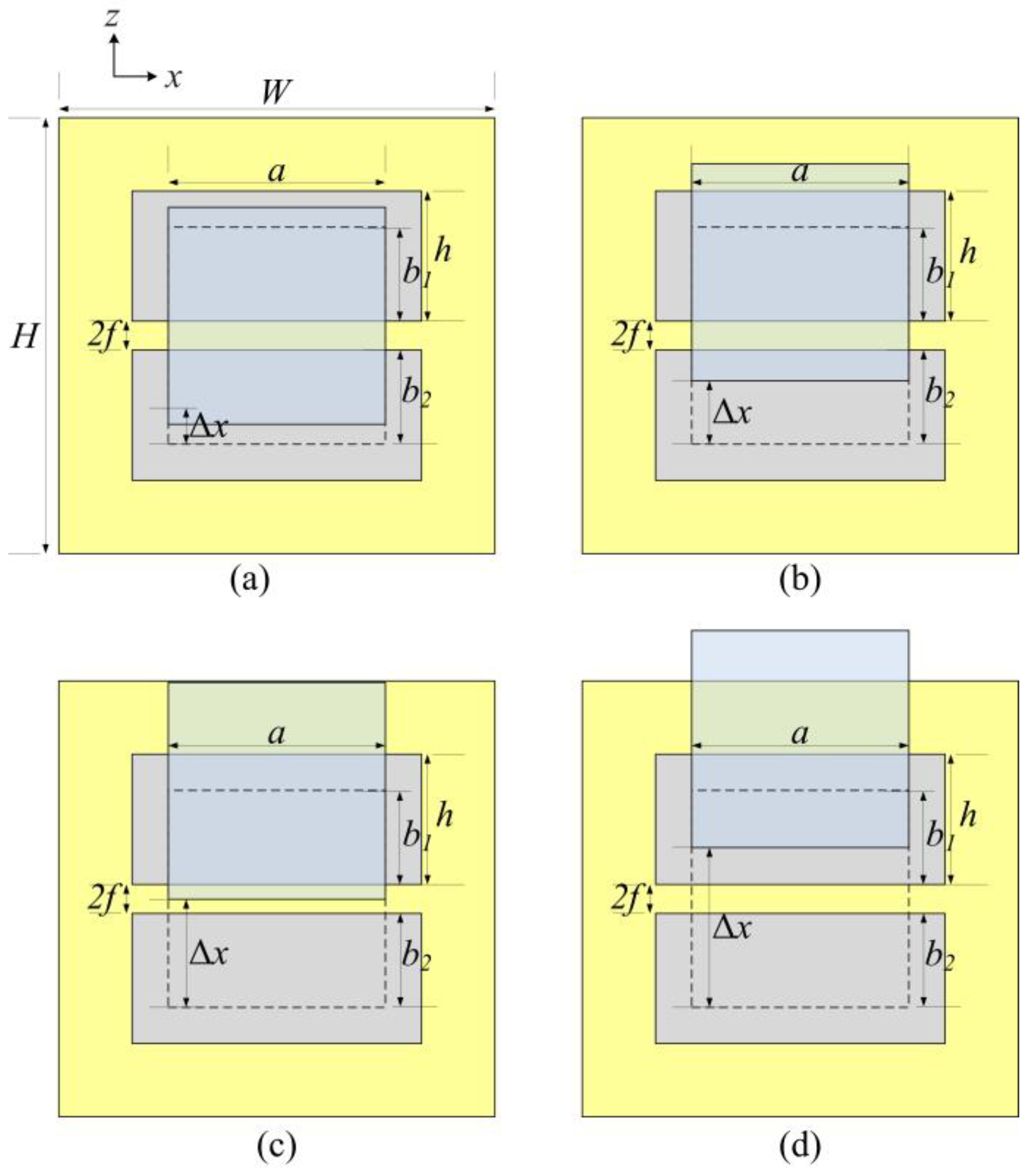
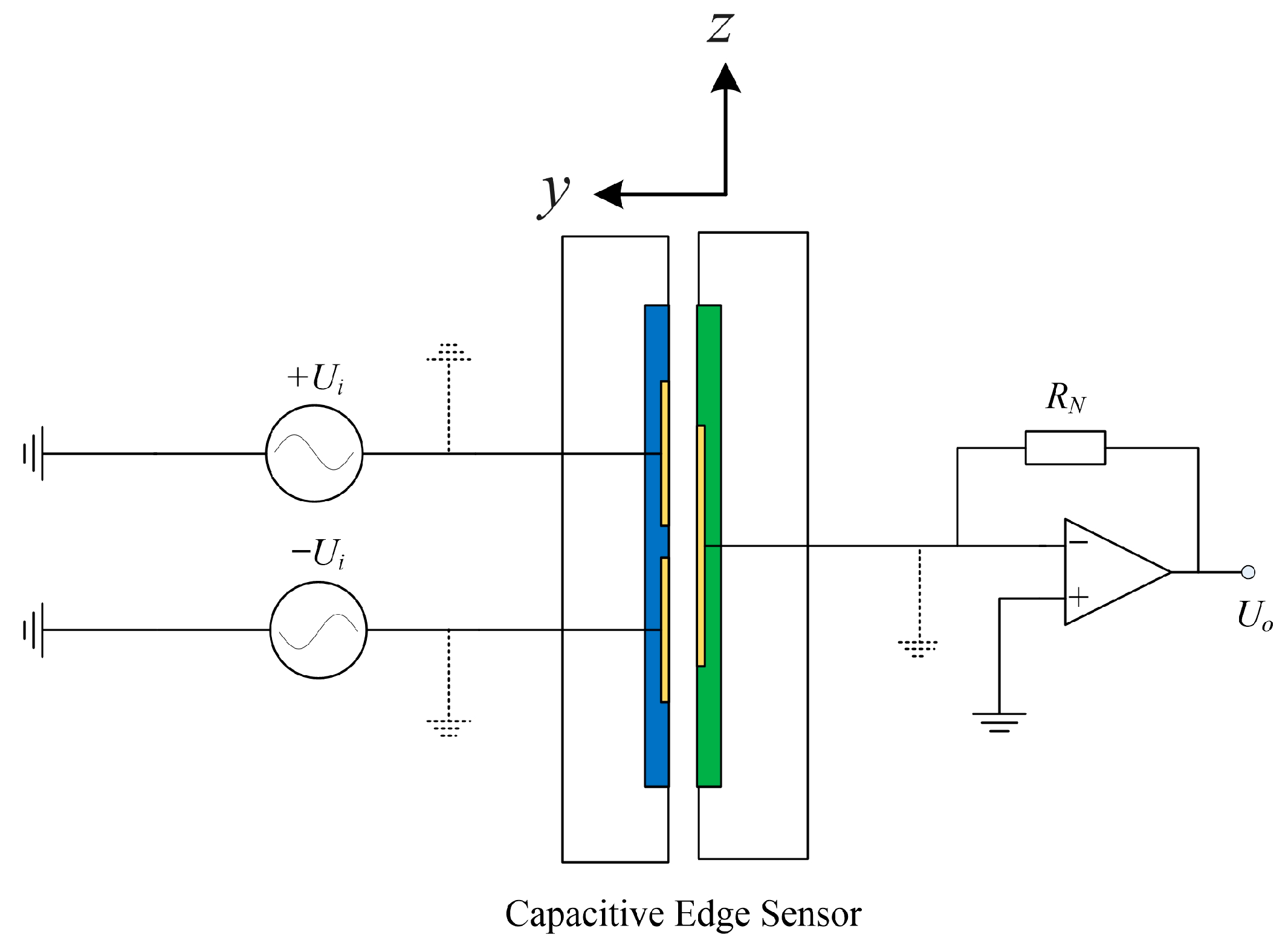
2.1. Design of the Edge Sensors
- (1)
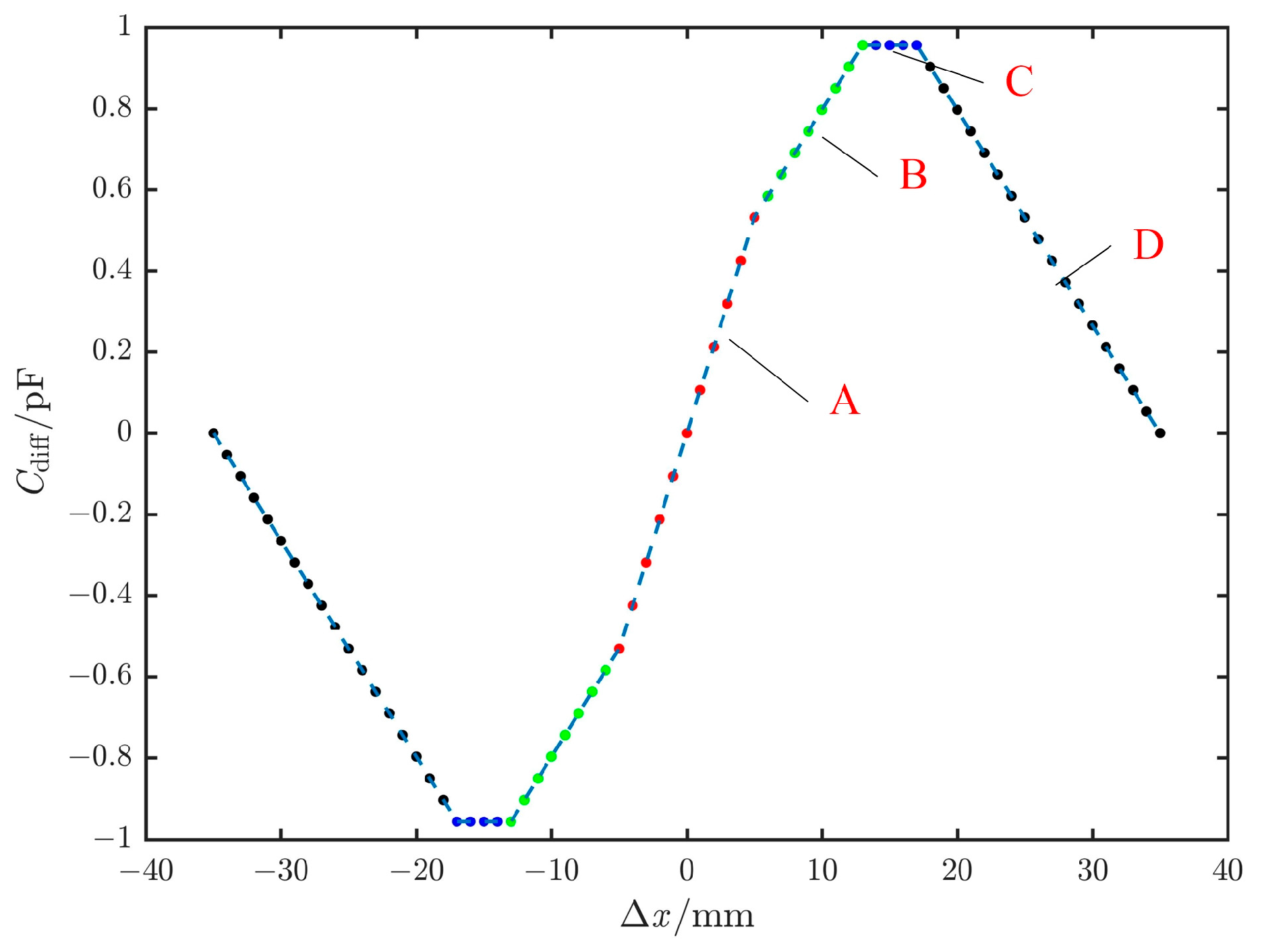
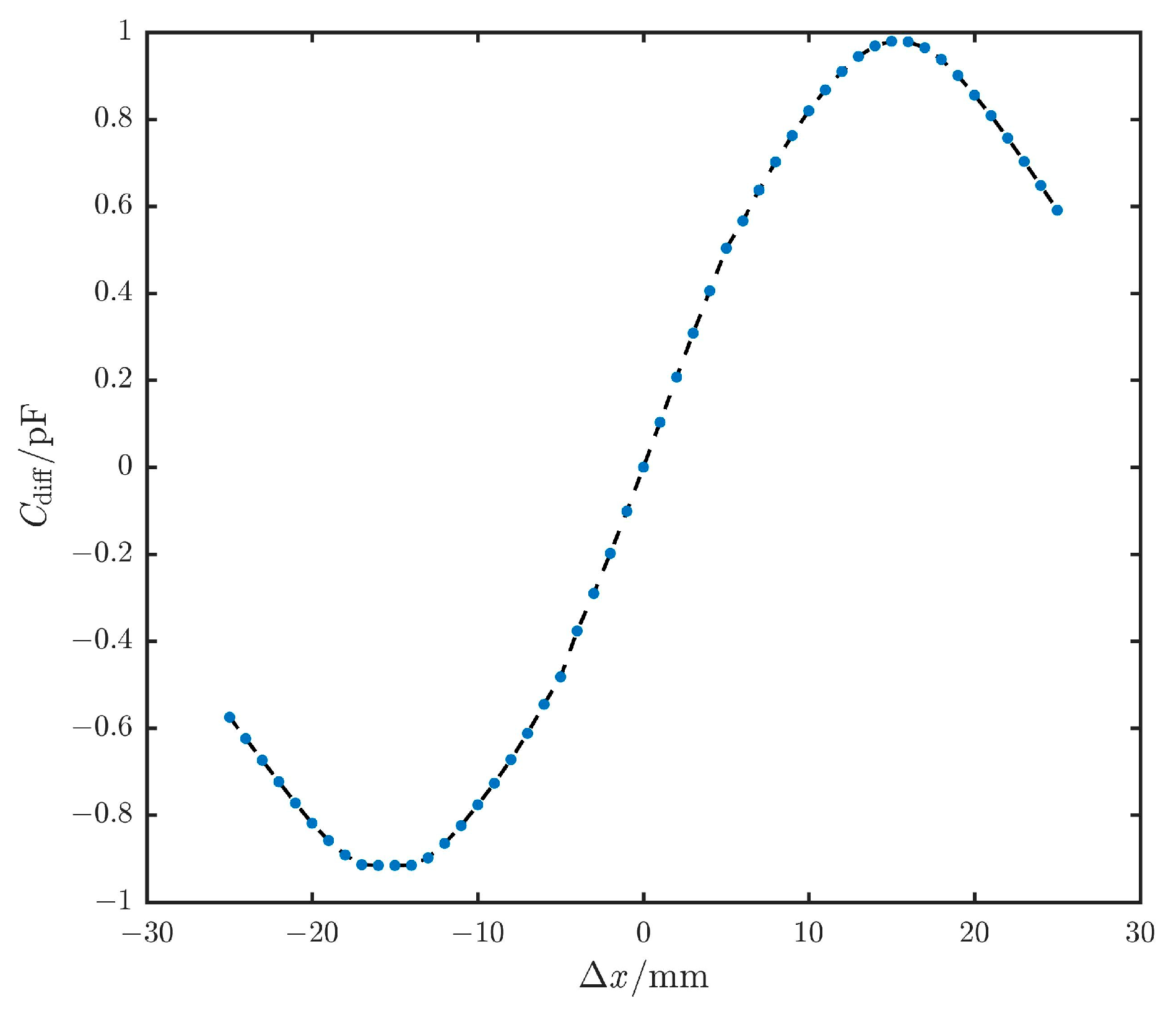
- Full Differential (Curve A): When 0 < Δx ≤ h − b1, the differential capacitance follows the corresponding relationship:
- (2)
- Partial Differential (Curve B): h−b1 < Δx ≤ b2.
- (3)
- Fixed (Curve C): b2 < Δx ≤ b2 + 2f.
- (4)
- Decrease (Curve D): b2 + 2f < Δx ≤ b2 + 2f + h.
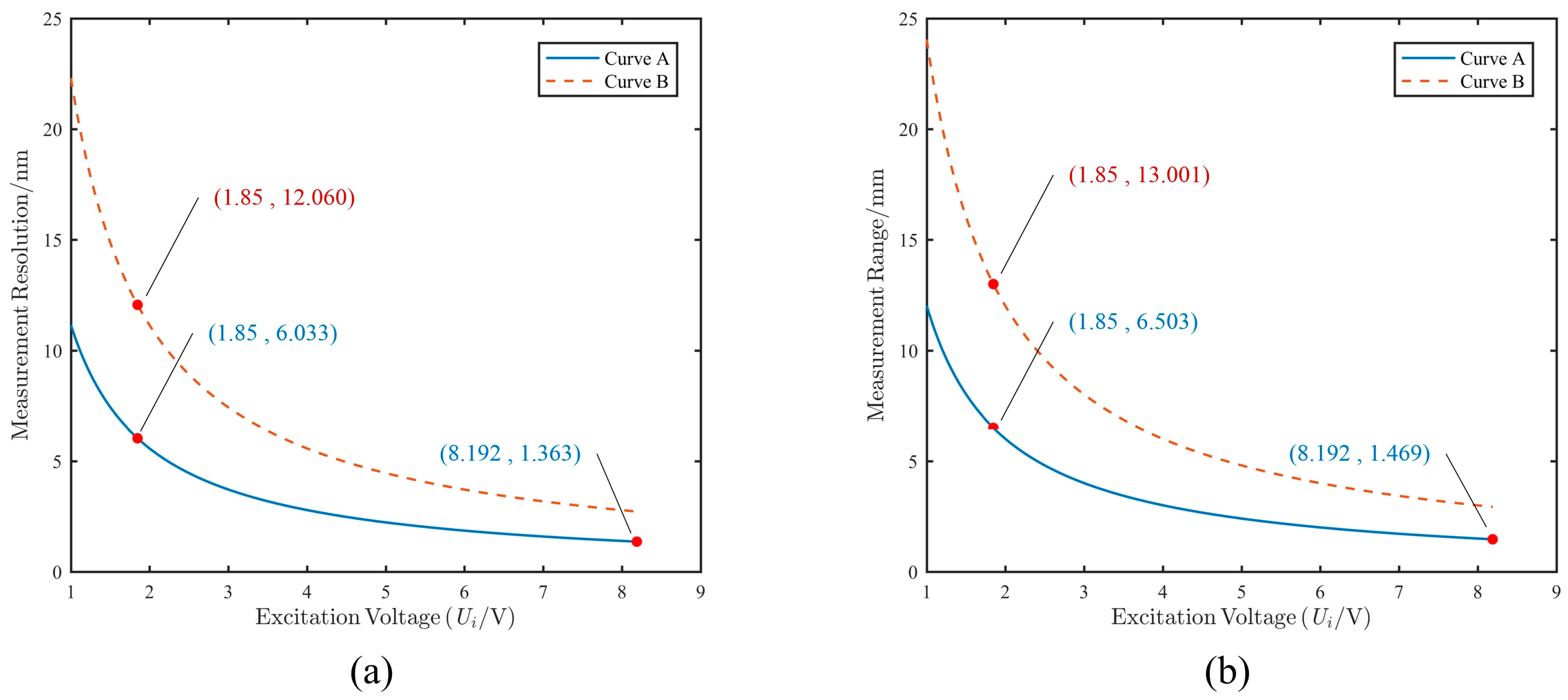
2.2. Implementation of Dynamic Measurement Range
- (1)
- In the range of curve A, the primary goal is to ensure detection resolution. Therefore, the excitation voltage is set to the maximum value of 8.192 V. At this setting, the detection resolution is 1.363 nm, and the measurement range is 1.469 mm.
- (2)
- In the range of curve B, the main objective is to extend the measurement range to match the effective measurement range of the sensor. Therefore, the voltage is set to 1.85 V. At this setting, the detection accuracy is 12.060 nm, and the measurement range is 13.001 mm.
- (3)
- Since the measurement range cannot cover a displacement of 5 mm when the excitation voltage is set to 8.192 V, the voltage is switched to 1.85 V when the displacement range exceeds 1 mm. The corresponding detection resolution decreases to 6.033 nm, and the measurement range expands to 6.503 mm.
3. Performance Evaluation
3.1. Experimental Setup
3.2. Differential Capacitance Response
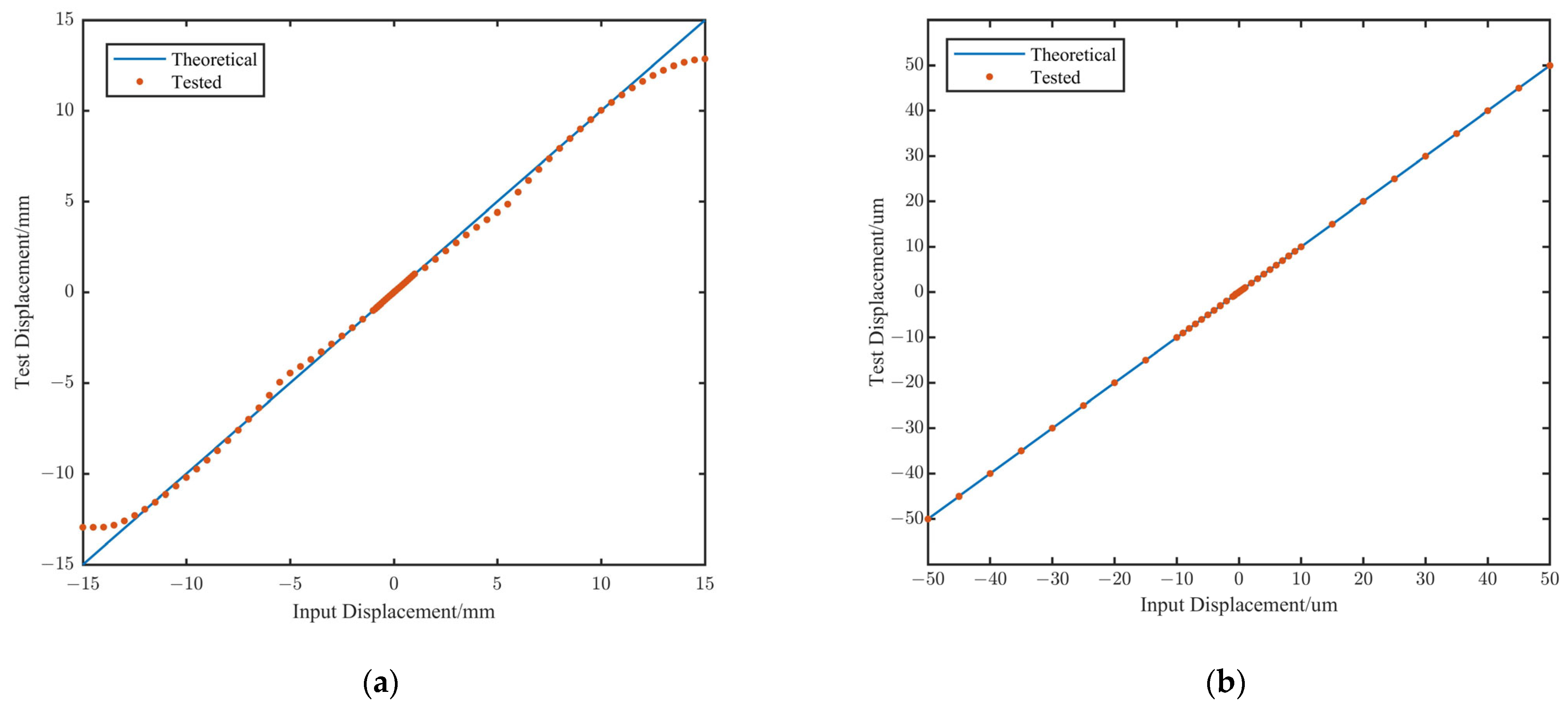
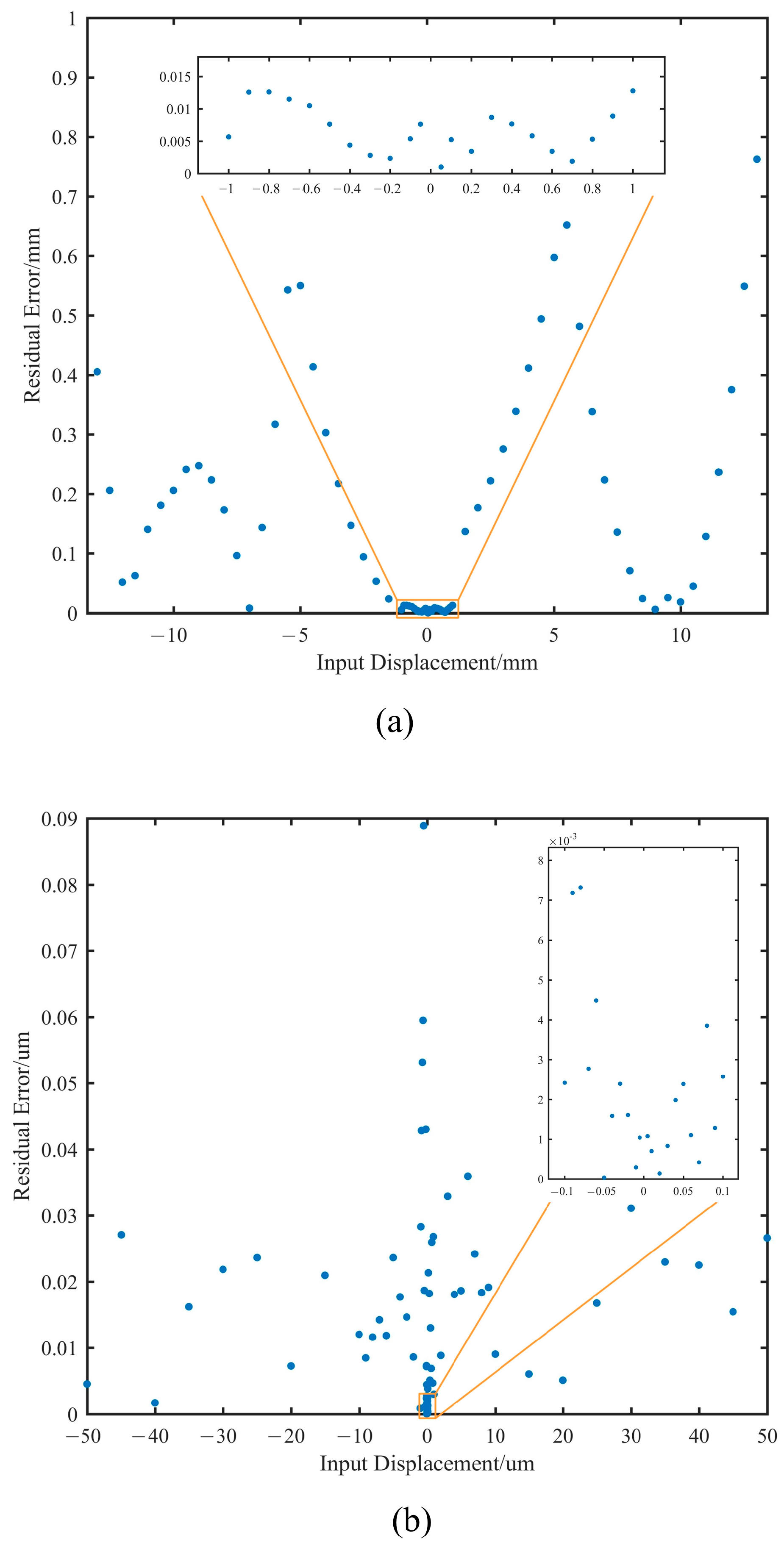
3.3. Displacement Detection Performance
- (1)
- ±1 mm to ±13 mm: The maximum residual is 0.76 mm, with an average residual of 0.24 mm.
- (2)
- ±50 μm to ±1 mm: The maximum residual is 12.8 μm, with an average residual of 6.7 μm.
- (3)
- ±100 nm to ±50 μm: The maximum residual is 88.9 nm, with an average residual of 14.7 nm.
- (4)
- ±5 nm to ±100 nm: The maximum residual is 7.3 nm, with an average residual of 2.2 nm.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pontoppidan, K.M.; Barrientes, J.; Blome, C.; Braun, H.; Brown, M.; Carruthers, M.; Coe, D.; DePasquale, J.; Espinoza, N.; Marin, M.G.; et al. The JWST early release observations. Astrophys. J. Lett. 2022, 936, L14. [Google Scholar] [CrossRef]
- Gardner, P.J.; Mather, J.C.; Clampin, M.; Doyon, R.; Greenhouse, M.A.; Hammel, H.B.; Hutchings, J.B.; Jakobsen, P.; Lilly, S.J.; Long, K.S.; et al. The james webb space telescope. Space Sci. Rev. 2006, 123, 485–606. [Google Scholar] [CrossRef]
- Hylan, J.E.; Bolcar, M.R.; Crooke, J.; Bronke, G.; Collins, C.; Corsetti, J.; Generie, J.; Gong, Q.; Groff, T.; Hayden, W.; et al. The large uv/optical/lnfrared surveyor (luvoir): Decadal mission concept study update. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–15. [Google Scholar]
- Leisawitz, D.; Amatucci, E.; Carter, R.; DiPirro, M.; Flores, A.; Staguhn, J.; Wu, C.; Allen, L.; Arenberg, J.; Armus, L.; et al. The origins space telescope: Mission concept overview. In Proceedings of the Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave, Austin, TX, USA, 24 July 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10698, pp. 363–375. [Google Scholar]
- Acton, D.S.; Knight, S.; Carrasquilla, M.; Weiser, N.; Masciarelli, M.; Jurczyk, S.; Rapp, G.; Mueckay, J.; Wolf, E.; Murphy, J.; et al. Phasing the Webb telescope. In Proceedings of the Space Telescopes and Instrumentation 2022: Optical, Infrared, and Millimeter Wave, Montréal, QC, Canada, 27 August 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12180, pp. 329–352. [Google Scholar]
- Acton, D.S.; Knight, J.S.; Contos, A.; Grimaldi, S.; Terry, J.; Lightsey, P.; Barto, A.; League, B.; Dean, B.; Smith, J.S.; et al. Wavefront sensing and controls for the James Webb Space Telescope. In Proceedings of the Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, Amsterdam, The Netherlands, 21 September 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8442, pp. 877–887. [Google Scholar]
- McElwain, M.W.; Feinberg, L.D.; Perrin, M.D.; Clampin, M.; Mountain, C.M.; Lallo, M.D.; Lajoie, C.-P.; Kimble, R.A.; Bowers, C.W.; Stark, C.C.; et al. The James Webb Space Telescope mission: Optical telescope element design, development, and performance. Publ. Astron. Soc. Pac. 2023, 135, 058001. [Google Scholar] [CrossRef]
- Perrin, M.D.; Acton, D.S.; Lajoie, C.-P.; Knight, J.S.; Lallo, M.D.; Allen, M.; Baggett, W.; Barker, E.; Comeau, T.; Coppock, E.; et al. Preparing for JWST wavefront sensing and control operations. In Proceedings of the Space Telescopes and Instrumentation 2016: Optical, Infrared, and Millimeter Wave, Edinburgh, UK, 19 July 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9904, pp. 142–160. [Google Scholar]
- Warden, R.M. Cryogenic nano-actuator for JWST. In Proceedings of the 38th Aerospace Mechanisms Symposium, Langley Research Center, Boulder, Colorado, 17–19 May 2006; pp. 239–252. [Google Scholar]
- Barto, A.; Acton, D.S.; Finley, P.; Gallagher, B.; Hardy, B.; Knight, J.S.; Lightsey, P. Actuator usage and fault tolerance of the James Webb Space Telescope optical element mirror actuators. In Proceedings of the Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, Amsterdam, The Netherlands, 21 September 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8442, pp. 888–903. [Google Scholar]
- Minor, R.H.; Arthur, A.A.; Gabor, G.; Jackson, J.H.G.; Jared, R.C.; Mast, T.S.; Schaefer, B.A. Displacement sensors for the primary mirror of the WM Keck telescope. In Proceedings of the Advanced Technology Optical Telescopes IV, Tucson, AZ, USA, 1 July 1990; SPIE: Bellingham, WA, USA, 1990; Volume 1236, pp. 1009–1017. [Google Scholar]
- Shelton, C.; Mast, T.; Chanan, G.; Nelson, J.; Roberts, J.L.C.; Troy, M.; Sirota, M.J.; Seo, B.-J.; MacDonald, D.R. Advances in edge sensors for the Thirty Meter Telescope primary mirror. In Proceedings of the Ground-based and Airborne Telescopes II, Marseille, France, 10 July 2008; SPIE: Bellingham, WA, USA, 2008; Volume 7012, pp. 390–402. [Google Scholar]
- Wang, B.; Dai, Y.; Jin, Z.; Yang, D.; Xu, F. Active maintenance of a segmented mirror based on edge and tip sensing. Appl. Opt. 2021, 60, 7421–7431. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Xu, H.; Wu, H.; Li, C.; Fan, X.; Tang, Y.; Chen, M.; Wang, S.; Xian, H. Radiation Resistant Capacitive Edge Sensors for Segmented Space Telescopes. IEEE Sens. J. 2024, 24, 10221–10229. [Google Scholar] [CrossRef]
- Peng, K.; Yu, Z.; Liu, X.; Chen, Z.; Pu, H. Features of capacitive displacement sensing that provide high-accuracy measurements with reduced manufacturing precision. IEEE Trans. Ind. Electron. 2017, 64, 7377–7386. [Google Scholar]
- Avramov-Zamurovic, S.; Dagalakis, N.G.; Lee, R.D.; Yoo, J.M.; Kim, Y.S.; Yang, S.H. Embedded capacitive displacement sensor for nanopositioning applications. IEEE Trans. Instrum. Meas. 2011, 60, 2730–2737. [Google Scholar] [CrossRef]
- Cromey, B.M.; Hicks, B.; Shugrue, J.; Ho, J.; Owen, C.; Grossman, A.; Fan, N.; Walters, B.; Knight, J.S.; Coyle, L.E. Picometer-scale edge sensing and actuation for ultra-stable mission concepts. In Proceedings of the Space Telescopes and Instrumentation 2022: Optical, Infrared, and Millimeter Wave, Montréal, QC, Canada, 27 August 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12180, pp. 2143–2154. [Google Scholar]
- Cayrel, M. E-ELT optomechanics: Overview. Ground-Based Airborne Telesc. IV 2012, 8444, 674–691. [Google Scholar]
- Mast, T.; Chanan, G.; Nelson, J.; Minor, R.; Jared, R. Edge sensor design for the TMT. In Proceedings of the Ground-based and Airborne Telescopes, Orlando, FL, USA, 23 June 2006; SPIE: Bellingham, WA, USA, 2006; Volume 6267, pp. 974–988. [Google Scholar]



| Activity | Prelaunch Plan | Actual |
|---|---|---|
| Mirror Deployments | 18 January 2022 | 20 January 2022 |
| Segment Identification | 7 February 2022 | 8 February 2022 |
| First Closed Loop Guiding | 12 February 2022 | 13 February 2022 |
| Segment Alignment (iteration 1) | 12 February 2022 | 19 February 2022 |
| Image Stacking (iteration 1) | 14 February 2022 | 22 February 2022 |
| Coarse Phasing (iteration 1) | 21 February 2022 | 28 February 2022 |
| Coarse Multi Field | 22 February 2022 | 3 March 2022 |
| Fine Phasing (iteration 1) | 1 March 2022 | 8 March 2022 |
| Fine Phasing (iteration 3) | 5 March 2022 | 11 March 2022 |
| Multi Field Multi Instrument Sensing 1 | 10 March 2022 | 20 March 2022 |
| LOS Jitter Measurement | 17 March 2022 | 21 March 2022 |
| Multi Field Multi Instrument Sensing 2 | 6 April 2022 | 19 April 2022 |
| OTE Alignment Complete | 24 April 2022 | 23 April 2022 |
| Name | Type of Edge Sensors | Measurement Range/μm | Measurement Accuracy/nm |
|---|---|---|---|
| KECK [11] | Capacitive | ±12 | 3 |
| ELT [18] | Inductive | ±200 ±1000 | 1 10 |
| TMT [19] | Capacitive | ±30 | 2.8 |
| Expected | -- | 21,000 | 7.7 |
| Parameters | Values | Units |
|---|---|---|
| Initial projection length (b1/b2) | 13 | mm |
| Projection width (a) | 30 | mm |
| Spacing between drive plates (2f) | 4 | mm |
| Single drive plate height (h) | 18 | mm |
| Distance of plates (d) | 5 | mm |
| Width of edge sensor (W) | 60 | mm |
| Height of edge sensor (H) | 60 | mm |
| Parameters | Values | Units |
|---|---|---|
| Driving voltage frequency (fc) | 50 | kHz |
| Amplification factor (RN) | 2.04 × 107 | Ω |
| Excitation voltage (Ui) | ≤8.192 | V |
| Resolution of ADC | 20 | bit |
| Maximum output voltage (Umax) | 8.192 | V |
| Minimum resolution voltage (Umin) | 7.8 | μV |
| Output frequency | 1 | Hz |
| Piston/mm | Excitation Voltage/V | Measurement Range/mm | Measurement Resolution/nm |
|---|---|---|---|
| [−13, −5] | 1.85 | 13 | 12.06 |
| [−5, −1] | 1.85 | 6.5 | 6.03 |
| [−1, 0] | 8.192 | 1.46 | 1.36 |
| [0, 1] | 8.192 | 1.46 | 1.36 |
| [1, 5] | 1.85 | 6.5 | 6.03 |
| [5, 13] | 1.85 | 13 | 12.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Fan, X.; Li, C.; Tang, Y.; Wang, S.; Xian, H.; Chen, M. Rapid Detection of Deployment Errors for Segmented Space Telescopes Based on Long-Range, High-Precision Edge Sensors. Sensors 2025, 25, 3391. https://doi.org/10.3390/s25113391
Jiang J, Fan X, Li C, Tang Y, Wang S, Xian H, Chen M. Rapid Detection of Deployment Errors for Segmented Space Telescopes Based on Long-Range, High-Precision Edge Sensors. Sensors. 2025; 25(11):3391. https://doi.org/10.3390/s25113391
Chicago/Turabian StyleJiang, Jisong, Xinlong Fan, Chenxu Li, Yuanyuan Tang, Shengqian Wang, Hao Xian, and Mo Chen. 2025. "Rapid Detection of Deployment Errors for Segmented Space Telescopes Based on Long-Range, High-Precision Edge Sensors" Sensors 25, no. 11: 3391. https://doi.org/10.3390/s25113391
APA StyleJiang, J., Fan, X., Li, C., Tang, Y., Wang, S., Xian, H., & Chen, M. (2025). Rapid Detection of Deployment Errors for Segmented Space Telescopes Based on Long-Range, High-Precision Edge Sensors. Sensors, 25(11), 3391. https://doi.org/10.3390/s25113391






