Pilot Study: Step Width Estimation with Body-Worn Magnetoelectric Sensors
Abstract
1. Introduction
2. Materials and Methods
- (1)
- Timing: To which phase (or phases) of the gait cycle does the step width refer?
- (2)
- Distance: What distance (in which coordinate frame) is considered?
- (3)
- Placement: What point on the feet (or even legs) is used as the reference point?
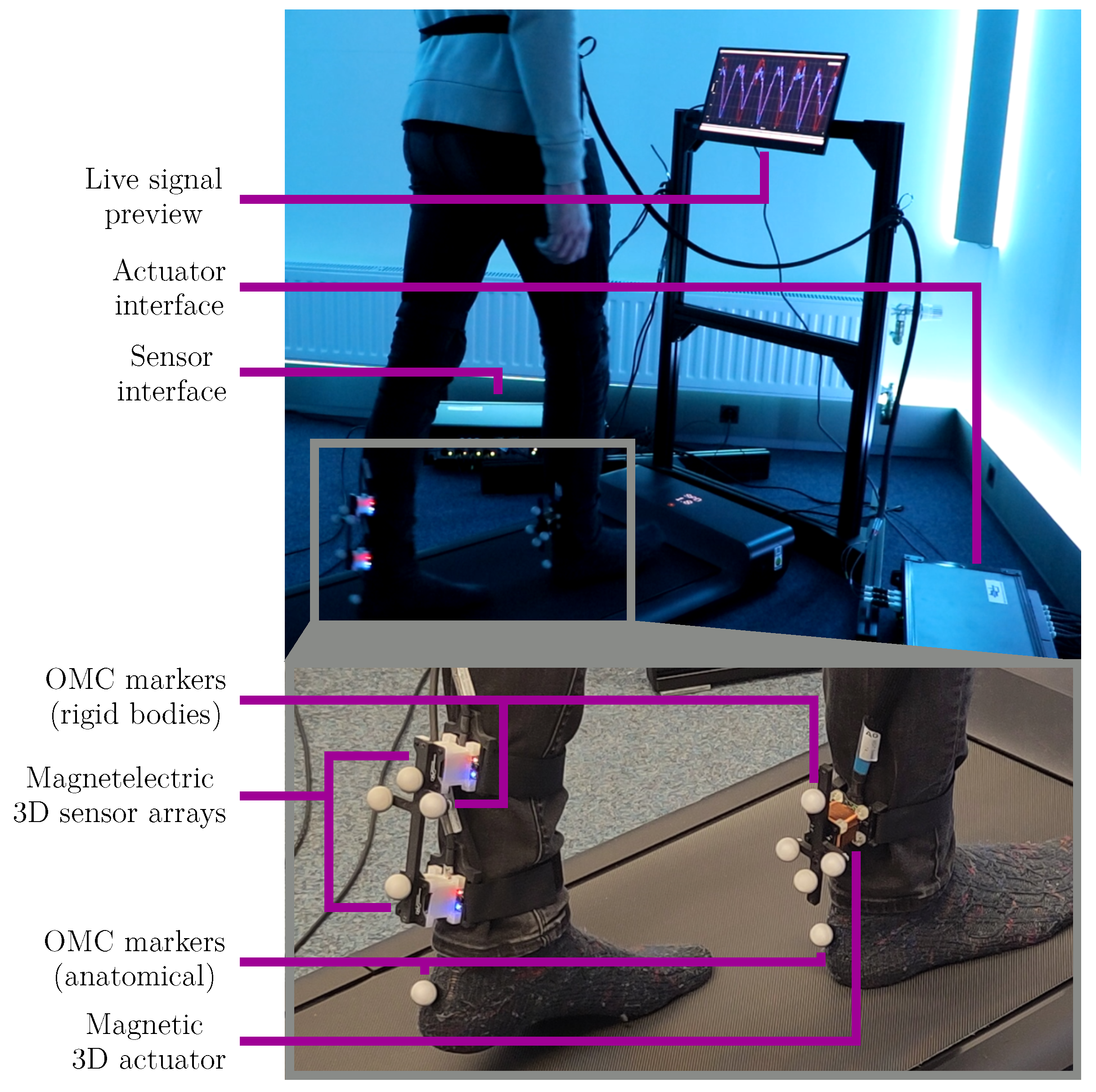
2.1. Measurement System
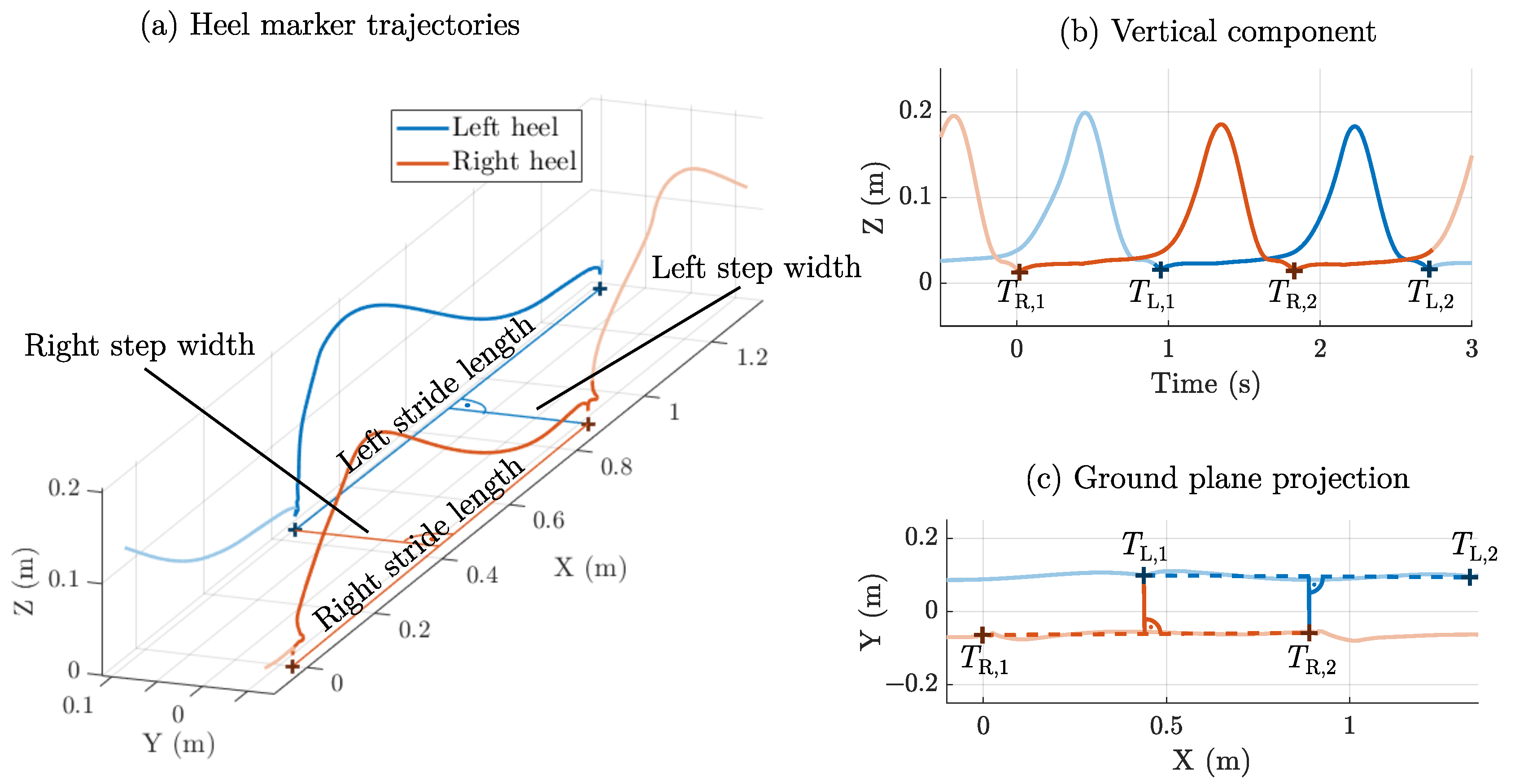
2.2. Step Width: Initial Contact Method
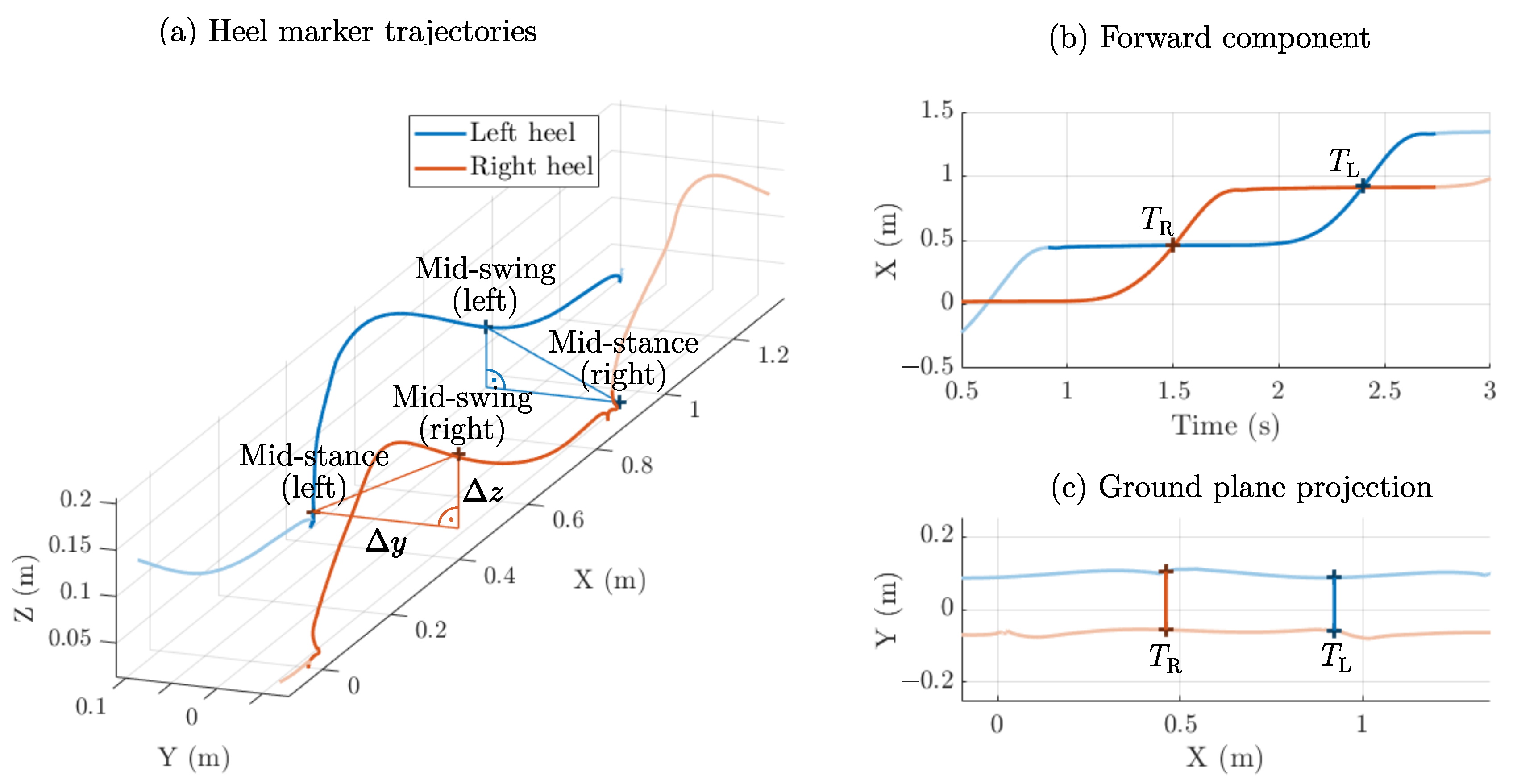
2.3. Step Width: Mid-Swing Method
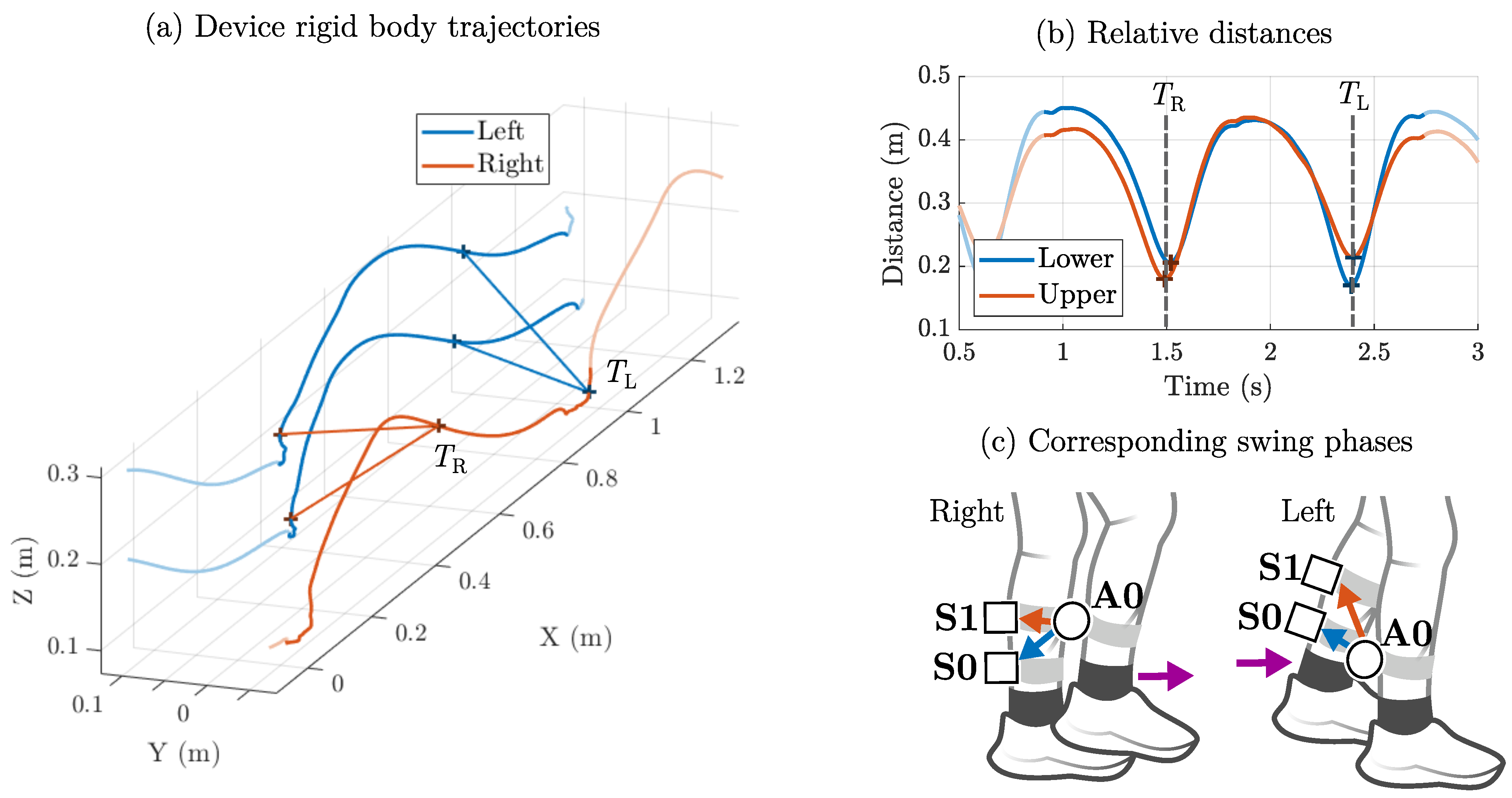
2.4. Step Width: Shank Clearance Method
2.5. Signal Conditioning and Feature Extraction
- (1)
- Mid-swing: The distance between both shanks is rather short (≈20 cm), and the foot in swing phase has not yet hit the ground (high signal, low noise).
- (2)
- Initial contact: The distance between both shanks reaches its maximum (≈40 cm), and the foot hits the ground (low signal, high noise).
2.6. Experimental Setup
2.7. Error Metrics
3. Results
3.1. Dataset Overview
3.2. Spatial Performance of the Magnetic Distance Estimation
3.3. Temporal Performance of the Gait Event Detection
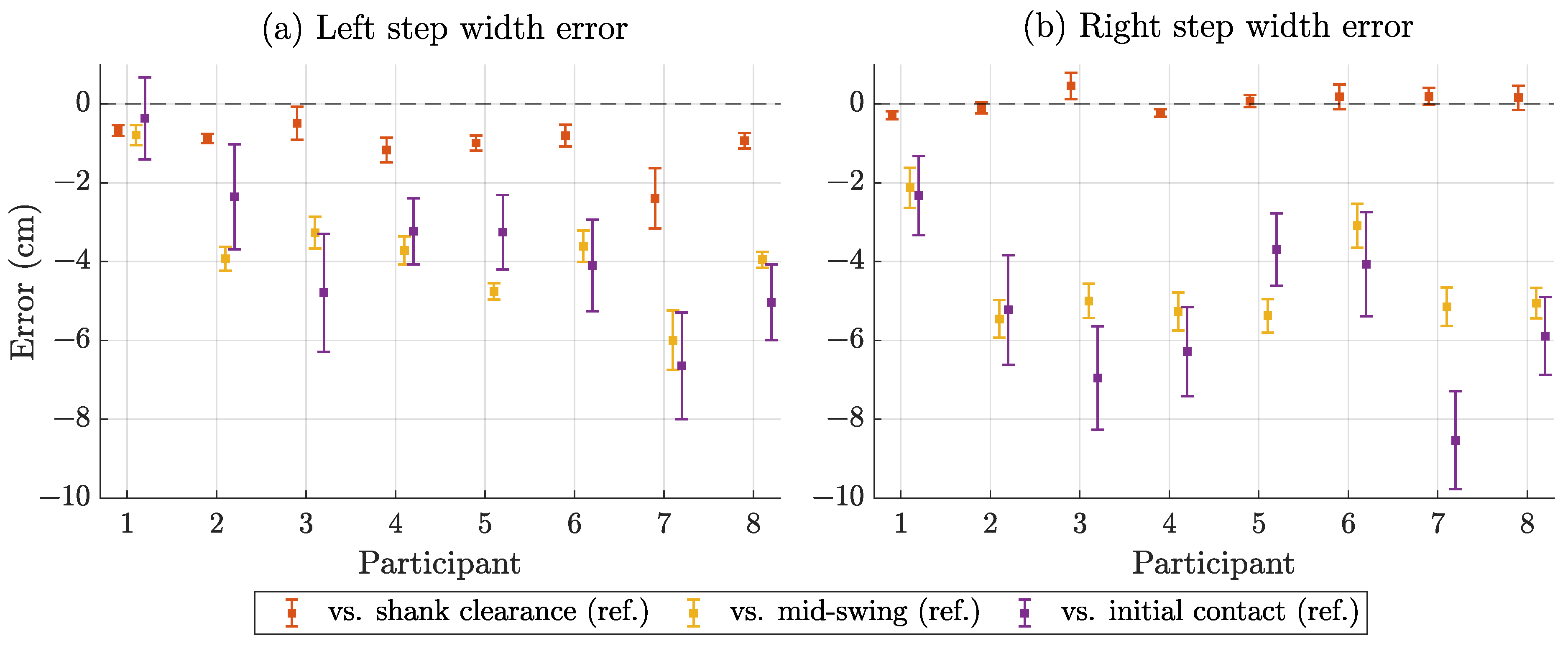
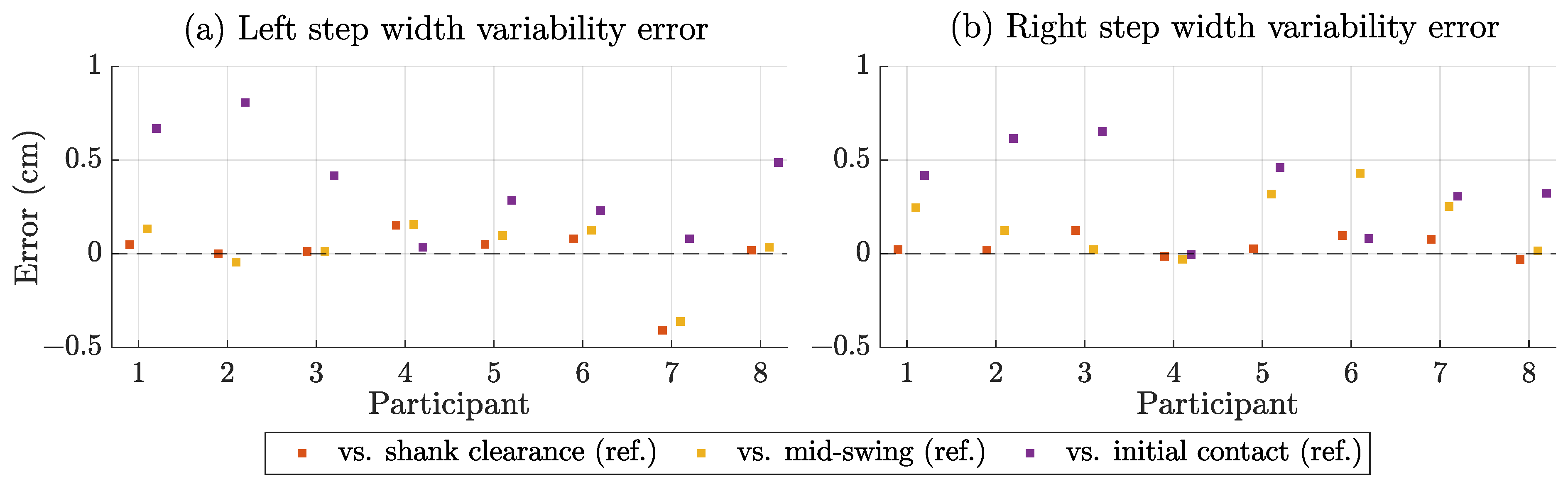
3.4. Step Width Estimation Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BIDS | Brain imaging data structure |
| IMU | Inertial measurement unit |
| KiRAT | Kiel real-time application toolkit |
| MAE | Mean absolute error |
| ME | Mean error |
| ME sensor | Magnetoelectric sensor |
| MEMS | Micro-electromechanical system |
| OMC | Optical motion capture |
| PD | Parkinson’s disease |
| (R)MSE | (Root) mean squared error |
| SCC | Spearman correlation coefficient |
| SD | Standard deviation |
| SNR | Signal-to-noise ratio |
| UWB | Ultra wideband |
References
- Bouça-Machado, R.; Jalles, C.; Guerreiro, D.; Pona-Ferreira, F.; Branco, D.; Guerreiro, T.; Matias, R.; Ferreira, J.J. Gait Kinematic Parameters in Parkinson’s Disease: A Systematic Review. J. Park. Dis. 2020, 10, 843–853. [Google Scholar] [CrossRef]
- Bello, O.; Sánchez, J.A.; Vazquez-Santos, C.; Fernandez-Del-Olmo, M. Spatiotemporal Parameters of Gait During Treadmill and Overground Walking in Parkinson’s Disease. J. Park. Dis. 2014, 4, 33–36. [Google Scholar] [CrossRef]
- Bower, K.; Thilarajah, S.; Pua, Y.H.; Williams, G.; Tan, D.; Mentiplay, B.; Denehy, L.; Clark, R. Dynamic balance and instrumented gait variables are independent predictors of falls following stroke. J. Neuroeng. Rehabil. 2019, 16, 3. [Google Scholar] [CrossRef]
- Eduardo Cofré Lizama, L.; Pijnappels, M.; Rispens, S.M.; Reeves, N.P.; Verschueren, S.M.; van Dieën, J.H. Mediolateral balance and gait stability in older adults. Gait Posture 2015, 42, 79–84. [Google Scholar] [CrossRef]
- Buckley, E.; Mazzà, C.; McNeill, A. A systematic review of the gait characteristics associated with Cerebellar Ataxia. Gait Posture 2025, 60, 154–163. [Google Scholar] [CrossRef]
- Kawami, Y.; Nikaido, Y.; Nose, S.; Unekawa, M.; Marumoto, K.; Kawami, M.; Matsugashita, S.; Kozuki, T.; Akisue, T. Mediolateral Postural Control during Gait in Parkinson’s Disease. Prog. Rehabil. Med. 2022, 7, 20220048. [Google Scholar] [CrossRef] [PubMed]
- Jansen, J.A.; Buurke, T.J.; van de Venis, L.; Weerdesteyn, V.; Keijsers, N.; Nonnekes, J. Narrow-based gait in people with Parkinson’s disease: Its mechanisms explored. J. Park. Dis. 2025, 15, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, J.M. Gait variability: Methods, modeling and meaning. J. Neuroeng. Rehabil. 2005, 2, 19. [Google Scholar] [CrossRef] [PubMed]
- Owings, T.M.; Grabiner, M.D. Step width variability, but not step length variability or step time variability, discriminates gait of healthy young and older adults during treadmill locomotion. J. Biomech. 2004, 37, 935–938. [Google Scholar] [CrossRef]
- Beauchet, O.; Allali, G.; Sekhon, H.; Verghese, J.; Guilain, S.; Steinmetz, J.P.; Kressig, R.W.; Barden, J.M.; Szturm, T.; Launay, C.P.; et al. Guidelines for Assessment of Gait and Reference Values for Spatiotemporal Gait Parameters in Older Adults: The Biomathics and Canadian Gait Consortiums Initiative. Front. Hum. Neurosci. 2017, 11, 353. [Google Scholar] [CrossRef]
- Eichelberger, P.; Ferraro, M.; Minder, U.; Denton, T.; Blasimann, A.; Krause, F.; Baur, H. Analysis of accuracy in optical motion capture—A protocol for laboratory setup evaluation. J. Biomech. 2016, 49, 2085–2088. [Google Scholar] [CrossRef] [PubMed]
- Parati, M.; Ambrosini, E.; De Maria, B.; Galotta, M.; Dalla Vecchia, L.A.; Ferriero, G.; Ferrante, S. The reliability of gait parameters captured via instrumented walkways: A systematic review and meta-analysis. Eur. J. Phys. Rehabil. Med. 2022, 58, 363–377. [Google Scholar] [CrossRef] [PubMed]
- Warmerdam, E.; Hansen, C.; Romijnders, R.; Hobert, M.A.; Welzel, J.; Maetzler, W. Full-Body Mobility Data to Validate Inertial Measurement Unit Algorithms in Healthy and Neurological Cohorts. Data 2022, 7, 136. [Google Scholar] [CrossRef]
- Cloete, T.; Scheffer, C. Benchmarking of a full-body inertial motion capture system for clinical gait analysis. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 4579–4582. [Google Scholar] [CrossRef]
- Benson, L.C.; Clermont, C.A.; Bošnjak, E.; Ferber, R. The use of wearable devices for walking and running gait analysis outside of the lab: A systematic review. Gait Posture 2018, 63, 124–138. [Google Scholar] [CrossRef]
- Salis, F.; Bertuletti, S.; Bonci, T.; Caruso, M.; Scott, K.; Alcock, L.; Buckley, E.; Gazit, E.; Hansen, C.; Schwickert, L.; et al. A multi-sensor wearable system for the assessment of diseased gait in real-world conditions. Front. Bioeng. Biotechnol. 2023, 11, 1143248. [Google Scholar] [CrossRef]
- Díez, L.E.; Bahillo, A.; Otegui, J.; Otim, T. Step Length Estimation Methods Based on Inertial Sensors: A Review. IEEE Sens. J. 2018, 18, 6908–6926. [Google Scholar] [CrossRef]
- Kluge, F.; Gaßner, H.; Hannink, J.; Pasluosta, C.; Klucken, J.; Eskofier, B.M. Towards Mobile Gait Analysis: Concurrent Validity and Test-Retest Reliability of an Inertial Measurement System for the Assessment of Spatio-Temporal Gait Parameters. Sensors 2017, 17, 1522. [Google Scholar] [CrossRef] [PubMed]
- Riek, P.M.; Best, A.N.; Wu, A.R. Validation of Inertial Sensors to Evaluate Gait Stability. Sensors 2023, 23, 1547. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Gaßmann, K.G.; Klucken, J.; Eskofier, B.M. Sensor-Based Gait Parameter Extraction With Deep Convolutional Neural Networks. IEEE J. Biomed. Health Inform. 2017, 21, 85–93. [Google Scholar] [CrossRef]
- Sharifi Renani, M.; Myers, C.A.; Zandie, R.; Mahoor, M.H.; Davidson, B.S.; Clary, C.W. Deep Learning in Gait Parameter Prediction for OA and TKA Patients Wearing IMU Sensors. Sensors 2020, 20, 5553. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ullah, Z.; Gazit, E.; Brozgol, M.; Tan, T.; Hausdorff, J.M.; Shull, P.B.; Ponger, P. Step Width Estimation in Individuals With and Without Neurodegenerative Disease Via a Novel Data-Augmentation Deep Learning Model and Minimal Wearable Inertial Sensors. IEEE J. Biomed. Health Inform. 2024, 29, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.; Shi, M.; Tan, V.Y.F.; Wang, Y. Mobile Gait Analysis Using Foot-Mounted UWB Sensors. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2019, 3, 73:1–73:22. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, B.; Park, S.; Kim, C.H. Estimation of Stride Length, Foot Clearance, and Foot Progression Angle Using UWB Sensors. Appl. Sci. 2023, 13, 4801. [Google Scholar] [CrossRef]
- Weenk, D.; Roetenberg, D.; van Beijnum, B.J.J.F.; Hermens, H.J.; Veltink, P.H. Ambulatory Estimation of Relative Foot Positions by Fusing Ultrasound and Inertial Sensor Data. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 817–826. [Google Scholar] [CrossRef]
- Trojaniello, D.; Cereatti, A.; Bourke, A.; Aminian, K.; Della Croce, U. A wearable system for the measurement of the inter-foot distance during gait. In Proceedings of the 20th IMEKO TC4 International Symposium, Benevento, Italy, 15–17 September 2014; pp. 15–17. [Google Scholar]
- Bäcklund, T.; Öhberg, F.; Johansson, G.; Grip, H.; Sundström, N. Novel, clinically applicable method to measure step-width during the swing phase of gait. Physiol. Meas. 2020, 41, 065005. [Google Scholar] [CrossRef]
- Chheng, C.; Wilson, D. Abnormal Gait Detection Using Wearable Hall-Effect Sensors. Sensors 2021, 21, 1206. [Google Scholar] [CrossRef]
- Zhang, Y.; Clark, W.W.; Tillman, B.; Chun, Y.J.; Liu, S.; Cho, S.K. A System to Track Stent Location in the Human Body by Fusing Magnetometer and Accelerometer Measurements. Sensors 2023, 23, 4887. [Google Scholar] [CrossRef]
- Paperno, E.; Sasada, I.; Leonovich, E. A new method for magnetic position and orientation tracking. IEEE Trans. Magn. 2001, 37, 1938–1940. [Google Scholar] [CrossRef]
- Niekiel, F.; Su, J.; Bodduluri, M.T.; Lisec, T.; Blohm, L.; Pieper, I.; Wagner, B.; Lofink, F. Highly sensitive MEMS magnetic field sensors with integrated powder-based permanent magnets. Sens. Actuators Phys. 2019, 297, 111560. [Google Scholar] [CrossRef]
- Roetenberg, D.; Slycke, P.; Veltink, P. Ambulatory Position and Orientation Tracking Fusing Magnetic and Inertial Sensing. IEEE Trans. Biomed. Eng. 2007, 54, 883–890. [Google Scholar] [CrossRef]
- Pasku, V.; De Angelis, A.; De Angelis, G.; Arumugam, D.D.; Dionigi, M.; Carbone, P.; Moschitta, A.; Ricketts, D.S. Magnetic Field-Based Positioning Systems. IEEE Commun. Surv. Tutor. 2017, 19, 2003–2017. [Google Scholar] [CrossRef]
- Lage, E.; Woltering, F.; Quandt, E.; Meyners, D. Exchange biased magnetoelectric composites for vector field magnetometers. J. Appl. Phys. 2013, 113, 17C725. [Google Scholar] [CrossRef]
- Zabel, S.; Kirchhof, C.; Yarar, E.; Meyners, D.; Quandt, E.; Faupel, F. Phase modulated magnetoelectric delta-E effect sensor for sub-nano tesla magnetic fields. Appl. Phys. Lett. 2015, 107, 152402. [Google Scholar] [CrossRef]
- Dong, C.; Liang, X.; Gao, J.L.; Chen, H.; He, Y.; Wei, Y.; Zaeimbashi, M.; Matyushov, A.; Sun, C.; Sun, N.X. Thin Film Magnetoelectric Sensors Toward Biomagnetism: Materials, Devices, and Applications. Adv. Electron. Mater. 2022, 8, 2200013. [Google Scholar] [CrossRef]
- Meyer, J.M.; Schell, V.; Su, J.; Fichtner, S.; Yarar, E.; Niekiel, F.; Giese, T.; Kittmann, A.; Thormählen, L.; Lebedev, V.; et al. Thin-Film-Based SAW Magnetic Field Sensors. Sensors 2021, 21, 8166. [Google Scholar] [CrossRef]
- Thormählen, L.; Hayes, P.; Elzenheimer, E.; Spetzler, E.; Schmidt, G.; Höft, M.; McCord, J.; Meyners, D.; Quandt, E. Low-noise inverse magnetoelectric magnetic field sensor. Appl. Phys. Lett. 2024, 124, 172402. [Google Scholar] [CrossRef]
- Spetzler, E.; Spetzler, B.; Seidler, D.; Arbustini, J.; Thormählen, L.; Elzenheimer, E.; Höft, M.; Bahr, A.; Meyners, D.; McCord, J. On the Origin of Signal and Bandwidth of Converse Magnetoelectric Magnetic Field Sensors. Adv. Sens. Res. 2025, 4, 2400109. [Google Scholar] [CrossRef]
- Hoffmann, J.; Wolframm, H.; Engelhardt, E.; Boueke, M.; Schmidt, T.; Welzel, J.; Höft, M.; Maetzler, W.; Schmidt, G. A Magnetoelectric Distance Estimation System for Relative Human Motion Tracking. Sensors 2025, 25, 495. [Google Scholar] [CrossRef]
- Perry, J.; Burnfield, J. Gait Analysis: Normal and Pathological Function; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Huxham, F.; Gong, J.; Baker, R.; Morris, M.; Iansek, R. Defining spatial parameters for non-linear walking. Gait Posture 2006, 23, 159–163. [Google Scholar] [CrossRef]
- Paperno, E.; Plotkin, A. Cylindrical induction coil to accurately imitate the ideal magnetic dipole. Sens. Actuators Phys. 2004, 112, 248–252. [Google Scholar] [CrossRef]
- Kadoya, S.; Nagaya, N.; Konyo, M.; Tadokoro, S. A precise gait phase detection based on high-frequency vibration on lower limbs. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1852–1857. [Google Scholar] [CrossRef]
- Reermann, J.; Schmidt, G.; Teliban, I.; Salzer, S.; Höft, M.; Knöchel, R.; Piorra, A.; Quandt, E. Adaptive Acoustic Noise Cancellation for Magnetoelectric Sensors. IEEE Sens. J. 2015, 15, 5804–5812. [Google Scholar] [CrossRef]
- Kiel Real-Time Application Tookit. Available online: https://dss-kiel.de/index.php/research/realtime-framework (accessed on 3 September 2024).
- Riffenburgh, R.H. Statistics in Medicine; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Stimpson, K.H.; Heitkamp, L.N.; Horne, J.S.; Dean, J.C. Effects of walking speed on the step-by-step control of step width. J. Biomech. 2018, 68, 78–83. [Google Scholar] [CrossRef] [PubMed]
- Desmet, D.M.; Sawers, A.; Grabiner, M.D. Ensuring accurate estimates of step width variability during treadmill walking requires more than 400 consecutive steps. J. Biomech. 2019, 91, 160–163. [Google Scholar] [CrossRef] [PubMed]
- Zachmann, G. Distortion correction of magnetic fields for position tracking. In Proceedings of the Computer Graphics International, Hasselt and Diepenbeek, Belgium, 23–27 June 1997; pp. 213–220. [Google Scholar] [CrossRef]
- Hoffmann, J.; Welzel, J.; Hansen, C.; Maetzler, W.; Schmidt, G. Magnetic Step Width Estimation with Magnetoelectric Sensors. Zenodo 2025. [Google Scholar] [CrossRef]
- Jeung, S.; Cockx, H.; Appelhoff, S.; Berg, T.; Gramann, K.; Grothkopp, S.; Warmerdam, E.; Hansen, C.; Oostenveld, R.; Welzel, J. Motion-BIDS: An extension to the brain imaging data structure to organize motion data for reproducible research. Sci. Data 2024, 11, 716. [Google Scholar] [CrossRef]
- Gorgolewski, K.J.; Auer, T.; Calhoun, V.D.; Craddock, R.C.; Das, S.; Duff, E.P.; Flandin, G.; Ghosh, S.S.; Glatard, T.; Halchenko, Y.O.; et al. The brain imaging data structure, a format for organizing and describing outputs of neuroimaging experiments. Sci. Data 2016, 3, 160044. [Google Scholar] [CrossRef]




| Category | Metric | Value |
|---|---|---|
| Participants | Number | 8 |
| Age | 27.5 ± 2.4 years | |
| Sex | 3 (f), 5 (m) | |
| Walking conditions | Speed | 0.5 m/s |
| Duration | 120 s | |
| Results (average) | Number of steps | 146 ± 13 |
| Step width | 9.76 ± 3.22 cm | |
| Step width variability | 1.26 ± 0.26 cm |
| Distance | Bias (cm) | SD (cm) | MAE (cm) | RMSE (cm) | SCC |
|---|---|---|---|---|---|
| Lower distance (A0-S0) | −0.5 | 0.30 | 0.5 | 0.6 | 1.00 |
| Upper distance (A0-S1) | −0.1 | 0.30 | 0.3 | 0.4 | 0.98 |
| All distances | −0.3 | 0.37 | 0.4 | 0.5 | 0.99 |
| Detected Time Points | Bias (ms) | SD (ms) | MAE (ms) | RMSE (ms) |
|---|---|---|---|---|
| Compared to shank clearance reference | ||||
| Lower distance minima (A0-S0) | 6 | 8 | 7 | 10 |
| Upper distance minima (A0-S1) | 0 | 13 | 10 | 14 |
| All minima | 3 | 11 | 9 | 12 |
| Compared to mid-swing reference | ||||
| Lower distance minima (A0-S0) | 3 | 13 | 11 | 14 |
| Upper distance minima (A0-S1) | 6 | 21 | 19 | 23 |
| All minima | 5 | 18 | 15 | 19 |
| Steps | Bias (cm) | SD (cm) | MAE (cm) | RMSE (cm) | SCC | MAE-VAR (cm) |
|---|---|---|---|---|---|---|
| Compared to shank clearance reference | ||||||
| Left | −1.0 | 0.35 | 1.0 | 1.2 | 0.92 | 0.09 |
| Right | 0.1 | 0.23 | 0.2 | 0.3 | 0.95 | 0.05 |
| All | −0.5 | 0.68 | 0.6 | 0.9 | 0.93 | 0.41 |
| Compared to mid-swing reference | ||||||
| Left | −3.7 | 0.39 | 3.7 | 4.0 | 0.90 | 0.12 |
| Right | −4.6 | 0.47 | 4.6 | 4.7 | 0.88 | 0.18 |
| All | −4.2 | 0.75 | 4.2 | 4.4 | 0.82 | 0.33 |
| Compared to initial contact reference | ||||||
| Left | −3.7 | 1.16 | 3.7 | 4.2 | 0.45 | 0.39 |
| Right | −5.3 | 1.17 | 5.3 | 5.7 | 0.42 | 0.37 |
| All | −4.5 | 1.52 | 4.5 | 5.0 | 0.33 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, J.; Engelhardt, E.; Boueke, M.; Welzel, J.; Hansen, C.; Maetzler, W.; Schmidt, G. Pilot Study: Step Width Estimation with Body-Worn Magnetoelectric Sensors. Sensors 2025, 25, 3390. https://doi.org/10.3390/s25113390
Hoffmann J, Engelhardt E, Boueke M, Welzel J, Hansen C, Maetzler W, Schmidt G. Pilot Study: Step Width Estimation with Body-Worn Magnetoelectric Sensors. Sensors. 2025; 25(11):3390. https://doi.org/10.3390/s25113390
Chicago/Turabian StyleHoffmann, Johannes, Erik Engelhardt, Moritz Boueke, Julius Welzel, Clint Hansen, Walter Maetzler, and Gerhard Schmidt. 2025. "Pilot Study: Step Width Estimation with Body-Worn Magnetoelectric Sensors" Sensors 25, no. 11: 3390. https://doi.org/10.3390/s25113390
APA StyleHoffmann, J., Engelhardt, E., Boueke, M., Welzel, J., Hansen, C., Maetzler, W., & Schmidt, G. (2025). Pilot Study: Step Width Estimation with Body-Worn Magnetoelectric Sensors. Sensors, 25(11), 3390. https://doi.org/10.3390/s25113390











