Tripartite: Tackling Realistic Noisy Labels with More Precise Partitions
Abstract
1. Introduction
- We propose a novel partition criterion, which divides training data into three subsets: uncertain, noisy, and clean. It alleviates the uncertain sample division problem of bipartition methods and minimizes the harm of noisy labels by improving the quality of the clean subset.
- We design a low-weight training strategy that aims to maximize the value of clean samples in the uncertain subset while minimizing the influence of potential noise. This strategy is particularly beneficial for vision systems operating in environments with ambiguous or noisy sensor data.
- To simulate the characteristics of noisy labels in real-world datasets, we design a synthetic class-dependent label noise model on CIFAR datasets, referred to as realistic noise. This model flips labels of samples from two different classes at controlled ratios based on their class similarity, providing a more accurate representation of label noise challenges faced by computer vision systems in practical scenarios.
2. Related Work
2.1. Loss Correction
2.2. Sample Selection
3. The Design of Realistic Label Noise
4. The Proposed Method
4.1. Preliminaries
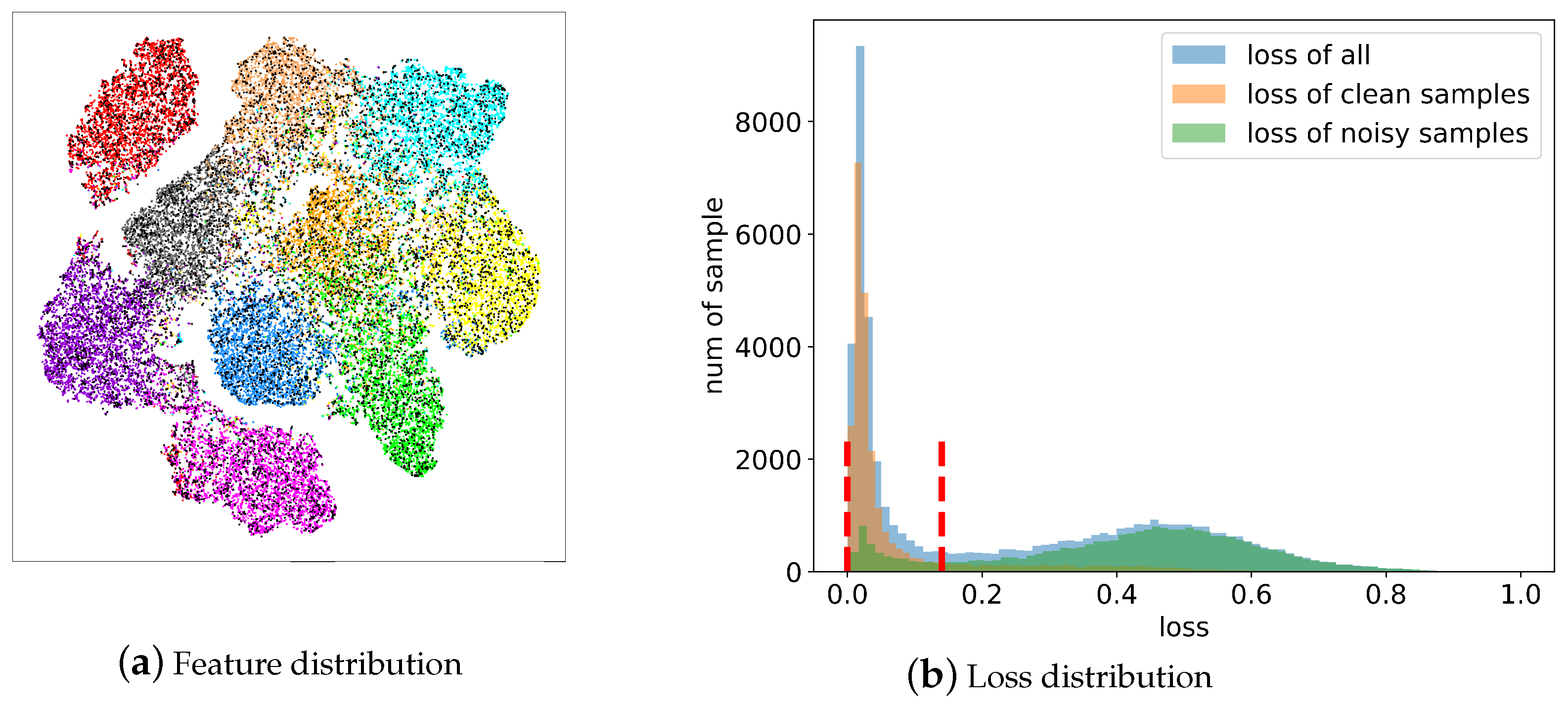
4.2. Distribution of Training Data and the Logic of Tripartite
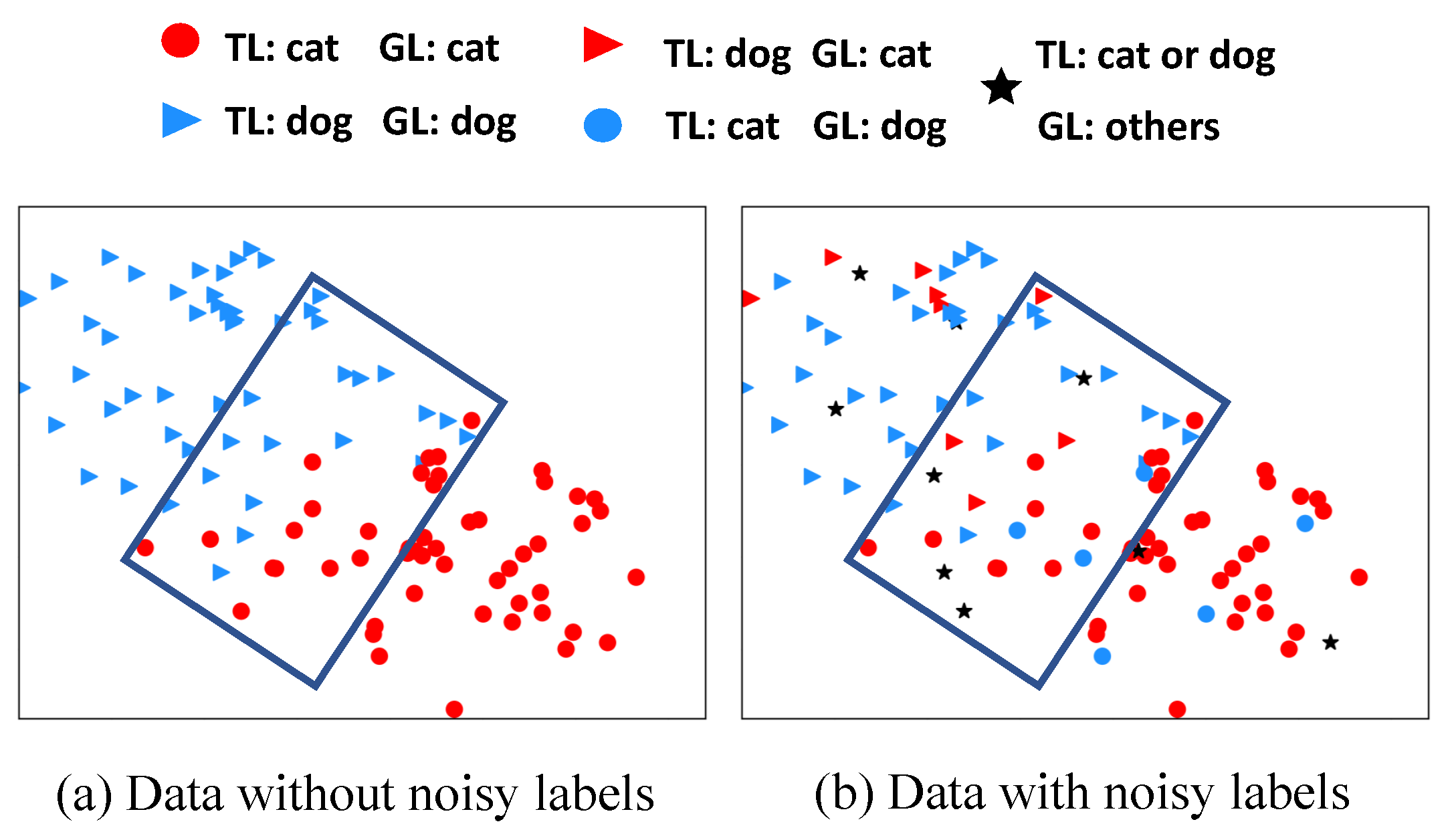
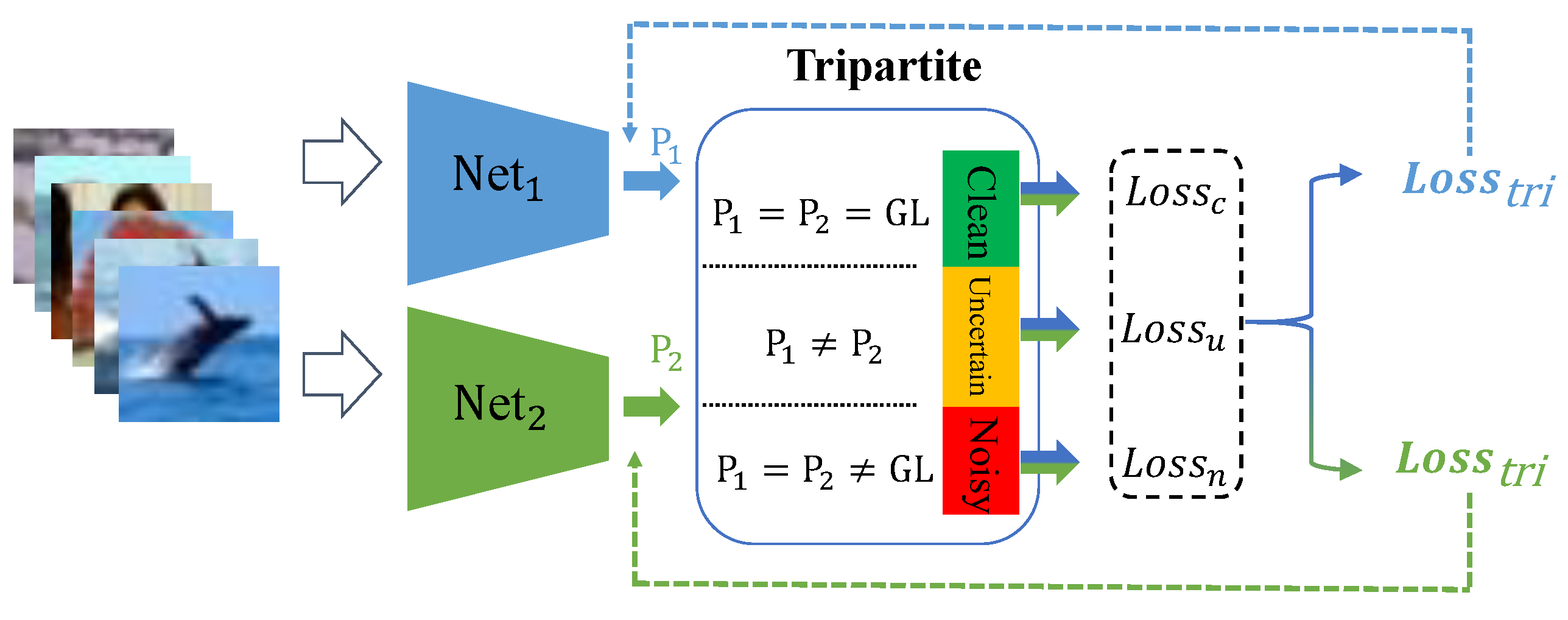
4.3. Tripartition Method and Criteria
4.3.1. The Selection Criterion for the Uncertain Subset
4.3.2. The Selection Criterion for the Noisy Subset
4.3.3. The Selection Criterion for the Clean Subset
4.4. Learning Strategies for the Three Subsets
4.4.1. The Learning Strategy for the Uncertain Subset
4.4.2. The Learning Strategy for the Noisy Subset
4.4.3. The Learning Strategy for the Clean Subset
4.5. Pseudo-Code
| Algorithm 1: Tripartite |
 |
5. Experiments
5.1. Datasets and Noise Types
5.2. Models and Parameters
5.3. Comparison with SOTA Methods
5.3.1. Results on CIFAR-10 and CIFAR-100
5.3.2. Results on Real-World Datasets
5.4. Visualization of Uncertain Samples
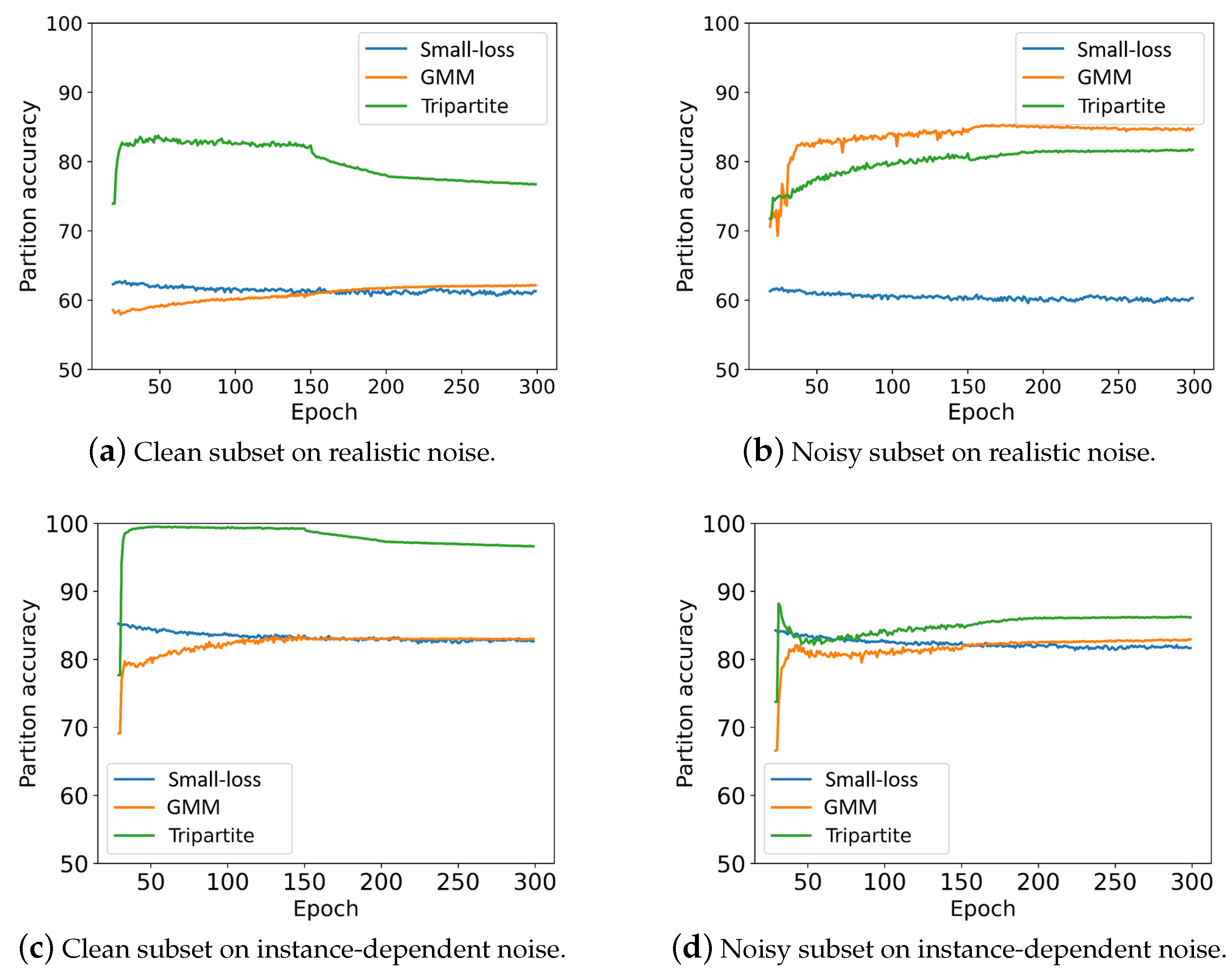
5.5. The Quality of Training Data Partition
5.6. The Effectiveness of Tripartition for the Other Methods
5.7. Ablation Study
5.7.1. The Training Strategy for the Uncertain Subset
5.7.2. The Training Strategy for the Noisy Subset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahajan, D.; Girshick, R.; Ramanathan, V.; He, K.; Paluri, M.; Li, Y.; Bharambe, A.; Van Der Maaten, L. Exploring the limits of weakly supervised pretraining. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 181–196. [Google Scholar]
- Blum, A.; Kalai, A.; Wasserman, H. Noise-tolerant learning, the parity problem, and the statistical query model. J. ACM 2003, 50, 506–519. [Google Scholar] [CrossRef]
- Thomee, B.; Shamma, D.A.; Friedland, G.; Elizalde, B.; Ni, K.; Poland, D.; Borth, D.; Li, L.J. YFCC100M: The new data in multimedia research. Commun. ACM 2016, 59, 64–73. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Li, W.; Agustsson, E.; Van Gool, L. Webvision database: Visual learning and understanding from web data. arXiv 2017, arXiv:1708.02862. [Google Scholar]
- Yan, Y.; Rosales, R.; Fung, G.; Subramanian, R.; Dy, J. Learning from multiple annotators with varying expertise. Mach. Learn. 2014, 95, 291–327. [Google Scholar] [CrossRef]
- Yu, X.; Liu, T.; Gong, M.; Tao, D. Learning with biased complementary labels. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 68–83. [Google Scholar]
- Li, J.; Wong, Y.; Zhao, Q.; Kankanhalli, M.S. Learning to learn from noisy labeled data. In Proceedings of the CVPR, Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5051–5059. [Google Scholar]
- Tanno, R.; Saeedi, A.; Sankaranarayanan, S.; Alexander, D.C.; Silberman, N. Learning from noisy labels by regularized estimation of annotator confusion. In Proceedings of the CVPR, Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 11244–11253. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
- Arpit, D.; Jastrzebski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y.; et al. A closer look at memorization in deep networks. In Proceedings of the ICML, Sydney, Australia, 6–11 August 2017; PMLR: Cambridge, MA, USA, 2017; pp. 233–242. [Google Scholar]
- Ahmed, M.T.; Monjur, O.; Khaliduzzaman, A.; Kamruzzaman, M. A comprehensive review of deep learning-based hyperspectral image reconstruction for agri-food quality appraisal. Artif. Intell. Rev. 2025, 58, 96. [Google Scholar] [CrossRef]
- Gimaletdinova, G.; Shaiakhmetov, D.; Akpaeva, M.; Abduzhabbarov, M.; Momunov, K. Training a Neural Network for Partially Occluded Road Sign Identification in the Context of Autonomous Vehicles. arXiv 2025, arXiv:2503.18177. [Google Scholar]
- González-Santoyo, C.; Renza, D.; Moya-Albor, E. Identifying and Mitigating Label Noise in Deep Learning for Image Classification. Technologies 2025, 13, 132. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, X.P.; Yu, H.G.; Liu, Q.S. A confident learning-based support vector machine for robust ground classification in noisy label environments. Tunn. Undergr. Space Technol. 2025, 155, 106128. [Google Scholar] [CrossRef]
- Huang, B.; Xie, Y.; Xu, C. Learning with noisy labels via clean aware sharpness aware minimization. Sci. Rep. 2025, 15, 1350. [Google Scholar] [CrossRef] [PubMed]
- Patrini, G.; Rozza, A.; Krishna Menon, A.; Nock, R.; Qu, L. Making deep neural networks robust to label noise: A loss correction approach. In Proceedings of the CVPR, Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1944–1952. [Google Scholar]
- Goldberger, J.; Ben-Reuven, E. Training deep neural-networks using a noise adaptation layer. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Reed, S.; Lee, H.; Anguelov, D.; Szegedy, C.; Erhan, D.; Rabinovich, A. Training deep neural networks on noisy labels with bootstrapping. In Proceedings of the ICLR, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Tanaka, D.; Ikami, D.; Yamasaki, T.; Aizawa, K. Joint optimization framework for learning with noisy labels. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5552–5560. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.W.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. In Proceedings of the NeurIPS, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Li, J.; Socher, R.; Hoi, S.C. DivideMix: Learning with Noisy Labels as Semi-supervised Learning. In Proceedings of the ICLR, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Yu, X.; Han, B.; Yao, J.; Niu, G.; Tsang, I.; Sugiyama, M. How does disagreement help generalization against label corruption? In Proceedings of the ICML, Long Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 7164–7173. [Google Scholar]
- Wei, H.; Feng, L.; Chen, X.; An, B. Combating noisy labels by agreement: A joint training method with co-regularization. In Proceedings of the CVPR, Seattle, WA, USA, 14–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 13726–13735. [Google Scholar]
- Yi, R.; Huang, Y. TC-Net: Detecting Noisy Labels Via Transform Consistency. IEEE Trans. Multimed. 2022, 24, 4328–4341. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Liu, F.; Yu, Y. Neighborhood collective estimation for noisy label identification and correction. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 128–145. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the ECCV, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Menon, A.; Van Rooyen, B.; Ong, C.S.; Williamson, B. Learning from corrupted binary labels via class-probability estimation. In Proceedings of the ICML, Lille, France, 6–11 July 2015; PMLR: Cambridge, MA, USA, 2015; pp. 125–134. [Google Scholar]
- Natarajan, N.; Dhillon, I.S.; Ravikumar, P.; Tewari, A. Learning with Noisy Labels. In Proceedings of the NeurIPS, Lake Tahoe, NV, USA, 5–10 December 2013. [Google Scholar]
- Xia, X.; Liu, T.; Wang, N.; Han, B.; Gong, C.; Niu, G.; Sugiyama, M. Are Anchor Points Really Indispensable in Label-Noise Learning? In Proceedings of the NeurIPS, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Ghosh, A.; Kumar, H.; Sastry, P. Robust loss functions under label noise for deep neural networks. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017; Volume 31, pp. 1919–1925. [Google Scholar]
- Xu, Y.; Cao, P.; Kong, Y.; Wang, Y. LDMI: A Novel Information-theoretic Loss Function for Training Deep Nets Robust to Label Noise. In Proceedings of the NeurIPS, Vancouver, BC, Canada, 8–14 December 2019; pp. 6222–6233. [Google Scholar]
- Wang, X.; Hua, Y.; Kodirov, E.; Robertson, N.M. IMAE for Noise-Robust Learning: Mean Absolute Error Does Not Treat Examples Equally and Gradient Magnitude’s Variance Matters. arXiv 2019, arXiv:1903.12141. [Google Scholar]
- Zhang, Z.; Sabuncu, M.R. Generalized cross entropy loss for training deep neural networks with noisy labels. In Proceedings of the NeurIPS, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Wang, Y.; Ma, X.; Chen, Z.; Luo, Y.; Yi, J.; Bailey, J. Symmetric cross entropy for robust learning with noisy labels. In Proceedings of the ICCV, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 322–330. [Google Scholar]
- Yi, K.; Wu, J. Probabilistic end-to-end noise correction for learning with noisy labels. In Proceedings of the CVPR, Long Beach, CA, USA, 15–21 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 7017–7025. [Google Scholar]
- Liu, S.; Niles-Weed, J.; Razavian, N.; Fernandez-Granda, C. Early-Learning Regularization Prevents Memorization of Noisy Labels. In Proceedings of the NeurIPS, Virtual, 6–12 December 2020. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Wilson, D.; Gimpel, K. Using Trusted Data to Train Deep Networks on Labels Corrupted by Severe Noise. In Proceedings of the NeurIPS, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Jiang, L.; Zhou, Z.; Leung, T.; Li, L.J.; Fei-Fei, L. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. In Proceedings of the ICML, Stockholm, Sweden, 10–15 July 2018; PMLR: Cambridge, MA, USA, 2018; pp. 2304–2313. [Google Scholar]
- Huang, Z.; Zhang, J.; Shan, H. Twin contrastive learning with noisy labels. In Proceedings of the CVPR, Vancouver, BC, Canada, 18–22 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 11661–11670. [Google Scholar]
- Bai, Y.; Yang, E.; Han, B.; Yang, Y.; Li, J.; Mao, Y.; Niu, G.; Liu, T. Understanding and improving early stopping for learning with noisy labels. In Proceedings of the NeurIPS, Virtual, 6–14 December 2021. [Google Scholar]
- Yang, H.; Jin, Y.Z.; Li, Z.Y.; Wang, D.B.; Geng, X.; Zhang, M.L. Learning from noisy labels via dynamic loss thresholding. IEEE Trans. Knowl. Data. Eng. 2023, 36, 6503–6516. [Google Scholar] [CrossRef]
- Albert, P.; Ortego, D.; Arazo, E.; O’Connor, N.E.; McGuinness, K. Addressing out-of-distribution label noise in webly-labelled data. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 392–401. [Google Scholar]
- Kim, D.; Ryoo, K.; Cho, H.; Kim, S. SplitNet: Learnable clean-noisy label splitting for learning with noisy labels. Int. J. Comput. Vis. 2025, 133, 549–566. [Google Scholar] [CrossRef]
- Garg, A.; Nguyen, C.; Felix, R.; Liu, Y.; Do, T.T.; Carneiro, G. AEON: Adaptive Estimation of Instance-Dependent In-Distribution and Out-of-Distribution Label Noise for Robust Learning. arXiv 2025, arXiv:2501.13389. [Google Scholar]
- Liu, Z.; Zhu, F.; Vasilakos, A.V.; Chen, X.; Zhao, Q.; Camacho, D. Discriminative approximate regression projection for feature extraction. Inf. Fusion 2025, 120, 103088. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Chen, Y.; Liu, J. Meta-learning collaborative optimization for lifetime prediction of lithium-ion batteries considering label noise. J. Energy Storage 2025, 107, 114928. [Google Scholar] [CrossRef]
- Zhang, R.; Cao, Z.; Huang, Y.; Yang, S.; Xu, L.; Xu, M. Visible-Infrared Person Re-identification with Real-world Label Noise. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 4857–4869. [Google Scholar] [CrossRef]
- Bukchin, G.; Schwartz, E.; Saenko, K.; Shahar, O.; Feris, R.S.; Giryes, R.; Karlinsky, L. Fine-grained Angular Contrastive Learning with Coarse Labels. In Proceedings of the CVPR, Virtual, 19–25 June 2021; pp. 8726–8736. [Google Scholar]
- van der Maaten, L.; Hinton, G.E. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Li, Y.; Han, H.; Shan, S.; Chen, X. Disc: Learning from noisy labels via dynamic instance-specific selection and correction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 24070–24079. [Google Scholar]
- Lee, K.; Yun, S.; Lee, K.; Lee, H.; Li, B.; Shin, J. Robust inference via generative classifiers for handling noisy labels. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 3763–3772. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Krizhevsky, A.; Hinton, G.E. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Xiao, T.; Xia, T.; Yang, Y.; Huang, C.; Wang, X. Learning from massive noisy labeled data for image classification. In Proceedings of the CVPR, Boston, MA, USA, 7–12 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2691–2699. [Google Scholar]
- Xia, X.; Liu, T.; Han, B.; Wang, N.; Gong, M.; Liu, H.; Niu, G.; Tao, D.; Sugiyama, M. Part-dependent label noise: Towards instance-dependent label noise. In Proceedings of the NeurIPS, Virtual, 6–12 December 2020. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the CVPR, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Chen, P.; Liao, B.B.; Chen, G.; Zhang, S. Understanding and utilizing deep neural networks trained with noisy labels. In Proceedings of the ICML, Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 1062–1070. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the CVPR, Las Vegas, NV, USA, 26 June–1 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- Arazo, E.; Ortego, D.; Albert, P.; O’Connor, N.; McGuinness, K. Unsupervised label noise modeling and loss correction. In Proceedings of the ICML, Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 312–321. [Google Scholar]
- Tan, C.; Xia, J.; Wu, L.; Li, S.Z. Co-learning: Learning from noisy labels with self-supervision. In Proceedings of the ACM MM, Virtual Event, China, 20–24 October 2021; ACM: New York, NY, USA, 2021; pp. 1405–1413. [Google Scholar]
- Kim, Y.; Yun, J.; Shon, H.; Kim, J. Joint Negative and Positive Learning for Noisy Labels. In Proceedings of the CVPR, Virtual, 19–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 9442–9451. [Google Scholar]
- Garg, A.; Nguyen, C.; Felix, R.; Do, T.T.; Carneiro, G. Instance-dependent noisy label learning via graphical modelling. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2023; pp. 2288–2298. [Google Scholar]
- Malach, E.; Shalev-Shwartz, S. Decoupling “when to update” from “how to update”. In Proceedings of the NeurIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ma, X.; Wang, Y.; Houle, M.E.; Zhou, S.; Erfani, S.; Xia, S.; Wijewickrema, S.; Bailey, J. Dimensionality-driven learning with noisy labels. In Proceedings of the ICML, Stockholm, Sweden, 10–15 July 2018; PMLR: Cambridge, MA, USA, 2018; pp. 3355–3364. [Google Scholar]



| Similar Classes | Similarity | |
|---|---|---|
| automobile | truck | 0.075 |
| automobile | ship | 0.062 |
| cat | dog | 0.062 |
| dog | horse | 0.054 |
| deer | horse | 0.052 |
| bird | frog | 0.046 |
| airplane | ship | 0.044 |
| horse | truck | 0.025 |
| cat | frog | 0.021 |
| airplane | truck | 0.016 |
| Similar Classes | Similarity | Similar Classes | Similarity | Similar Classes | Similarity | |||
|---|---|---|---|---|---|---|---|---|
| maple_tree | oak_tree | 0.337 | poppy | tulip | 0.249 | beaver | otter | 0.222 |
| dolphin | whale | 0.312 | bed | couch | 0.246 | lion | tiger | 0.220 |
| plain | sea | 0.306 | poppy | rose | 0.245 | clock | plate | 0.220 |
| bus | pickup_truck | 0.301 | snake | worm | 0.245 | pickup_truck | tank | 0.219 |
| girl | woman | 0.298 | bottle | can | 0.242 | flatfish | ray | 0.217 |
| bus | streetcar | 0.296 | apple | pear | 0.242 | plain | road | 0.216 |
| bicycle | motorcycle | 0.275 | dolphin | shark | 0.237 | chimpanzee | woman | 0.216 |
| baby | girl | 0.273 | baby | boy | 0.232 | shark | trout | 0.215 |
| maple_tree | willow_tree | 0.270 | poppy | sunflower | 0.232 | lawn_mower | tractor | 0.214 |
| castle | house | 0.260 | bowl | plate | 0.231 | house | streetcar | 0.211 |
| oak_tree | pine_tree | 0.258 | cloud | plain | 0.231 | leopard | lion | 0.210 |
| cloud | sea | 0.257 | hamster | mouse | 0.230 | otter | seal | 0.210 |
| oak_tree | willow_tree | 0.255 | chair | couch | 0.230 | beetle | spider | 0.209 |
| orchid | tulip | 0.255 | bowl | cup | 0.229 | bed | chair | 0.209 |
| beetle | cockroach | 0.254 | rose | tulip | 0.229 | orange | pear | 0.209 |
| streetcar | train | 0.253 | apple | orange | 0.229 | maple_tree | rose | 0.207 |
| leopard | tiger | 0.253 | television | wardrobe | 0.227 | pickup_truck | tractor | 0.205 |
| man | woman | 0.251 | keyboard | telephone | 0.227 | forest | willow_tree | 0.205 |
| orange | sweet_pepper | 0.250 | boy | girl | 0.224 | crab | lobster | 0.205 |
| apple | sweet_pepper | 0.250 | mouse | shrew | 0.223 | mountain | sea | 0.204 |
| Datasets | # of Training | # of Test | # of Class | Size |
|---|---|---|---|---|
| CIFAR-10 | 50,000 | 10,000 | 10 | 32 × 32 |
| CIFAR-100 | 50,000 | 10,000 | 100 | 32 × 32 |
| Clothing1M | 1,000,000 | 10,526 | 14 | * |
| WebVision1.0 | 2,400,000 | 50,000 | 1000 | * |
| Dataset Symmetric | CIFAR-10 | CIFAR-100 | |||
|---|---|---|---|---|---|
| Method | 20% | 50% | 20% | 50% | |
| Standard CE | 86.8 | 79.4 | 62.0 | 46.7 | |
| Bootstrap (2015) [18] | 86.8 | 79.8 | 62.1 | 46.6 | |
| F-correction (2017) [16] | 86.8 | 79.8 | 61.5 | 46.6 | |
| Co-teaching + (2019) [22] | 89.5 | 85.7 | 65.6 | 51.8 | |
| P-correction (2019) [35] | 92.4 | 89.1 | 69.4 | 57.5 | |
| Meta-Learning (2019) [7] | 92.9 | 89.3 | 68.5 | 59.2 | |
| M-correction (2019) [60] | 94.0 | 92.0 | 73.9 | 66.1 | |
| DivideMix (2020) [21] | 96.1 | 94.6 | 77.3 | 74.6 | |
| ELR + (2020) [36] | 95.8 | 94.8 | 77.6 | 73.6 | |
| Co-learning (2021) [61] | 92.5 | 84.8 | 66.7 | 55.0 | |
| PES(semi) (2021) [40] | 95.9 | 95.1 | 77.4 | 74.3 | |
| DSOS (2022) [42] | 92.7 | 87.4 | 75.1 | 66.2 | |
| TCL + (2023) [39] | 96.0 | 94.5 | 79.3 | 74.6 | |
| DLT (2023) [41] | 96.3 | * | 77.1 | * | |
| Tripartite | 96.4 | 95.1 | 81.1 | 76.6 | |
| Dataset Inst | CIFAR-10 | CIFAR-100 | |||
|---|---|---|---|---|---|
| Method | 20% | 40% | 20% | 40% | |
| Standard CE | 87.5 | 78.9 | 56.8 | 48.2 | |
| DivideMix (2020) [21] | 95.5 | 94.5 | 75.2 | 70.9 | |
| ELR + (2020) [36] | 94.9 | 94.3 | 75.8 | 74.3 | |
| PES(semi) (2021) [40] | 95.9 | 95.3 | 77.6 | 76.1 | |
| InstanceGM (2023) [63] | 96.7 | 96.4 | 79.7 | 78.5 | |
| Tripartite | 96.8 | 96.6 | 80.1 | 78.8 | |
| Dataset Realistic | CIFAR-10 | CIFAR-100 | |||||
|---|---|---|---|---|---|---|---|
| Method | 20% | 40% | 50% | 20% | 40% | 50% | |
| Co-teaching (2018) [20] | 82.7 | 74.4 | 55.8 | 50.3 | 40.9 | 32.5 | |
| JoCoR (2020) [23] | 82.2 | 68.7 | 55.8 | 49.7 | 35.1 | 29.1 | |
| DivideMix (2020) [21] | 91.1 | 92.3 | 91.8 | 76.2 | 66.1 | 59.5 | |
| ELR + (2020) [36] | 95.1 | 92.9 | 91.2 | 75.8 | 72.5 | 60.6 | |
| Co-learning (2021) [61] | 91.6 | 75.5 | 61.7 | 68.5 | 58.5 | 50.2 | |
| PES(semi) (2021) [40] | 95.9 | 93.9 | 91.1 | 76.3 | 73.2 | 66.7 | |
| DSOS (2022) [42] | 92.5 | 89.0 | 81.1 | 75.3 | 64.8 | 52.6 | |
| Tripartite | 96.2 | 95.9 | 94.4 | 80.9 | 75.5 | 71.4 | |
| Clothing1M | |
|---|---|
| Methods | Acc. |
| Standard CE | 69.21 |
| F-correction (2017) [16] | 69.84 |
| Joint (2018) [19] | 72.16 |
| Meta-Learning (2019) [7] | 73.47 |
| P-correction (2019) [35] | 73.49 |
| DivideMix (2020) [21] | 74.76 |
| ELR + (2020) [36] | 74.81 |
| JNPL (2021) [62] | 74.15 |
| PES(semi) (2021) [40] | 74.99 |
| DSOS (2022) [42] | 73.63 |
| TCL (2023) [39] | 74.80 |
| Tripartite | 75.23 |
| Dataset | WebVision | ILSVRC12 | |||
|---|---|---|---|---|---|
| Method | Top-1 | Top-5 | Top-1 | Top-5 | |
| F-correction (2017) [16] | 61.12 | 82.68 | 57.36 | 82.36 | |
| Decoupling (2017) [64] | 62.54 | 84.74 | 58.26 | 82.26 | |
| D2L (2018) [65] | 62.68 | 84.00 | 57.80 | 81.36 | |
| MentorNet (2018) [38] | 63.00 | 81.40 | 57.80 | 79.92 | |
| Co-teaching (2018) [20] | 63.58 | 85.20 | 61.48 | 84.70 | |
| Iterative-CV (2019) [57] | 65.24 | 85.34 | 61.60 | 84.98 | |
| DivideMix (2020) [21] | 77.32 | 91.64 | 75.20 | 90.84 | |
| ELR+ (2020) [36] | 77.78 | 91.68 | 70.29 | 89.76 | |
| DSOS (2022) [42] | 77.76 | 92.04 | 74.36 | 90.80 | |
| TCL (2023) [39] | 79.10 | 92.30 | 75.40 | 92.40 | |
| Tripartite | 80.12 | 93.88 | 76.40 | 93.20 | |
| Epoch | Acc. (%) | Clean Subset | Noisy Subset | Uncertain Subset | ||
|---|---|---|---|---|---|---|
| Partition Acc. | Total Nums | Partition Acc. | Total Nums | |||
| 20 | 46.47 | 73.94 | 12,896 | 71.75 | 9597 | 27,507 |
| 50 | 59.45 | 83.34 | 18,927 | 77.66 | 19,902 | 11,171 |
| 100 | 62.57 | 82.69 | 20,722 | 79.81 | 19,551 | 9727 |
| 150 | 64.77 | 82.31 | 21,634 | 81.16 | 19,085 | 9281 |
| 200 | 66.15 | 78.01 | 25,936 | 81.55 | 20,369 | 3695 |
| 250 | 65.99 | 77.22 | 26,501 | 81.51 | 20,537 | 2962 |
| 300 | 65.80 | 76.75 | 26,831 | 81.73 | 20,370 | 2799 |
| Epoch | Acc. (%) | Clean Subset | Noisy Subset | Uncertain Subset | ||
|---|---|---|---|---|---|---|
| Partition Acc. | Total Nums | Partition Acc. | Total Nums | |||
| 30 | 49.42 | 78.15 | 21,954 | 77.71 | 3647 | 24,399 |
| 50 | 67.13 | 99.48 | 21,585 | 82.58 | 17,871 | 10,544 |
| 100 | 70.23 | 99.44 | 23,077 | 84.26 | 18,487 | 8436 |
| 150 | 71.57 | 99.23 | 23,836 | 85.09 | 18,492 | 7672 |
| 200 | 75.03 | 97.42 | 27,218 | 86.07 | 20,170 | 2612 |
| 250 | 75.70 | 96.93 | 27,554 | 86.14 | 20,335 | 2111 |
| 300 | 75.40 | 96.61 | 27,732 | 86.20 | 20,344 | 1924 |
| Noisy Type | Method | Partition Criterion | Acc. % |
|---|---|---|---|
| Instance-dependent 30% | Co-teaching | Small-loss | 71.30 |
| Tripartition | 72.34 | ||
| DivideMix | GMM | 75.94 | |
| Tripartition | 76.29 | ||
| Realistic 30% | Co-teaching | Small-loss | 71.04 |
| Tripartition | 72.03 | ||
| DivideMix | GMM | 76.44 | |
| Tripartition | 76.49 |
| 1 | 0.5 | 0.3 | 0.1 | 0 | ||
|---|---|---|---|---|---|---|
| Noise Type | ||||||
| Symmetric | 20% | 78.11 | 79.95 | 81.14 | 80.60 | 78.84 |
| 50% | 67.80 | 75.26 | 76.63 | 75.04 | 72.53 | |
| Realistic | 20% | 77.53 | 80.01 | 80.85 | 80.00 | 77.63 |
| 50% | 67.78 | 70.07 | 71.40 | 70.99 | 64.6 |
| Noise Type | Symmetric | Realistic | |||
|---|---|---|---|---|---|
| Strategy | 20% | 50% | 20% | 50% | |
| Drop | 79.8 | 72.97 | 79.7 | 68.6 | |
| Semi-supervised | 81.14 | 76.63 | 80.85 | 71.40 | |
| 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | ||
|---|---|---|---|---|---|---|---|
| Noise Type | |||||||
| Symmetric | 20% | 80.10 | 80.26 | 80.53 | 81.00 | 81.14 | 80.29 |
| 50% | 75.91 | 76.63 | 76.46 | 76.03 | 74.97 | 74.85 | |
| Realistic | 20% | 79.96 | 80.02 | 80.60 | 80.85 | 80.65 | 79.93 |
| 50% | 70.60 | 71.40 | 71.12 | 71.37 | 70.19 | 69.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Liang, X.; Cao, C.; Yao, L.; Liu, X. Tripartite: Tackling Realistic Noisy Labels with More Precise Partitions. Sensors 2025, 25, 3369. https://doi.org/10.3390/s25113369
Yu L, Liang X, Cao C, Yao L, Liu X. Tripartite: Tackling Realistic Noisy Labels with More Precise Partitions. Sensors. 2025; 25(11):3369. https://doi.org/10.3390/s25113369
Chicago/Turabian StyleYu, Lida, Xuefeng Liang, Chang Cao, Longshan Yao, and Xingyu Liu. 2025. "Tripartite: Tackling Realistic Noisy Labels with More Precise Partitions" Sensors 25, no. 11: 3369. https://doi.org/10.3390/s25113369
APA StyleYu, L., Liang, X., Cao, C., Yao, L., & Liu, X. (2025). Tripartite: Tackling Realistic Noisy Labels with More Precise Partitions. Sensors, 25(11), 3369. https://doi.org/10.3390/s25113369








