Design of Refractive Index Sensors Based on Valley Photonic Crystal Mach–Zehnder Interferometer
Abstract
Highlights
- For the first time, a valley photonic crystal Mach–Zehnder interferometry refractive index sensor with a high forward transmittance of 91% is demonstrated.
- The refractive index sensor exhibits high sensitivity, 1534%/RIU, with micrometer-scale dimensions.
- Valley photonic crystals can be utilized in the design of optical sensors with high transmittance and sensitivity.
- The design is suitable for various on-chip sensing applications.
Abstract
1. Introduction
2. The Design of the Valley Photonic Crystal
3. The Design of the MZI Structure
4. Refractive Index Sensing Using the MZI Structure
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, M.Z.; Zhang, Y.; Fu, W.L.; He, J.C. Microfludic Refractive Index Sensor Based on Terahertz Metamaterials. Spectrosc. Spect. Anal. 2021, 41, 1039–1043. [Google Scholar]
- Yan, D.X.; Li, J.S.; Wang, Y. High sensitivity terahertz refractive index sensor based on sunflower-shaped circular photonic crystal. Acta Phys. Sin. 2019, 68, 207801. [Google Scholar] [CrossRef]
- Li, W.; Long, Y.; Yan, Y.; Xiao, K.; Wang, Z.; Zheng, D.; Leal-Junior, A.; Kumar, S.; Ortega, B.; Marques, C.; et al. Wearable photonic smart wristband for cardiorespiratory function assessment and biometric identification. Opto-Electron. Adv. 2025, 8, 240254. [Google Scholar] [CrossRef]
- Alsharari, M.; Wekalao, J.; Patel, S.K.; Kumar, U.A.; Aliqab, K.; Armghan, A. Enhanced Sensing Efficiency of Ultra-Narrow Band Graphene-Based Surface lasmon Resonance Refractive Index Sensor for Biochemical Applications and Environmental Monitoring. Plasmonics 2024, 20, 1273–1284. [Google Scholar] [CrossRef]
- Sequeira, F.; Duarte, D.; Bilro, L.; Rudnitskaya, A.; Pesavento, M.; Zeni, L.; Cennamo, N. Refractive Index Sensing with D-Shaped Plastic Optical Fibers for Chemical and Biochemical Applications. Sensors 2016, 16, 2119. [Google Scholar] [CrossRef]
- Tsigara, A.; Athanasekos, L.; Manasis, J.; Hands, M.; Mousdis, G.; Pispas, S.; Vainos, N.A. Inorganic and hybrid polymer-inorganic nanostructured materials, for optical physicochemical sensing applications. In Proceedings of the ROMOPTO 2006: Eighth Conference on Optics, Sibiu, Romania, 11 September 2007; pp. 386–394. [Google Scholar]
- Liang, R.B.; Sun, Q.Z.; Wo, J.H.; Liu, D.M. Theoretical investigation on refractive index sensor based on Bragg grating in micro/nanofiber. Acta Phys. Sin. 2011, 60, 104221. [Google Scholar] [CrossRef]
- Liao, J.; Feng, W.L. Compatibility defects of the fiber-optic liquid level and refractive index sensors based on modal interference. Phys. B 2022, 624, 413398. [Google Scholar] [CrossRef]
- Yuan, D.; Dong, Y.; Liu, Y.; Li, T. Mach-Zehnder Interferometer Biochemical Sensor Based on Silicon-on-Insulator Rib Waveguide with Large Cross Section Sensors. Sensors 2015, 15, 21500–21517. [Google Scholar] [CrossRef]
- Zhao, Y.; Tong, R.J.; Xia, F.; Peng, Y. Current status of optical fiber biosensor based on surface plasmon resonance. Biosens. Bioelectron. 2019, 142, 111505. [Google Scholar] [CrossRef]
- Baldini, F.; Brenci, M.; Chiavaioli, F.; Giannetti, A.; Trono, C. Optical fibre gratings as tools for chemical and biochemical sensing. Anal. Bioanal. Chem. 2012, 402, 109–116. [Google Scholar] [CrossRef]
- Wang, R.; Tang, T.T.; Shen, J.; Li, C.Y. Refractive index sensing based on Mach-Zehnder interferometer with a hybrid silica/polymer waveguide. Superlatt. Microstruct. 2019, 130, 117–121. [Google Scholar] [CrossRef]
- Jiang, L.Z.; Wu, J.Y.; Li, Q.; Deng, G.W.; Zhang, X.L.; Li, Z.H.; Chen, K.X.; Chiang, K.S. A photochromic dye doped polymeric Mach-Zehnder interferometer for UV light detection. J. Mater. Chem. C 2019, 7, 6257–6265. [Google Scholar] [CrossRef]
- Luff, B.J.; Wilkinson, J.S.; Piehler, J.; Hollenbach, U.; Ingenhoff, J.; Fabricius, N. Integrated Optical Mach-Zehnder Biosensor. J. Light. Technol. 1998, 16, 583. [Google Scholar] [CrossRef]
- Miyazaki, C.M.; Shimizu, F.M.; Ferreira, M. Surface Plasmon Resonance (SPR) for Sensors and Biosensors. Nanocharact. Tech. 2017, 13, 183–200. [Google Scholar]
- Phiri, I.K.; Zekriti, M. Design and theoretical analysis of SPR biosensors based on gold-silver alloy and protective top layer for enhanced biosensing applications. Phys. B 2024, 689, 416196. [Google Scholar] [CrossRef]
- Zhong, X.; Xie, Q.; Liu, Y.; He, Y.; Zhong, N.; Zhang, Z.; Karimi-Maleh, H.; Peng, X.; Lichtfouse, E. Recent advances in optical fiber grating sensors for detection of organic substances. Chem. Eng. J. 2024, 492, 152260. [Google Scholar] [CrossRef]
- Tong, R.; Zhao, Y.; Hu, H.; Qu, J. Large measurement range and high sensitivity temperature sensor with FBG cascaded Mach-Zehnder interferometer. Opt. Laser Technol. 2020, 125, 106034. [Google Scholar] [CrossRef]
- Li, B.Y.; Jiang, L.; Wang, S.M.; Zhou, L.Y.; Xiao, H.; Tsai, H.L. Ultra-Abrupt Tapered Fiber Mach-Zehnder Interferometer Sensors. Sensors 2011, 11, 5729–5739. [Google Scholar] [CrossRef]
- Kaiyue, Q.; Yundong, Z.; Jianfeng, S.; Guo, Y. All-Fiber high temperature and refractive index sensor based on three microspheres array Michelson interferometer. Opt. Laser Technol. 2020, 129, 106300. [Google Scholar]
- Wang, P.; Pan, Y.; Zhang, J.; Zhai, J.; Liu, D.; Lu, P. Miniaturized and highly sensitive fiber-optic Fabry–Perot sensor for mHz infrasound detection. Photon. Res. 2024, 12, 969–978. [Google Scholar] [CrossRef]
- Guan, X.; Wang, X.; Frandsen, L.H. Optical temperature sensor with enhanced sensitivity by employing hybrid waveguides in a silicon Mach-Zehnder interferometer. Opt. Express 2016, 24, 16349–16356. [Google Scholar] [CrossRef] [PubMed]
- Nohoji, A.H.A.; Danaie, M. Highly sensitive refractive index sensor based on photonic crystal ring resonators nested in a Mach-Zehnder interferometer. Opt. Quantum Electron. 2022, 54, 574. [Google Scholar] [CrossRef]
- Sepúlveda, B.; del Río, J.S.; Moreno, M.; Blanco, F.J.; Mayora, K.; Domínguez, C.; Lechuga, L.M. Optical biosensor microsystems based on the integration of highly sensitive Mach-Zehnder interferometer devices. J. Opt. A Pure Appl. Opt. 2006, 8, S561–S566. [Google Scholar] [CrossRef]
- Krauss, T.F.; De La Rue, R.M. Photonic crystals in the optical regime—past, present and future. Prog. Quantum Electron. 1999, 23, 51–96. [Google Scholar] [CrossRef]
- Noda, S.; Chutinan, A.; Imada, M. Trapping and emission of photons by a single defect in a photonic bandgap structure. Nature 2000, 407, 608–610. [Google Scholar] [CrossRef]
- Beggs, D.M.; O’Faolain, L.; Krauss, T.F. Accurate determination of hole sizes in photonic crystal slabs using an optical measurement. Phys. E 2009, 41, 1115–1117. [Google Scholar] [CrossRef]
- Wang, X.R.; Fei, H.M.; Lin, H.; Wu, M.; Kang, L.J.; Zhang, M.D.; Liu, X.; Yang, Y.B.; Xiao, L.T. High-performance chiral all-optical OR logic gate based on topological edge states of valley photonic crystal. Chin. Phys. B 2023, 32, 074205. [Google Scholar] [CrossRef]
- Wu, M.; Yang, Y.B.; Fei, H.M.; Lin, H.; Han, Y.H.; Zhao, X.D.; Chen, Z.H. Unidirectional transmission of visible region topological edge states in hexagonal boron nitride valley photonic crystals. Opt. Express 2022, 30, 6275–6283. [Google Scholar] [CrossRef]
- Wu, M.; Yang, Y.B.; Fei, H.M.; Lin, H.; Zhao, X.D.; Kang, L.J.; Xiao, L.T. On-Chip Ultra-Compact Hexagonal Boron Nitride Topological Ring-Resonator in Visible Region. J. Light. Technol. 2022, 40, 7610–7618. [Google Scholar] [CrossRef]
- Bai, J.; Fei, H.; Lin, H.; Wang, Y.; Zhang, M.; Liu, X.; Cao, B.; Tian, Y.; Xiao, L. Design of a temperature sensor based on a valley photonic crystal Mach–Zehnder interferometer. Appl. Opt. 2024, 63, 4940–4945. [Google Scholar] [CrossRef]
- Han, Y.H.; Fei, H.M.; Lin, H.; Zhang, Y.M.; Zhang, M.D.; Yang, Y.B. Design of broadband all-dielectric valley photonic crystals at telecommunication wavelength. Opt. Commun. 2021, 488, 126847. [Google Scholar] [CrossRef]
- Kang, L.J.; Fei, H.M.; Lin, H.; Wu, M.; Wang, X.R.; Zhang, M.D.; Liu, X.; Sun, F.; Chen, Z.H. Thermal tunable silicon valley photonic crystal ring resonators at the telecommunication wavelength. Opt. Express 2023, 31, 2807–2815. [Google Scholar] [CrossRef]
- Wang, X.R.; Han, Y.H.; Fei, H.M.; Lin, H.; Zhang, M.D.; Liu, X.; Cao, B.Z.; Yang, Y.B.; Chen, Z.H.; Xiao, L.T. Design of wavelength division multiplexing devices based on tunable edge states of valley photonic crystals. Opt. Express 2023, 31, 13933–13942. [Google Scholar] [CrossRef]
- Wang, Y.; Fei, H.; Lin, H.; Bai, J.; Zhang, M.; Liu, X.; Cao, B.; Tian, Y.; Xiao, L. Ultra-compact electro-optic phase modulator based on a lithium niobate topological slow light waveguide. Opt. Express 2024, 32, 3980–3988. [Google Scholar] [CrossRef]
- Ya, M.Z.; Hong, M.F.E.I.; Han, L.I.N.; Han, Y.-H.; Ming, D.Z.; Xue, M.L.I.; Yi, B.Y. Design of all-dielectric valley photonic crystals with low symmetry elliptical lattice. J. Infrared Millim. Terahertz Waves 2021, 40, 547–553. [Google Scholar]
- Cheng, Q.; Wang, S.T.; Lv, J.T.; Liu, N. Topological photonic crystal biosensor with valley edge modes based on a silicon-on-insulator slab. Opt. Express 2022, 30, 10792–10801. [Google Scholar] [CrossRef]
- Peng, Y.G.; Geng, Z.G.; Zhu, X.F. Topologically protected bound states in one-dimensional Floquet acoustic waveguide systems. J. Appl. Phys. 2018, 123, 091716. [Google Scholar] [CrossRef]
- Dong, J.; Chen, X.; Zhu, H. Valley photonic crystals for control of spin and topology. Nat. Mater. 2017, 16, 298–302. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Walasik, W.; Tsukernik, A.; Xu, Y.; Litchinitser, N.M. Robust topologically protected transport in photonic crystals at telecommunication wavelengths. Nat. Nanotechnol. 2019, 14, 31–34. [Google Scholar] [CrossRef]
- He, X.-T.; Liang, E.-T.; Yuan, J.-J.; Qiu, H.-Y.; Chen, X.-D.; Zhao, F.-L.; Dong, J.-W. A silicon-on-insulator slab for topological valley transport. Nat. Commun. 2019, 10, 872. [Google Scholar] [CrossRef]
- Guan, W.; Wu, Y.; Xie, C.; Fang, L.; Liu, X.; Chen, Y. Performance analysis and enhancement for visible light communication using CMOS sensors. Opt. Commun. 2018, 410, 531–551. [Google Scholar]
- Zhi, J.L.; Gui, H.; Cheng, F.Q.; You, Y.F.; Hong, Y.W.; Zhao, J.L. CMOS monolithic photodetector with a built-in 2-dimensional light direction sensor for laser diode based underwater wireless optical communications. Opt. Express 2021, 29, 16197–16204. [Google Scholar]
- Jiang, D.; Yu, D.-Y.; Zheng, Z.; Cao, X.-C.; Lin, Q.; Liu, W.-M. Research progress of material, physics, and device of topological superconductors for quantum computing. Acta Phys. Sin. 2022, 71, 160302. [Google Scholar] [CrossRef]
- Ioudashkin, E.; Malka, D. High-Performance O-Band Angled Multimode Interference Splitter with Buried Silicon Nitride Waveguide for Advanced Data Center Optical Networks. Photonics 2025, 12, 322. [Google Scholar] [CrossRef]
- Sun, X.; Thylén, L.; Wosinski, L. Hollow hybrid plasmonic Mach–Zehnder sensor. Opt. Lett. 2017, 42, 807–810. [Google Scholar] [CrossRef]
- Sun, X.; Dai, D.; Thylén, L.; Wosinski, L. High-sensitivity liquid refractive-index sensor based on a Mach-Zehnder interferometer with a double-slot hybrid plasmonic waveguide. Opt. Express 2015, 23, 25688–25699. [Google Scholar] [CrossRef]
- Zhang, Y.-N.; Zhao, Y.; Wang, Q.; Xue, K. Liquid refractive index sensor based on slow light in slotted photonic crystal waveguide. Optik 2013, 124, 5443–5446. [Google Scholar] [CrossRef]
- Gao, P.A.; Rong, Q.Z.; Sun, H.; Hu, M.L. High-sensitive fiber-optic refractometer constructed by core-diameter-mismatch welding. J. Appl. Opt. 2013, 34, 542–546. [Google Scholar]
- Tang, C.P.; Deng, M.; Zhu, T.; Rao, Y.J. Photonic crystal fiber based M-Z interferometer for refractive index measurement. J. Optoelectron. Laser 2011, 22, 1304–1308. [Google Scholar]
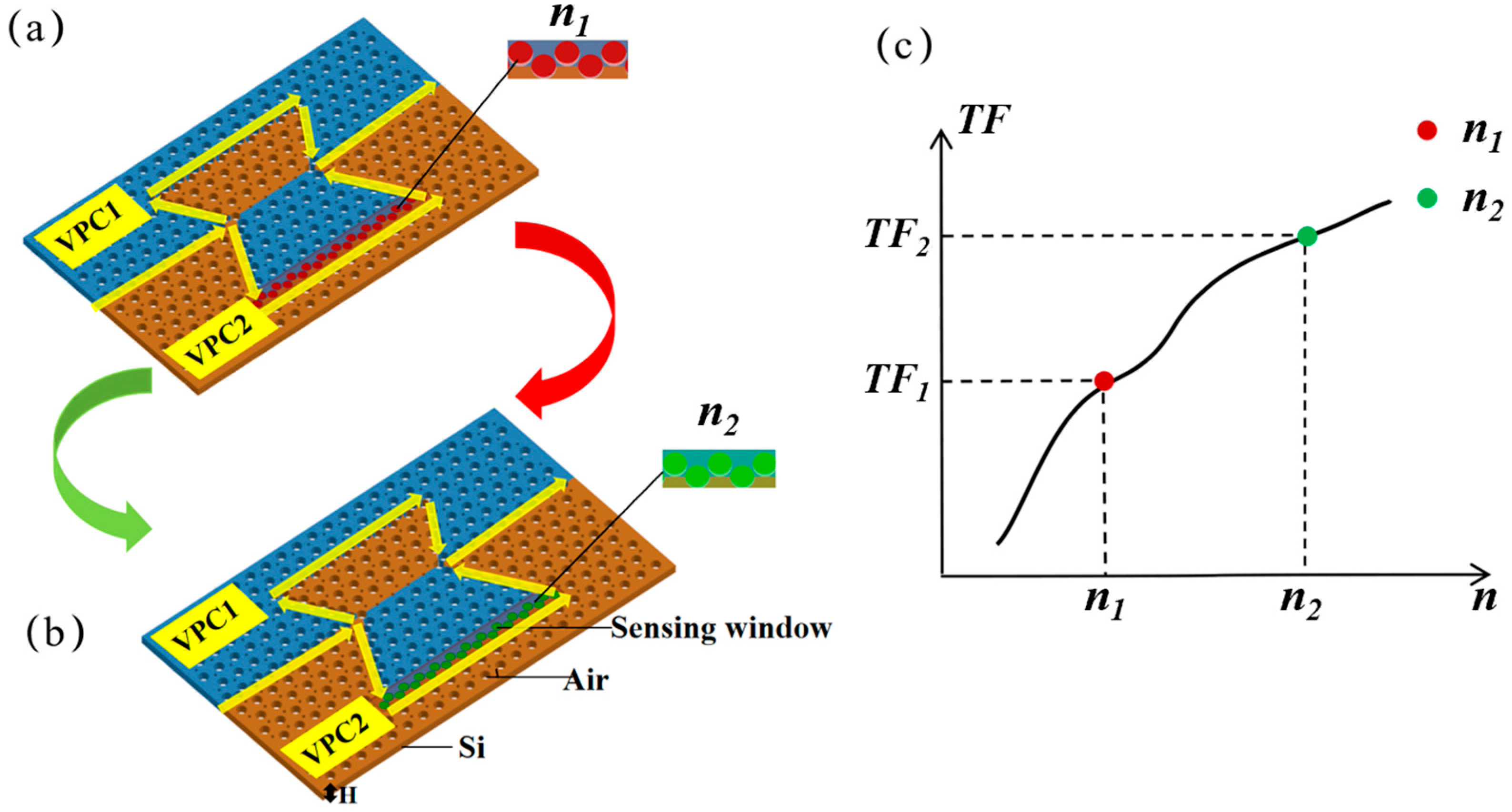
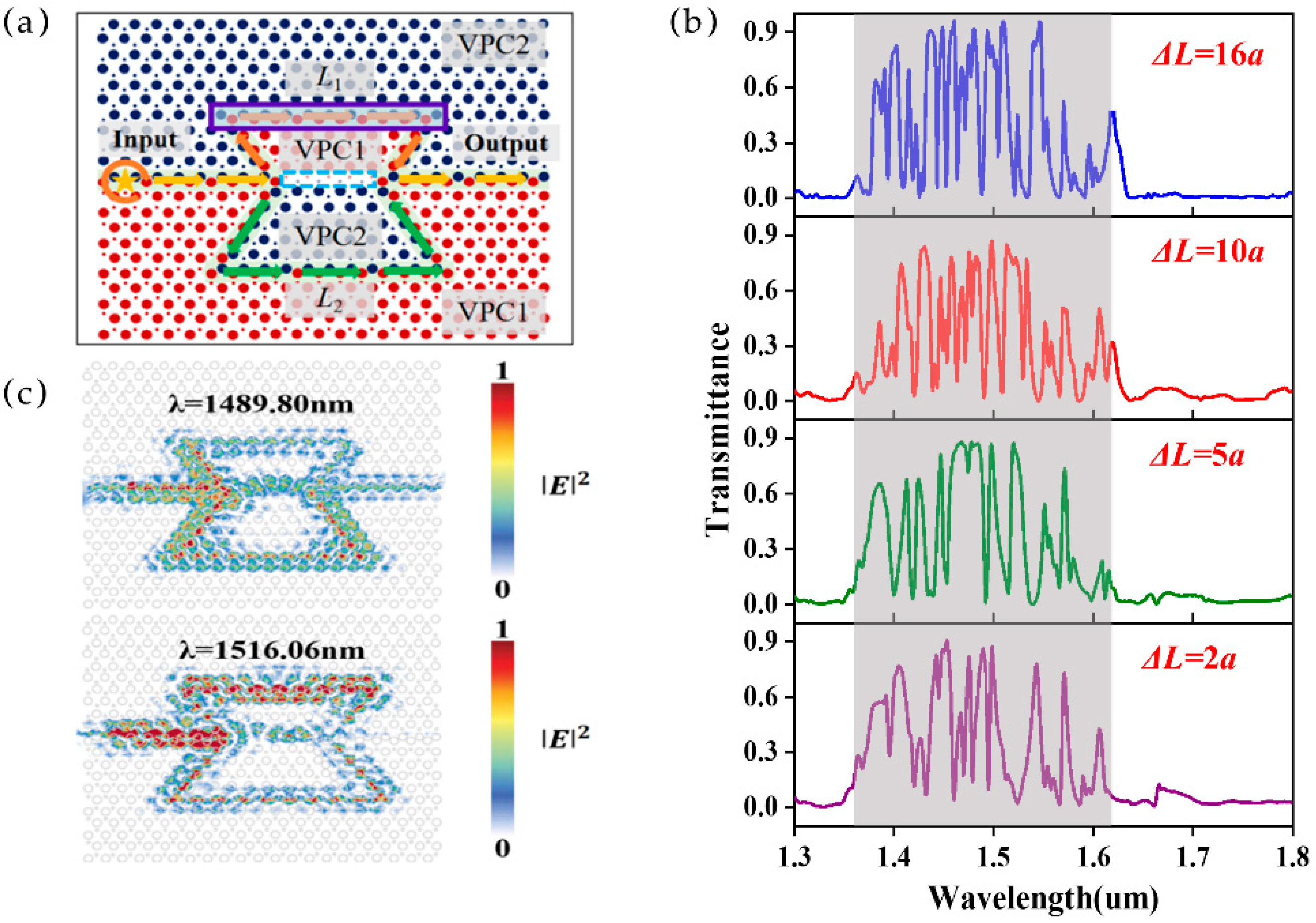
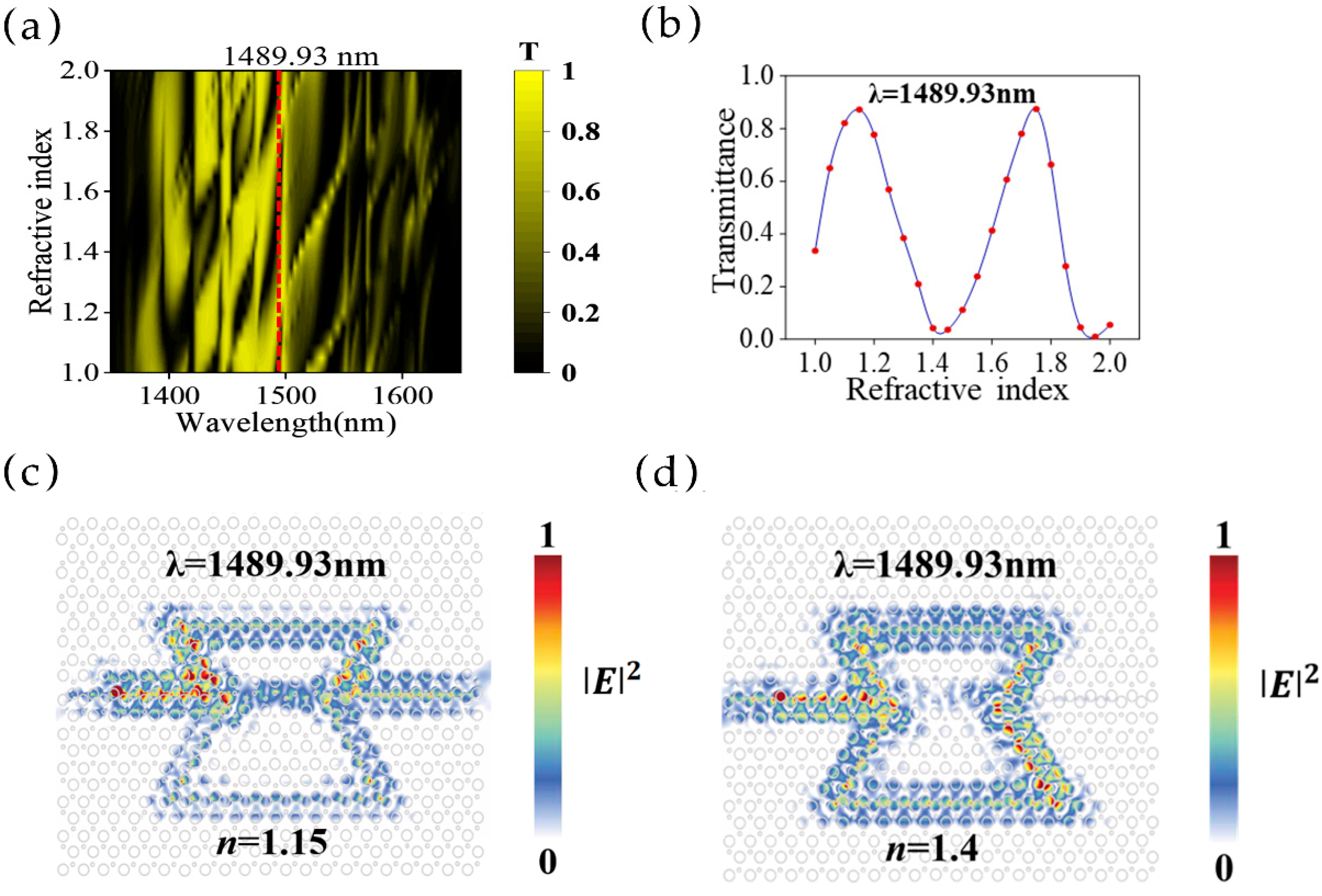

| Materials | Structures | Sensitivity (For Comparison, Unify the Unit) | Footprint (Size) | Reference |
|---|---|---|---|---|
| SOI waveguide | HP-MZI | 7.56 dB/RIU (160 nm/RIU) | 20 μm | [46] |
| SOI waveguide | DSHP-MZI | 2 dB/RIU (1061 nm/RIU) | 40 μm | [47] |
| Photonic crystal | S-PhCW-MZI | 187 dB/RIU (2.3 × 109 nm/RIU) | 1 mm | [48] |
| Fiber | TCF-SMF-TCF MZI | 189 dB/RIU (159 nm/RIU) | 5 mm | [49] |
| Photonic crystal fiber | PCF-SMFs MZI | 120 dB/RIU (198.77 nm/RIU) | 3.2 cm | [50] |
| Silicon | VPC MZI | 159 dB/RIU (1534%/RIU) | 9.26 × 7.99 μm2 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Fei, H.; Liu, X.; Lin, H. Design of Refractive Index Sensors Based on Valley Photonic Crystal Mach–Zehnder Interferometer. Sensors 2025, 25, 3289. https://doi.org/10.3390/s25113289
Li Y, Fei H, Liu X, Lin H. Design of Refractive Index Sensors Based on Valley Photonic Crystal Mach–Zehnder Interferometer. Sensors. 2025; 25(11):3289. https://doi.org/10.3390/s25113289
Chicago/Turabian StyleLi, Yuru, Hongming Fei, Xin Liu, and Han Lin. 2025. "Design of Refractive Index Sensors Based on Valley Photonic Crystal Mach–Zehnder Interferometer" Sensors 25, no. 11: 3289. https://doi.org/10.3390/s25113289
APA StyleLi, Y., Fei, H., Liu, X., & Lin, H. (2025). Design of Refractive Index Sensors Based on Valley Photonic Crystal Mach–Zehnder Interferometer. Sensors, 25(11), 3289. https://doi.org/10.3390/s25113289





