Exploring New Ways to Analyze Data on the Spontaneous Physical Activity of Rodents Through a Weighing Balance
Abstract
Highlights
- We showed that it is possible to develop a cost-effective and robust SPA measurement system using user-friendly Arduino-based instrumentation.
- We analyzed SPA data in ways never explored before, adapting mathematical strategies, exploring SPA on a minute-by-minute basis, and classifying it into four distinct domains.
- By offering a measurement method based on accessible instrumentation, we are contributing to the advancement of SPA-related research.
- Our expectation is that constant SPA monitoring could become a standard practice in both scientific research and veterinary settings.
Abstract
1. Introduction
2. Materials and Methods
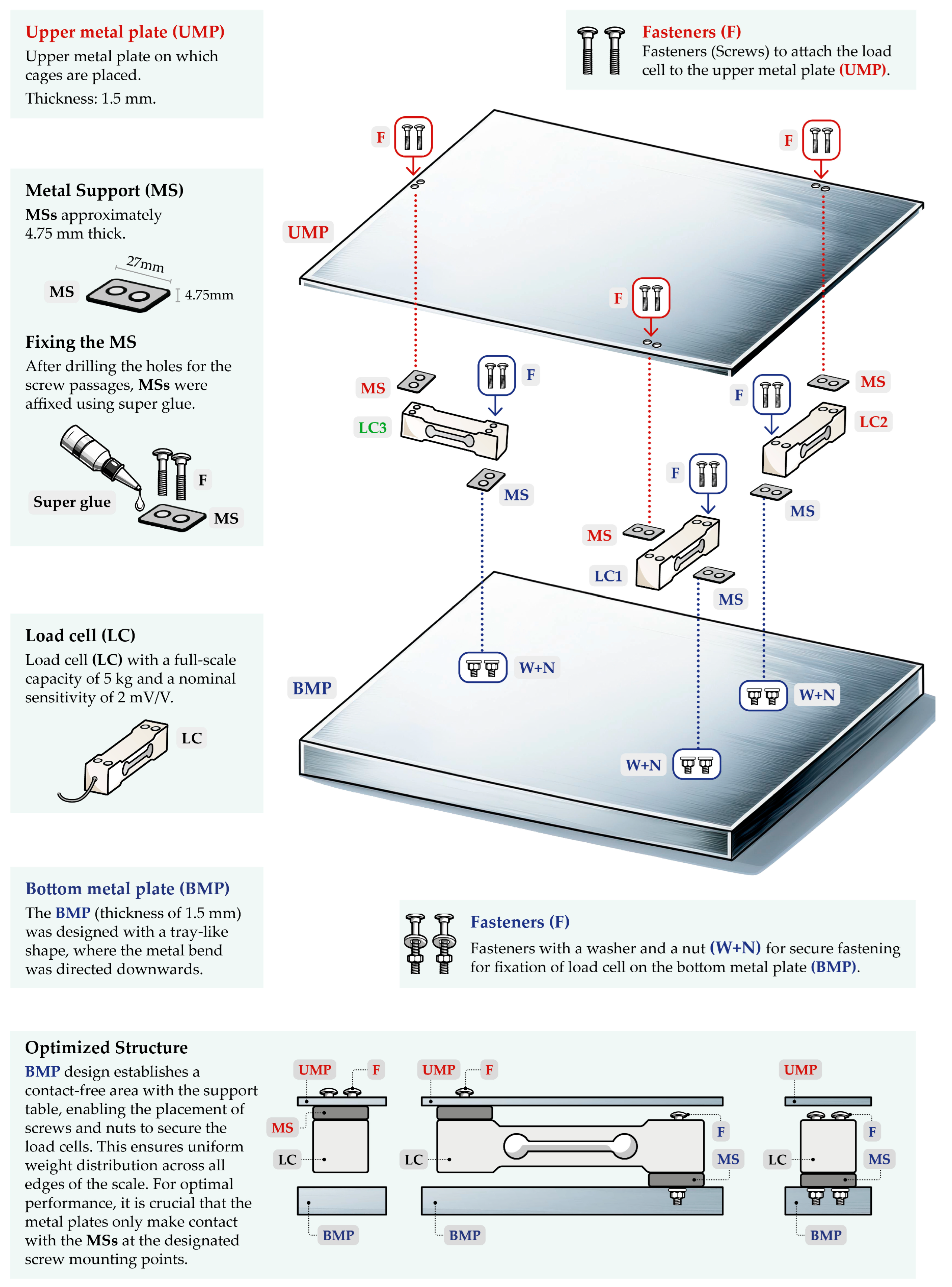
2.1. Construction and Development of the Weighing Balance
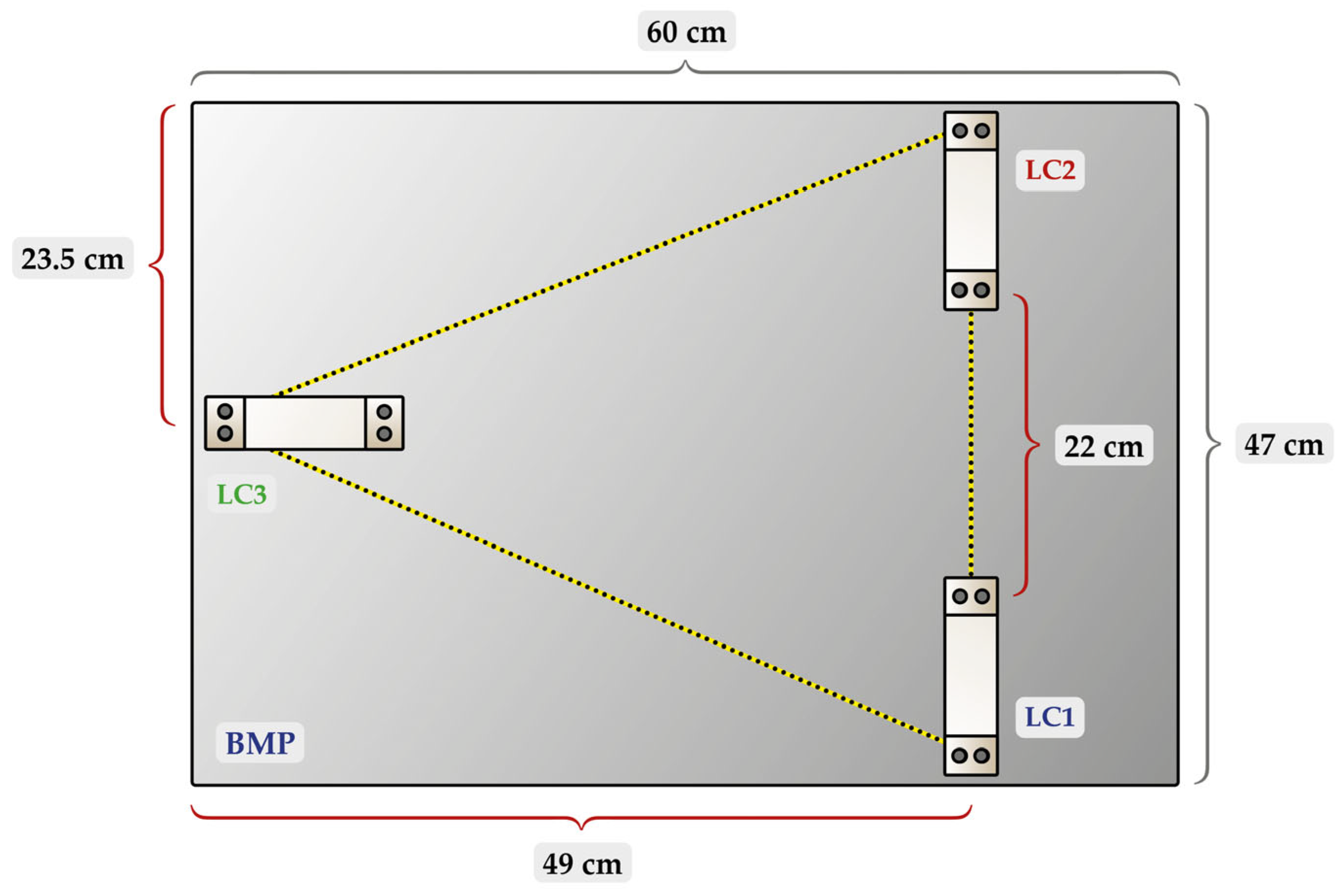
2.2. Arrangement of Load Cells
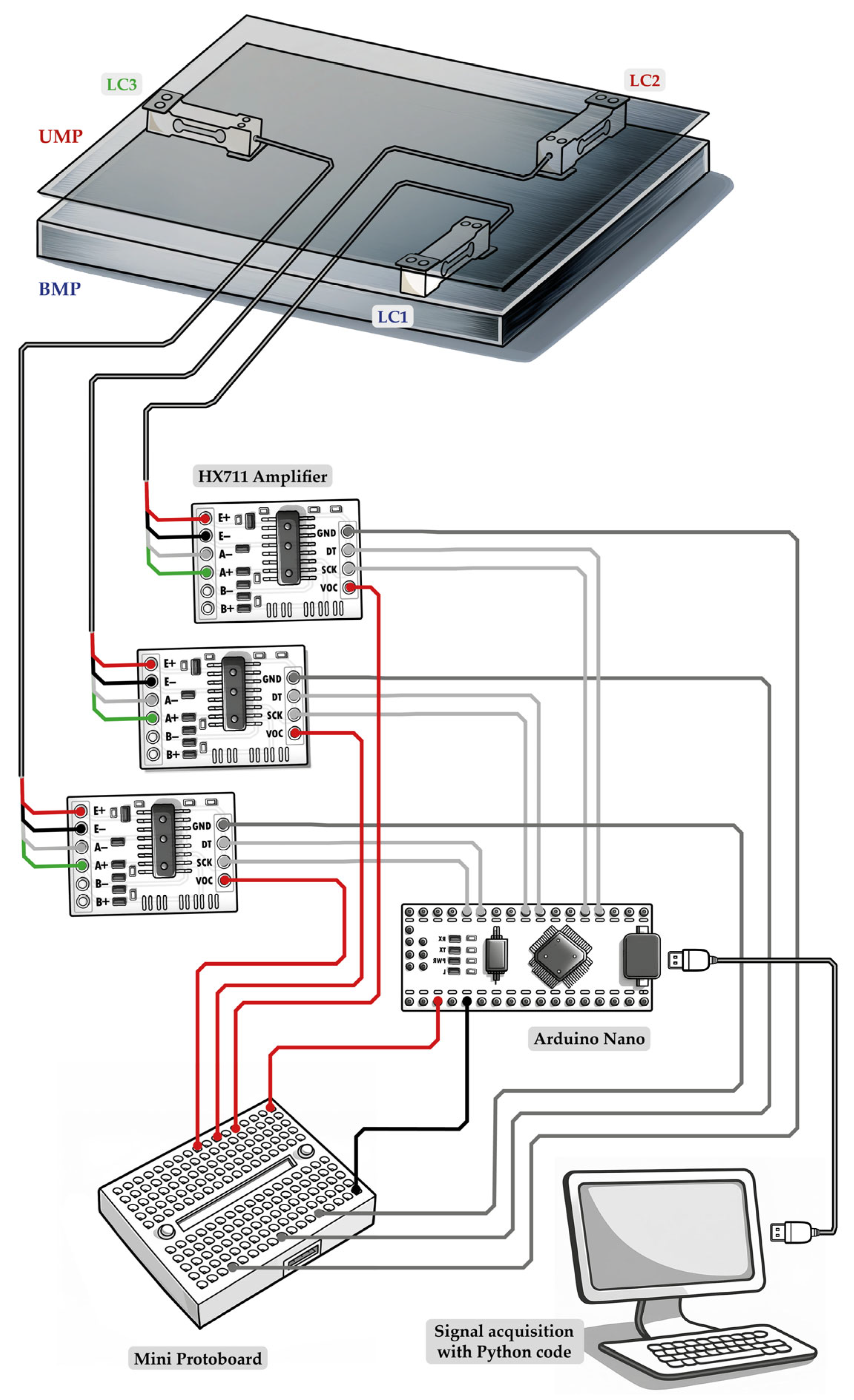
2.3. Signal Acquisition System
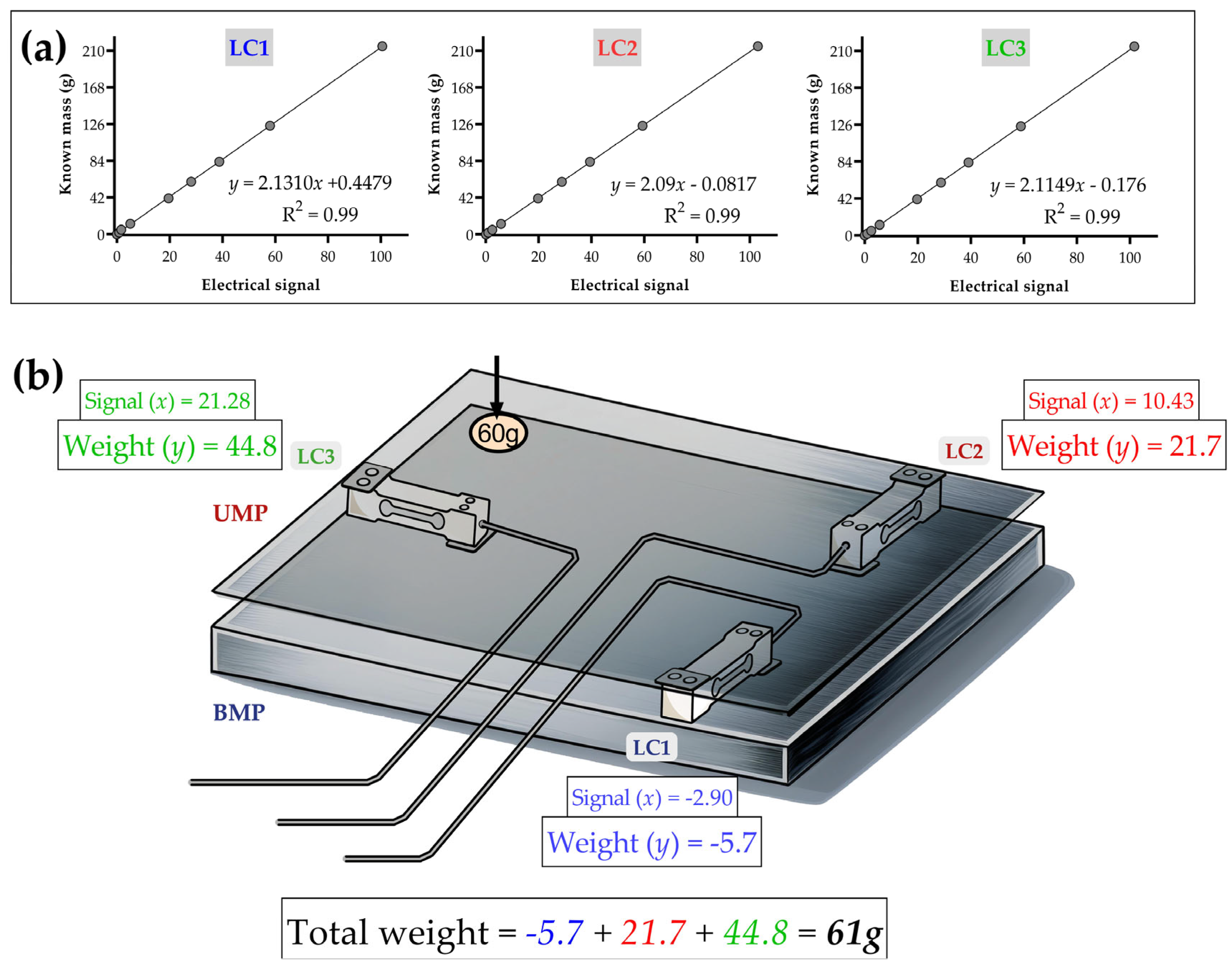
2.4. Transforming Raw Data into Weight Values Through the Calibration of Load Cells
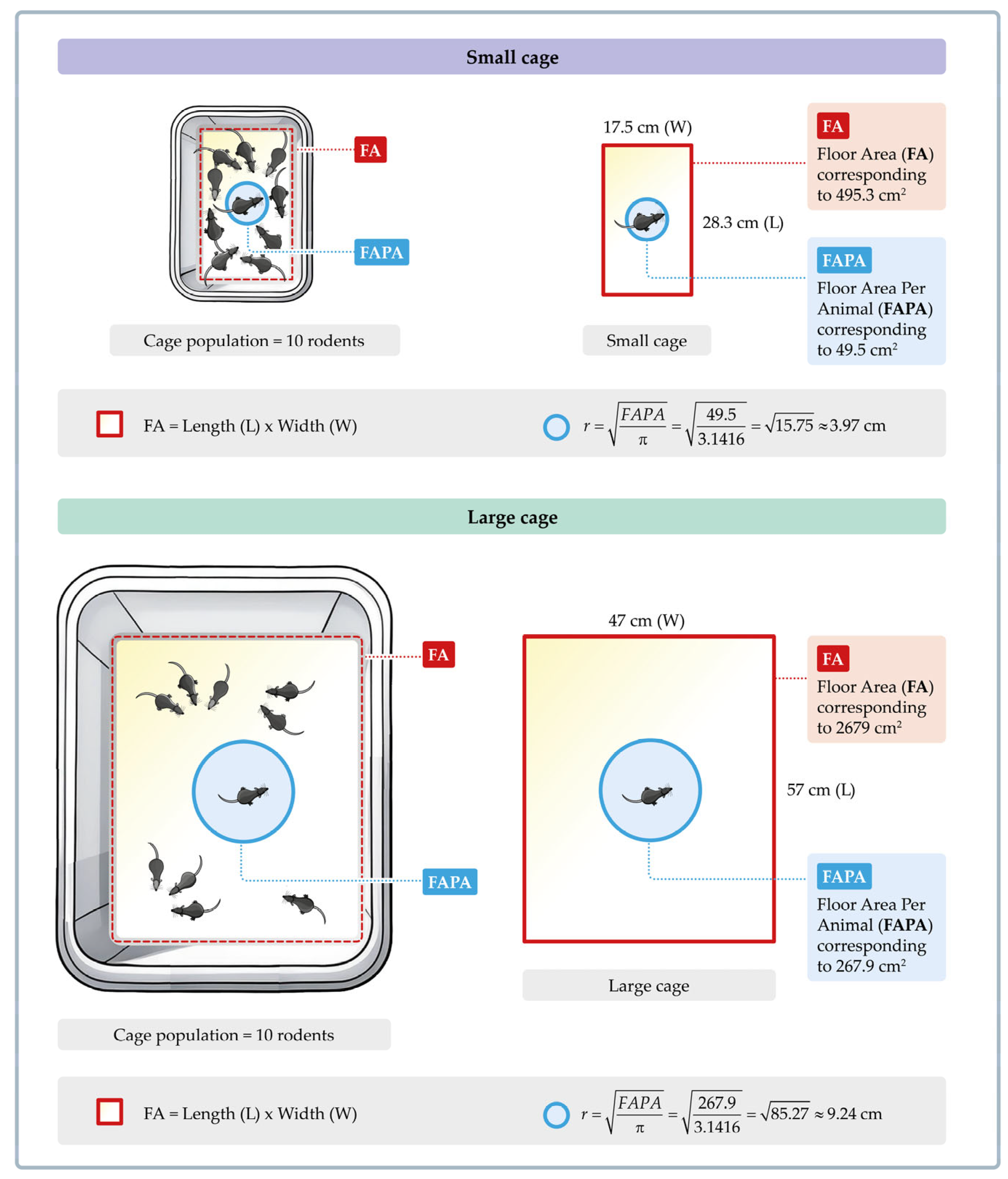
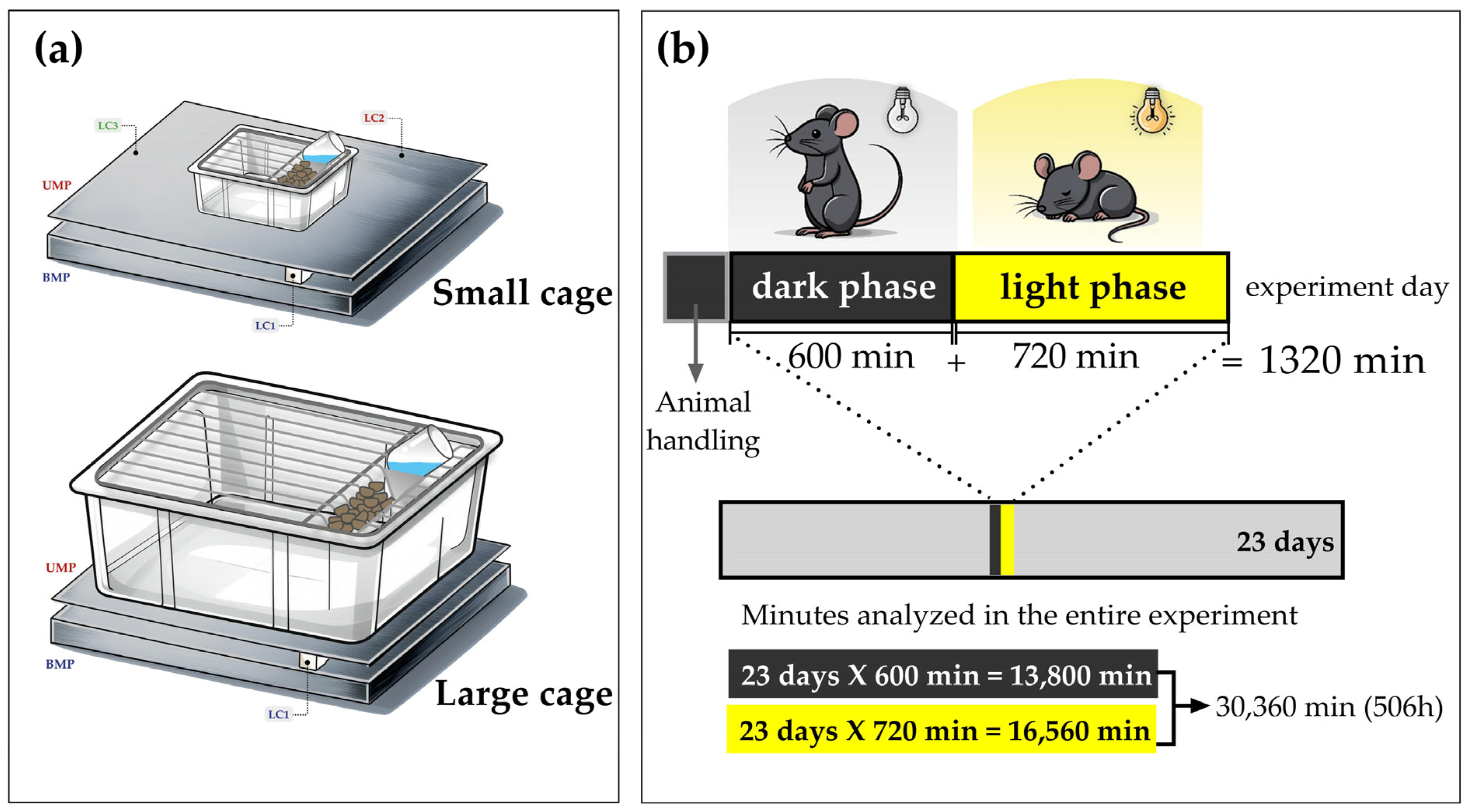
2.5. Rodents, Experimental Conditions, and SPA Recordings
2.6. Algorithm for Analyzing SPA
2.7. Mathematical Basis for Determining SPA: Biesiadecki’s Summation Strategy
2.8. Mathematical Basis for Determining SPA: Mean of Weight Changes (MWC)
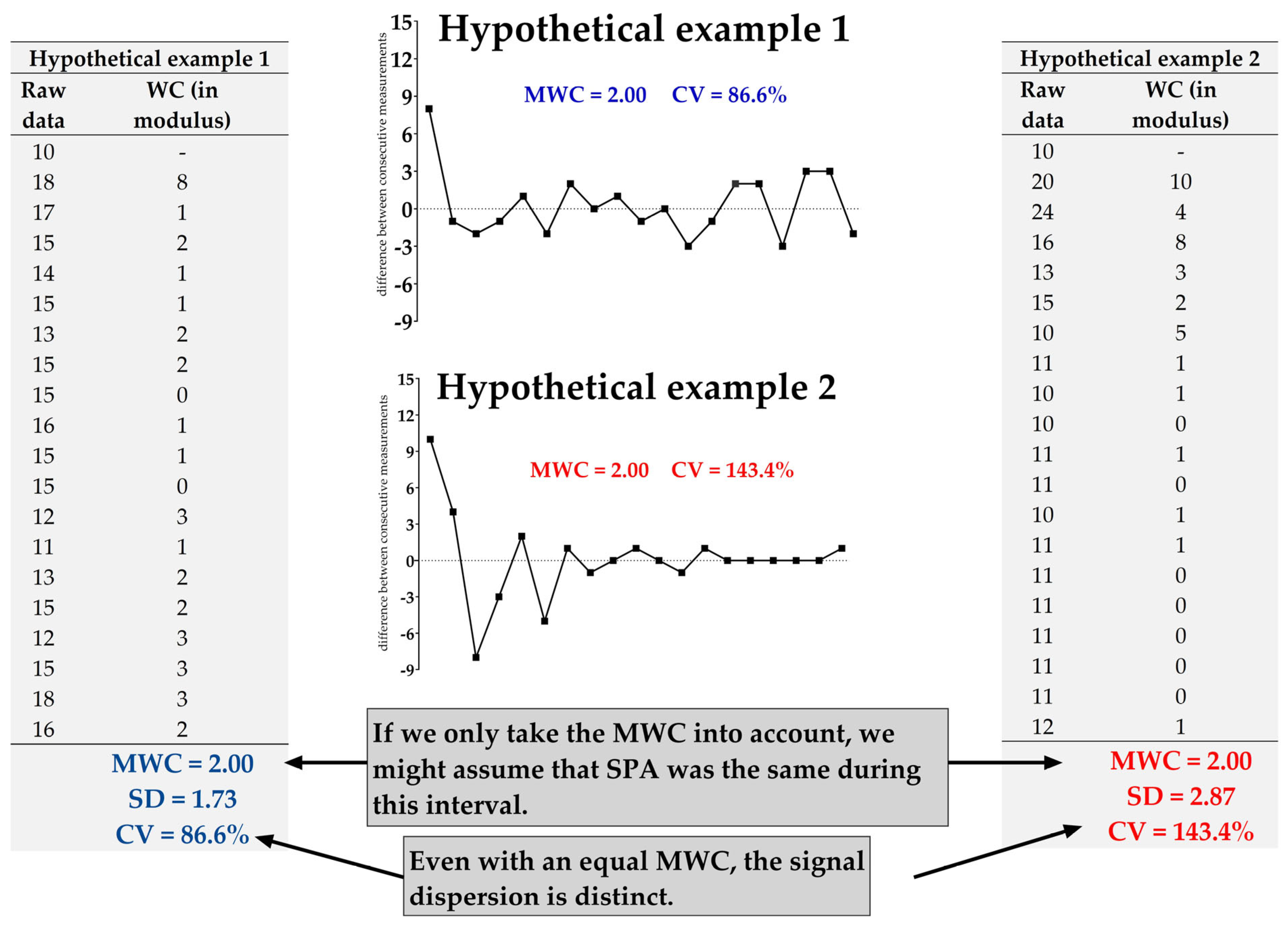
2.9. Exploring Beyond MWC: A Look at Signal Dispersion
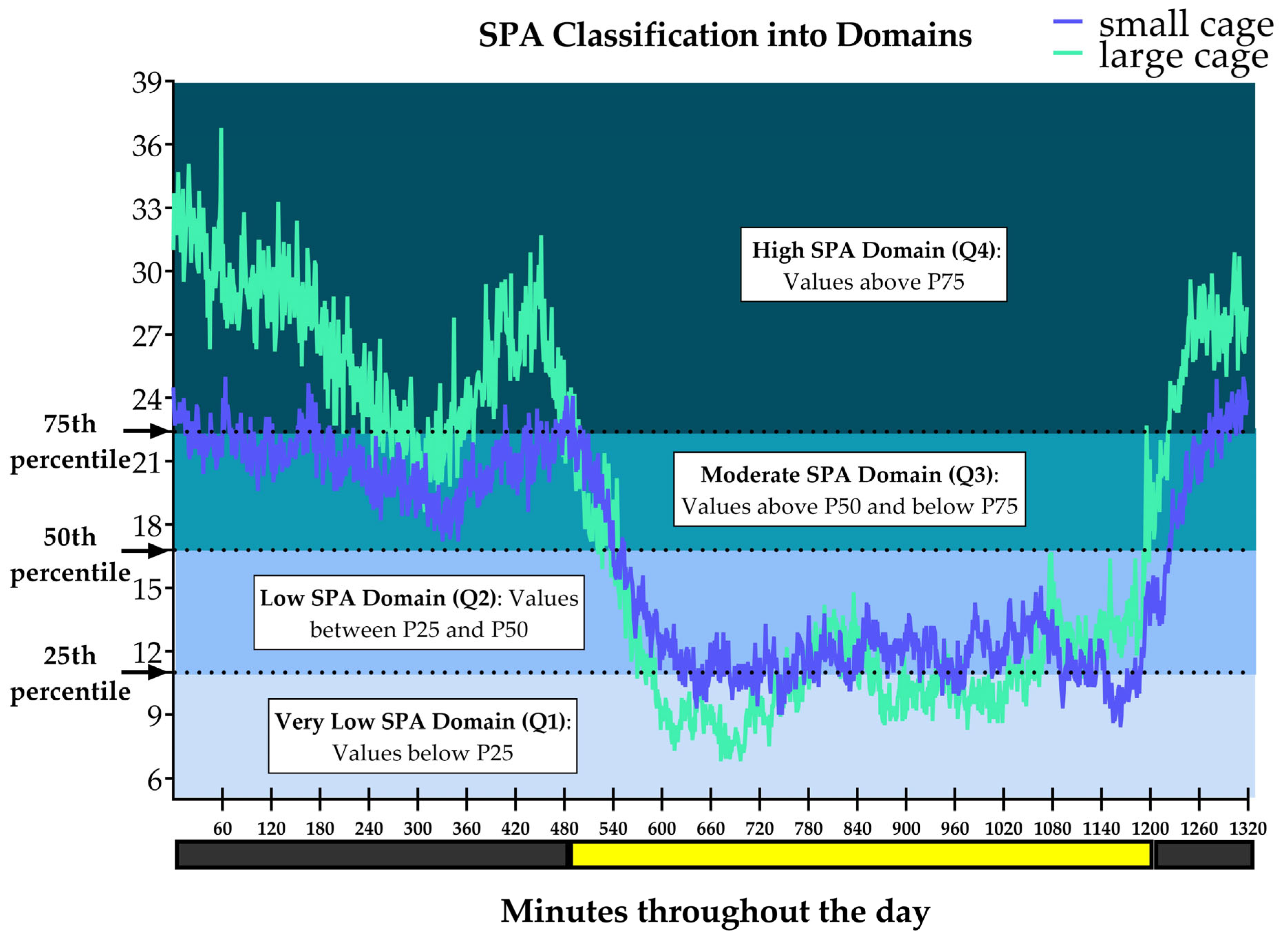
2.10. SPA Classification into Domains
2.11. Minute-by-Minute Heat Maps of SPA Domains
2.12. Statistical Procedures
3. Results
3.1. Comparative Analysis of Mathematical Strategies (SWC vs. MWC)
3.2. A Panoramic View on the 23-Day Experiment
3.3. Exploring Analyses Across Light and Dark Phases
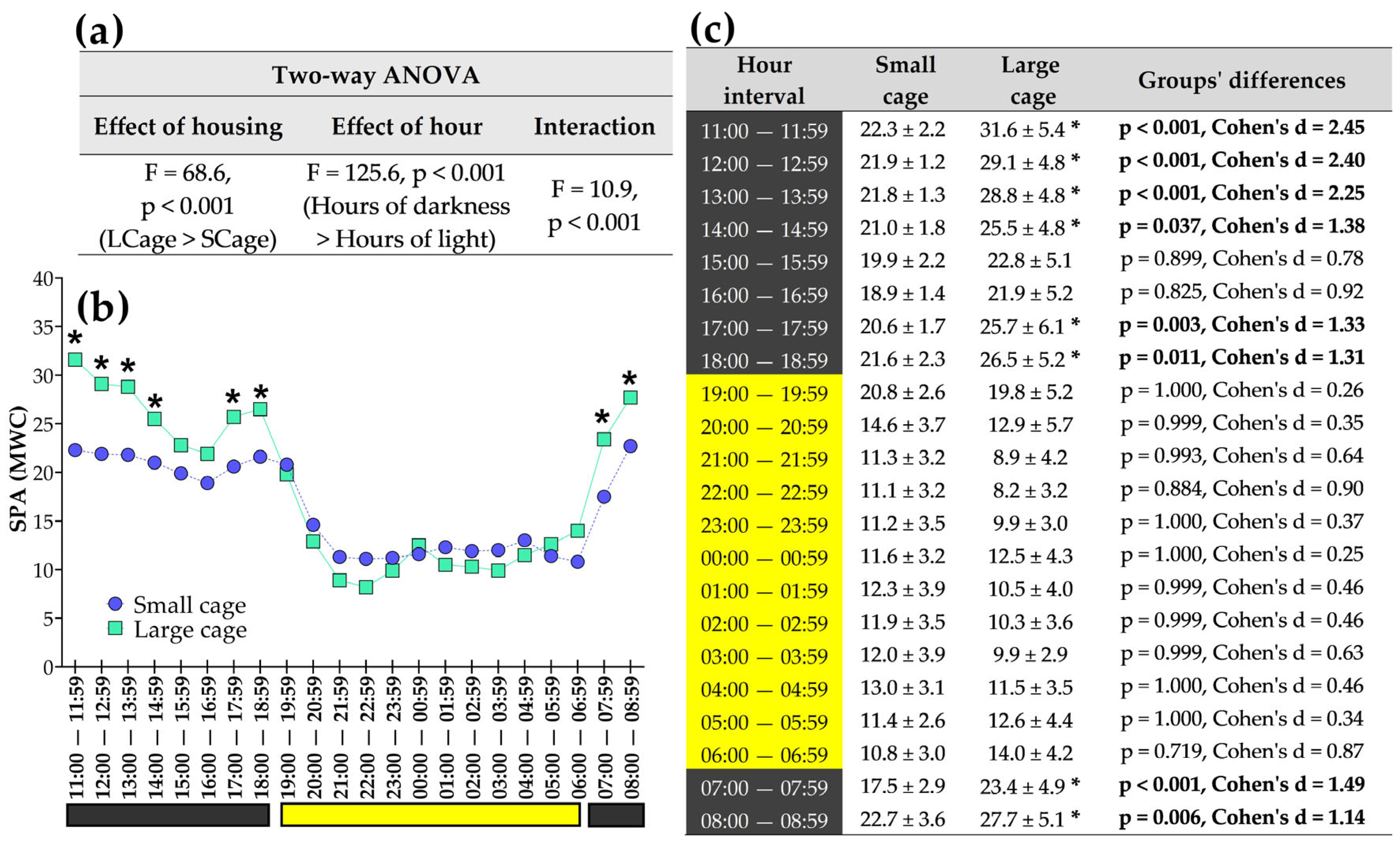
3.4. Exploring Analyses Across Different Hours of the Day
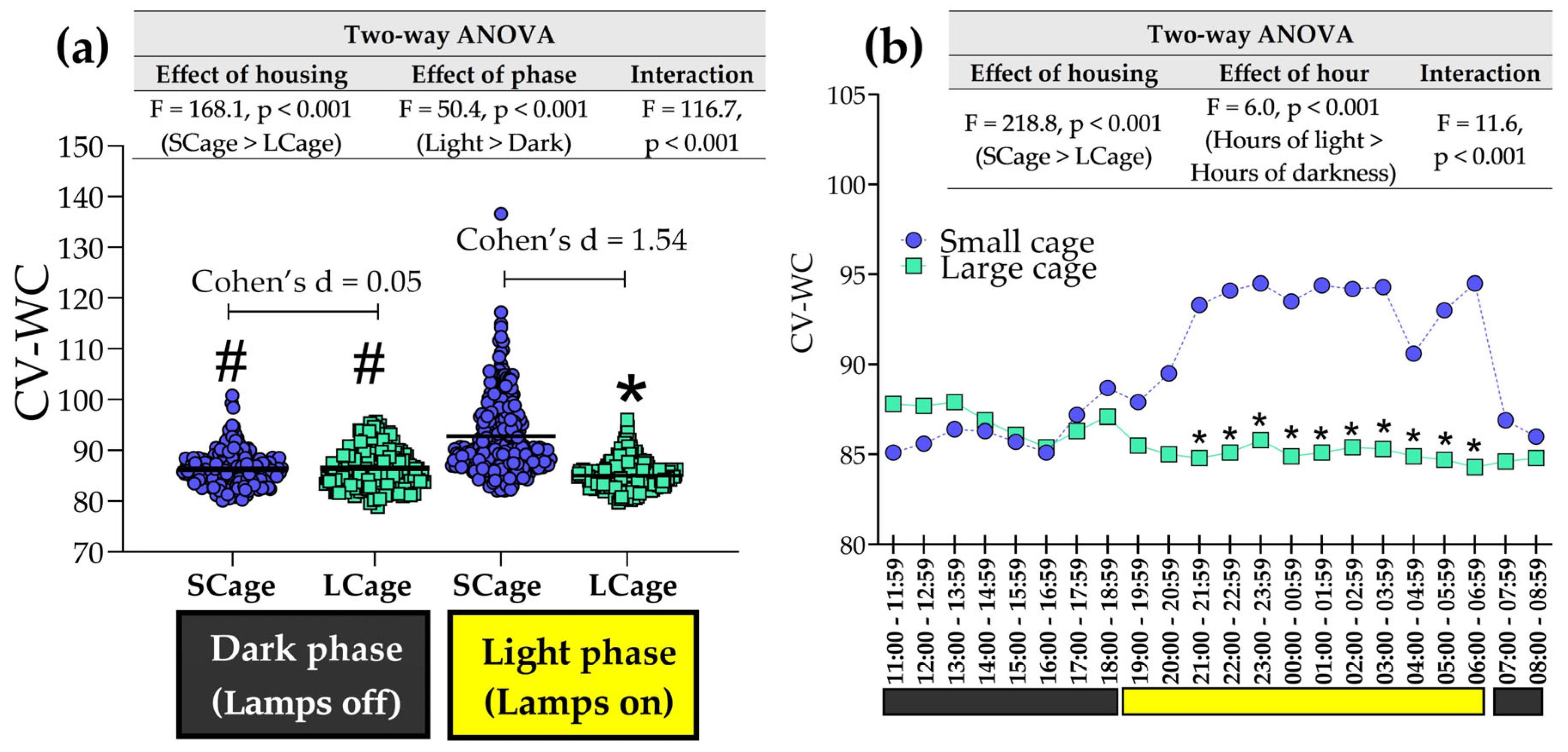
3.5. Signal Dispersion Analyses
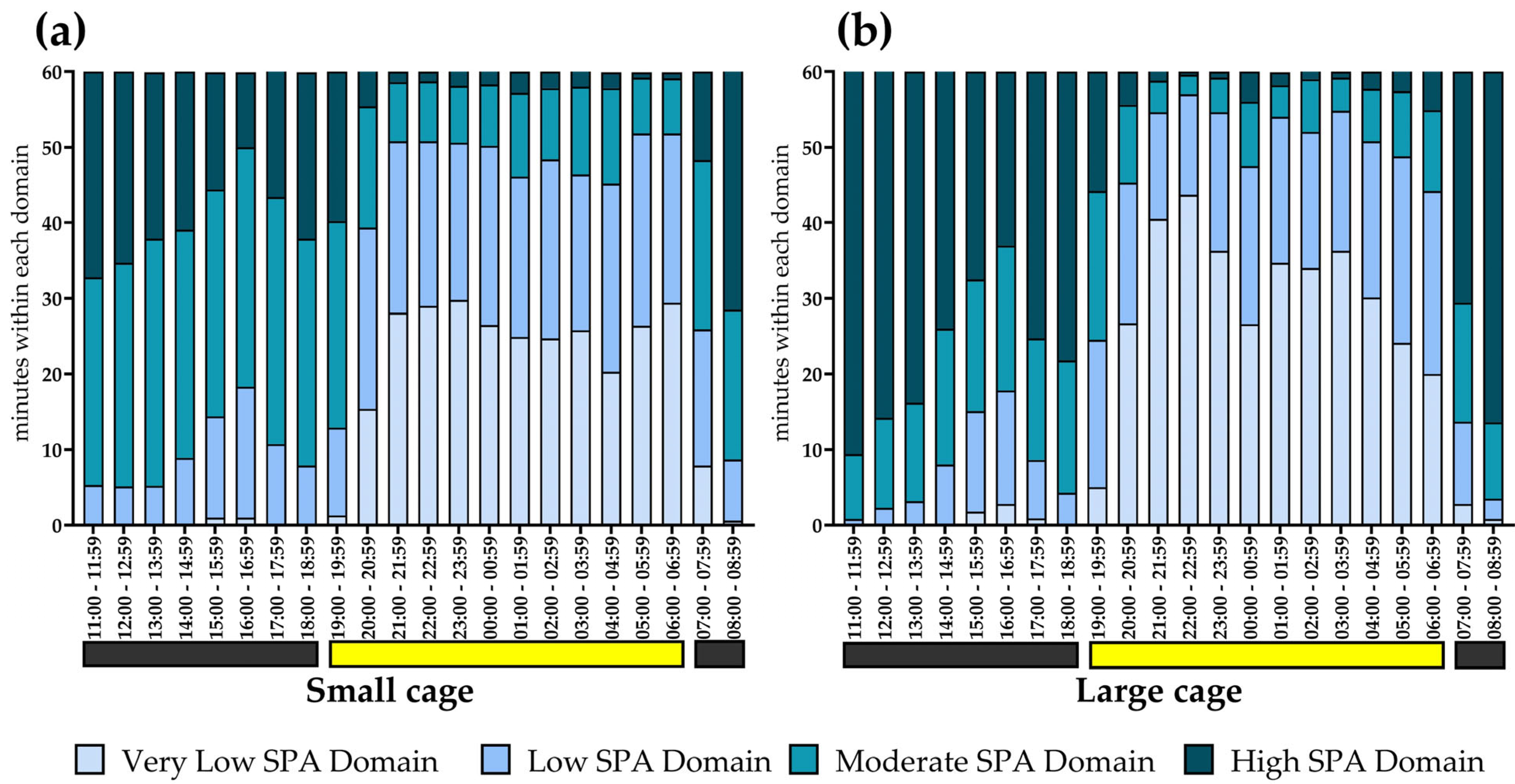
3.6. SPA Classification into Domains Within Hours
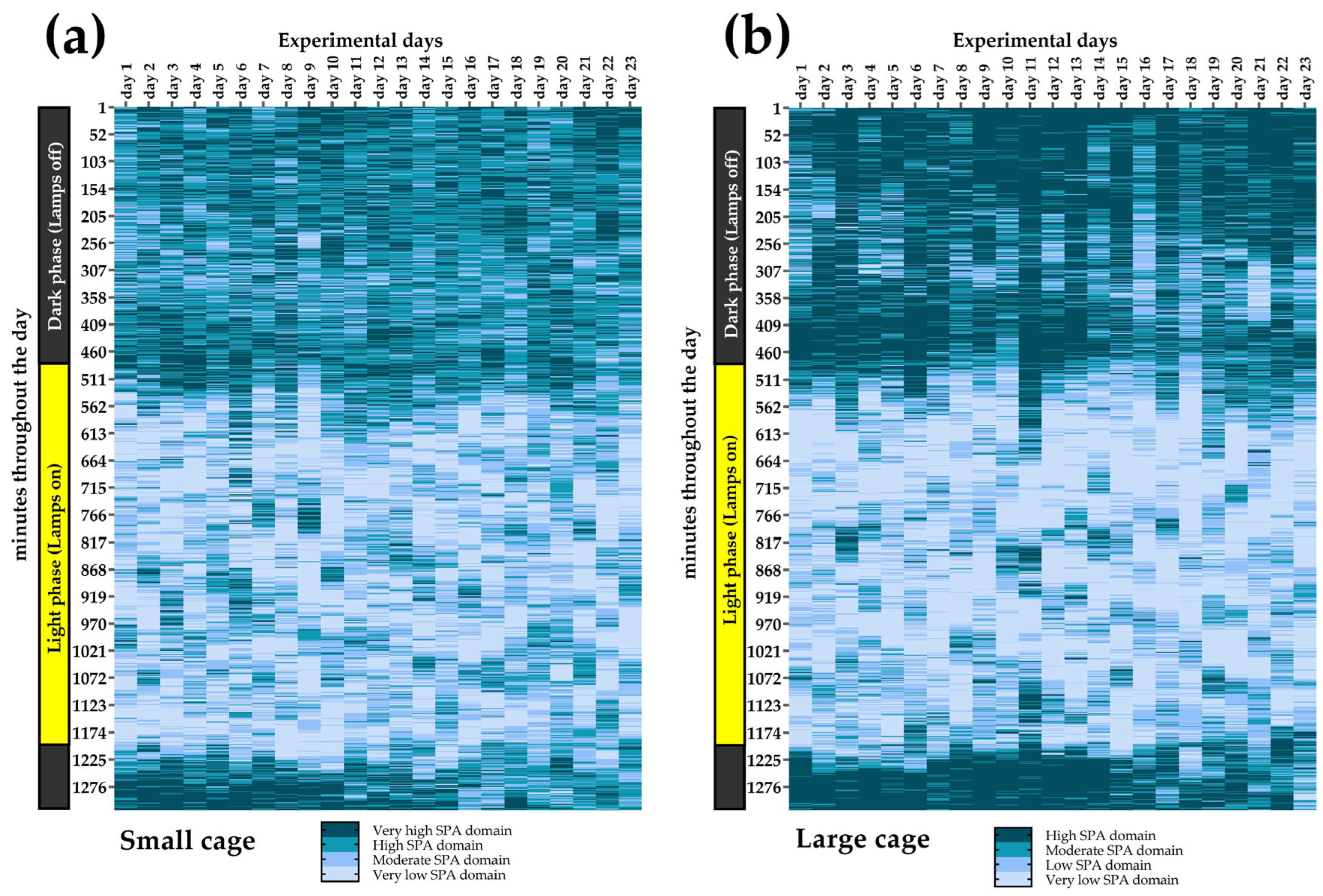
3.7. SPA Classification into Domains Across All Experimental Days
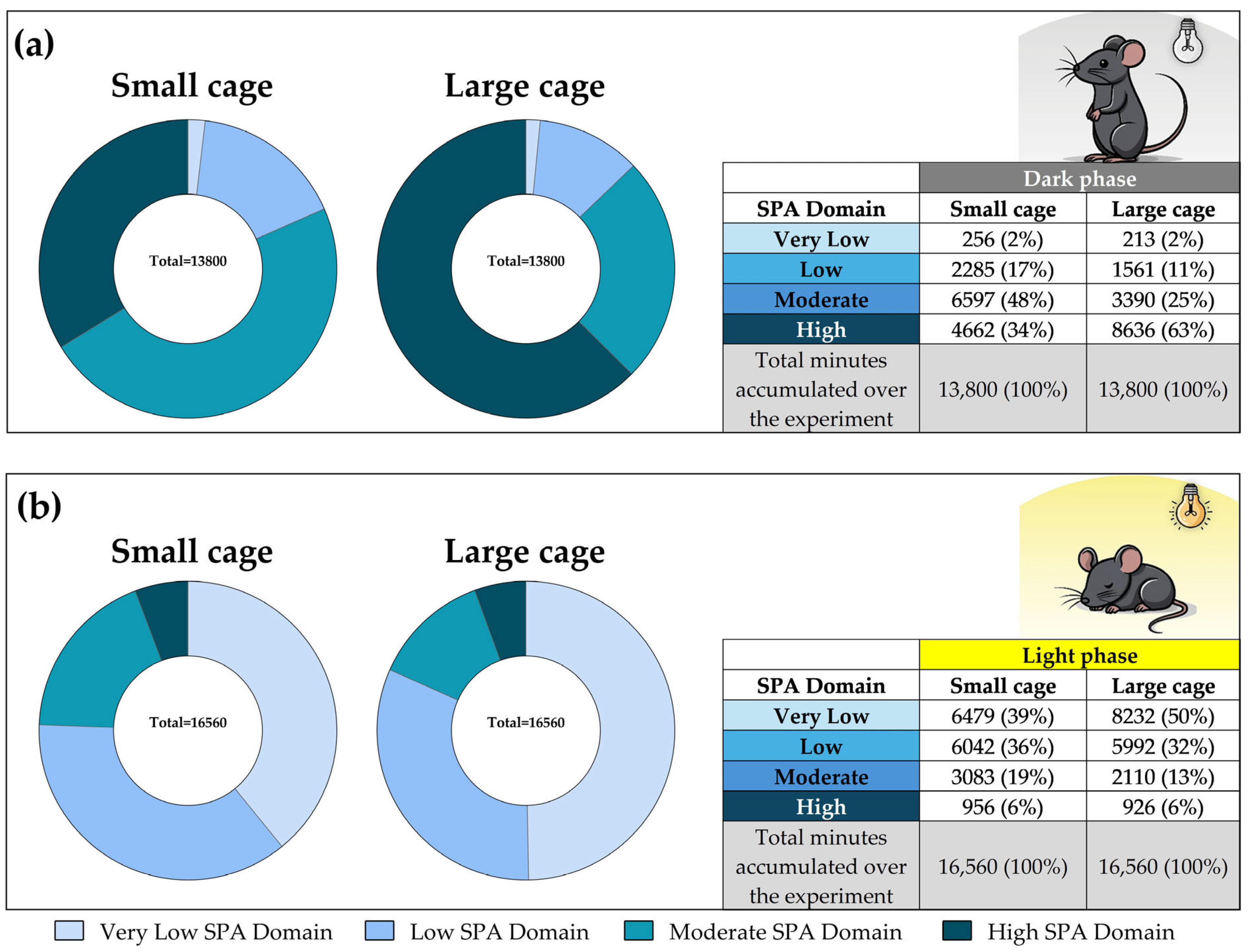
3.8. SPA Classification into Domains Throughout the Experiment
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPA | Spontaneous physical activity |
| WC | Weight changes |
| MWC | Mean of Weight Changes |
| SWC | Sum of Weight Changes |
| SD-WC | Standard deviation of weight changes |
| CV-WC | Coefficient of variation of weight changes |
| MS | Metal support |
| UMP | Upper metal plate |
| BMP | Bottom metal plate |
| LC | Load cell |
| SCage | Small cage |
| LCage | Large cage |
| FA | Floor area |
| FAPA | Floor area per animal |
| Hz | Hertz |
| SEE | Standard Error of the Estimate |
| AUC | Area under the curve |
| VLSPAD | Very Low Spontaneous Physical Activity Domain |
| LSPAD | Low Spontaneous Physical Activity Domain |
| MSPAD | Moderate Spontaneous Physical Activity Domain |
| HSPAD | High Spontaneous Physical Activity Domain |
References
- Bradbury, A.J.; Costall, B.; Naylor, R.J.; Onaivi, E.S. 5-Hydroxytryptamine involvement in the locomotor activity suppressant effects of amphetamine in the mouse. Psychopharmacology 1987, 93, 457–465. [Google Scholar] [CrossRef] [PubMed]
- Levin, B.E. Spontaneous motor activity during the development and maintenance of diet-induced obesity in the rat. Physiol. Behav. 1991, 50, 573–581. [Google Scholar] [CrossRef] [PubMed]
- Garland, T., Jr.; Schutz, H.; Chappell, M.A.; Keeney, B.K.; Meek, T.H.; Copes, L.E.; Acosta, W.; Drenowatz, C.; Maciel, R.C.; van Dijk, G.; et al. The biological control of voluntary exercise, spontaneous physical activity and daily energy expenditure in relation to obesity: Human and rodent perspectives. J. Exp. Biol. 2011, 214, 206–229. [Google Scholar] [CrossRef] [PubMed]
- Kotz, C.M. Integration of feeding and spontaneous physical activity: Role for orexin. Physiol. Behav. 2006, 88, 294–301. [Google Scholar] [CrossRef]
- Kotz, C.M.; Perez-Leighton, C.E.; Teske, J.A.; Billington, C.J. Spontaneous Physical Activity Defends Against Obesity. Curr. Obes. Rep. 2017, 6, 362–370. [Google Scholar] [CrossRef]
- Kotz, C.M.; Teske, J.A.; Billington, C.J. Neuroregulation of nonexercise activity thermogenesis and obesity resistance. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, R699–R710. [Google Scholar] [CrossRef]
- Kotz, C.M.; Teske, J.A.; Levine, J.A.; Wang, C. Feeding and activity induced by orexin A in the lateral hypothalamus in rats. Regul. Pept. 2002, 104, 27–32. [Google Scholar] [CrossRef]
- Levine, J.A. Non-exercise activity thermogenesis (NEAT). Best Pract. Res. Clin. Endocrinol. Metab. 2002, 16, 679–702. [Google Scholar] [CrossRef]
- Levine, J.A. Nonexercise activity thermogenesis (NEAT): Environment and biology. Am. J. Physiol. Endocrinol. Metab. 2004, 286, E675–E685. [Google Scholar] [CrossRef]
- Novak, C.M.; Escande, C.; Burghardt, P.R.; Zhang, M.; Barbosa, M.T.; Chini, E.N.; Britton, S.L.; Koch, L.G.; Akil, H.; Levine, J.A. Spontaneous activity, economy of activity, and resistance to diet-induced obesity in rats bred for high intrinsic aerobic capacity. Horm. Behav. 2010, 58, 355–367. [Google Scholar] [CrossRef]
- Novak, C.M.; Kotz, C.M.; Levine, J.A. Central orexin sensitivity, physical activity, and obesity in diet-induced obese and diet-resistant rats. Am. J. Physiol. Endocrinol. Metab. 2006, 290, E396–E403. [Google Scholar] [CrossRef]
- Perez-Leighton, C.E.; Boland, K.; Billington, C.J.; Kotz, C.M. High and low activity rats: Elevated intrinsic physical activity drives resistance to diet-induced obesity in non-bred rats. Obesity 2013, 21, 353–360. [Google Scholar] [CrossRef] [PubMed]
- Teske, J.A.; Billington, C.J.; Kotz, C.M. Mechanisms underlying obesity resistance associated with high spontaneous physical activity. Neuroscience 2014, 256, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Teske, J.A.; Billington, C.J.; Kuskowski, M.A.; Kotz, C.M. Spontaneous physical activity protects against fat mass gain. Int. J. Obes. 2012, 36, 603–613. [Google Scholar] [CrossRef]
- Cho, M.H. Quantitation of spontaneous movements of animals given psychotropic drugs. J. Appl. Physiol. 1961, 16, 390–391. [Google Scholar] [CrossRef] [PubMed]
- Scariot, P.P.M.; Gobatto, C.A.; Polisel, E.E.C.; Gomes, A.E.C.; Beck, W.R.; Manchado-Gobatto, F.B. Early-life mice housed in standard stocking density reduce the spontaneous physical activity and increase visceral fat deposition before reaching adulthood. Lab. Anim. 2022, 56, 344–355. [Google Scholar] [CrossRef]
- Scariot, P.P.M.; Manchado-Gobatto, F.B.; Prolla, T.A.; Masselli Dos Reis, I.G.; Gobatto, C.A. Housing conditions modulate spontaneous physical activity, feeding behavior, aerobic running capacity and adiposity in C57BL/6J mice. Horm. Behav. 2019, 115, 104556. [Google Scholar] [CrossRef]
- Dhillon, R.S.; Qin, Y.A.; van Ginkel, P.R.; Fu, V.X.; Vann, J.M.; Lawton, A.J.; Green, C.L.; Manchado-Gobatto, F.B.; Gobatto, C.A.; Lamming, D.W.; et al. SIRT3 deficiency decreases oxidative metabolism capacity but increases lifespan in male mice under caloric restriction. Aging Cell 2022, 21, e13721. [Google Scholar] [CrossRef]
- Beck, W.R.; Scariot, P.P.M.; Carmo, S.S.; Manchado-Gobatto, F.B.; Gobatto, C.A. Metabolic profile and spontaneous physical activity modulation under short-term food restriction in young rats. Mot. Rev. Educ. Física Motriz. 2017, 23, e101606. [Google Scholar] [CrossRef][Green Version]
- Chausse, B.; Solon, C.; Caldeira da Silva, C.C.; Masselli Dos Reis, I.G.; Manchado-Gobatto, F.B.; Gobatto, C.A.; Velloso, L.A.; Kowaltowski, A.J. Intermittent fasting induces hypothalamic modifications resulting in low feeding efficiency, low body mass and overeating. Endocrinology 2014, 155, 2456–2466. [Google Scholar] [CrossRef]
- Scariot, P.P.M.; Manchado-Gobatto, F.B.; Beck, W.R.; Papoti, M.; Van Ginkel, P.R.; Gobatto, C.A. Monocarboxylate transporters (MCTs) in skeletal muscle and hypothalamus of less or more physically active mice exposed to aerobic training. Life Sci. 2022, 307, 120872. [Google Scholar] [CrossRef] [PubMed]
- Scariot, P.P.M.; Manchado-Gobatto, F.B.; Van Ginkel, P.R.; Prolla, T.A.; Gobatto, C.A. Aerobic training associated with an active lifestyle exerts a protective effect against oxidative damage in hypothalamus and liver: The involvement of energy metabolism. Brain Res. Bull. 2021, 175, 116–129. [Google Scholar] [CrossRef] [PubMed]
- Polisel, E.E.C.; Beck, W.R.; Scariot, P.P.M.; Pejon, T.M.M.; Gobatto, C.A.; Manchado-Gobatto, F.B. Effects of high-intensity interval training in more or less active mice on biomechanical, biophysical and biochemical bone parameters. Sci. Rep. 2021, 11, 6414. [Google Scholar] [CrossRef] [PubMed]
- Koch, L.G.; Green, C.L.; Lee, A.D.; Hornyak, J.E.; Cicila, G.T.; Britton, S.L. Test of the principle of initial value in rat genetic models of exercise capacity. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2005, 288, R466–R472. [Google Scholar] [CrossRef]
- Pejon, T.M.M.; Scariot, P.P.M.; Selistre-de-Araujo, H.S.; Gobatto, C.A.; Cornachione, A.S.; Beck, W.R. Effects of Moderate–Intensity Physical Training on Skeletal Muscle Substrate Transporters and Metabolic Parameters of Ovariectomized Rats. Metabolites 2022, 12, 402. [Google Scholar] [CrossRef]
- Silvennoinen, M.; Rantalainen, T.; Kainulainen, H. Validation of a method to measure total spontaneous physical activity of sedentary and voluntary running mice. J. Neurosci. Methods 2014, 235, 51–58. [Google Scholar] [CrossRef]
- Moes, J.R.; Holden, J.E. Characterizing Activity and Muscle Atrophy Changes in Rats With Neuropathic Pain:A Pilot Study. Biol. Res. Nurs. 2014, 16, 16–22. [Google Scholar] [CrossRef]
- Siviy, S.M.; Kritikos, A.; Atrens, D.M.; Shepherd, A. Effects of norepinephrine infused in the paraventricular hypothalamus on energy expenditure in the rat. Brain Res. 1989, 487, 79–88. [Google Scholar] [CrossRef]
- Biesiadecki, B.J.; Brand, P.H.; Koch, L.G.; Britton, S.L. A gravimetric method for the measurement of total spontaneous activity in rats. Proc. Soc. Exp. Biol. Med. 1999, 222, 65–69. [Google Scholar] [CrossRef]
- Nejat, M.A.; Stiedl, O.; Smit, A.B.; van Kesteren, R.E. Continuous locomotor activity monitoring to assess animal welfare following intracranial surgery in mice. Front. Behav. Neurosci. 2024, 18, 1457894. [Google Scholar] [CrossRef]
- Ikeda, M.; Sagara, M.; Inoué, S. Continuous exposure to dim illumination uncouples temporal patterns of sleep, body temperature, locomotion and drinking behavior in the rat. Neurosci. Lett. 2000, 279, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Spangenberg, E.M.; Augustsson, H.; Dahlborn, K.; Essén-Gustavsson, B.; Cvek, K. Housing-related activity in rats: Effects on body weight, urinary corticosterone levels, muscle properties and performance. Lab. Anim. 2005, 39, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Teske, J.A.; Perez-Leighton, C.E.; Billington, C.J.; Kotz, C.M. Methodological considerations for measuring spontaneous physical activity in rodents. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2014, 306, R714–R721. [Google Scholar] [CrossRef] [PubMed]
- Chabert, C.; Bottelin, P.; Pison, C.; Dubouchaud, H. A low-cost system to easily measure spontaneous physical activity in rodents. J. Appl. Physiol. 2016, 120, 1097–1103. [Google Scholar] [CrossRef][Green Version]
- Beck, W.; Gobatto, C. Effect of high wavelengths low intensity light during dark period on physical exercise performance, biochemical and haematological parameters of swimming rats. Physiol. Int. 2016, 103, 112–119. [Google Scholar] [CrossRef]
- Templeton, G.F. A two-step approach for transforming continuous variables to normal: Implications and recommendations for IS research. J. Commun. Assoc. Inf. Syst. 2011, 28, 4. [Google Scholar] [CrossRef]
- Conover, W.J.; Iman, R.L. Rank transformations as a bridge between parametric and nonparametric statistics. Am. Stat. 1981, 35, 124–129. [Google Scholar] [CrossRef]
- Tai, M.M. A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves. Diabetes Care 1994, 17, 152–154. [Google Scholar] [CrossRef]
- Farsi, H.; Achaâban, M.R.; Piro, M.; Bothorel, B.; Ouassat, M.; Challet, E.; Pévet, P.; El Allali, K. Entrainment of circadian rhythms of locomotor activity by ambient temperature cycles in the dromedary camel. Sci. Rep. 2020, 10, 19515. [Google Scholar] [CrossRef]
- Yamanaka, Y.; Honma, S.; Honma, K. Mistimed wheel running interferes with re-entrainment of circadian Per1 rhythms in the mouse skeletal muscle and lung. Genes Cells Devoted Mol. Cell. Mech. 2016, 21, 264–274. [Google Scholar] [CrossRef]
- Meng, Q.J.; Maywood, E.S.; Bechtold, D.A.; Lu, W.Q.; Li, J.; Gibbs, J.E.; Dupré, S.M.; Chesham, J.E.; Rajamohan, F.; Knafels, J.; et al. Entrainment of disrupted circadian behavior through inhibition of casein kinase 1 (CK1) enzymes. Proc. Natl. Acad. Sci. USA 2010, 107, 15240–15245. [Google Scholar] [CrossRef] [PubMed]
- Helm, B.; Gwinner, E.; Koolhaas, A.; Battley, P.; Schwabl, I.; Dekinga, A.; Piersma, T. Avian migration: Temporal multitasking and a case study of melatonin cycles in waders. Prog. Brain Res. 2012, 199, 457–479. [Google Scholar] [CrossRef] [PubMed]
- Agostino, P.V.; Bussi, I.L.; Caldart, C.S.; Vatakis, A.; Balcı, F.; Di Luca, M.; Correa, Á. Circadian Timing: From Genetics to Behavior. In Timing and Time Perception: Procedures, Measures, & Applications; Brill: Leiden, The Netherlands, 2018; pp. 1–31. [Google Scholar] [CrossRef]
- Guideline. Guidelines for accomodation and care of animals (Article 5 of the Convention). In European Convention for the Protection of Vertebrate Animals Used for Experimental and Other Scientific Purposes (ETS N. 123); Council of Europe: Strasbourg, France, 2006. [Google Scholar]
- Guideline. National Research Council, Guide for the Care and Use of Laboratory Animals, 8th ed.; The National Academies Press: Washington, DC, USA, 2011; p. 248. [Google Scholar]
- Parker, V.; Morinan, A. The socially-isolated rat as a model for anxiety. Neuropharmacology 1986, 25, 663–664. [Google Scholar] [CrossRef]
- Goldsmith, J.F.; Brain, P.F.; Benton, D. Effects of the duration of individual or group housing on behavioural and adrenocortical reactivity in male mice. Physiol. Behav. 1978, 21, 757–760. [Google Scholar] [CrossRef]
- Weiss, I.C.; Pryce, C.R.; Jongen-Rêlo, A.L.; Nanz-Bahr, N.I.; Feldon, J. Effect of social isolation on stress-related behavioural and neuroendocrine state in the rat. Behav. Brain Res. 2004, 152, 279–295. [Google Scholar] [CrossRef]
- Clement, J.G.; Mills, P.; Brockway, B. Use of telemetry to record body temperature and activity in mice. J. Pharmacol. Methods 1989, 21, 129–140. [Google Scholar] [CrossRef]
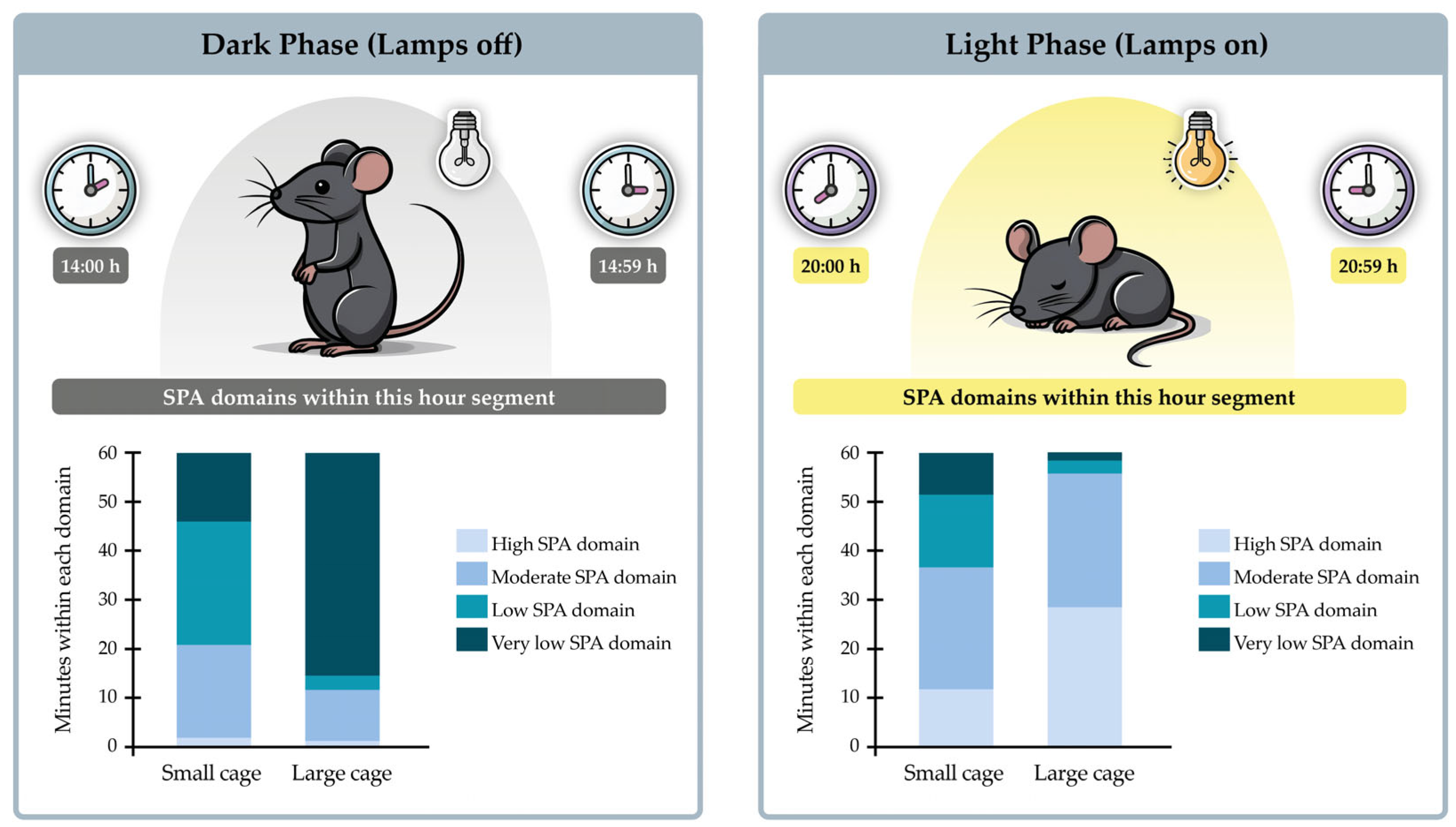
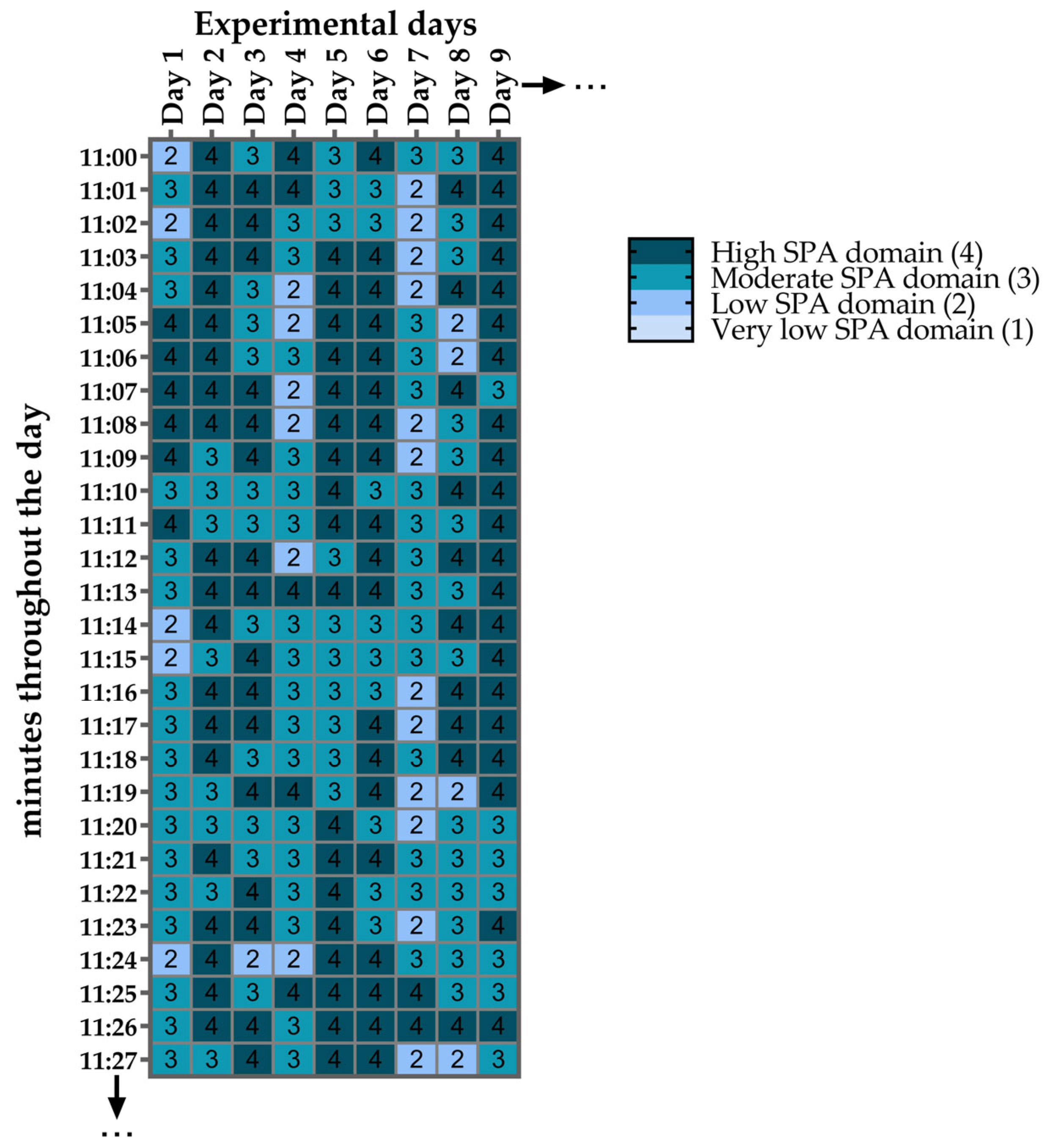

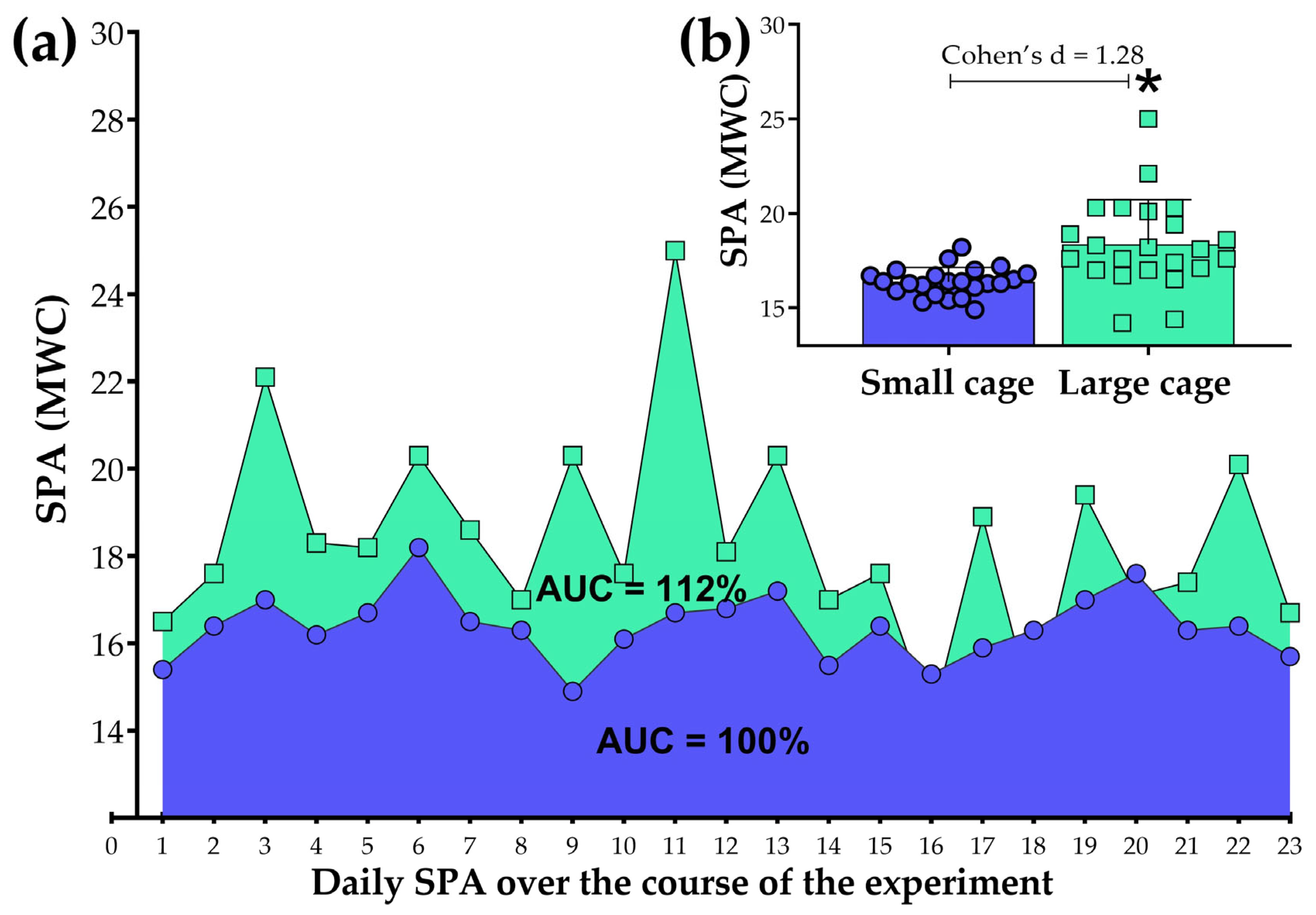
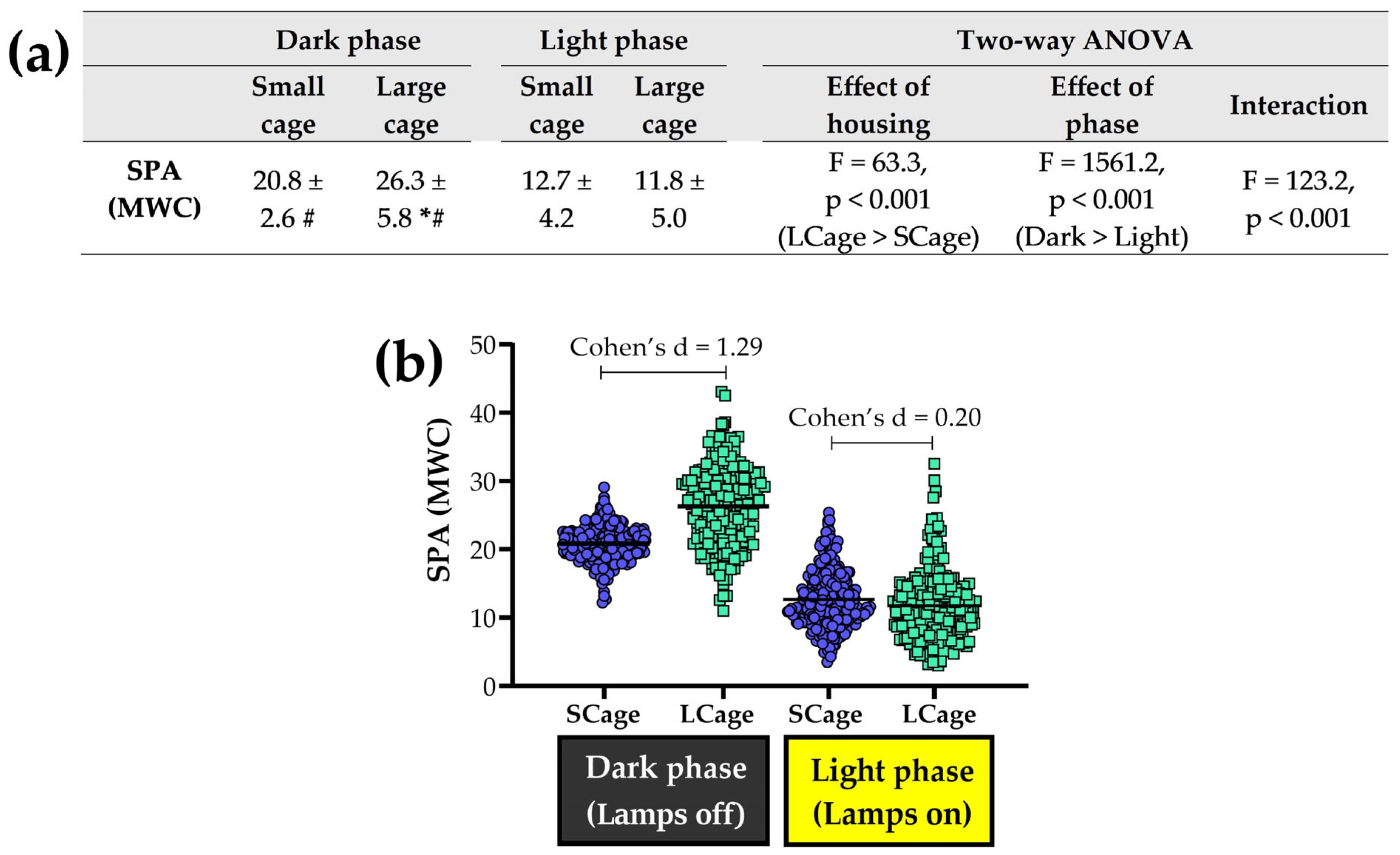

| Dark Phase | Light Phase | All Phases | ||||
|---|---|---|---|---|---|---|
| SCage | LCage | SCage | LCage | SCage | LCage | |
| SD-WC | 18.1 ± 2.6 | 23.1 ± 5.7 | 11.3 ± 3.6 | 10.1 ± 4.5 | 14.4 ± 4.6 | 16.0 ± 8.3 |
| Small Cage | Large Cage | |||||||
|---|---|---|---|---|---|---|---|---|
| VLSPAD | LSPAD | MSPAD | HSPAD | VLSPAD | LSPAD | MSPAD | HSPAD | |
| 11:00–11:59 | 0.1 ± 0.6 | 5.2 ± 6.0 | 27.5 ± 8.4 &¥ | 27.2 ± 13.4 &¥ | 0.0 ± 0.0 | 0.8 ± 1.2 | 8.6 ± 7.5 &¥$ | 50.7 ± 8.3 &¥£ |
| 12:00–12:59 | 0.0 ± 0.0 | 5.1 ± 4.7 & | 29.6 ± 6.4 &¥ | 25.3 ± 8.4 &¥ | 0.0 ± 0.0 | 2.3 ± 4.5 | 11.9 ± 9.9 &¥$ | 45.9 ± 13.3 &¥£ |
| 13:00–13:59 | 0.0 ± 0.0 | 5.2 ± 4.5 & | 32.7 ± 6.2 &¥ | 22.0 ± 7.5 &¥ | 0.0 ± 0.0 | 3.2 ± 4.4 | 13.0 ± 9.4 &¥$ | 43.8 ± 12.8 &¥£ |
| 14:00–14:59 | 0.1 ± 0.5 | 8.8 ± 8.0 & | 30.2 ± 6.8 &¥ | 20.9 ± 10.4 &¥ | 0.2 ± 0.5 | 7.8 ± 8.8 & | 18.0 ± 8.9 &¥ | 34.1 ± 14.6 &¥ |
| 15:00–15:59 | 1.0 ± 2.3 | 13.4 ± 7.7 & | 30.0 ± 7.2 &¥ | 15.5 ± 10.2 &£ | 1.8 ± 2.9 | 13.3 ± 11.1 & | 17.4 ± 7.2 & | 27.5 ± 17.0 & |
| 16:00–16:59 | 1.0 ± 0.9 | 17.3 ± 6.0 & | 31.7 ± 6.0 & | 9.9 ± 7.1 &£ | 2.8 ± 7.2 | 15.0 ± 10.6 & | 19.2 ± 8.5 & | 23.0 ± 16.7 & |
| 17:00–17:59 | 0.2 ± 0.7 | 10.5 ± 6.2 & | 32.7 ± 6.2 &¥ | 16.6 ± 8.1 &£ | 0.9 ± 3.2 | 7.7 ± 11.3 & | 16.1 ± 8.9 &$ | 35.3 ± 17.3 &¥£ |
| 18:00–18:59 | 0.2 ± 0.9 | 7.7 ± 7.1 & | 30.0 ± 6.5 &¥ | 22.0 ± 10.3 &¥ | 0.0 ± 0.0 | 4.3 ± 6.1 | 17.5 ± 10.6 & | 38.2 ± 15.1 &¥£ |
| 19:00–19:59 | 1.3 ± 3.2 | 11.6 ± 8.9 & | 27.3 ± 5.9 &¥ | 19.8 ± 10.8 & | 5.0 ± 7.4 | 19.5 ± 13.1 & | 19.7 ± 9.6 & | 15.8 ± 14.1 & |
| 20:00–20:59 | 15.4 ± 15.0 | 24.0 ± 9.4 | 16.0 ± 10.1 | 4.7 ± 6.1 &¥£ | 26.7 ± 19.8 | 18.6 ± 9.7 | 10.3 ± 10.4 | 4.4 ± 8.4 &¥ |
| 21:00–21:59 | 28.1 ± 16.0 | 22.7 ± 9.4 | 7.8 ± 7.1 &¥ | 1.4 ± 2.4 &¥ | 40.5 ± 18.4 | 14.1 ± 10.7 & | 4.2 ± 7.2 &¥ | 1.3 ± 3.1 &¥ |
| 22:00–22:59 | 29.0 ± 14.5 | 21.8 ± 8.4 | 7.9 ± 7.8 &¥ | 1.3 ± 3.3 &¥£ | 43.7 ± 15.4 | 13.3 ± 11.8 & | 2.6 ± 4.5 &¥ | 0.4 ± 0.9 &¥ |
| 23:00–23:59 | 29.8 ± 14.5 | 20.8 ± 8.1 | 7.5 ± 7.7 &¥ | 2.0 ± 4.6 &¥ | 36.3 ± 15.4 | 18.3 ± 11.5 & | 4.6 ± 6.1 &¥ | 0.8 ± 1.3 &¥ |
| 00:00–00:59 | 26.5 ± 15.9 | 23.7 ± 10.5 | 8.1 ± 7.0 &¥ | 1.8 ± 3.1 &¥ | 26.6 ± 15.8 | 20.9 ± 10.3 | 8.5 ± 7.2 &¥ | 4.0 ± 6.6 &¥ |
| 01:00–01:59 | 24.9 ± 16.0 | 21.2 ± 8.2 | 11.1 ± 9.7 | 2.8 ± 3.9 &¥£ | 34.7 ± 15.8 | 19.3 ± 11.8 | 4.2 ± 4.7 &¥ | 1.7 ± 5.0 &¥ |
| 02:00–02:59 | 24.7 ± 15.2 | 23.7 ± 9.5 | 9.4 ± 8.3 &¥ | 2.2 ± 4.5 &¥£ | 34.0 ± 17.4 | 18.0 ± 10.9 | 7.0 ± 7.8 &¥ | 1.1 ± 1.9 &¥ |
| 03:00–03:59 | 25.8 ± 17.6 | 20.6 ± 8.4 | 11.6 ± 10.7 | 2.0 ± 2.6 &¥£ | 36.3 ± 14.8 | 18.5 ± 10.7 | 4.4 ± 4.9 &¥ | 0.8 ± 1.4 &¥ |
| 04:00–04:59 | 20.3 ± 13.3 | 24.9 ± 7.8 | 12.6 ± 9.9 | 2.1 ± 2.3 &¥£ | 30.1 ± 14.7 | 20.7 ± 9.0 | 6.9 ± 6.2 &¥ | 2.3 ± 2.8 &¥ |
| 05:00–05:59 | 26.4 ± 12.9 | 25.4 ± 9.4 | 7.4 ± 5.6 &¥ | 0.7 ± 1.2 &¥£ | 24.1 ± 16.2 | 24.7 ± 10.4 | 8.6 ± 7.3 &¥ | 2.7 ± 7.5 &¥ |
| 06:00–06:59 | 29.4 ± 14.3 | 22.4 ± 9.1 | 7.3 ± 7.4 &¥ | 0.8 ± 1.4 &¥£ | 20.0 ± 15.5 | 24.2 ± 11.0 | 10.7 ± 7.0 ¥ | 5.1 ± 7.5 &¥ |
| 07:00–07:59 | 7.9 ± 9.4 | 18.0 ± 7.7 & | 22.4 ± 8.1 & | 11.7 ± 8.0 | 2.8 ± 4.5 | 10.9 ± 8.7 | 15.7 ± 8.2 & | 30.6 ± 15.1 &¥$ |
| 08:00–08:59 | 0.6 ± 1.4 | 8.1 ± 9.6 & | 19.8 ± 11.0 &¥ | 31.6 ± 18.5 &¥ | 0.8 ± 4.0 | 2.7 ± 6.1 | 10.1 ± 8.5 &¥ | 46.4 ± 15.2 &¥£ |
| Dark Phase | ||||||||
|---|---|---|---|---|---|---|---|---|
| Small Cage | Large Cage | |||||||
| Day | VLSPAD | LSPAD | MSPAD | HSPAD | VLSPAD | LSPAD | MSPAD | HSPAD |
| 1st | 7 (1%) | 156 (26%) | 283 (47%) | 154 (26%) | 7 (1%) | 100 (17%) | 172 (29%) | 321 (54%) |
| 2nd | 2 (0%) | 107 (18%) | 269 (45%) | 222 (37%) | 5 (1%) | 64 (11%) | 141 (24%) | 390 (65%) |
| 3rd | 3 (1%) | 79 (13%) | 234 (39%) | 284 (47%) | 10 (2%) | 35 (6%) | 62 (10%) | 493 (82%) |
| 4th | 7 (1%) | 113 (19%) | 282 (47%) | 198 (33%) | 18 (3%) | 59 (10%) | 163 (27%) | 360 (60%) |
| 5th | 4 (1%) | 99 (17%) | 298 (50%) | 199 (33%) | 7 (1%) | 88 (15%) | 128 (21%) | 377 (63%) |
| 6th | 11 (2%) | 78 (13%) | 242 (40%) | 269 (45%) | 2 (0.3%) | 32 (5%) | 103 (17%) | 463 (77%) |
| 7th | 7 (1%) | 85 (14%) | 276 (46%) | 232 (39%) | 5 (1%) | 31 (5%) | 112 (19%) | 452 (75%) |
| 8th | 27 (5%) | 105 (18%) | 219 (37%) | 249 (42%) | 0 (0%) | 54 (9%) | 187 (31%) | 359 (60%) |
| 9th | 36 (6%) | 98 (16%) | 258 (43%) | 208 (35%) | 3 (1%) | 48 (8%) | 106 (18%) | 443 (74%) |
| 10th | 27 (5%) | 76 (13%) | 243 (41%) | 254 (42%) | 2 (0.3%) | 64 (11%) | 173 (29%) | 361 (60%) |
| 11th | 1 (0.2%) | 118 (20%) | 303 (51%) | 178 (30%) | 0 (0%) | 4 (1%) | 56 (9%) | 540 (90%) |
| 12th | 20 (3%) | 69 (12%) | 269 (45%) | 242 (40%) | 7 (1%) | 65 (11%) | 118 (20%) | 410 (68%) |
| 13th | 0 (0%) | 67 (11%) | 307 (51%) | 226 (38%) | 0 (0%) | 12 (2%) | 65 (11%) | 523 (87%) |
| 14th | 8 (1%) | 132 (22%) | 331 (55%) | 129 (22%) | 2 (0.3%) | 86 (14%) | 208 (35%) | 304 (51%) |
| 15th | 32 (5%) | 65 (11%) | 296 (49%) | 207 (35%) | 12 (2%) | 56 (9%) | 123 (21%) | 409 (68%) |
| 16th | 9 (2%) | 107 (18%) | 341 (57%) | 143 (24%) | 24 (4%) | 182 (30%) | 234 (39%) | 160 (27%) |
| 17th | 4 (1%) | 117 (20%) | 297 (50%) | 182 (30%) | 0 (0%) | 50 (8%) | 162 (27%) | 388 (65%) |
| 18th | 2 (0.3%) | 89 (15%) | 322 (54%) | 187 (31%) | 24 (4%) | 168 (28%) | 211 (35%) | 197 (33%) |
| 19th | 6 (1%) | 127 (21%) | 301 (50%) | 166 (28%) | 4 (1%) | 57 (10%) | 185 (31%) | 354 (59%) |
| 20th | 7 (1%) | 84 (14%) | 308 (51%) | 201 (34%) | 7 (1%) | 66 (11%) | 195 (33%) | 332 (55%) |
| 21th | 8 (1%) | 102 (17%) | 329 (55%) | 161 (27%) | 50 (8%) | 96 (16%) | 165 (28%) | 289 (48%) |
| 22th | 24 (4%) | 81 (14%) | 268 (45%) | 227 (38%) | 0 (0%) | 29 (5%) | 139 (23%) | 432 (72%) |
| 23th | 4 (1%) | 131 (22%) | 321 (54%) | 144 (24%) | 24 (4%) | 115 (19%) | 182 (30%) | 279 (47%) |
| Overall average | 11 ± 11 | 99 ± 24 & | 287 ± 33 &¥ | 203 ± 42 &¥£ | 9 ± 12 | 68 ± 43 & | 147 ± 49 *&¥ | 375 ± 94 *&¥£ |
| Light Phase | ||||||||
|---|---|---|---|---|---|---|---|---|
| Small Cage | Large Cage | |||||||
| Day | VLSPAD | LSPAD | MSPAD | HSPAD | VLSPAD | LSPAD | MSPAD | HSPAD |
| 1st | 359 (50%) | 256 (36%) | 82 (11%) | 23 (3%) | 404 (56%) | 223 (31%) | 62 (9%) | 31 (4%) |
| 2nd | 340 (47%) | 223 (31%) | 111 (15%) | 46 (6%) | 378 (53%) | 242 (34%) | 80 (11%) | 20 (3%) |
| 3rd | 343 (48%) | 216 (30%) | 96 (13%) | 65 (9%) | 298 (41%) | 211 (29%) | 136 (19%) | 75 (10%) |
| 4th | 317 (44%) | 255 (35%) | 103 (14%) | 45 (6%) | 308 (43%) | 262 (36%) | 126 (18%) | 24 (3%) |
| 5th | 237 (33%) | 310 (43%) | 136 (19%) | 37 (5%) | 409 (57%) | 224 (31%) | 60 (8%) | 27 (4%) |
| 6th | 224 (31%) | 204 (28%) | 176 (24%) | 116 (16%) | 291 (40%) | 259 (36%) | 93 (13%) | 77 (11%) |
| 7th | 308 (43%) | 248 (34%) | 135 (19%) | 29 (4%) | 436 (61%) | 204 (28%) | 55 (8%) | 25 (3%) |
| 8th | 325 (45%) | 253 (35%) | 99 (14%) | 43 (6%) | 405 (56%) | 233 (32%) | 64 (9%) | 18 (3%) |
| 9th | 399 (55%) | 202 (28%) | 87 (12%) | 32 (4%) | 308 (43%) | 295 (41%) | 98 (14%) | 19 (3%) |
| 10th | 330 (46%) | 224 (31%) | 127 (18%) | 39 (5%) | 330 (46%) | 278 (39%) | 93 (13%) | 19 (3%) |
| 11th | 240 (33%) | 288 (40%) | 138 (19%) | 54 (8%) | 241 (33%) | 144 (20%) | 126 (18%) | 209 (29%) |
| 12th | 237 (33%) | 285 (40%) | 156 (22%) | 42 (6%) | 430 (60%) | 178 (25%) | 86 (12%) | 26 (4%) |
| 13th | 233 (32%) | 283 (39%) | 145 (20%) | 59 (8%) | 430 (60%) | 174 (24%) | 90 (13%) | 26 (4%) |
| 14th | 306 (43%) | 225 (31%) | 145 (20%) | 44 (6%) | 352 (49%) | 244 (34%) | 101 (14%) | 23 (3%) |
| 15th | 243 (34%) | 320 (44%) | 128 (18%) | 29 (4%) | 432 (60%) | 218 (30%) | 52 (7%) | 18 (3%) |
| 16th | 334 (46%) | 231 (32%) | 127 (18%) | 28 (4%) | 424 (59%) | 246 (34%) | 44 (6%) | 6 (1%) |
| 17th | 323 (45%) | 244 (34%) | 111 (15%) | 42 (6%) | 347 (48%) | 238 (33%) | 97 (13%) | 38 (5%) |
| 18th | 238 (33%) | 319 (44%) | 145 (20%) | 18 (3%) | 477 (66%) | 209 (29%) | 23 (3%) | 11 (2%) |
| 19th | 170 (24%) | 350 (49%) | 166 (23%) | 34 (5%) | 253 (35%) | 248 (34%) | 172 (24%) | 47 (7%) |
| 20th | 156 (22%) | 334 (46%) | 183 (25%) | 47 (7%) | 374 (52%) | 178 (25%) | 115 (16%) | 53 (7%) |
| 21th | 252 (35%) | 244 (34%) | 179 (25%) | 45 (6%) | 234 (33%) | 320 (44%) | 131 (18%) | 35 (5%) |
| 22th | 251 (35%) | 276 (38%) | 174 (24%) | 19 (3%) | 303 (42%) | 234 (33%) | 117 (16%) | 66 (9%) |
| 23th | 314 (44%) | 252 (35%) | 134 (19%) | 20 (3%) | 368 (51%) | 230 (32%) | 89 (12%) | 33 (5%) |
| Overall average | 282 ± 62 | 263 ± 42 | 134 ± 30 &¥ | 42 ± 20 &¥£ | 358 ± 69 * | 230 ± 40 & | 92 ± 35 *&¥ | 40 ± 41 &¥£ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scariot, P.P.M.; dos Reis, I.G.M.; Monteiro, W.A.P.; dos Reis, M.C.; Bertolucci, V.; Manchado-Gobatto, F.B.; Gobatto, C.A.; Messias, L.H.D. Exploring New Ways to Analyze Data on the Spontaneous Physical Activity of Rodents Through a Weighing Balance. Sensors 2025, 25, 3290. https://doi.org/10.3390/s25113290
Scariot PPM, dos Reis IGM, Monteiro WAP, dos Reis MC, Bertolucci V, Manchado-Gobatto FB, Gobatto CA, Messias LHD. Exploring New Ways to Analyze Data on the Spontaneous Physical Activity of Rodents Through a Weighing Balance. Sensors. 2025; 25(11):3290. https://doi.org/10.3390/s25113290
Chicago/Turabian StyleScariot, Pedro Paulo Menezes, Ivan Gustavo Masselli dos Reis, Walter Aparecido Pimentel Monteiro, Maria Clara dos Reis, Vanessa Bertolucci, Fulvia Barros Manchado-Gobatto, Claudio Alexandre Gobatto, and Leonardo Henrique Dalcheco Messias. 2025. "Exploring New Ways to Analyze Data on the Spontaneous Physical Activity of Rodents Through a Weighing Balance" Sensors 25, no. 11: 3290. https://doi.org/10.3390/s25113290
APA StyleScariot, P. P. M., dos Reis, I. G. M., Monteiro, W. A. P., dos Reis, M. C., Bertolucci, V., Manchado-Gobatto, F. B., Gobatto, C. A., & Messias, L. H. D. (2025). Exploring New Ways to Analyze Data on the Spontaneous Physical Activity of Rodents Through a Weighing Balance. Sensors, 25(11), 3290. https://doi.org/10.3390/s25113290









