Preparation and Performance of a Grid-Based PCL/TPU@MWCNTs Nanofiber Membrane for Pressure Sensor
Abstract
1. Introduction
2. Mechanical Simulation of the Nanofibre Membrane
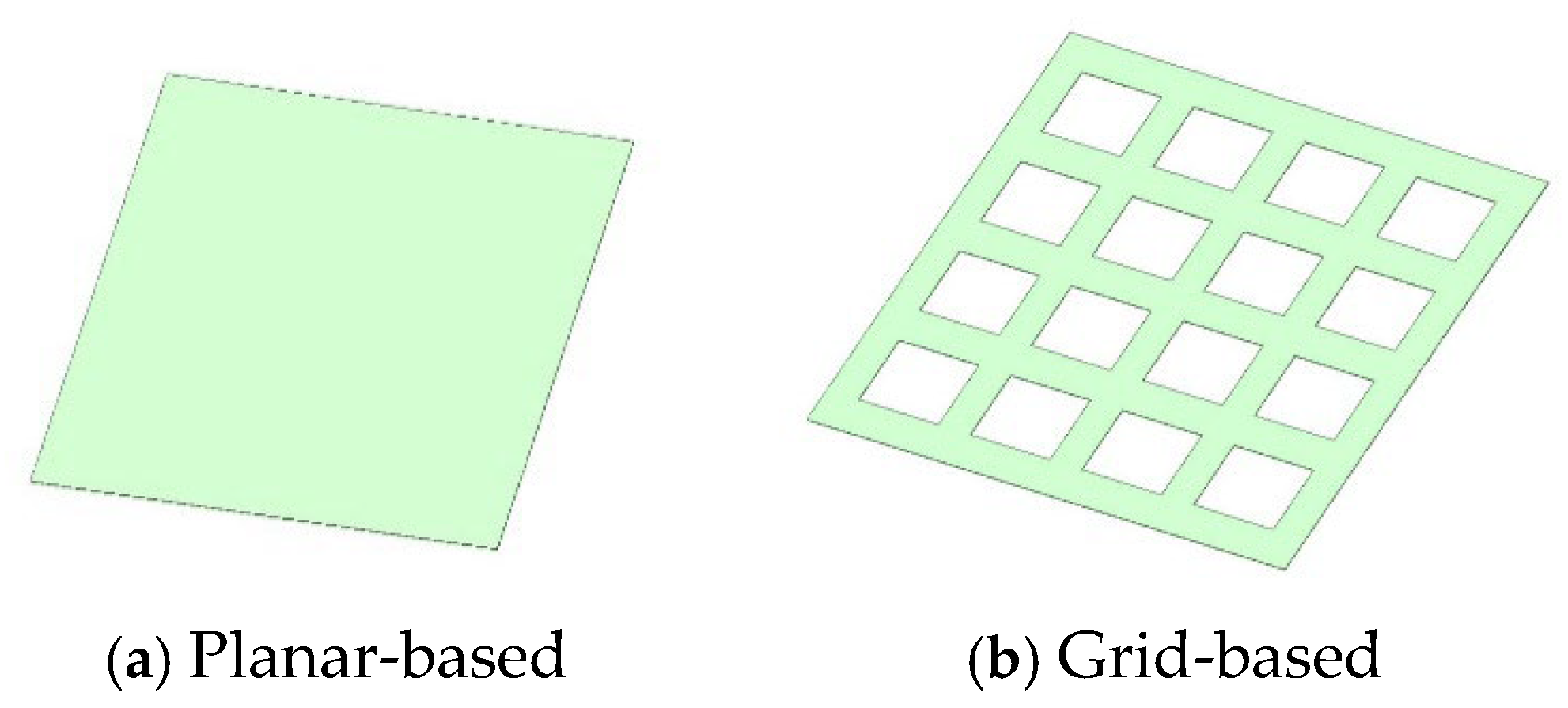
2.1. Model Construction and Parameter Settings
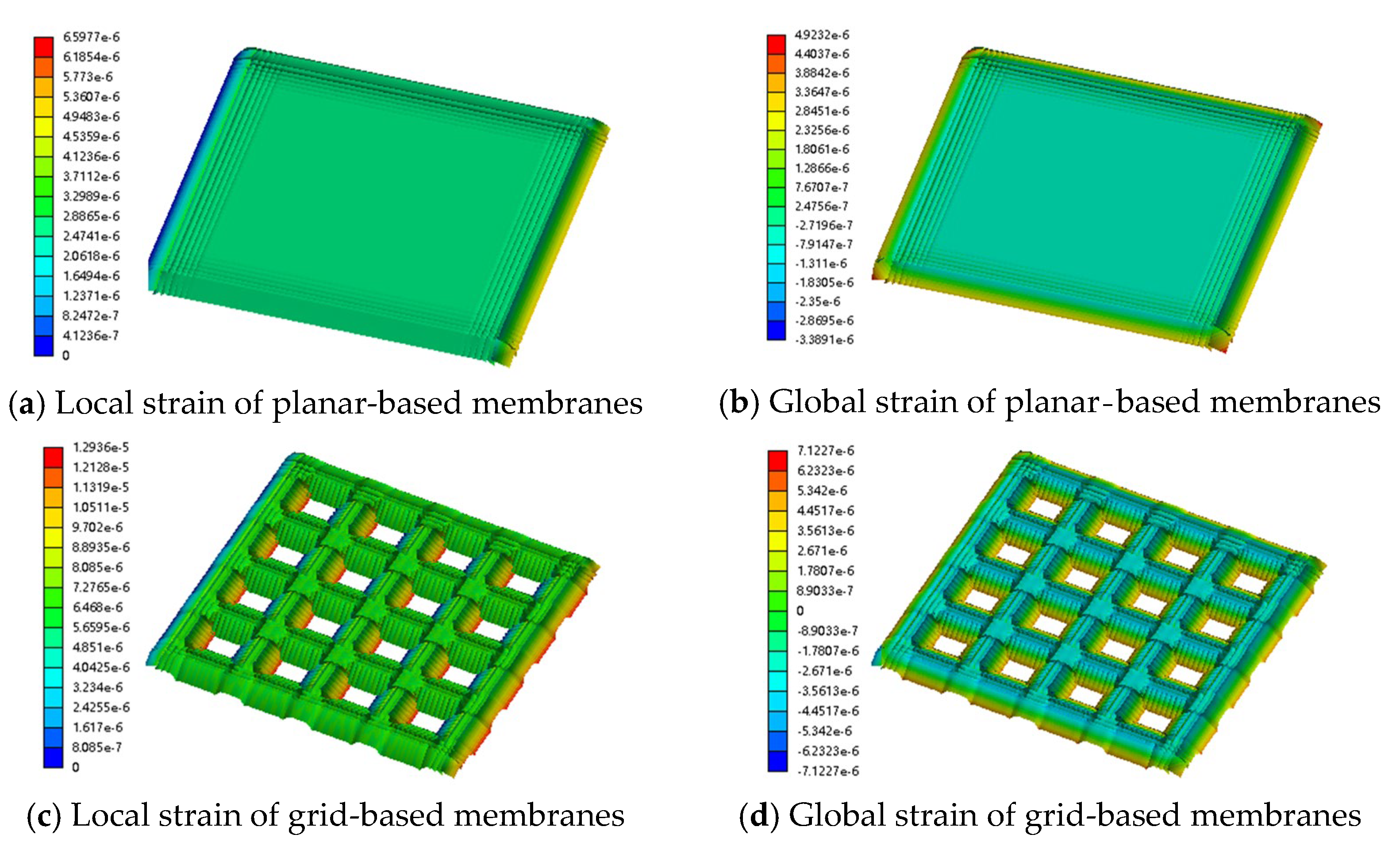
2.2. Stress Distribution Mechanism and Sensitivity Performance Analysis
3. Fabrication and Measurement of the PCL/TPU@MWCNTs Nanofiber-Based Pressure Sensor
3.1. Preparation of PCL/TPU@MWCNTs Nanofiber Membrane
3.1.1. Dispersion of MWCNT
3.1.2. Fabrication of the PCL/TPU@MWCNT Nanofibre Membrane and Assembly of the Pressure Sensor
3.2. Testing Methods
4. Test Results
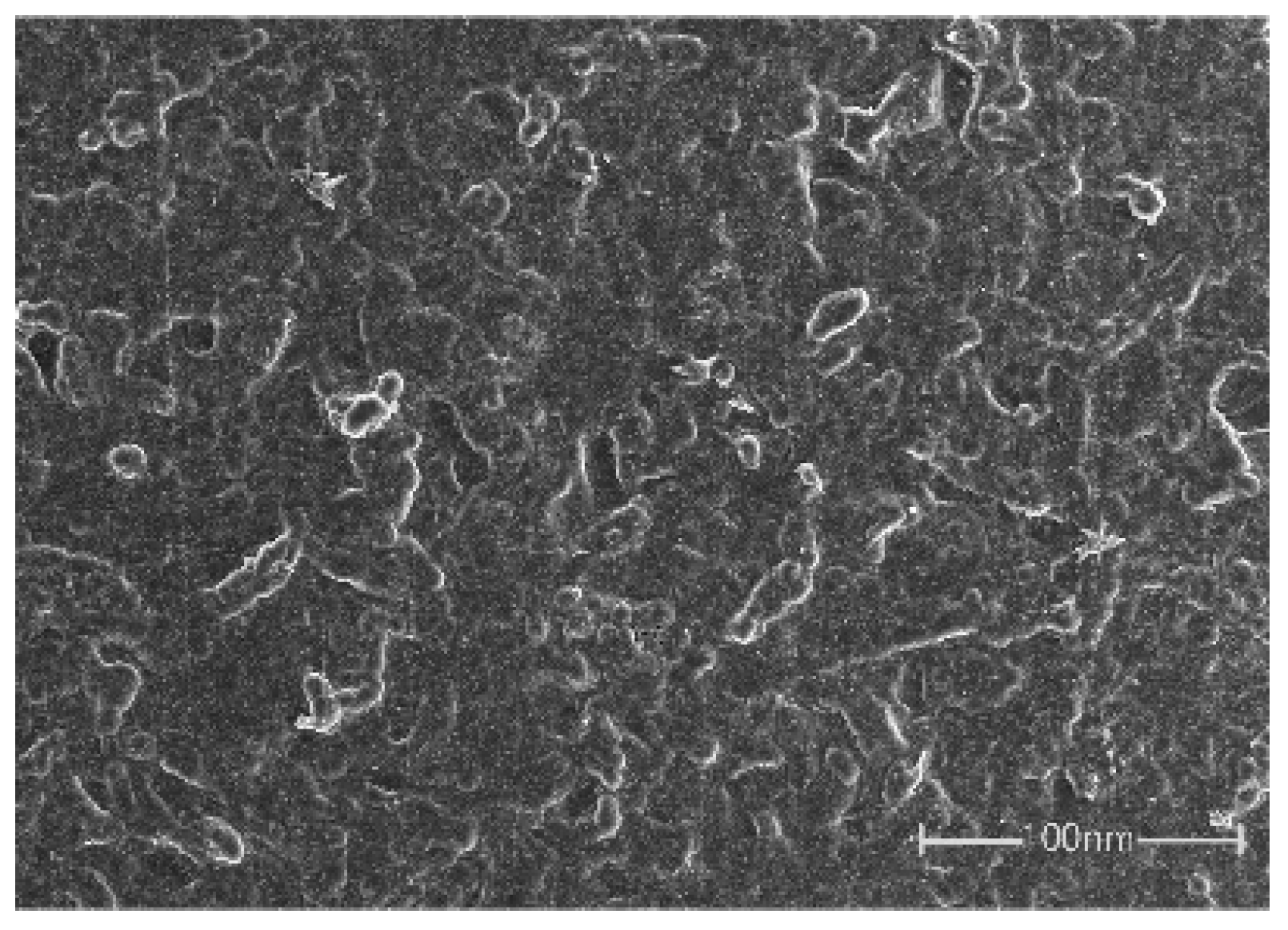
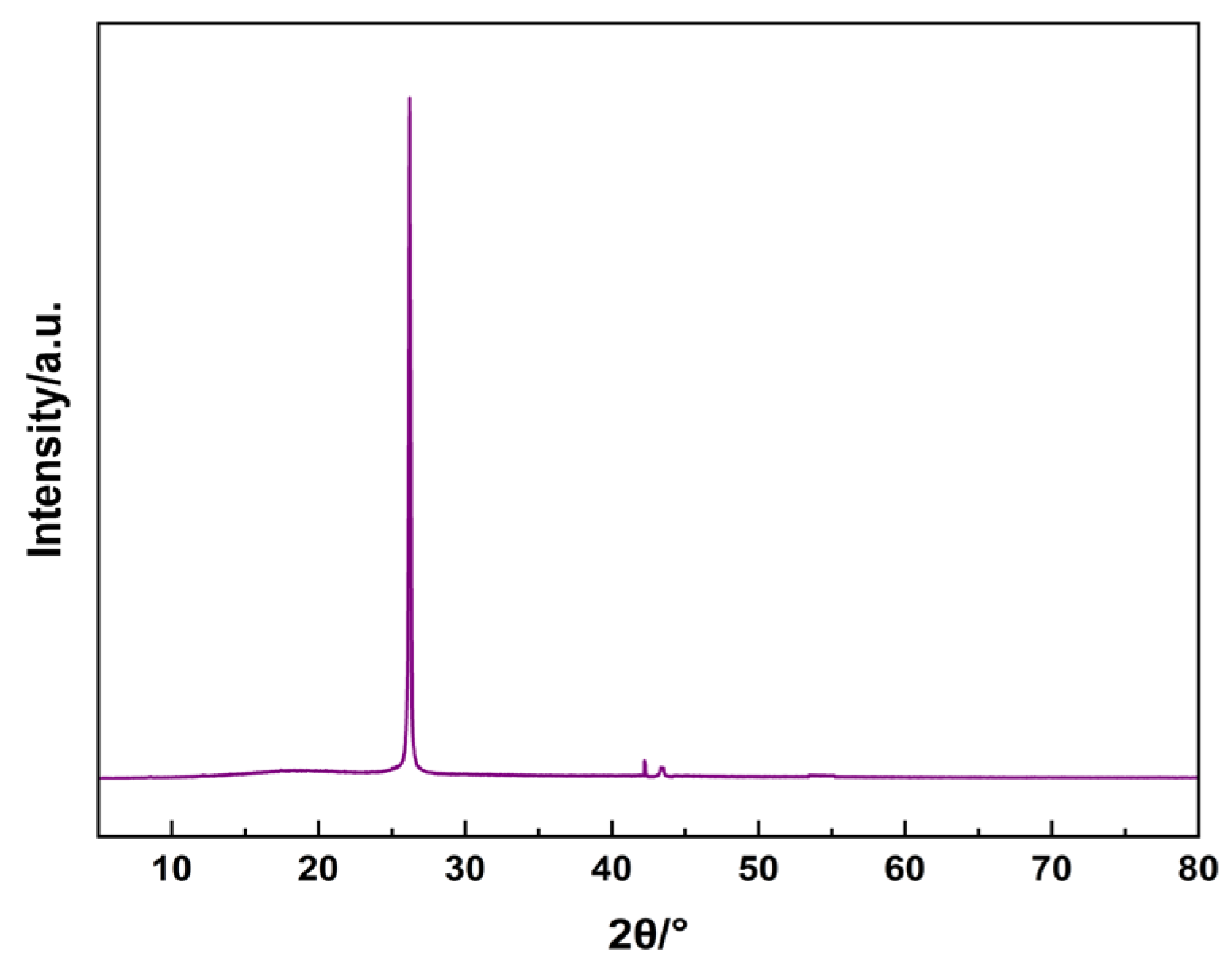
4.1. SEM and XRD of Membranes
4.2. Mechanical Response Analysis
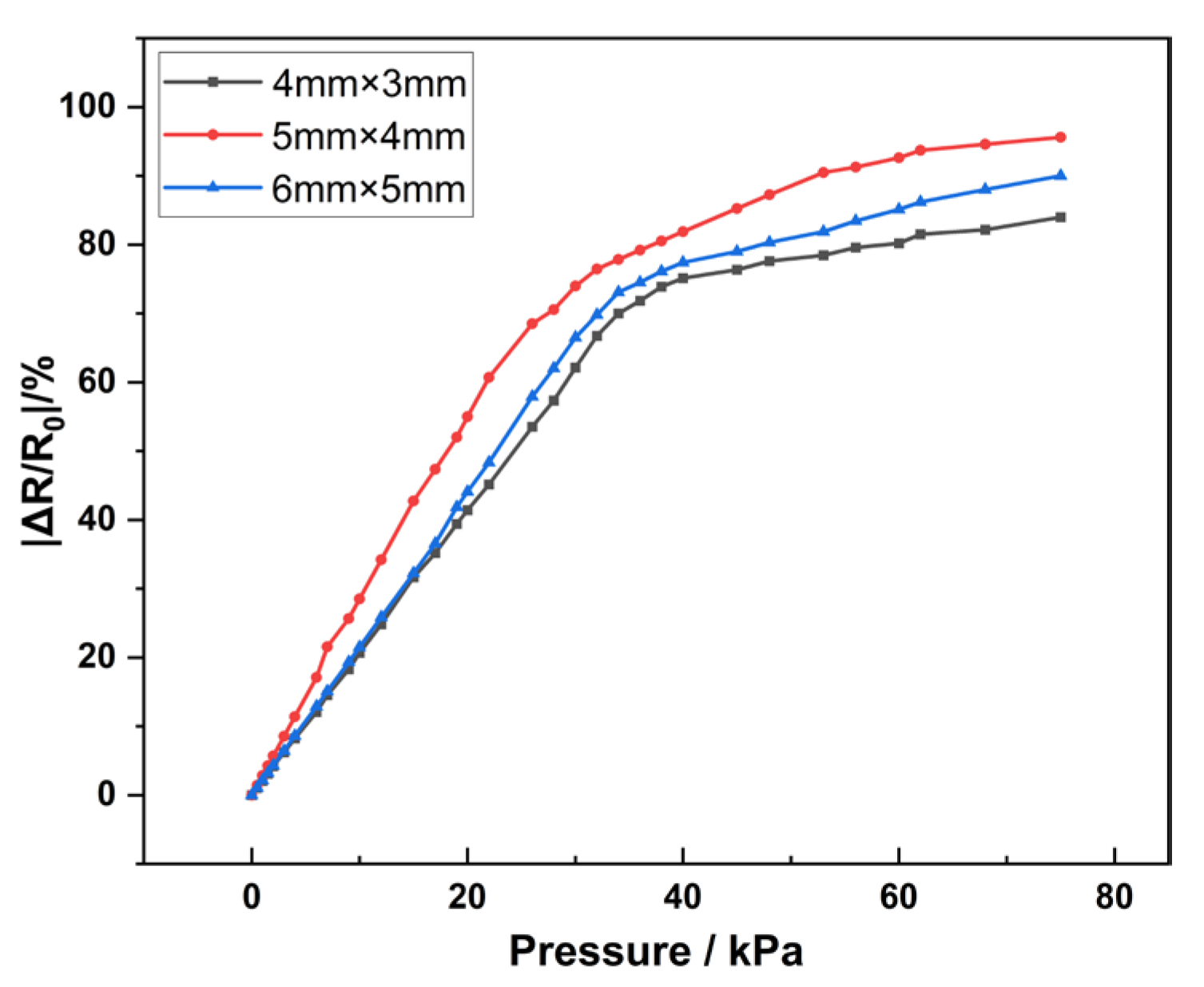
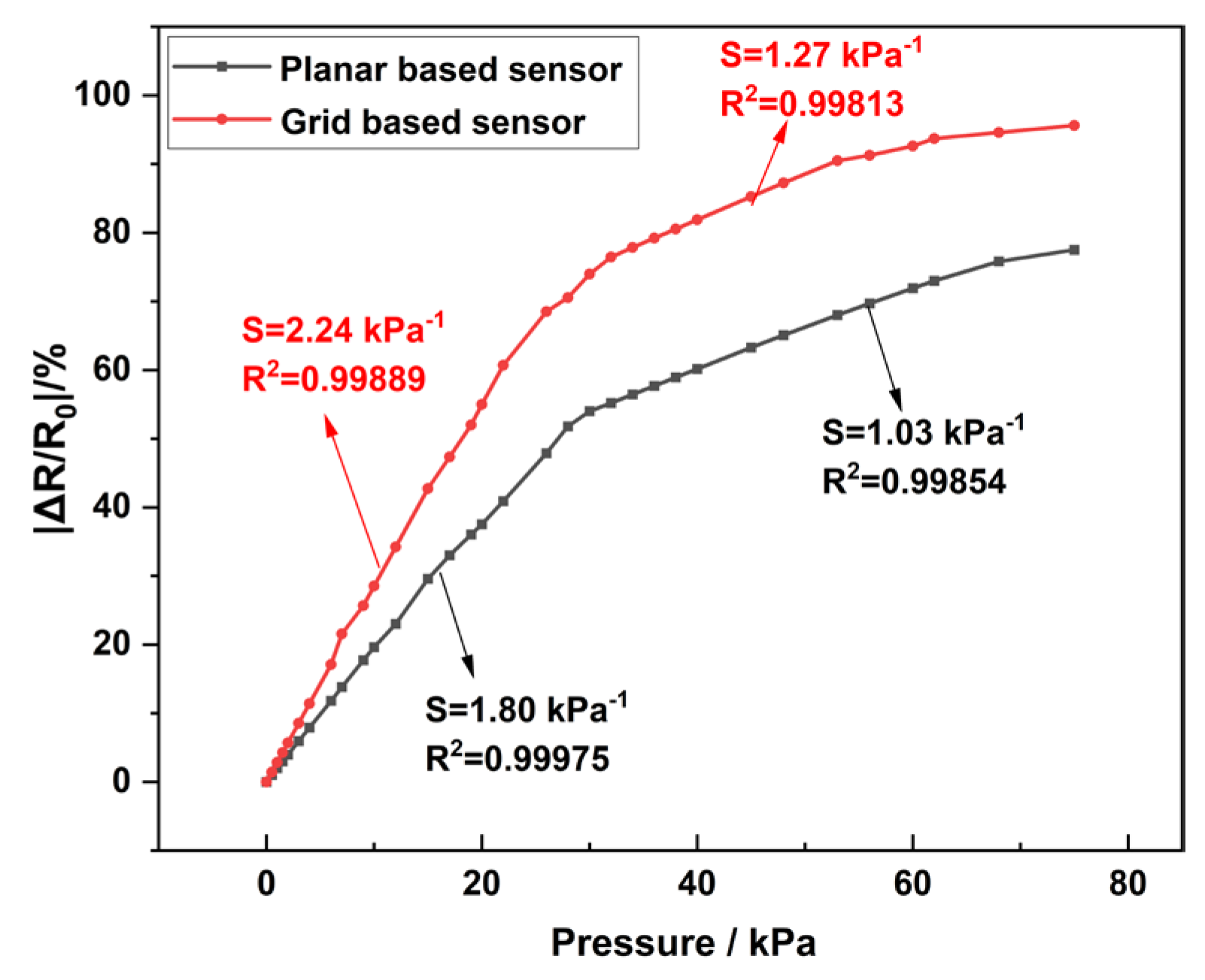
4.3. Sensitivity Analysis
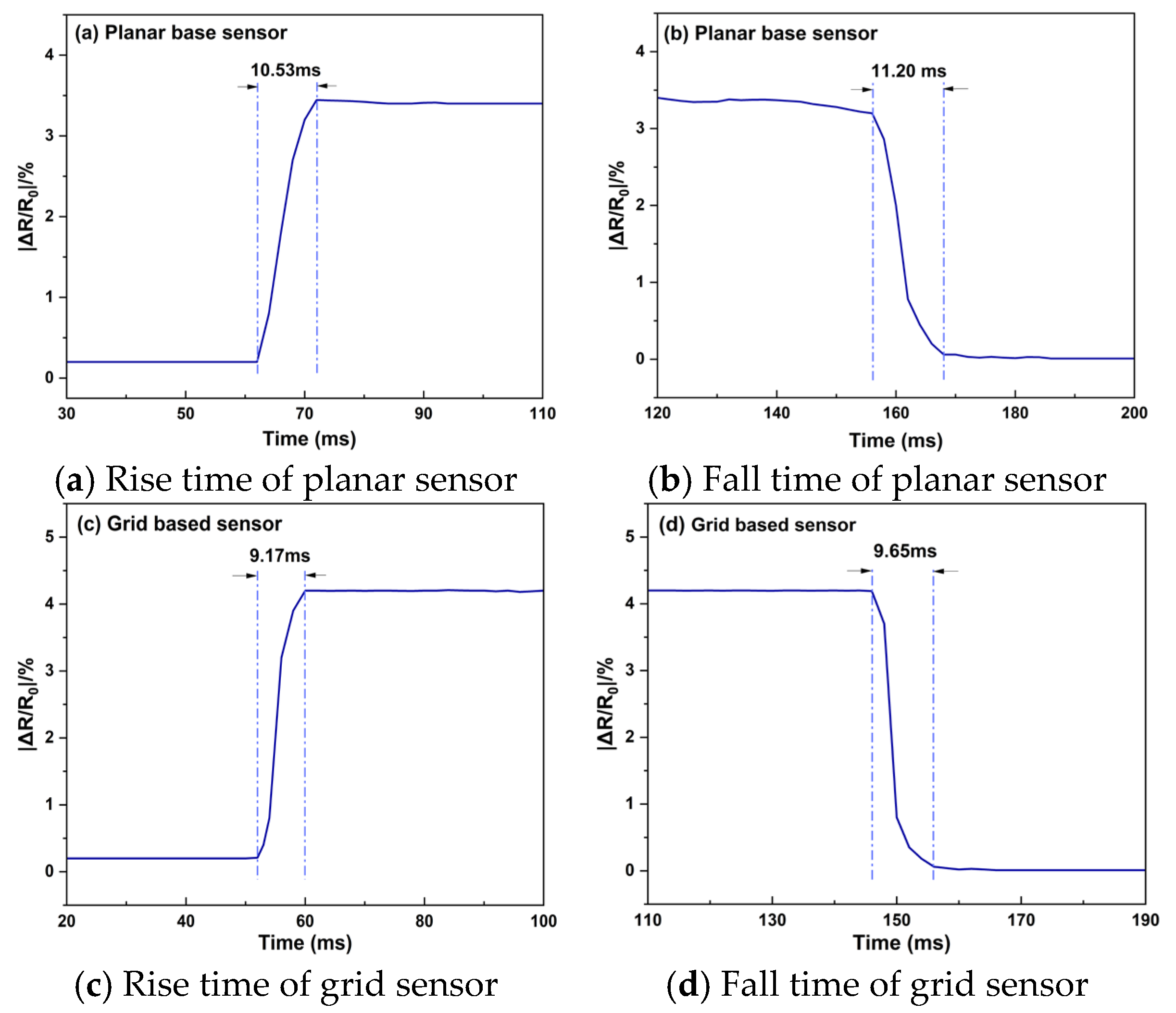
4.4. Output-Response Analysis
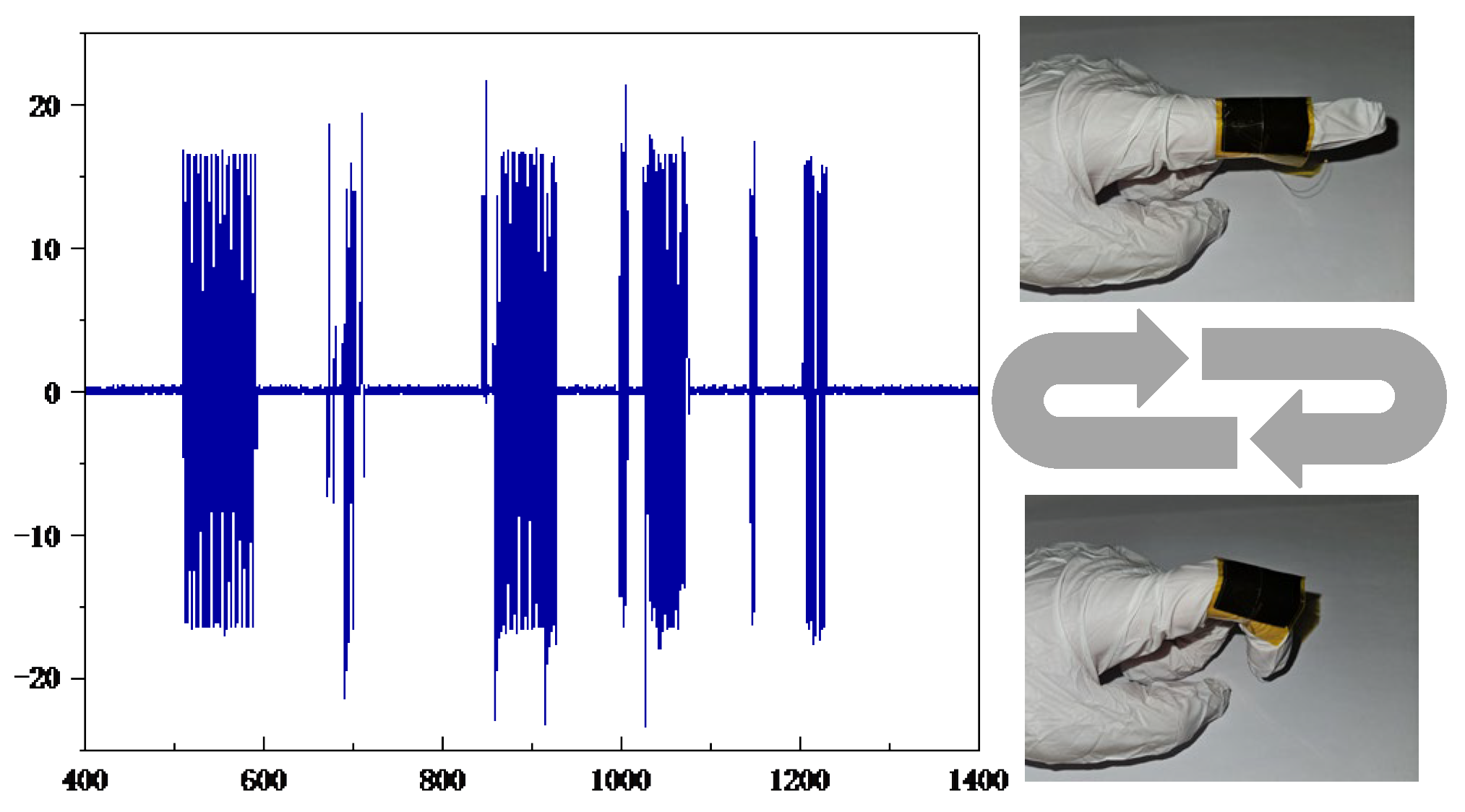
4.5. Index Finger Simple Motion Analysis
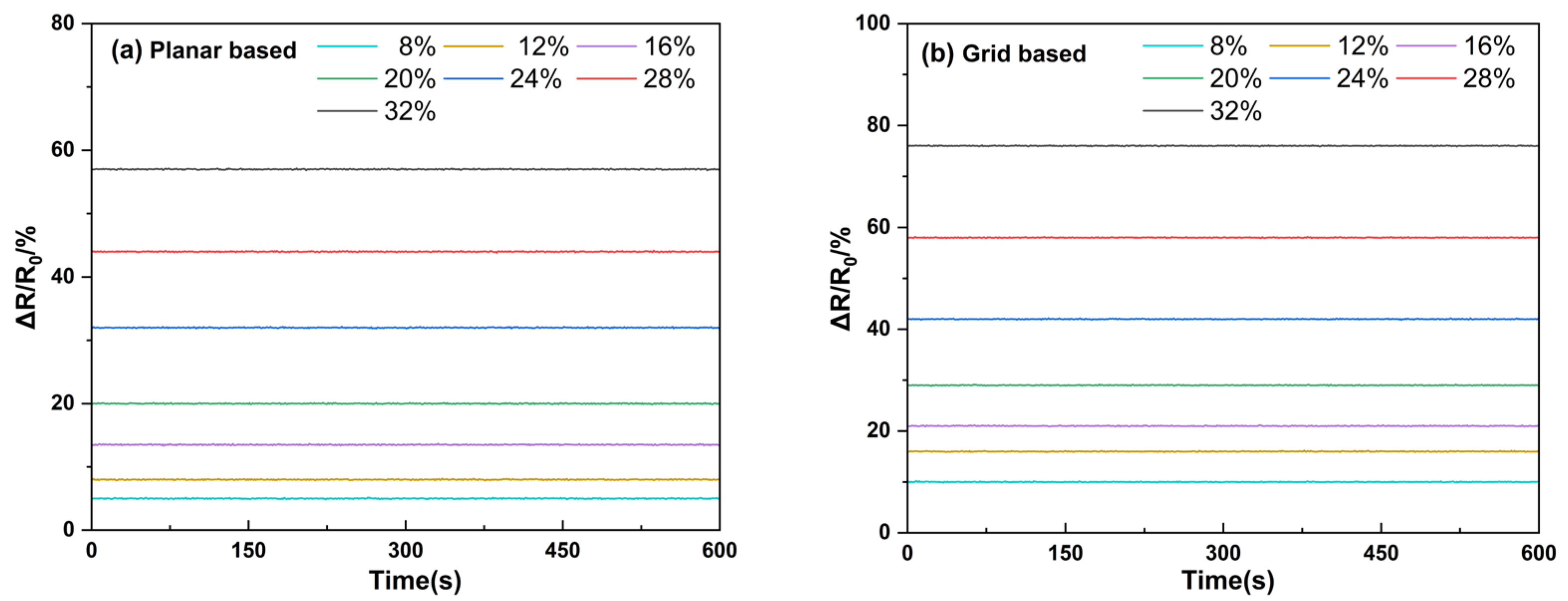
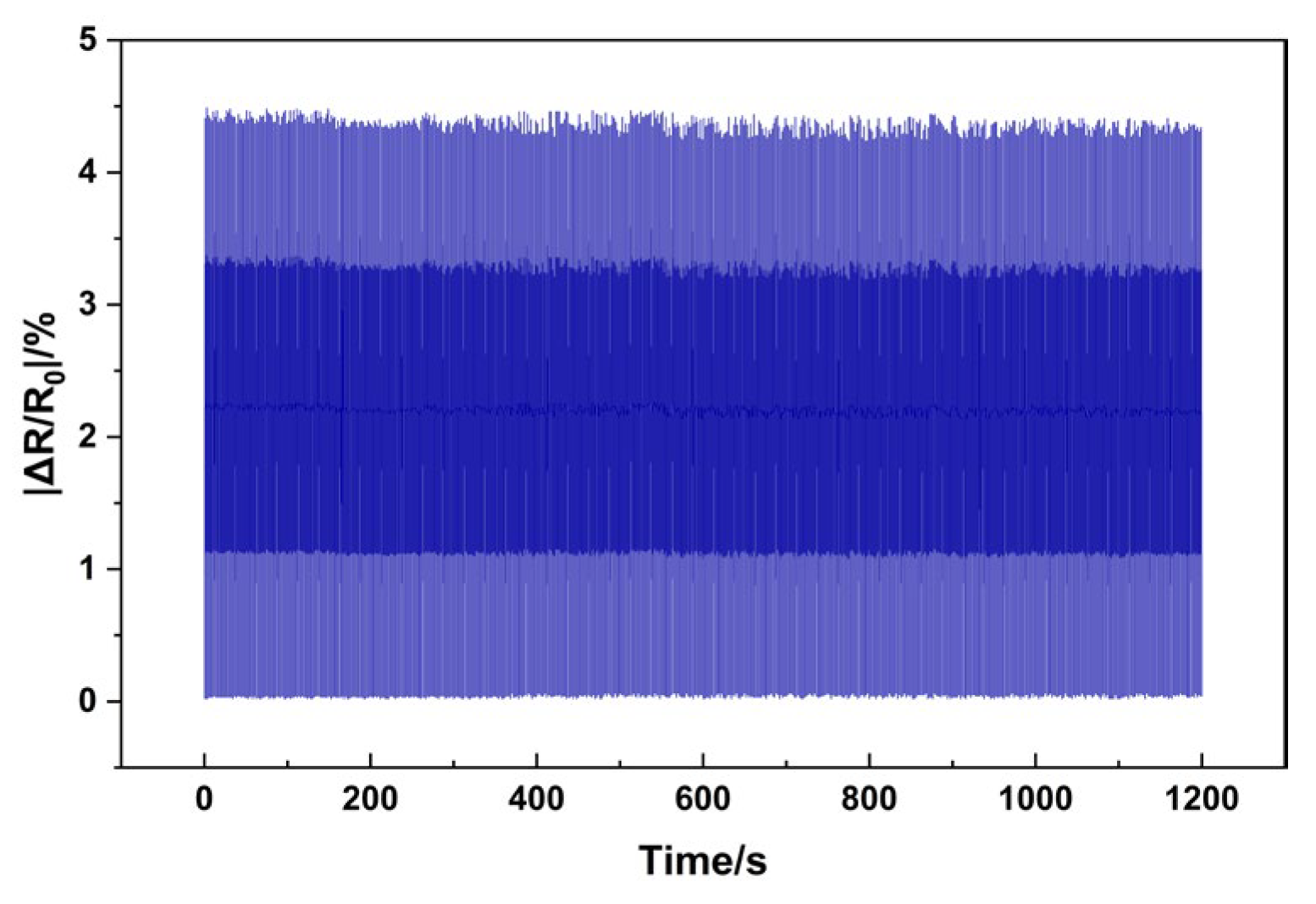
4.6. Cycling Stability of the Grid Sensor
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, X.; Chen, T.; Gong, D.; Ma, P.; Chen, B.; Cai, J. Skin-inspired interface modification strategy toward a structure-function integrated hybrid smart fabric system with self-powered sensing property for versatile applications. Nano Res. 2024, 17, 8200–8208. [Google Scholar] [CrossRef]
- Mahmud, M.P.; Tat, T.; Xiao, X.; Adhikary, P.; Chen, J. Advances in 4D-printed physiological monitoring sensors. Exploration 2021, 1, 20210033. [Google Scholar] [CrossRef]
- Xiao, W.; Lu, L.; Xu, Z.; Huang, Y.; Zhuang, Q.; Qian, X.; Liu, X.; Zhou, H.; Zhang, Y.; Yang, Y.; et al. A superelastic ceramic aerogel for flexible pressure sensor in harsh environment. Compos. Part B Eng. 2025, 292, 112110. [Google Scholar] [CrossRef]
- Lin, Q.; Shi, Q.; Fu, J.; Zhang, W.; Liu, Q.; Wu, Y. A flexible wearable sensor based on improving the piezoelectric layer performance of sandwich structures with micro-/mesopores for communication with the deaf-mute. J. Alloys Compd. 2025, 1010, 177646. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, W.; Wen, Y.; Zhao, J.; Chen, C.; Chen, Z.; Zhang, X.S. Wearable, washable piezoresistive pressure sensor based on polyurethane sponge coated with composite CNT/CB/TPU. Mater. Today Phys. 2025, 52, 101681. [Google Scholar] [CrossRef]
- Zhuang, Y.; Guo, Y.; Li, J.; Yu, Y.; Jiang, K.; Zhang, H.; Guo, S. Study on the forming and sensing properties of laser-sintered TPU/CNT composites for plantar pressure sensors. Int. J. Adv. Manuf. Technol. 2021, 112, 2211–2222. [Google Scholar] [CrossRef]
- Ryspayeva, A.; Jones, T.D.; Esfahani, M.N.; Shuttleworth, M.P.; Harris, R.A.; Kay, R.W.; Desmulliez, M.P.; Marques-Hueso, J. A rapid technique for the direct metallization of PDMS substrates for flexible and stretchable electronics applications. Microelectron. Eng. 2019, 209, 35–40. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Wu, Z.K.; Bai, S.L. Study on thermal properties of graphene foam/graphene sheets filled polymer composites. Compos. Part A Appl. Sci. Manuf. 2015, 72, 200–206. [Google Scholar] [CrossRef]
- Guo, Y.; Zeng, S.; Liu, Q.; Sun, J.; Zhu, M.; Li, L.; Deng, T. Review of the pressure sensor based on graphene and its derivatives. Microelectron. Eng. 2024, 288, 112167. [Google Scholar] [CrossRef]
- Mackin, C.; Fasoli, A.; Xue, M.; Lin, Y.; Adebiyi, A.; Bozano, L.; Palacios, T. Chemical sensor systems based on 2D and thin film materials. 2D Mater. 2020, 7, 022002. [Google Scholar] [CrossRef]
- Chen, J.; Song, T.; Wang, X.; Zhou, Y.; Wang, T.; Zhang, X.; Zhao, Y.; Yang, B.; Zhang, Y.; Chen, J.; et al. Ultrasensitive and wide-range MXene/PDMS piezoresistive sensors inspired by rose petals. Nano Energy 2024, 131, 110285. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, X.; Hu, Z.; Sun, Q.; Liu, M.; Gu, P.; Yang, X.; Huang, J.; Zu, G. Highly sensitive broad-range battery-type all-in-one self-powered stretchable pressure sensors based on porous electrodes. Mater. Chem. 2023, 1, 1–30. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, M.; Du, W.; Zhou, C.; Xiao, Y.; Zhang, S.; Chan, M. Sensing-range-tunable pressure sensors realized by self-patterned-spacer design and vertical CNT arrays embedded in PDMS. RSC Adv. 2020, 10, 33558–33565. [Google Scholar] [CrossRef] [PubMed]
- Niu, H.; Yin, F.; Kim, E.S.; Wang, W.; Yoon, D.Y.; Wang, C.; Liang, J.; Li, Y.; Kim, N.Y. Advances in flexible sensors for intelligent perception system enhanced by artificial intelligence. InfoMat 2023, 5, e12412. [Google Scholar] [CrossRef]
- Tanusha, D.; Badhulika, S. Comparative analysis of micro patterned PDMS-based piezoresistive pressure sensors with multifunctional strain and health monitoring applications. Sens. Actuators A Phys. 2024, 369, 115139. [Google Scholar] [CrossRef]
- Kim, T.K.; Kim, J.K.; Jeong, O.C. Measurement of nonlinear mechanical properties of PDMS elastomer. Microelectron. Eng. 2011, 88, 1982–1985. [Google Scholar] [CrossRef]
- Jia, M.; Yi, C.; Han, Y.; Wang, L.; Li, X.; Xu, G.; He, K.; Li, N.; Hou, Y.; Wang, Z.; et al. Hierarchical network enabled flexible textile pressure sensor with ultrabroad response range and high-temperature resistance. Adv. Sci. 2022, 9, 2105738. [Google Scholar] [CrossRef]
- Chen, J.H.; Shen, L.; Wang, Q.B.; Ge, J.B. Design and application of biodegradable coronarystents: What will be brought by further innovations in materials science? Chin. J. Tissue Eng. Res. 2014, 18, 4878–4887. [Google Scholar]
- Rigotti, D.; Dorigato, A.; Pegoretti, A. Multifunctional 3D-printed thermoplastic polyurethane (TPU)/multiwalled carbon nanotube (MWCNT) nanocomposites for thermal management applications. Appl. Sci. 2024, 14, 9614. [Google Scholar] [CrossRef]
- Lv, Y.; Margulies, D.S.; Villringer, A.; Zang, Y.F. Effects of finger tapping frequency on regional homogeneity of sensorimotor cortex. PLoS ONE 2013, 8, e64115. [Google Scholar] [CrossRef]
- Chen, B.; Li, H.; Zhang, S.; Lai, X.; Zeng, X.; Wu, X.; Cheng, X.; Liu, H. High-performance and superhydrophobic piezoresistive pressure sensor based on mountain ridge-like microstructure by silver nanoparticles and reduced graphene oxide. Compos. Part A 2022, 162, 107171. [Google Scholar] [CrossRef]
- Kwon, D.; Lee, T.I.; Shim, J.; Ryu, S.; Kim, M.S.; Kim, S.; Kim, T.S.; Park, I. Highly Sensitive, flexible, and wearable pressure sensor based on a giant piezocapacitive effect of three-dimensional microporous elastomeric dielectric layer. ACS Appl. Mater. Interfaces 2016, 8, 16922–16931. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, S.; Chaitoglou, S.; Serafin, J.; Farid, G.; Ospina, R.; Ma, Y.; Rovira, R.A.; Bertran-Serra, E. Enhancing hydrogen evolution: Carbon nanotubes as a scaffold for Mo2C deposition via magnetron sputtering and chemical vapor deposition. Int. J. Hydrog. Energy 2024, 89, 977–989. [Google Scholar] [CrossRef]
- Bagheri, M.; Mahmoodzadeh, A. Polycaprolactone/graphene nanocomposites: Synthesis, characterization and mechanical properties of electrospun nanofibers. J. Inorg. Organomet. Polym. Mater. 2020, 30, 1566–1577. [Google Scholar] [CrossRef]




| Elastic Modulus GPa | Poisson’s Ratio | Thermal Conductivity Coefficient W/m·K | Density g/cm3 | |
|---|---|---|---|---|
| PCL/TPU@MWCNTs | 1 | 0.35 | 0.7 | 1.15 |
| Material Name | Specification | Manufacturer |
|---|---|---|
| Polycaprolactone (PCL) | 6800 | Swedish Bersto Specialty Chemicals Company |
| Thermoplastic Polyurethane (TPU) | 1195a | BASF AG, Germany |
| Multi walled carbon Nanotubes (MWCNTs) | >98% | Merck Darmstadt, Germany |
| Sodium Dodecyl Sulfonate | Chemically pure | Tianjin Kemio Chemical Reagent Co., Ltd., China |
| Dichloromethane (DCM) | Chemically pure | Chengdu Cologne Chemical Co., Ltd., China |
| Dimethylformamide (DMF) | Chemically pure | Chengdu Cologne Chemical Co., Ltd., China |
| Equipment Name | Model | Manufacturer |
|---|---|---|
| Functional electrospinning equipment | NS-1 | Qingdao Junada Technology Co., Ltd., China |
| Analytical balance | JJ124BC | Changshu Shuangjie Testing Instrument Factory, China |
| Four way magnetic heating stirrer | CJJ-4 | Changzhou Guowang Instrument Equipment Co., Ltd., China |
| Ultrasonic cleaning machine | JP020 | Shenzhen Jiemeng Technology Co., Ltd., China |
| Vacuum filtration machine | R410-MF31 | Xiamen Loken Instrument Co., Ltd., China |
| SEM | Apreo 2C | Thermo Fisher Scientific, USA |
| Touch screen measurement and control tensile strength tester | JSM-7900F | Guangdong Zhongye Jingke Instrument Equipment Co., Ltd., China |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Lan, Q. Preparation and Performance of a Grid-Based PCL/TPU@MWCNTs Nanofiber Membrane for Pressure Sensor. Sensors 2025, 25, 3201. https://doi.org/10.3390/s25103201
Zhu P, Lan Q. Preparation and Performance of a Grid-Based PCL/TPU@MWCNTs Nanofiber Membrane for Pressure Sensor. Sensors. 2025; 25(10):3201. https://doi.org/10.3390/s25103201
Chicago/Turabian StyleZhu, Ping, and Qian Lan. 2025. "Preparation and Performance of a Grid-Based PCL/TPU@MWCNTs Nanofiber Membrane for Pressure Sensor" Sensors 25, no. 10: 3201. https://doi.org/10.3390/s25103201
APA StyleZhu, P., & Lan, Q. (2025). Preparation and Performance of a Grid-Based PCL/TPU@MWCNTs Nanofiber Membrane for Pressure Sensor. Sensors, 25(10), 3201. https://doi.org/10.3390/s25103201






