Configurable Multi-Layer Perceptron-Based Soft Sensors on Embedded Field Programmable Gate Arrays: Targeting Diverse Deployment Goals in Fluid Flow Estimation †
Abstract
1. Introduction and Related Work
- Increased Model Configurability and Complexity: We enhance the flexibility of MLP accelerators for embedded FPGAs by enabling customizable configurations of layer count, neuron count, and quantization bitwidth. This configurability allows developers to adapt models to different deployment requirements, balancing metrics like precision, inference speed, and resource usage.
- Cross-Platform FPGA Support and Optimized Toolchain Integration: We introduce an open-source, user-friendly toolchain that integrates Quantization-Aware Training (QAT), integer-only inference, automated accelerator generation through VHDL templates, along with synthesis and performance estimation across diverse FPGA platforms. This toolchain simplifies deployment, making it accessible for users without deep FPGA expertise to optimize and deploy models across multiple hardware configurations.
- Case Study in Fluid Flow Estimation: Using fluid flow estimation as a case study, we validate our configurable MLP-based soft sensors on two FPGA platforms: the AMD Spartan-7 XC7S15 and the Lattice iCE40UP5K. Our experiments highlight the trade-offs across different configurations, providing insights into the effects of varying model complexity on precision, inference time, power, and energy consumption.
2. System Architecture
3. Fundamentals
3.1. Multi-Layer Perceptron Architecture
3.2. Integer-Only Quantization
4. Software–Hardware Co-Design
4.1. Customized Software Implementation
4.1.1. Quantization-Aware Training
4.1.2. Enhanced Integer-Only Inference
Integer-Only Fully Connected Layer
Integer-Only ReLU
4.2. Optimized Model Inference on FPGAs
4.2.1. Linear Layer Optimization
Configurable Parameters
Pipelined Matrix Multiplication
| Algorithm 1: MAC Algorithm in the fully connected layer |
Input: x is an K-element vector, W is an matrix, B is an J-element vector
Output: Y |
4.2.2. ReLU Optimization
4.2.3. Network Component Integration
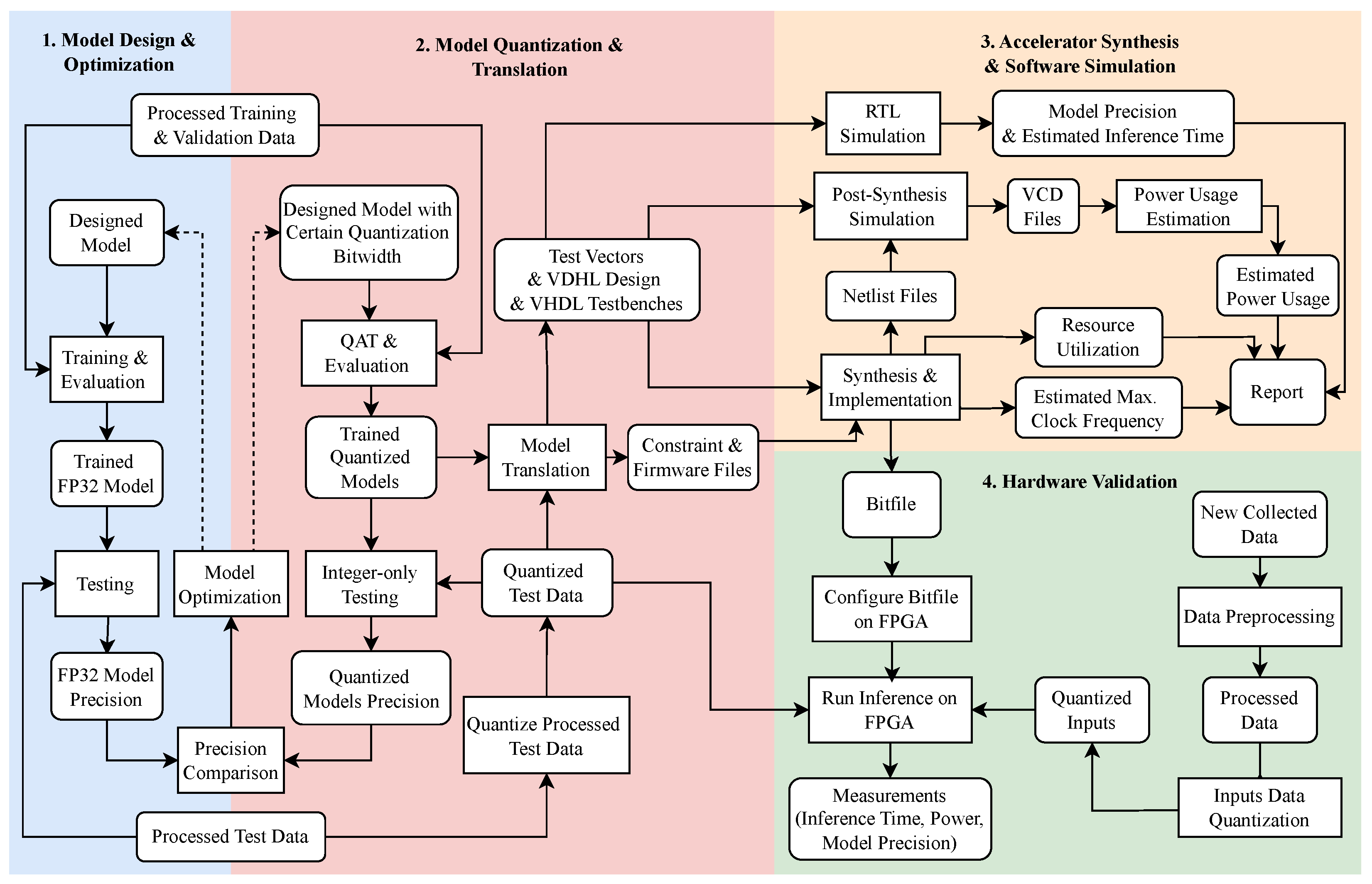
5. End-to-End Workflow and Open-Source Toolchain
- Model Design and Optimization in PyTorch: Users design and train initial FP32 models in PyTorch, utilizing a dataset representative of the target application. This stage focuses on building a robust and accurate baseline model to serve as the foundation for further quantization and deployment, ensuring the model’s adaptability to integer-only processing requirements.
- Model Quantization and Translation in ElasticAI.Creator: Users employ QAT to configure a quantized model mirroring the architecture of the previously trained FP32 model. Depending on specific deployment objectives, the quantized model can be trained from scratch or initialized using the pre-trained FP32 model parameters. After quantization, ElasticAI.Creator translates the integer-only quantized model into a set of VHDL files tailored for the corresponding FPGA accelerator.
- Accelerator Synthesis and Software Simulation: The generated VHDL files are subjected to simulation to verify model precision. During the synthesis process, resource usage and power estimation reports are produced, with which we can identify performance bottlenecks and ensure the model aligns with real-time and resource constraints, enabling further fine-tuning to enhance model efficiency.
- Hardware Validation: The bitfile generated during synthesis is deployed onto the selected FPGA. By executing the accelerator on real hardware, inference latency, power usage, and precision are validated to confirm the accelerator’s overall performance.
6. Testbed Platforms and FPGA Comparative Analysis
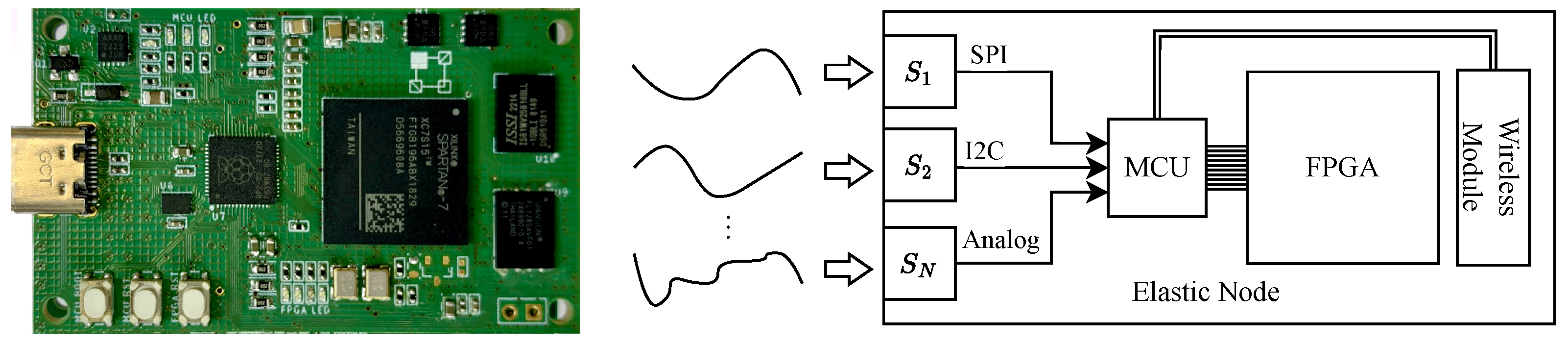
6.1. Elastic Node V5 Hardware Platform
6.2. Elastic Node V5 SE Hardware Platform
6.3. Comparison of FPGA Platforms
7. Experimental Design
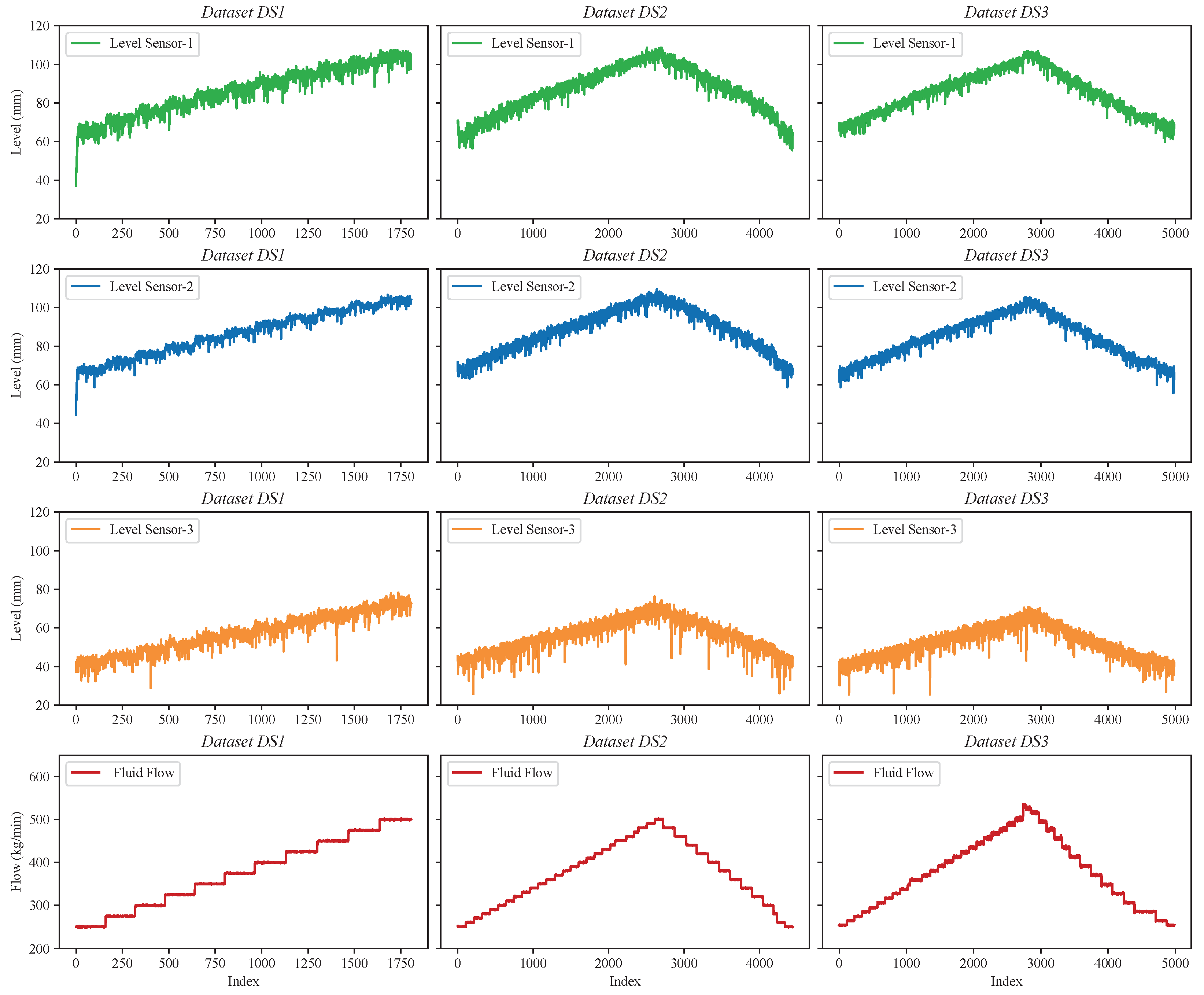
7.1. Case Study and Datasets
7.2. Training Settings
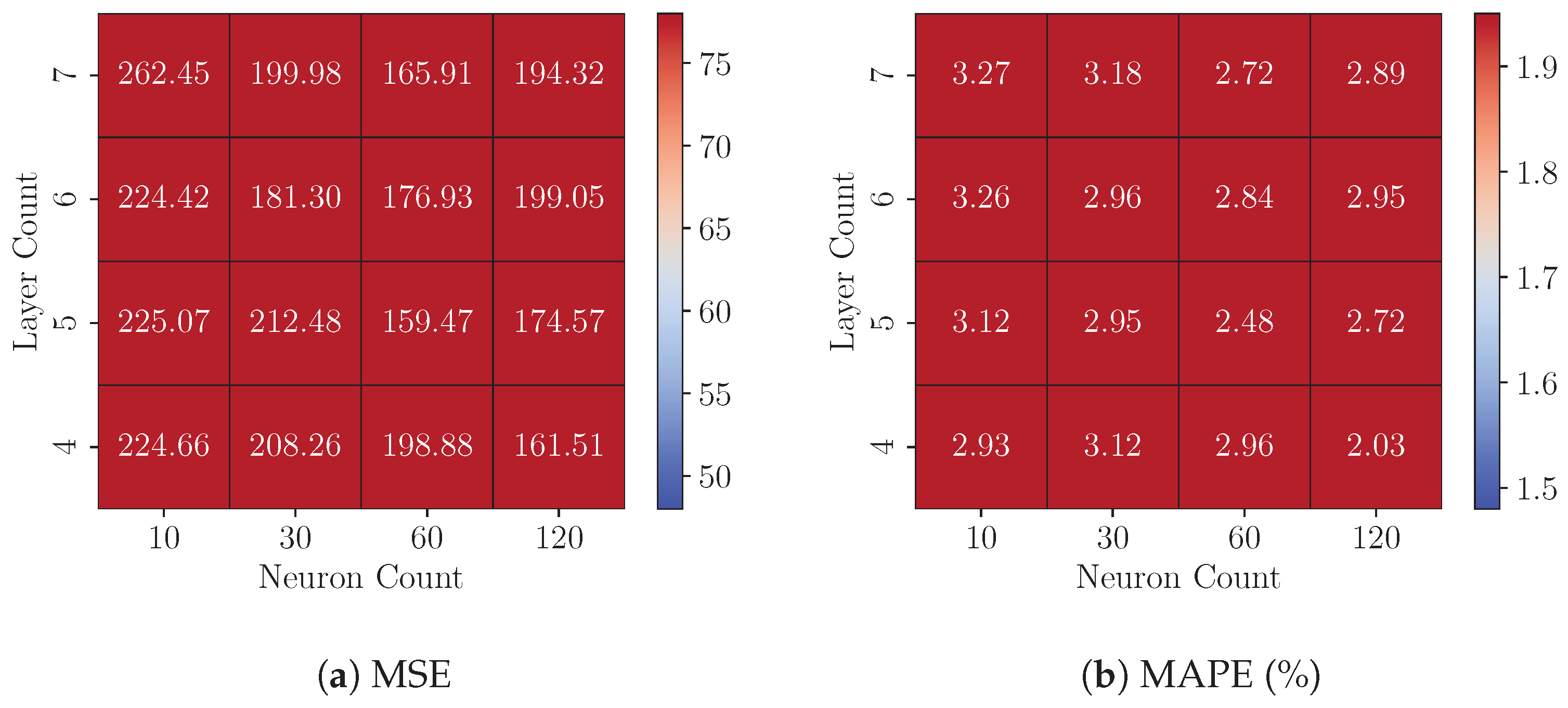
7.3. Evaluation Metrics
7.3.1. Model Precision Metrics
- Mean Squared Error (MSE): Defined in Equation (13), MSE calculates the average squared deviation between predictions () and target values (), offering a scale-sensitive measure of precision.
- Mean Absolute Percentage Error (MAPE): Defined in Equation (14), MAPE measures average absolute percentage differences between predictions () and targets (), providing a scale-independent assessment.
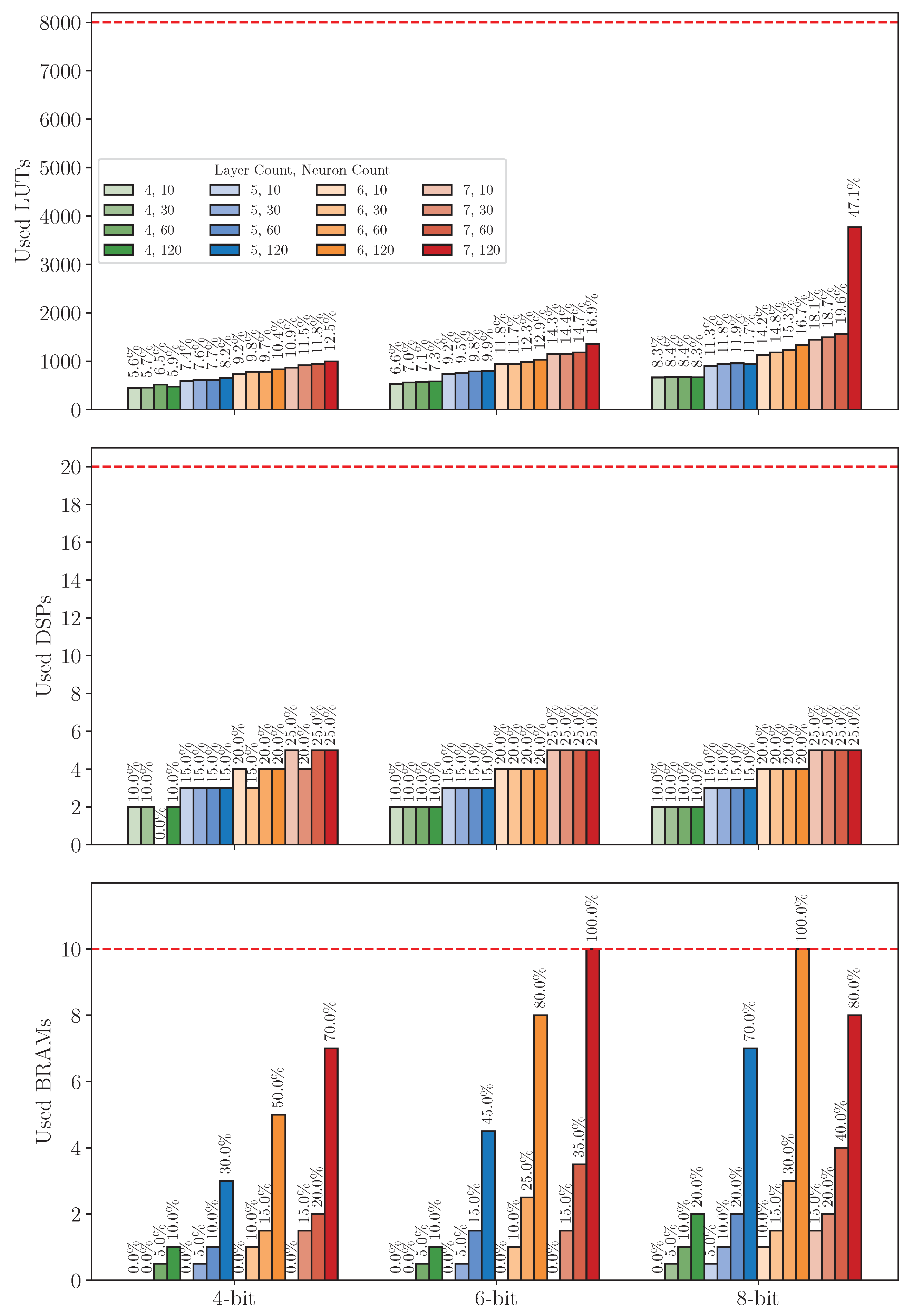
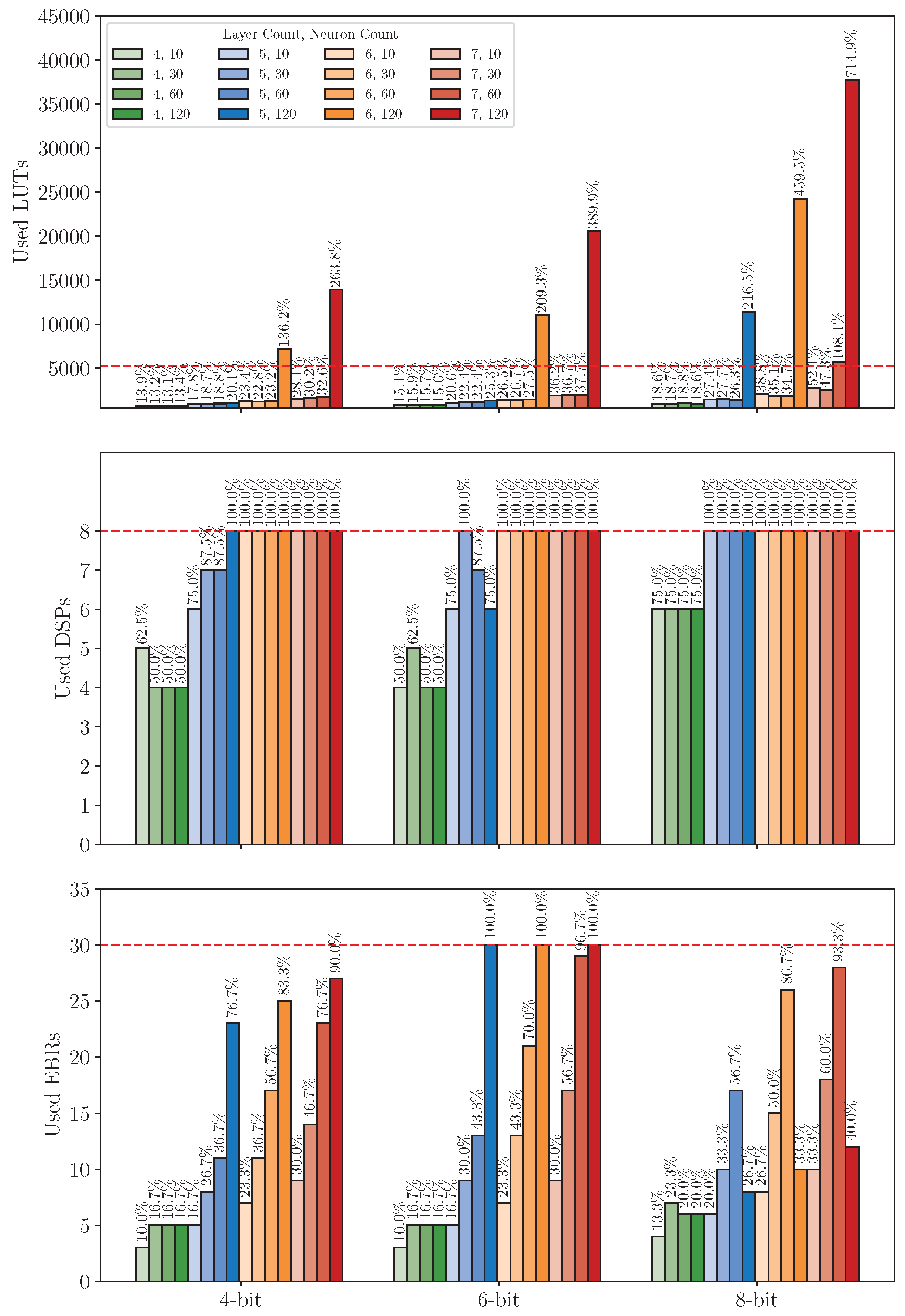
7.3.2. Hardware Evaluation Metrics
Resource Usage
Inference Time
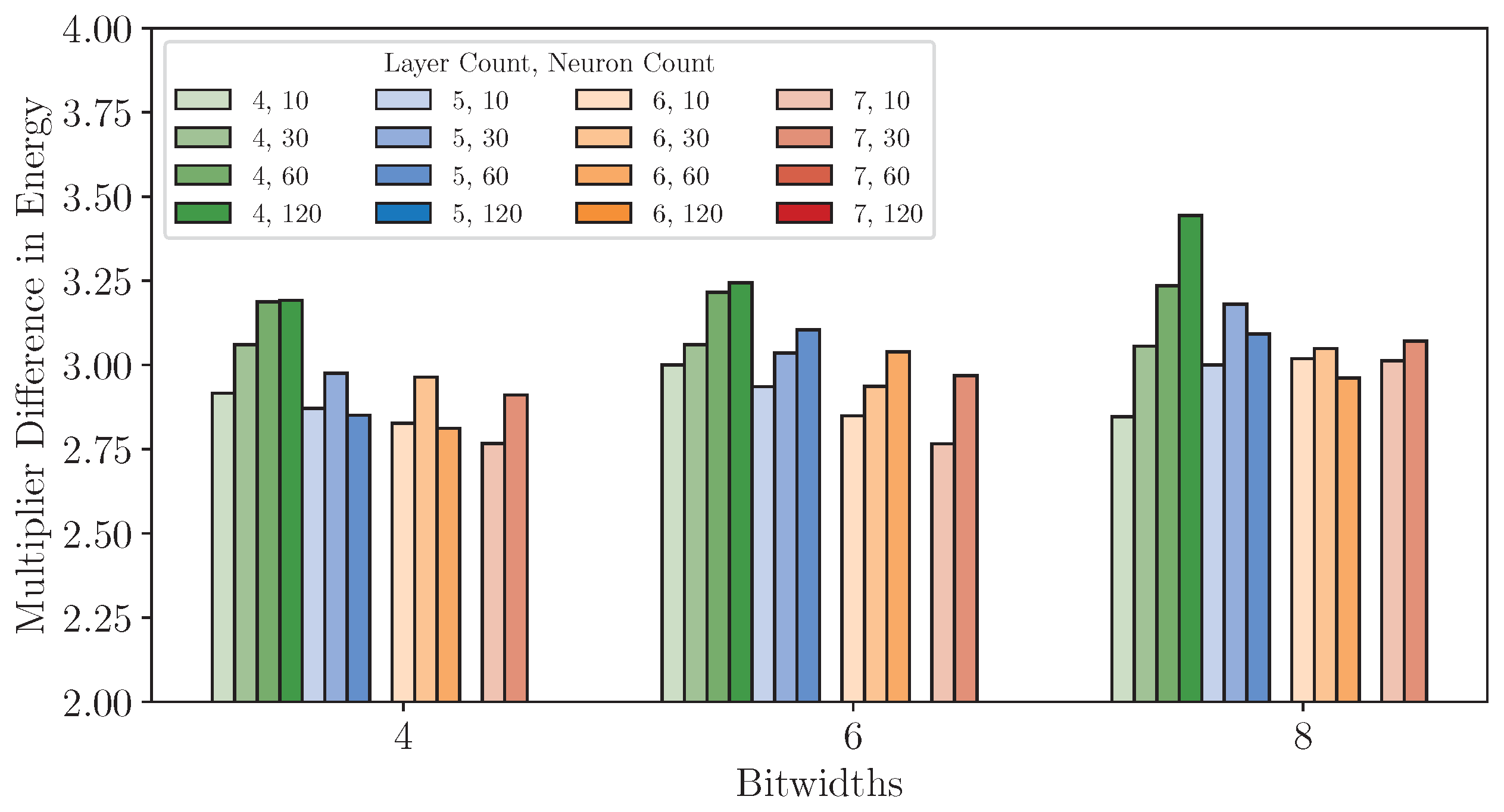
Power and Energy Consumption
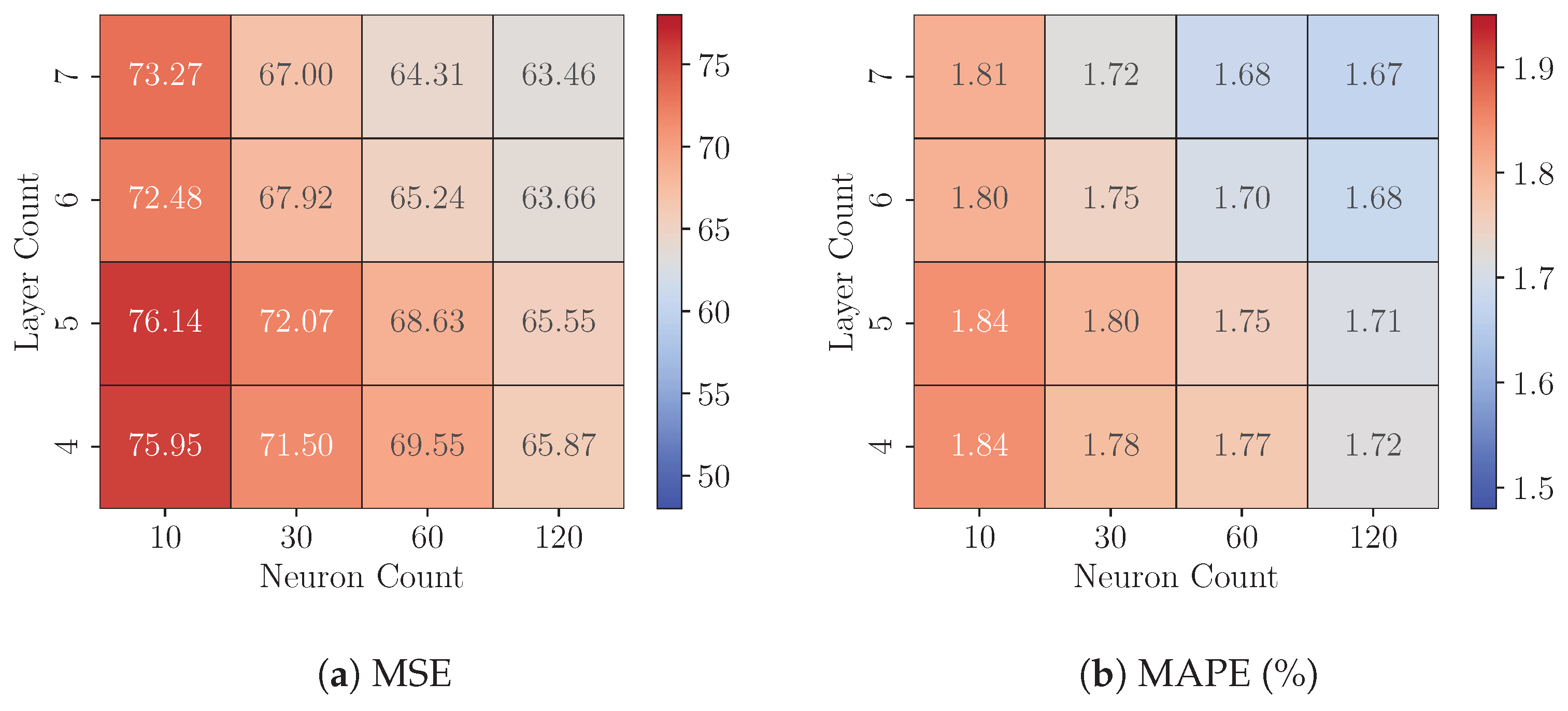
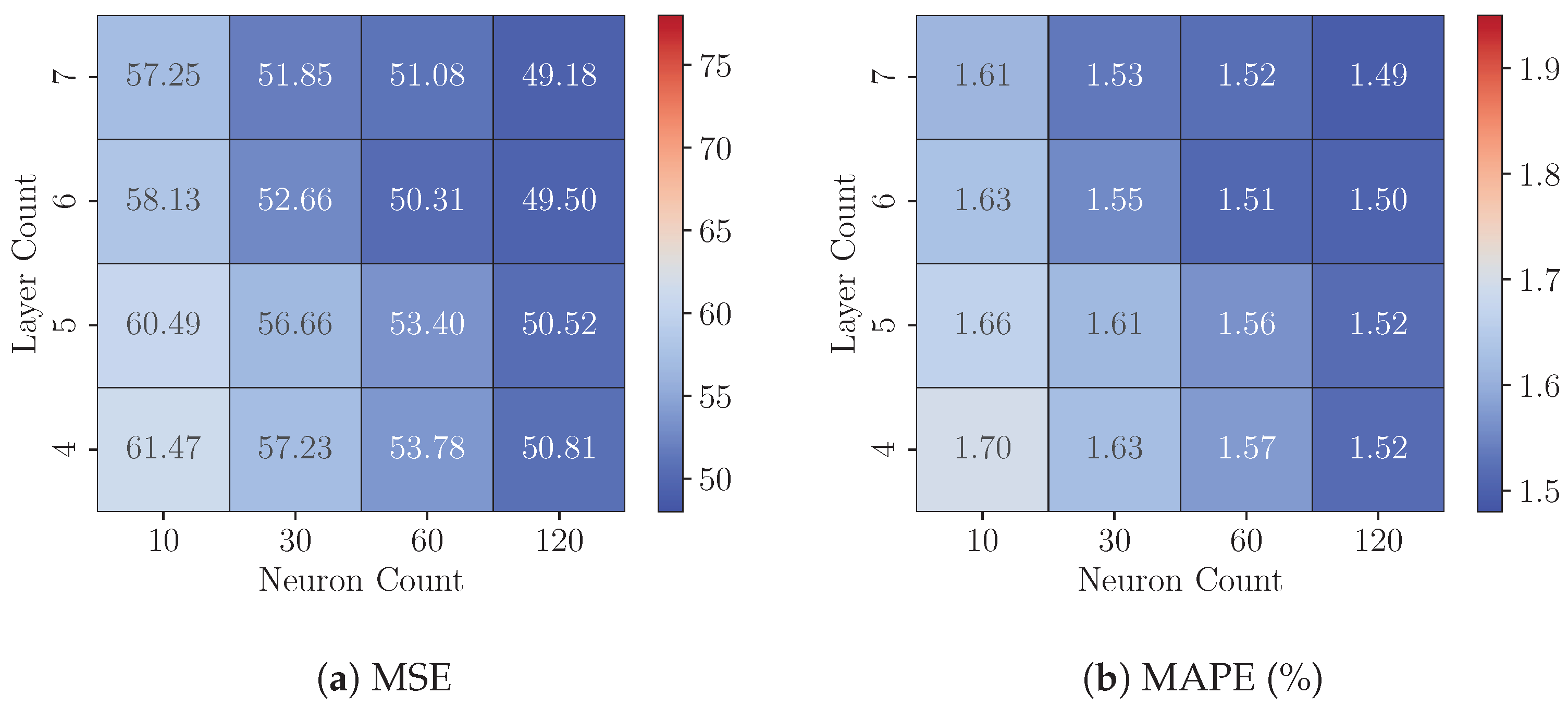
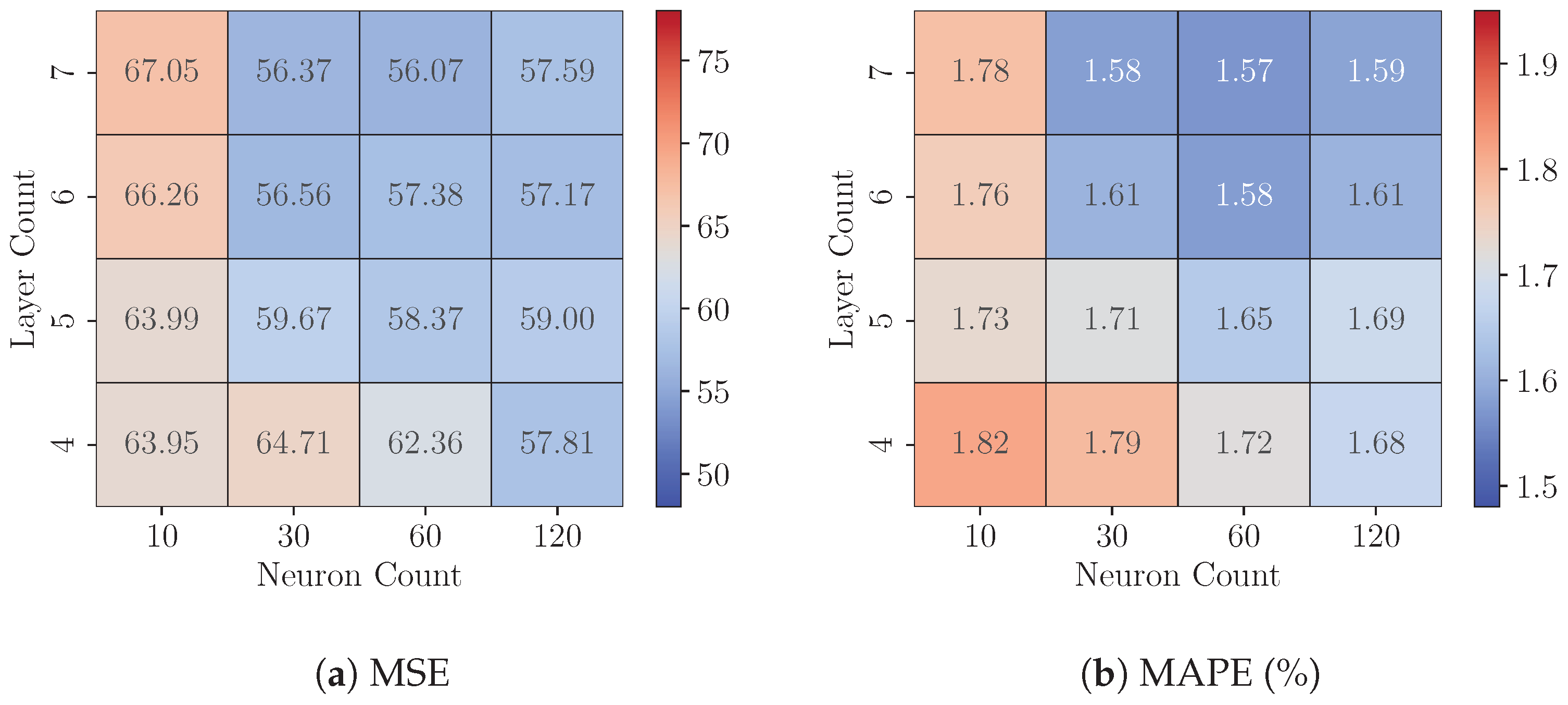
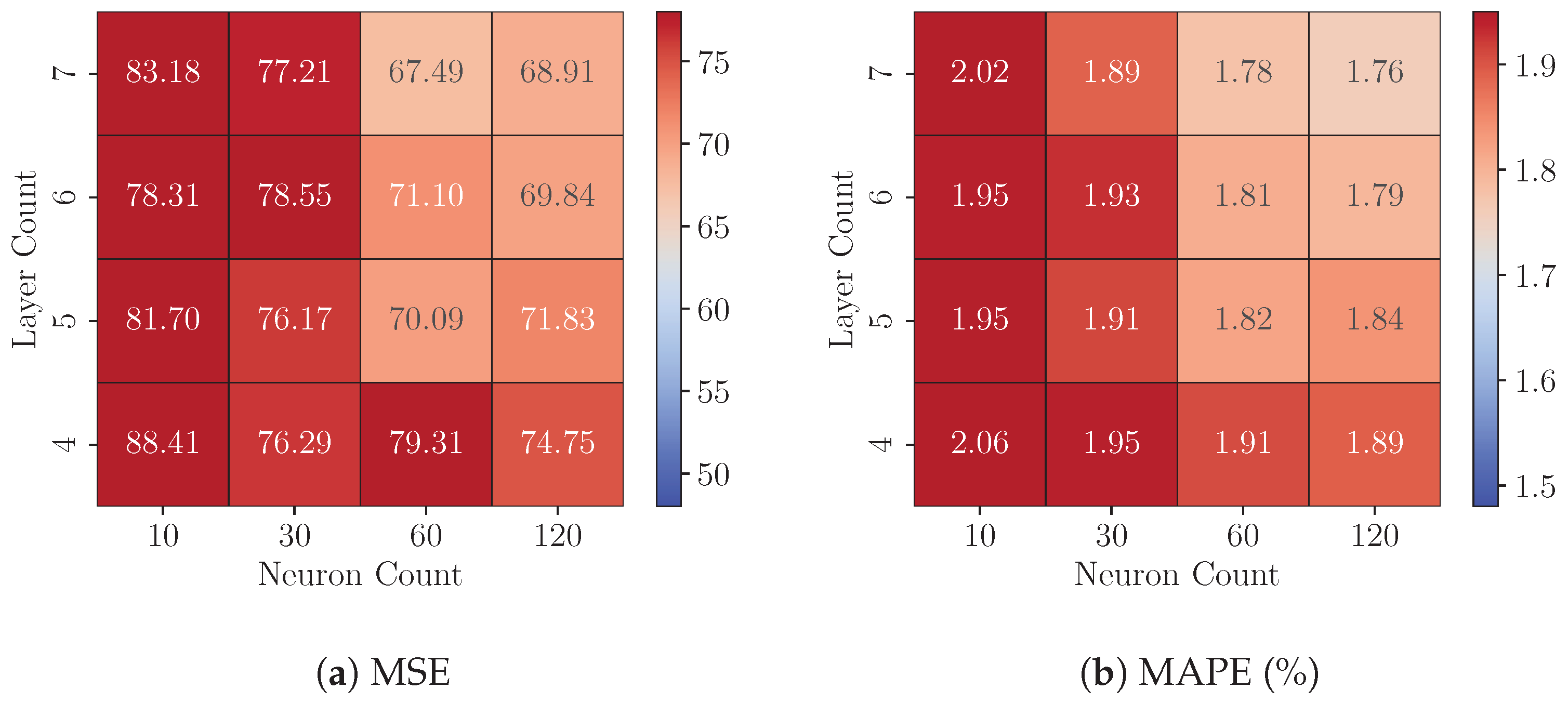
8. Results and Analysis
8.1. Experiments 1: FP32 Model Analysis
8.2. Experiments 2: Quantized Models Analysis
8.3. Experiments 3: Cross-Platform Performance Comparison
8.3.1. Resource Usage Analysis
8.3.2. Timing Analysis
8.3.3. Power and Energy Analysis
8.3.4. Deployment Analysis
9. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leon, M.A.; Castro, A.R.; Ascencio, R.L. An artificial neural network on a field programmable gate array as a virtual sensor. In Proceedings of the Third International Workshop on Design of Mixed-Mode Integrated Circuits and Applications (Cat. No. 99EX303), Puerto Vallarta, Mexico, 28–28 July 1999; pp. 114–117. [Google Scholar] [CrossRef]
- Becker, T.; Krause, D. Softsensorsysteme–Mathematik als Bindeglied zum Prozessgeschehen (in German). Chem. Ing. Tech. 2010, 82, 429–440. [Google Scholar] [CrossRef]
- Abeykoon, C. Design and applications of soft sensors in polymer processing: A review. IEEE Sensors J. 2018, 19, 2801–2813. [Google Scholar] [CrossRef]
- Lin, B.; Recke, B.; Knudsen, J.K.; Jørgensen, S.B. A systematic approach for soft sensor development. Comput. Chem. Eng. 2007, 31, 419–425. [Google Scholar] [CrossRef]
- Ma, M.D.; Ko, J.W.; Wang, S.J.; Wu, M.F.; Jang, S.S.; Shieh, S.S.; Wong, D.S.H. Development of adaptive soft sensor based on statistical identification of key variables. Control Eng. Pract. 2009, 17, 1026–1034. [Google Scholar] [CrossRef]
- Sun, Q.; Ge, Z. A survey on deep learning for data-driven soft sensors. IEEE Trans. Ind. Inform. 2021, 17, 5853–5866. [Google Scholar] [CrossRef]
- Yuan, X.; Qi, S.; Wang, Y.; Xia, H. A dynamic CNN for nonlinear dynamic feature learning in soft sensor modeling of industrial process data. Control Eng. Pract. 2020, 104, 104614. [Google Scholar] [CrossRef]
- Alencar, G.M.R.d.; Fernandes, F.M.L.; Moura Duarte, R.; Melo, P.F.d.; Cardoso, A.A.; Gomes, H.P.; Villanueva, J.M.M. A Soft Sensor for Flow Estimation and Uncertainty Analysis Based on Artificial Intelligence: A Case Study of Water Supply Systems. Automation 2024, 5, 106–127. [Google Scholar] [CrossRef]
- Jia, M.; Jiang, L.; Guo, B.; Liu, Y.; Chen, T. Physical-anchored graph learning for process key indicator prediction. Control Eng. Pract. 2025, 154, 106167. [Google Scholar] [CrossRef]
- Graziani, S.; Xibilia, M.G. Deep learning for soft sensor design. In Development and Analysis of Deep Learning Architectures; Springer: Berlin/Heidelberg, Germany, 2020; pp. 31–59. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, V.; Jaiswal, M.; Wang, H.C.; Jayakody, D.N.K.; Basnayaka, C.M.W.; Muthanna, A. Recent trends in AI-based intelligent sensing. Electronics 2022, 11, 1661. [Google Scholar] [CrossRef]
- Phung, K.H.; Tran, H.; Nguyen, Q.; Huong, T.T.; Nguyen, T.L. Analysis and assessment of LoRaWAN. In Proceedings of the 2018 2nd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing, Ho Chi Minh City, Vietnam, 29–31 January 2018; pp. 241–246. [Google Scholar] [CrossRef]
- Manzano, S.A.; Sundaram, V.; Xu, A.; Ly, K.; Rentschler, M.; Shepherd, R.; Correll, N. Toward smart composites: Small-scale, untethered prediction and control for soft sensor/actuator systems. J. Compos. Mater. 2022, 56, 4025–4039. [Google Scholar] [CrossRef]
- Flores, T.; Silva, M.; Andrade, P.; Silva, J.; Silva, I.; Sisinni, E.; Ferrari, P.; Rinaldi, S. A TinyML soft-sensor for the internet of intelligent vehicles. In Proceedings of the 2022 IEEE International Workshop on Metrology for Automotive, Modena, Italy, 4–6 July 2022; pp. 18–23. [Google Scholar] [CrossRef]
- Schizas, N.; Karras, A.; Karras, C.; Sioutas, S. TinyML for ultra-low power AI and large scale IoT deployments: A systematic review. Future Internet 2022, 14, 363. [Google Scholar] [CrossRef]
- Balaji, A.N.; Peh, L.S. AI-On-Skin: Towards Enabling Fast and Scalable On-body AI Inference for Wearable On-Skin Interfaces. Proc. ACM Hum.-Comput. Interact. 2023, 7, 1–34. [Google Scholar] [CrossRef]
- Ling, T.; Qian, C.; Schiele, G. On-device soft sensors: Real-time fluid flow estimation from level sensor data. In Proceedings of the International Conference on Mobile and Ubiquitous Systems: Computing, Networking, and Services, Melbourne, Australia, 14–17 November 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 529–537. [Google Scholar] [CrossRef]
- Ling, T.; Hoever, J.; Qian, C.; Schiele, G. FlowPrecision: Advancing FPGA-based real-time fluid flow estimation with linear quantization. In Proceedings of the 2024 IEEE International Conference on Pervasive Computing and Communications Workshops and other Affiliated Events, Biarritz, France, 11–15 March 2024; pp. 733–738. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Hara, K.; Saito, D.; Shouno, H. Analysis of function of rectified linear unit used in deep learning. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Ron, D.A.; Freire, P.J.; Prilepsky, J.E.; Kamalian-Kopae, M.; Napoli, A.; Turitsyn, S.K. Experimental implementation of a neural network optical channel equalizer in restricted hardware using pruning and quantization. Sci. Rep. 2022, 12, 8713. [Google Scholar] [CrossRef] [PubMed]
- Shuvo, M.M.H.; Islam, S.K.; Cheng, J.; Morshed, B.I. Efficient acceleration of deep learning inference on resource-constrained edge devices: A review. Proc. IEEE 2022, 111, 42–91. [Google Scholar] [CrossRef]
- Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar] [CrossRef]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of Neural Networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Yin, P.; Lyu, J.; Zhang, S.; Osher, S.; Qi, Y.; Xin, J. Understanding straight-through estimator in training activation quantized Neural Nets. arXiv 2019, arXiv:1903.05662. [Google Scholar] [CrossRef]
- Hettiarachchi, D.L.N.; Davuluru, V.S.P.; Balster, E.J. Integer vs. floating-point processing on modern FPGA technology. In Proceedings of the 2020 10th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 6–8 January 2020; pp. 0606–0612. [Google Scholar] [CrossRef]
- Qian, C.; Ling, T.; Schiele, G. ElasticAI: Creating and deploying energy-efficient Deep Learning accelerator for pervasive computing. In Proceedings of the 2023 IEEE International Conference on Pervasive Computing and Communications Workshops and other Affiliated Events, Atlanta, GA, USA, 13–17 March 2023; pp. 297–299. [Google Scholar] [CrossRef]
- AMD. 7 Series FPGAs Data Sheet: Overview (DS180). 2020. Available online: https://docs.amd.com/v/u/en-US/ds180_7Series_Overview (accessed on 5 November 2024).
- Lattice Semiconductor. iCE40 UltraPlus Family Data Sheet. 2023. FPGA-DS-02008-2.3. Available online: https://www.latticesemi.com/view_document?document_id=51968 (accessed on 5 November 2024).
- AMD. Spartan-7 FPGAs Data Sheet: DC and AC Switching Characteristics. 2022. Available online: https://docs.amd.com/r/en-US/ds189-spartan-7-data-sheet (accessed on 5 November 2024).
- Baker, R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, And Applications; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- LaNasa, P.J.; Upp, E.L. Fluid Flow Measurement: A Practical Guide to Accurate Flow Measurement; Butterworth-Heinemann: Woburn, MA, USA, 2014. [Google Scholar] [CrossRef]
- Karimi, H.S.; Natarajan, B.; Ramsey, C.L.; Henson, J.; Tedder, J.L.; Kemper, E. Comparison of learning-based wastewater flow prediction methodologies for smart sewer management. J. Hydrol. 2019, 577, 123977. [Google Scholar] [CrossRef]
- Tomperi, J.; Rossi, P.M.; Ruusunen, M. Estimation of wastewater flowrate in a gravitational sewer line based on a low-cost distance sensor. Water Pract. Technol. 2023, 18, 40–52. [Google Scholar] [CrossRef]
- Stone, K.A.; He, Q.P.; Wang, J. Two experimental protocols for accurate measurement of gas component uptake and production rates in bioconversion processes. Sci. Rep. 2019, 9, 5899. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Zhang, Y.; Zhao, W.; Liu, E. Analysis of the influence of rectifier blockage on the metering performance during shale gas extraction. Energy Fuels 2021, 35, 2134–2143. [Google Scholar] [CrossRef]
- Noori, N.; Waag, T.; Viumdal, H.; Sharma, R.; Jondahl, M.; Jinasena, A. Non-Newtonian fluid flow measurement in open venturi channel using Shallow Neural Network time series and non-contact level measurement radar sensors. In Proceedings of the SPE Norway Subsurface Conference, OnePetro, Virtual, 2–3 November 2020. [Google Scholar] [CrossRef]
- Ling, T.; Qian, C.; Schiele, G. Towards Auto-Building of Embedded FPGA-based Soft Sensors for Wastewater Flow Estimation. In Proceedings of the 2024 IEEE Annual Congress on Artificial Intelligence of Things (AIoT), Melbourne, Australia, 24–26 July 2024; pp. 248–249. [Google Scholar] [CrossRef]
- Ahm, M.; Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Estimation of combined sewer overflow discharge: A software sensor approach based on local water level measurements. Water Sci. Technol. 2016, 74, 2683–2696. [Google Scholar] [CrossRef] [PubMed]

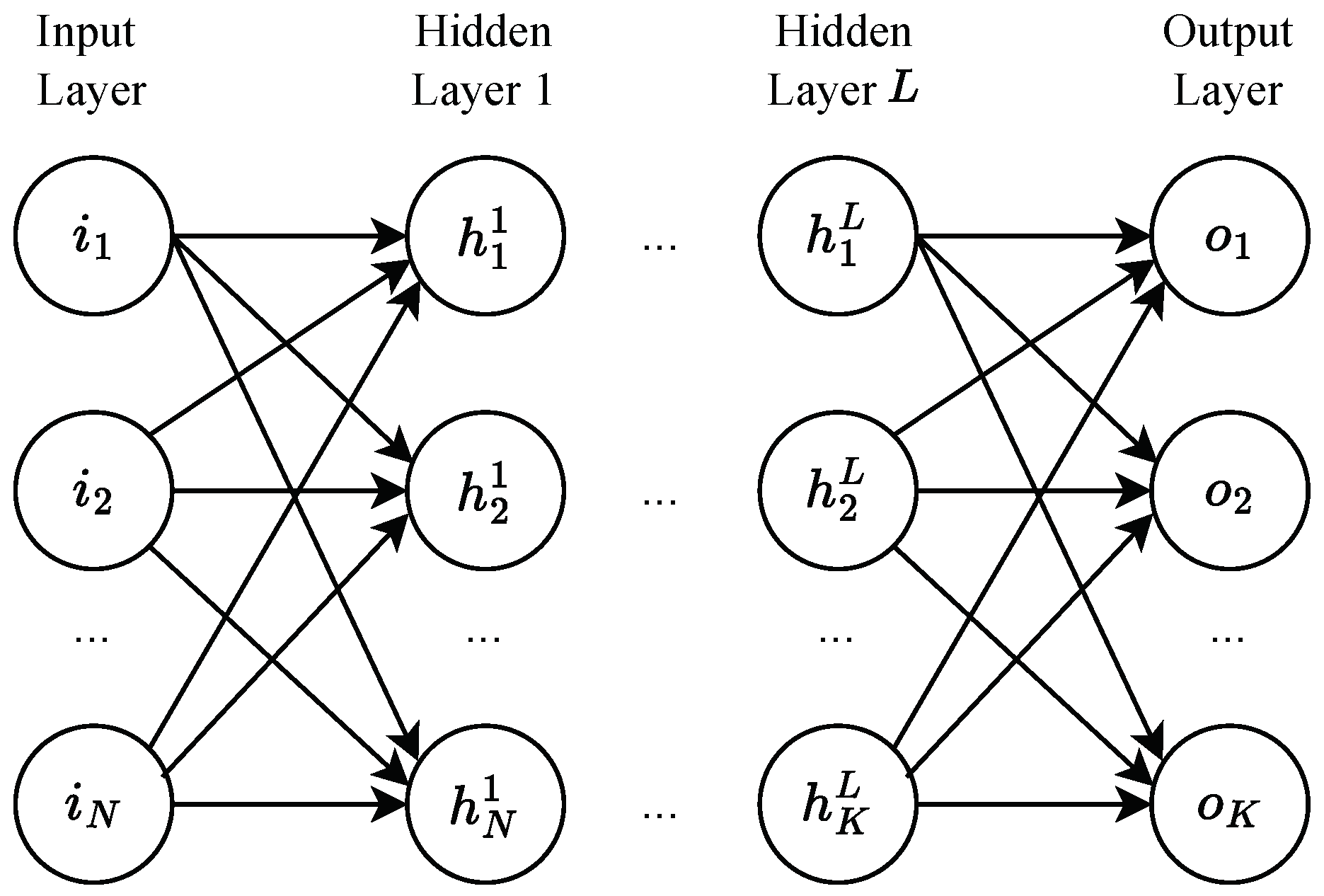





| Layers | Quantization Objects | Quantization Parameters |
|---|---|---|
| Input Layer | X | , |
| Hidden Layer 1 | , | |
| , | ||
| A | , | |
| Hidden Layer 2 | , | |
| , | ||
| Output Layer | , |
| XC7S15 [28] | iCE40UP5K [29] | ||
|---|---|---|---|
| LUTs | Type | LUT6 | LUT4 |
| Count | 12,800 | 5280 | |
| Total size (Kbits) | 360 | 120 | |
| BRAMs/EBRs | Blocks | 10 | 30 |
| DSPs | Width (bits) | 25 × 18 + 48 | 16 × 16 + 32 |
| Maximum frequency (MHz) | 741 | 50 | |
| Count | 20 | 8 | |
| Price (€) | 22.58 | 6.96 |
| Datasets | Description |
|---|---|
| DS1 | 1800 samples with upward trend only |
| DS2 | 4439 samples with upward and downward trends |
| DS3 | 4985 samples with upward and downward trends |
| FPGAs | Layer Count | Neuron Count | Bitwidth | Clock Cycles | Time (s) | Power (mW) | Energy (J) | ||
|---|---|---|---|---|---|---|---|---|---|
| Static | Dynamic | Total | |||||||
| XC7S15 @100 MHz | 4 | 10 | 4 | 10,100 | 1.01 | 30.0 | 5.0 | 35.0 | 0.035 |
| 6 | 10,100 | 1.01 | 30.0 | 5.0 | 35.0 | 0.035 | |||
| 8 | 10,100 | 1.01 | 30.0 | 6.0 | 37.0 | 0.037 | |||
| 30 | 4 | 28,100 | 2.81 | 30.0 | 5.0 | 36.0 | 0.101 | ||
| 6 | 28,100 | 2.81 | 30.0 | 6.0 | 36.0 | 0.101 | |||
| 8 | 28,100 | 2.81 | 30.0 | 9.0 | 39.0 | 0.110 | |||
| 60 | 4 | 55,100 | 5.51 | 30.0 | 7.0 | 37.0 | 0.204 | ||
| 6 | 55,100 | 5.51 | 30.0 | 7.0 | 38.0 | 0.209 | |||
| 8 | 55,100 | 5.51 | 30.0 | 9.0 | 40.0 | 0.220 | |||
| 120 | 4 | 109,100 | 10.91 | 30.0 | 8.0 | 38.0 | 0.415 | ||
| 6 | 109,100 | 10.91 | 31.0 | 8.0 | 39.0 | 0.425 | |||
| 8 | 109,100 | 10.91 | 31.0 | 12.0 | 42.0 | 0.458 | |||
| 5 | 10 | 4 | 25,400 | 2.54 | 30.0 | 5.0 | 35.0 | 0.089 | |
| 6 | 25,400 | 2.54 | 30.0 | 6.0 | 36.0 | 0.091 | |||
| 8 | 25,400 | 2.54 | 30.0 | 8.0 | 39.0 | 0.099 | |||
| 30 | 4 | 13,340 | 13.34 | 30.0 | 6.0 | 37.0 | 0.494 | ||
| 6 | 13,340 | 13.34 | 30.0 | 8.0 | 38.0 | 0.507 | |||
| 8 | 13,340 | 13.34 | 30.0 | 10.0 | 40.0 | 0.547 | |||
| 60 | 4 | 44,540 | 44.54 | 30.0 | 7.0 | 37.0 | 1.648 | ||
| 6 | 44,540 | 44.54 | 30.0 | 9.0 | 40.0 | 1.782 | |||
| 8 | 44,540 | 44.54 | 30.0 | 12.0 | 42.0 | 1.871 | |||
| 120 | 4 | 1,609,400 | 160.94 | 30.0 | 11.0 | 41.0 | 6.599 | ||
| 6 | 1,609,400 | 160.94 | 31.0 | 15.0 | 46.0 | 7.403 | |||
| 6 | 10 | 4 | 40,700 | 4.07 | 30.0 | 6.0 | 36.0 | 0.147 | |
| 6 | 40,700 | 4.07 | 30.0 | 6.0 | 36.0 | 0.147 | |||
| 8 | 40,700 | 4.07 | 30.0 | 10.0 | 40.0 | 0.163 | |||
| 30 | 4 | 238,700 | 23.87 | 30.0 | 8.0 | 38.0 | 0.907 | ||
| 6 | 238,700 | 23.87 | 30.0 | 9.0 | 39.0 | 0.931 | |||
| 8 | 238,700 | 23.87 | 30.0 | 12.0 | 42.0 | 1.003 | |||
| 60 | 4 | 835,700 | 83.57 | 30.0 | 9.0 | 39.0 | 3.259 | ||
| 6 | 835,700 | 83.57 | 30.0 | 12.0 | 42.0 | 3.510 | |||
| 8 | 835,700 | 83.57 | 30.0 | 15.0 | 45.0 | 3.761 | |||
| 7 | 10 | 4 | 56,900 | 5.60 | 30.0 | 6.0 | 36.0 | 0.202 | |
| 6 | 56,900 | 5.60 | 30.0 | 8.0 | 38.0 | 0.213 | |||
| 8 | 56,900 | 5.60 | 30.0 | 12.0 | 42.0 | 0.235 | |||
| 30 | 4 | 344,000 | 34.40 | 30.0 | 9.0 | 39.0 | 1.342 | ||
| 6 | 344,000 | 34.40 | 30.0 | 11.0 | 41.0 | 1.410 | |||
| 8 | 344,000 | 34.40 | 30.0 | 14.0 | 44.0 | 1.514 | |||
| 60 | 4 | 1,226,000 | 122.60 | 31.0 | 10.0 | 41.0 | 5.207 | ||
| 6 | 1,226,000 | 122.60 | 31.0 | 15.0 | 45.0 | 5.517 | |||
| iCE40UP5K @16 MHz | 4 | 10 | 4 | 10,100 | 6.31 | 0.73 | 1.16 | 1.89 | 0.012 |
| 6 | 10,100 | 6.31 | 0.73 | 1.20 | 1.93 | 0.012 | |||
| 8 | 10,100 | 6.31 | 0.76 | 1.27 | 2.04 | 0.013 | |||
| 30 | 4 | 28,100 | 17.56 | 0.75 | 1.13 | 1.89 | 0.033 | ||
| 6 | 28,100 | 17.56 | 0.76 | 1.13 | 1.90 | 0.033 | |||
| 8 | 28,100 | 17.56 | 0.81 | 1.23 | 2.04 | 0.036 | |||
| 60 | 4 | 55,100 | 34.44 | 0.75 | 1.11 | 1.86 | 0.064 | ||
| 6 | 55,100 | 34.44 | 0.76 | 1.14 | 1.90 | 0.065 | |||
| 8 | 55,100 | 34.44 | 0.79 | 1.18 | 1.97 | 0.068 | |||
| 120 | 4 | 109,100 | 68.19 | 0.75 | 1.16 | 1.91 | 0.130 | ||
| 6 | 109,100 | 68.19 | 0.76 | 1.16 | 1.92 | 0.131 | |||
| 8 | 109,100 | 68.19 | 0.78 | 1.16 | 1.94 | 0.133 | |||
| 5 | 10 | 4 | 25,400 | 15.88 | 0.77 | 1.20 | 1.97 | 0.031 | |
| 6 | 25,400 | 15.88 | 0.78 | 1.19 | 1.97 | 0.031 | |||
| 8 | 25,400 | 15.88 | 0.81 | 1.29 | 2.10 | 0.033 | |||
| 30 | 4 | 13,340 | 83.37 | 0.81 | 1.18 | 1.99 | 0.166 | ||
| 6 | 13,340 | 83.37 | 0.84 | 1.16 | 2.00 | 0.167 | |||
| 8 | 13,340 | 83.37 | 0.87 | 1.19 | 2.06 | 0.172 | |||
| 60 | 4 | 44,540 | 278.38 | 0.85 | 1.22 | 2.08 | 0.578 | ||
| 6 | 44,540 | 278.38 | 0.89 | 1.17 | 2.06 | 0.574 | |||
| 8 | 44,540 | 278.38 | 0.96 | 1.21 | 2.17 | 0.605 | |||
| 120 | 4 | 1,609,400 | 1005.88 | 1.02 | 1.17 | 2.19 | 2.200 | ||
| 6 | 1,609,400 | 1005.88 | 1.13 | 1.28 | 2.40 | 2.417 | |||
| 6 | 10 | 4 | 40,700 | 25.44 | 0.81 | 1.24 | 2.05 | 0.052 | |
| 6 | 40,700 | 25.44 | 0.82 | 1.27 | 2.09 | 0.053 | |||
| 8 | 40,700 | 25.44 | 0.87 | 1.25 | 2.12 | 0.054 | |||
| 30 | 4 | 238,700 | 149.19 | 0.86 | 1.18 | 2.05 | 0.306 | ||
| 6 | 238,700 | 149.19 | 0.91 | 1.22 | 2.13 | 0.317 | |||
| 8 | 238,700 | 149.19 | 0.96 | 1.24 | 2.20 | 0.329 | |||
| 60 | 4 | 835,700 | 522.31 | 0.95 | 1.27 | 2.22 | 1.159 | ||
| 6 | 835,700 | 522.31 | 1.02 | 1.20 | 2.21 | 1.155 | |||
| 8 | 835,700 | 522.31 | 1.11 | 1.32 | 2.43 | 1.270 | |||
| 7 | 10 | 4 | 56,900 | 35.00 | 0.86 | 1.24 | 2.10 | 0.073 | |
| 6 | 56,900 | 35.00 | 0.88 | 1.32 | 2.19 | 0.077 | |||
| 8 | 56,900 | 35.00 | 0.93 | 1.29 | 2.22 | 0.078 | |||
| 30 | 4 | 344,000 | 215.00 | 0.93 | 1.21 | 2.14 | 0.461 | ||
| 6 | 344,000 | 215.00 | 0.99 | 1.22 | 2.21 | 0.475 | |||
| 8 | 344,000 | 215.00 | 1.04 | 1.25 | 2.29 | 0.493 | |||
| 60 | 4 | 1,226,000 | 766.25 | 1.06 | 1.20 | 2.25 | 1.740 | ||
| 6 | 1,226,000 | 766.25 | 1.15 | 1.30 | 2.45 | 1.880 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, T.; Qian, C.; Klann, T.M.; Hoever, J.; Einhaus, L.; Schiele, G. Configurable Multi-Layer Perceptron-Based Soft Sensors on Embedded Field Programmable Gate Arrays: Targeting Diverse Deployment Goals in Fluid Flow Estimation. Sensors 2025, 25, 83. https://doi.org/10.3390/s25010083
Ling T, Qian C, Klann TM, Hoever J, Einhaus L, Schiele G. Configurable Multi-Layer Perceptron-Based Soft Sensors on Embedded Field Programmable Gate Arrays: Targeting Diverse Deployment Goals in Fluid Flow Estimation. Sensors. 2025; 25(1):83. https://doi.org/10.3390/s25010083
Chicago/Turabian StyleLing, Tianheng, Chao Qian, Theodor Mario Klann, Julian Hoever, Lukas Einhaus, and Gregor Schiele. 2025. "Configurable Multi-Layer Perceptron-Based Soft Sensors on Embedded Field Programmable Gate Arrays: Targeting Diverse Deployment Goals in Fluid Flow Estimation" Sensors 25, no. 1: 83. https://doi.org/10.3390/s25010083
APA StyleLing, T., Qian, C., Klann, T. M., Hoever, J., Einhaus, L., & Schiele, G. (2025). Configurable Multi-Layer Perceptron-Based Soft Sensors on Embedded Field Programmable Gate Arrays: Targeting Diverse Deployment Goals in Fluid Flow Estimation. Sensors, 25(1), 83. https://doi.org/10.3390/s25010083







