An Innovative Linear Wireless Sensor Network Reliability Evaluation Algorithm
Abstract
1. Introduction
2. Related Works
3. Problem Statement
- All ordinary nodes are produced in the same batch and are identical except for their identifiers .
- All ordinary nodes can only be in one of two possible states: 1, representing operational, and 0, representing failed.
- All ordinary nodes follow the same failure probability distribution function.
- The nodes are stationary and spaced evenly.
4. Math-Based Evaluation Methods
4.1. Status Classification
4.2. State Analysis
4.3. Calculate the Number of States
| Algorithm 1: y splitting of x |
 |
4.4. Probability Calculation
5. Test and Analysis of the Results
5.1. Feasibility Verification
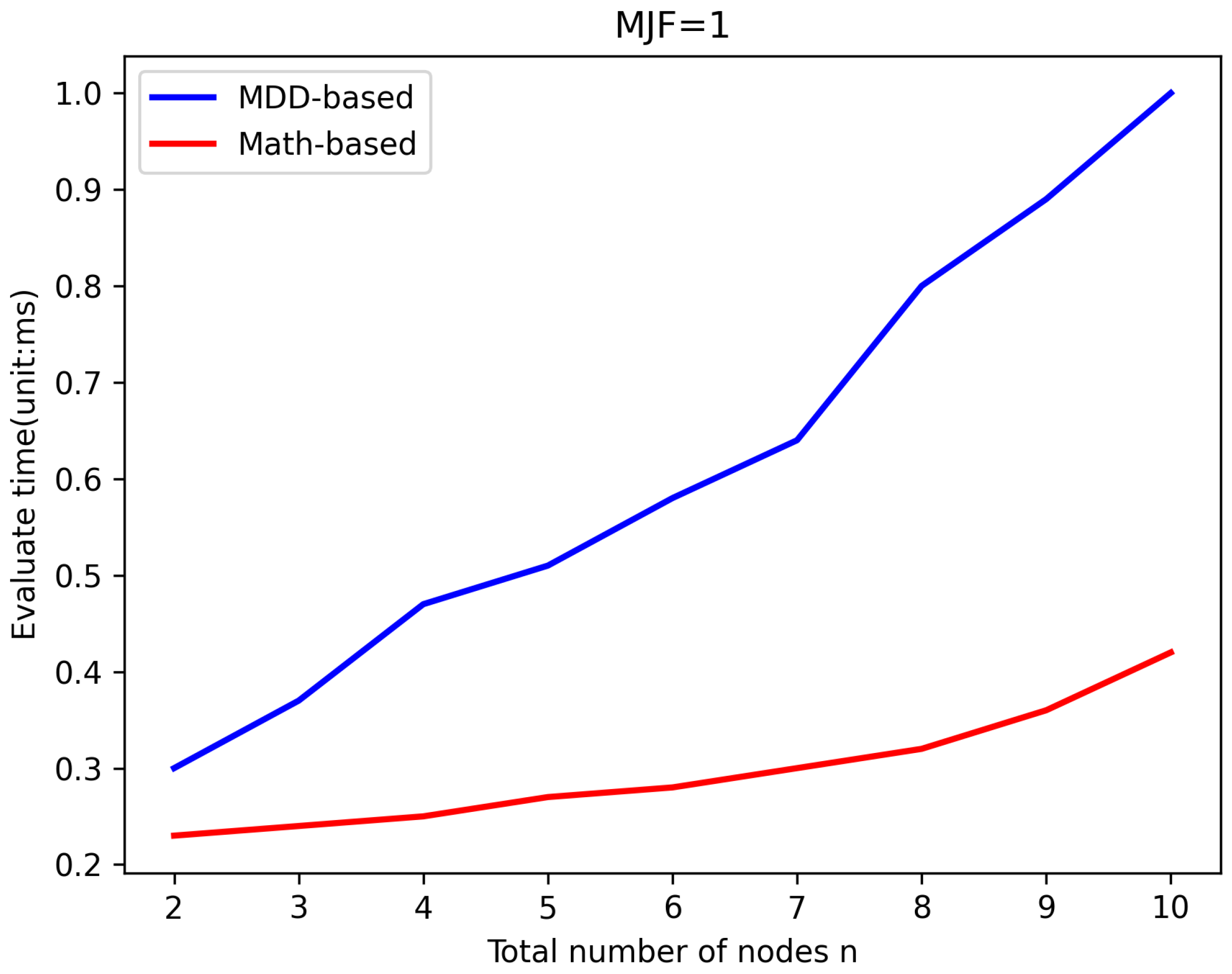
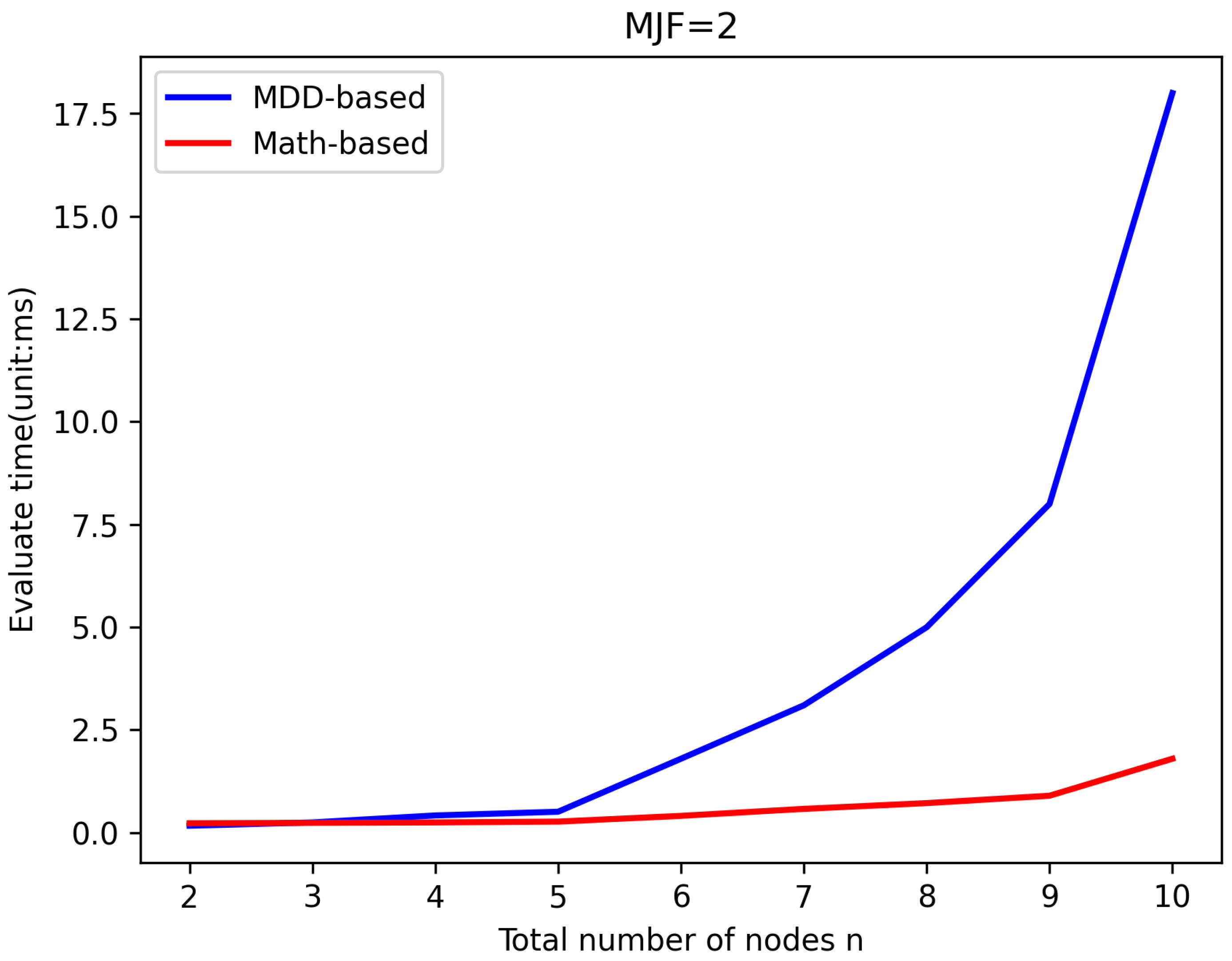
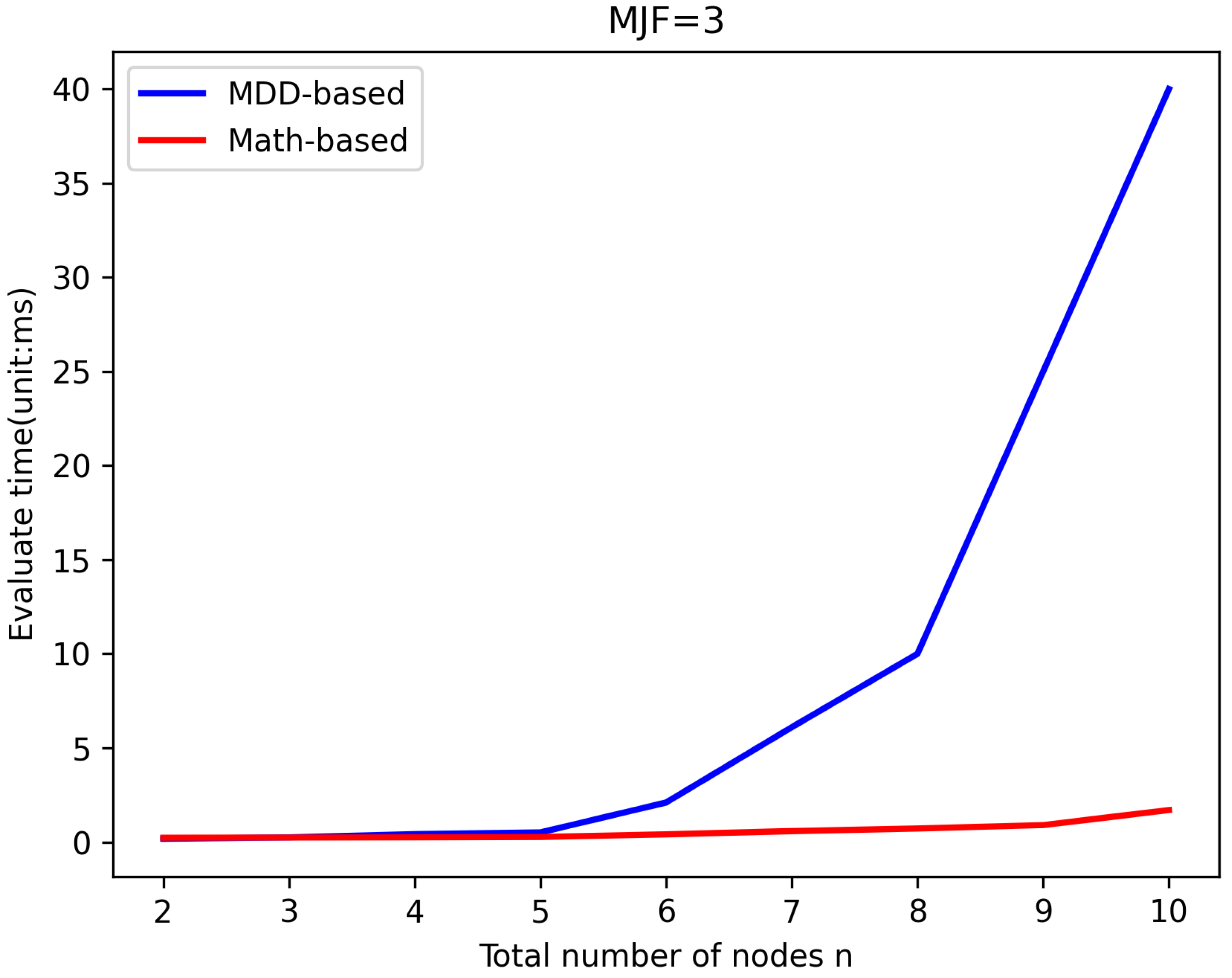
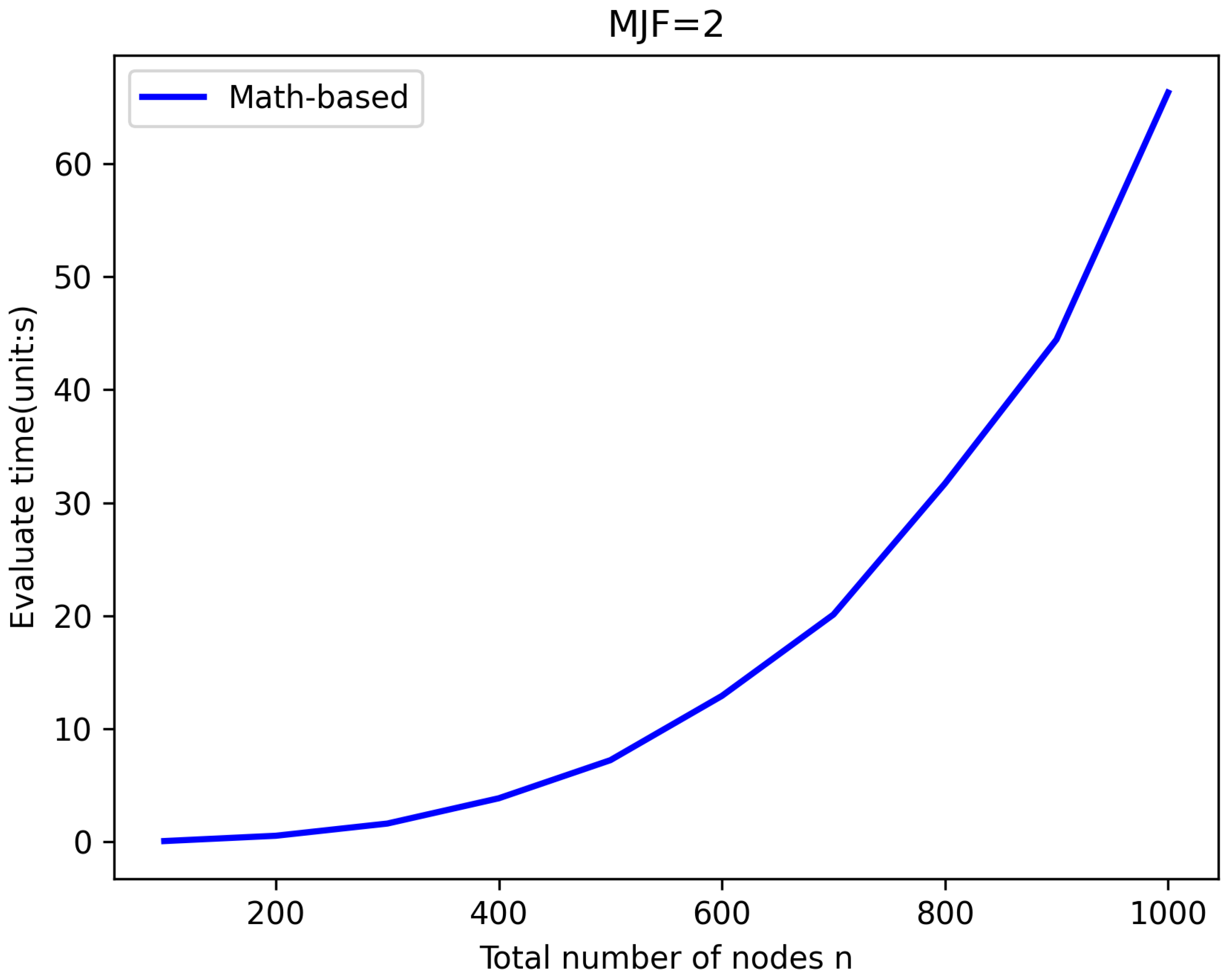
5.2. Efficiency Verification
5.3. Analysis of Applicable Scope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, A.; Zhao, M.; Wong, K.J.; Guan, Y.L.; Chong, P.H.J. A comprehensive study of IoT and WSN MAC protocols: Research issues, challenges and opportunities. IEEE Access 2018, 6, 76228–76262. [Google Scholar] [CrossRef]
- Khan, I.; Belqasmi, F.; Glitho, R.; Crespi, N.; Morrow, M.; Polakos, P. Wireless sensor network virtualization: A survey. IEEE Commun. Surv. Tutor. 2015, 18, 553–576. [Google Scholar] [CrossRef]
- Bapat, V.; Kale, P.; Shinde, V.; Deshpande, N.; Shaligram, A. WSN application for crop protection to divert animal intrusions in the agricultural land. Comput. Electron. Agric. 2017, 133, 88–96. [Google Scholar] [CrossRef]
- Jamshed, M.A.; Ali, K.; Abbasi, Q.H.; Imran, M.A.; Ur-Rehman, M. Challenges, applications, and future of wireless sensors in Internet of Things: A review. IEEE Sens. J. 2022, 22, 5482–5494. [Google Scholar] [CrossRef]
- Verma, G.; Sharma, V. A novel thermoelectric energy harvester for wireless sensor network application. IEEE Trans. Ind. Electron. 2018, 66, 3530–3538. [Google Scholar]
- Subhan, F.; Noreen, M.; Imran, M.; Tariq, M.; Khan, A.; Shoaib, M. Impact of node deployment and routing for protection of critical infrastructures. IEEE Access 2019, 7, 11502–11514. [Google Scholar] [CrossRef]
- Xiang, S.; Yang, J. Reliability evaluation and reliability-based optimal design for wireless sensor networks. IEEE Syst. J. 2019, 14, 1752–1763. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, J.; Wang, N. Timely reliability modeling and evaluation of wireless sensor networks with adaptive N-policy sleep scheduling. Reliab. Eng. Syst. Saf. 2023, 235, 109270. [Google Scholar] [CrossRef]
- Koriem, S.M.; Bayoumi, M.A. Detecting and measuring holes in wireless sensor network. J. King Saud-Univ.-Comput. Inf. Sci. 2020, 32, 909–916. [Google Scholar] [CrossRef]
- Qiu, C.; Shen, H.; Chen, K. An energy-efficient and distributed cooperation mechanism for k-coverage hole detection and healing in WSNs. IEEE Trans. Mob. Comput. 2017, 17, 1247–1259. [Google Scholar] [CrossRef]
- Behera, T.M.; Mohapatra, S.K.; Samal, U.C.; Khan, M.S.; Daneshmand, M.; Gandomi, A.H. Residual energy-based cluster-head selection in WSNs for IoT application. IEEE Internet Things J. 2019, 6, 5132–5139. [Google Scholar] [CrossRef]
- Du, T.; Qu, S.; Liu, F.; Wang, Q. An energy efficiency semi-static routing algorithm for WSNs based on HAC clustering method. Inf. Fusion 2015, 21, 18–29. [Google Scholar] [CrossRef]
- Rebaiaia, M.L.; Ait-Kadi, D. A new technique for generating minimal cut sets in nontrivial network. AASRI Procedia 2013, 5, 67–76. [Google Scholar] [CrossRef]
- Dash, R.K.; Barpanda, N.K.; Tripathy, P.K.; Tripathy, C.R. Network reliability optimization problem of interconnection network under node-edge failure model. Appl. Soft Comput. 2012, 12, 2322–2328. [Google Scholar] [CrossRef]
- Rei, A.M.; Schilling, M.T. Reliability assessment of the Brazilian power system using enumeration and Monte Carlo. IEEE Trans. Power Syst. 2008, 23, 1480–1487. [Google Scholar] [CrossRef]
- Kawahara, J.; Sonoda, K.; Inoue, T.; Kasahara, S. Efficient construction of binary decision diagrams for network reliability with imperfect vertices. Reliab. Eng. Syst. Saf. 2019, 188, 142–154. [Google Scholar] [CrossRef]
- Xing, L.; Dai, Y. A new decision-diagram-based method for efficient analysis on multistate systems. IEEE Trans. Dependable Secur. Comput. 2008, 6, 161–174. [Google Scholar] [CrossRef]
- Mo, Y.; Xing, L.; Jiang, J. Modeling and analyzing linear wireless sensor networks with backbone support. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3912–3924. [Google Scholar] [CrossRef]
- He, W.; Hu, G.Y.; Zhou, Z.J.; Qiao, P.L.; Han, X.X.; Qu, Y.Y.; Wei, H.; Shi, C. A new hierarchical belief-rule-based method for reliability evaluation of wireless sensor network. Microelectron. Reliab. 2018, 87, 33–51. [Google Scholar] [CrossRef]
- Díez-González, J.; Alvarez, R.; Prieto-Fernandez, N.; Perez, H. Local wireless sensor networks positioning reliability under sensor failure. Sensors 2020, 20, 1426. [Google Scholar] [CrossRef] [PubMed]
- Tong, F.; Zhang, Y.; Tao, J.; Wang, G.; Shi, X.; Cheng, G. EPDC: An Enhanced Pipelined Data Collection MAC for Duty-Cycled Linear Sensor Networks. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 4–7 October 2020; IEEE: Dundas, ON, Canada, 2020; pp. 1–5. [Google Scholar]
- Villordo-Jimenez, I.; Torres-Cruz, N.; Menchaca-Mendez, R.; Rivero-Angeles, M.E. A scalable and energy-efficient MAC protocol for linear sensor networks. IEEE Access 2022, 10, 36697–36710. [Google Scholar] [CrossRef]





| L | Z (b = 0/1) |
| 0 | (0, 0, b, b, b, b) |
| 1 | (1, 0, 0, b, b, b), (0, 1, b, b, b, b) |
| 2 | (1, 1, 0, 0, b, b), (1, 0, 1, 0, 0, b), (0, 1, 1, 0, 0, b), (0, 1, 0, 1, 0, 0) |
| 3 | (1, 1, 1, 0, 0, b), (1, 1, 0, 1, 0, 0), (1, 0, 1, 1, 0, 0), (1, 0, 1, 0, 1, 0), (0, 1, 1, 1, 0, 0), (0, 1, 1, 0, 1, 0), (0, 1, 0, 1, 1, 0), (0, 1, 0, 1, 0, 1) |
| 4 | (1, 1, 1, 1, 0, 0), (1, 1, 1, 0, 1, 0), (1, 1, 0, 1, 1, 0), (1, 1, 0, 1, 0, 1), (1, 0, 1, 1, 1, 0), (1, 0, 1, 0, 1, 1), (0, 1, 1, 1, 1, 0), (0, 1, 1, 1, 0, 1), (0, 1, 1, 0, 1, 1), (0, 1, 0, 1, 1, 1) |
| 5 | (1, 1, 1, 1, 1, 0), (1, 1, 1, 1, 0, 1), (1, 1, 1, 0, 1, 1), (1, 1, 0, 1, 1, 1), (1, 0, 1, 1, 1, 1), (0, 1, 1, 1, 1, 1) |
| 6 | (1, 1, 1, 1, 1, 1) |
| Z | |||||
|---|---|---|---|---|---|
| 0 | 3 | 2 | 1 | 0 | (0, 0, 1, 0, 1, 1) |
| 2 | 0 | 1 | (0, 0, 1, 1, 0, 1) | ||
| 1 | 2 | 0 | (0, 1, 0, 0, 1, 1) | ||
| 1 | 0 | 2 | (0, 1, 1, 0, 0, 1) | ||
| 0 | 1 | 2 | (1, 0, 1, 0, 0, 1) | ||
| 0 | 2 | 1 | (1, 0, 0, 1, 0, 1) | ||
| 1 | 1 | 1 | (0, 1, 0, 1, 0, 1) | ||
| 1 | 2 | 2 | 0 | 0 | (0, 0, 1, 1, 1, 1) |
| 0 | 2 | 0 | (1, 0, 0, 1, 1, 0) | ||
| 0 | 0 | 2 | (1, 1, 0, 0, 1, 0) | ||
| 1 | 1 | 0 | (0, 1, 0, 1, 1, 0) | ||
| 1 | 0 | 1 | (0, 1, 1, 0, 1, 0) | ||
| 0 | 1 | 1 | (1, 0, 1, 0, 1, 0) | ||
| 2 | 1 | 1 | 0 | 0 | (0, 1, 1, 1, 0, 0) |
| 0 | 1 | 0 | (1, 0, 1, 0, 0, 0) | ||
| 0 | 0 | 1 | (1, 1, 0, 1, 0, 0) | ||
| 3 | 0 | 0 | 0 | 0 | (1, 1, 1, 0, 0, 0) |
| G | Sn | |||
|---|---|---|---|---|
| 0 | 3 | (0, 1,2) | (1, 1, 1) | 6 |
| (1, 1, 1) | (0,3, 0) | 1 | ||
| 1 | 2 | (0, 0,2) | (2, 0, 1) | 3 |
| (0, 1, 1) | (1,2, 0) | 3 | ||
| 2 | 1 | (0, 0, 1) | (2, 1, 0) | 3 |
| 3 | 0 | (0, 0, 0) | (3, 0, 0) | 1 |
| Performance Level | t = 1000 h | t = 5000 h | t = 10,000 h |
|---|---|---|---|
| 2.180909 | 9.515355 | 4.412608 | |
| 2.180433 | 9.424813 | 4.217897 | |
| 2.179958 | 9.335133 | 4.031778 | |
| 2.179483 | 9.246304 | 3.853871 | |
| 2.179007 | 9.158324 | 3.683815 | |
| 2.178571 | 9.100270 | 3.582978 | |
| 2.193153 | 1.059404 | 4.788920 | |
| 3.793584 | 3.314570 | 1.205509 | |
| 7.163870 | 1.548905 | 2.475374 | |
| 1.291712 | 3.872890 | 2.515847 | |
| 8.617584 | 3.583005 | 9.460838 |
| n | 11 | 15 | 20 | 25 | 30 |
| MDD-Based (s) | 0.01 | 0.18 | 2.71 | 38.15 | — |
| n | 200 | 400 | 600 | 800 | 1000 |
| Math-Based (s) | 0.52 | 3.84 | 12.91 | 31.7 | 66.23 |
| n | 11 | 15 | 20 | 21 | 25 |
| MDD-Based (s) | 0.06 | 0.91 | 25.53 | 49.82 | — |
| n | 20 | 30 | 40 | 50 | 60 |
| Math-Based (s) | 0.01 | 0.08 | 0.76 | 7.52 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Guo, H.; Li, X. An Innovative Linear Wireless Sensor Network Reliability Evaluation Algorithm. Sensors 2025, 25, 285. https://doi.org/10.3390/s25010285
Ma T, Guo H, Li X. An Innovative Linear Wireless Sensor Network Reliability Evaluation Algorithm. Sensors. 2025; 25(1):285. https://doi.org/10.3390/s25010285
Chicago/Turabian StyleMa, Tao, Huidong Guo, and Xin Li. 2025. "An Innovative Linear Wireless Sensor Network Reliability Evaluation Algorithm" Sensors 25, no. 1: 285. https://doi.org/10.3390/s25010285
APA StyleMa, T., Guo, H., & Li, X. (2025). An Innovative Linear Wireless Sensor Network Reliability Evaluation Algorithm. Sensors, 25(1), 285. https://doi.org/10.3390/s25010285





