Predictive Maintenance and Fault Detection for Motor Drive Control Systems in Industrial Robots Using CNN-RNN-Based Observers
Abstract
1. Introduction
- Enhanced feature extraction and temporal learning: CNN excels at automatically extracting spatial and temporal features from raw sensor data, while RNN tracks how faults evolve over time and identifies gradual changes or trends that may indicate emerging issues.
- Improved fault detection accuracy: The integration enables the system to detect both immediate anomalies and subtle, evolving faults, improving the overall accuracy of the fault detection system.
- Real-time detection with contextual awareness: CNN can process sensor data in real time, identifying immediate faults, while RNN provides contextual awareness by using past time steps, helping the model understand event sequences, which is crucial in robotics where faults develop over time.
- Enhances predictive maintenance: The combined model enhances predictive maintenance by not only detecting faults early but also predicting errors, which can help in planning maintenance before critical failures happen.
- CNN can recognize complex patterns that traditional models are hard to identify, and RNN can capture how these faults evolve and how mechanical wear affects performance over time.
2. Related Work
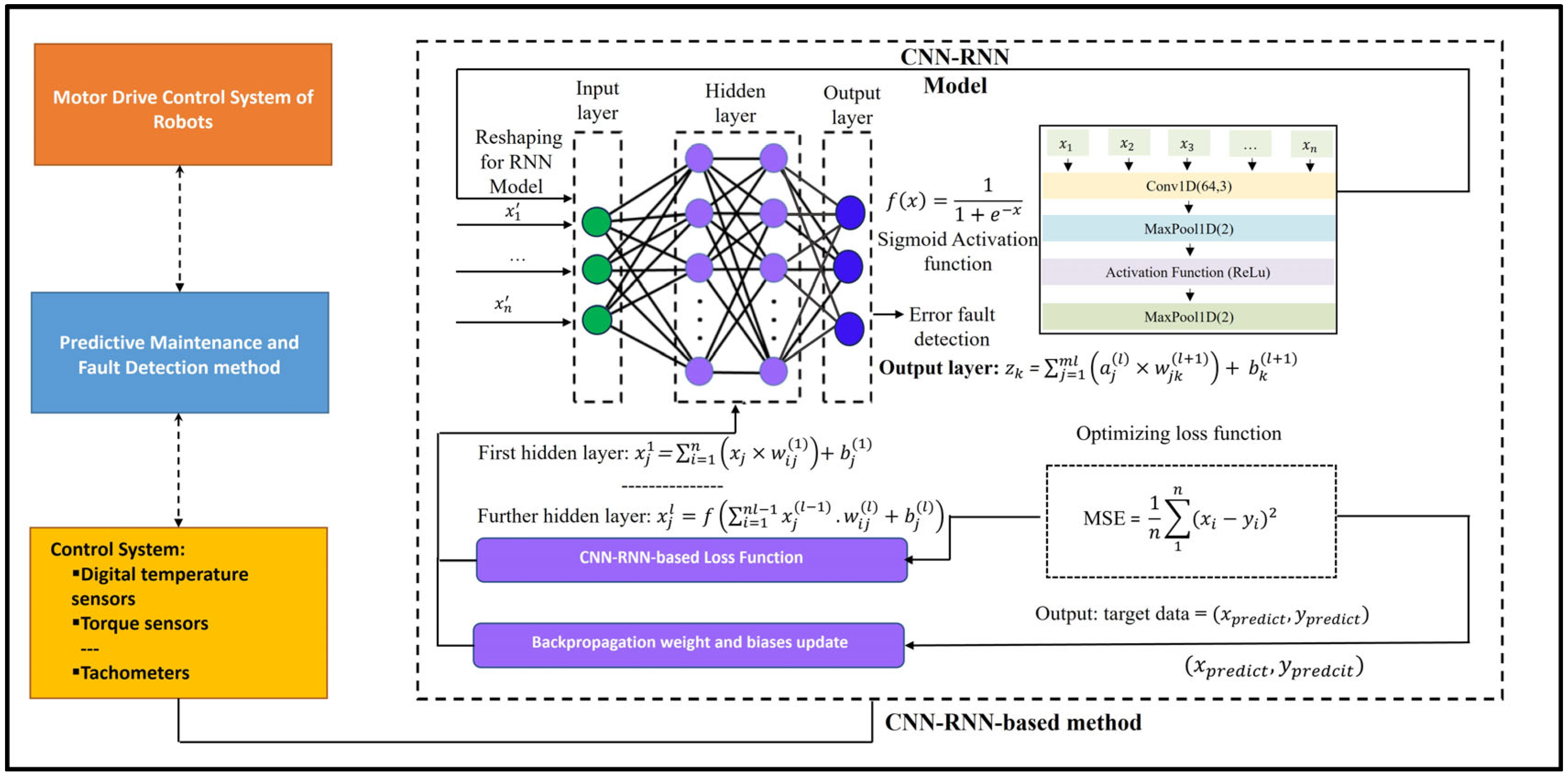
3. Proposed Methodology
3.1. System Architecture
3.2. Dataset Description
3.3. Existing Research and Proposed Fault Detection Algorithms
3.3.1. Traditional and Existing Research Models
3.3.2. Long Short-Term Memory (LSTM) Networks
3.3.3. Convolution Neural Networks
3.3.4. CNN-LSTM Fault Diagnosis Model
| Algorithm 1 CNN-LSTM-based |
 |
3.3.5. Recurrent Neural Networks (RNN)
3.3.6. Proposed CNN-RNN Method
| Algorithm 2 CNN-RNN-based |
 |
4. Experiment Result and Analysis
4.1. Datasets and Evaluation Metrics
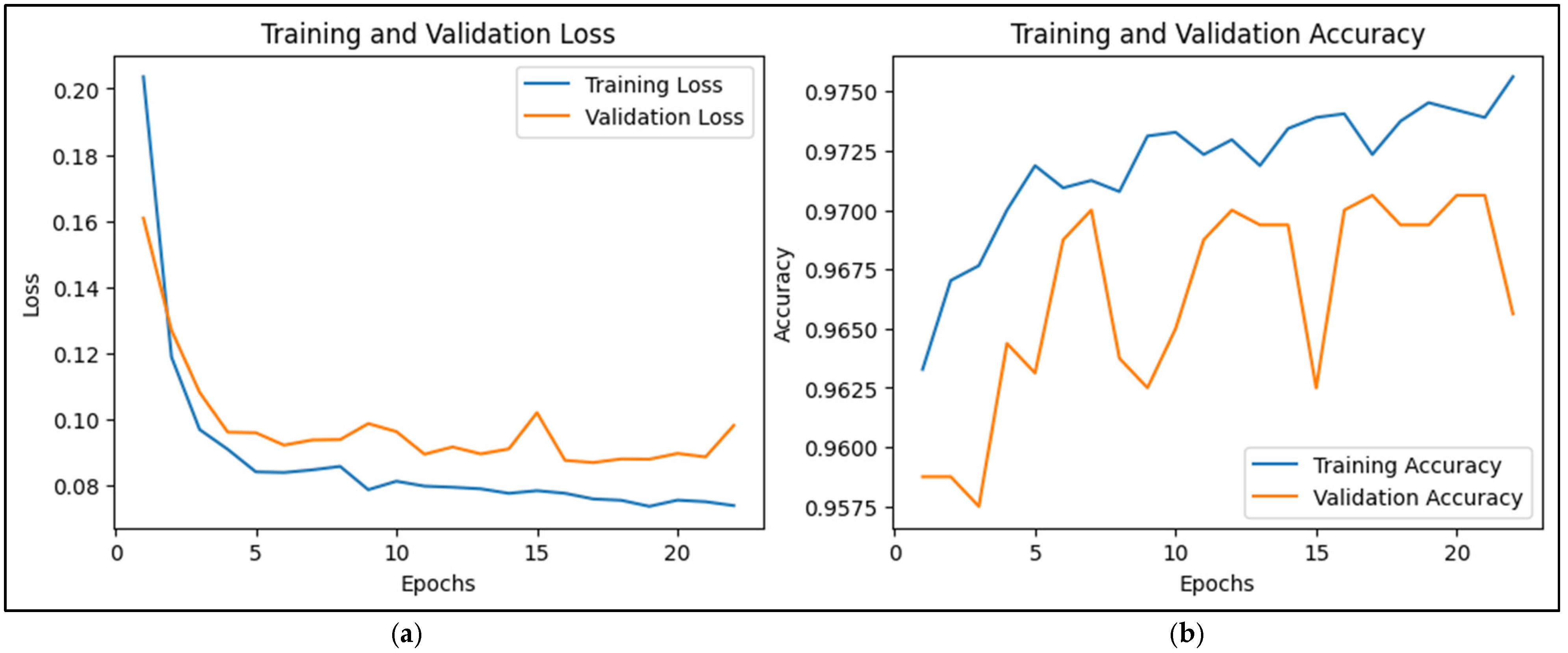
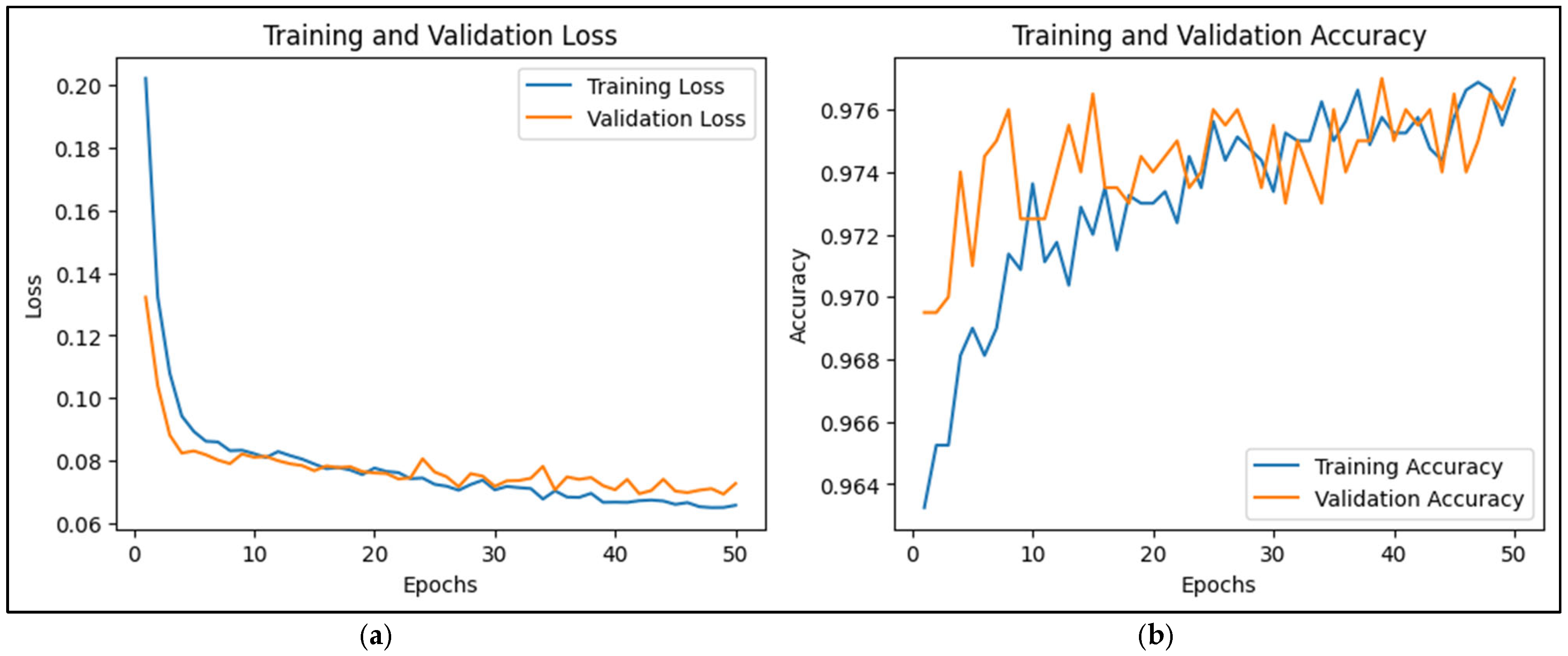
4.2. Experiments and Parameter Settings
4.3. Results and Discussion
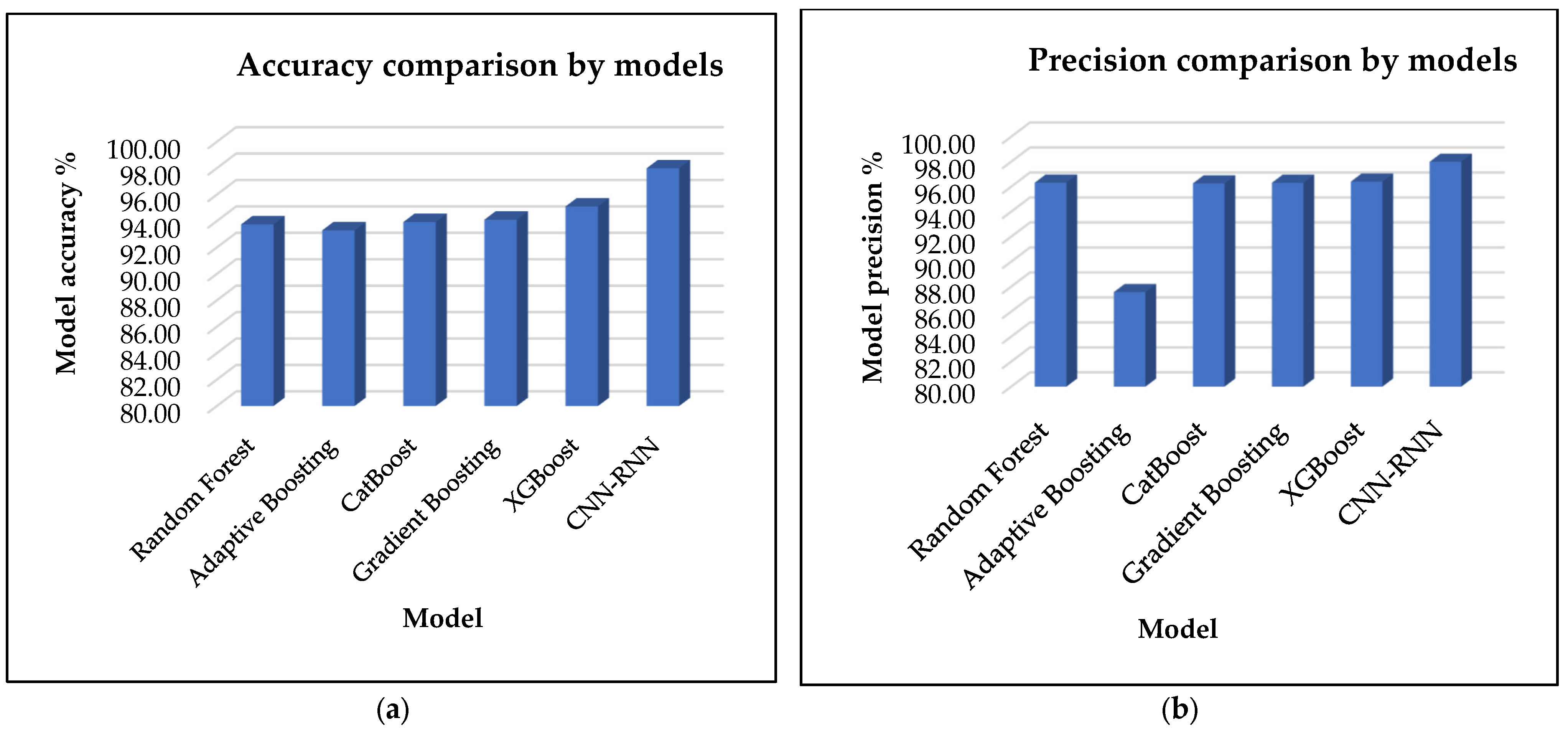
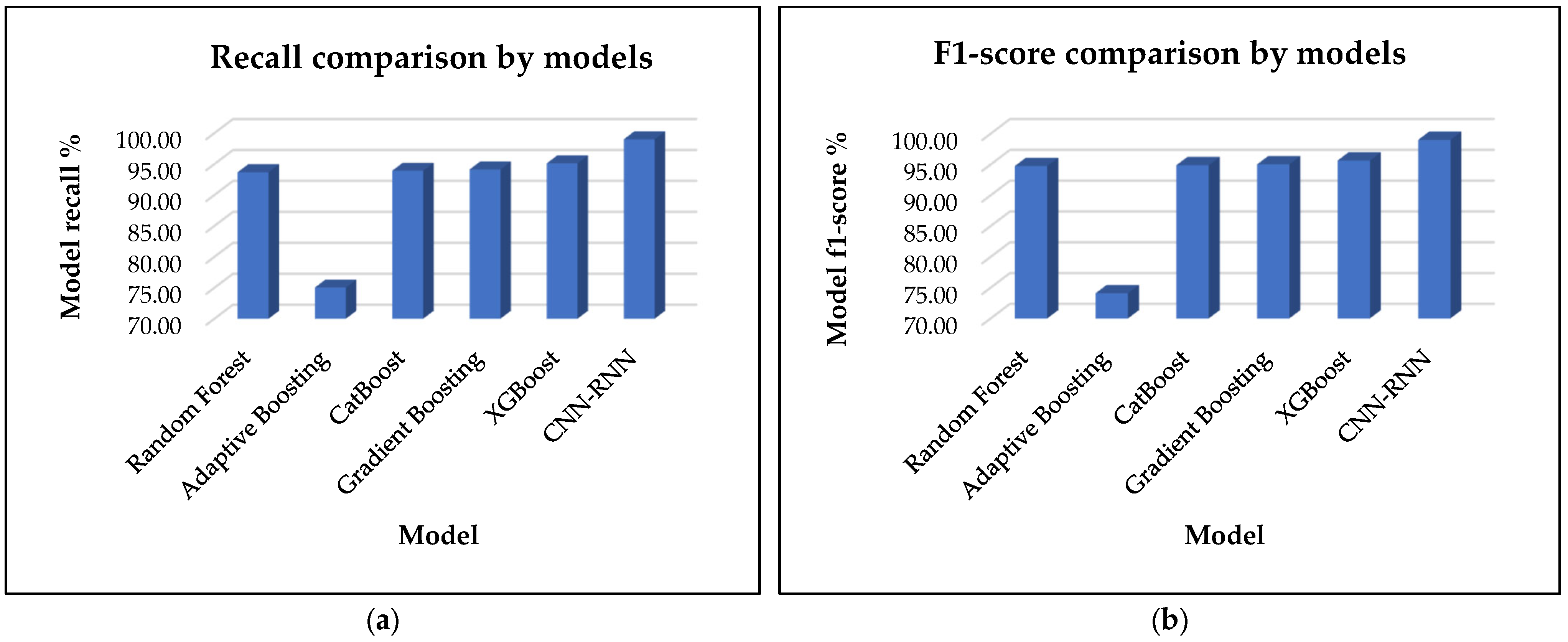
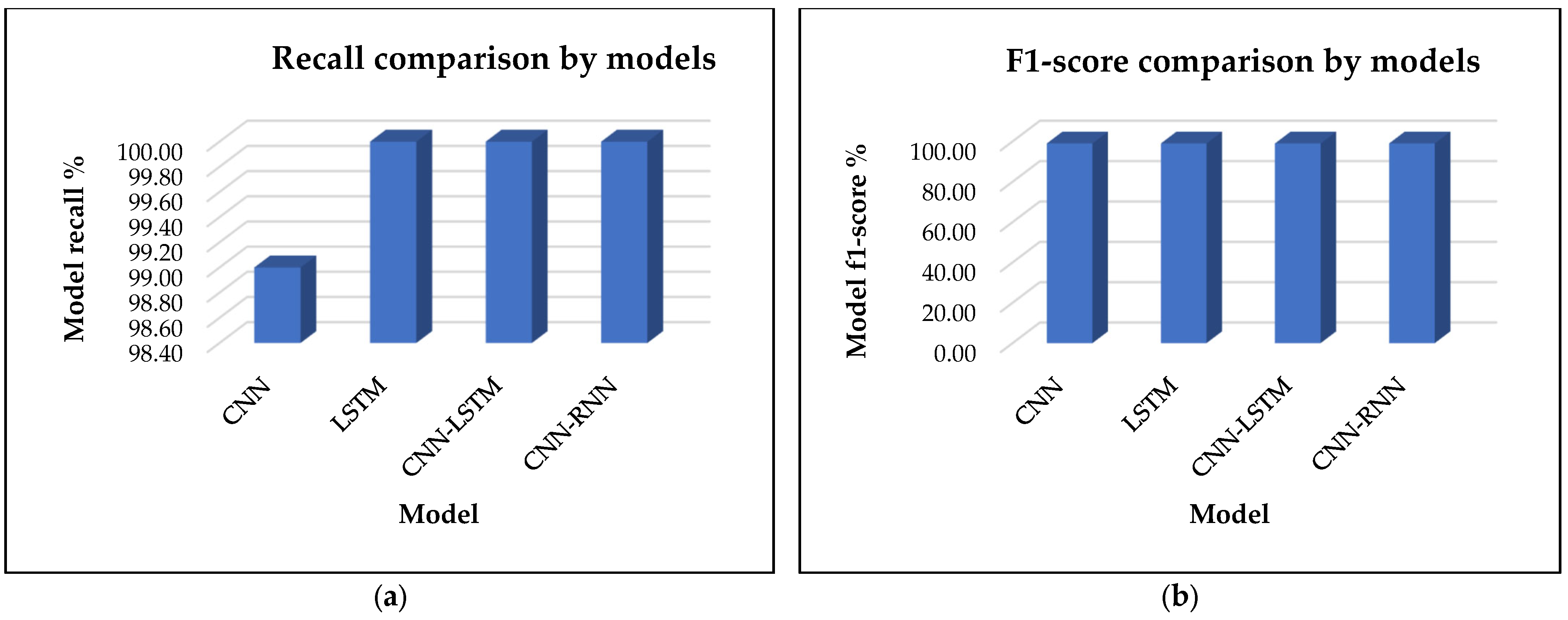
4.3.1. Proposed CNN-RNN-Base and Traditional Models
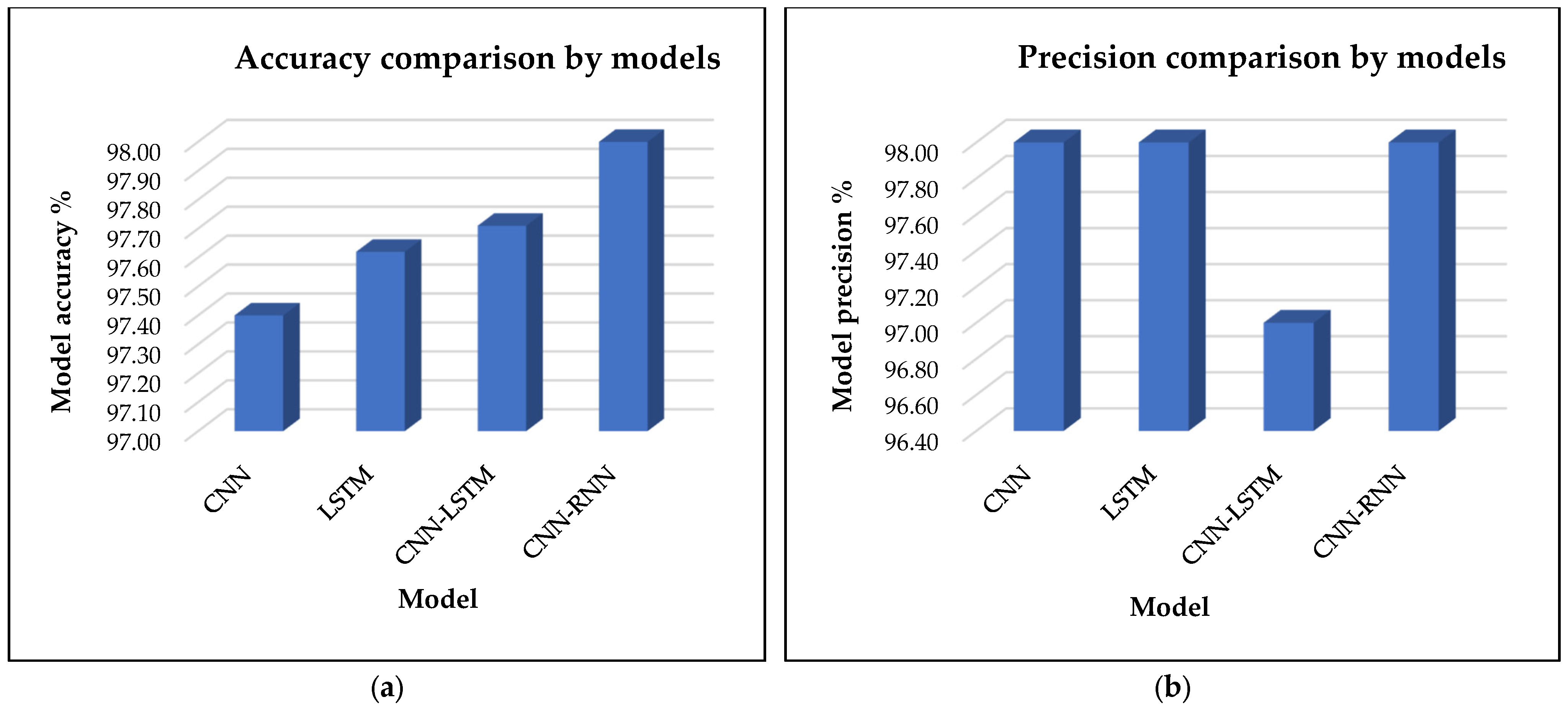
4.3.2. Proposed CNN-RNN-Base and Other Current Existing Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaber, A.A.; Bicker, R. Fault Diagnosis of Industrial Robot Gears Based on Discrete Wavelet Transform and Artificial Neural Network. Insight—Non-Destr. Test. Cond. Monit. 2016, 58, 179–186. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A Deep Learning Method for Bearing Fault Diagnosis Based on Cyclic Spectral Coherence and Convolutional Neural Networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Zhuang, Z.; Lv, H.; Xu, J.; Huang, Z.; Qin, W. A Deep Learning Method for Bearing Fault Diagnosis through Stacked Residual Dilated Convolutions. Appl. Sci. 2019, 9, 1823. [Google Scholar] [CrossRef]
- Yang, K.; Yang, W.; Wang, C. Inverse Dynamic Analysis and Position Error Evaluation of the Heavy-Duty Industrial Robot with Elastic Joints: An Efficient Approach Based on Lie Group. Nonlinear Dyn. 2018, 93, 487–504. [Google Scholar] [CrossRef]
- Purbowaskito, W.; Wu, P.-Y.; Lan, C.-Y. Permanent Magnet Synchronous Motor Driving Mechanical Transmission Fault Detection and Identification: A Model-Based Diagnosis Approach. Electronics 2022, 11, 1356. [Google Scholar] [CrossRef]
- Cho, S.; Seo, H.-R.; Lee, G.; Choi, S.-K.; Choi, H.-J. A Rapid Learning Model Based on Selected Frequency Range Spectral Subtraction for the Data-Driven Fault Diagnosis of Manufacturing Systems. Int. J. Precis. Eng. Manuf.-Smart Technol. 2023, 1, 49–62. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Jiang, B.; Pillay, P.; Rakheja, S. A Comprehensive Review on Signal-Based and Model-Based Condition Monitoring of Wind Turbines: Fault Diagnosis and Lifetime Prognosis. Proc. IEEE 2022, 110, 754–806. [Google Scholar] [CrossRef]
- Yang, K.; Yang, W.; Cheng, G.; Lu, B. A New Methodology for Joint Stiffness Identification of Heavy Duty Industrial Robots with the Counterbalancing System. Robot. Comput.-Integr. Manuf. 2018, 53, 58–71. [Google Scholar] [CrossRef]
- Liu, H.; Lei, Y.; Yang, X.; Song, W.; Cao, J. Deflection Estimation of Industrial Robots with Flexible Joints. Fundam. Res. 2022, 2, 447–455. [Google Scholar] [CrossRef]
- Quarta, D.; Pogliani, M.; Polino, M.; Maggi, F.; Zanchettin, A.M.; Zanero, S. An Experimental Security Analysis of an Industrial Robot Controller. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Yi, H.; Lu, N. Data-Driven Fault Diagnosis for Dynamic Traction Systems in High-Speed Trains. Sci. Sin. Informationis 2020, 50, 496–510. [Google Scholar] [CrossRef]
- Lin, K.-Y.; Jamrus, T. Industrial Data-Driven Modeling for Imbalanced Fault Diagnosis. Ind. Manag. Data Syst. 2024, 124, 3108–3137. [Google Scholar] [CrossRef]
- Bi, K.; Liao, A.; Hu, D.; Shi, W.; Liu, R.; Sun, C. Simulation Data-Driven Fault Diagnosis Method for Metro Traction Motor Bearings under Small Samples and Missing Fault Samples. Meas. Sci. Technol. 2024, 35, 105117. [Google Scholar] [CrossRef]
- Buizza Avanzini, G.; Ceriani, N.M.; Zanchettin, A.M.; Rocco, P.; Bascetta, L. Safety Control of Industrial Robots Based on a Distributed Distance Sensor. IEEE Trans. Control. Syst. Technol. 2014, 22, 2127–2140. [Google Scholar] [CrossRef]
- Frizzo Stefenon, S.; Zanetti Freire, R.; Henrique Meyer, L.; Picolotto Corso, M.; Sartori, A.; Nied, A.; Rodrigues Klaar, A.C.; Yow, K.C. Fault Detection in Insulators Based on Ultrasonic Signal Processing Using a Hybrid Deep Learning Technique. IET Sci. Meas. Technol. 2020, 14, 953–961. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, L.; Wang, X. Fault Detection for Motor Drive Control System of Industrial Robots Using CNN-LSTM-Based Observers. CES Trans. Electr. Mach. Syst. 2023, 7, 144–152. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Wang, Y.; Sun, Y.; Sun, G. Intelligent Joint Actuator Fault Diagnosis for Heavy-Duty Industrial Robots. IEEE Sens. J. 2024, 24, 15292–15301. [Google Scholar] [CrossRef]
- Shoorkand, H.D.; Nourelfath, M.; Hajji, A. A Hybrid CNN-LSTM Model for Joint Optimization of Production and Imperfect Predictive Maintenance Planning. Reliab. Eng. Syst. Saf. 2024, 241, 109707. [Google Scholar] [CrossRef]
- Bi, Z.M.; Luo, C.; Miao, Z.; Zhang, B.; Zhang, W.J.; Wang, L. Safety Assurance Mechanisms of Collaborative Robotic Systems in Manufacturing. Robot. Comput.-Integr. Manuf. 2021, 67, 102022. [Google Scholar] [CrossRef]
- Ferraguti, F.; Talignani Landi, C.; Costi, S.; Bonfè, M.; Farsoni, S.; Secchi, C.; Fantuzzi, C. Safety Barrier Functions and Multi-Camera Tracking for Human–Robot Shared Environment. Robot. Auton. Syst. 2020, 124, 103388. [Google Scholar] [CrossRef]
- Jaber, A.A.; Bicker, R. Development of a Condition Monitoring Algorithm for Industrial Robots Based on Artificial Intelligence and Signal Processing Techniques. Int. J. Electr. Comput. Eng. (IJECE) 2018, 8, 996. [Google Scholar] [CrossRef]
- Chen, Z.; Gryllias, K.; Li, W. Mechanical Fault Diagnosis Using Convolutional Neural Networks and Extreme Learning Machine. Mech. Syst. Signal Process. 2019, 133, 106272. [Google Scholar] [CrossRef]
- Zhang, X.; Rane, K.P.; Kakaravada, I.; Shabaz, M. Research on Vibration Monitoring and Fault Diagnosis of Rotating Machinery Based on Internet of Things Technology. Nonlinear Eng. 2021, 10, 245–254. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep Learning and Its Applications to Machine Health Monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Xiao, C.; Liu, Z.; Zhang, T.; Zhang, X. Deep Learning Method for Fault Detection of Wind Turbine Converter. Appl. Sci. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, Q.; Si, X.-S.; Sun, G.-X.; Qin, A.-S. Intelligent Fault Diagnosis Approach Based on Composite Multi-Scale Dimensionless Indicators and Affinity Propagation Clustering. IEEE Sens. J. 2020, 20, 11439–11453. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Luo, C.; Miao, Q. Deep Learning Domain Adaptation for Electro-Mechanical Actuator Fault Diagnosis under Variable Driving Waveforms. IEEE Sens. J. 2022, 22, 10783–10793. [Google Scholar] [CrossRef]
- Yang, R.; Huang, M.; Lu, Q.; Zhong, M. Rotating Machinery Fault Diagnosis Using Long-Short-Term Memory Recurrent Neural Network. IFAC-PapersOnLine 2018, 51, 228–232. [Google Scholar] [CrossRef]
- Shi, H.; Guo, L.; Tan, S.; Bai, X. Rolling Bearing Initial Fault Detection Using Long Short-Term Memory Recurrent Network. IEEE Access 2019, 7, 171559–171569. [Google Scholar] [CrossRef]
- Abdul, Z.K.; Al-Talabani, A.K.; Ramadan, D.O. A Hybrid Temporal Feature for Gear Fault Diagnosis Using the Long Short Term Memory. IEEE Sens. J. 2020, 20, 14444–14452. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, C.; Wang, S. Sparse One-Dimensional Convolutional Neural Network-Based Feature Learning for Fault Detection and Diagnosis in Multivariable Manufacturing Processes. Neural Comput. Appl. 2022, 34, 4343–4366. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, S.; Ma, Y.; Huang, B.; Liu, F.; Luan, X. Sensor Fault Estimation in a Probabilistic Framework for Industrial Processes and Its Applications. IEEE Trans. Ind. Inform. 2021, 18, 387–396. [Google Scholar] [CrossRef]
- Tang, X.; Xu, Z.; Wang, Z. A Novel Fault Diagnosis Method of Rolling Bearing Based on Integrated Vision Transformer Model. Sensors 2022, 22, 3878. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L.; Qian, S. A Small Sample Bearing Fault Diagnosis Method Based on Variational Mode Decomposition, Autocorrelation Function, and Convolutional Neural Network. Int. J. Adv. Manuf. Technol. 2023, 124, 3887–3898. [Google Scholar] [CrossRef]
- Ai, T.; Liu, Z.; Zhang, J.; Liu, H.; Jin, Y.; Zuo, M. Fully Simulated-Data-Driven Transfer-Learning Method for Rolling-Bearing-Fault Diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 3526111. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, X.; Gong, W.; Chen, Y.; Gao, H. Efficient Federated Convolutional Neural Network with Information Fusion for Rolling Bearing Fault Diagnosis. Control Eng. Pract. 2021, 116, 104913. [Google Scholar] [CrossRef]
- Pan, J.; Qu, L.; Peng, K. Sensor and Actuator Fault Diagnosis for Robot Joint Based on Deep CNN. Entropy 2021, 23, 751. [Google Scholar] [CrossRef]
- Liu, C.; Meerten, Y.; Declercq, K.; Gryllias, K. Vibration-Based Gear Continuous Generating Grinding Fault Classification and Interpretation with Deep Convolutional Neural Network. J. Manuf. Process. 2022, 79, 688–704. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A Deep Convolutional Neural Network with New Training Methods for Bearing Fault Diagnosis under Noisy Environment and Different Working Load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Alhussein, M.; Aurangzeb, K.; Haider, S.I. Hybrid CNN-LSTM Model for Short-Term Individual Household Load Forecasting. IEEE Access 2020, 8, 180544–180557. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A Novel Fault Diagnosis Method Based on CNN and LSTM and Its Application in Fault Diagnosis for Complex Systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Xu, J. Robust Amplitude Control Set Model Predictive Control with Low-Cost Error for SPMSM Based on Nonlinear Extended State Observer. IEEE Trans. Power Electron. 2024, 39, 7016–7028. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, C.; Liu, S.; Song, Z. A New Cascaded Adaptive Deadbeat Control Method for PMSM Drive. IEEE Trans. Ind. Electron. 2022, 70, 3384–3393. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.-C.; Wu, C.-H.; Wang, Y.; Cui, Z.-X.; Niu, C. A Data-Driven Approach to RUL Prediction of Tools. Adv. Manuf. 2024, 12, 6–18. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Othman, M.L.; Padmanaban, S.; Sekar, K.; Ramachandran, R.; Hizam, H.; Vinayagam, A.; Islam, M.Z. LSTM Recurrent Neural Network Classifier for High Impedance Fault Detection in Solar PV Integrated Power System. IEEE Access 2021, 9, 32672–32687. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Lee, K.B.; Cheon, S.; Kim, C.O. A Convolutional Neural Network for Fault Classification and Diagnosis in Semiconductor Manufacturing Processes. IEEE Trans. Semicond. Manuf. 2017, 30, 135–142. [Google Scholar] [CrossRef]
- Han, P.; Li, G.; Skulstad, R.; Skjong, S.; Zhang, H. A Deep Learning Approach to Detect and Isolate Thruster Failures for Dynamically Positioned Vessels Using Motion Data. IEEE Trans. Instrum. Meas. 2020, 70, 3501511. [Google Scholar] [CrossRef]
- Grezmak, J.; Zhang, J.; Wang, P.; Gao, R.X. Multi-Stream Convolutional Neural Network-Based Fault Diagnosis for Variable Frequency Drives in Sustainable Manufacturing Systems. Procedia Manuf. 2020, 43, 511–518. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Feng, T.; Sun, Y.; Zhang, X. Research on Rotating Machinery Fault Diagnosis Method Based on Energy Spectrum Matrix and Adaptive Convolutional Neural Network. Processes 2020, 9, 69. [Google Scholar] [CrossRef]


| Number | Parameter | Value |
|---|---|---|
| 1 | Conv1D layer | 64 filters, kernel size of 3, ReLU activation |
| 2 | Dropout rate | 20% |
| 3 | RNN layer | 32 units, no sequence output |
| 4 | Dense layer | 1 unit with sigmoid activation |
| 5 | Optimizer | Adam |
| 6 | Loss function | Binary cross-entropy |
| 7 | Batch size | 32 |
| 8 | Epochs | 50 |
| Number | Model | Value |
|---|---|---|
| 1 | CNN | 0.0440 |
| 2 | LSTM | 0.0420 |
| 3 | CNN-LSTM | 0.0400 |
| 4 | CNN-RNN | 0.0354 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eang, C.; Lee, S. Predictive Maintenance and Fault Detection for Motor Drive Control Systems in Industrial Robots Using CNN-RNN-Based Observers. Sensors 2025, 25, 25. https://doi.org/10.3390/s25010025
Eang C, Lee S. Predictive Maintenance and Fault Detection for Motor Drive Control Systems in Industrial Robots Using CNN-RNN-Based Observers. Sensors. 2025; 25(1):25. https://doi.org/10.3390/s25010025
Chicago/Turabian StyleEang, Chanthol, and Seungjae Lee. 2025. "Predictive Maintenance and Fault Detection for Motor Drive Control Systems in Industrial Robots Using CNN-RNN-Based Observers" Sensors 25, no. 1: 25. https://doi.org/10.3390/s25010025
APA StyleEang, C., & Lee, S. (2025). Predictive Maintenance and Fault Detection for Motor Drive Control Systems in Industrial Robots Using CNN-RNN-Based Observers. Sensors, 25(1), 25. https://doi.org/10.3390/s25010025









