Research on SPAD Estimation Model for Spring Wheat Booting Stage Based on Hyperspectral Analysis
Abstract
1. Introduction
2. Data and Methods
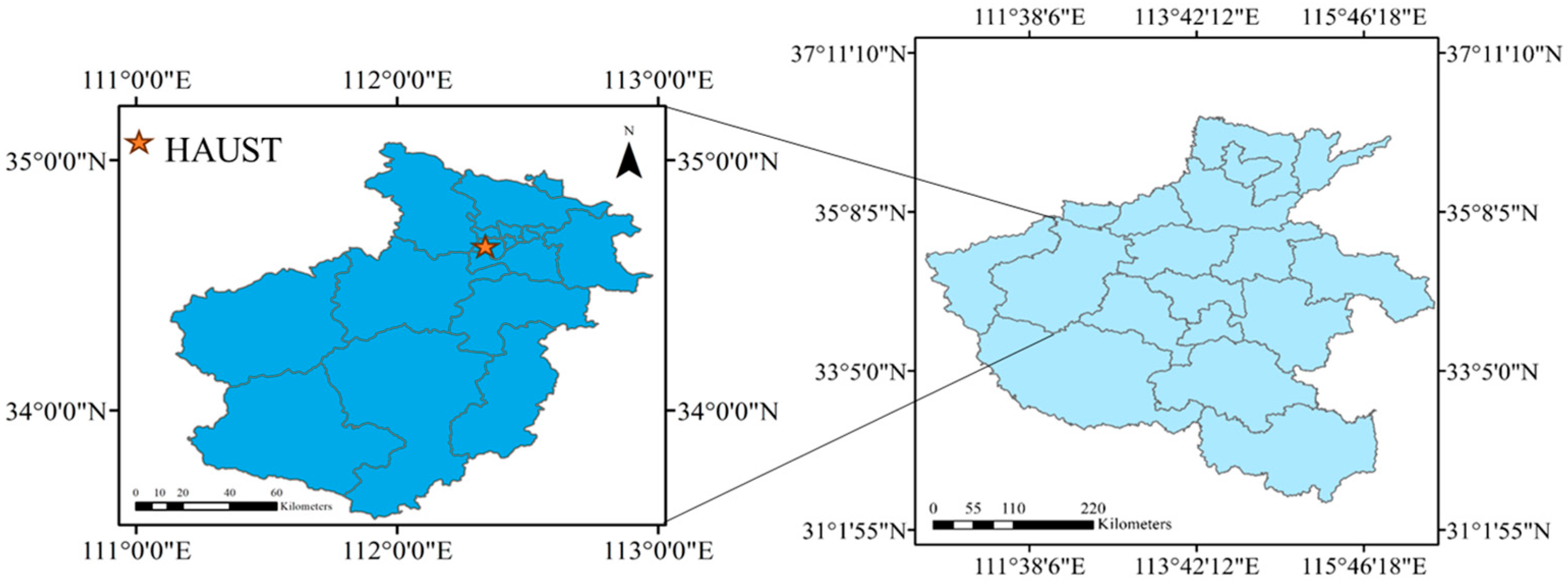
2.1. Experimental Material
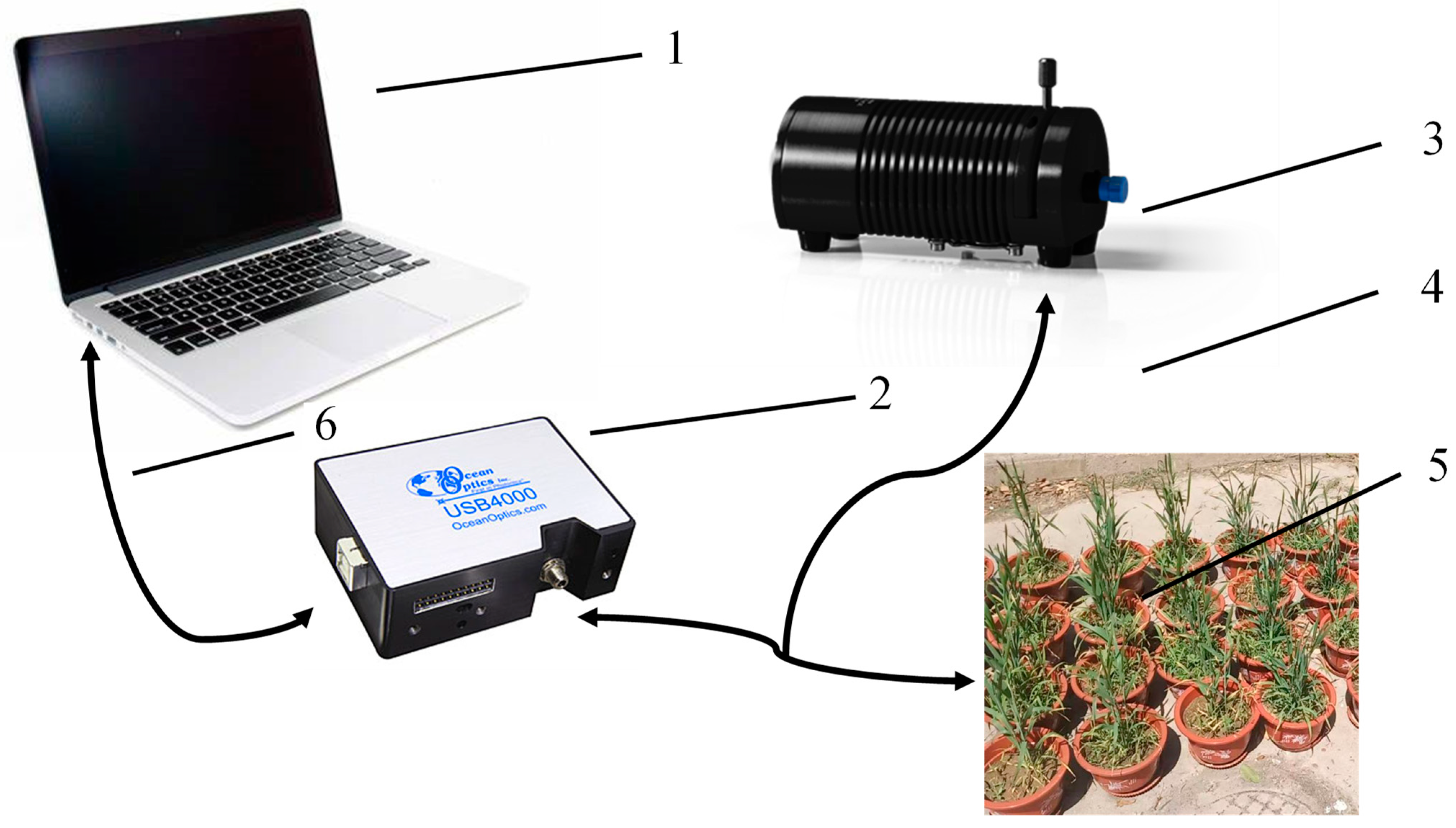
2.2. Data Acquisition
2.3. Fractional-Order Differentiation
2.4. Fractional-Order Differential Spectral Index
2.5. Slime Mold Alrorithm [26] (SMA)
2.6. SMA-LSSVM Prediction Model
2.7. Model Construction Method and Accuracy
3. Results and Discussion
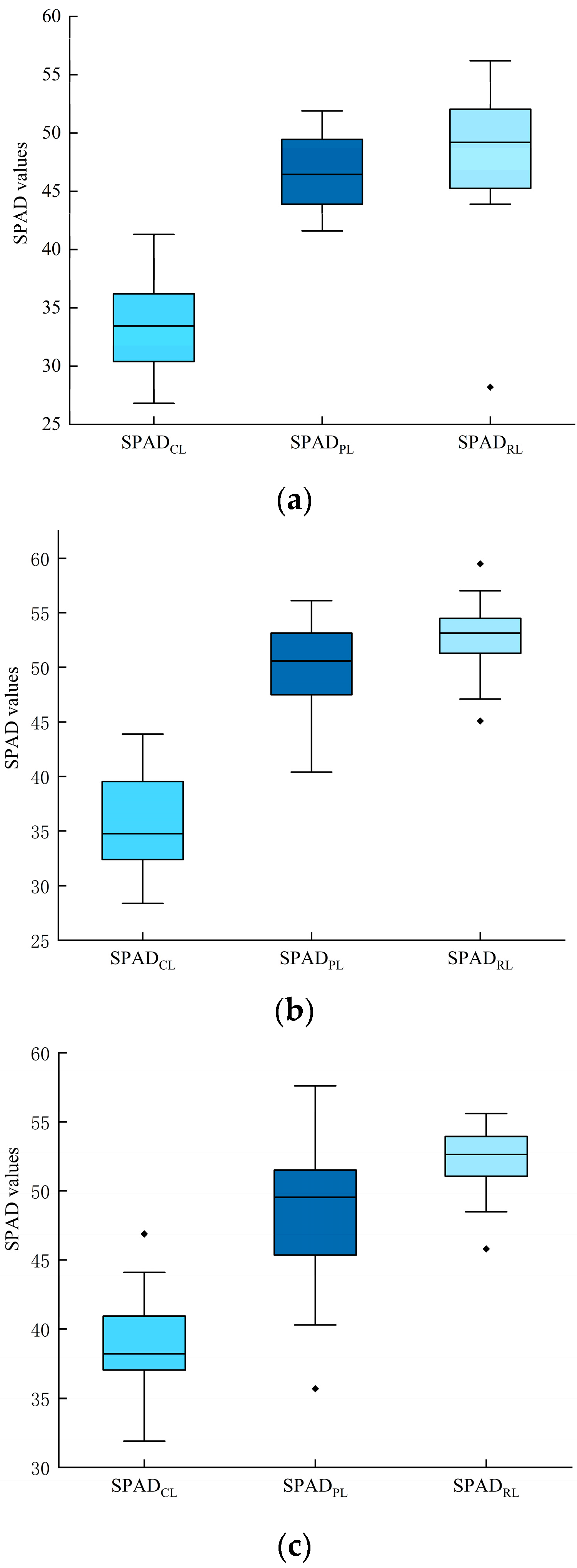
3.1. Analysis of SPAD Content at Different Spatial Vertical Scales
3.2. Fractional-Order Differential Spectroscopy
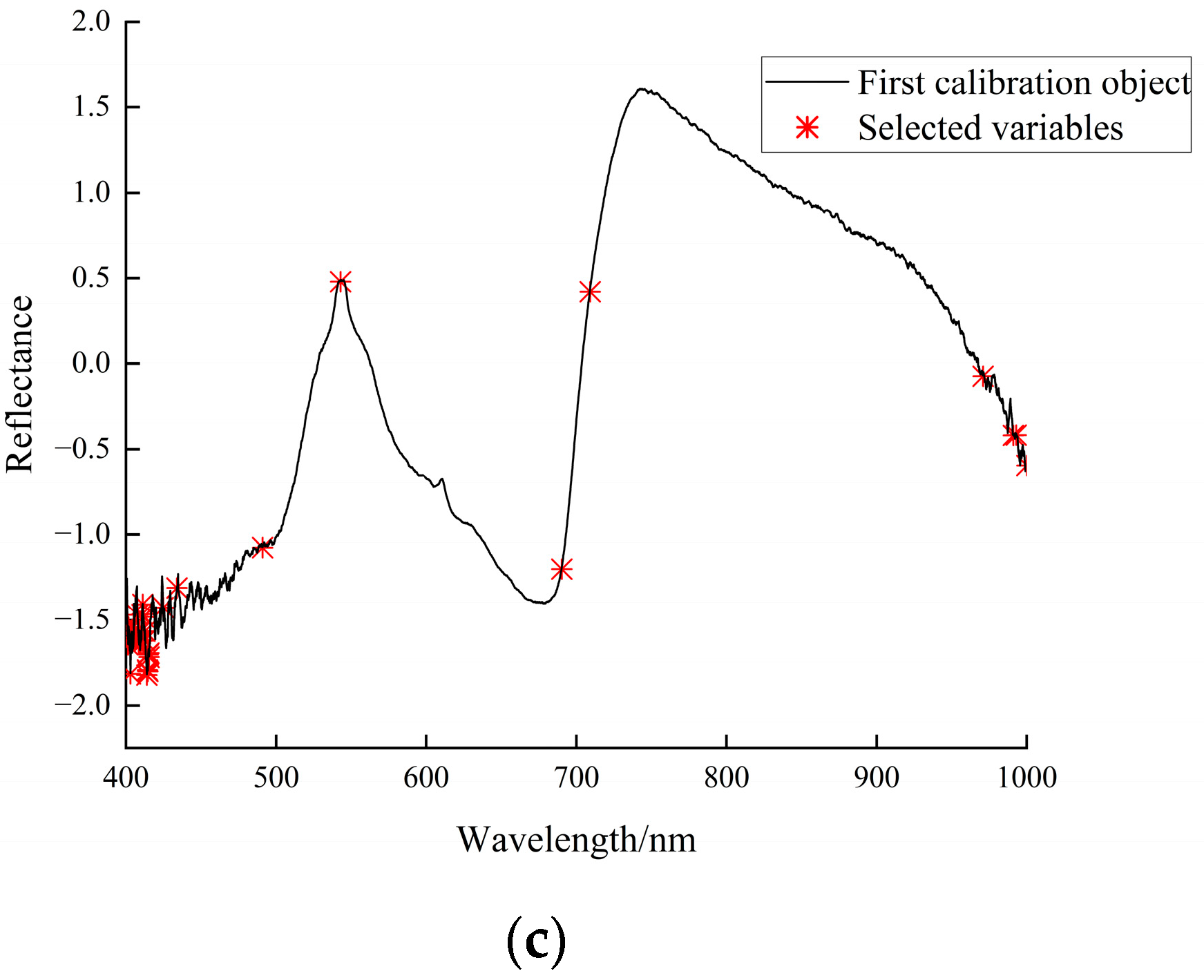
3.2.1. Fractional-Order Differential Spectral Downscaling
3.2.2. Correlation of Fractional-Order Differential Spectra with SPAD
3.3. The Construction of Fractional-Order Differential Spectral Index
3.4. Model Construction and Evaluation
3.4.1. Fractional-Order Differential Spectral Reflectance
3.4.2. Fractional-Order Differential Spectral Index
3.4.3. Feature Fusion
3.5. Discussion
4. Conclusions
- The correlation between spectral reflectance and wheat SPAD was promoted by fractional-order differentiation of the raw spectra, and the maximum correlation coefficient was of the order of 0.4, corresponding to a wavelength of 433.2 nm, with a value of −0.568, which is 9.3% higher than the maximum correlation coefficient of the original spectra.
- Among the three fractional-order differential spectral indices, the optimal correlation between the single-band and wheat SPAD was −0.568, and the optimal correlation coefficients between the FDI, FRI and FNDI and wheat SPAD were 0.724, 0.700 and 0.680, respectively, suggesting that the two-band differential spectral indices can reflect wheat SPAD more sensitively than the optimal fractional-order wavelengths.
- The SMA-LSSSVM prediction model constructed on the basis of two-band fractional-order differential spectral indices is superior to the optimal fractional-order wavelength and the mixture of the two and better realizes the accomplishment of wheat SPAD.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, L. A Spectral and Image-Based Approach for Phenotypic Information Perception in Wheat. Bachelor’s Thesis, Zhejiang University, Hangzhou, China, 2022. [Google Scholar]
- Liu, T.; Zhang, H.; Wang, Z.Y.; He, C.; Zhang, Q.G.; Jiao, Y.Z. Estimation of leaf area index and chlorophyll content in wheat using unmanned aerial vehicle multispectral estimation. J. Agric. Eng. 2021, 37, 65–72. [Google Scholar]
- Cai, Q.H. Remote Sensing Inversion of Leaf Area Index and Chlorophyll Content in Winter Wheat Based on Wavelet Transformation. Bachelor’s Thesis, China University of Mining and Technology, Beijing, China, 2015. [Google Scholar]
- Liang, H.X.; Ma, Y.H.; Huang, W.J.; Liu, L.Y.; Wang, C.J.; Xue, X.Z. Research progress on monitoring winter wheat growth and variable fertilization based on remote sensing data. J. Wheat Crops 2005, 25, 119–124. [Google Scholar]
- Wang, Y.L. Modeling of Winter Wheat Growth Parameters and Yield Estimation Based on Hyperspectral Remote Sensing. Master’s Thesis, Henan University of Science and Technology, Zhengzhou, China, 2022. [Google Scholar]
- Wang, J.Z.; Tashpolat, T.; Ding, J.L.; Zhang, D.; Liu, W. Estimation of organic carbon content in desert soils based on fractional-order differential preprocessed hyperspectral data. J. Agric. Eng. 2016, 32, 161–169. [Google Scholar]
- Fu, C.B.; Gan, S.; Yuan, X.P.; Xiong, H.G.; Tian, A.H. Impact of fractional calculus on correlation coefficient between available potassium and spectrum data in ground hyperspectral and Landsat 8 image. Mathematics 2019, 7, 488. [Google Scholar] [CrossRef]
- Tong, P.J.; Du, Y.P.; Zheng, K.Y.; Wu, T.; Wang, J.J. Improvement of NIR model by Fractional Order Savitzky Golay Derivation (FOSGD) coupled with wavelength selection. Chemom. Intell. Lab. Syst. 2015, 143, 40–48. [Google Scholar] [CrossRef]
- Jing, X.; Zhang, T.; Zhou, Q.; Yan, J.M.; Huang, Y.Y. Construction of a remote sensing monitoring model for wheat stripe rust based on fractional-order differential spectral indexes. J. Agric. Eng. 2021, 37, 142–151. [Google Scholar]
- Wang, L.M.; Liu, J.; Shao, J.; Yang, F.G.; Gao, J.M. Hyperspectral-based index selection for remote sensing monitoring of spring corn big spot disease. J. Agric. Eng. 2017, 33, 170–177. [Google Scholar]
- Wang, X.P.; Zhang, F.; Kung, H.T.; Johnson, V.C. New methods for improving the remote sensing estimation of Soil Organic Matter Content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in Northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Rukya, S.; Abduaini, A.; Negati, K.; Li, H.; Umuti, A.; Yasenjiang, K.; Li, X.H. Hyperspectral estimation of chlorophyll content in spring wheat based on fractional differentiation. J. Wheat Crops 2019, 39, 738–746. [Google Scholar]
- Liu, Y.; Zhang, Y.W.; Lu, H.Z.; Yang, Y.; Xie, J.Y.; Chen, D.Y. Application of fractional-order differential and ensemble learning to predict soil organic matter from hyperspectra. J. Soils Sediments 2023, 49, 377–392. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.Y.; Chen, D.Y.; Zheng, W.; Ma, Y.X.; Pan, X.Z. Simultaneous estimation of multiple soil properties under moist conditions using fractional-order derivative of vis-NIR spectra and deep learning. Geoderma 2023, 438, 116653. [Google Scholar] [CrossRef]
- Zhao, H.L.; Gan, S.; Yuan, X.P.; Hu, L.; Wang, J.J.; Liu, S. Application of a Fractional Order Differential to the Hyperspectral Inversion of Soil Iron Oxide. Agriculture 2022, 12, 1163. [Google Scholar] [CrossRef]
- Tian, A.H.; Zhao, J.S.; Tang, B.H.; Zhu, D.M.; Fu, C.B.; Xiong, H.G. Hyperspectral Prediction of Soil Total Salt Content by Different Disturbance Degree under a Fractional-Order Differential Model with Differing Spectral Transformations. Remote Sens. 2021, 13, 4283. [Google Scholar] [CrossRef]
- Lin, X.; Sue, Y.C.; Shang, J.L.; Sha, J.M.; Li, X.M.; Sun, Y.Y.; Ji, J.W.; Jin, B. Geographically Weighted Regression Effects on Soil Zinc Content Hyperspectral Modeling by Applying the Fractional-Order Differential. Remote Sens. 2019, 11, 636. [Google Scholar] [CrossRef]
- Ding, W.J. Hyperspectral Remote Sensing Monitoring of Winter Wheat Scab at Different Scales. Master’s Thesis, Anhui University, Hefei, China, 2019. [Google Scholar]
- Chen, H.Y.; Xiang, L.; Gao, H.; Mou, J.Y.; Suo, X.J.; Hua, B.W. Hyperspectral inversion of soil total nitrogen based on fractional differentiation. Remote Sens. Nat. Resour. 2023, 35, 170–178. [Google Scholar]
- Li, C.C.; Wang, Y.L.; Ma, C.Y.; Ding, F.; Li, Y.C.; Chen, W.A.; Li, J.B.; Xiao, Z. Hyperspectral Estimation of Winter Wheat Leaf Area Index Based on Continuous Wavelet Transform and Fractional Order Differentiation. Sensors 2021, 21, 8497. [Google Scholar] [CrossRef]
- Peng, Y.F.; Zhu, X.C.; Xiong, J.L.; Yu, R.Y.; Liu, T.L.; Jiang, Y.M.; Yang, G.J. Estimation of Nitrogen Content on Apple Tree Canopy through Red-Edge Parameters from Fractional-Order Differential Operators using Hyperspectral Reflectance. J. Soc. Remote Sens. 2020, 49, 377–392. [Google Scholar] [CrossRef]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Ma, C.Y. A possible fractional order derivative and optimized spectral indices for assessing total nitrogen content in cotton. Comput. Electron. Agric. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Liang, H.Y. Effects of Drought Stress on Wheat Grain Filling and Its Relationship with Hormones. Master’s Thesis, Northwest Agriculture and Forestry University, Xi’an, China, 2016. [Google Scholar]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Appl. Math. Comput. 2015, 257, 2–11. [Google Scholar] [CrossRef]
- Wang, Y.N. Estimation of Nitrogen Nutrition Index of Winter Wheat by Hyperspectral Remote Sensing. Master’s Thesis, Northwest Agriculture and Forestry University, Xi’an, China, 2022. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machines classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Gao, C.C.; Chen, X.C.; Zhang, R.; Song, Q.Y.; Yi, D.; Wu, Y.Z. Application of three new intelligent algorithms in epidemic early warning model—COVID-19 early warning based on Baidu search Index. Comput. Eng. Appl. 2021, 57, 256–263. [Google Scholar]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Yun, Y.H.; Li, H.D.; Deng, B.C.; Cao, D.S. An overview of variable selection methods in multivariate analysis of near-infrared spectra. TrAC Trends Anal. Chem. 2019, 113, 102–115. [Google Scholar] [CrossRef]
- Ding, Y.J.; Li, M.Z.; Zheng, L.H.; Zhao, R.J.; Li, X.H.; An, D.K. Prediction of chlorophyll content of greenhouse tomato using wavelet transform combined with Nir spectra. Spectrosc. Spectr. Anal. 2011, 31, 2936. [Google Scholar]
- Han, S. Winter Wheat Growth Monitoring and Yield Prediction Based on Multi Platform Remote Sensing Data. Bachelor’s Thesis, Henan Agricultural University, Zhengzhou, China, 2023. [Google Scholar]



| DS | Maximum | Minimum | Mean | Standard Deviation |
|---|---|---|---|---|
| SPADCL(11) | 41.3 | 26.8 | 33.57 | 4.29 |
| SPADPL(11) | 51.9 | 41.6 | 46.63 | 3.24 |
| SPADRL(11) | 56.2 | 43.9 | 49.29 | 3.75 |
| SPADCL(9) | 43.9 | 28.4 | 35.75 | 4.57 |
| SPADPL(9) | 56.1 | 40.4 | 50.16 | 3.92 |
| SPADRL(9) | 59.5 | 45.1 | 52.68 | 3.53 |
| SPADCL(23) | 46.9 | 31.9 | 38.76 | 3.79 |
| SPADPL(23) | 57.6 | 35.7 | 48.43 | 5.27 |
| SPADRL(23) | 55.6 | 45.8 | 52.18 | 2.68 |
| Wavelength/nm | Cc | Wavelength/nm | Cc | Wavelength/nm | Cc | Wavelength/nm | Cc |
|---|---|---|---|---|---|---|---|
| 408.4 | 0.453 ** | 410.76 | 0.441 ** | 407.76 | 0.442 ** | 401.53 | 0.475 ** |
| 408.19 | 0.447 ** | 410.12 | 0.444 ** | 709.22 | −0.452 ** | 434.05 | 0.419 ** |
| 414.62 | 0.444 ** | 411.62 | 0.422 ** | 424.88 | 0.420 ** | 412.69 | 0.420 ** |
| 414.4 | 0.449 ** | 409.69 | 0.444 ** | 414.83 | 0.443 ** | 491.07 | 0.101 |
| 412.47 | 0.431 ** | 411.19 | 0.452 ** | 542.97 | −0.312 * | 993.05 | 0.419 ** |
| 415.26 | 0.425 ** | 413.97 | 0.441 ** | 991.07 | 0.430 ** | 970.98 | 0.302 * |
| 403.03 | 0.457 ** | 402.39 | 0.467 ** | 1000.11 | 0.448 ** | ||
| 415.47 | 0.430 ** | 403.46 | 0.453 ** | 408.61 | 0.447 ** | ||
| 401.74 | 0.470 ** | 409.04 | 0.446 ** | 690.42 | −0.056 |
| Orders | Correlation Coefficient | Wavelength/nm | Orders | Correlation Coefficient | Wavelength/nm |
|---|---|---|---|---|---|
| 0.1 | 0.462 | 718.28 | 0.6 | 0.375 | 441.71 |
| 0.2 | 0.511 | 976.66 | 0.7 | 0.432 | 442.35 |
| 0.3 | 0.423 | 400.45 | 0.8 | 0.405 | 455.5 |
| 0.4 | −0.568 | 443.2 | 0.9 | 0.495 | 415.05 |
| 0.5 | 0.414 | 442.78 | 1.0 | 0.422 | 747.7 |
| Orders | FDI | FRI | FNDI | |||
|---|---|---|---|---|---|---|
| Correlation Coefficient | Band Combination /nm | Correlation Coefficient | Band Combination /nm | Correlation Coefficient | Band Combination /nm | |
| 0 | 0.618 | (509.86, 510.07) | 0.645 | (838.46, 822.98) | 0.644 | (838.46, 822.98) |
| 0.1 | 0.614 | (858.12, 848.58) | 0.590 | (864.03, 850.21) | 0.590 | (864.03, 850.21) |
| 0.2 | 0.634 | (858.12, 849.67) | 0.571 | (861.52, 845.7) | 0.590 | (516.72, 966.46) |
| 0.3 | 0.674 | (989.59, 438.1) | 0.610 | (443.63, 450.2) | 0.632 | (444.47, 937.33) |
| 0.4 | 0.662 | (968.98, 442.78) | 0.676 | (443.41, 912.68) | 0.637 | (468.81, 937.33) |
| 0.5 | 0.685 | (927.72, 468.81) | 0.696 | (475.12, 888.7) | 0.672 | (468.81, 927.72) |
| 0.6 | 0.691 | (989.59, 483.74) | −0.687 | (899.77, 468.81) | 0.680 | (468.81, 851.65) |
| 0.7 | 0.724 | (989.59, 488.35) | 0.700 | (475.12, 841.72) | 0.672 | (468.81, 824.62) |
| 0.8 | 0.669 | (989.59, 488.35) | −0.671 | (870.05, 628.52) | 0.637 | (675.38, 754.14) |
| 0.9 | 0.661 | (837.37, 853.63) | 0.650 | (996.34, 411.62) | 0.622 | (789.04, 649.19) |
| 1.0 | 0.667 | (989.59, 437.89) | 0.649 | (475.12, 643.25) | 0.619 | (453.59, 751.87) |
| Differential Spectral Indices | Algorithm | Test | Validation | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| 3 differential spectra | LSSVM | 0.914 | 3.119 | 0.888 | 4.494 |
| SMA-LSSVM | 0.914 | 3.124 | 0.889 | 4.421 | |
| 4 differential spectra | LSSVM | 0.910 | 3.250 | 0.889 | 4.439 |
| SMA-LSSVM | 0.924 | 2.735 | 0.915 | 3.411 | |
| 5 differential spectra | LSSVM | 0.909 | 3.282 | 0.894 | 4.255 |
| SMA-LSSVM | 0.900 | 3.625 | 0.906 | 3.744 | |
| Differential Spectral Indices | Algorithm | Test | Validation | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| 7 differential spectral indices | LSSVM | 0.934 | 2.405 | 0.909 | 3.643 |
| SMA-LSSVM | 0.989 | 0.409 | 0.937 | 2.504 | |
| 8 differential spectral indices | LSSVM | 0.939 | 2.202 | 0.910 | 3.611 |
| SMA-LSSVM | 0.997 | 0.093 | 0.931 | 2.754 | |
| 9 differential spectral indices | LSSVM | 0.936 | 2.303 | 0.909 | 3.646 |
| SMA-LSSVM | 0.959 | 1.474 | 0.927 | 2.906 | |
| Algorithm | Test | Validation | ||
|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |
| LSSVM | 0.942 | 2.093 | 0.896 | 4.175 |
| SMA-LSSVM | 0.981 | 0.684 | 0.903 | 3.899 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Zhang, H.; Ma, H.; Ji, J. Research on SPAD Estimation Model for Spring Wheat Booting Stage Based on Hyperspectral Analysis. Sensors 2024, 24, 1693. https://doi.org/10.3390/s24051693
Cui H, Zhang H, Ma H, Ji J. Research on SPAD Estimation Model for Spring Wheat Booting Stage Based on Hyperspectral Analysis. Sensors. 2024; 24(5):1693. https://doi.org/10.3390/s24051693
Chicago/Turabian StyleCui, Hongwei, Haolei Zhang, Hao Ma, and Jiangtao Ji. 2024. "Research on SPAD Estimation Model for Spring Wheat Booting Stage Based on Hyperspectral Analysis" Sensors 24, no. 5: 1693. https://doi.org/10.3390/s24051693
APA StyleCui, H., Zhang, H., Ma, H., & Ji, J. (2024). Research on SPAD Estimation Model for Spring Wheat Booting Stage Based on Hyperspectral Analysis. Sensors, 24(5), 1693. https://doi.org/10.3390/s24051693






