UAV Trajectory Control and Power Optimization for Low-Latency C-V2X Communications in a Federated Learning Environment
Abstract
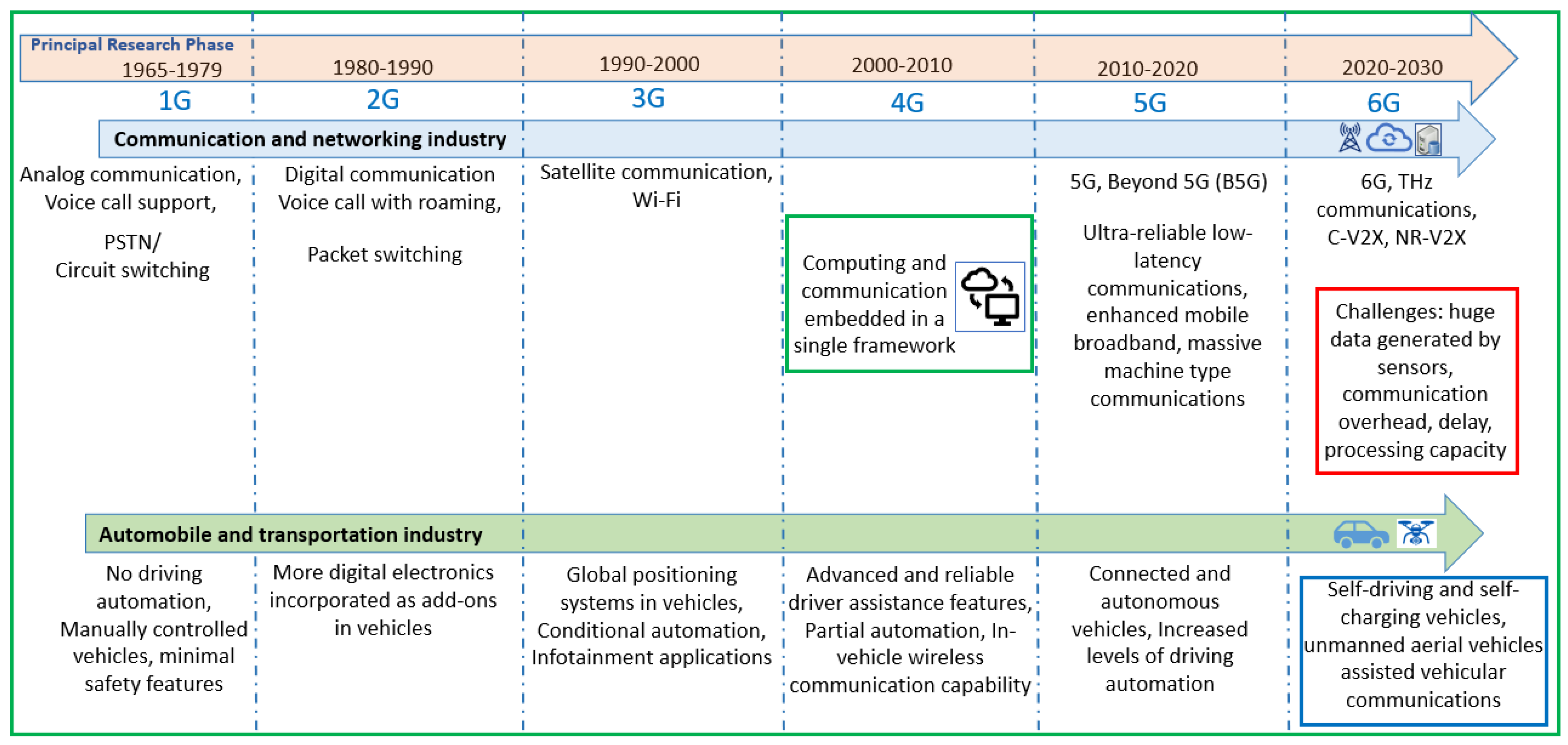
1. Introduction
1.1. Contributions
- We propose to examine end-to-end packet latency as well as UAV energy consumption based on FL with varying numbers of vehicles. From the FL iterations, we study the probability of the optimal trajectory prediction of the UAV using different neural network models. This is a significant extension of our previous work in [28] where we analyzed the variation in the UAV transmit power for a varying number of vehicles in a gross data offloading scenario.
- As a function of computation offloading to UAV and the local vehicle model computation time, we plot the average task completion latency for varying numbers of vehicles. Using long short-term memory (LSTM), gated recurrent unit (GRU), recurrent neural network (RNN) and convolutional neural network (CNN)-LSTM models, we compare the average task completion latency for gross data offloading and FL, and the probability of optimal UAV trajectory prediction.
- We validate the proposed solution by calculating the number of training iterations required to satisfy the service-time constraint for LSTM, GRU, RNN, and CNN-LSTM models. Here, we use the V2X-Sim and LTE I/Q datasets and based on the number of vehicles that exceed a specified time frame to process a task, we conclude the maximum number of vehicles a UAV can support without violating the identified constraints. Furthermore, we utilize the V2X-Sim dataset to verify the FL model convergence characteristics and performance trade-offs [29] for the proposed UAV-assisted C-V2X communications.
- Unlike existing works where the device-to-device communication largely depends on neighbor discovery [30], in this work, the TTI is selected using the distributed scheduling protocol known as sensing-based semi-persistent scheduling (SPS) [31]. Since the vehicles and the UAV operate at different speeds, SPS is utilized to enable vehicles to independently select and manage the available bandwidth and the UAV communication and computational resources.
1.2. Organization
2. Related Work
- In NOMA, multiple vehicles share the same time and frequency resources, and their signals are distinguished by different power levels. Vehicles with stronger channel conditions are assigned lower power, while vehicles with weaker channel conditions are assigned higher power [41]. This leads to the efficient utilization of the available resources and enhances the throughput [42].
- OFDM divides the spectrum into multiple orthogonal subcarriers in the frequency domain and uses them to transmit data simultaneously. However, OFDM faces challenges in high-mobility environments, where Doppler spread is significant and the performance degrades in NLoS conditions and multipath environments [43].
- OTFS modulation improves communication performance in scenarios with high mobility, NLoS conditions, and multipath environments [9]. OTFS transforms the wireless channel into a new domain called the delay-Doppler domain, where the instantaneous channel conditions appear to be stationary in high-mobility scenarios [10].
3. System Model
3.1. Packet Arrival at the UAV
3.2. UAV Power Consumption
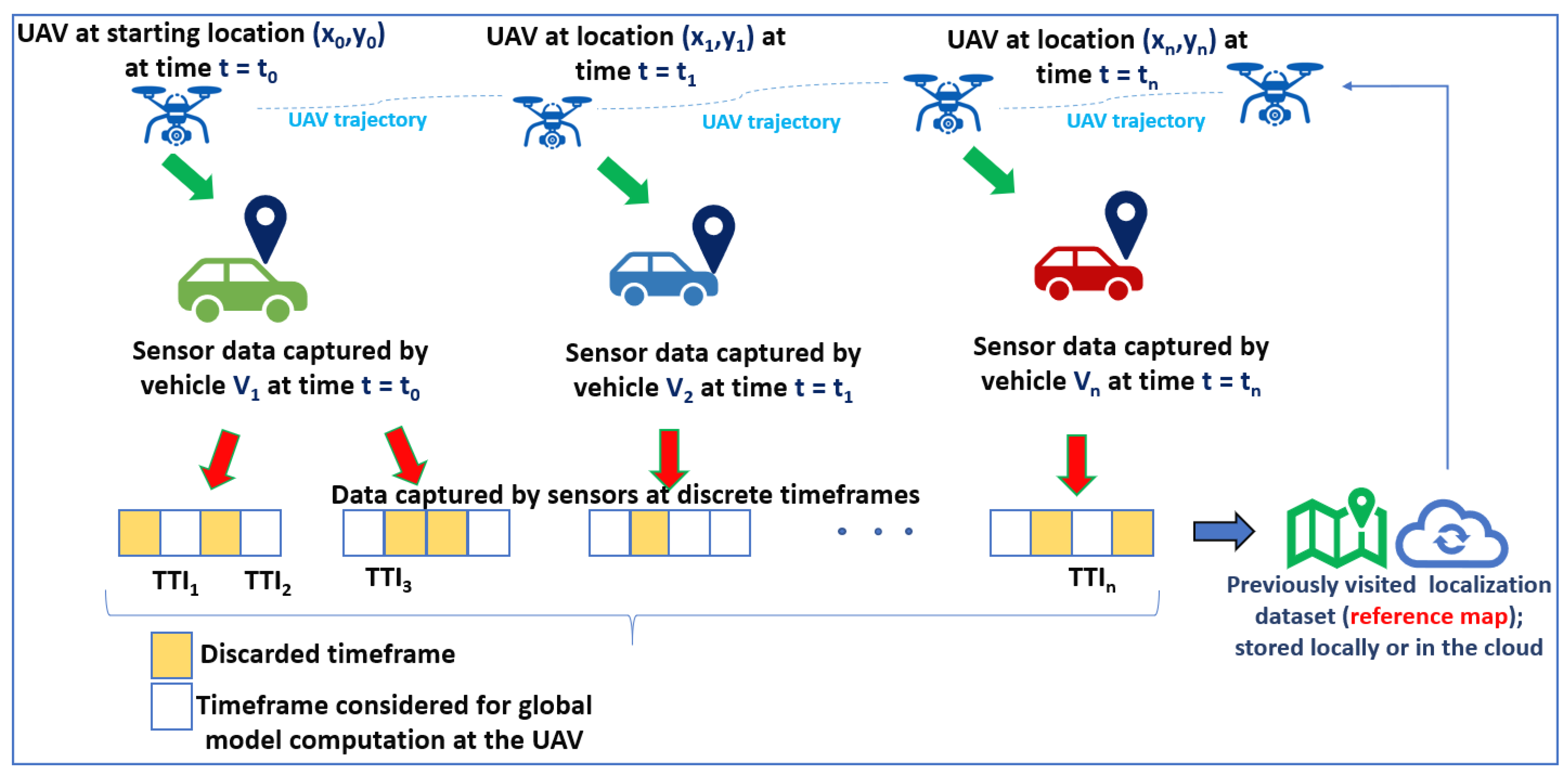
3.3. Distance Between Vehicles and UAV
3.4. Channel State and UAV Energy Consumption
4. Problem Formulation
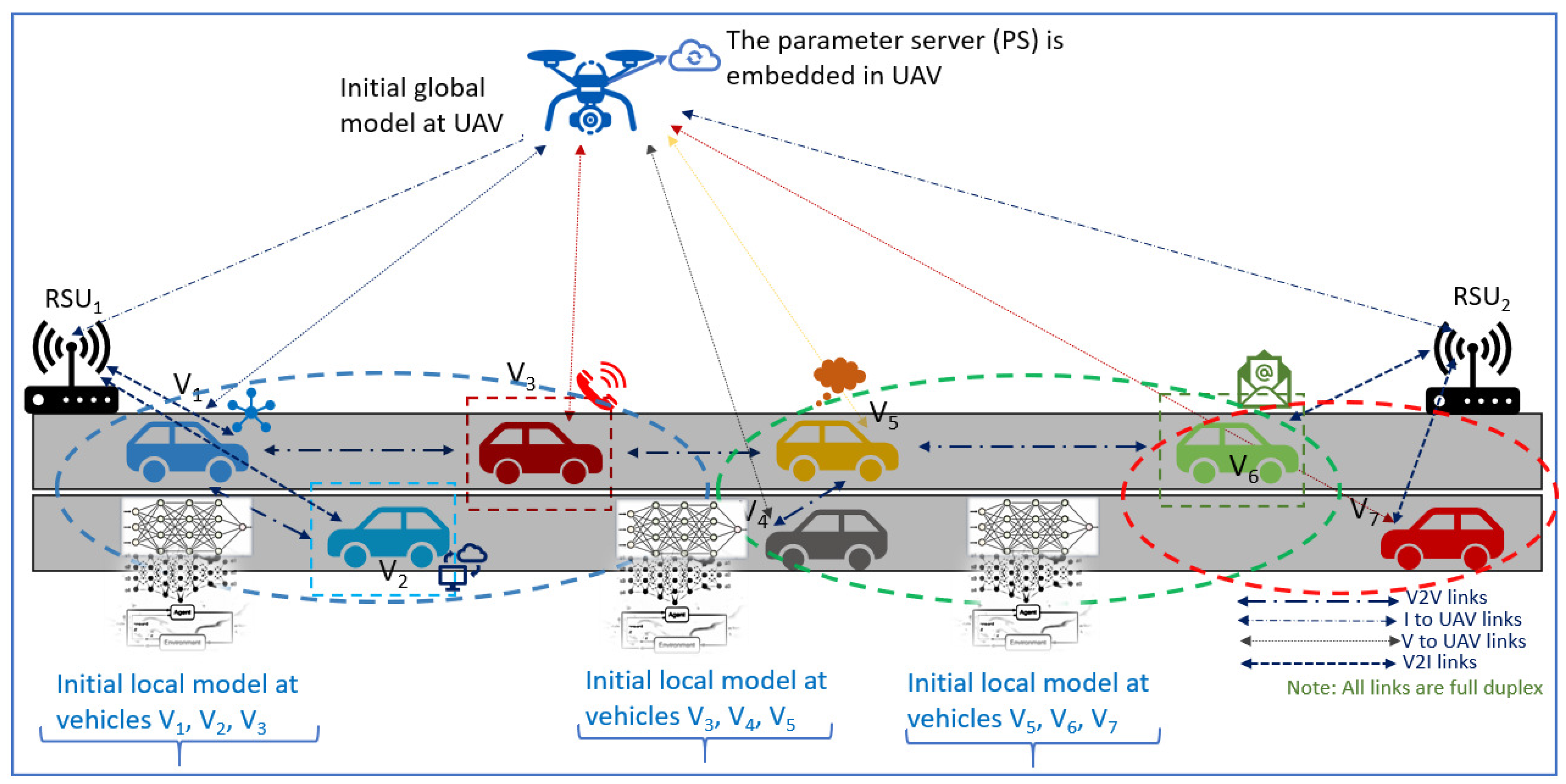
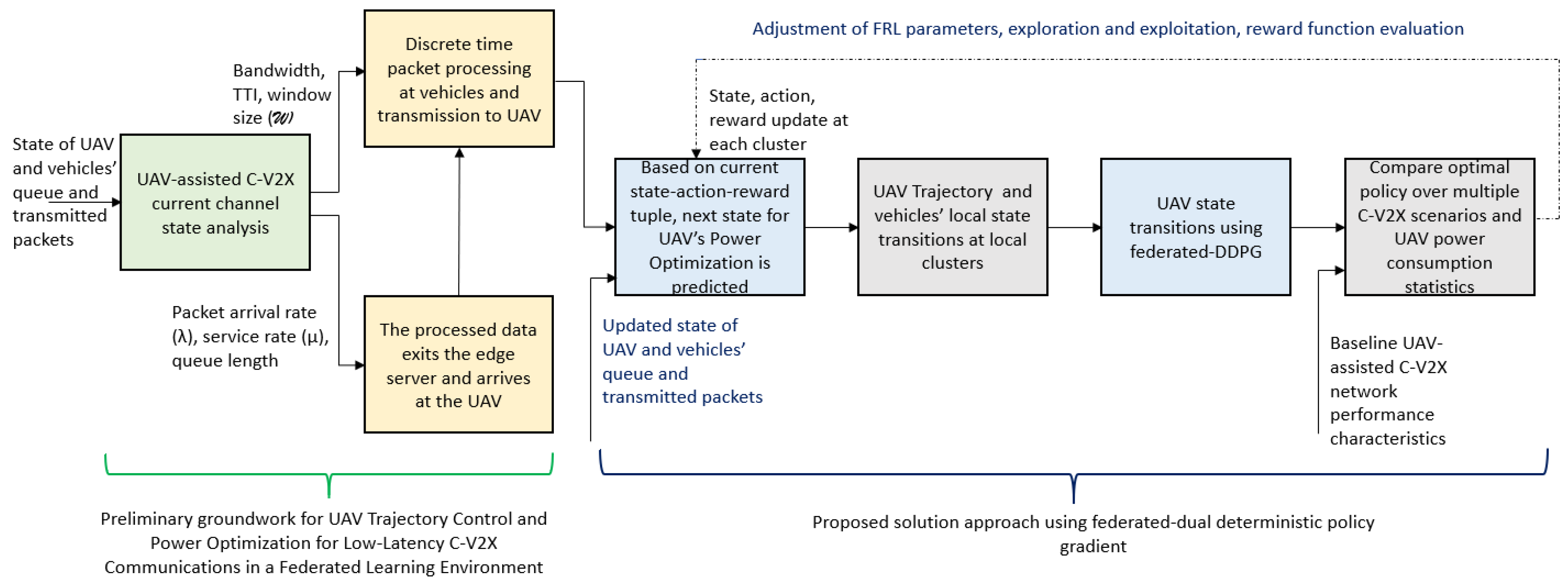
5. Proposed Solution
5.1. Long Short-Term Memory to Approximate the UAV Trajectory Parameters
5.2. Federated Deep Deterministic Policy Gradient (Fed-DDPG)
5.3. Experience Replay and Fed-DDPG
5.4. Reward Function
6. Simulation Results and Discussion
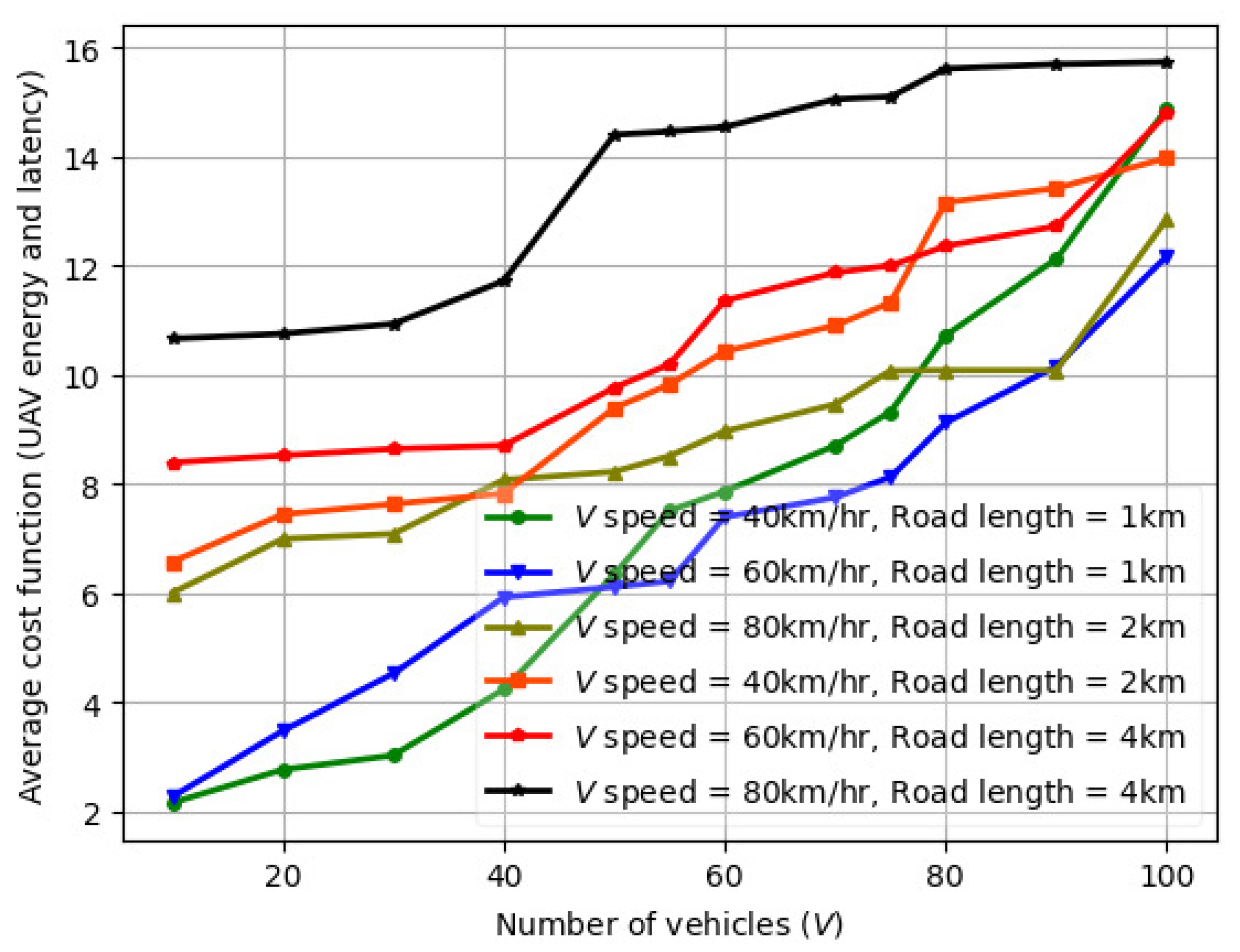
6.1. Variation in Average Cost Function (UAV Energy and Latency) with Number of Vehicles (V)
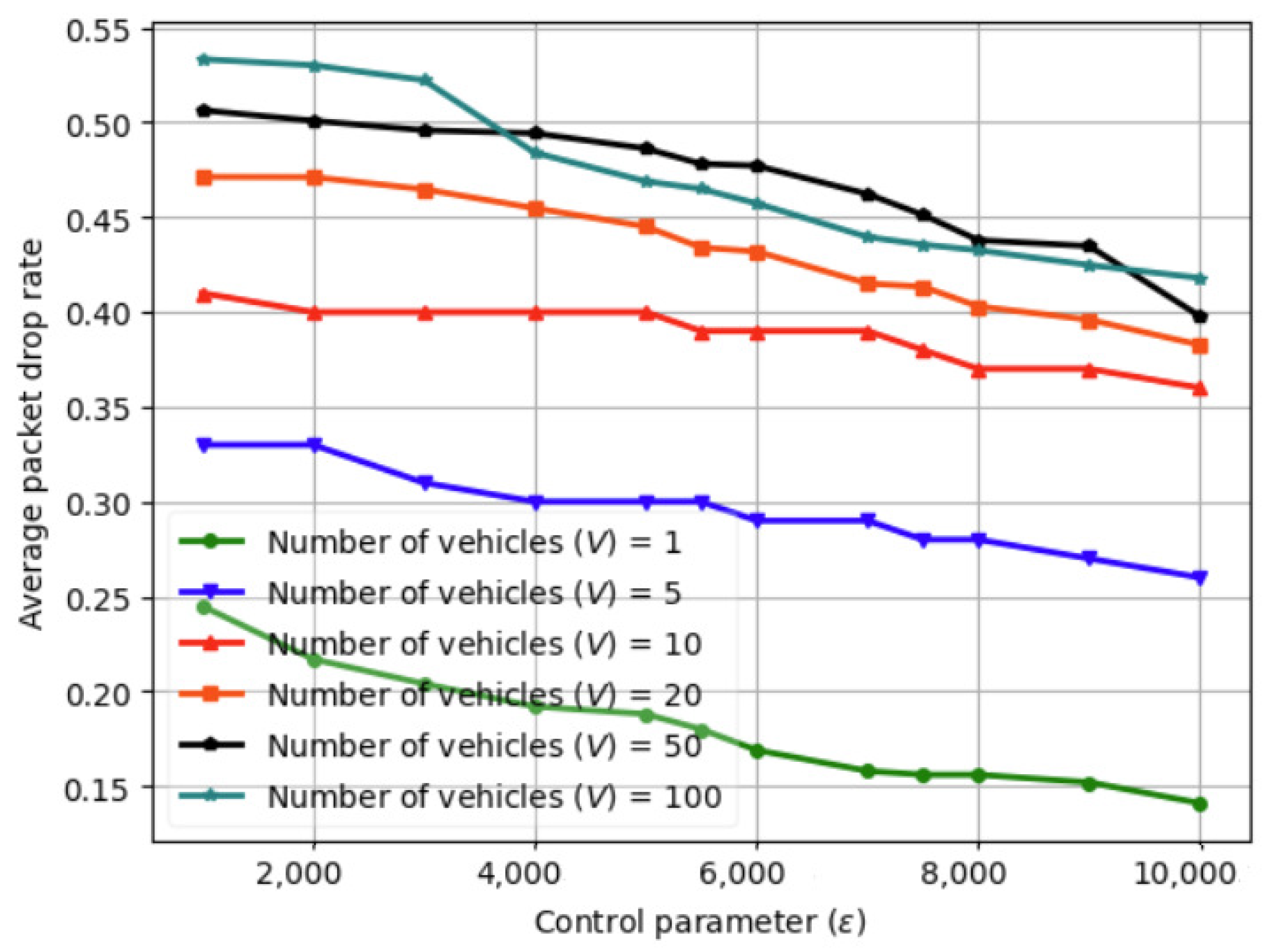
6.2. Variation in Average Packet Drop Rate with Control Parameter () Using Fed-DDPG
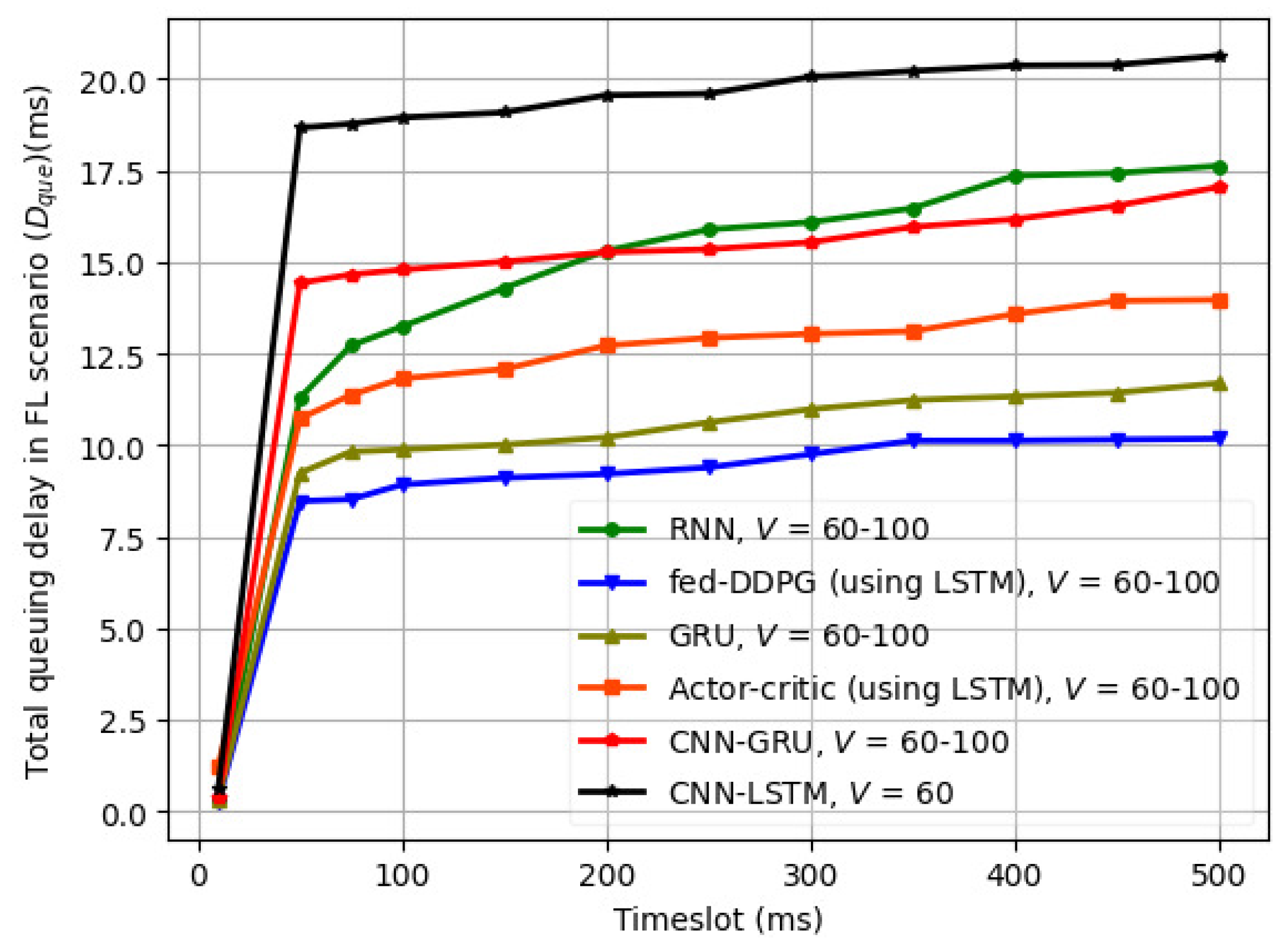
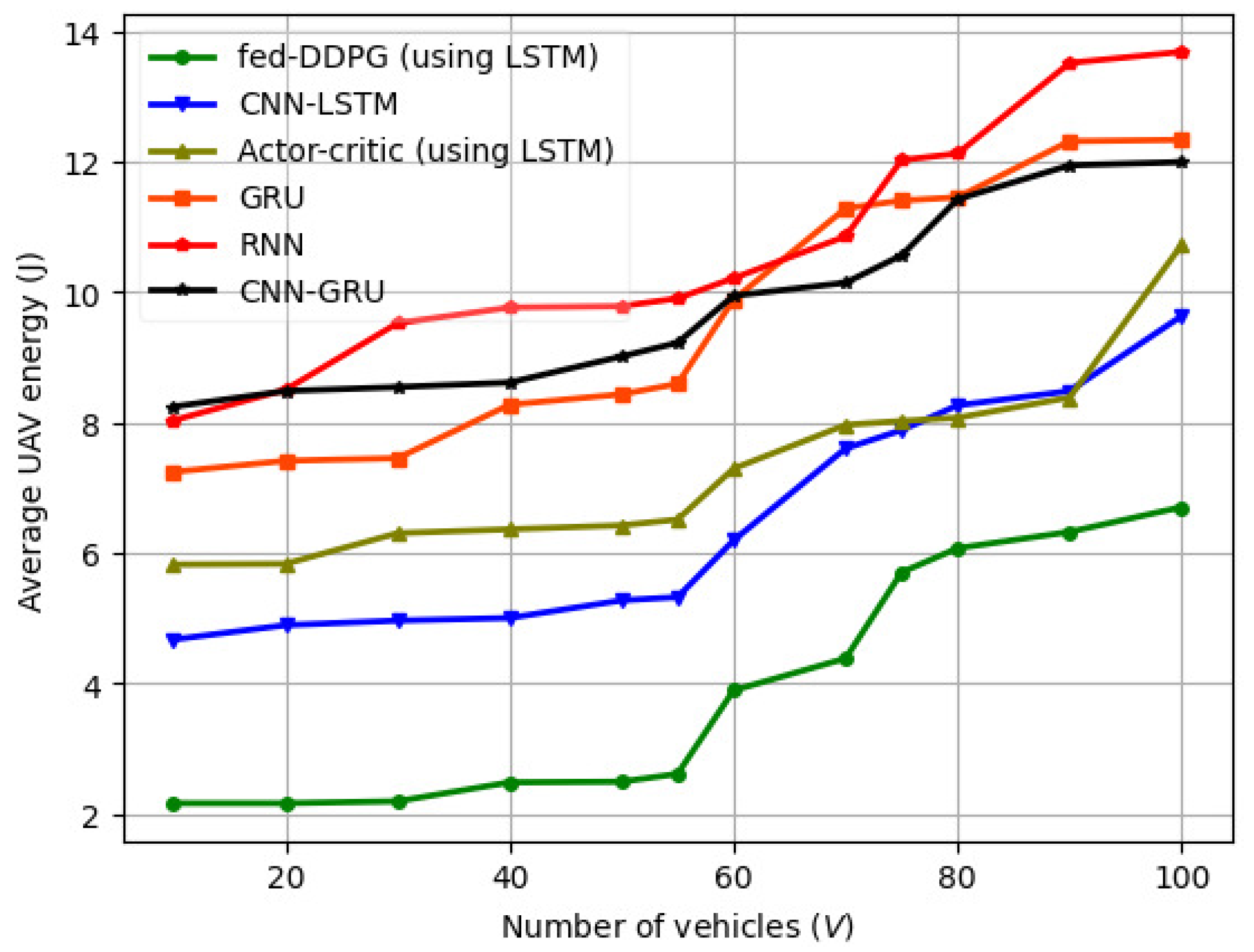
6.3. Variation in FL Computation Rate and Average UAV Energy with V for Different Machine Learning Models
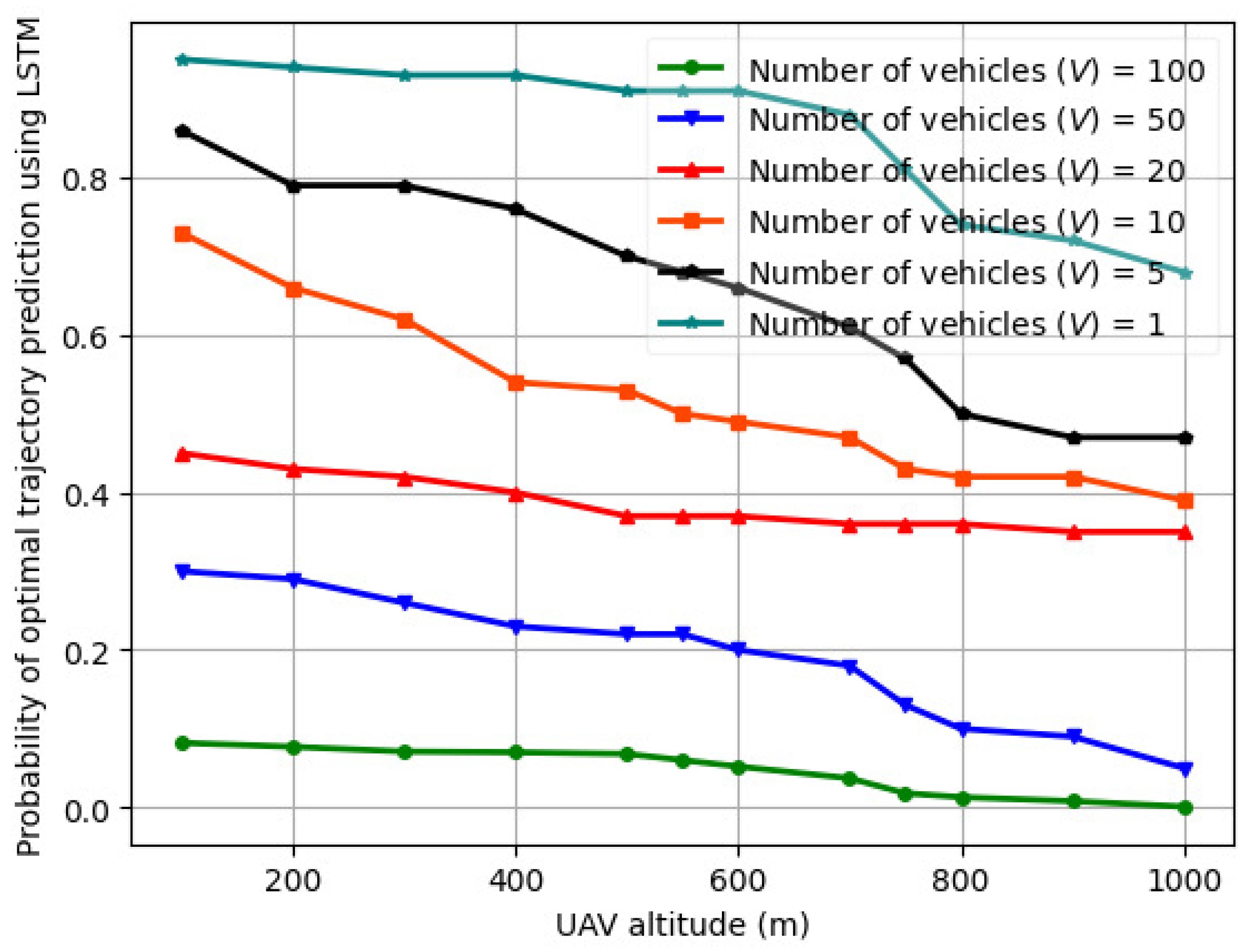
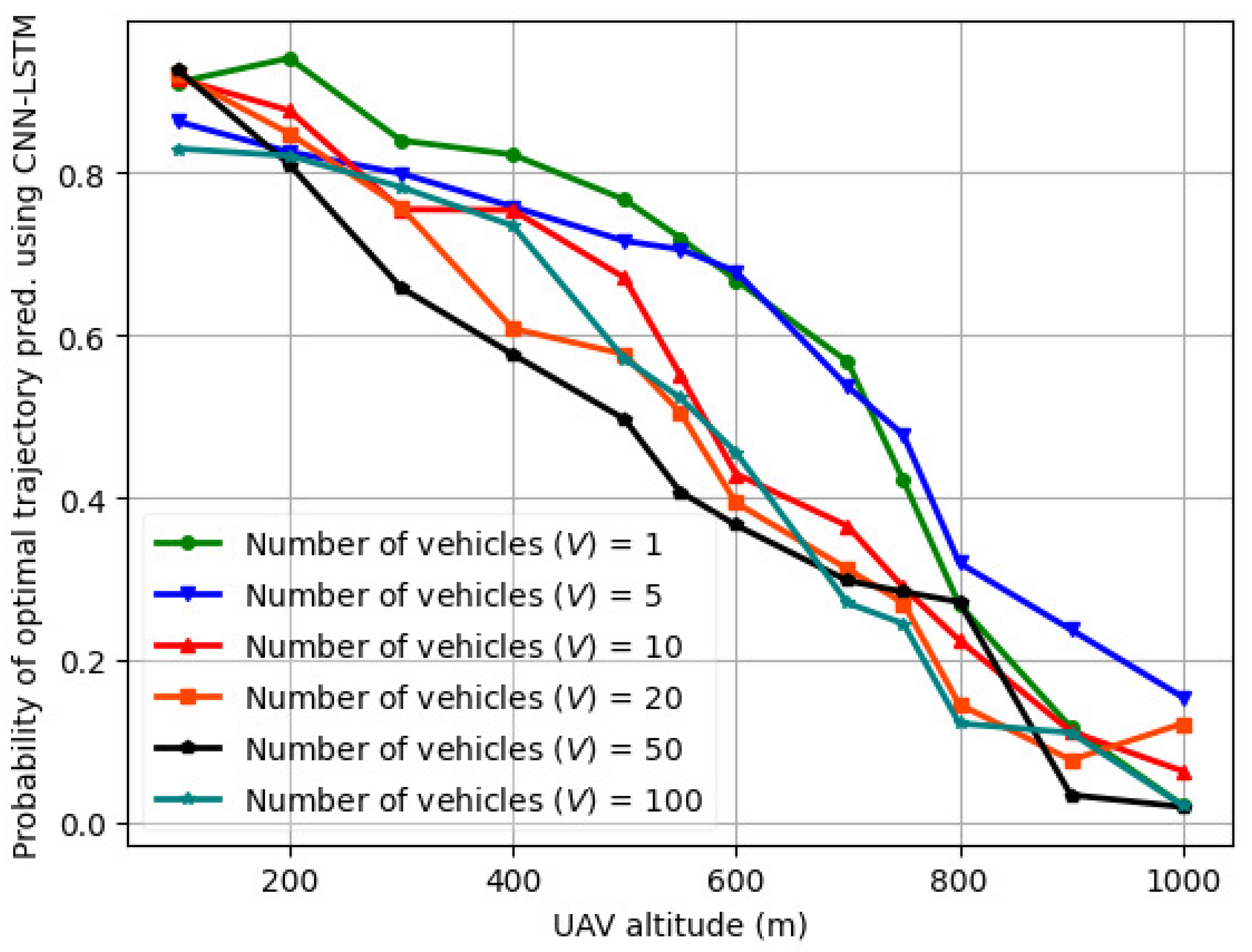
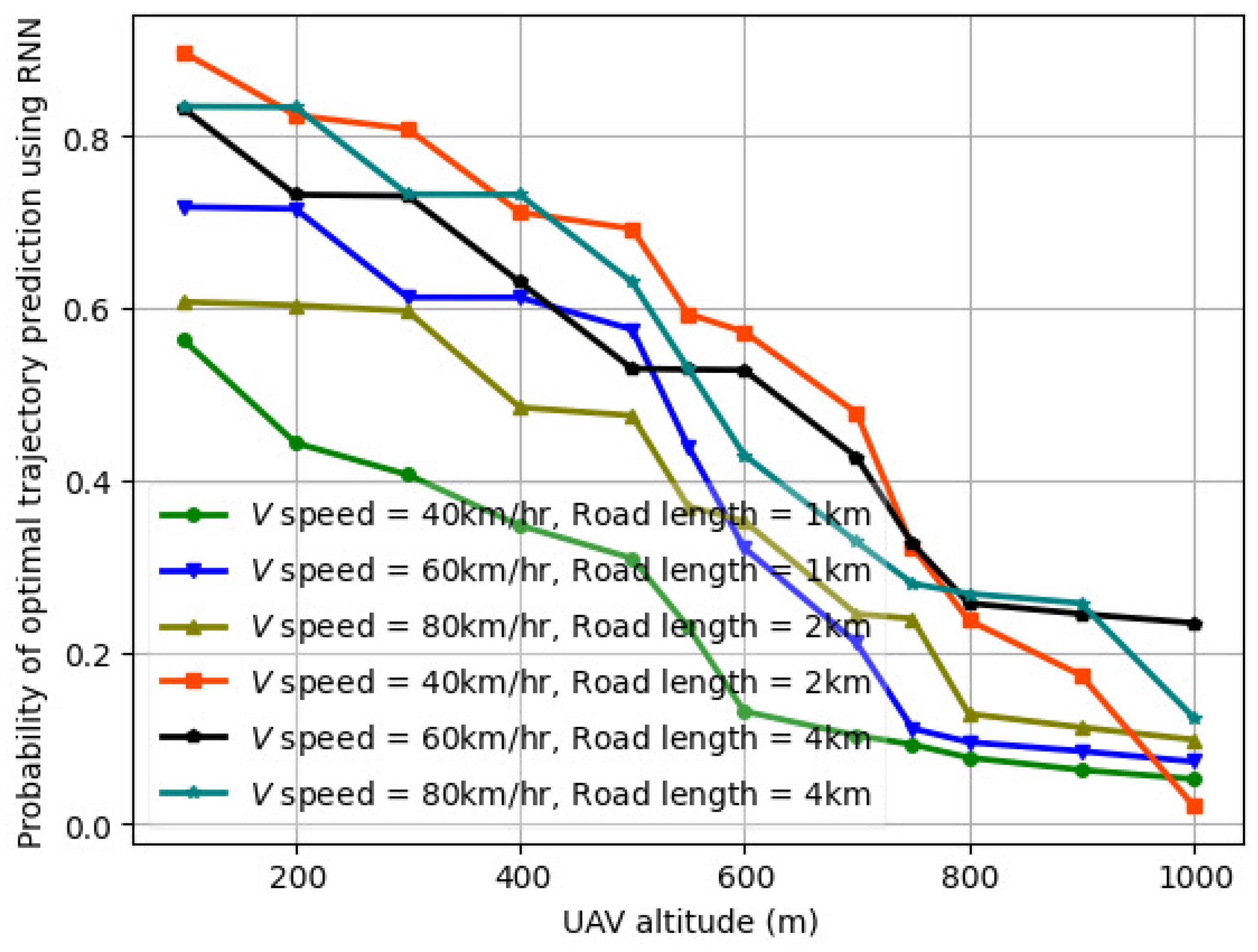
6.4. Probability of Optimal Trajectory Prediction
6.5. UAV Transmit Power () vs. SNR for OTFS Modulation
6.6. Discussion and Comparison with Existing Works
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chafii, M.; Bariah, L.; Muhaidat, S.; Debbah, M. Twelve Scientific Challenges for 6G: Rethinking the Foundations of Communications Theory. IEEE Commun. Surv. Tutor. 2023, 25, 868–904. [Google Scholar] [CrossRef]
- Labib, N.S.; Brust, M.R.; Danoy, G.; Bouvry, P. The Rise of Drones in Internet of Things: A Survey on the Evolution, Prospects and Challenges of Unmanned Aerial Vehicles. IEEE Access 2021, 9, 115466–115487. [Google Scholar] [CrossRef]
- Liu, R.; Liu, A.; Qu, Z.; Xiong, N.N. An UAV-Enabled Intelligent Connected Transportation System with 6G Communications for Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2045–2059. [Google Scholar] [CrossRef]
- Bai, L.; Liu, J.; Wang, J.; Han, R.; Choi, J. Data Aggregation in UAV-Aided Random Access for Internet of Vehicles. IEEE Internet Things J. 2022, 9, 5755–5764. [Google Scholar] [CrossRef]
- Amadeo, M.; Campolo, C.; Molinaro, A.; Harri, J.; Rothenberg, C.E.; Vinel, A. Enhancing the 3GPP V2X Architecture with Information-Centric Networking. Future Internet 2019, 11, 199. [Google Scholar] [CrossRef]
- Garcia-Roger, D.; Gonzalez, E.E.; Martin-Sacristan, D.; Monserrat, J.F. V2X Support in 3GPP Specifications: From 4G to 5G and Beyond. IEEE Access 2020, 8, 190946–190963. [Google Scholar] [CrossRef]
- Moreira, I.; Pimentel, C.; Barros, F.P.; Chaves, D.P.B. Modeling Fading Channels with Binary Erasure Finite-State Markov Channels. IEEE Trans. Veh. Technol. 2017, 66, 4429–4434. [Google Scholar] [CrossRef]
- Qiao, D.; Liu, G.; Guo, S.; He, J. Adaptive Federated Learning for Non-Convex Optimization Problems in Edge Computing Environment. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3478–3491. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, G.; Ai, B.; Liu, J.; Wang, N.; Zhong, Z. OTFCS-Modulated Waveform Design for Joint Grant-Free Random Access and Positioning in C-V2X. IEEE J. Sel. Areas Commun. 2024, 42, 103–119. [Google Scholar] [CrossRef]
- Wang, B.; Yuan, Z.; Zheng, S.; Liu, Y. Data-Driven Intelligent Receiver for OTFS Communication in Internet of Vehicles. IEEE Trans. Veh. Technol. 2023, 73, 6968–6979. [Google Scholar] [CrossRef]
- Muñoz, J.; López, B.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Multi UAV Coverage Path Planning in Urban Environments. Sensors 2021, 21, 7365. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Li, T.; Jin, R.; Dai, H. Delay-Optimal Coded Offloading for Distributed Edge Computing in Fading Environments. IEEE Trans. Wirel. Commun. 2022, 21, 10796–10808. [Google Scholar] [CrossRef]
- Chen, Z.; Yi, W.; Shin, H.; Nallanathan, A.; Li, G.Y. Efficient Wireless Federated Learning with Partial Model Aggregation. IEEE Trans. Commun. 2024, 72, 6271–6286. [Google Scholar] [CrossRef]
- Sun, C.; Fontanesi, G.; Canberk, B.; Mohajerzadeh, A.; Chatzinotas, S.; Grace, D.; Ahmadi, H. Advancing UAV Communications: A Comprehensive Survey of Cutting-Edge Machine Learning Techniques. IEEE Open J. Veh. Technol. 2024, 5, 825–854. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, G. A survey on UAV-assisted wireless communications: Recent advances and future trends. Comput. Commun. 2023, 208, 44–78. [Google Scholar] [CrossRef]
- Ng, J.S.; Lim, W.Y.B.; Dai, H.N.; Xiong, Z.; Huang, J.; Niyato, D.; Hua, X.S.; Leung, C.; Miao, C. Joint Auction-Coalition Formation Framework for Communication-Efficient Federated Learning in UAV-Enabled Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2326–2344. [Google Scholar] [CrossRef]
- Li, Z.; Lu, J.; Luo, S.; Zhu, D.; Shao, Y.; Li, Y.; Zhang, Z.; Wang, Y.; Wu, C. Towards Effective Clustered Federated Learning: A Peer-to-peer Framework with Adaptive Neighbor Matching. IEEE Trans. Big Data 2024, 10, 812–826. [Google Scholar] [CrossRef]
- Tang, Q.; Yang, Y.; Yang, H.; Cao, D.; Yang, K. Energy Consumption Minimization for Hybrid Federated Learning and Offloadable Tasks in UAV-Enabled WPCN. IEEE Trans. Netw. Sci. Eng. 2024, 11, 4639–4650. [Google Scholar] [CrossRef]
- Duan, Q.; Huang, J.; Hu, S.; Deng, R.; Lu, Z.; Yu, S. Combining Federated Learning and Edge Computing Toward Ubiquitous Intelligence in 6G Network: Challenges, Recent Advances, and Future Directions. IEEE Commun. Surv. Tutor. 2023, 25, 2892–2950. [Google Scholar] [CrossRef]
- Nasr-Azadani, M.; Abouei, J.; Plataniotis, K.N. Distillation and Ordinary Federated Learning Actor-Critic Algorithms in Heterogeneous UAV-Aided Networks. IEEE Access 2023, 11, 44205–44220. [Google Scholar] [CrossRef]
- Li, X.C.; Song, S.; Li, Y.; Li, B.; Shao, Y.; Yang, Y.; Zhan, D.C. MAP: Model Aggregation and Personalization in Federated Learning with Incomplete Classes. IEEE Trans. Knowl. Data Eng. 2024, 36, 6560–6573. [Google Scholar] [CrossRef]
- Xu, X.; Feng, G.; Qin, S.; Liu, Y.; Sun, Y. Joint UAV Deployment and Resource Allocation: A Personalized Federated Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2024, 73, 1–14. [Google Scholar] [CrossRef]
- Pakrooh, R.; Bohlooli, A. A Survey on Unmanned Aerial Vehicles-Assisted Internet of Things: A Service-Oriented Classification. Wirel. Pers. Commun. 2021, 119, 1541–1575. [Google Scholar] [CrossRef]
- Le, N.P.; Huang, X.; Dutkiewicz, E.; Ritz, C.; Phung, S.L.; Bouzerdoum, A.; Franklin, D.; Hanzo, L. Energy-Harvesting Aided Unmanned Aerial Vehicles for Reliable Ground User Localization and Communications Under Lognormal-Nakagami-m Fading Channels. IEEE Trans. Veh. Technol. 2021, 70, 1632–1647. [Google Scholar] [CrossRef]
- Kang, B.; Yang, J.; Paek, J.; Bahk, S. ATOMIC: Adaptive Transmission Power and Message Interval Control for C-V2X Mode 4. IEEE Access 2021, 9, 12309–12321. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Federated Reinforcement Learning for Collaborative Intelligence in UAV-assisted C-V2X Communications. Drones 2024, 8, 321. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Analysis of Unmanned Aerial Vehicle-Assisted Cellular Vehicle-to-Everything Communication Using Markovian Game in a Federated Learning Environment. Drones 2024, 8, 238. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Latency Analysis of Drone-Assisted C-V2X Communications for Basic Safety and Co-Operative Perception Messages. Drones 2024, 8, 600. [Google Scholar] [CrossRef]
- Wei, W.; Gu, H.; Li, B. Congestion Control: A Renaissance with Machine Learning. IEEE Netw. 2021, 35, 262–269. [Google Scholar] [CrossRef]
- Albasry, H.; Ahmed, Q.Z. Network-Assisted D2D Discovery Method by Using Efficient Power Control Strategy. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Shimizu, T.; Cheng, B.; Lu, H.; Kenney, J. Comparative Analysis of DSRC and LTE-V2X PC5 Mode 4 with SAE Congestion Control. In Proceedings of the 2020 IEEE Vehicular Networking Conference (VNC), New York, NY, USA, 16–18 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Gupta, A.; Fernando, X. Simultaneous Localization and Mapping (SLAM) and Data Fusion in Unmanned Aerial Vehicles: Recent Advances and Challenges. Drones 2022, 6, 85. [Google Scholar] [CrossRef]
- Pasternak, G.; Pasternak, K.; Koda, E.; Ogrodnik, P. Unmanned Aerial Vehicle Photogrammetry for Monitoring the Geometric Changes of Reclaimed Landfills. Sensors 2024, 24, 7247. [Google Scholar] [CrossRef] [PubMed]
- Kandregula, V.R.; Zaharis, Z.D.; Ahmed, Q.Z.; Khan, F.A.; Loh, T.H.; Schreiber, J.; Serres, A.J.R.; Lazaridis, P.I. A Review of Unmanned Aerial Vehicle Based Antenna and Propagation Measurements. Sensors 2024, 24, 7395. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Qin, Y.; Du, C.; Wang, W.; Zhang, Z. Deep Reinforcement Learning-Driven Jamming-Enhanced Secure Unmanned Aerial Vehicle Communications. Sensors 2024, 24, 7328. [Google Scholar] [CrossRef]
- Ponte, S.; Ariante, G.; Greco, A.; Del Core, G. Differential Positioning with Bluetooth Low Energy (BLE) Beacons for UAS Indoor Operations: Analysis and Results. Sensors 2024, 24, 7170. [Google Scholar] [CrossRef]
- Luong, P.; Gagnon, F.; Tran, L.N.; Labeau, F. Deep Reinforcement Learning-Based Resource Allocation in Cooperative UAV-Assisted Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 7610–7625. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, K.; Xu, H.; Ji, J. Deep Reinforcement Learning for Multi-Objective Resource Allocation in Multi-Platoon Cooperative Vehicular Networks. IEEE Trans. Wirel. Commun. 2023, 22, 6185–6198. [Google Scholar] [CrossRef]
- Xie, J.; Chang, Z.; Guo, X.; Hamalainen, T. Energy Efficient Resource Allocation for Wireless Powered UAV Wireless Communication System with Short Packet. IEEE Trans. Green Commun. Netw. 2023, 7, 101–113. [Google Scholar] [CrossRef]
- Zheng, H.; Atia, M.; Yanikomeroglu, H. A Positioning System in an Urban Vertical Heterogeneous Network (VHetNet). IEEE J. Radio Freq. Identif. 2023, 7, 352–363. [Google Scholar] [CrossRef]
- Qin, P.; Wu, X.; Cai, Z.; Zhao, X.; Fu, Y.; Wang, M.; Geng, S. Joint Trajectory Plan and Resource Allocation for UAV-Enabled C-NOMA in Air-Ground Integrated 6G Heterogeneous Network. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3421–3434. [Google Scholar]
- Liu, Z.; Qi, J.; Shen, Y.; Ma, K.; Guan, X. Maximizing Energy Efficiency in UAV-Assisted NOMA-MEC Networks. IEEE Internet Things J. 2023, 10, 22208–22222. [Google Scholar] [CrossRef]
- Zhang, M.; Xiong, Y.; Ng, S.X.; El-Hajjar, M. Content-Aware Transmission in UAV-Assisted Multicast Communication. IEEE Trans. Wirel. Commun. 2023, 22, 7144–7157. [Google Scholar] [CrossRef]
- Yang, D.; Wu, Q.; Zeng, Y.; Zhang, R. Energy Tradeoff in Ground-to-UAV Communication via Trajectory Design. IEEE Trans. Veh. Technol. 2018, 67, 6721–6726. [Google Scholar] [CrossRef]
- Bithas, P.S.; Nikolaidis, V.; Kanatas, A.G.; Karagiannidis, G.K. UAV-to-Ground Communications: Channel Modeling and UAV Selection. IEEE Trans. Commun. 2020, 68, 5135–5144. [Google Scholar] [CrossRef]
- Hua, B.; Ni, H.; Zhu, Q.; Wang, C.X.; Zhou, T.; Mao, K.; Bao, J.; Zhang, X. Channel Modeling for UAV-to-Ground Communications with Posture Variation and Fuselage Scattering Effect. IEEE Trans. Commun. 2023, 71, 3103–3116. [Google Scholar] [CrossRef]
- Park, H.; Lim, Y. Deep Reinforcement Learning Based Resource Allocation with Radio Remote Head Grouping and Vehicle Clustering in 5G Vehicular Networks. Electronics 2021, 10, 3015. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Gong, J.; Xia, N.; Guo, J.; Peng, M. Amplitude Barycenter Calibration of Delay-Doppler Spectrum for OTFS Signal—An Endeavor to Integrated Sensing and Communication Waveform Design. IEEE Trans. Wirel. Commun. 2023, 23, 2622–2637. [Google Scholar] [CrossRef]
- Xia, X.; Xu, K.; Wang, Y.; Xu, Y.; Xie, W. Achieving Better Accuracy with Less Computations: A Delay-Doppler Spectrum Matching Assisted Active Sensing Framework for OTFS Based ISAC Systems. IEEE Trans. Wirel. Commun. 2023, 23, 6204–6220. [Google Scholar] [CrossRef]
- Stefanovic, C.; Panic, S.; Bhatia, V.; Kumar, N. On Second-Order Statistics of the Composite Channel Models for UAV-to-Ground Communications with UAV Selection. IEEE Open J. Commun. Soc. 2021, 2, 534–544. [Google Scholar] [CrossRef]
- Qu, G.; Xie, A.; Liu, S.; Zhou, J.; Sheng, Z. Reliable Data Transmission Scheduling for UAV-Assisted Air-to-Ground Communications. IEEE Trans. Veh. Technol. 2023, 72, 13787–13792. [Google Scholar] [CrossRef]
- Li, Z.; Giorgetti, A.; Kandeepan, S. Multiple Radio Transmitter Localization via UAV-Based Mapping. IEEE Trans. Veh. Technol. 2021, 70, 8811–8822. [Google Scholar] [CrossRef]
- Al-Quraan, M.; Mohjazi, L.; Bariah, L.; Centeno, A.; Zoha, A.; Arshad, K.; Assaleh, K.; Muhaidat, S.; Debbah, M.; Imran, M.A. Edge-Native Intelligence for 6G Communications Driven by Federated Learning: A Survey of Trends and Challenges. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 957–979. [Google Scholar] [CrossRef]
- Feng, J.; Liu, L.; Pei, Q.; Li, K. Min-Max Cost Optimization for Efficient Hierarchical Federated Learning in Wireless Edge Networks. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 2687–2700. [Google Scholar] [CrossRef]
- Hu, Z.; Shaloudegi, K.; Zhang, G.; Yu, Y. Federated Learning Meets Multi-Objective Optimization. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2039–2051. [Google Scholar] [CrossRef]
- Taik, A.; Mlika, Z.; Cherkaoui, S. Clustered Vehicular Federated Learning: Process and Optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25371–25383. [Google Scholar] [CrossRef]
- Deng, D.; Wang, C.; Wang, W. Joint Air-to-Ground Scheduling in UAV-Aided Vehicular Communication: A DRL Approach with Partial Observations. IEEE Commun. Lett. 2022, 26, 1628–1632. [Google Scholar] [CrossRef]
- Shen, S.; Yang, K.; Wang, K.; Zhang, G. UAV-Aided Vehicular Short-Packet Communication and Edge Computing System Under Time-Varying Channel. IEEE Trans. Veh. Technol. 2023, 72, 6625–6638. [Google Scholar] [CrossRef]
- Almutairi, J.; Aldossary, M.; Alharbi, H.A.; Yosuf, B.A.; Elmirghani, J.M.H. Delay-Optimal Task Offloading for UAV-Enabled Edge-Cloud Computing Systems. IEEE Access 2022, 10, 51575–51586. [Google Scholar] [CrossRef]
- Hosseini, M.; Ghazizadeh, R. Stackelberg Game-Based Deployment Design and Radio Resource Allocation in Coordinated UAVs-Assisted Vehicular Communication Networks. IEEE Trans. Veh. Technol. 2023, 72, 1196–1210. [Google Scholar] [CrossRef]
- Khazali, A.; Bozorgchenani, A.; Tarchi, D.; Shayesteh, M.G.; Kalbkhani, H. Joint Task Assignment, Power Allocation and Node Grouping for Cooperative Computing in NOMA-mmWave Mobile Edge Computing. IEEE Access 2023, 11, 93664–93678. [Google Scholar] [CrossRef]
- Shinde, S.S.; Tarchi, D. Joint Air-Ground Distributed Federated Learning for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9996–10011. [Google Scholar] [CrossRef]
- Hu, C.; Qu, G.; Shin, H.S.; Tsourdos, A. Distributed synchronous cooperative tracking algorithm for ground moving target in urban by UAVs. Int. J. Syst. Sci. 2021, 52, 832–847. [Google Scholar] [CrossRef]
- Shinde, S.S.; Tarchi, D. A Markov Decision Process Solution for Energy-Saving Network Selection and Computation Offloading in Vehicular Networks. IEEE Trans. Veh. Technol. 2023, 72, 12031–12046. [Google Scholar] [CrossRef]
- Kumar, A.S.; Zhao, L.; Fernando, X. Multi-Agent Deep Reinforcement Learning-Empowered Channel Allocation in Vehicular Networks. IEEE Trans. Veh. Technol. 2022, 71, 1726–1736. [Google Scholar] [CrossRef]
- Kumar, A.S.; Zhao, L.; Fernando, X. Mobility Aware Channel Allocation for 5G Vehicular Networks using Multi-Agent Reinforcement Learning. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Virtual, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Kumar, A.S.; Zhao, L.; Fernando, X. Task Offloading and Resource Allocation in Vehicular Networks: A Lyapunov-based Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2023, 72, 13360–13373. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, G.; Zhong, Q.; Zheng, H.; Zhao, S. UAV-Aided Vehicular Communication Design with Vehicle Trajectory’s Prediction. IEEE Wirel. Commun. Lett. 2021, 10, 1212–1216. [Google Scholar] [CrossRef]
- Maeng, S.J.; Ozdemir, O.; Guvenc, I.; Sichitiu, M.L.; Mushi, M.; Dutta, R. LTE I/Q Data Set for UAV Propagation Modeling, Communication, and Navigation Research. IEEE Commun. Mag. 2023, 61, 90–96. [Google Scholar] [CrossRef]
- Li, Y.; Ma, D.; An, Z.; Wang, Z.; Zhong, Y.; Chen, S.; Feng, C. V2X-Sim: Multi-Agent Collaborative Perception Dataset and Benchmark for Autonomous Driving. IEEE Robot. Autom. Lett. 2022, 7, 10914–10921. [Google Scholar] [CrossRef]
- Roshdi, M.; Bhadauria, S.; Hassan, K.; Fischer, G. Deep Reinforcement Learning based Congestion Control for V2X Communication. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Virtual, 13–16 September 2021; pp. 1–6. [Google Scholar]
- Chen, M.; Poor, H.V.; Saad, W.; Cui, S. Convergence Time Optimization for Federated Learning Over Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 2457–2471. [Google Scholar] [CrossRef]
- Samarakoon, S.; Bennis, M.; Saad, W.; Debbah, M. Distributed Federated Learning for Ultra-Reliable Low-Latency Vehicular Communications. IEEE Trans. Commun. 2020, 68, 1146–1159. [Google Scholar] [CrossRef]
- Jayanetti, A.; Halgamuge, S.; Buyya, R. Deep reinforcement learning for energy and time optimized scheduling of precedence-constrained tasks in edge–cloud computing environments. Future Gener. Comput. Syst. 2022, 137, 14–30. [Google Scholar] [CrossRef]
- Gyawali, S.; Qian, Y.; Hu, R. Deep Reinforcement Learning Based Dynamic Reputation Policy in 5G Based Vehicular Communication Networks. IEEE Trans. Veh. Technol. 2021, 70, 6136–6146. [Google Scholar] [CrossRef]
- Sial, M.N.; Deng, Y.; Ahmed, J.; Nallanathan, A.; Dohler, M. Stochastic Geometry Modeling of Cellular V2X Communication Over Shared Channels. IEEE Trans. Veh. Technol. 2019, 68, 11873–11887. [Google Scholar] [CrossRef]






| Symbol | Definition |
|---|---|
| 3GPP | Third generation partnership project |
| 5G | Fifth generation (communication networks) |
| 6G | Sixth generation (communication networks) |
| AoI | Age of information |
| BER | Bit error rate |
| BS | Base station |
| BSM | Basic safety messages |
| CNN | Convolutional neural network |
| CPM | Co-operative perception messages |
| C-V2X | Cellular vehicle-to-everything |
| DQN | Deep Q-network |
| DRL | Deep reinforcement learning |
| FDRL | Federated deep reinforcement learning |
| FedAvg | Federated averaging |
| FedSGD | Federated stochastic gradient descent |
| FL | Federated learning |
| FL-DDPG | FL-based dual deterministic policy gradient |
| FRL | Federated reinforcement learning |
| GNSS | Global navigation satellite system |
| GRU | Gated recurrent unit |
| i.i.d. | independent-and-identically-distributed |
| ITU-R | International Telecommunication Union |
| LoS | Line of sight |
| LSTM | long short-term memory |
| MADRL | Multi-agent deep reinforcement learning |
| MDP | Markov decision process |
| MEC | Mobile edge computing |
| ML | Machine learning |
| MSE | Mean square error |
| NLoS | Non-line of sight |
| NOMA | Non-orthogonal multiple access |
| NTNs | Non-terrestrial networks |
| OFDM | Orthogonal frequency division multiplexing |
| OFDMA | Orthogonal frequency division multiple access |
| OTFS | Orthogonal time–frequency space |
| QoS | Quality of service |
| RL | Reinforcement learning |
| RNN | Recurrent neural networks |
| RSSI | Received signal strength indicator |
| SCA | Successive convex approximation |
| SINR | Signal-to-interference-plus-noise ratio |
| SPS | Sensing-based semi-persistent scheduling |
| SNR | Signal-to-noise ratio |
| SQP | Successive quadratic programming |
| TDD | Time-delay-doppler |
| TTI | Transmission time interval |
| UAV | Unmanned aerial vehicle |
| Benefit | Short Description |
|---|---|
| Collaborative learning at the vehicles and the UAV | Co-operative learning enables collaboration between multiple vehicle clusters and edge servers for enhanced intelligence [61]. Furthermore, FRL can be utilized to optimize UAV trajectories and data transmission strategies, adapt UAV mobility, optimize computing resources, and make optimal scheduling decisions. |
| Distributed learning at the vehicles and the UAV | The existing works have demonstrated that FL enhances intelligence and learning across distributed nodes and edge servers. FL has been used in jointly optimizing the UAV flying speed, flying locations, and bandwidth allocation for efficient data collection [62]. |
| Decentralized learning at the vehicles and the UAV | In FL, the vehicles and the vehicle–UAV server pairs train their own models without a centralized aggregator. The vehicles usually collect sensing information, and the timely processing of the sensed information and transmission to the UAV using actor–critic DRL approaches minimizes the AoI by adapting the UAV scheduling strategies [63]. |
| Data availability, reliability, and network scalability; energy-optimal computation offloading | FL allows to leverage the driving decisions obtained from massive amounts of vehicular data, without locally hosting the data [64]. Hence, using FL, new vehicles can easily be integrated into existing clusters to maximize the uplink and downlink capacity of all vehicles [65]. |
| Fault recovery and minimal packet drops | In FL, the global model aggregation is based on local data from multiple vehicles in a cluster. Consequently, it is feasible to rapidly recover the losses due to vehicles experiencing connectivity issues and interference, or if a vehicle’s sensors malfunction. Further, multi-agent FL is used to minimize the UAV flight time by learning the UAV–vehicle association strategies [66]. |
| Communication efficiency and shorter timeouts | Using FL, the model updates and hyper-parameters are communicated to the UAV server rather than gross data offloading. Using asynchronous FL, vehicles can be trained to drop redundant packets. Short-packet transmission can be harnessed to maximize computation efficiency, jointly optimize communication scheduling, and mitigate the impact of intermittent coverage [67]. |
| Symbol | Definition |
|---|---|
| Time period | |
| UAV has available battery power | |
| UAV flying at a height in meters (m) | |
| Transmission windows | |
| Number of vehicles in a cluster | |
| Data rate in bits/Hz transmitted by each vehicle over UAV flight time | |
| Binary variable indicating if a vehicle transmits to the UAV in a transmission window | |
| Delay which is the sum of the queuing delay and processing delay | |
| Bandwidth | |
| Power consumed by the UAV while communicating with the ith vehicle | |
| Noise power density at the receiver of the vehicle | |
| Channel gains of UAV at time slot t | |
| Instantaneous transmission rate for the ith vehicle in a time slot | |
| Instantaneous bandwidth utilized by ith vehicle in jth transmission window | |
| SNR | |
| Inter-arrival time between successive packets | |
| Local models considered for federated averaging | |
| Total power consumption during time period t | |
| Power required for operating the UAV during time period t | |
| Power consumption in the ith time slot | |
| Local models arrive at the queue which accumulates at a rate | |
| Uplink transmission window | |
| Binary variable; 1 indicates UAV is processing data from a vehicle; 0 indicates UAV is idle | |
| Size of the kth type of vehicular data served by the UAV in the ith time slot | |
| Coefficient of power consumption during uplink and downlink of kth type of vehicular data | |
| UAV trajectory | |
| Maximum speed of UAV in meter/second (m/s) | |
| Limiting parameter for UAV distance traveled in a TTI | |
| Channel-gain experienced by the ith vehicle in jth window considering Rician K-factor | |
| Weight values scaling factor | |
| Distance between the UAV and the ith vehicle | |
| Upper bound on delay | |
| Size of packets | |
| Assignment coefficient; 1 denotes vehicle scheduled for transmission, 0 denotes waiting | |
| Control parameter for the data rates to reduce the computational complexity of the solution | |
| Policy function | |
| Value functions | |
| Mean vector | |
| Covariance matrix for each sampling value on the trajectory point | |
| UAV selects action to move to the next coordinates; maximizes expected delay minimization | |
| Expected maximum value function when UAV visited the past coordinates | |
| UAV overall reward function | |
| Discount factor | |
| Reward that achieves optimal model transmission from vehicles to UAV | |
| UAV action in each TTI | |
| Entropy | |
| Actor–critic Q-function | |
| Learning rate |
| Parameter | Value |
|---|---|
| Vehicle Mobility | Manhattan Mobility |
| Number of vehicles (V) | 1–100 |
| Number of UAV | 1 |
| UAV deployment altitude | 100 m–3 km |
| Edge server location | In-vehicle |
| Communication frequency | 5.9 GHz |
| Distance between vehicles | 30–100 m |
| Road length | 1–5 km |
| Vehicle speed | 0–100 km/h |
| Payload size for BSM, CPM | 1 byte–3 Megabytes |
| Payload size of FL models | 1 byte–10 Megabytes |
| Dataset used | V2X-Sim, LTE I/Q |
| 100 ms–1000 ms | |
| 100, 200, 300, 500 ms | |
| Packet arrival rate () | 1000, 2000 packets/s |
| Speed of UAV | 20–50 km/h |
| UAV transmission power | 20 dBm (100 mW) |
| UAV receiving threshold | −80 dBm |
| Vehicle transmission power | 25 dBm (316.2 mW) |
| Standard deviation in speed | 10 km/h |
| Noise power, | −110 dBm |
| SNR threshold | 3 dB |
| Size of static obstacles | 20 m × 20 m |
| Channel gain | −30 dBm |
| BER threshold | |
| Doppler speed | 30 km/h |
| Reference | Proposed Method | Objectives | Cost Function | Reported Results |
|---|---|---|---|---|
| [71] |
|
|
|
|
| [72] |
|
|
|
|
| [73] |
|
|
|
|
| [74] |
|
|
|
|
| [75,76] |
|
|
|
|
| Our Work |
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernando, X.; Gupta, A. UAV Trajectory Control and Power Optimization for Low-Latency C-V2X Communications in a Federated Learning Environment. Sensors 2024, 24, 8186. https://doi.org/10.3390/s24248186
Fernando X, Gupta A. UAV Trajectory Control and Power Optimization for Low-Latency C-V2X Communications in a Federated Learning Environment. Sensors. 2024; 24(24):8186. https://doi.org/10.3390/s24248186
Chicago/Turabian StyleFernando, Xavier, and Abhishek Gupta. 2024. "UAV Trajectory Control and Power Optimization for Low-Latency C-V2X Communications in a Federated Learning Environment" Sensors 24, no. 24: 8186. https://doi.org/10.3390/s24248186
APA StyleFernando, X., & Gupta, A. (2024). UAV Trajectory Control and Power Optimization for Low-Latency C-V2X Communications in a Federated Learning Environment. Sensors, 24(24), 8186. https://doi.org/10.3390/s24248186






