Communication Link Analysis of a Low-Earth Orbit Satellites Considering Interference Sources Moving Along Various Parabola-Curved Paths
Abstract
:1. Introduction
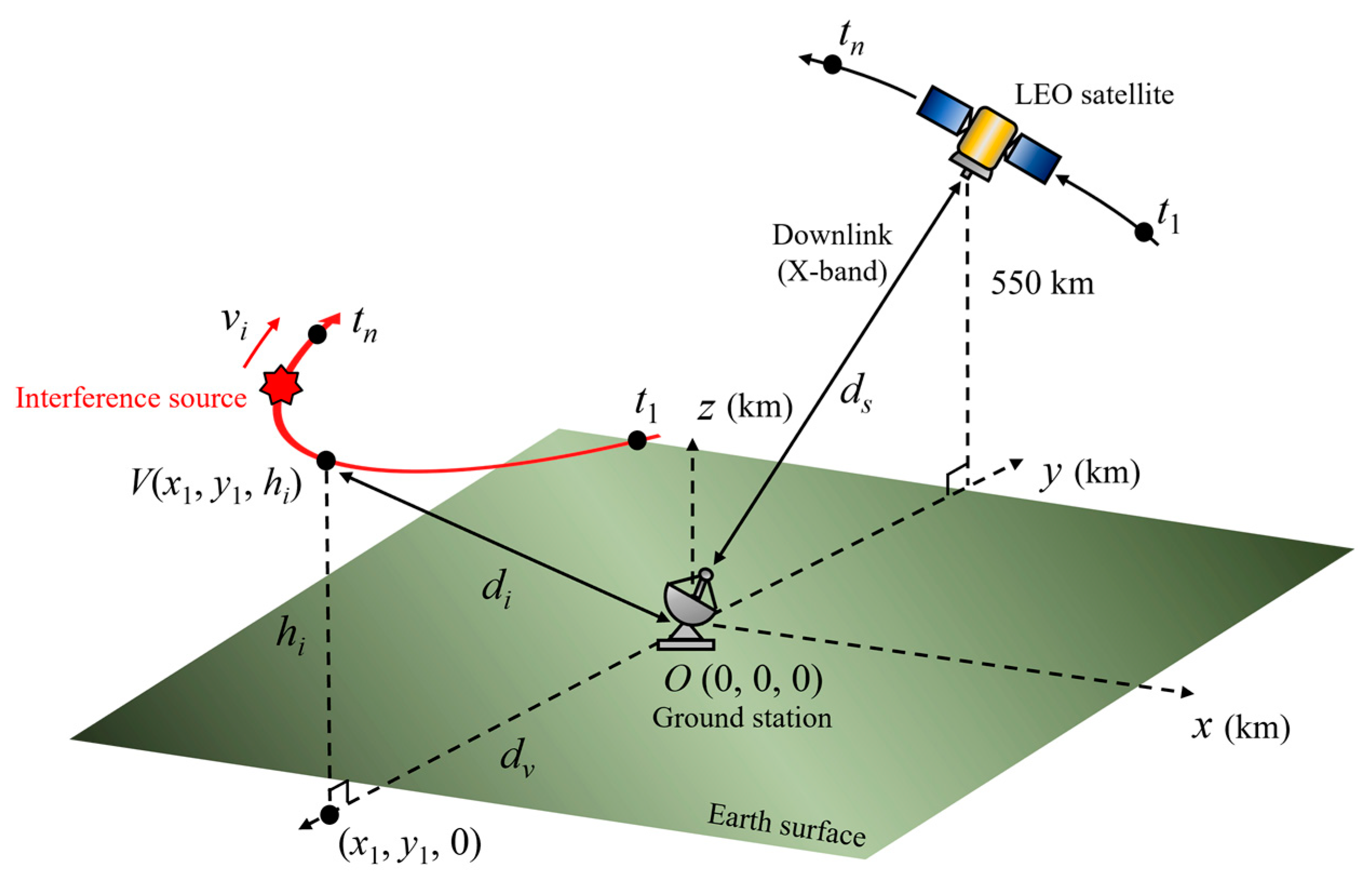
2. Analysis of LEO Satellite Communication Links Under Interference Situations
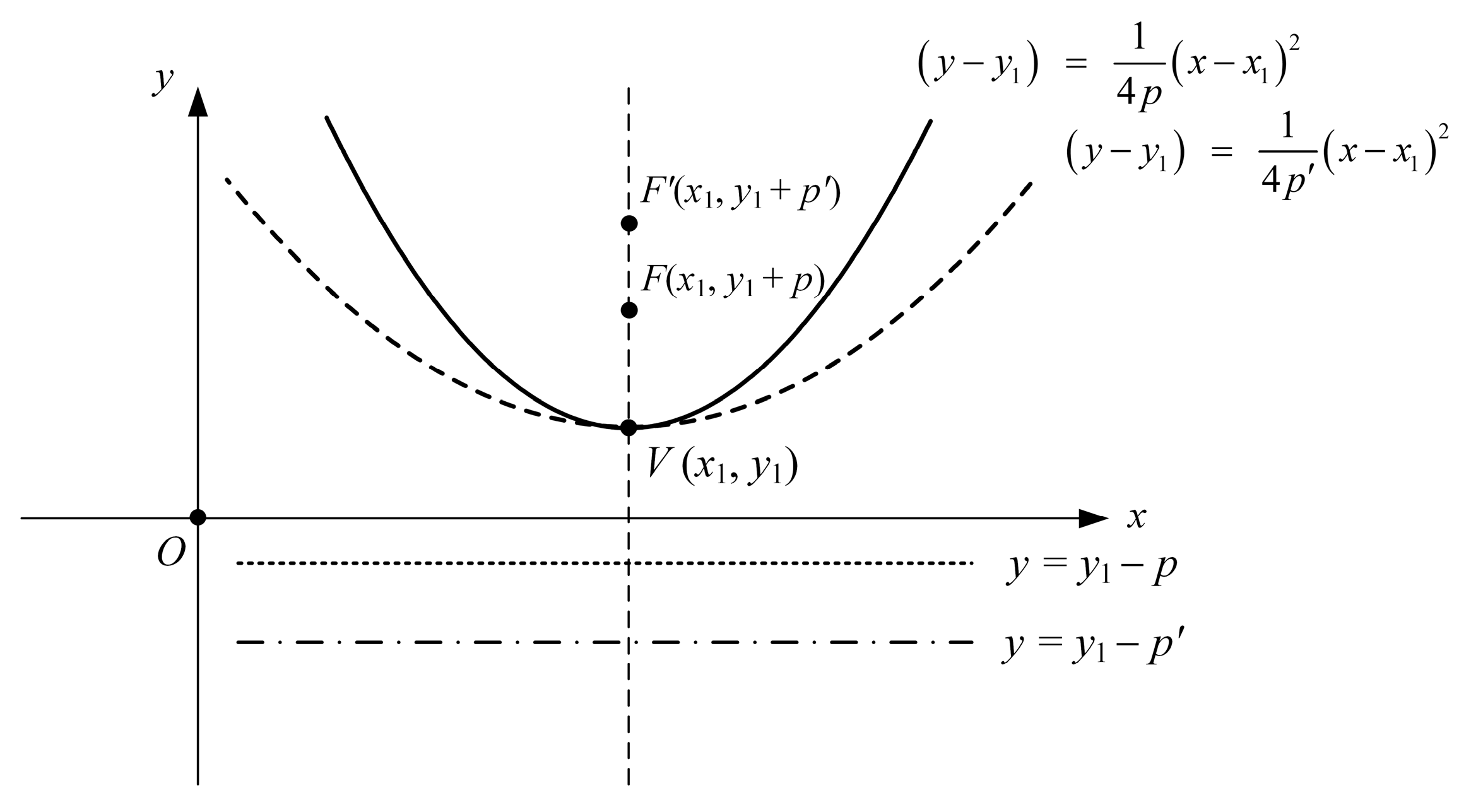
2.1. Communication Link Considering Parabola-Curved Paths of Airborne Interference Source
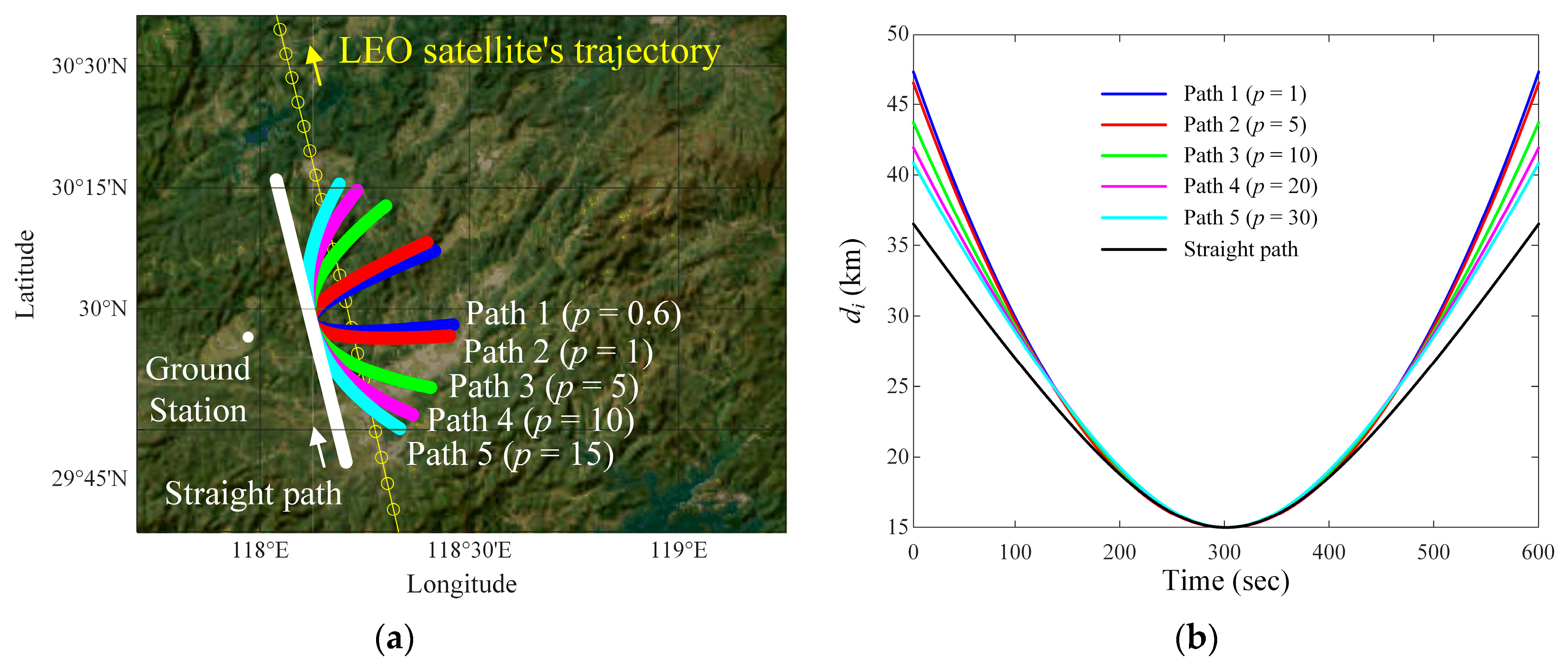
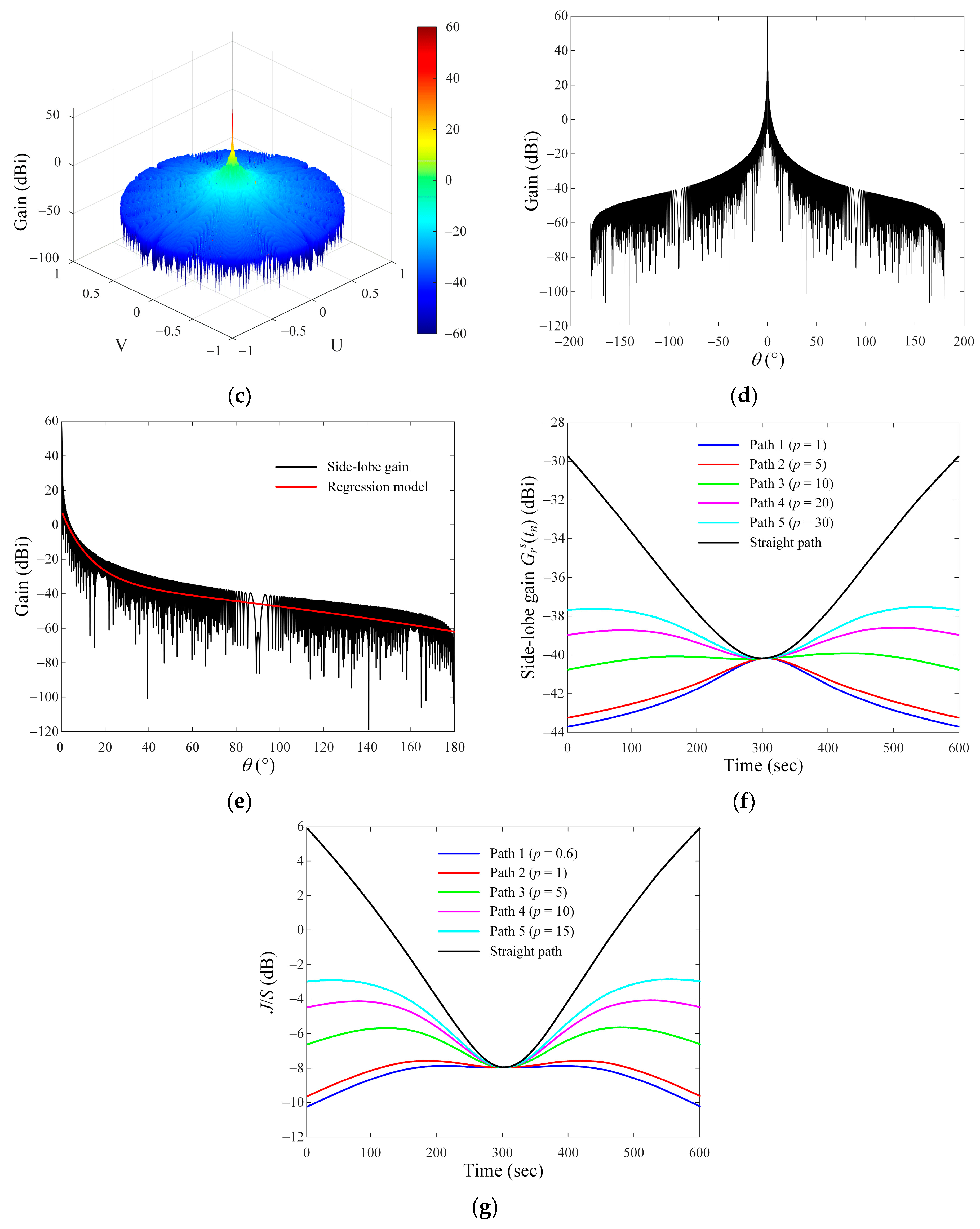
2.2. Analysis of Communication Links According to Various Paths of the Airborne Interference Source
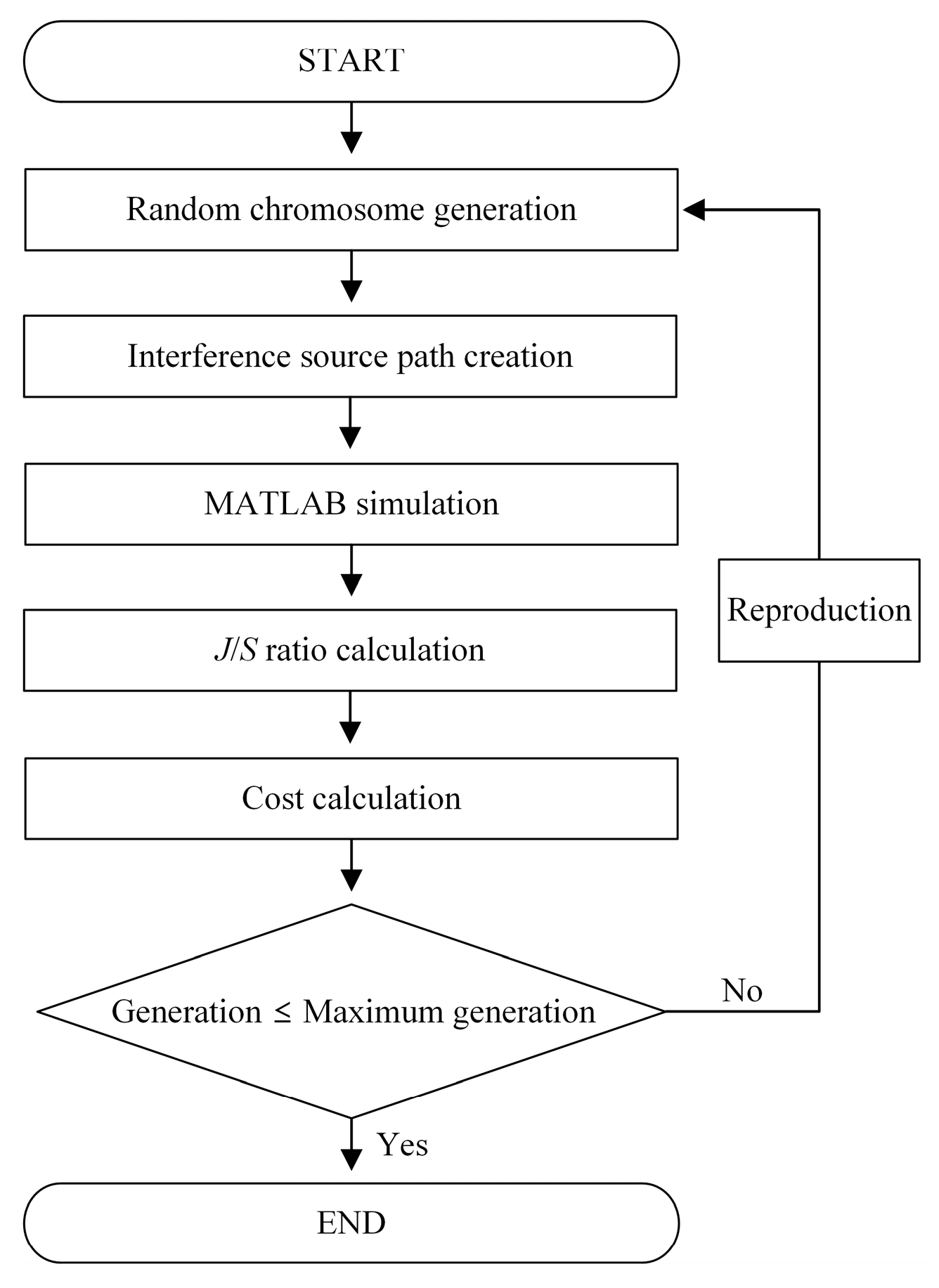
3. Investigation of the Interference Situation Using the Genetic Algorithm
- Setting LEO satellite trajectories and the location of the ground station.
- −
- Loading the information of LEO satellite trajectories from the JSpOC at Vandenberg Air Force Base (TLE data).
- −
- Specifying the location of the ground station that communicates with the LEO satellite.
- Expression of interference source paths.
- −
- Expressing airborne interference source paths based on the parabola equations.
- −
- Considering conditions such as speed and altitude of actually operable airborne interference sources.
- Calculation of the J/S ratio.
- −
- Calculating the power ratio of the interference and the satellite signal received by the ground station.
- −
- Considering LEO satellites trajectories and airborne interference source paths.
- Optimization of airborne interference source paths.
- −
- Setting the key parameters that determine the interference source path as GA parameters.
- −
- Setting the Cost to obtain a path with a constant J/S ratio during communication time using GA.
- Analysis of LEO satellite communications links.
- −
- Predicting the interference source paths that could seriously affect LEO satellite communications.
- −
- Providing a database for operating an anti-jamming system based on the obtained optimized path.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Townsend, W. An initial assessment of the performance achieved by the Seasat-1 radar altimeter. IEEE J. Ocean. Eng. 1980, 5, 80–92. [Google Scholar] [CrossRef]
- Ellis, P.; Rheeden, D.V.; Dowla, F. Use of Doppler and Doppler rate for RF geolocation using a single LEO satellite. IEEE Access 2020, 8, 12907–12920. [Google Scholar] [CrossRef]
- Seo, S.M.; Choi, Y.; Lim, H.; Park, J.H. A deep learning-based compact weighted binary classification technique to discriminate between targets and clutter in SAR images. J. Electromagn. Eng. Sci. 2022, 22, 412–418. [Google Scholar] [CrossRef]
- Seo, S.M.; Choi, Y.; Lim, H.; Chae, D.Y. A measurement image translation-automatic target recognition technique based on CycleGAN with SAR simulation DB. J. Electromagn. Eng. Sci. 2022, 22, 326–334. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, B.; Han, X.; Wang, R.; Song, H.; Deng, Y. A novel high-order range model and imaging approach for high-resolution LEO SAR. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3473–3485. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR processing and products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Ali, I.; Al-Dhahir, N.; Hershey, J.E. Predicting the visibility of LEO satellites. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1183–1190. [Google Scholar] [CrossRef]
- Radzik, J.; Maral, G. A methodology for rapidly evaluating the performance of some low earth orbit satellite systems. IEEE J. Sel. Areas Commun. 1995, 13, 301–309. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Luo, T. AsyncFLEO: Asynchronous federated learning for LEO satellite constellations with high-altitude platforms. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 17–20 December 2022; pp. 5478–5487. [Google Scholar]
- Keim, W. Scientific satellite ground station at 2 GHz in urban environment. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2004. [Google Scholar]
- Kang, E.; Yang, J.; Park, Y.; Kim, J.; Shin, W.; Park, Y.B.; Choo, H. Analysis of a low-Earth orbit satellite downlink considering antenna radiation patterns and space environment in interference situations. Remote Sens. 2023, 15, 1748–1758. [Google Scholar] [CrossRef]
- Akhtaruzzaman, M.; Bari, S.M.S.; Hossain, S.A.; Rahman, M.M. Link budget analysis in designing a web-application tool for military X-band satellite communication. Maejo Int. J. Sci. Technol. 2020, 8, 17–33. [Google Scholar] [CrossRef]
- Gongora-Torres, J.M.; Vargas-Rosales, C.; Aragón-Zavala, A.; Villalpando-Hernandez, R. Link budget analysis for LEO satellites based on the statistics of the elevation angle. IEEE Access 2022, 10, 14518–14528. [Google Scholar] [CrossRef]
- Castanet, L.; Bolea-Alamañac, A.; Bousquet, M. Interference and fade mitigation techniques for Ka and Q/V band satellite communication systems. In Proceedings of the 2nd International Workshop Satellite Communication of COST Action from Fade Mitigation to Service Provision, Noordwijk, The Netherlands, 26–28 May 2003; pp. 238–241. [Google Scholar]
- Ali, I.; Al-Dhahir, N.; Hershey, J.E. Doppler characterization for LEO satellites. IEEE Trans. Commun. 1998, 46, 309–313. [Google Scholar] [CrossRef]
- Ning, Q.; Yang, X.; Chen, B.; Zhou, X. The performance analysis of NOMA in LEO satellite rain attenuation and fading hybrid channel. Int. J. Satell. Commun. Netw. 2022, 40, 256–267. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Lyu, D. Estimation of Moist Atmospheric Profiles from Refraction and Attenuation Measurements by Using Centimeter and Millimeter Wave Links between LEO Satellites. Remote Sens. 2023, 15, 391–408. [Google Scholar] [CrossRef]
- Kim, K.Y. Analysis of anti-jamming techniques for satellite navigation systems. J. Korean Inst. Commun. Inf. Sci. 2013, 38, 1216–1227. [Google Scholar]
- Lichtman, M.; Reed, J.H. Analysis of reactive jamming against satellite communications. Trans. Emerg. Telecommun. Technol. 2016, 32, 195–210. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, L.; Ki, Z.; Ma, R.; Ou, J. Cooperative jamming in downlink satellite network with hardware impairments. Int. J. Satell. Commun. Netw. 2021, 34, 4372–4392. [Google Scholar] [CrossRef]
- Taricco, G.; Alagha, N. On jamming detection methods for satellite Internet of Things networks. Int. J. Satell. Commun. Netw. 2022, 40, 177–190. [Google Scholar] [CrossRef]
- Han, C.; Liu, A.; An, K.; Wang, H.; Zheng, G.; Chatzinotas, S.; Huo, L.; Tong, X. Satellite-assisted UAV trajectory control in hostile jamming environments. IEEE Trans. Veh. Technol. 2021, 71, 3760–3775. [Google Scholar] [CrossRef]
- Bankey, V.; Upadhyay, P.K. Improving secrecy performance of land mobile satellite systems via a UAV friendly jammer. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications Networking Conference, Las Vegas, NV, USA, 10–13 January 2020; pp. 1–4. [Google Scholar]
- Leonardi, M.; Strohmeier, M.; Lenders, V. On jamming attacks in crowdsourced air traffic surveillance. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 44–54. [Google Scholar] [CrossRef]
- Kang, E.; Park, Y.; Kim, J.; Choo, H. Downlink analysis of a Low-Earth Orbit satellite considering an airborne interference source moving on various trajectory. Remote Sens. 2024, 16, 321–334. [Google Scholar] [CrossRef]
- Kelecy, T.; Hall, D.; Hamada, K.; Stocker, D. Satellite maneuver detection using Two-line Element (TLE) data. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 12–15 September 2007. [Google Scholar]
- Chronopoulos, S.K.; Angelis, C.T.; Koumasis, A.; Drakou, P. Satellite coverage analysis for the investigation of real-time communication in selected areas. WSEAS Trans. Commun. 2006, 5, 1965–1972. [Google Scholar]
- Ippolito, L.J., Jr. Satellite Communications Systems Engineering: Atmospheric Effects, Satellite Link Design and System Performance; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Merabtine, N.; Boualleg, A.; Benslama, M. Analysis of radiation patterns and feed illumination of the reflector antenna using the physical and geometrical optics. Semicond. Phys. Quant. 2006, 9, 53–57. [Google Scholar] [CrossRef]
- Piu, H.; Rahmat Samii, Y. Analysis and characterization of multilayered reflector antennas: Rain/snow accumulation and deployable membrane. IEEE Trans. Antennas Propagat. 1998, 46, 1593–1605. [Google Scholar]
- Hung, C.; Mittra, R. Secondary pattern and focal region distribution of reflector antennas under wide-angle scaning. IEEE Trans. Antennas Propagat. 1983, 31, 756–763. [Google Scholar] [CrossRef]
- Erceg, V.; Greenstein, L.J.; Tjandra, S.; Parkoff, S.R.; Gupta, A.; Kulic, B.; Julius, B.; Jastrzab, R. An empirically-based path loss model for wireless channels in suburban environments. In Proceedings of the IEEE GLOBECOM’98, Sydney, NSW, Australia, 8–12 November 1998; Volume 2, pp. 922–927. [Google Scholar]
- Famoriji; Oluwole, J.; Shongwe, T. Channel characterization and modeling for wireless communication link planning and design in the tropics. Indones. J. Electr. Eng. Comput. Sci. 2023, 31, 1433–1441. [Google Scholar] [CrossRef]
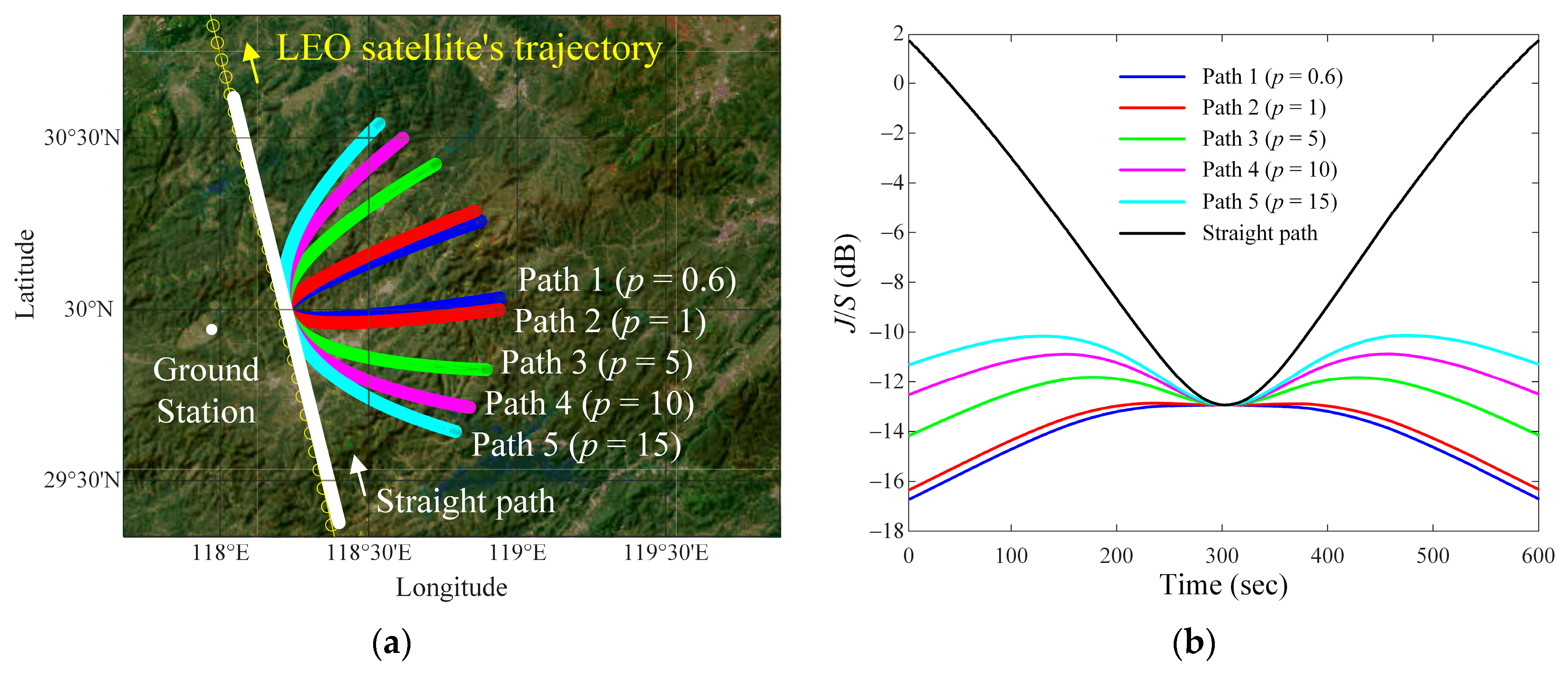

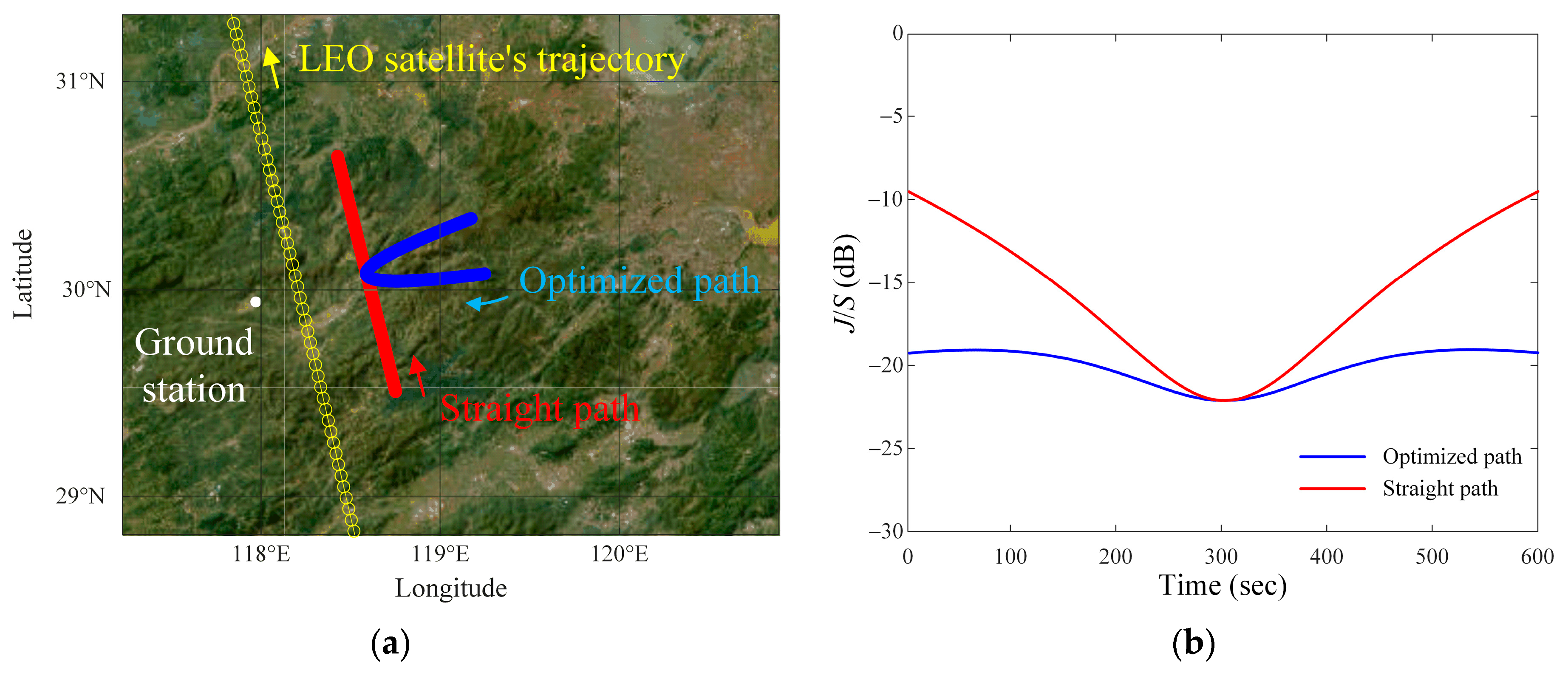
| Interference Source Paths | Values | |
|---|---|---|
| Max. Value of di (km) | Min. Value of di (km) | |
| Path 1 (p = 0.6) | 47.3 | 15 |
| Path 2 (p = 1) | 46.6 | 15 |
| Path 3 (p = 5) | 43.8 | 15 |
| Path 4 (p = 10) | 42 | 15 |
| Path 5 (p = 15) | 40.9 | 15 |
| Straight path | 36.6 | 15 |
| Parameters | Values |
|---|---|
| Frequency (GHz) | 8.025 |
| Bore-sight gain (dBi) | 59 |
| LEO satellite altitude (km) | 550 |
| (dBm) | 30 |
| Bore-sight gain (dBi) | 4.4 |
| Free-space path loss (dB) | |
| Interference source velocity vi (km/h) | 400~850 |
| Interference source altitude hi (km) | 9~15 |
| (dBm) | 70 |
| Bore-sight gain (dBi) | 30 |
| Interference Source Paths | J/S Ratios (dB) | ||
|---|---|---|---|
| Max. Value | Min. Value | Average Difference | |
| Path 1 (p = 1) | −7.9 | −10.2 | 0.6 |
| Path 2 (p = 5) | −7.6 | −9.6 | 0.4 |
| Path 3 (p = 10) | −5.6 | −7.9 | 1.5 |
| Path 4 (p = 20) | −4.1 | −7.9 | 2.6 |
| Path 5 (p = 30) | −2.8 | −7.9 | 3.3 |
| Straight path | 5.9 | −7.9 | 6.7 |
| Interference Source Paths | Values | ||
|---|---|---|---|
| Max. Value | Min. Value | Average Difference | |
| Path 1 (p = 1) | −12.9 | −16.7 | 1.2 |
| Path 2 (p = 5) | −12.8 | −16.3 | 1 |
| Path 3 (p = 10) | −11.8 | −14.1 | 0.6 |
| Path 4 (p = 20) | −10.9 | −12.9 | 1.3 |
| Path 5 (p = 30) | −10.1 | −12.9 | 1.9 |
| Straight path | 1.7 | −12.9 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.; Kang, E.; Choo, H. Communication Link Analysis of a Low-Earth Orbit Satellites Considering Interference Sources Moving Along Various Parabola-Curved Paths. Sensors 2024, 24, 8185. https://doi.org/10.3390/s24248185
Kang H, Kang E, Choo H. Communication Link Analysis of a Low-Earth Orbit Satellites Considering Interference Sources Moving Along Various Parabola-Curved Paths. Sensors. 2024; 24(24):8185. https://doi.org/10.3390/s24248185
Chicago/Turabian StyleKang, Hyunmu, Eunjung Kang, and Hosung Choo. 2024. "Communication Link Analysis of a Low-Earth Orbit Satellites Considering Interference Sources Moving Along Various Parabola-Curved Paths" Sensors 24, no. 24: 8185. https://doi.org/10.3390/s24248185
APA StyleKang, H., Kang, E., & Choo, H. (2024). Communication Link Analysis of a Low-Earth Orbit Satellites Considering Interference Sources Moving Along Various Parabola-Curved Paths. Sensors, 24(24), 8185. https://doi.org/10.3390/s24248185






