Enhance the Concrete Crack Classification Based on a Novel Multi-Stage YOLOV10-ViT Framework
Abstract
:1. Introduction
1.1. Related Work
- The recent literature lacks the effective implementation of the idea of multi-stage detection and multi-class classification based on hybrid lightweight models.
- Current and historical studies often focus on specific tasks (either detection or classification).
- The modern ViT classification models outperform the traditional CNNs and available transfer-learning models and guarantee robust and efficient performance.
- The most recent YOLO model (YOLOV10) model has not yet received high attention in the field of crack detection and still needs more investigations.
- All previous attempts to develop multi-stage systems focus on one mission (detection, classification, segmentation), and few studies considered the detection-classification issue. However, the literature is short of region-based detection and classification frameworks.
1.2. Contribution
- Creating a novel deep learning framework utilizing the capability of two detection and classification models (YOLOV10 and ViT) called the “YOLOV10-ViT” framework.
- Utilizing of new concrete crack detection dataset for training the YOLOV10 model, and depending on a multi-class classification concrete crack classification dataset for training the ViT model. The aim of the combination of two-source datasets to train and test the proposed YOLOV10-ViT model provide more efficient identification with boosted generalization abilities.
- Comparison of the performance with and without the pre-detection stage of the YOLOV10 model to show the superiority of the proposed multi-stage technique.
2. Materials and Methods
2.1. Main Methodology
2.2. The Datasets
2.3. Deep Learning Methodologies
2.3.1. YOLOV10 Detection Model
2.3.2. Vision Transformer Model
2.3.3. Training Options
2.3.4. Performance Evaluation
3. Results
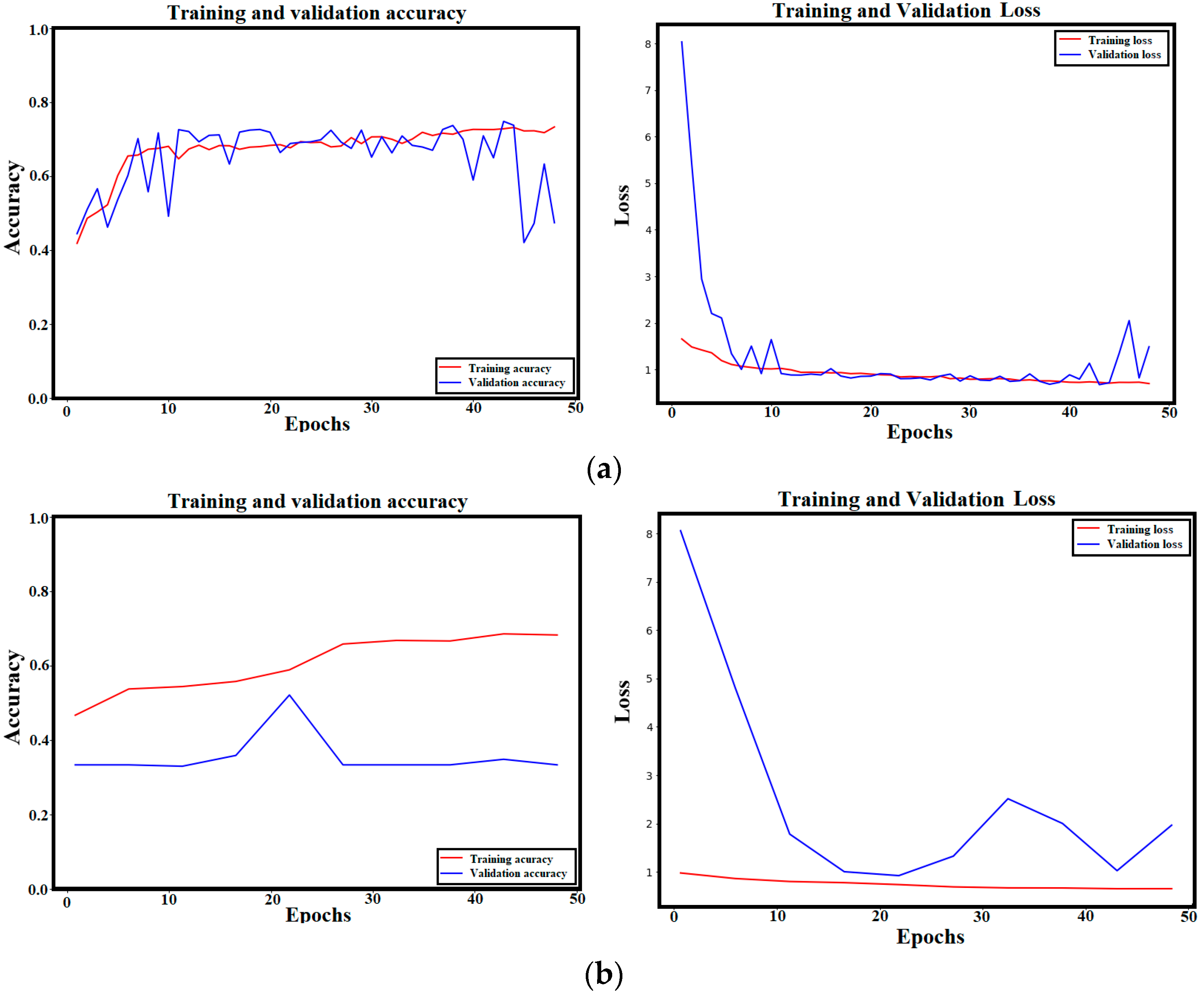
3.1. ViT Classification Model’s Results
3.2. YOLOV10 Detection Model’s Results
3.3. The Multi-Stage Model Results
4. Discussion
4.1. Individual Models Discussion
4.2. Multi-Stage Model Results’ Discussion
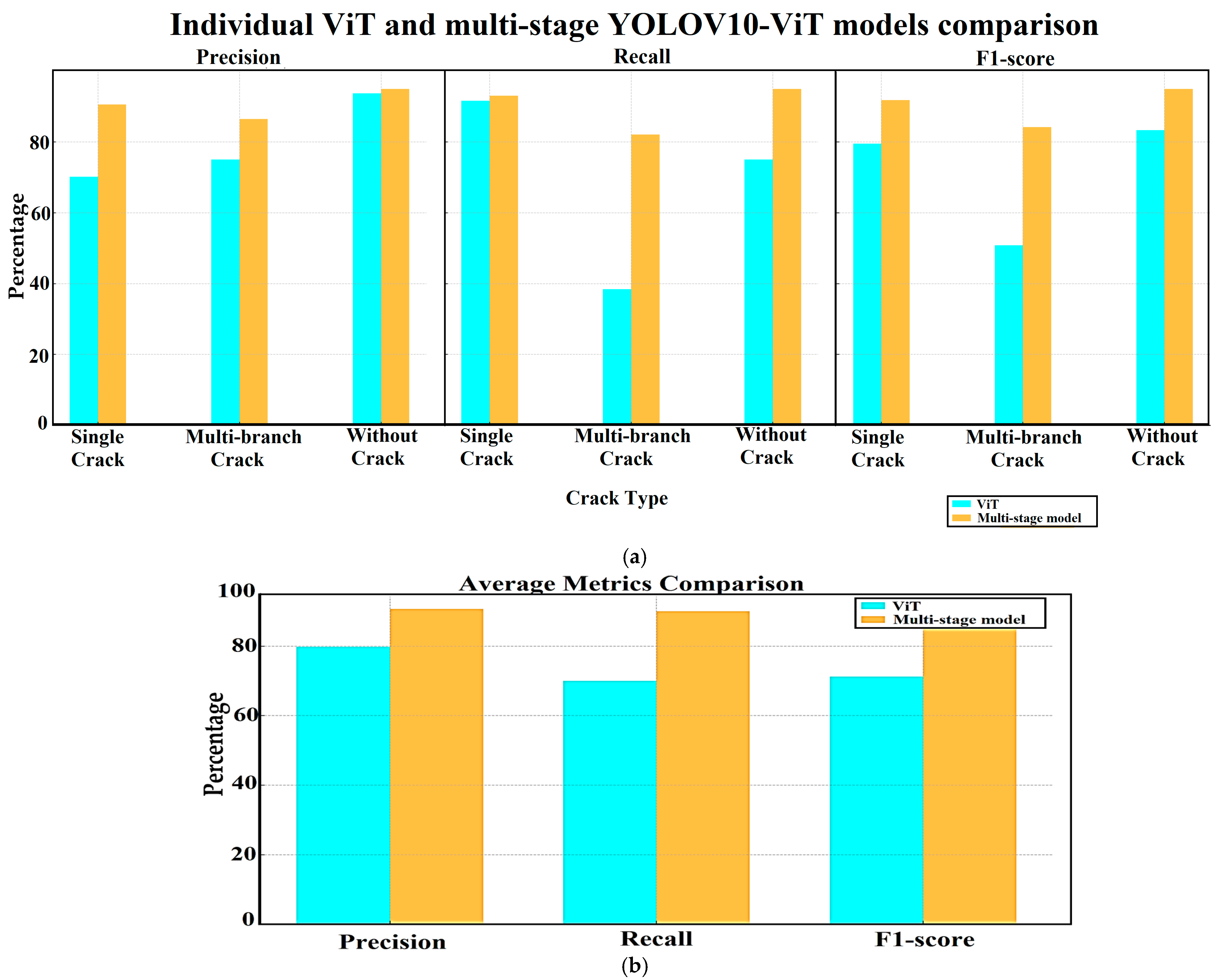
4.3. Individual and Multi-Stage Models Numerical Comparison
4.4. Ablation Study
4.4.1. Changing the Input and Batch Size
4.4.2. Fine Tuning the ViT Model
4.4.3. Changing the Learning Rate and Optimizer
4.4.4. Changing the Stop Condition
4.4.5. Changing the Hyperparameters of the YOLO Model
4.5. Limitations
4.6. Comparison with Previous Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Peng, L.; Wen, S.; Huang, S. A Review on Concrete Structural Properties and Damage Evolution Monitoring Techniques. Sensors 2024, 24, 620. [Google Scholar] [CrossRef]
- Amirkhani, D.; Allili, M.S.; Hebbache, L.; Hammouche, N.; Lapointe, J.-F. Visual Concrete Bridge Defect Classification and Detection Using Deep Learning: A Systematic Review. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10483–10505. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Shen, L.; Mayya, A.; Asteris, P.G.; Fu, R.; Di Luzio, G.; Strauss, A.; Cao, M. Prediction of concrete and FRC properties at high temperature using machine and deep learning: A review of recent advances and future perspectives. J. Build. Eng. 2023, 83, 108369. [Google Scholar] [CrossRef]
- Abualigah, S.M.; Al-Naimi, A.F.; Sachdeva, G.; AlAmri, O.; Abualigah, L. IDSDeep-CCD: Intelligent decision support system based on deep learning for concrete cracks detection. Multimed. Tools Appl. 2024, 1–14. [Google Scholar] [CrossRef]
- Al-hababi, T.; Cao, M.; Alkayem, N.F.; Shi, B.; Wei, Q.; Cui, L.; Šumarac, D. The dual Fourier transform spectra (DFTS): A new nonlinear damage indicator for identification of breathing cracks in beam-like structures. Nonlinear Dyn. 2022, 110, 2611–2633. [Google Scholar] [CrossRef]
- Fu, Y.; Li, L. Study on mechanism of thermal spalling in concrete exposed to elevated temperatures. Mater. Struct. 2011, 44, 361–376. [Google Scholar] [CrossRef]
- Biradar, G.; Ramanna, N.; Madduru, S.R.C. An in-depth examination of fire-related damages in reinforced concrete structures-A review. J. Build. Pathol. Rehabil. 2024, 9, 81. [Google Scholar] [CrossRef]
- Elkady, N.; Nelson, L.A.; Weekes, L.; Makoond, N.; Buitrago, M. Progressive collapse: Past, present, future and beyond. Structures 2024, 62, 106131. [Google Scholar] [CrossRef]
- Forest, F.; Porta, H.; Tuia, D.; Fink, O. From classification to segmentation with explainable AI: A study on crack detection and growth monitoring. Autom. Constr. 2024, 165, 105497. [Google Scholar] [CrossRef]
- Sarkar, K.; Shiuly, A.; Dhal, K.G. Revolutionizing concrete analysis: An in-depth survey of AI-powered insights with image-centric approaches on comprehensive quality control, advanced crack detection and concrete property exploration. Constr. Build. Mater. 2024, 411, 134212. [Google Scholar] [CrossRef]
- Guo, J.; Liu, P.; Xiao, B.; Deng, L.; Wang, Q. Surface defect detection of civil structures using images: Review from data perspective. Autom. Constr. 2024, 158, 105186. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Z.; Kang, H.; Tang, Y. 3D vision technologies for a self-developed structural external crack damage recognition robot. Autom. Constr. 2024, 159, 105262. [Google Scholar] [CrossRef]
- Wan, S.; Guan, S.; Tang, Y. Advancing bridge structural health monitoring: Insights into knowledge-driven and data-driven approaches. J. Data Sci. Intell. Syst. 2024, 2, 129–140. [Google Scholar] [CrossRef]
- Wu, Z.; Tang, Y.; Hong, B.; Liang, B.; Liu, Y. Enhanced Precision in Dam Crack Width Measurement: Leveraging Advanced Lightweight Network Identification for Pixel-Level Accuracy. Int. J. Intell. Syst. 2023, 2023, 9940881. [Google Scholar] [CrossRef]
- Moreh, F.; Lyu, H.; Rizvi, Z.H.; Wuttke, F. Deep neural networks for crack detection inside structures. Sci. Rep. 2024, 14, 4439. [Google Scholar] [CrossRef] [PubMed]
- Alkayem, N.F.; Mayya, A.; Shen, L.; Zhang, X.; Asteris, P.G.; Wang, Q.; Cao, M. Co-CrackSegment: A New Collaborative Deep Learning Framework for Pixel-Level Semantic Segmentation of Concrete Cracks. Mathematics 2024, 12, 3105. [Google Scholar] [CrossRef]
- Duan, S.; Zhang, M.; Qiu, S.; Xiong, J.; Zhang, H.; Li, C.; Kou, Y. Tunnel lining crack detection model based on improved YOLOv5. Tunn. Undergr. Space Technol. 2024, 147, 105713. [Google Scholar] [CrossRef]
- Yuan, Q.; Shi, Y.; Li, M. A Review of Computer Vision-Based Crack Detection Methods in Civil Infrastructure: Progress and Challenges. Remote Sens. 2024, 16, 2910. [Google Scholar] [CrossRef]
- Yadav, D.P.; Kishore, K.; Gaur, A.; Kumar, A.; Singh, K.U.; Singh, T.; Swarup, C. A novel multi-scale feature fusion-based 3SCNet for building crack detection. Sustainability 2022, 14, 16179. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Wang, G.; Huo, J.; Li, Y.; Li, L. Automatic concrete infrastructure crack semantic segmentation using deep learning. Autom. Constr. 2023, 152, 104950. [Google Scholar] [CrossRef]
- Yadav, D.P.; Sharma, B.; Chauhan, S.; Dhaou, I.B. Bridging Convolutional Neural Networks and Transformers for Efficient Crack Detection in Concrete Building Structures. Sensors 2024, 24, 4257. [Google Scholar] [CrossRef] [PubMed]
- Shahin, M.; Chen, F.F.; Maghanaki, M.; Hosseinzadeh, A.; Zand, N.; Koodiani, H.K. Improving the Concrete Crack Detection Process via a Hybrid Visual Transformer Algorithm. Sensors 2024, 24, 3247. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Zhou, X.; Liu, Y.; Liu, D.; Lu, Y.; Su, M. Identification of the Surface Cracks of Concrete Based on ResNet-18 Depth Residual Network. Appl. Sci. 2024, 14, 3142. [Google Scholar] [CrossRef]
- Mayya, A.; Alkayem, N.F.; Shen, L.; Zhang, X.; Fu, R.; Wang, Q.; Cao, M. Efficient hybrid ensembles of CNNs and transfer learning models for bridge deck image-based crack detection. Structures 2024, 64, 106538. [Google Scholar] [CrossRef]
- Wang, Z.; Leng, Z.; Zhang, Z. A weakly-supervised transformer-based hybrid network with multi-attention for pavement crack detection. Constr. Build. Mater. 2024, 411, 134134. [Google Scholar] [CrossRef]
- Abubakr; Rady, M.; Badran, K.; Mahfouz, S.Y. Application of deep learning in damage classification of reinforced concrete bridges. Ain Shams Eng. J. 2024, 15, 102297. [Google Scholar] [CrossRef]
- Russel, N.S.; Selvaraj, A. MultiScaleCrackNet: A parallel multiscale deep CNN architecture for concrete crack classification. Expert Syst. Appl. 2024, 249, 123658. [Google Scholar] [CrossRef]
- Dong, X.; Liu, Y.; Dai, J. Concrete Surface Crack Detection Algorithm Based on Improved YOLOv8. Sensors 2024, 24, 5252. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Dong, Q. Detection of asphalt pavement cracks based on vision transformer improved YOLO V5. J. Transp. Eng. Part B Pavements 2023, 149, 04023004. [Google Scholar] [CrossRef]
- Nguyen, N.H.T.; Perry, S.; Bone, D.; Le, H.T.; Nguyen, T.T. Two-stage convolutional neural network for road crack detection and segmentation. Expert Syst. Appl. 2021, 186, 115718. [Google Scholar] [CrossRef]
- Sohaib, M.; Jamil, S.; Kim, J.-M. An ensemble approach for robust automated crack detection and segmentation in concrete structures. Sensors 2024, 24, 257. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Ou, L.; Yi, S.; Wang, L. Multi-stage damage identification method for PC structures based on machine learning driven by piezoelectric singular feature. Eng. Fail. Anal. 2024, 165, 108769. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Wu, R.-T.; Puranam, A. Multi-task deep learning for crack segmentation and quantification in RC structures. Autom. Constr. 2024, 166, 105599. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Z.; Shen, H. A three-stage detection algorithm for automatic crack-width identification of fine concrete cracks. J. Civ. Struct. Health Monit. 2024, 14, 1373–1382. [Google Scholar] [CrossRef]
- Jabbari, H.; Bigdeli, N.; Shojaei, M. Cracks in Concrete Structures (CICS) Dataset, Mendeley Data, V1. 2023. Available online: https://data.mendeley.com/datasets/9brnm3c39k/1 (accessed on 1 August 2024).
- Karimi, N.; Mishra, M.; Lourenço, P.B. Deep learning-based automated tile defect detection system for Portuguese cultural heritage buildings. J. Cult. Herit. 2024, 68, 86–98. [Google Scholar] [CrossRef]
- Karimi, N. Deterioration Detection in Historical Buildings. Kaggle. Available online: https://www.kaggle.com/datasets/nargeskarimii/deterioration-detection-in-historical-buildings (accessed on 20 August 2024).
- Hussain, M.; Khanam, R. In-depth review of yolov1 to yolov10 variants for enhanced photovoltaic defect detection. Solar 2024, 4, 351–386. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. Yolov10: Real-time end-to-end object detection. arXiv 2024, arXiv:2405.14458. [Google Scholar]
- Vijayakumar, A.; Vairavasundaram, S.; Koilraj, J.A.S.; Rajappa, M.; Kotecha, K.; Kulkarni, A. Real-time visual intelligence for defect detection in pharmaceutical packaging. Sci. Rep. 2024, 14, 18811. [Google Scholar] [CrossRef] [PubMed]
- Geetha, A.S.; Alif, M.A.R.; Hussain, M.; Allen, P. Comparative Analysis of YOLOv8 and YOLOv10 in Vehicle Detection: Performance Metrics and Model Efficacy. Vehicles 2024, 6, 1364–1382. [Google Scholar] [CrossRef]
- Hussain, M. YOLOv8 and YOLOv10: The Go-To Detectors for Real-time Vision. arXiv 2024, arXiv:2407.02988. [Google Scholar]
- Tang, S.; Yan, W. Utilizing RT-DETR Model for Fruit Calorie Estimation from Digital Images. Information 2024, 15, 469. [Google Scholar] [CrossRef]
- Maurício, J.; Domingues, I.; Bernardino, J. Comparing vision transformers and convolutional neural networks for image classification: A literature review. Appl. Sci. 2023, 13, 5521. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Amjoud, A.B.; Amrouch, M. Object detection using deep learning, CNNs and vision transformers: A review. IEEE Access 2023, 11, 35479–35516. [Google Scholar] [CrossRef]
- Elgazzar, K.; Mostafi, S.; Dennis, R.; Osman, Y. Quantitative Analysis of Deep Learning-Based Object Detection Models. IEEE Access 2024, 12, 70025–70044. [Google Scholar] [CrossRef]
- You, J.; Korhonen, J. Transformer for image quality assessment. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1389–1393. [Google Scholar]
- Hemalatha, S.; Jayachandran, J.J.B. A Multitask Learning-Based Vision Transformer for Plant Disease Localization and Classification. Int. J. Comput. Intell. Syst. 2024, 17, 188. [Google Scholar] [CrossRef]
- Hassan, N.M.; Hamad, S.; Mahar, K. YOLO-based CAD framework with ViT transformer for breast mass detection and classification in CESM and FFDM images. Neural Comput. Appl. 2024, 36, 6467–6496. [Google Scholar] [CrossRef]
- Vujović, Ž. Classification model evaluation metrics. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 599–606. [Google Scholar] [CrossRef]
- Hassan, S.U.; Ahamed, J.; Ahmad, K. Analytics of machine learning-based algorithms for text classification. Sustain. Oper. Comput. 2022, 3, 238–248. [Google Scholar] [CrossRef]
- Erickson, B.J.; Kitamura, F. Magician’s corner: 9. Performance metrics for machine learning models. Radiol. Soc. North Am. 2021, 3, e200126. [Google Scholar] [CrossRef]
- Yucesoy, Y.F.; Sahin, C. Object Detection in Infrared Images with Different Spectra. In Proceedings of the 2024 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Istanbul, Turkey, 23–25 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Antunes, S.N.; Okano, M.T.; Nääs, I.d.A.; Lopes, W.A.C.; Aguiar, F.P.L.; Vendrametto, O.; Fernandes, J.C.L.; Fernandes, M.E. Model Development for Identifying Aromatic Herbs Using Object Detection Algorithm. AgriEngineering 2024, 6, 1924–1936. [Google Scholar] [CrossRef]
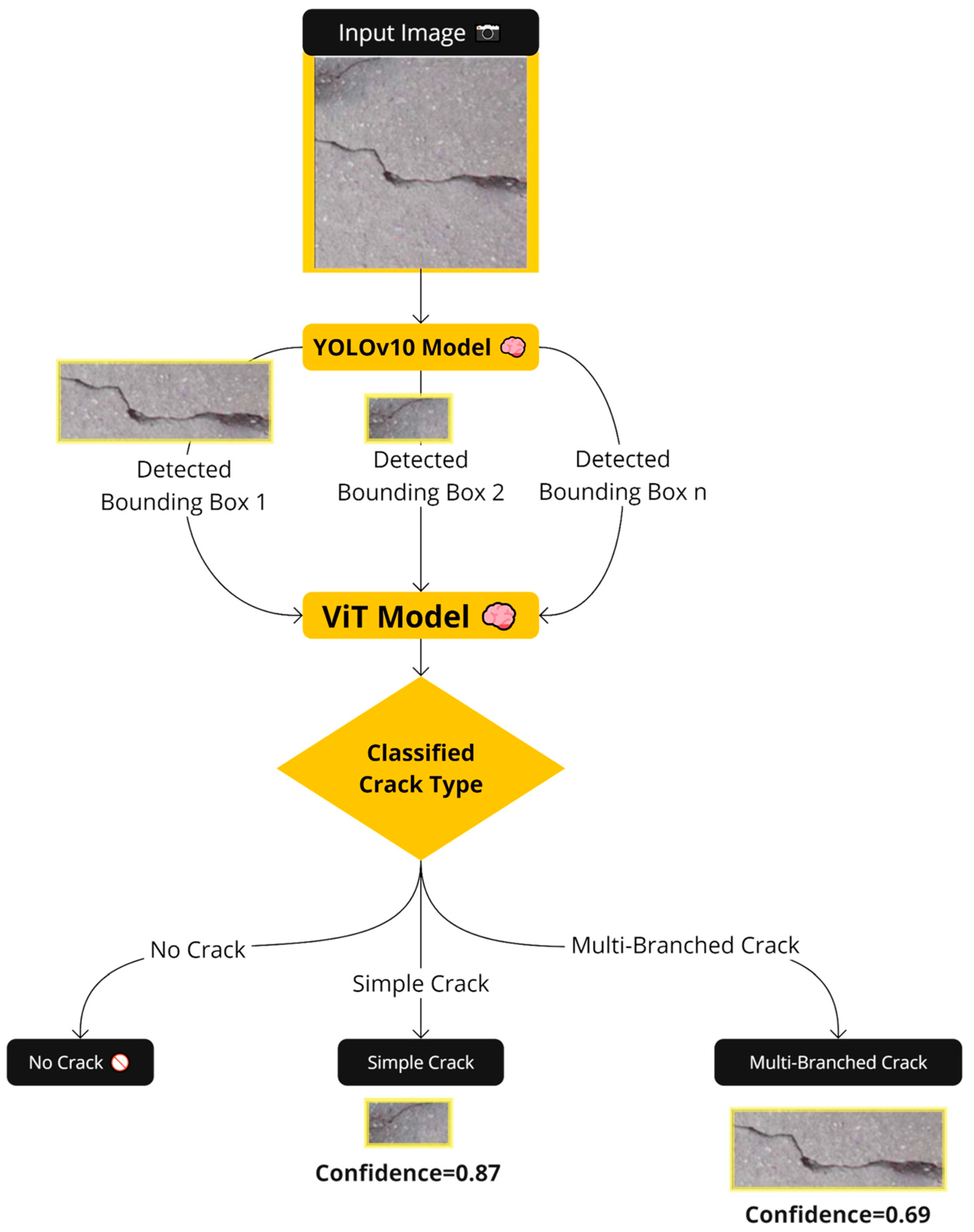



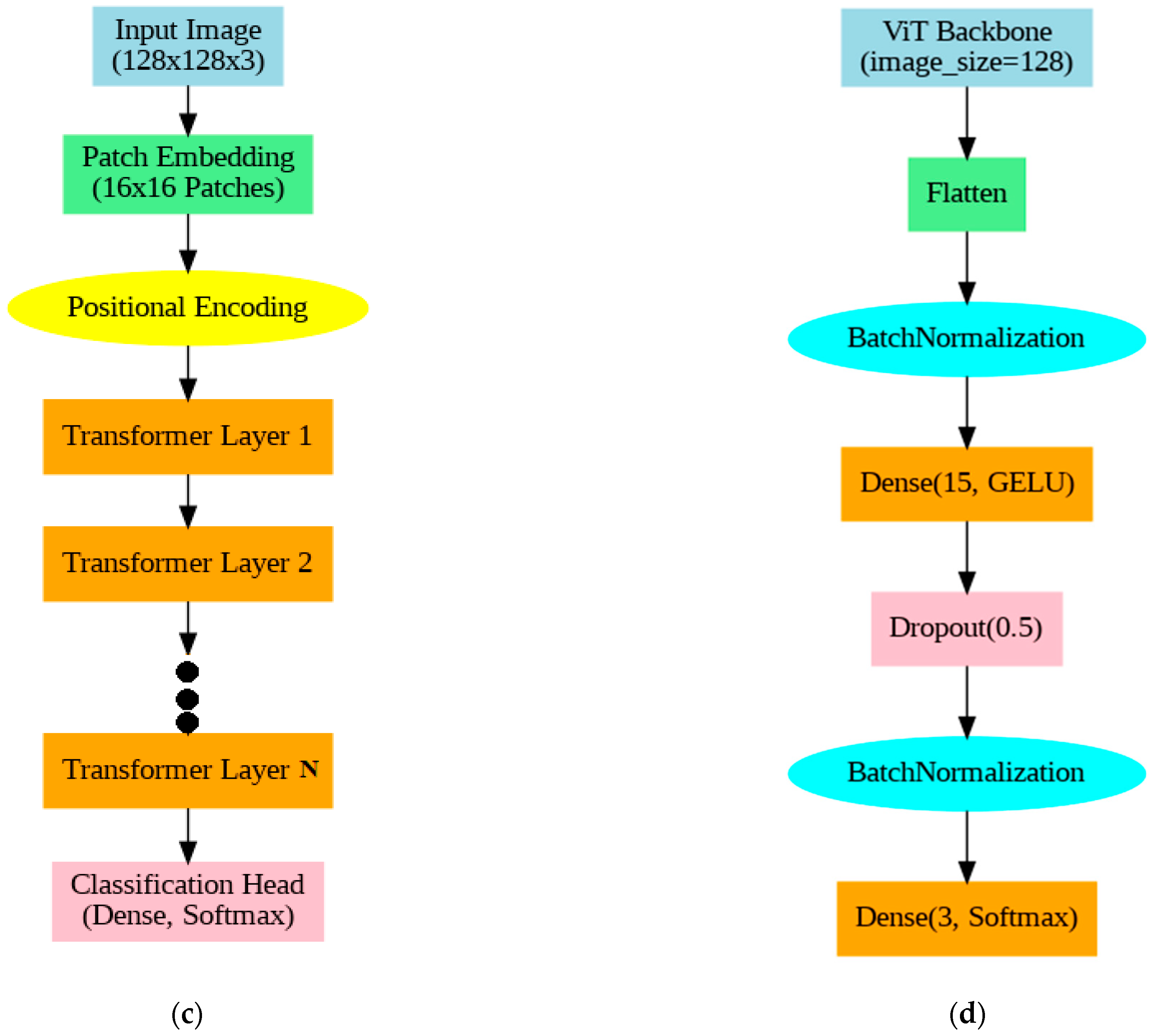

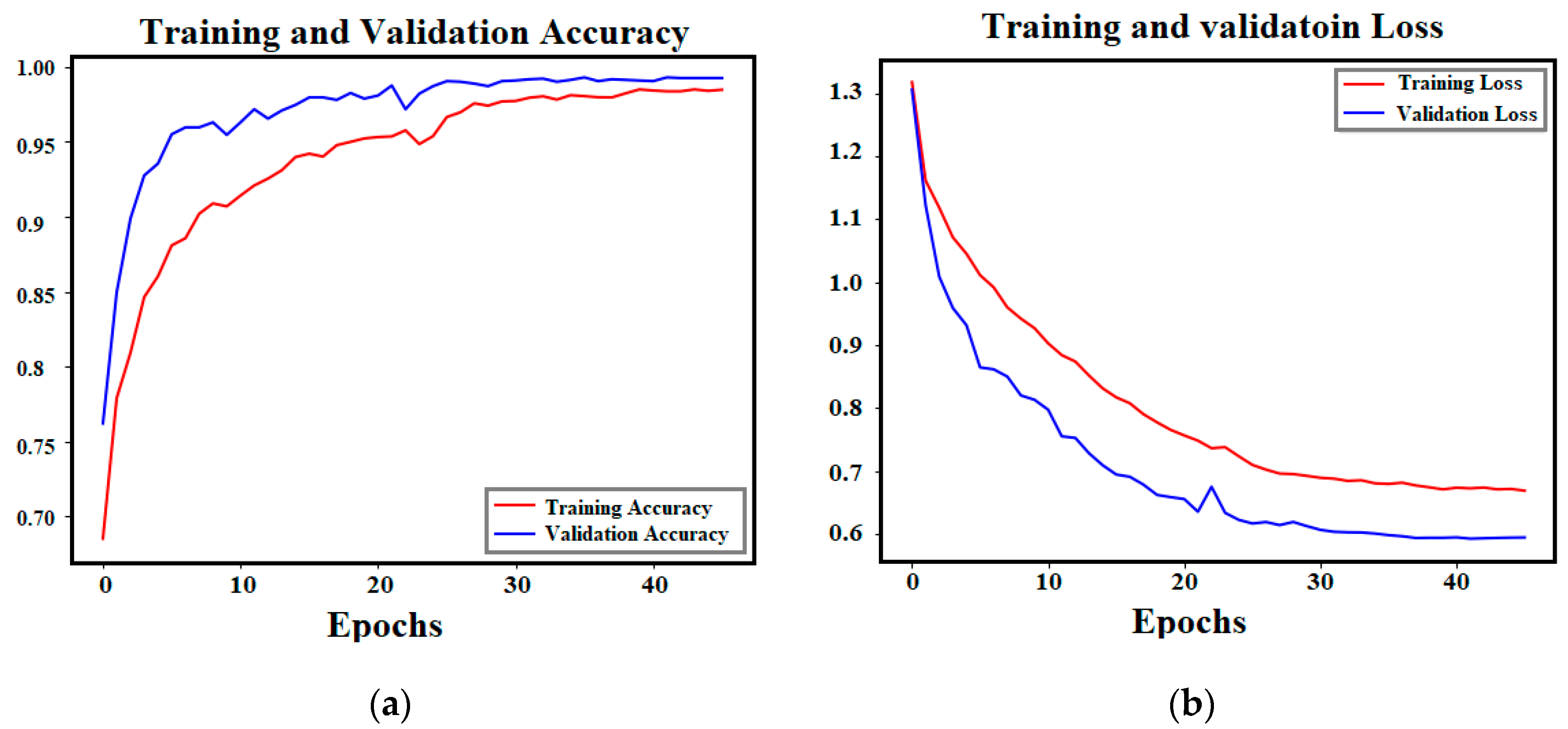
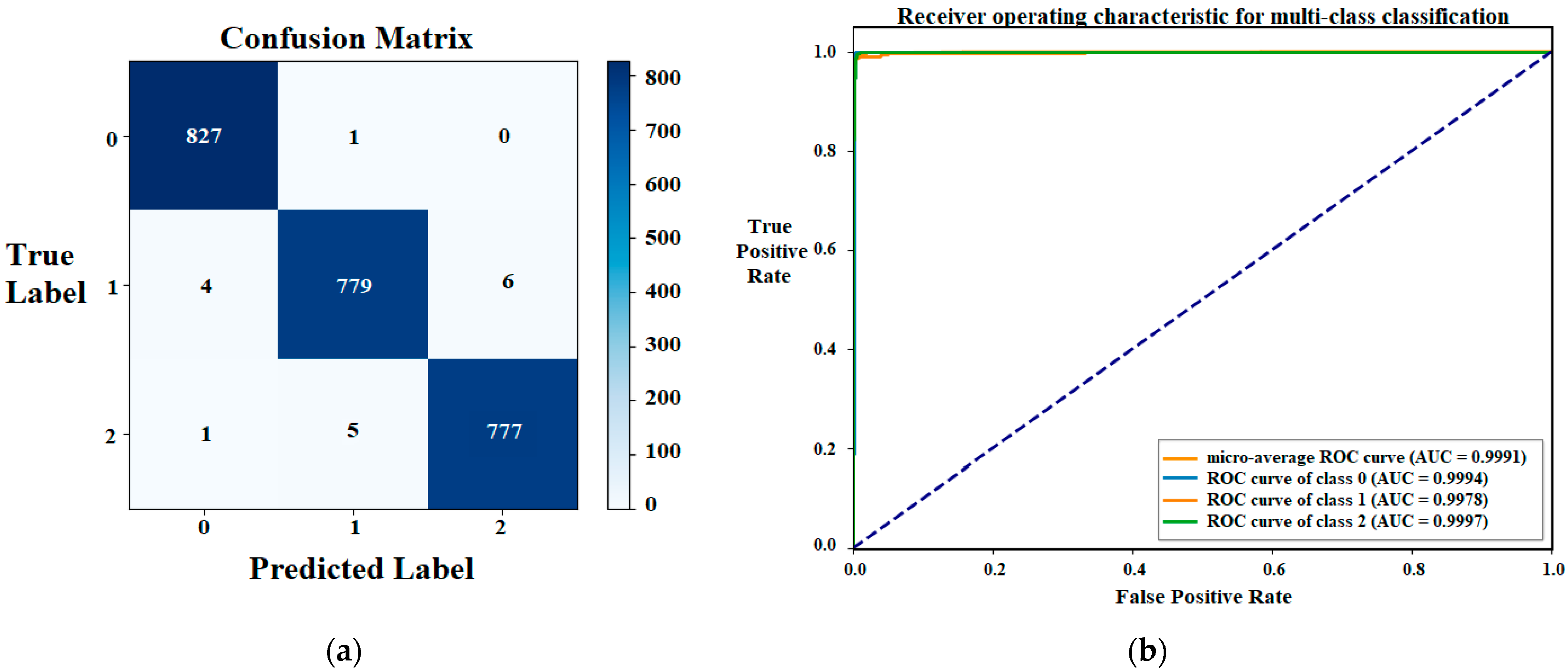














| Parameter | Value |
|---|---|
| Image size | 640 × 640 |
| Epochs | 50 |
| Batch Size | 32 |
| Learning Rate | 0.001 |
| Optimizer | Adam |
| Number of classes | 2 (Crack region and Background) |
| Parameter | Value |
|---|---|
| Image size | 128 × 128 × 3 |
| Test size | 20% |
| Batch size | 256 |
| Activation (Decision layer) | Softmax |
| Pretrained ViT | True |
| Number of classes | 3 |
| Optimizer | Adam |
| Loss function | Categorical Cross entropy |
| Learning rate | 0.0001 |
| Early stop condition | Yes |
| Early stop condition patience | 5 |
| Epochs | 50 |
| Class | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|
| Multi-branched crack | 99.4 | 99.88 | 99.64 |
| Simple crack | 99.24 | 98.73 | 98.98 |
| Without crack | 99.23 | 99.23 | 99.23 |
| Macro Average | 99.29 | 99.28 | 99.29 |
| Weighted Average | 99.29 | 99.29 | 99.29 |
| Samples/Models | ViT | Multi-Stage YOLOV10-ViT | Metrics (ViT) | Metrics (Multi-Stage) | |
|---|---|---|---|---|---|
| ‘single’ crack test samples | Correct classification | 66 | 67 | P: 66/(66 + 24 + 4) = 70.21% R: 66/(66 + 6) = 91.66% F: 79.51% | P: 67/(67 + 6+1) = 90.54% R: 67/(67 + 5) = 93.05% F: 91.77% |
| Misclassified as Multi-branch crack | 5 | 5 | |||
| Misclassified as without crack | 1 | - | |||
| Total | 72 | 72 | |||
| ‘multi-branch’ crack samples | Correct classification | 15 | 32 | P: 15/(15 + 5) = 75% R: 15/(15 + 24) = 38.46% F: 50.84% | P: 32/(32 + 5) = 86.48% R: 32/(32 + 7) = 82.05% F: 84.2% |
| Misclassified as Single-crack | 24 | 6 | |||
| Misclassified as without crack | - | 1 | |||
| Total | 39 | 39 | |||
| ‘Without crack’ samples | Correct classification | 15 | 19 | P: 15/(15 + 1) = 93.75% R: 15/(15 + 5) = 75% F: 83.33% | P: 19/(19 + 1) = 95% R: 19/(19 + 1) = 95% F: 95% |
| Misclassified as Single-crack | 5 | 1 | |||
| Misclassified as Multi-branch crack | - | - | |||
| Total | 20 | 20 | |||
| Average Metrics | P: 79.77% R: 70.04% F: 71.22% | P: 90.67% R: 90.03% F: 90.34% | |||
| Class | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| ’Adam’, Lr = 0.01 | 33.33 | 33.33 | 33.33 | 33.33 |
| ’Adam’, Lr = 0.001 | 75.6 | 75.5 | 75.6 | 75.54 |
| ’Adam’, Lr = 0.0001 | 99.29 | 99.23 | 99.23 | 99.23 |
| ’Adam’, Lr = 0.00001 | 99.9 | 99.9 | 99.9 | 99.9 |
| ’SGD’, Lr = 0.0001 | 85.07 | 85.07 | 85.07 | 85.07 |
| ’ RMSprop’, Lr = 0.0001 | 98.4 | 98.93 | 98.93 | 98.93 |
| Researcher | Multi-Stage Technology | Methodology | Dataset | Results | Limitations |
|---|---|---|---|---|---|
| Yadav et al. [19] | Multi-feature extraction parts | LBP, iterative clustering, 3ScaleNetwork | Historical_Building_Crack_2019 3886 (757 crack images) | Precision: 98.9%, Recall: 99.18%, Accuracy: 99.69% | Unstable performance due to unbalanced dataset |
| Chen et al. [20] | Multi-resolution segmentation methodology | multi-resolution semantic segmentation | 2000 images of bridge, dam, and spillway materials | Precision: 94.51%, Recall: 86.39% | Small dataset, High false negative ratio |
| Wang et al. [29] | Integrating ViT as backbone for YOLO | YOLOV8 with ViT backbone | 1994 asphalt pavement images | Precision: 87.2% | Too many false positive errors |
| Nguyen et al. [30] | Crack detection and segmentation | CNN, U-Net | DeepCrack: 537 images The CrackIT: 84 pavement surface images | F1-score: 91% | Small dataset size with some FP and FN errors |
| Dai et al. [32] | Damage detection | machine learning and piezoelectric singular feature analysis | A signal-based dataset of 1344 signals | Accuracy:92%, Precision: 95.4%, Recall: 92.9% | Small dataset size, stages considered only the detection |
| Chen et al. [33] | Crack segmentation and quantification | U-Net and multi-task DeepLabV3+ | DeepCrack dataset | Improved the concrete crack quantification by above 2% | High computational time compared to mall improvement |
| Current study | Detection and classification | YOLOV10 and ViT | CICS: 12,000 images, Crack in various Materials from Historic Buildings: 1116 images | ViT: accuracy: 99.93% YOLOV10: Precision:90.7%, Recall: 83.4%, mAP50: 91.6% Multi-stage: precision: 90.67%, Recall: 90.03%, F1: 90.34% | Some errors happen due to different sizes of the detected crack regions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayya, A.M.; Alkayem, N.F. Enhance the Concrete Crack Classification Based on a Novel Multi-Stage YOLOV10-ViT Framework. Sensors 2024, 24, 8095. https://doi.org/10.3390/s24248095
Mayya AM, Alkayem NF. Enhance the Concrete Crack Classification Based on a Novel Multi-Stage YOLOV10-ViT Framework. Sensors. 2024; 24(24):8095. https://doi.org/10.3390/s24248095
Chicago/Turabian StyleMayya, Ali Mahmoud, and Nizar Faisal Alkayem. 2024. "Enhance the Concrete Crack Classification Based on a Novel Multi-Stage YOLOV10-ViT Framework" Sensors 24, no. 24: 8095. https://doi.org/10.3390/s24248095
APA StyleMayya, A. M., & Alkayem, N. F. (2024). Enhance the Concrete Crack Classification Based on a Novel Multi-Stage YOLOV10-ViT Framework. Sensors, 24(24), 8095. https://doi.org/10.3390/s24248095







