Design and Study of Pulsed Eddy Current Sensor for Detecting Surface Defects in Small-Diameter Bars
Abstract
:1. Introduction
2. Principle of Pulsed Eddy Current Testing Based on Tx-Rx Sensor
3. Finite Element Simulation
3.1. Simulation Model
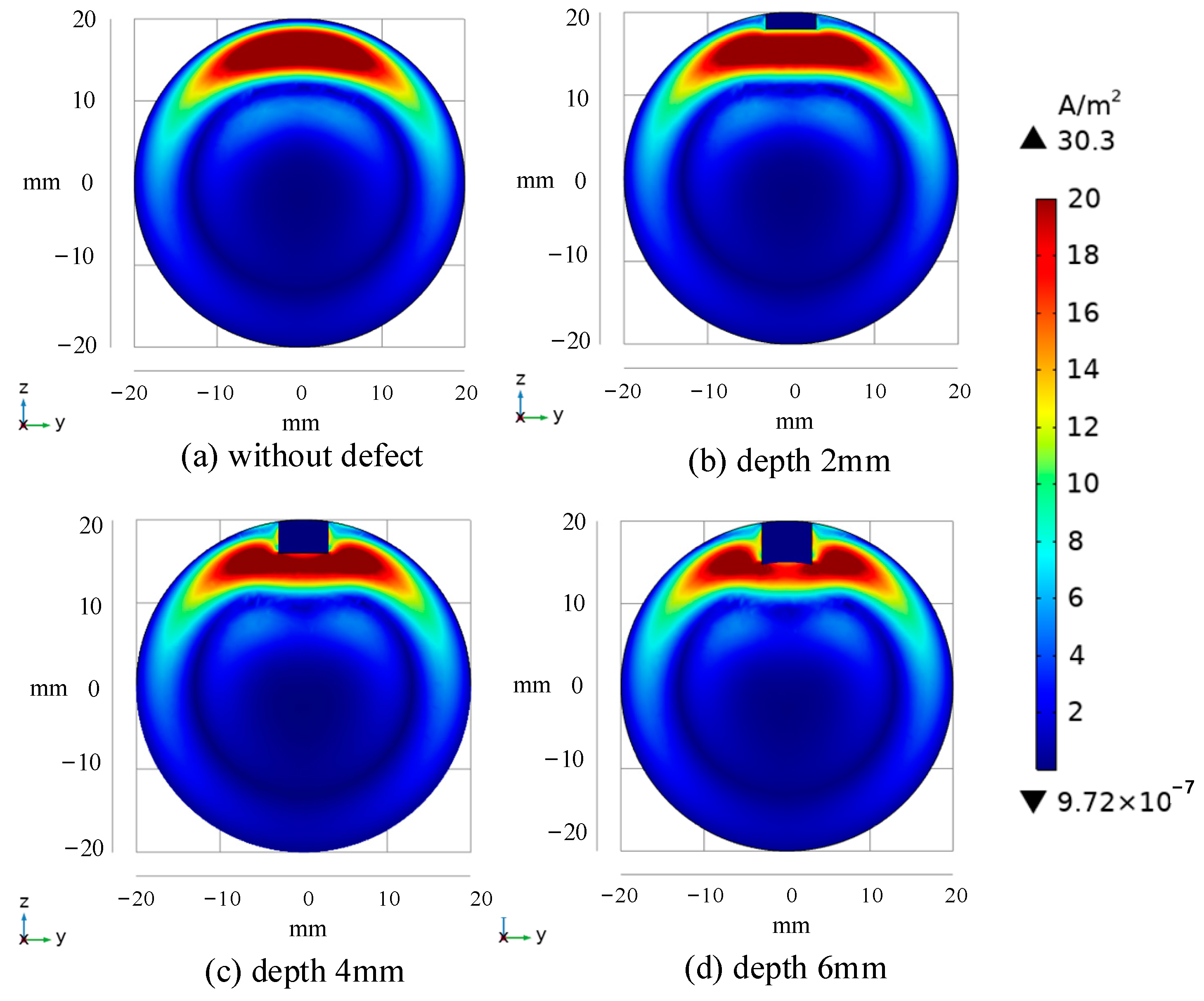
3.2. Analysis of Electromagnetic Field Distribution Simulation Results
3.3. Results and Analysis of Defect Response Signal
4. Probe Design
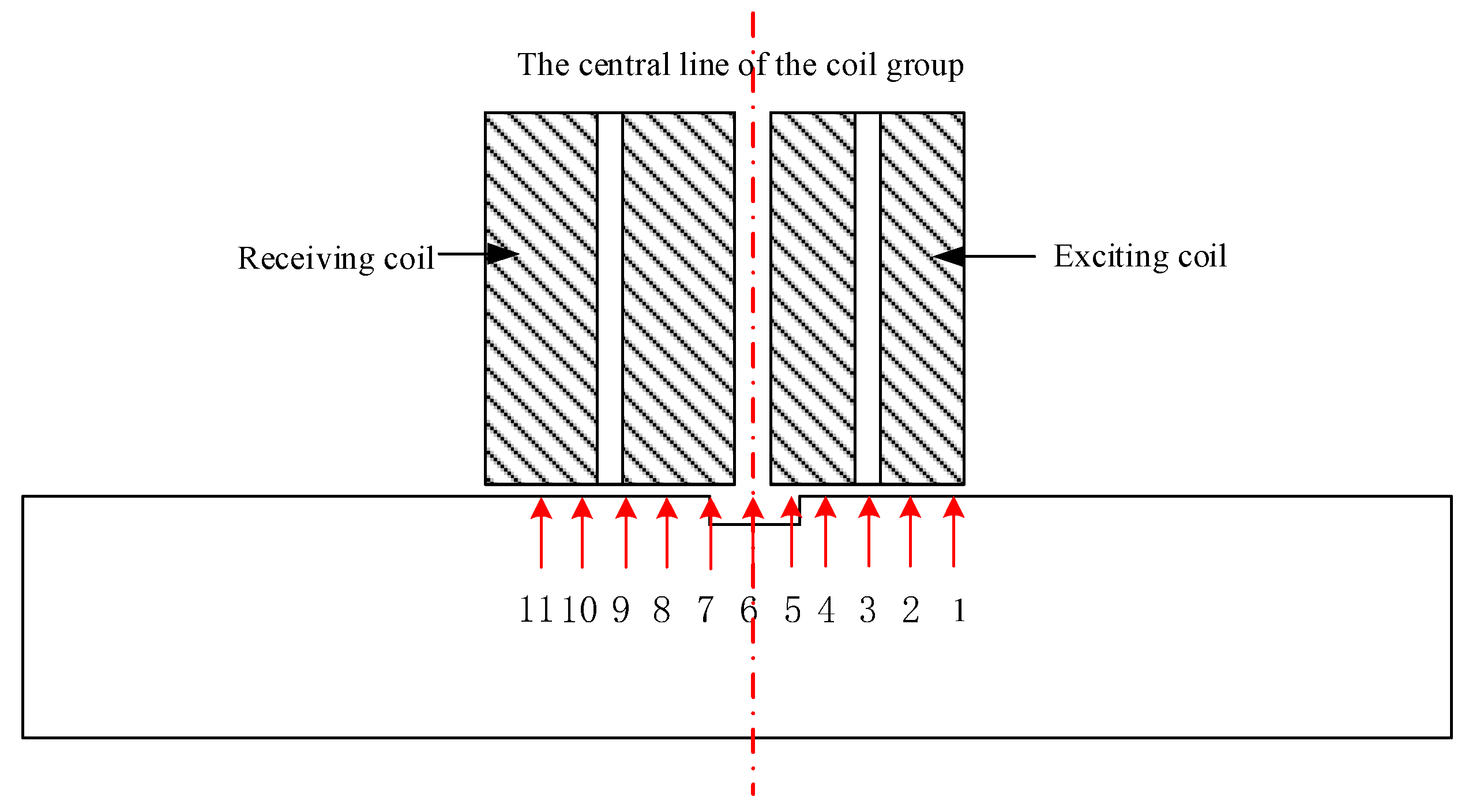
4.1. Signal Influencing by Coil Structure
4.2. The Influence of Coil Combination on Detection
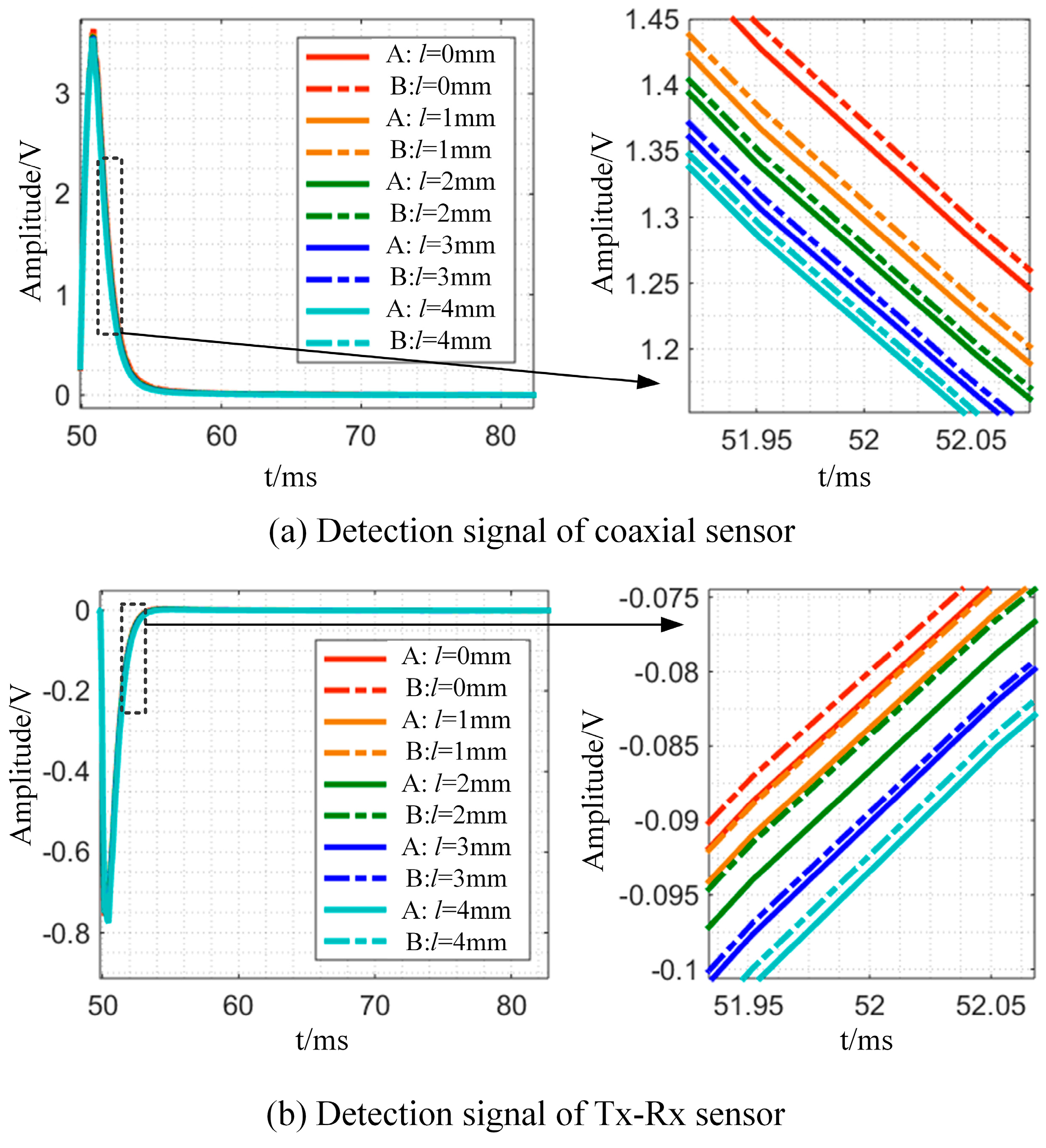
4.3. The Influence of Coil Spacing on Detection
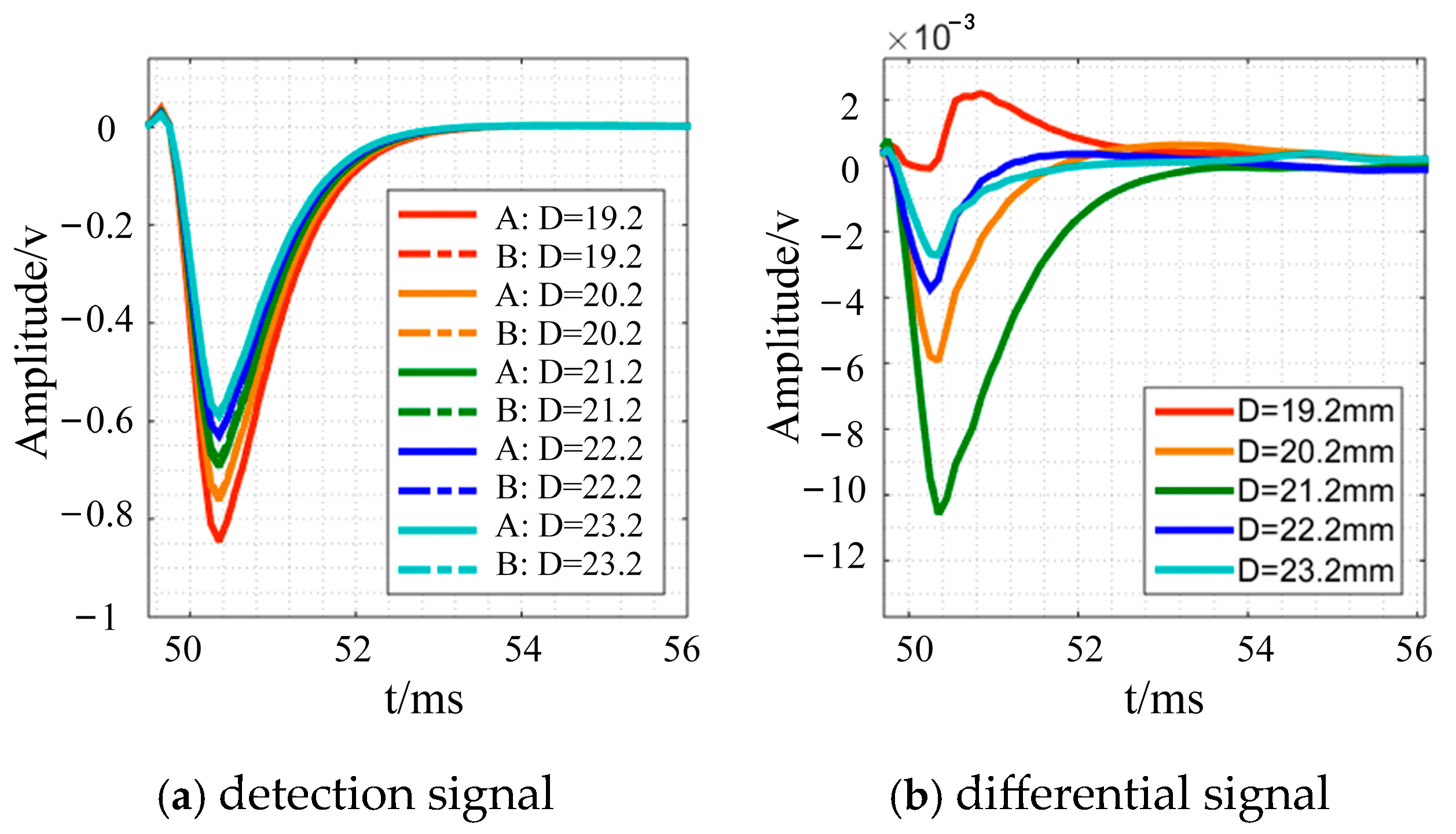
4.4. The Influence of the Relative Position of Coil and Defect on Detection
5. Pulsed Eddy Current Testing System and Result Analysis
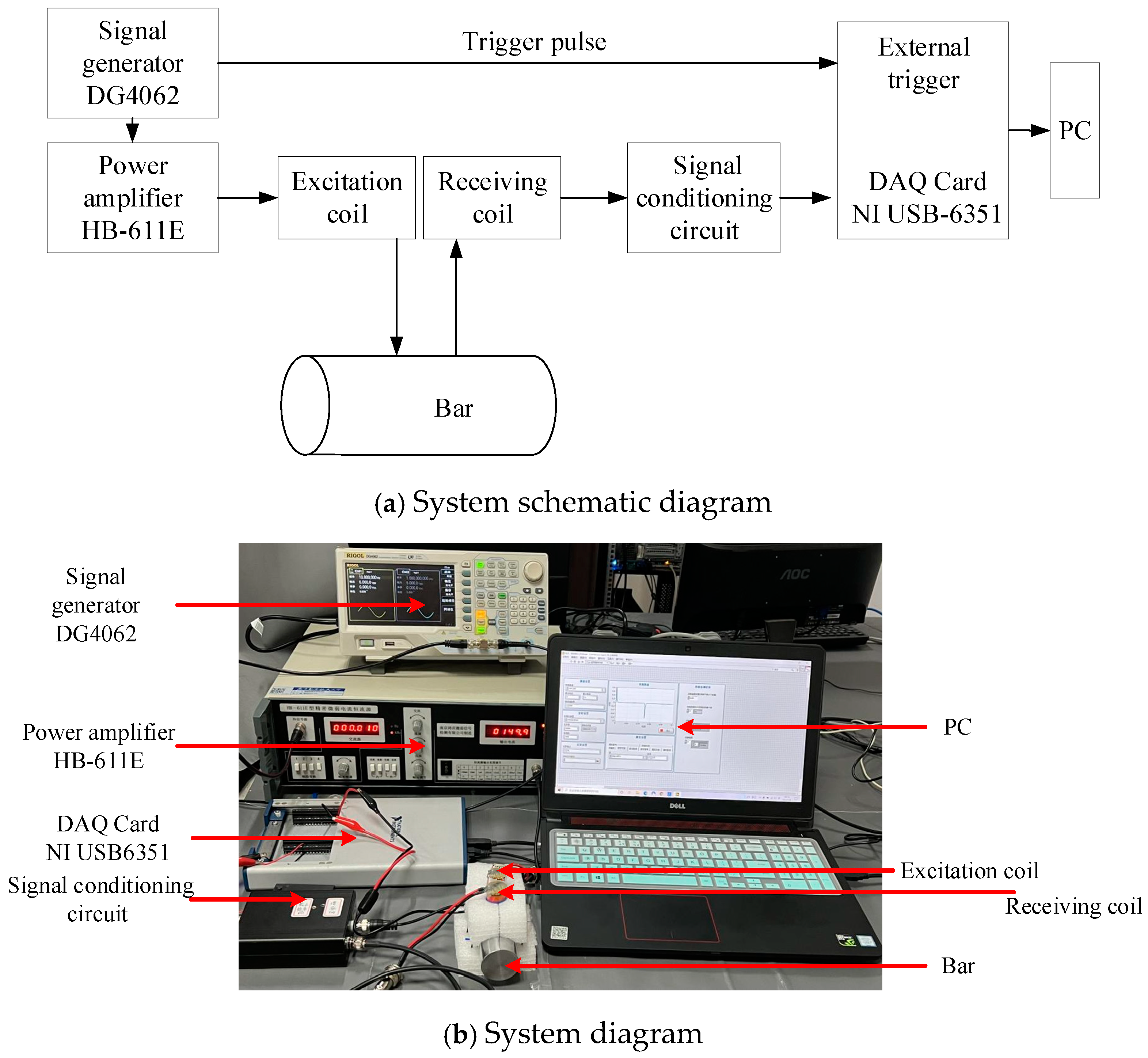
5.1. Experimental System
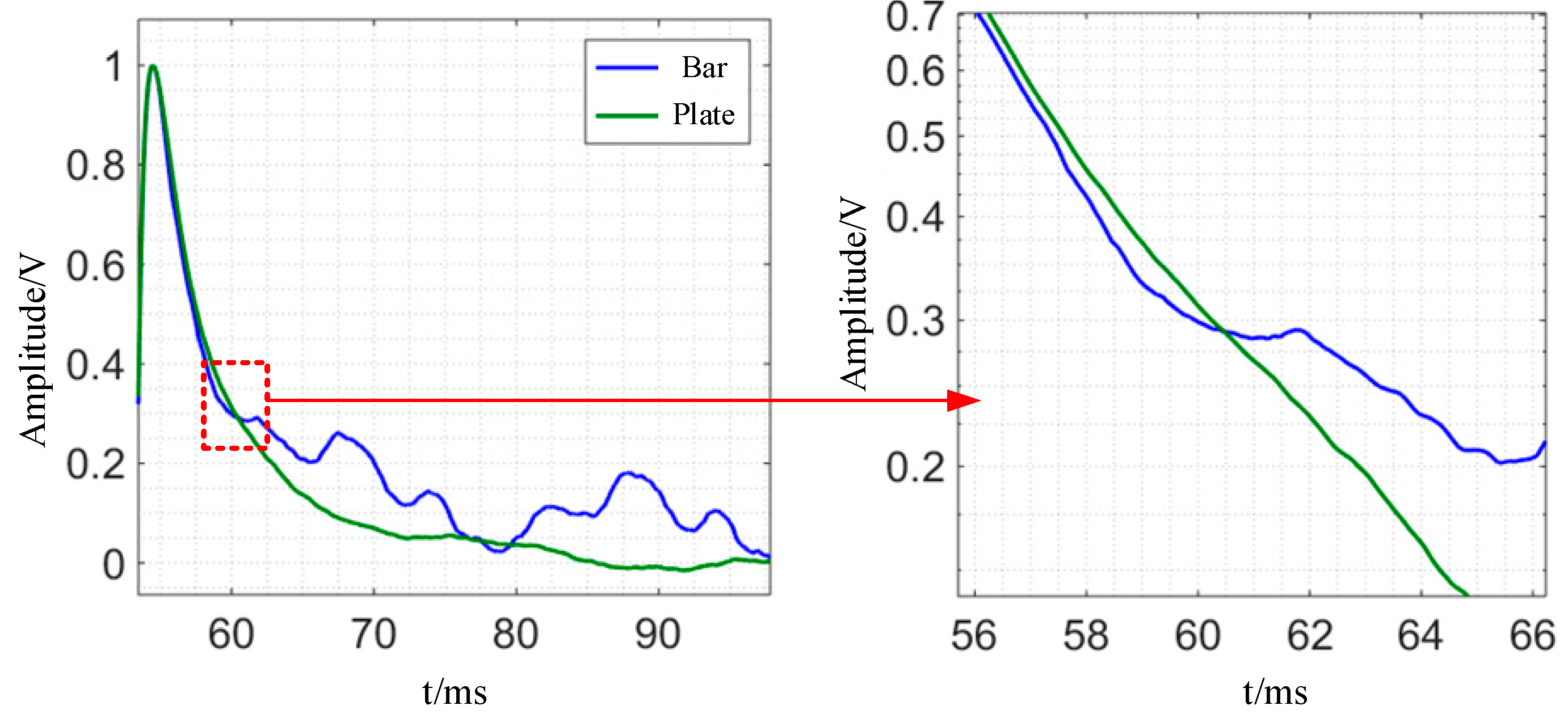
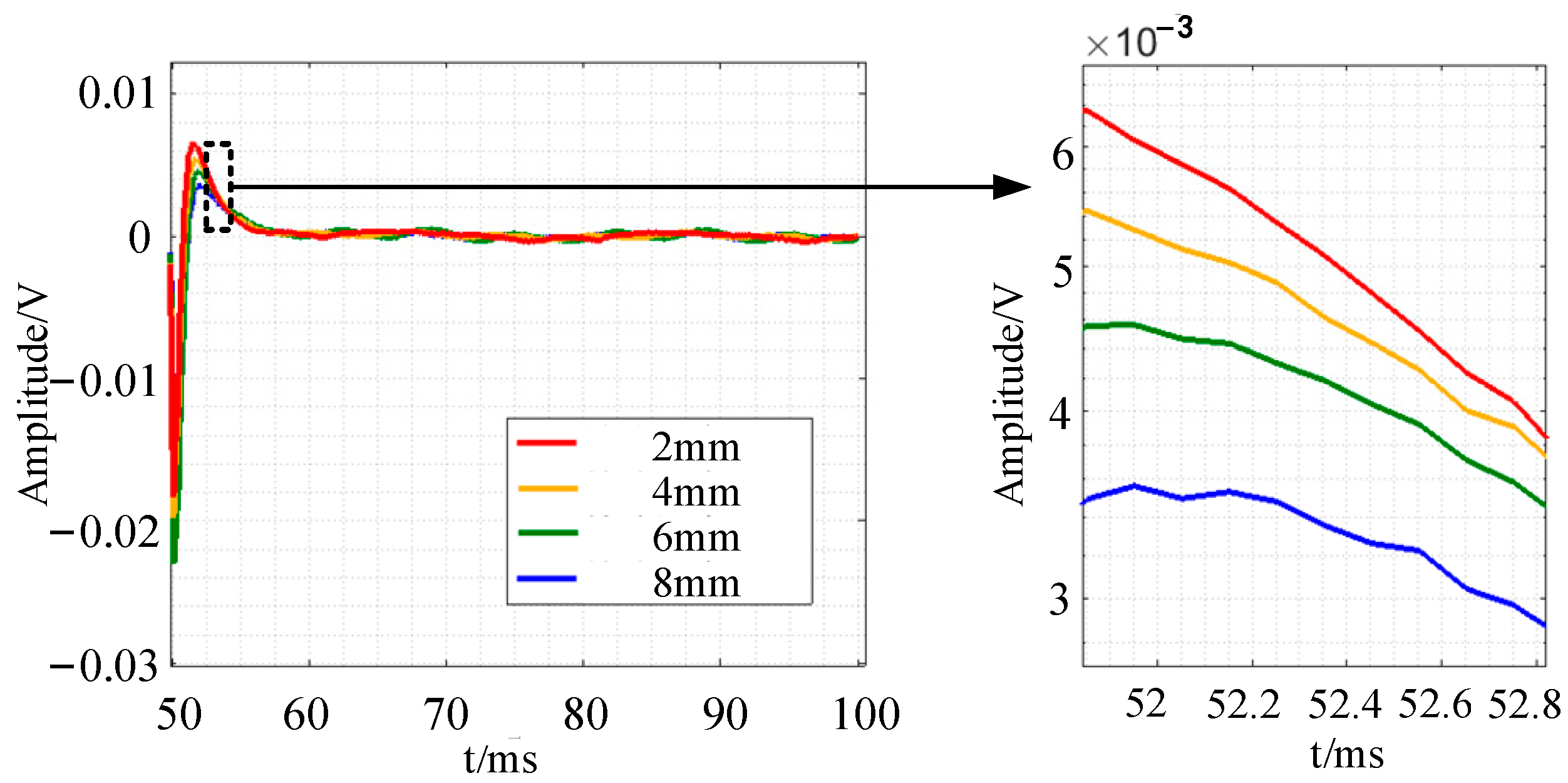
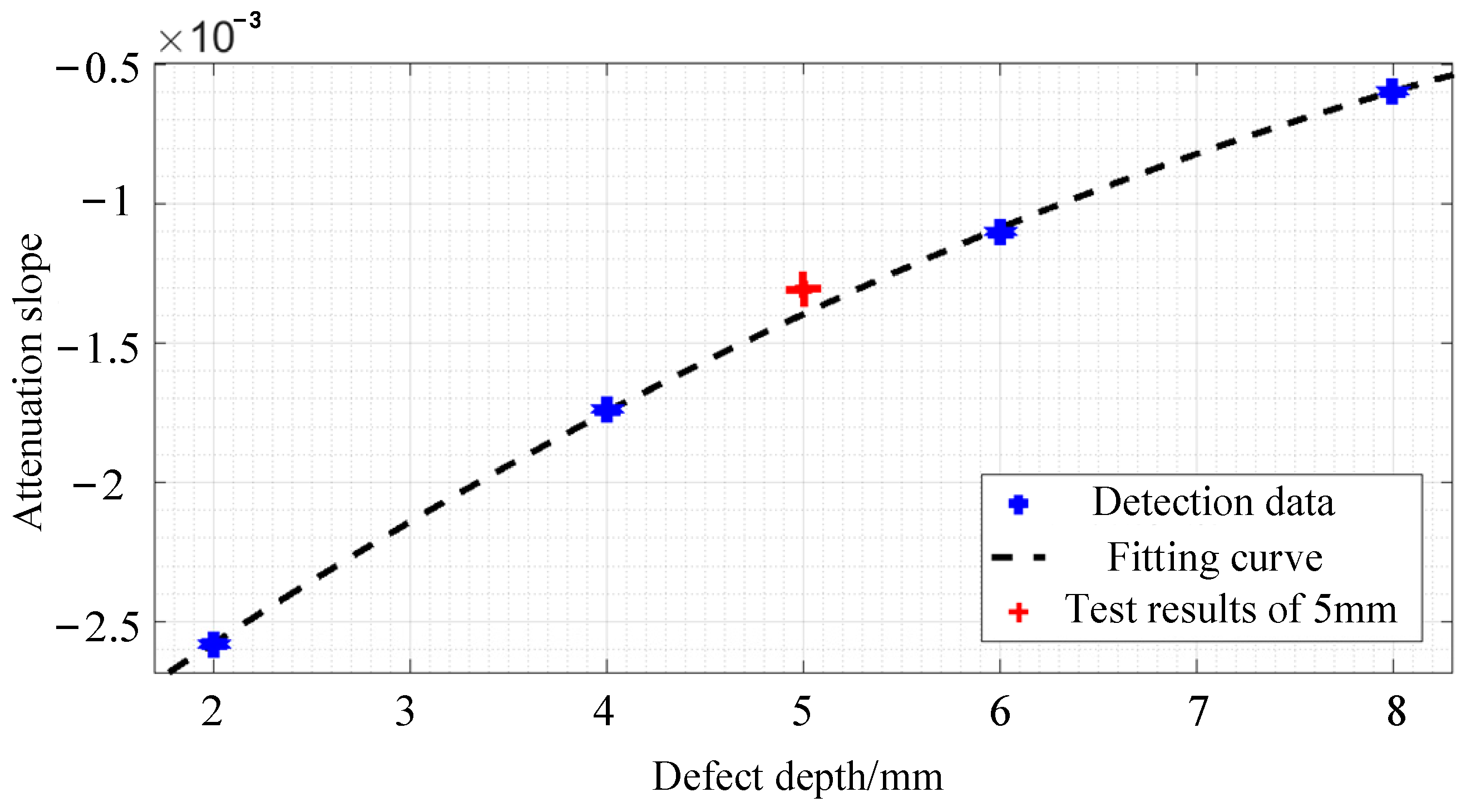
5.2. Experimental Results
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, P.; Wang, C.; Li, Y.; Cong, Z. Electromagnetic and eddy current NDT in weld inspection: A review. Insight 2015, 57, 337–345. [Google Scholar] [CrossRef]
- Yu, Z.H.; Fu, Y.W.; Jiang, L.; Yang, F. Study on inspection for small diameter tubes using pulsed remote field eddy current method. J. Mech. Eng. 2021, 57, 10–18. [Google Scholar]
- Pei, C.; Xiao, P.; Zhao, S.; Chen, Z. Development of a flexible film electromagnetic acoustic transducer for nondestructive testing. Sens. Actuators A Phys. 2017, 258, 68–73. [Google Scholar] [CrossRef]
- Zhou, Z.G.; Li, Y.; Zhou, W.B. Ultrasonic phased array post-processing imaging techniques: An review. J. Mech. Eng. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Heim, K.; Bernier, F.; Pelletier, R.; Lefebvre, L.-P. High-resolution pore size analysis in metallic powders by X-ray tomography. Case Stud. Nondestruct. Test. Eval. 2016, 6, 45–52. [Google Scholar] [CrossRef]
- Zeng, W.; Qi, S.; Liu, L.; Yao, F. A quantitative inspection method for internal defects based on laser ultrasonic technology. Optik 2020, 216, 164873. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, H.T.; Chen, S.; Zhang, Q.; Hu, P.; Li, X.; Zheng, K.; Wang, H. Quantitative imaging detection of Additive Manufactured Parts Using laser ultrasonic testing. IEEE Access 2020, 8, 186071–186079. [Google Scholar] [CrossRef]
- Li, Y.; Yan, B.; Li, D.; Jing, H.; Li, Y.; Chen, Z. Pulse-modulation eddy current inspection of subsurface corrosion in conductive structures. NDT E Int. 2016, 79, 142–149. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, W.J.; Xie, S.J.; Wang, X.; Kong, Y.; Ma, Q.; Chen, Z. Swept-frequency ET and innovative feature extraction of abrasion defects for thimble tubes in nuclear power plants. J. Mech. Eng. 2021, 32, 18–25. [Google Scholar]
- Peng, Z. Research progress in ultrasonic imaging detection technology. Laser Optoelectron. Prog. 2022, 59, 1–15. [Google Scholar]
- Yang, Y.; Wang, P.; Song, T.-L.; Jiang, Y.; Zhou, W.-T.; Xu, W.-L. Evaluation of the Transverse Crack Depth of Rail Bottoms Based on the Ultrasonic Guided Waves of Piezoelectric Sensor Arrays. Sensors 2022, 22, 7023. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Han, L.; Wang, Z.; Wang, H.; Shen, Z. Finite Element Simulation of Laser-Synthetic Aperture Focusing Technique (SAFT) Detection of Additive Manufactured Parts. Russ. J. Nondestruct. Test. 2023, 59, 332–345. [Google Scholar] [CrossRef]
- Chen, X.; Niu, H. Pulsed eddy current testing for gap measurement of metal casing. Meas. Sci. Technol. 2022, 33, 075108. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J.; Liu, L.; Qin, S.; Fu, Z. A Novel Pulsed Eddy Current Criterion for Non-Ferromagnetic Metal Thickness Quantifications under Large Liftoff. Sensors 2022, 22, 614. [Google Scholar] [CrossRef]
- Ha, N.; Lee, H.-S.; Lee, S. Development of a Wireless Corrosion Detection System for Steel-Framed Structures Using Pulsed Eddy Currents. Sensors 2021, 21, 8199. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Guo, Y.; Cheng, S.; Kang, Y.; Hu, Y.; Chen, Y.; Li, Y.; Feng, B. A lift-off measurement and compensation method based on a comprehensive EMAT-PEC probe. Sens. Actuators A Phys. 2024, 372, 115319. [Google Scholar] [CrossRef]
- Guo, Y.; Hu, Y.; Wang, K.; Song, Y.; Feng, B.; Kang, Y.; Duan, Z. Bottom Crack Detection with Real-Time Signal Amplitude Correction Using EMAT-PEC Composite Sensor. Sensors 2024, 24, 5196. [Google Scholar] [CrossRef] [PubMed]
- Le, M.; Lee, J.; Jun, J.; Kim, J. Estimation of sizes of cracks on pipes in nuclear power plants using dipole moment and finite element methods. NDT E Int. 2013, 58, 56–63. [Google Scholar] [CrossRef]
- Xing, L.L. Computation of 3D Transient Eddy Current by Time-Stepping Finite-Element Boundary-Element Coupling Method. Proc. CSEE 2005, 19, 131–134. [Google Scholar]
- Zhou, D.Q.; Tian, G.Y.; Wang, H.T.; You, L.-H. The Recent Developments of Pulsed Eddy Current Nondestructive Testing Technology. NDT Test. 2011, 33, 25–29+35. [Google Scholar]
- Chen, Z.; Yusa, N.; Miya, K. Some advances in numerical analysis techniques for quantitative electromagnetic nondestructive evaluation. Nondestruct. Test. Eval. 2009, 24, 69–102. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Tian, G.Y.; You, L.H.; Wang, H. Study on pulsed eddy current defect signal detection technology based on spectrum analysis. Chin. J. Sci. Instrum. 2011, 32, 1948–1953. [Google Scholar]
- Santos, G.; Laurindo, B.M.; Fortes, M.Z.; França, B.W. A model for calculating losses in transformer related to orders and harmonic amplitude under analysis of joule effect, eddy current and hysteresis. Int. J. Emerg. Electr. Power Syst. 2020, 21, 20200006. [Google Scholar] [CrossRef]
- Preda, G.; Cranganu-Cretu, B.; Hantila, F.I.; Mihalache, O.; Chen, Z.; Miya, K. Nonlinear FEM-BEM formulation and model-free inversion procedure for reconstruction of cracks using pulse eddy currents. IEEE Trans. Magn. 2002, 38, 1241–1244. [Google Scholar] [CrossRef]
- Wang, L.; Xie, S.; Chen, Z.; Li, Y.; Wang, X.; Takagi, T. Reconstruction of stress corrosion cracks using signals of pulsed eddy current testing. Nondestruct. Test. Eval. 2013, 28, 145–154. [Google Scholar] [CrossRef]
- Heba, E.F.; Ehsan, T.; Behrad, K.M. Non-Destructive Testing Using Eddy Current Sensors for Defect Detection in Additively Manufactured Titanium and Stainless-Steel Parts. Sensors 2022, 22, 5440. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wu, X. Analytical Modeling for the Plate with a Flat-Bottom Hole Based on the Reflection and Transmission Theory in Pulsed Eddy Current Testing. Acta Phys. Sin. 2017, 3, 038102. [Google Scholar] [CrossRef]
- Xie, S.; Tian, M.; Xiao, P.; Pei, C.; Chen, Z.; Takagi, T. A hybrid nondestructive testing method of pulsed eddy current testing and electromagnetic acoustic transducer techniques for simultaneous surface and volumetric defects inspection. NDT E Int. 2017, 86, 153–163. [Google Scholar] [CrossRef]
- Klein, G.; Morelli, J.; Krause, T.W. Analytical model of the eddy current response of a drive-receive coil system inside two concentric tubes-Highlights. NDT E Int. 2018, 96, 18–25. [Google Scholar] [CrossRef]
- Yang, C.A. Comparison of eddy current testing of heat transfer tube of steam generator by rotating probe and array probe. Nondestruct. Test. 2017, 39, 64–66, 71. [Google Scholar]
- Lee, H.J.; Nam, M.W.; Cho, C.H.; Jee, D.H. Optimized design parameters of eddy current Bobbin probe for steam generator tube in NPPs. Mod. Phys. Lett. B 2008, 22, 1057–1061. [Google Scholar] [CrossRef]
- Ye, C.; Xin, J.; Su, Z.; Udpa, L.; Udpa, S.S. Novel transceiver rotating field nondestructive inspection probe. IEEE Trans. Magn. 2015, 51, 6201006. [Google Scholar] [CrossRef]
- Ye, C.; Huang, Y.; Udpa, L.; Udpa, S.S. Novel rotating current probe with GMR array sensors for steam generate tube inspection. IEEE Sens. J. 2016, 16, 4995–5002. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.M.; Wu, B.; He, C. A novel generation method of oscillatory rotating eddy current for crack orientation determination and detection in metal plates. NDT E Int. 2018, 97, 1–10. [Google Scholar]
- Obrutsky, L.; Renaud, J.; Lakhan, R. Overview of steam generator tube-inspection technology. CINDE J. 2014, 35, 5–13. [Google Scholar]
- Chen, T.; He, Y.; Du, J. A high-sensitivity flexible EC array sensor for crack monitoring of welded structures under varying environment. Sensors 2018, 18, 1780. [Google Scholar] [CrossRef]
- Wang, T.J.; Lou, Z.W. A continuum damage model for weld heat affected zone under low cycle fatigue loading. Eng. Fract. Mech. 1990, 37, 825–829. [Google Scholar] [CrossRef]
- Wang, T.J. A continuum damage model for ductile fracture of weld heat affected zone. Eng. Fract. Mech. 1991, 40, 1075–1082. [Google Scholar] [CrossRef]
- Desjardins, D.; Krause, T.W.; Clapham, L. Transient response of a driver-pickup coil probe in transient eddy current testing. NDT E Int. 2015, 75, 8–14. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, J.; He, Y.; Chen, D.; Li, K. Influence of metallic shields on pulsed eddy current sensor for ferromagnetic materials defect detection. Sens. Actuators A Phys. 2017, 248, 162–172. [Google Scholar] [CrossRef]

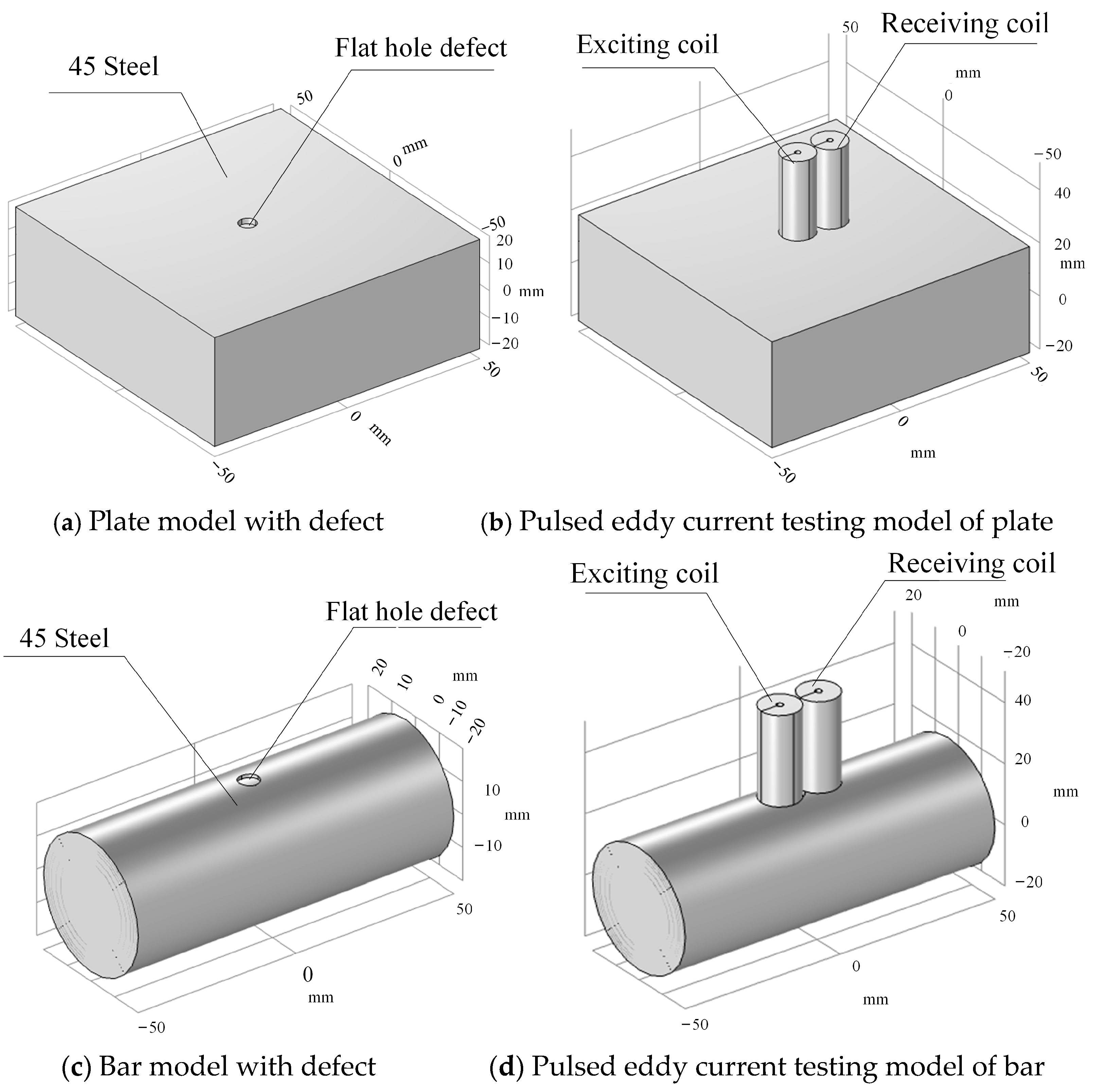
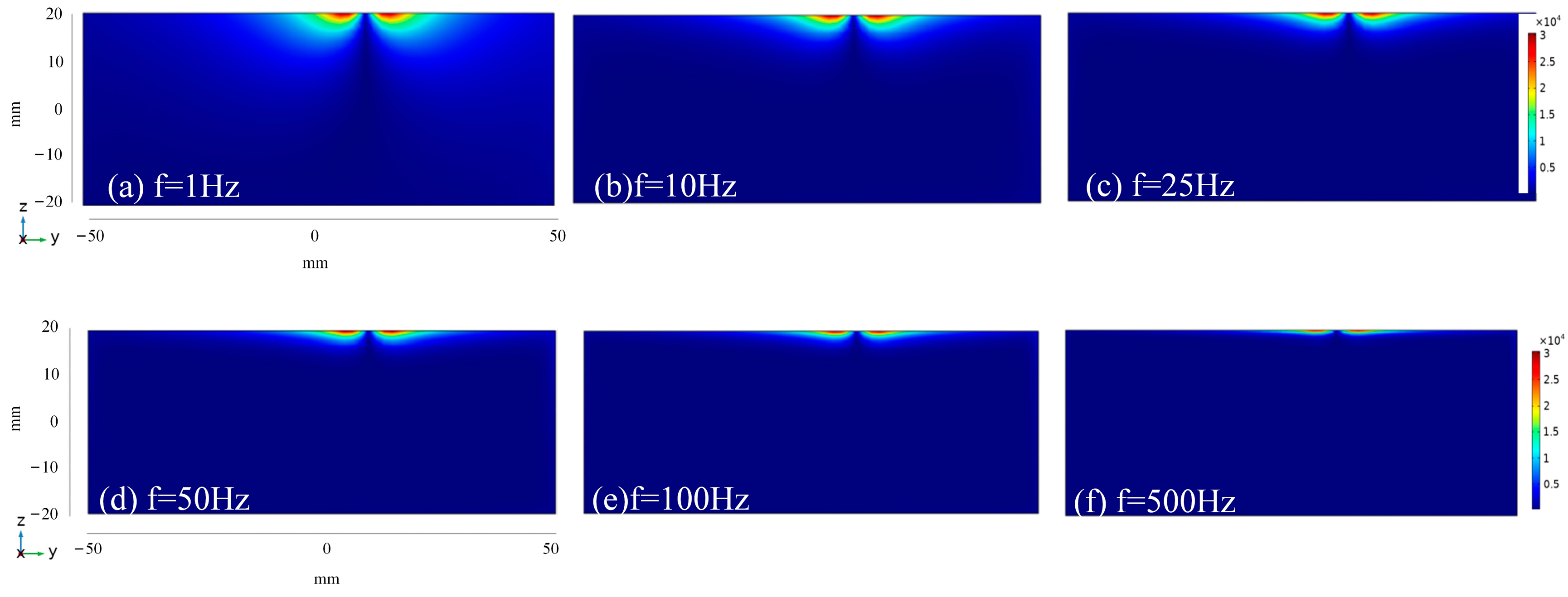
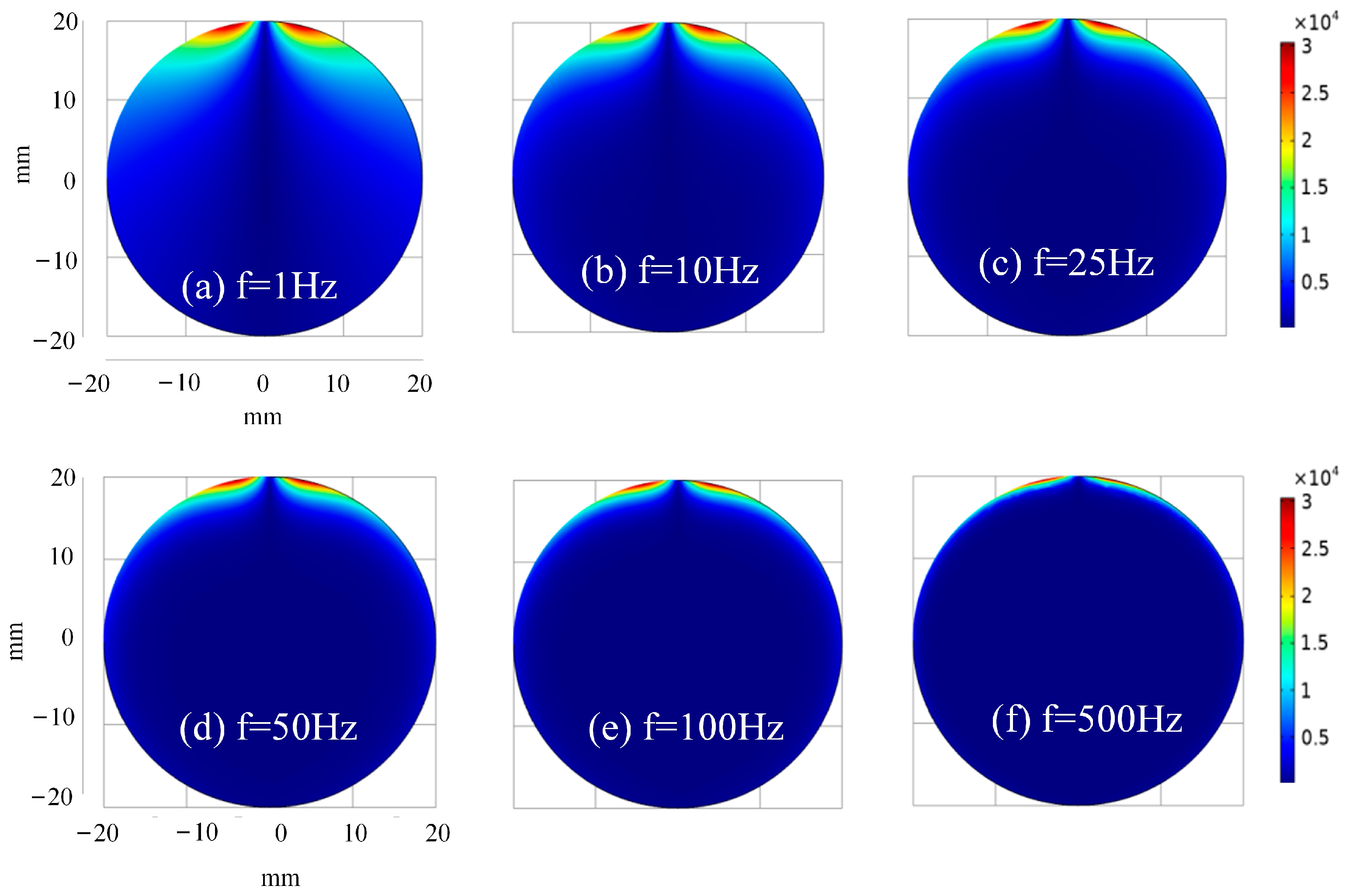

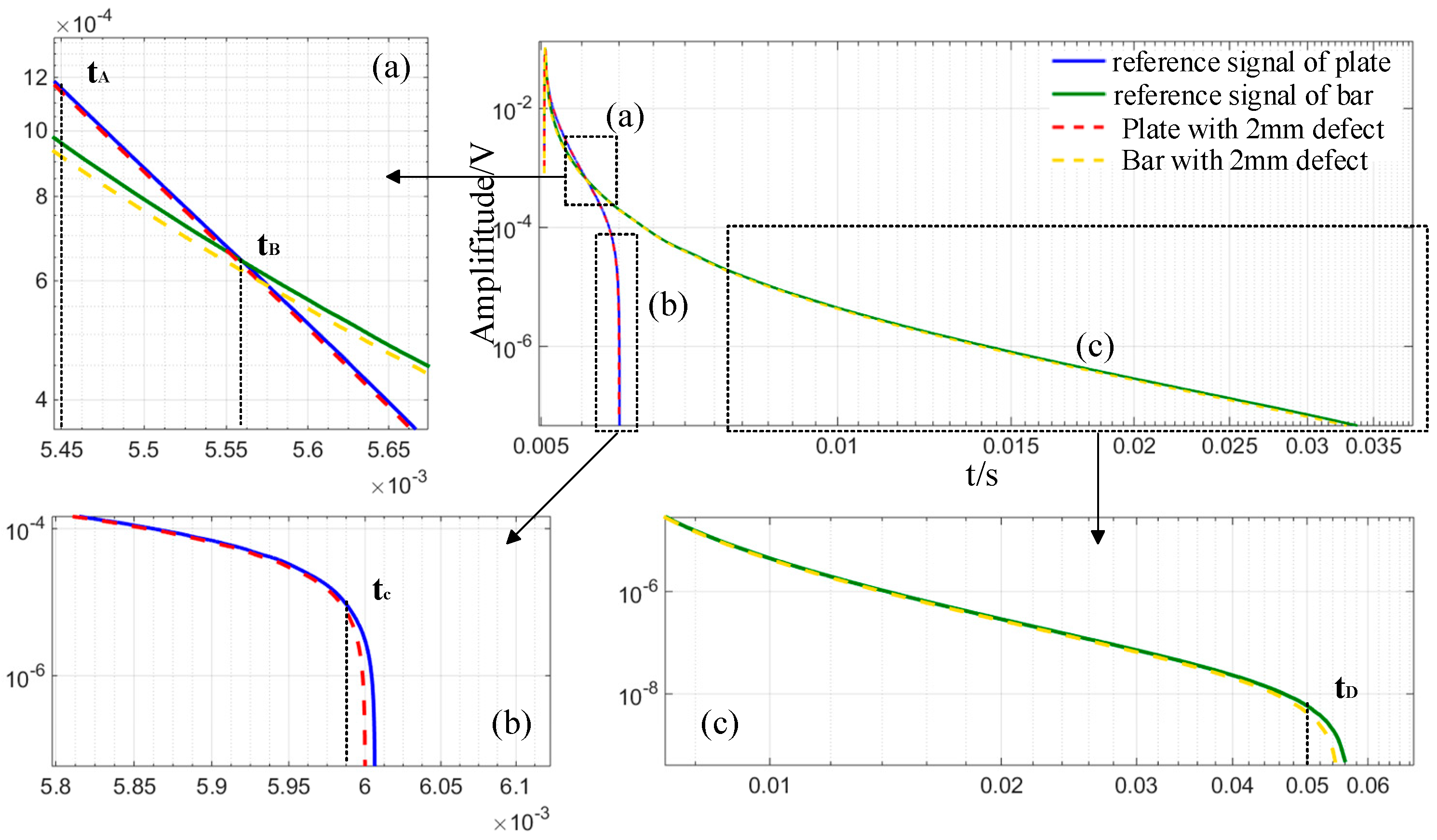
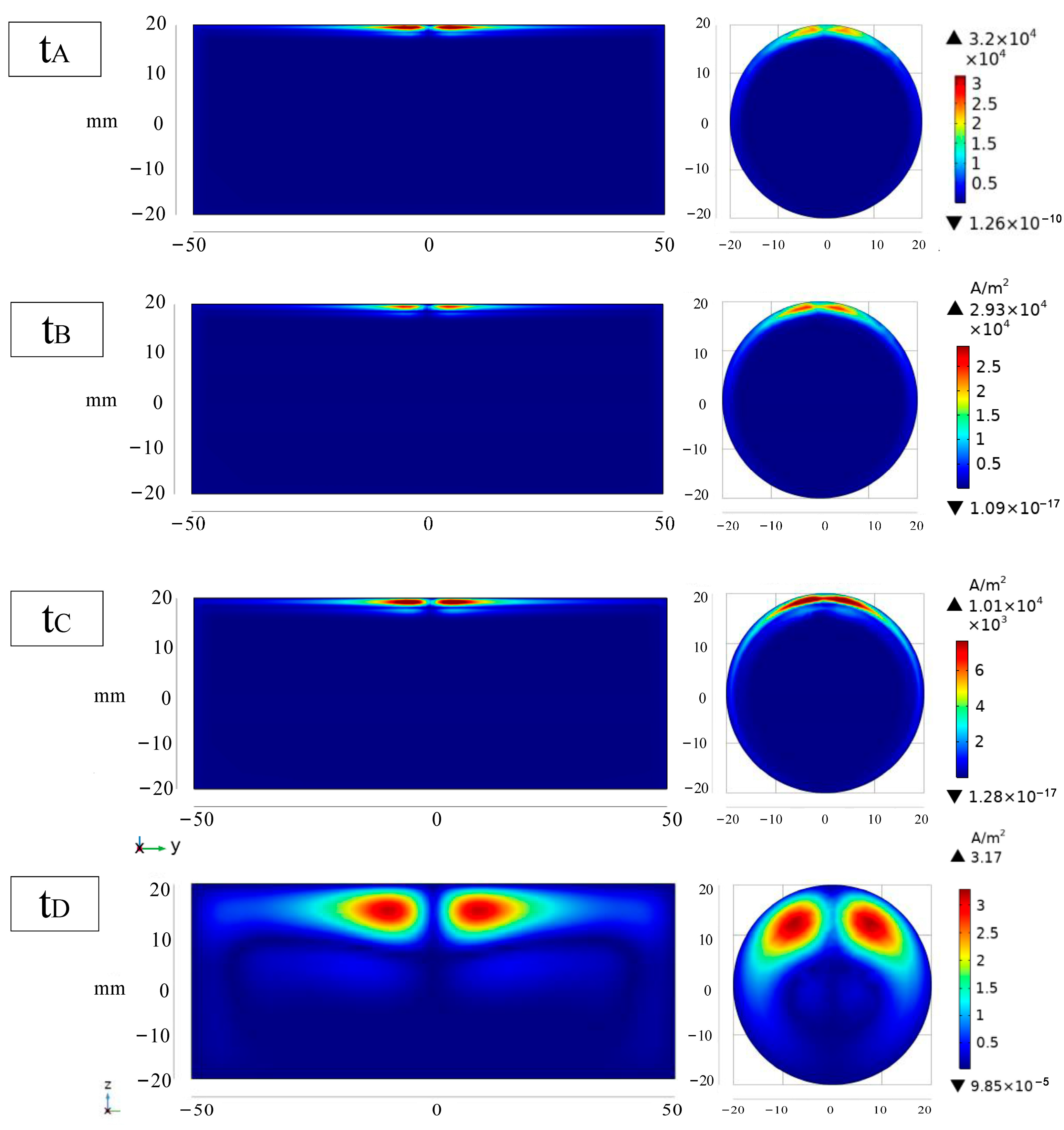
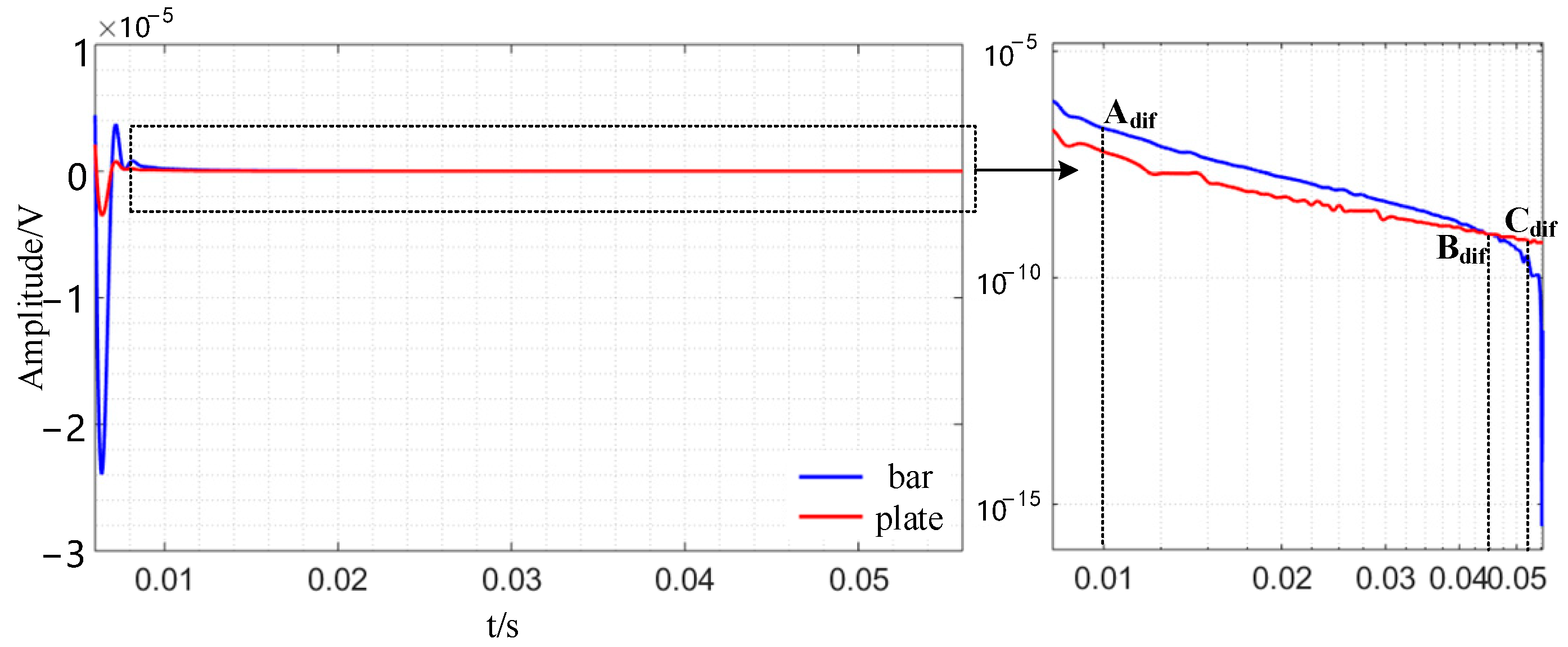
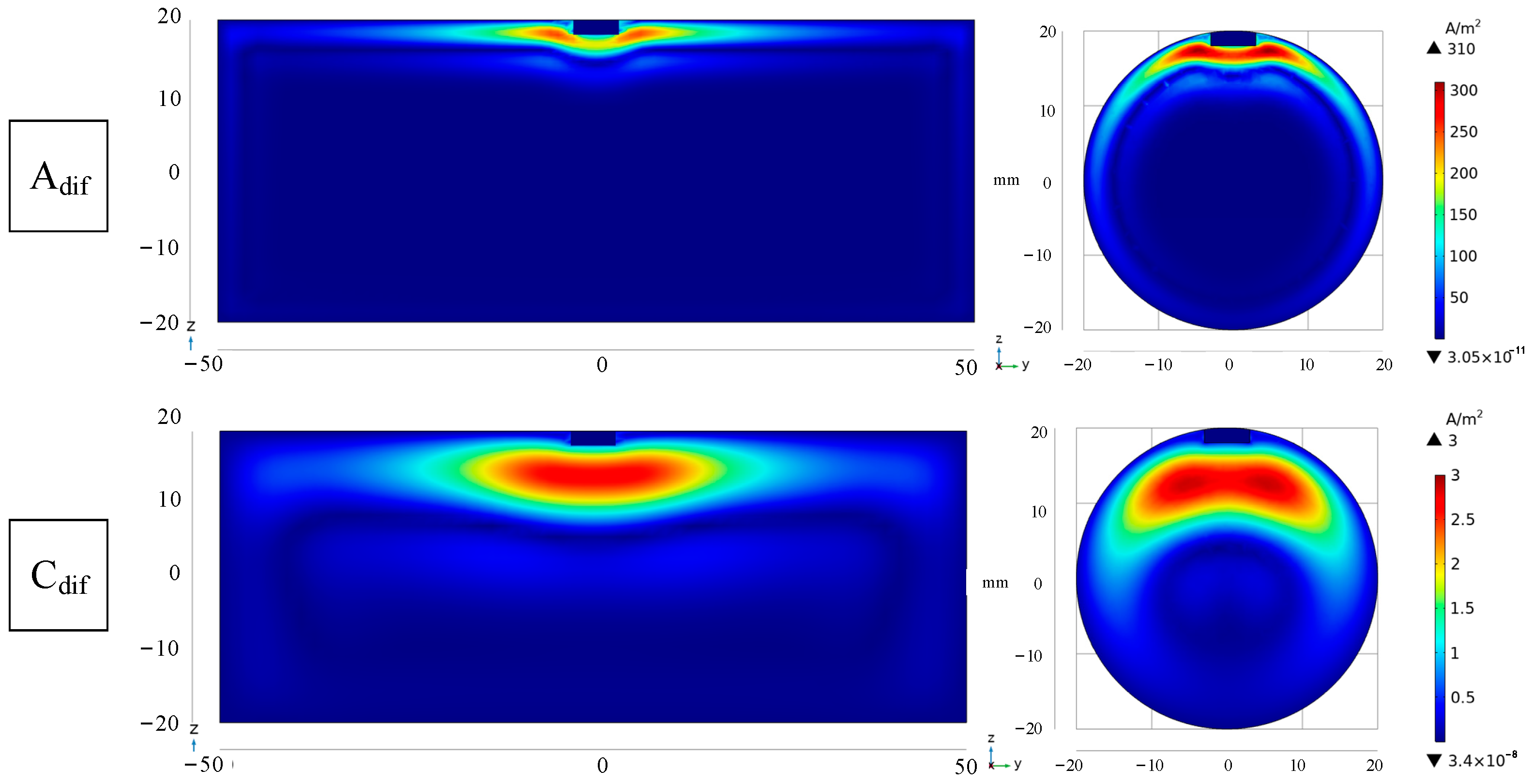
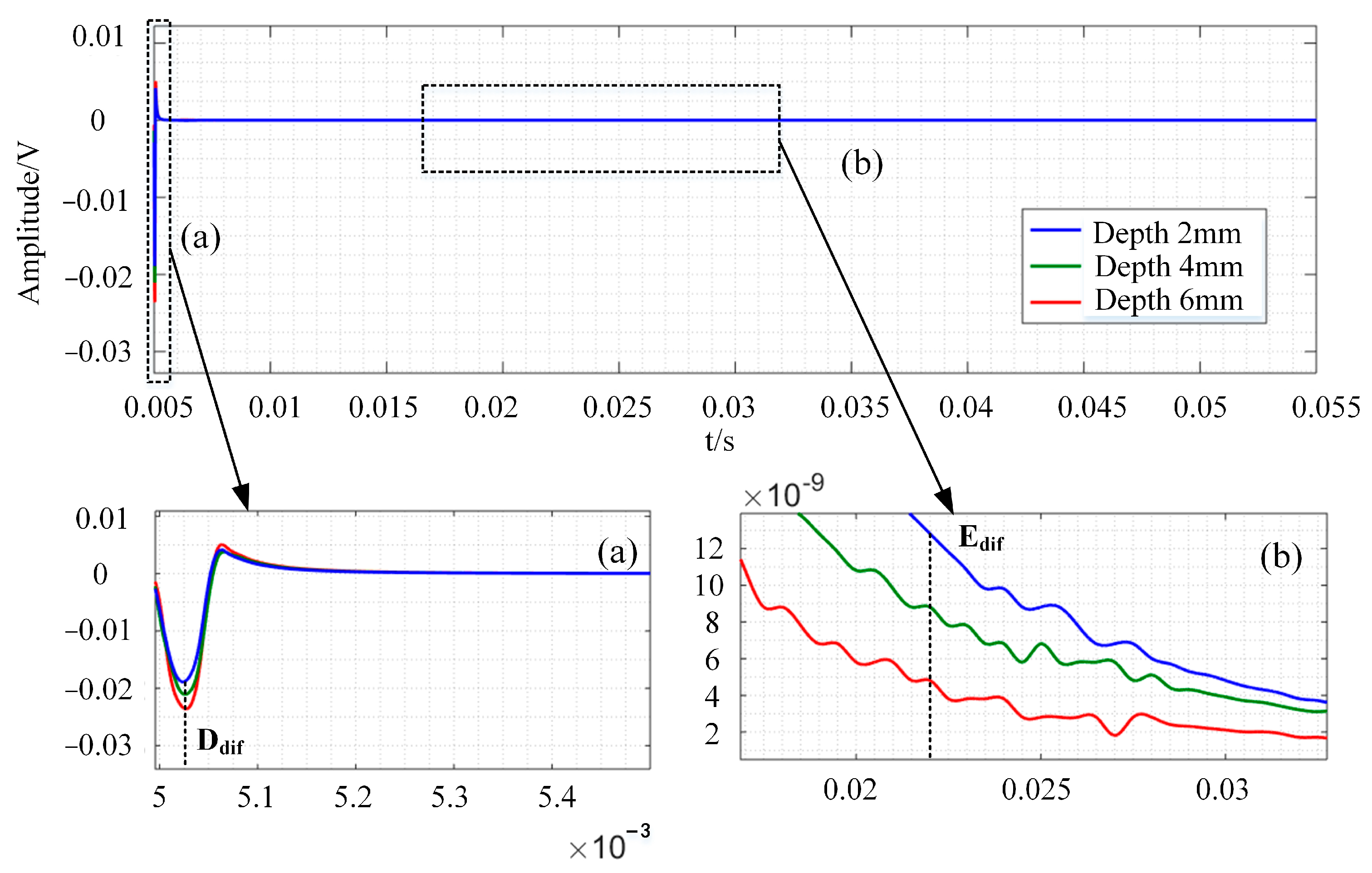





| Name | Relative Permeability | Electrical Conductivity/(S/m) | Relative Dielectric Constant |
|---|---|---|---|
| 45 steel | 300 | 5 × 106 | 1 |
| Air | 1 | 1 | 1 |
| Parameter | Inner Diameter/mm | Outer Diameter/mm | Height/mm | Number of Turns | Wire Diameter/mm |
|---|---|---|---|---|---|
| Exciting coil | 2 | 16 | 30 | 3800 | 0.2 |
| Receiving coil | 2 | 22 | 30 | 5000 | 0.2 |
| Sensor | Outer Diameter | Inner Diameter | Height | Number of Turns | Wire Diameter |
|---|---|---|---|---|---|
| Small size coil | 16 mm | 2 mm | 30 mm | 3800 | 0.2 mm |
| Large size coil | 22 mm | 2 mm | 30 mm | 5000 | 0.2 mm |
| Actual Defect Depth | Attenuation Slope | Calculated Defect Depth | Relative Error |
|---|---|---|---|
| 5 mm | −0.0013 | 5.26 mm | 4.94% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Jiang, Y.; Yuan, M. Design and Study of Pulsed Eddy Current Sensor for Detecting Surface Defects in Small-Diameter Bars. Sensors 2024, 24, 8063. https://doi.org/10.3390/s24248063
Han L, Jiang Y, Yuan M. Design and Study of Pulsed Eddy Current Sensor for Detecting Surface Defects in Small-Diameter Bars. Sensors. 2024; 24(24):8063. https://doi.org/10.3390/s24248063
Chicago/Turabian StyleHan, Lei, Yi Jiang, and Ming Yuan. 2024. "Design and Study of Pulsed Eddy Current Sensor for Detecting Surface Defects in Small-Diameter Bars" Sensors 24, no. 24: 8063. https://doi.org/10.3390/s24248063
APA StyleHan, L., Jiang, Y., & Yuan, M. (2024). Design and Study of Pulsed Eddy Current Sensor for Detecting Surface Defects in Small-Diameter Bars. Sensors, 24(24), 8063. https://doi.org/10.3390/s24248063






