Modelling, Analysis and Validation of Hydraulic Self-Adaptive Bearings for Elevated Floating Bridges
Abstract
1. Introduction
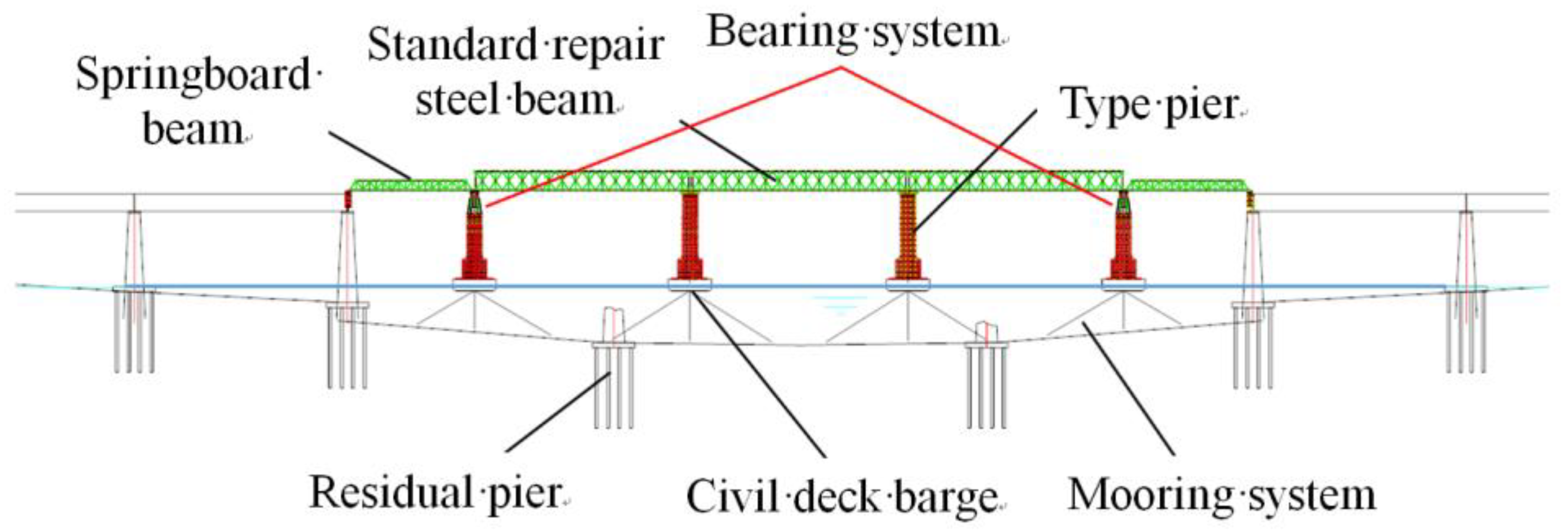
2. The Proposed Hydraulic Self-Adaptive Bearing System (HABS)
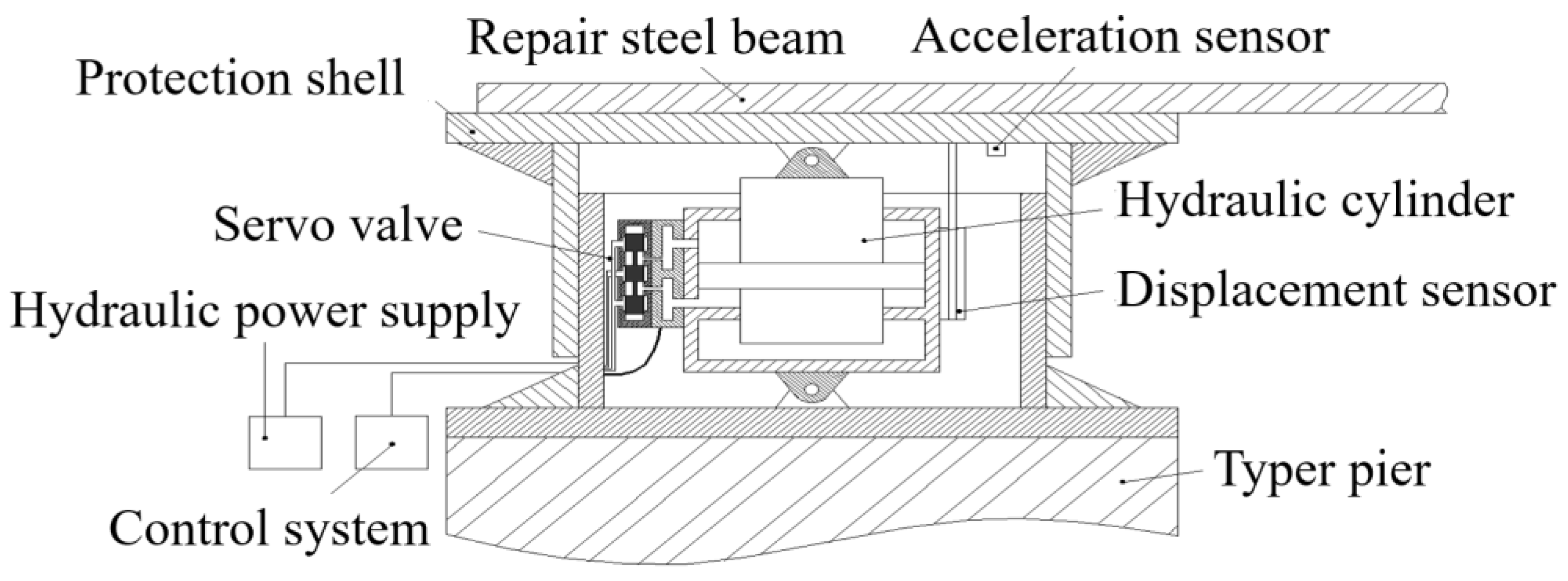
2.1. Overview of HABS Design
2.2. Dynamic Modelling of HABS
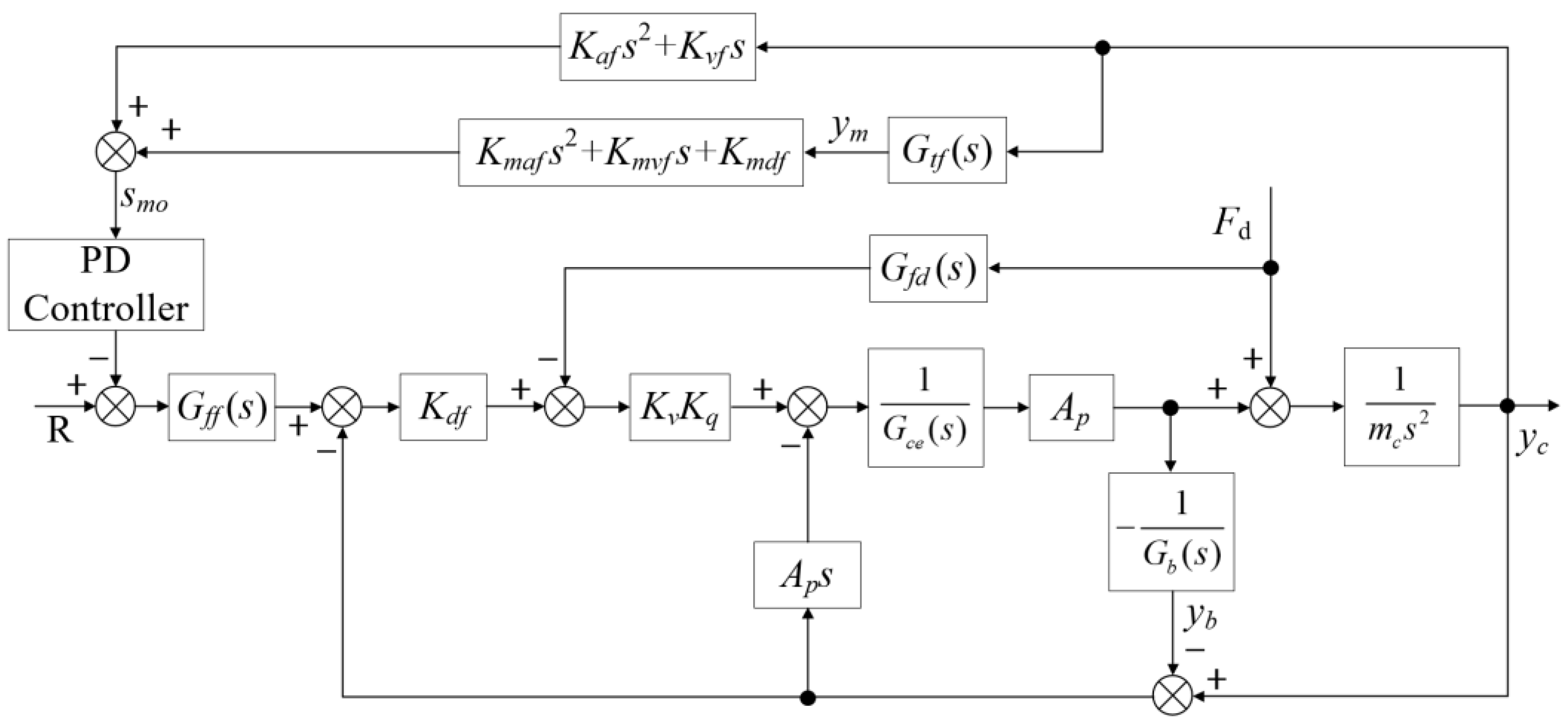
3. Control Strategy Design
3.1. Position Closed-Loop Control Approach
3.2. Disturbance Observers and Vibration Control Strategies
4. Co-Simulation Study
4.1. Co-Simulation Model Development
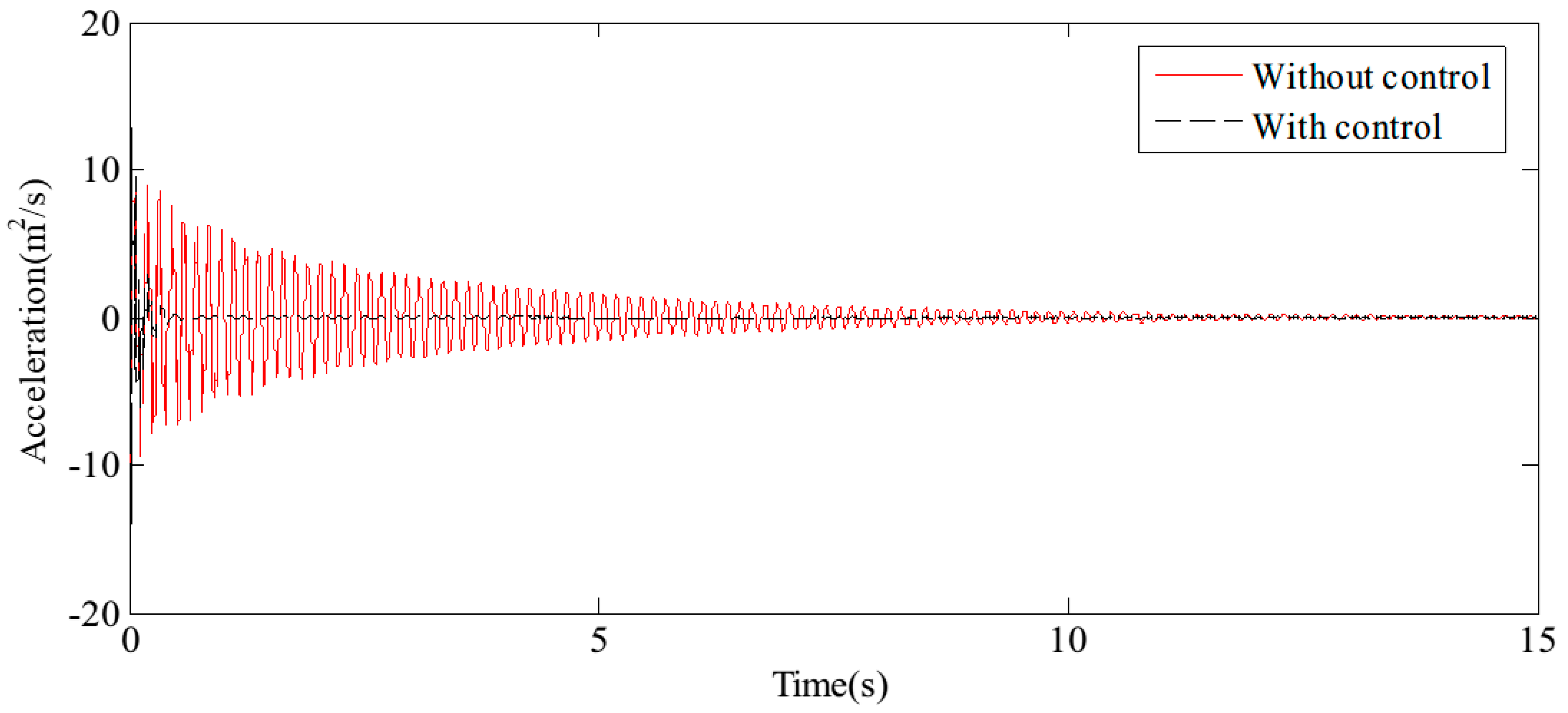
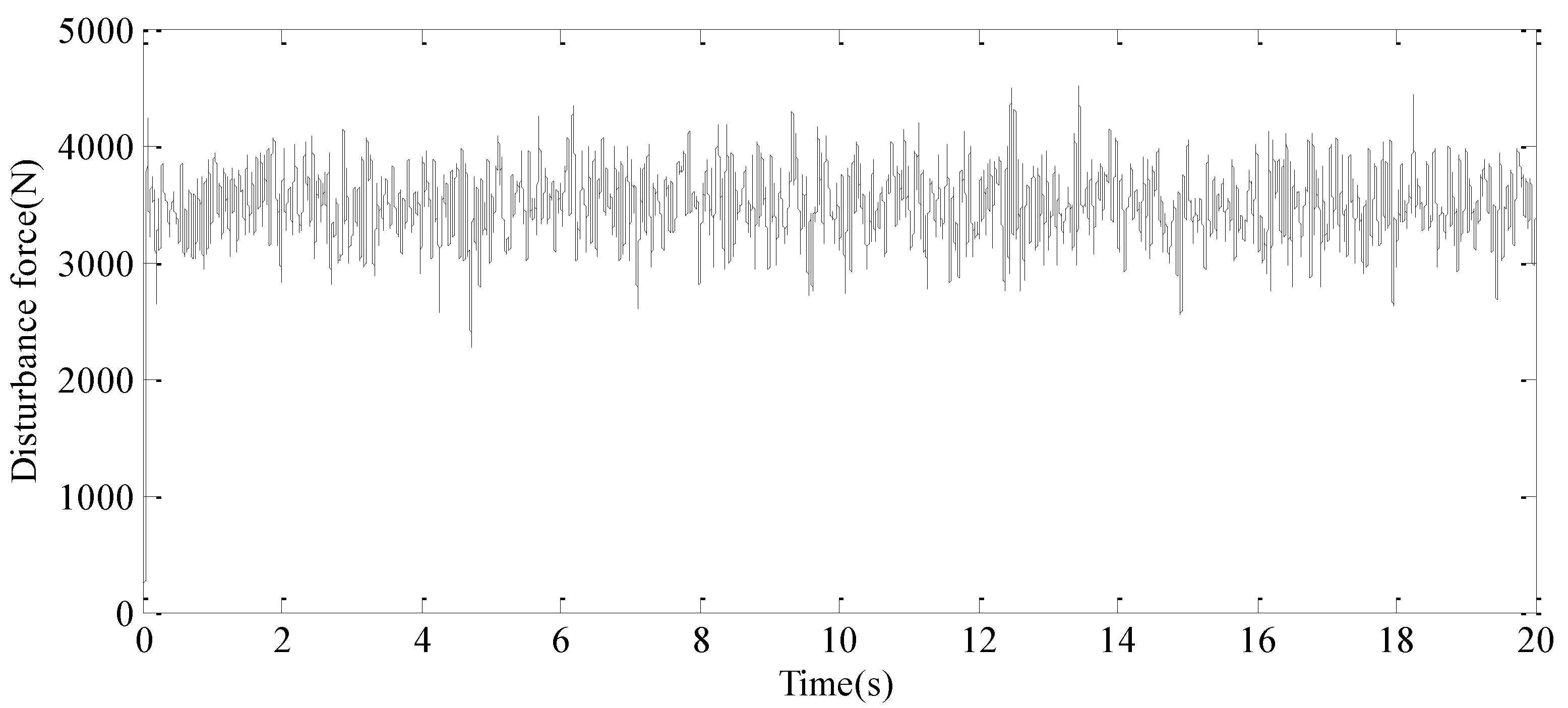
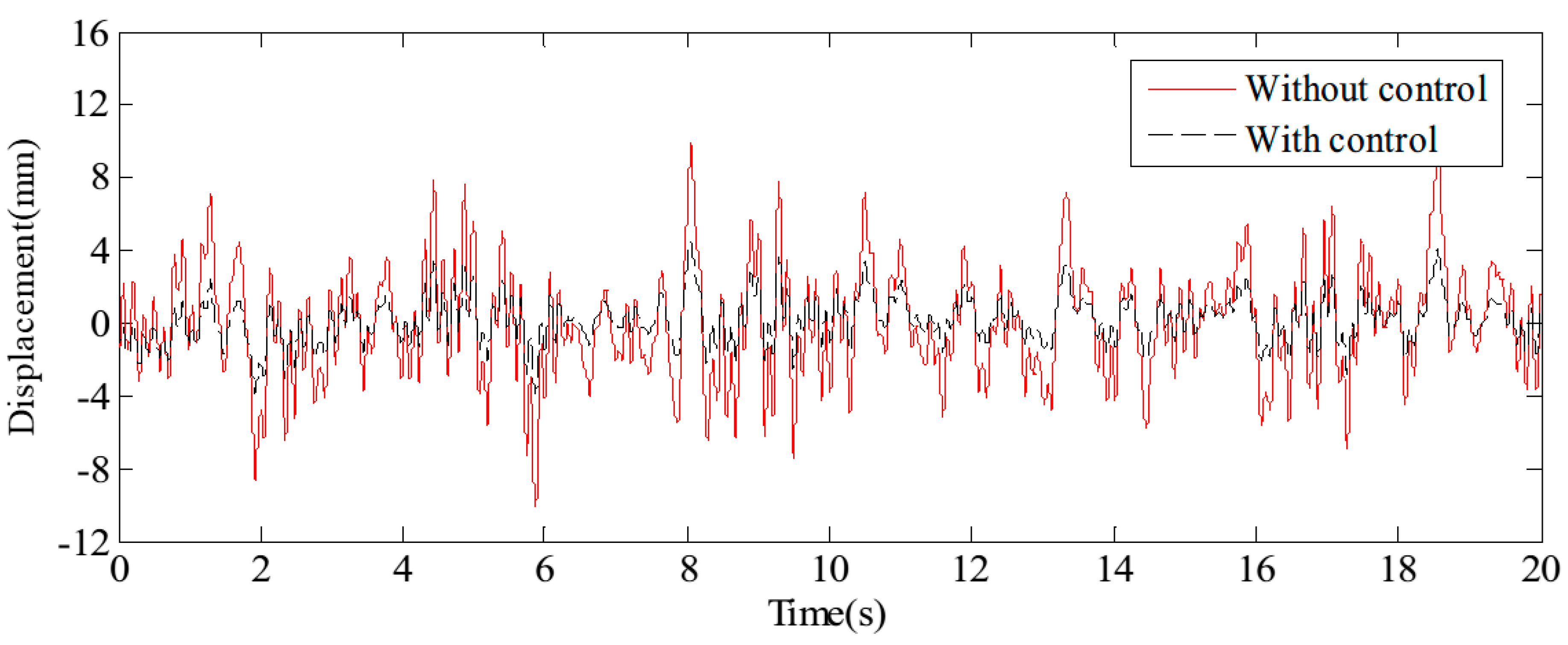
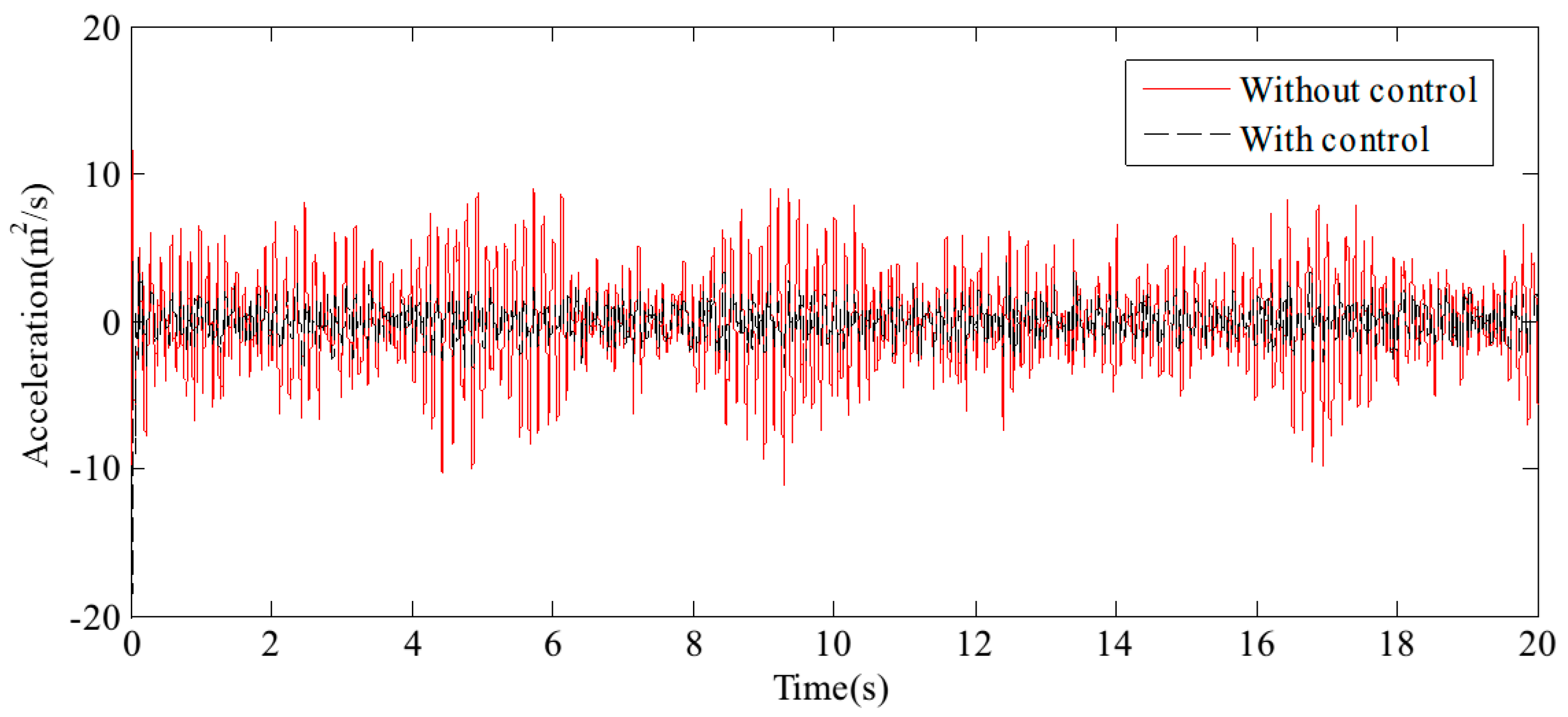
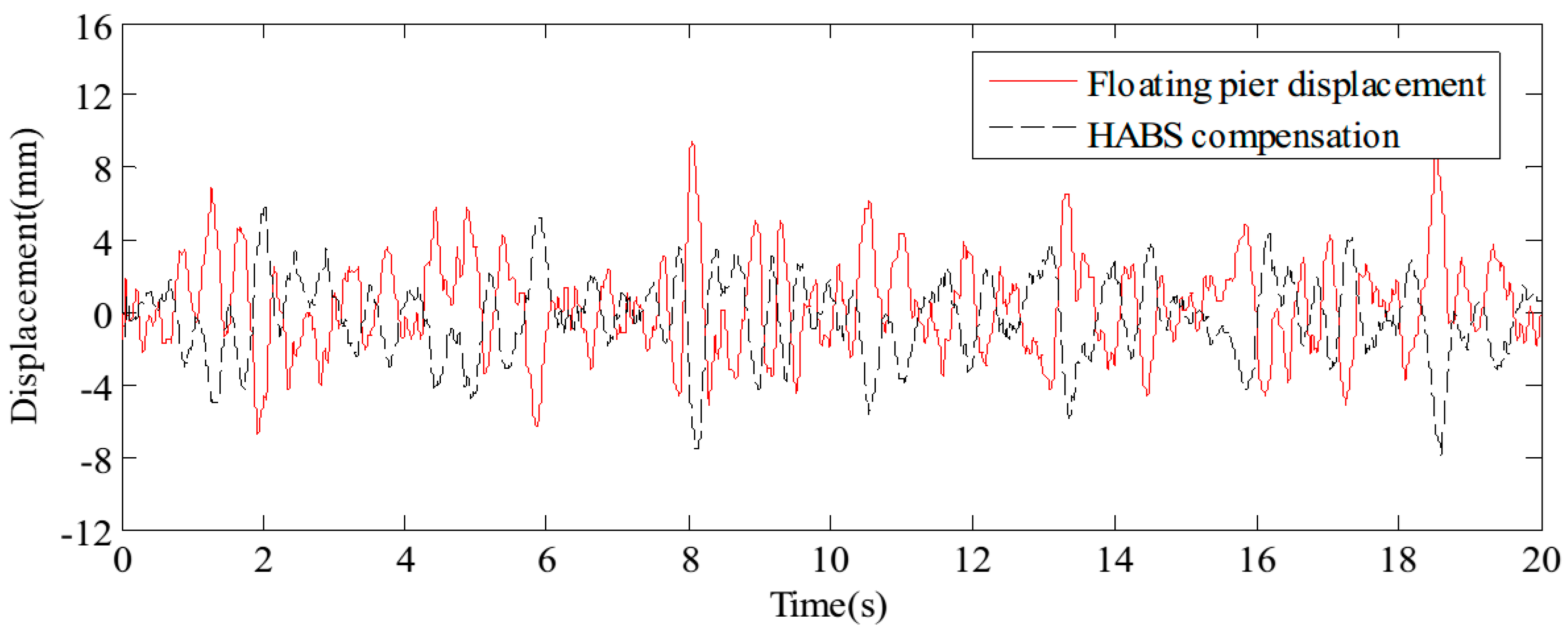
4.2. Performance Analysis and Results
5. Test-Rig Setup and Validation
5.1. Prototype Development
5.1.1. Scaling and Dynamic Similarity Principles
5.1.2. System Components and Setup
5.2. The Experiment Tests Research
5.2.1. Sine Signal Test
5.2.2. Random Signal Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Purcell, M.J.; Forrester, N.C. Bobbing crane heave compensation for the deep towed fiber optic survey system. In Proceedings of the Fiftieth Anniversary of the Society of Naval Architects and Marine Engineers, Wood Hole, MA, USA, 6–8 May 1994; pp. 1–16. [Google Scholar]
- Ma, B. Research on Electro-Hydraulic Control System of Wave Compensation for Deep Sea Hoists. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2019. [Google Scholar]
- Li, S.; Wei, J.; Guo, K.; Zhu, W.-L. Nonlinear robust prediction control of hybrid active–passive heave compensator with extended disturbance observer. IEEE Trans. Ind. Electron. 2017, 64, 6684–6694. [Google Scholar] [CrossRef]
- Do, K.; Pan, J. Nonlinear control of an active heave compensation system. Ocean Eng. 2008, 35, 558–571. [Google Scholar] [CrossRef]
- Neupert, J.; Mahl, T.; Haessig, B.; Sawodny, O.; Schneider, K. A heave compensation approach for offshore cranes. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 538–543. [Google Scholar]
- Liu, Z.; Zhang, Y.; Yu, X.; Chen, J.; Wang, Z.; Wang, D.; Duan, M.; Mu, X.; Huang, L. Study on the control strategies of offshore drilling crown-block heave compensation system with compound cylinders. IEEE Access 2020, 8, 149270–149281. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Li, Y.; Meng, Q.; Li, J. ADRC-ESMPC active heave compensation control strategy for offshore cranes. Ships Offshore Struct. 2020, 15, 1098–1106. [Google Scholar] [CrossRef]
- Sánchez, W.H.C.; Neto, A.B.; Fortaleza, E.L.F. Effects of nonlinear friction of passive heave compensator on drilling operation—Part I: Modeling and analysis. Ocean Eng. 2020, 213, 107743. [Google Scholar] [CrossRef]
- Sánchez, W.H.C.; Fortaleza, E.L.F.; Neto, A.B.; Vargas, J.A.R. Effects of nonlinear friction of passive heave compensator on drilling operation—Part II: Active robust control. Ocean Eng. 2021, 227, 108837. [Google Scholar] [CrossRef]
- Yu, H.; Chen, Y.; Shi, W.; Xiong, Y.; Wei, J. State constrained variable structure control for active heave compensators. IEEE Access 2019, 7, 54770–54779. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, S.; Li, X. Realization of Hydraulic Control System of Horizontal Rotary Forging Machine. In Proceedings of the 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 25–27 August 2020; pp. 496–499. [Google Scholar]
- Wang, Q.; Shi, T. Study on electro-hydraulic control system of advanced support in large section roadway. J. Phys. Conf. Ser. 2020, 1633, 012101. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Li, X.; Wang, L. Internal leakage analysis and experiment in hydraulic control system of steam turbine inlet valve. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 571–581. [Google Scholar] [CrossRef]
- Ni, T.-W.; Yang, Z.-G. Failure analysis on unexpected leakage of electro-hydraulic servo valve in digital electric hydraulic control system of 300 MW thermal power plant. Eng. Fail. Anal. 2021, 119, 104992. [Google Scholar] [CrossRef]
- Yang, H.; Xu, Y.; Chen, Z.; Wang, W.; Aung, N.Z.; Li, S. Cavitation suppression in the nozzle-flapper valves of the aircraft hydraulic system using triangular nozzle exits. Aerosp. Sci. Technol. 2021, 112, 106598. [Google Scholar] [CrossRef]
- Zhang, F. Design of Hydraulic Control System for Press Machine and Analysis on Its Fluid Transmission Features. Int. J. Heat Technol. 2021, 39, 161–169. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Liu, Y.; Zhu, H.; Liu, Y.; Shao, H.; Yang, C.; Li, H.; Mo, T. Optimal sensor placement methodology of hydraulic control system for fault diagnosis. Mech. Syst. Signal Process. 2022, 174, 109069. [Google Scholar] [CrossRef]
- An, Z.; Zhang, N.; Du, Y. Design of hydraulic pneumatic control system for rail grinding car. J. Phys. Conf. Ser. 2022, 2403, 012001. [Google Scholar] [CrossRef]
- Ma, W.; Ma, S.; Qiao, W.; Cao, D.; Yin, C. Research on PID controller of excavator electro-hydraulic system based on improved differential evolution. Machines 2023, 11, 143. [Google Scholar] [CrossRef]
- Guo, S.; Xue, Y.; Xie, J.; Zhou, X. Development of servo electro-hydraulic control system for heavy-duty horizontal extruder. In Proceedings of the Fourth International Conference on Mechanical, Electronics, and Electrical and Automation Control (METMS 2024), Xi’an, China, 26–28 January 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13163, pp. 1705–1712. [Google Scholar]
- Kajiwara, K.; Sato, E.; Mitsuta, T.; Watanabe, S.; Tagawa, Y.; Takai, S. Design methodology of the three-variable control method for shaking-table control with acceleration feedback. In Proceedings of the Fourth Symposium on Enhancement of Earthquake Performance of Infrastructures Based on Investigation into the Fracturing Process, Tokyo, Japan; 2003; pp. 53–58. (In Japanese). [Google Scholar]
- Tangwa, Y.; Kajiwara, K. Controller development for the E-Defense shaking table. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2007, 221, 171–181. [Google Scholar]
- Yang, Z.D. Research on Control Technologies of Simulation of Vibration Environment Using Hydraulic Vibration Table. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2009. [Google Scholar]
- Gang, S.; Zhen-Cai, Z.; Lei, Z.; Yu, T.; Chi-Fu, Y.; Jin-Song, Z.; Guang-Da, L.; Jun-Wei, H. Adaptive feed-forward compensation for hybrid control with acceleration time waveform replication on electro-hydraulic shaking table. Control Eng. Pract. 2013, 21, 1128–1142. [Google Scholar] [CrossRef]
- Yang, H.; Cong, D.; Yang, Z.; Han, J. Continuous swept-sine vibration realization combining adaptive sliding mode control and inverse model compensation for electro-hydraulic shake table. J. Vib. Eng. Technol. 2022, 10, 1007–1019. [Google Scholar] [CrossRef]
- Zhang, B.; Wei, W.; Qian, P.; Jiang, Z.; Li, J.; Han, J.; Mujtaba, M. Research on the control strategy of hydraulic shaking table based on the structural flexibility. IEEE Access 2019, 7, 43063–43075. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Chen, X. Neural-network-based adaptive finite-time output feedback control for spacecraft attitude tracking. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8116–8123. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, S.; Zou, J. Integral sliding mode control based deadbeat predictive current control for PMSM drives with disturbance rejection. IEEE Trans. Power Electron. 2021, 37, 2845–2856. [Google Scholar] [CrossRef]
- Ghadiri, H.; Mohammadi, A.; Khodadadi, H. Fast terminal sliding mode control based on SDRE observer for two-axis gimbal with external disturbances. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 70. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Dao, H.V.; Ahn, K.K. Adaptive robust position control of electro-hydraulic servo systems with large uncertainties and disturbances. Appl. Sci. 2022, 12, 794. [Google Scholar] [CrossRef]
- Benevides, J.R.S.; Paiva, M.A.D.; Simplicio, P.V.G.; Inoue, R.S.; Terra, M.H. Disturbance observer-based robust control of a quadrotor subject to parametric uncertainties and wind disturbance. IEEE Access 2022, 10, 7554–7565. [Google Scholar] [CrossRef]
- Yogi, S.C.; Tripathi, V.K.; Behera, L. Adaptive integral sliding mode control using fully connected recurrent neural network for position and attitude control of quadrotor. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5595–5609. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, P.; Jing, F.; Liu, B.; Peng, W.; Guo, M.; Xie, M. Sliding mode robust active disturbance rejection control for single-link flexible arm with large payload variations. Electronics 2021, 10, 2995. [Google Scholar] [CrossRef]
- Chen, C.-F.; Du, Z.-J.; He, L.; Wang, J.-Q.; Wu, D.-M.; Dong, W. Active disturbance rejection with fast terminal sliding mode control for a lower limb exoskeleton in swing phase. IEEE Access 2019, 7, 72343–72357. [Google Scholar] [CrossRef]
- Du, C.; Yin, Z.; Zhang, Y.; Liu, J.; Sun, X.-D.; Zhong, Y. Research on active disturbance rejection control with parameter autotune mechanism for induction motors based on adaptive particle swarm optimization algorithm with dynamic inertia weight. IEEE Trans. Power Electron. 2018, 34, 2841–2855. [Google Scholar] [CrossRef]
- Fareh, R.; Al-Shabi, M.; Bettayeb, M.; Ghommam, J. Robust active disturbance rejection control for flexible link manipulator. Robotica 2020, 38, 118–135. [Google Scholar] [CrossRef]
- Feliu, V.; Castillo, F.J.; Ramos, F.; Somolinos, J.A. Robust tip trajectory tracking of a very lightweight single-link flexible arm in presence of large payload changes. Mechatronics 2012, 22, 594–613. [Google Scholar] [CrossRef]
- Morales, R.; Feliu, V.; Jaramillo, V. Position control of very lightweight single-link flexible arms with large payload variations by using disturbance observers. Robot. Auton. Syst. 2012, 60, 532–547. [Google Scholar] [CrossRef]
- Pereira, E.; Aphale, S.S.; Feliu, V.; Moheimani, S.O.R. Integral resonant control for vibration damping and precise tip-positioning of a single-link flexible manipulator. IEEE/ASME Trans. Mechatron. 2010, 16, 232–240. [Google Scholar] [CrossRef]
- Sayahkarajy, M.; Mohamed, Z.; Faudzi, A.; Supriyanto, E. Hybrid vibration and rest-to-rest control of a two-link flexible robotic arm using H∞ loop-shaping control design. Eng. Comput. 2016, 33, 395–409. [Google Scholar] [CrossRef]
- Gao, H.; He, W.; Song, Y.; Zhang, S.; Sun, C. Modeling and neural network control of a flexible beam with unknown spatiotemporally varying disturbance using assumed mode method. Neurocomputing 2018, 314, 458–467. [Google Scholar] [CrossRef]
- Copot, C.; Ionescu, C.; Vanlanduit, S.; De Keyser, R. Vibration suppression in multi-body systems by means of disturbance filter design methods. J. Vib. Control 2018, 24, 2957–2969. [Google Scholar] [CrossRef]
- Liu, Y.; Zhan, W.; Gao, H.; Liu, H. Vibration suppression of an Euler–Bernoulli beam by backstepping iterative learning control. IET Control Theory Appl. 2019, 13, 2630–2637. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, W.; Xing, Y.; Li, N.; Yang, X. Research on vibration suppression of the long flexible arm based on three tilt sensors. Math. Probl. Eng. 2021, 2021, 7882357. [Google Scholar] [CrossRef]
- Han, J.W.; Yu, L.M.; Zhao, H.; Wang, Z.Y. Study of three state controller of Seismic simulating shaking table. JHIT 1999, 31, 21–28. [Google Scholar]
















| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Effective area of hydraulic cylinder | 8.64 cm2 | Mass of 87-type beam model | 400 Kg |
| Stroke of hydraulic cylinder | ±100 mm | Pressure of hydraulic source | 21 MPa |
| Rated flow of servo valve | 64 L/min | Stiffness of spring model | 40 kg/mm |
| Natural frequency of servo valve | 200 Hz | Load range of spring stiffness | 800–1200 Kg |
| Damping ratio of servo valve | 0.6 | First mode frequency of beam | 31 Hz |
| Density of hydraulic oil | 845 kg/m3 | Size of beam model | 0.2 × 0.3 × 4 m |
| Elasticity bulk modulus | 6.9 × 108 Pa | Step time of control system | 1 ms |
| mm/(m∙s−2) | RMS | The Maximum Value(abs) | ||||
|---|---|---|---|---|---|---|
| Without Control | With Control | Control Effect | Without Control | With Control | Control Effect | |
| End displacement | 2.95 | 1.56 | 52.88% | 10.27 | 5.62 | 54.72% |
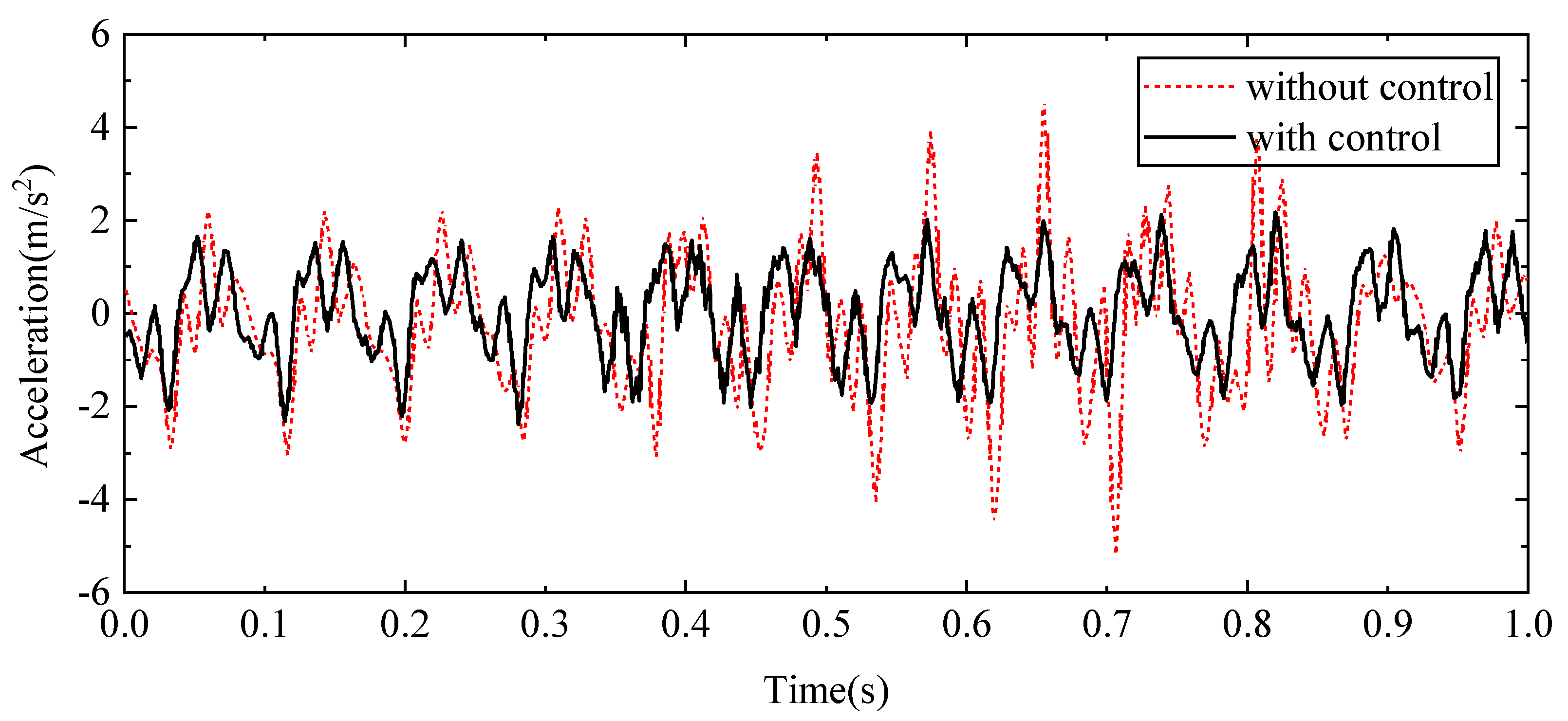
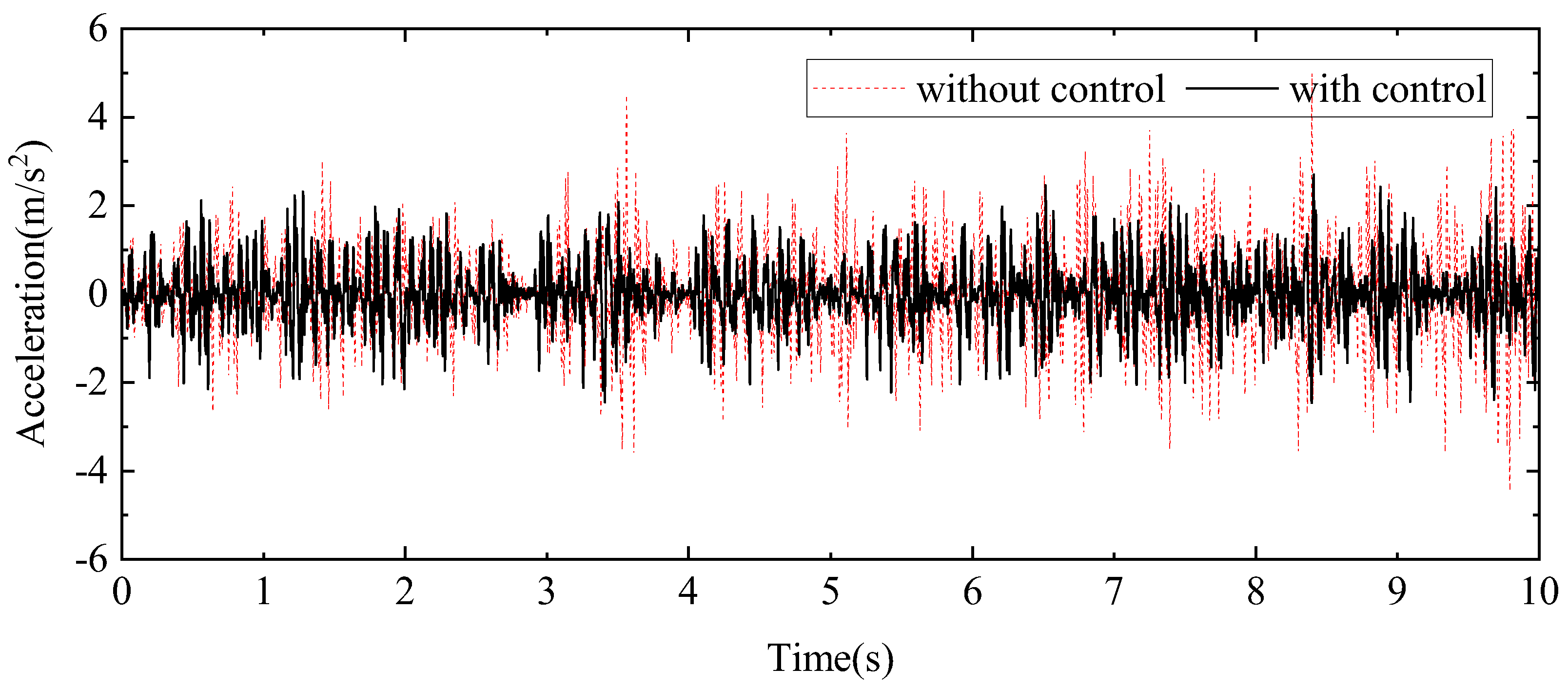
| End acceleration | 3.17 | 1.07 | 33.75% | 11.17 | 3.93 | 35.18% |
| Middle displacement | 1.93 | 1.36 | 64.98% | 6.16 | 3.39 | 55.03% |
| Middle acceleration | 1.86 | 0.81 | 43.55% | 5.77 | 2.66 | 46.10% |
| mm/(m∙s−2) | RMS | The Maximum Value | ||||
|---|---|---|---|---|---|---|
| Without Control | With Control | Control Effect | Without Control | With Control | Control Effect | |
| End displacement | 1.70 | 0.33 | 80.27% | 3.56 | 1.33 | 62.73% |
| Middle acceleration | 1.43 | 0.96 | 33.01% | 5.19 | 2.38 | 54.19% |
| mm/(m∙s−2) | RMS | The Maximum Value | ||||
|---|---|---|---|---|---|---|
| Without Control | With Control | Control Effect | Without Control | With Control | Control Effect | |
| End displacement | 1.14 | 0.23 | 79.23% | 3.02 | 0.82 | 72.83% |
| Middle acceleration | 0.97 | 0.67 | 30.32% | 4.99 | 2.46 | 50.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, Y.; Yang, T.; Wang, R.; Feng, J.; Crosbee, D. Modelling, Analysis and Validation of Hydraulic Self-Adaptive Bearings for Elevated Floating Bridges. Sensors 2024, 24, 8079. https://doi.org/10.3390/s24248079
Zhang L, Liu Y, Yang T, Wang R, Feng J, Crosbee D. Modelling, Analysis and Validation of Hydraulic Self-Adaptive Bearings for Elevated Floating Bridges. Sensors. 2024; 24(24):8079. https://doi.org/10.3390/s24248079
Chicago/Turabian StyleZhang, Lianpeng, Yuan Liu, Tailai Yang, Ruichen Wang, Jie Feng, and David Crosbee. 2024. "Modelling, Analysis and Validation of Hydraulic Self-Adaptive Bearings for Elevated Floating Bridges" Sensors 24, no. 24: 8079. https://doi.org/10.3390/s24248079
APA StyleZhang, L., Liu, Y., Yang, T., Wang, R., Feng, J., & Crosbee, D. (2024). Modelling, Analysis and Validation of Hydraulic Self-Adaptive Bearings for Elevated Floating Bridges. Sensors, 24(24), 8079. https://doi.org/10.3390/s24248079







