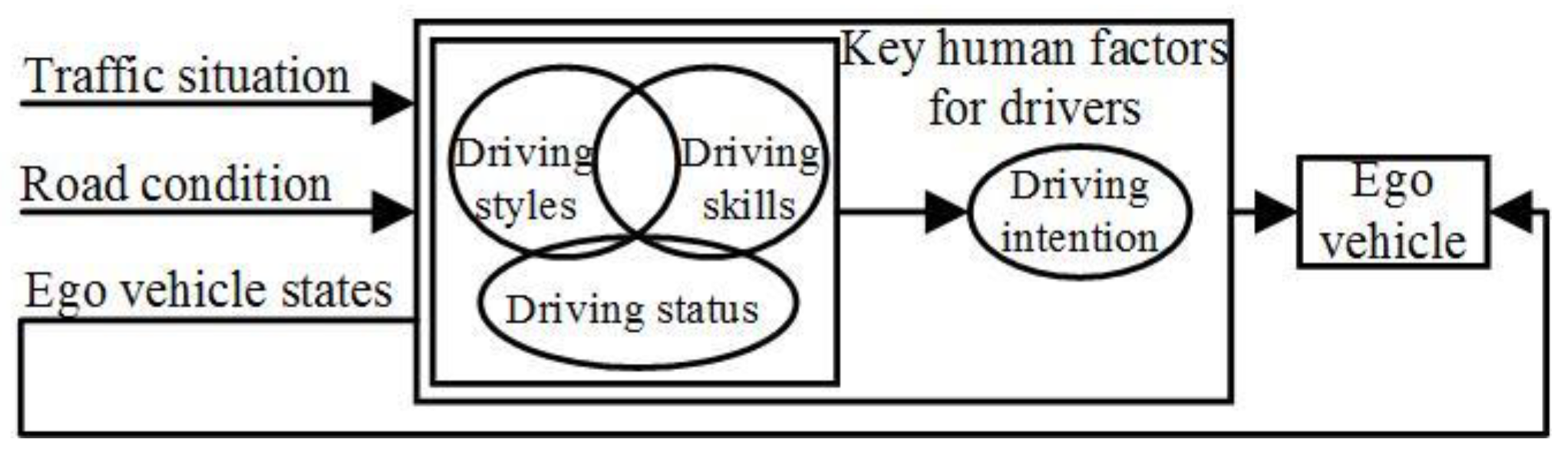
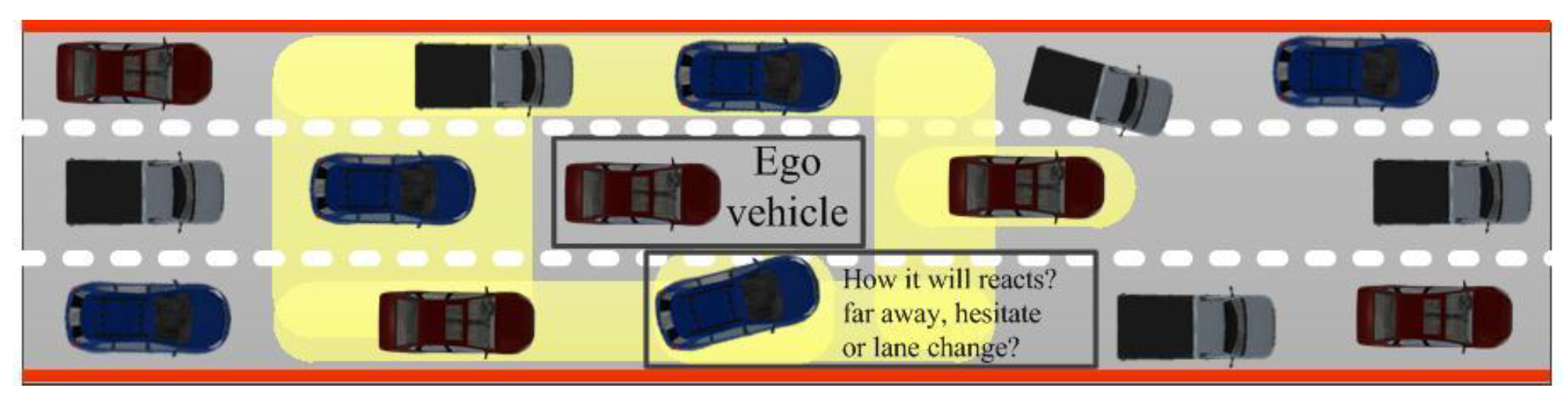
1. Introduction
Automated vehicles have become a dominant trend in improving traffic safety and transportation efficiency, given their advantages in reducing drivers’ driving loads and predicting traffic situations [
1,
2]. However, some obstacles still exist in enhancing the safety and adaptability of fully automated vehicles. Social dilemmas, represented by the tram issue and driver complacency, are technical problems that human society and ethics present to artificial intelligence theory in automated vehicles [
3]. The technique limitations of automated vehicles, such as poor perception accuracy and decision-making ability, restrict the transition process as well [
4,
5]. Therefore, the use of highly automated vehicles with a human-in-the-loop, which is called shared control, is likely to last for a long time and has been attracting increasing attention. Shared control can be defined as a safe, efficient, friendly, and stable driving mode formed by overcoming the decision-making conflict between the driver with social attributes and the automated system with logical attributes. The human–machine cooperation mechanism constitutes the theory foundation of the shared control system, and the human factors are required to be evaluated in detail.
As the key technique to overcoming the human–machine conflict in shared control, the driving authority allocation strategy (DAAS) needs to be analyzed in depth. The DAAS can be defined as the weight distribution method between the driver and the automated system, with the aim of achieving a safe, efficient, and stable system configuration [
6]. The DAAS consists of a switched type and a shared type, and the latter is subdivided into direct and indirect shared controls [
7]. With the development of by-wire and intelligent sensing techniques, the basic functionality of the DAAS has been improved, and indirect shared control has developed rapidly by virtue of its framework advantage, signal identification, velocity optimization, and H∞ control theories [
8,
9]. In recent years, in order to improve system safety, adaptability, and driver acceptability, the DAAS has gradually focused on the cognitive mechanism of human factor attributes, the cognitive capability of complex scenarios, and switching smoothness [
10,
11]. Drivers’ driving skills are modeled and evaluated based on the optimal driver preview model, overtaking model, and accident assessment model and the drivers’ learning processes and levels are revealed, mainly based on typical physical models [
12,
13]. Drivers’ driving statuses focus on drivers’ fatigue, sleepiness, distraction, and mood and are identified accurately based on biological signals, vehicle states, and driving actions, such as eye and head movements. Image detection and machine learning theories are used to analyze drivers’ take-over and reaction abilities, and they reveal the inducement and externalization of the driving status [
14,
15]. Drivers’ driving styles are classified and identified based on physical modeling or a data-driven approach, and the technique details are discussed in the next section. It can be seen that key human factors are analyzed and evaluated in a decoupled way, and few studies were conducted on the comprehensive representation of driving skills, statuses, and styles. The rationality of the DAAS still needs to be improved due to the lack of comprehensive human factors reflecting drivers’ time-varying abilities for vehicle control.
As the main component of a human-like automated driving pattern, a personalized driving pattern is produced by a driver’s driving style [
16]. Understanding the drivers’ driving styles that make the shared control more human-like is the key to improving system performance, in particular, driver adaption and acceptance [
17]. Four human-like degrees, namely, none, low, medium, and high levels, were researched, and the medium degree received more attention based on its advantage of high computational efficiency and distinct personalized results [
18]). The classification and identification methods were mainly developed to obtain up to six typical driving styles [
19,
20]. The classification mode of driving styles is the primary task used to reflect the intrinsic mechanism of the human-like driving pattern and is mainly affected by scenarios, modal datasets, and characteristic parameter sets [
21]. No more than five types of driving styles produce optimal computational efficiency but are mainly used for fuel economy instead of drivers’ acceptability [
22]. Subjective and objective classification methods were researched individually by online or offline methods, and the average accuracy was about 85%, which was based on data-driven algorithms, and 80% was based on a questionnaire [
23]. The identification process of driving styles takes the moment-based array or time-series-based high-dimensional data as the model inputs, and the identification method is mainly based on machine learning and system modeling [
19,
24]. Data-driven methods have advantages in processing the human factor data with high-order nonlinearity and uncertainty, and the framework of the system model has low-order nonlinearity and certain physical interpretations. Considering the model’s complexity, related methods are mainly conducted using offline methods to obtain analysis results [
25]. Furthermore, few studies focused on scenario generation methods specific to human factors, which are the main factors restricting the evaluation accuracy of human factors as well. Therefore, a combination of classification and identification processes for driving styles needs to be developed in depth, and its evaluation method combining online and offline methods and simulated scenarios for the personalized system needs to be established to improve evaluation accuracy.
The decision-making process is required to generate efficient and stable driving tasks in complex scenarios and becomes the core-level component in shared control [
26]. The DAAS and driving styles constitute internal constraints and determine the system features together with the external ones, such as scenarios or vehicle states [
27]. Thus, the system features of the decision-making process consist of self-learning, high-order nonlinearity, high data dependency, and personality, and the key challenge is how to deal with the uncertainties and improve driver acceptance [
28]. Two typical methods, the physical modeling-based and data-driven-based, are researched for decision-making logic. The physical modeling-based methods, such as the car-following model, the Pipes and Forbes model, and the overtaking maneuver model, aim to reveal the decision-making mechanisms of the human–vehicle closed loop system [
29]. The model’s accuracy is improved with the gradual refinement of driving skill sub-models, such as the driver preview model, the unified driver model, or the driver control model [
30]. The physical modeling-based decision-making models have clear physical meaning and can realize real-time and strong, robust decision-making tasks. However, these models poorly adapt to scenarios with high uncertainty due to the deterministic internal model structure and the neglect of data support. Data-driven-based methods, such as the multi-criteria, Bayesian network, or deep learning decision-making, are trained and operated based on datasets for the online decision-making of automated vehicles [
31,
32]. Artificial intelligence and research theories, such as game theory, the Markov decision-making process (MDP), or deep learning, are used to examine high-order nonlinearity and personality characteristics occurring in the decision-making process based on large-scale datasets [
33]. However, few studies combine intention-aware uncertainty and personalized factors into the decision-making process in shared control, which affects the acceptance and adaption of shared control to a certain extent. As a result, the data-driven-based decision-making paradigm needs to be developed in depth, where the personality of a driver should be merged.
Motivated by the above-mentioned observations, a personalized shared control framework considering a person’s driving capability and style is proposed. The contributions are as follows.
(1) Drivers’ driving capability is defined and evaluated to improve the rationality of the DAAS. Driving styles combining classification and identification processes are analyzed, characterized, and evaluated in both online and offline ways. The simulated scenario generation method for human factors is established.
(2) The personalized framework of shared control for the automated vehicle is proposed, considering drivers’ driving capabilities and style, and its evaluation criteria are established considering driving safety, comfort, and workload. The intention-aware decision-making logic is proposed based on the mixed observable Markov decision process (MOMDP).
6. Conclusions
A personalized shared control, while considering drivers’ driving capabilities and styles, is proposed to improve the acceptance and adaptation of shared control by human drivers. As per theoretical and validation analyses, the following conclusions can be obtained:
The simulation scenario generation method for human factors was established. The RVRF theory reveals a wave-particle duality of macro- and micro-traffic flows. Stimuli and the RVRF achieved the ability to motivate driving capability and styles to the maximum extent. Drivers’ driving capability was defined and evaluated, the average accuracy of both Aid and Apr were above 85%, and its physical properties with nonlinearity, time gradient, randomness, and predictive ability were extracted and analyzed. Drivers’ driving styles were analyzed, characterized, and evaluated, and their accuracy was higher than 95% within a short identification period.
The MOMDP-based decision-making process shows advantages in dealing with uncertain motion intention and personalized logic. The personalized shared control system obtained excellent performance in both the human-in-the-loop simulation platform and field tests. The proposed system combines the randomness of human factor attributes in a single test, multi-objective optimization, and personalized characteristics of the driver and the automated driving system. Personalized shared control can achieve better performance in driving safety, comfort, and workload, corresponding to different driving capability degrees and driving style types than those only driven by human drivers or automated systems.
With the advantage of deep mixing decision-making between human and automated systems, personalized shared control will achieve better driver acceptance in future automated driving tasks.