Quantum Positioning Scheme Based on Microwave–Optical Entanglement
Abstract
1. Introduction
2. EOM Converter and M–O Entanglement
2.1. Cavity Optomechanical Systems and EOM Converter
2.2. Propagating Modes and Entanglement Degree
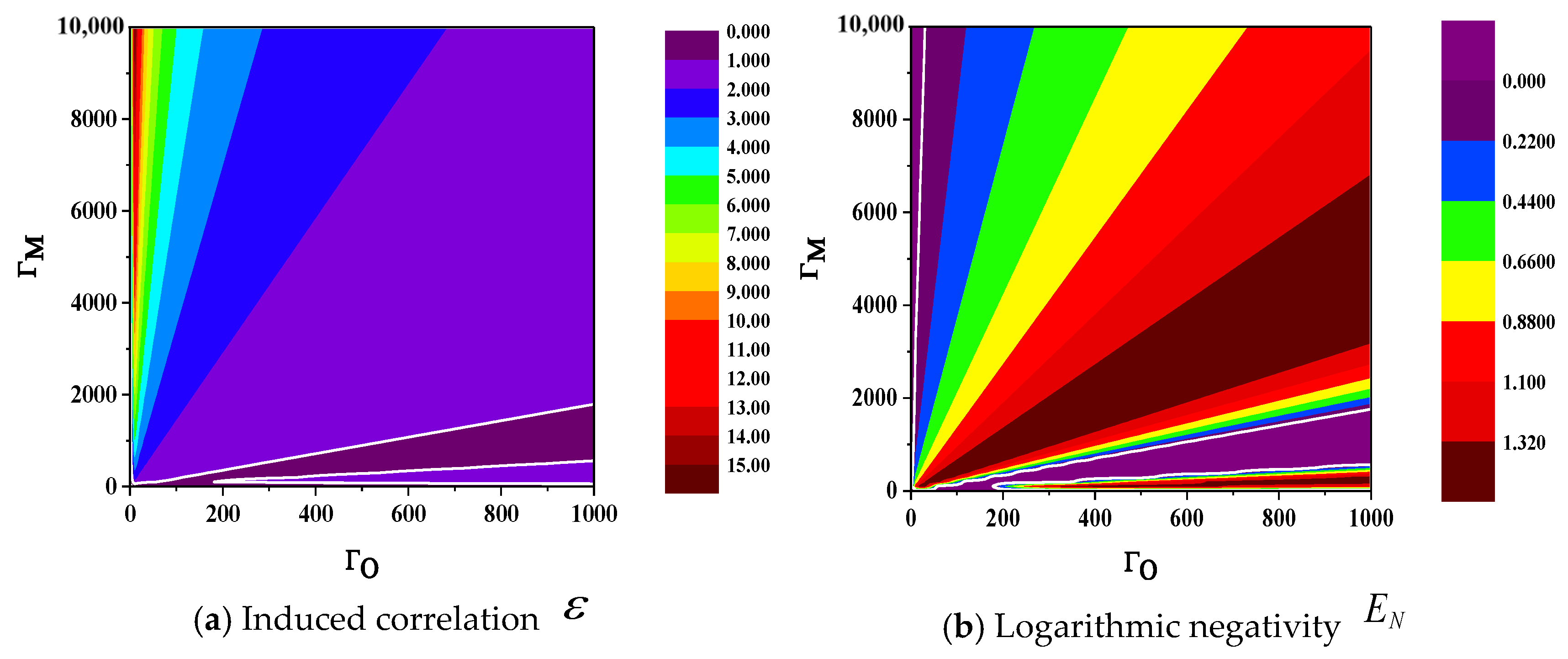
2.2.1. Metric of Induced Correlation
2.2.2. Metric of Logarithmic Negativity
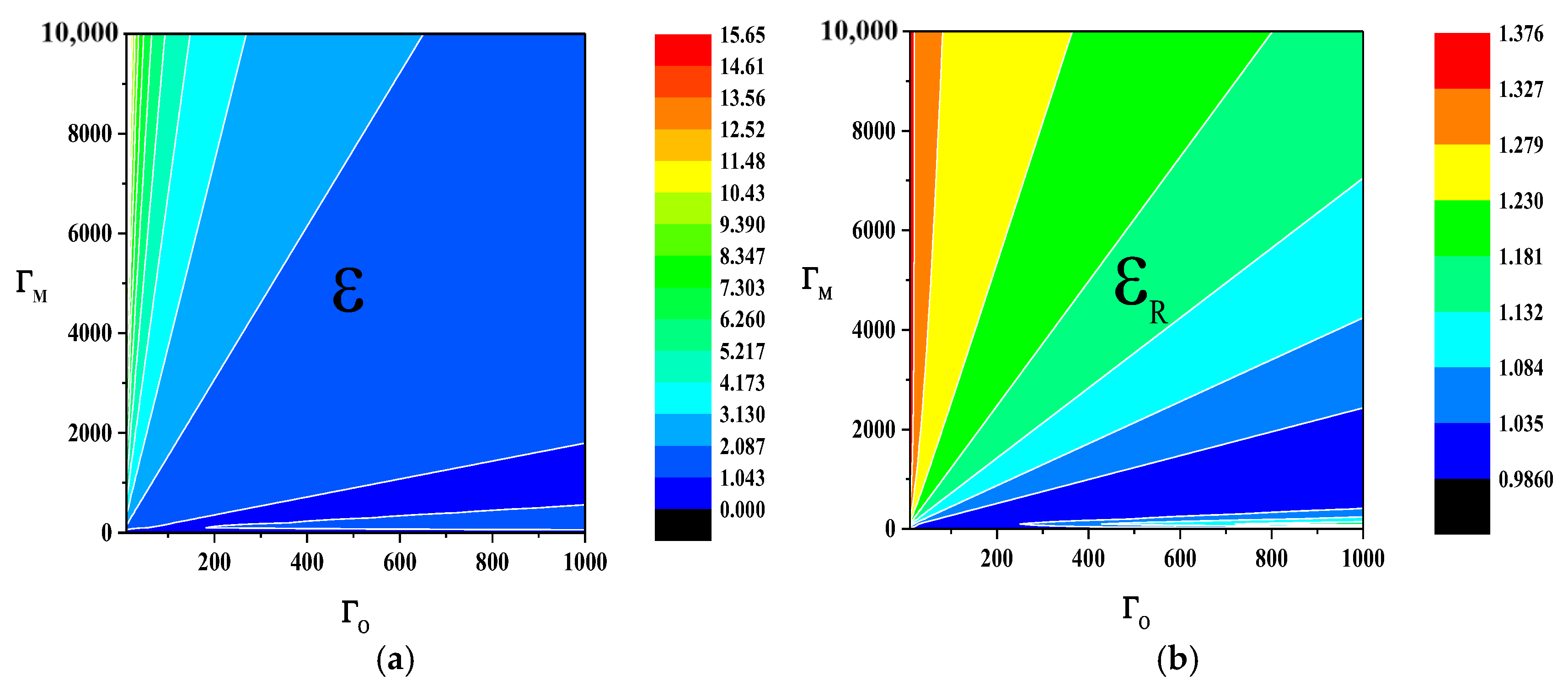
2.2.3. Comparison of Two Metrics: and
3. QPS Scheme Utilizing EOM Converters
3.1. Principle of Distance-Based Positioning
3.2. QPS Scheme Based on EOM Converters
3.2.1. Transmission
3.2.2. Reception
3.2.3. Coincidence Measurement
4. Results and Discussions
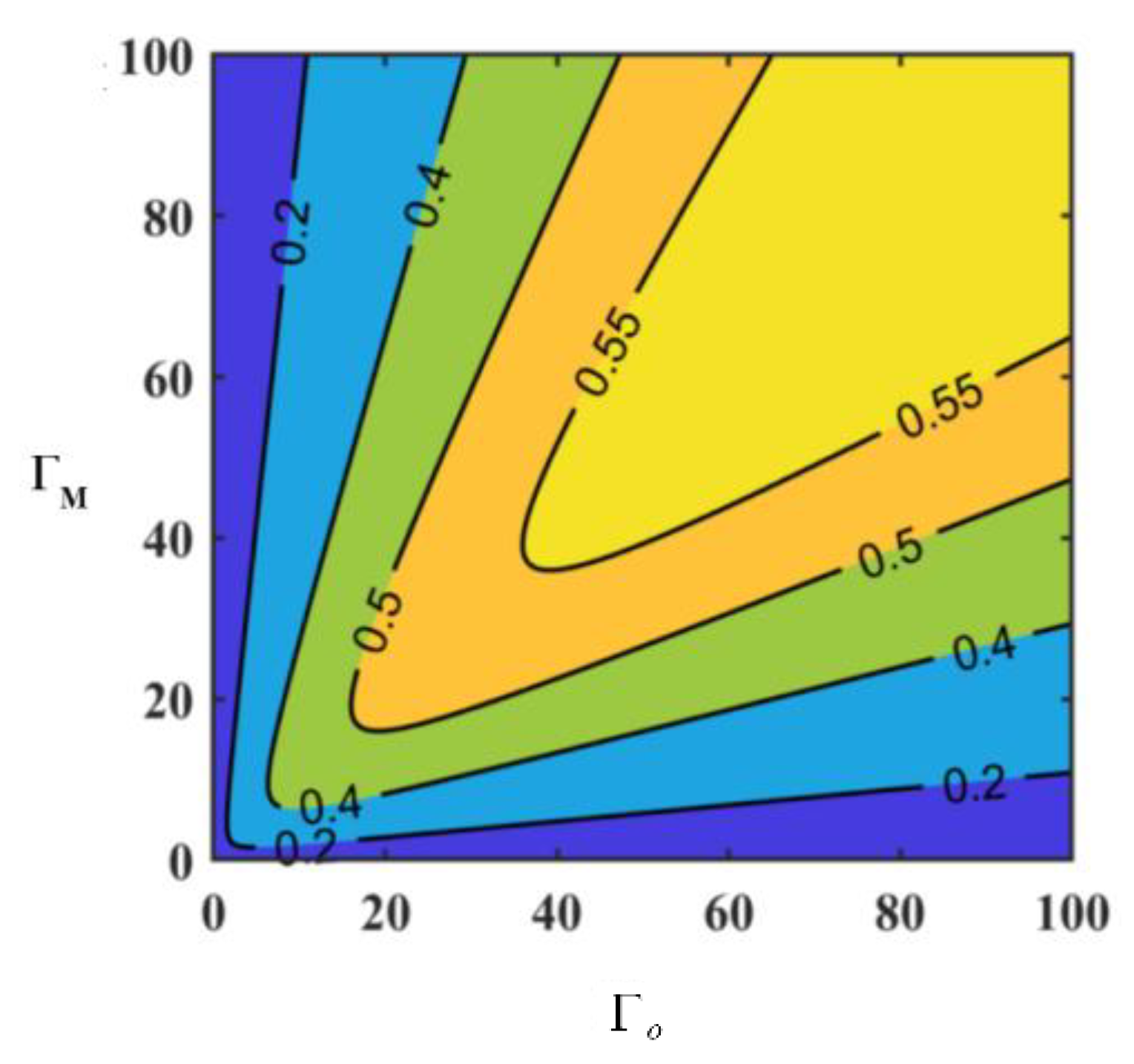
4.1. Entanglement Feature
4.2. System Stability
4.3. Quantum Positioning Feature
4.3.1. Performance of Positioning
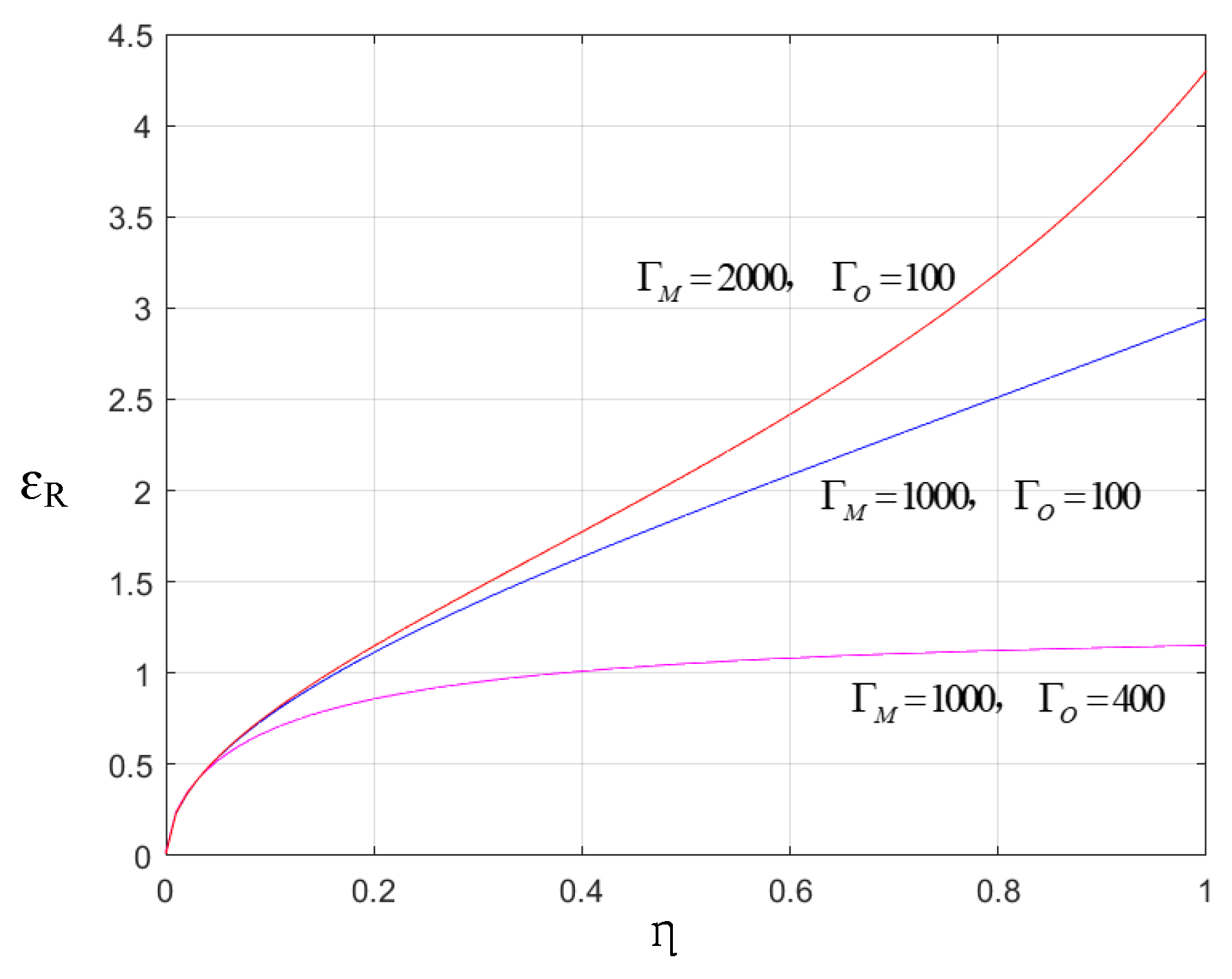
4.3.2. Impact of Key Parameter
- (1)
- Impact of the transmissivity
- (2)
- Impact of the photon conversion efficiency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete. Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Liu, C.C.; Wang, D.; Sun, W.Y.; Ye, L. Quantum Fisher information, quantum entanglement and correlation close to quantum critical phenomena. Quantum Inf. Process. 2017, 16, 219. [Google Scholar] [CrossRef]
- Nande, S.S.; Rossi, T.; Habibie, M.I.; Barhoumi, M.; Palaparthy, K.; Mansouri, W.; Raju, A.; Bassoli, R.; Cianca, E.; Fitzek, F.H.P.; et al. Satellite-based positioning enhanced by quantum synchronization. Comput. Netw. 2024, 254, 110734. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced positioning and clock synchronization. Nature 2001, 412, 417. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, M. Position measuring interactions and the Heisenberg uncertainty principle. Phys. Lett. A 2002, 299, 1–7. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Positioning and clock synchronization through entanglement. Phys. Rev. A 2002, 65, 022309. [Google Scholar] [CrossRef]
- Hofheinz, M.; Huard, B.; Portier, F. Quantum microwaves/Micro-ondes quantiques. Comptes Rendus Phys. 2016, 17, 679–804. [Google Scholar] [CrossRef]
- Bochmann, J.; Vainsencher, A.; Awschalom, D.D.; Cleland, A.N. Nanomechanical coupling between microwave and optical photons. Nat. Phys. 2013, 9, 712. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity optomechanics: Back-action at the mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Balram, K.C.; Davanço, M.; Lim, J.Y.; Song, J.D.; Srinivasan, K. Moving boundary and photoelastic coupling in GaAs optomechanical resonators. Optica 2014, 1, 414–420. [Google Scholar] [CrossRef]
- Gröblacher, S.; Hammerer, K.; Vanner, M.R.; Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 2009, 460, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.S.; Huang, S.M. The electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 2010, 81, 041803. [Google Scholar] [CrossRef]
- Eisaman, M.D.; André, A.; Massou, F.; Fleischhauer, M.; Zibrov, A.S.; Lukin, M.D. Electromagnetically induced transparency with tunable single-photon pulses. Nature 2005, 438, 837–841. [Google Scholar] [CrossRef]
- Weis, S.; Riviere, R.; Deléglise, S.; Gavartin, E.; Arcizet, O.; Schliesser, A.; Kippenberg, T.J. Optomechanically induced transparency. Science 2010, 330, 1520–1523. [Google Scholar] [CrossRef]
- Lau, H.K.; Clerk, A.A. Macroscale entanglement and measurement. Science 2021, 372, 570–571. [Google Scholar] [CrossRef]
- de Lépinay, L.M.; Ockeloen-Korppi, C.F.; Woolley, M.J.; Sillanpää, M.A. Quantum mechanics–free subsystem with mechanical oscillators. Science 2021, 372, 625–629. [Google Scholar] [CrossRef]
- Kotler, S.; Peterson, G.A.; Shojaee, E.; Lecocq, F.; Cicak, K.; Kwiatkowski, A.; Geller, S.; Glancy, S.; Knell, E.; Simmonds, R.W.; et al. Direct observation of deterministic macroscopic entanglement. Science 2021, 372, 622–625. [Google Scholar] [CrossRef]
- Riedinger, R.; Wallucks, A.; Marinkovic, I.; Löschnauer, C.; Aspelmeyer, M.; Hong, S.; Gröblacher, S. Remote quantum entanglement between two micromechanical oscillators. Nature 2018, 556, 473–477. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.S.; Chen, A.X. Large and robust mechanical squeezing of optomechanical systems in a highly unresolved sideband regime via Duffing nonlinearity and intracavity squeezed light. Opt. Express 2020, 28, 36620–36631. [Google Scholar] [CrossRef] [PubMed]
- Clark, J.B.; Lecocq, F.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature 2017, 541, 191–195. [Google Scholar] [CrossRef]
- Lau, H.K.; Clerk, A.A. Ground-state cooling and high-fidelity quantum transduction via parametrically driven bad-cavity opto-mechanics. Phys. Rev. Lett. 2020, 124, 103602. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.; Alegre, T.; Safavi-Naeini, A.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Fong, K.Y.; Tang, H.X. A 10-GHz film-thickness-mode cavity optomechanical resonator. Appl. Phys. Lett. 2015, 106, 161108. [Google Scholar] [CrossRef]
- Shen, M.; Xie, J.; Zou, C.-L.; Xu, Y.; Fu, W.; Tang, H.X. High frequency lithium niobate film-thickness-mode optomechanical resonator. Appl. Phys. Lett. 2020, 117, 131104. [Google Scholar] [CrossRef]
- Deotare, P.B.; Bulu, I.; Frank, I.W.; Quan, Q.; Zhang, Y.; Ilic, R.; Loncar, M. All optical reconfiguration of optomechanical filters. Nat. Commun. 2012, 3, 846. [Google Scholar] [CrossRef]
- Krause, A.; Winger, M.; Blasius, T.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 2012, 6, 768–772. [Google Scholar] [CrossRef]
- Richardson, L.; Hines, A.; Schaffer, A.; Anderson, B.P.; Guzman, F. Quantum hybrid optomechanical inertial sensing. Appl. Opt. 2020, 59, G160–G166. [Google Scholar] [CrossRef]
- Zhong, C.C.; Han, X.; Tang, H.X.; Jiang, L. Entanglement of microwave-optical modes in a strongly coupled electro-optomechanical system. Phys. Rev. A 2020, 101, 032345. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhang, R.; Chesi, S.; Wang, Y.D. Reservoir-engineered entanglement in an unresolved-sideband optomechanical system. Commun. Theor. Phys. 2021, 73, 055105. [Google Scholar] [CrossRef]
- Hill, J.T.; Safavi-Naeini, A.H.; Chan, J.; Painter, O. Coherent optical wavelength conversion via cavity-opto-mechanics. Nat. Commun. 2012, 3, 1196. [Google Scholar] [CrossRef]
- Wang, Y.D.; Clerk, A.A. Using dark modes for high-fidelity optomechanical quantum state transfer. New J. Phys. 2012, 14, 105010. [Google Scholar] [CrossRef]
- Palomaki, T.A.; Harlow, J.W.; Teufel, J.D.; Simmonds, R.W.; Lehnert, K.W. Coherent state transfer between itinerant microwave fields and a mechanical oscillator. Nature 2013, 495, 210. [Google Scholar] [CrossRef] [PubMed]
- Bhatti, U.; Ochieng, W.; Feng, S. Performance of rate detector algorithms for an integrated GPS/INS system in the presence of slowly growing error. GPS Solut. 2011, 16, 293. [Google Scholar] [CrossRef]
- Ji, K.H.; Herring, T.A. A method for detecting transient signals in GPS position time-series: Smoothing and principal component analysis. Geophys. J. Int. 2013, 193, 171. [Google Scholar] [CrossRef]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Guha, S.; Weedbrook, C.; Vitali, D.; Shapiro, J.H.; Pirandola, S. Microwave quantum illumination. Phys. Rev. Lett. 2015, 114, 080503. [Google Scholar] [CrossRef]
- Alejandra, V.; Maria, V.C.; Alexei, T.; Shih, Y.H. Entangled two-photon wave packet in a dispersive medium. Phys. Rev. Lett. 2002, 88, 183601. [Google Scholar]
- Zhu, J.; Chen, X.X.; Huang, P.; Zeng, G.H. Thermal-light-based ranging using second-order coherence. Appl. Optics. 2012, 51, 4885. [Google Scholar] [CrossRef]
- Plenio, M.B. Logarithmic negativity: A full entanglement monotone that is not convex. Phys. Rev. Lett. 2005, 95, 090503. [Google Scholar] [CrossRef] [PubMed]
- Lecocq, F.; Clark, J.B.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Mechanically mediated microwave frequency conversion in the quantum regime. Phys. Rev. Lett. 2016, 116, 043601. [Google Scholar] [CrossRef] [PubMed]
- Cernotik, O.; Mahmoodian, S.; Hammerer, K. Spatially adiabatic frequency conversion in opto-electro-mechanical arrays. Phys. Rev. Lett. 2018, 121, 110506. [Google Scholar] [CrossRef] [PubMed]
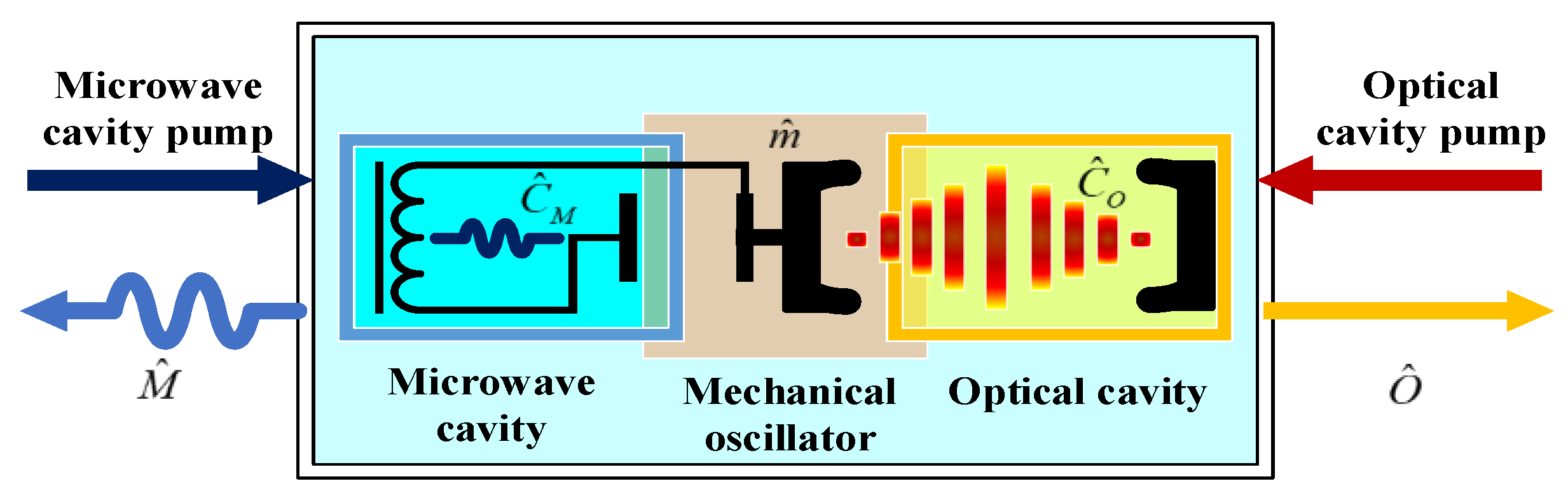






| Microwave Cavity | Mechanical Oscillator | Optical Cavity | |
|---|---|---|---|
| Cavity/vibration mode | |||
| Cavity/vibration mode frequency | |||
| Damping rate | |||
| Driving mode frequency | — | ||
| Detuning of frequency | — |
| Microwave Cavity | Mechanical Oscillator | Optical Cavity | |
|---|---|---|---|
| Frequency | 6.982 GHz | 32.5 MHz | 282 THz |
| Driving power | mW | — | mW |
| Coupling rate | Hz | — | Hz |
| Damping rate | |||
| Detuning of frequency | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Q.; Wu, D. Quantum Positioning Scheme Based on Microwave–Optical Entanglement. Sensors 2024, 24, 7712. https://doi.org/10.3390/s24237712
Miao Q, Wu D. Quantum Positioning Scheme Based on Microwave–Optical Entanglement. Sensors. 2024; 24(23):7712. https://doi.org/10.3390/s24237712
Chicago/Turabian StyleMiao, Qiang, and Dewei Wu. 2024. "Quantum Positioning Scheme Based on Microwave–Optical Entanglement" Sensors 24, no. 23: 7712. https://doi.org/10.3390/s24237712
APA StyleMiao, Q., & Wu, D. (2024). Quantum Positioning Scheme Based on Microwave–Optical Entanglement. Sensors, 24(23), 7712. https://doi.org/10.3390/s24237712





