Automatic Detection and Classification of Natural Weld Defects Using Alternating Magneto-Optical Imaging and ResNet50
Abstract
1. Introduction
2. Experimental Methods
2.1. Experimental Setup
2.2. Principle of MO Imaging for Weld Defects
2.3. Preprocessing of MO Images for Weld Defect Analysis
3. Detection and Classification by BP Neural Network and SVM
3.1. Feature Extraction Based on PCA
- (1)
- Resize: Resize the original image either horizontally or vertically.
- (2)
- Rotation: Make the original image rotate clockwise or counterclockwise according to a certain angle.
- (3)
- Flip: Flip the original images along the horizontal or vertical axes at their center coordinates.
- (4)
- Brightness change: Change the brightness of the original image.
- (5)
- Contrast adjustment: Change the intensity of the brightness difference in the original image.
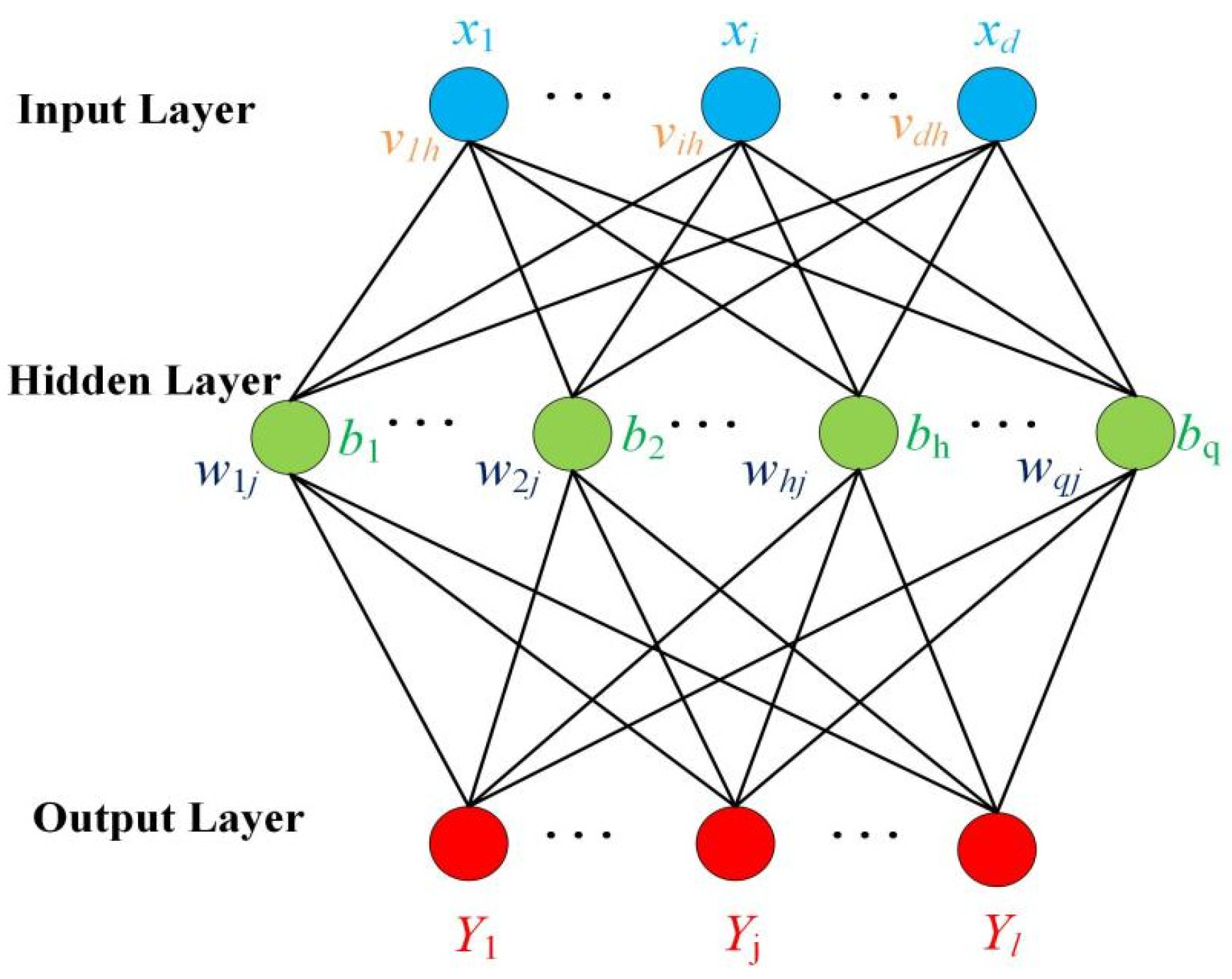
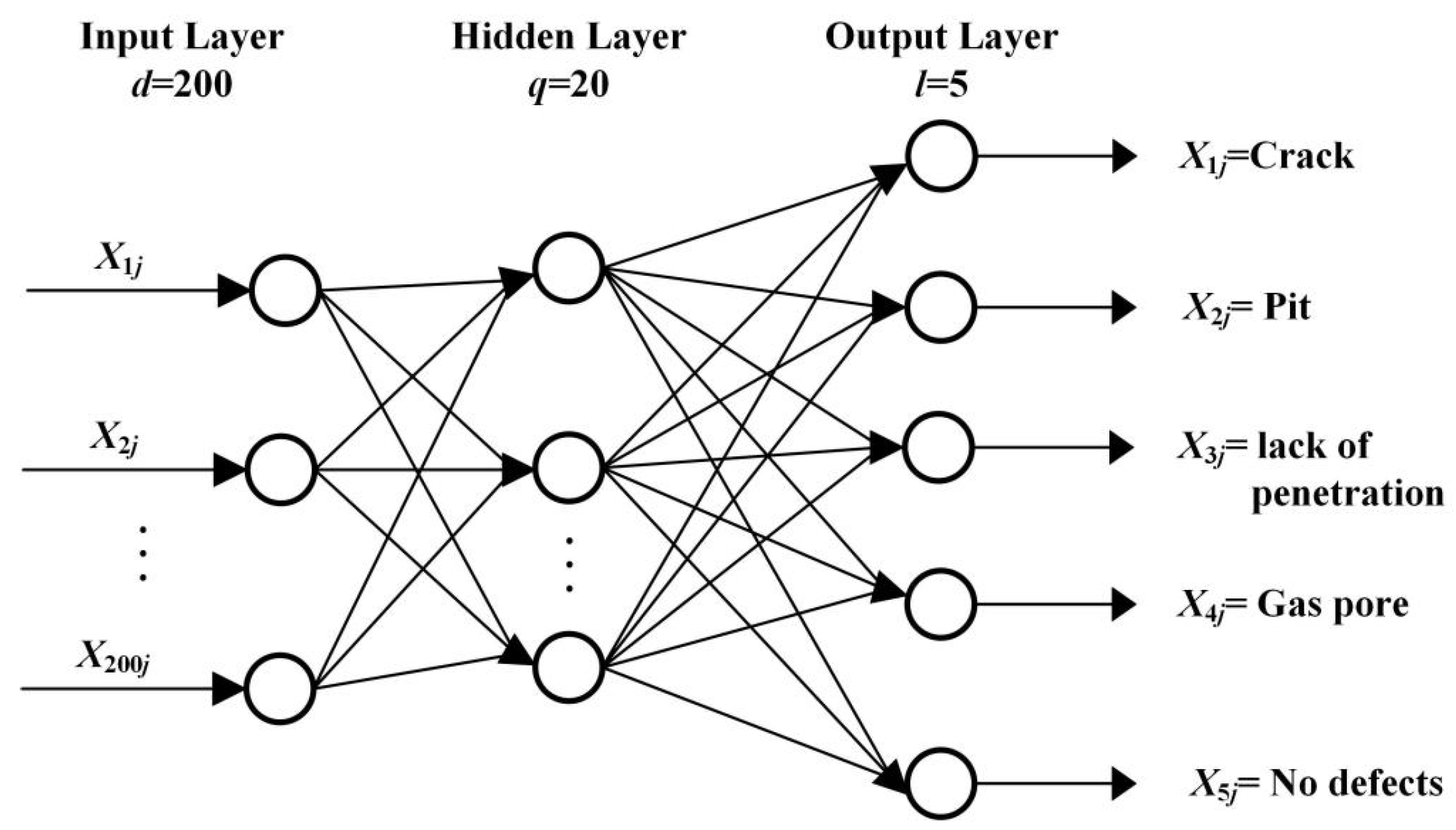
3.2. Classification by the PCA + BP Model
3.3. Classification by the PCA + SVM Model
4. Detection and Classification by CNN and ResNet50
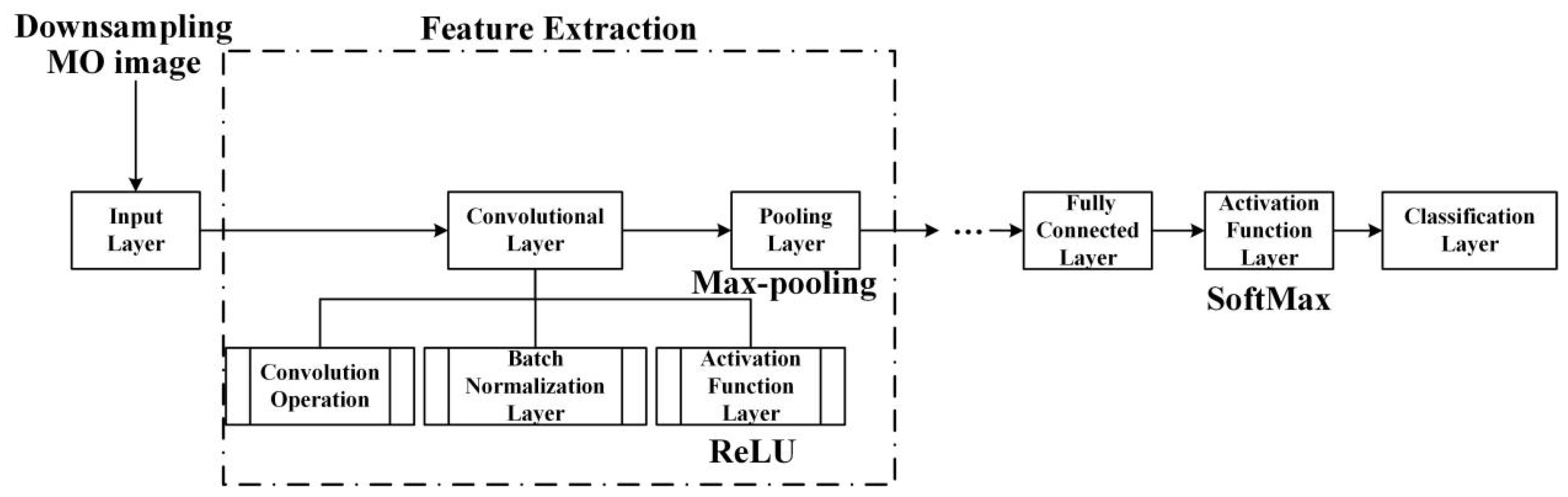
4.1. The Architecture of CNN
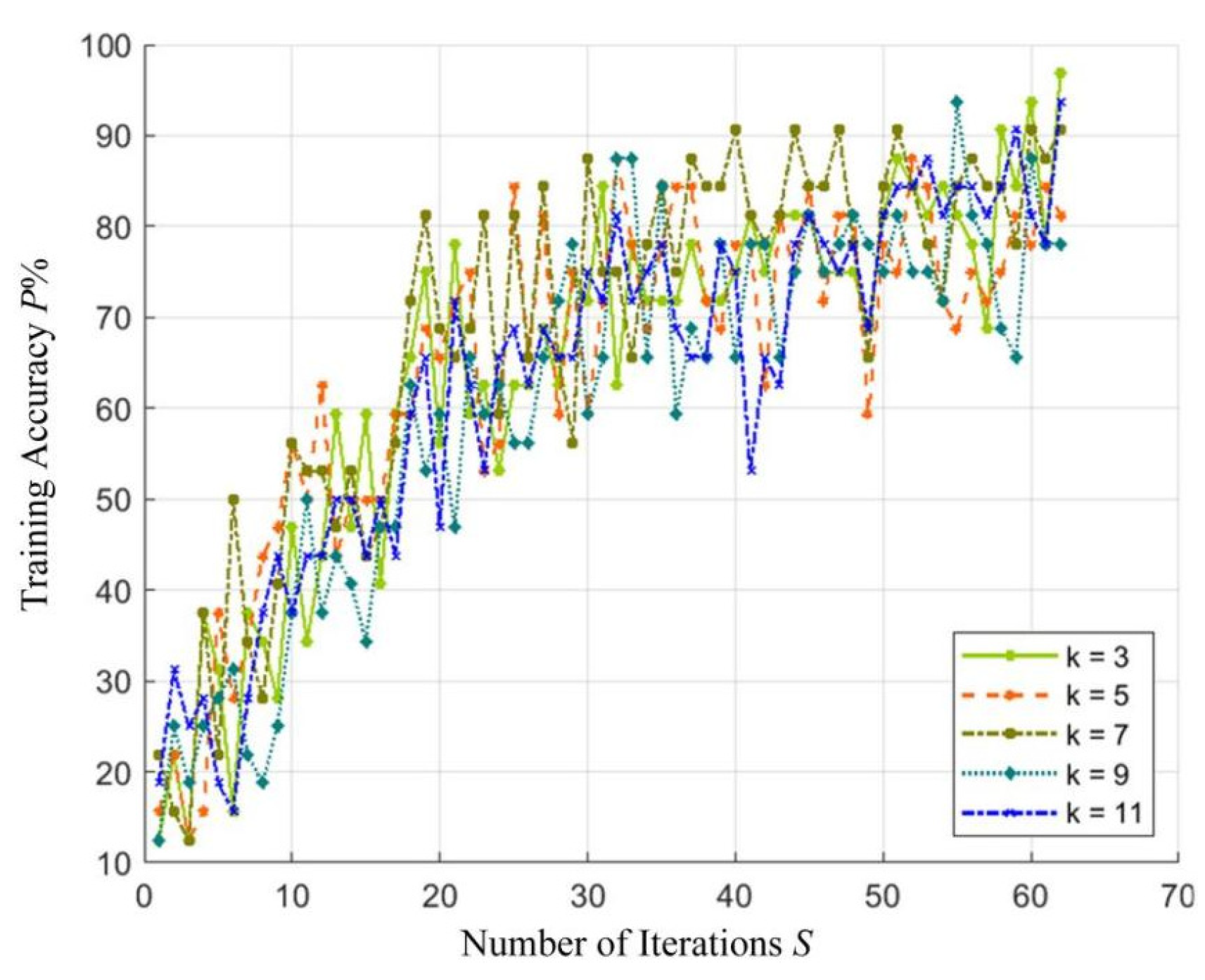
4.2. Parameter Evaluation of CNN Models
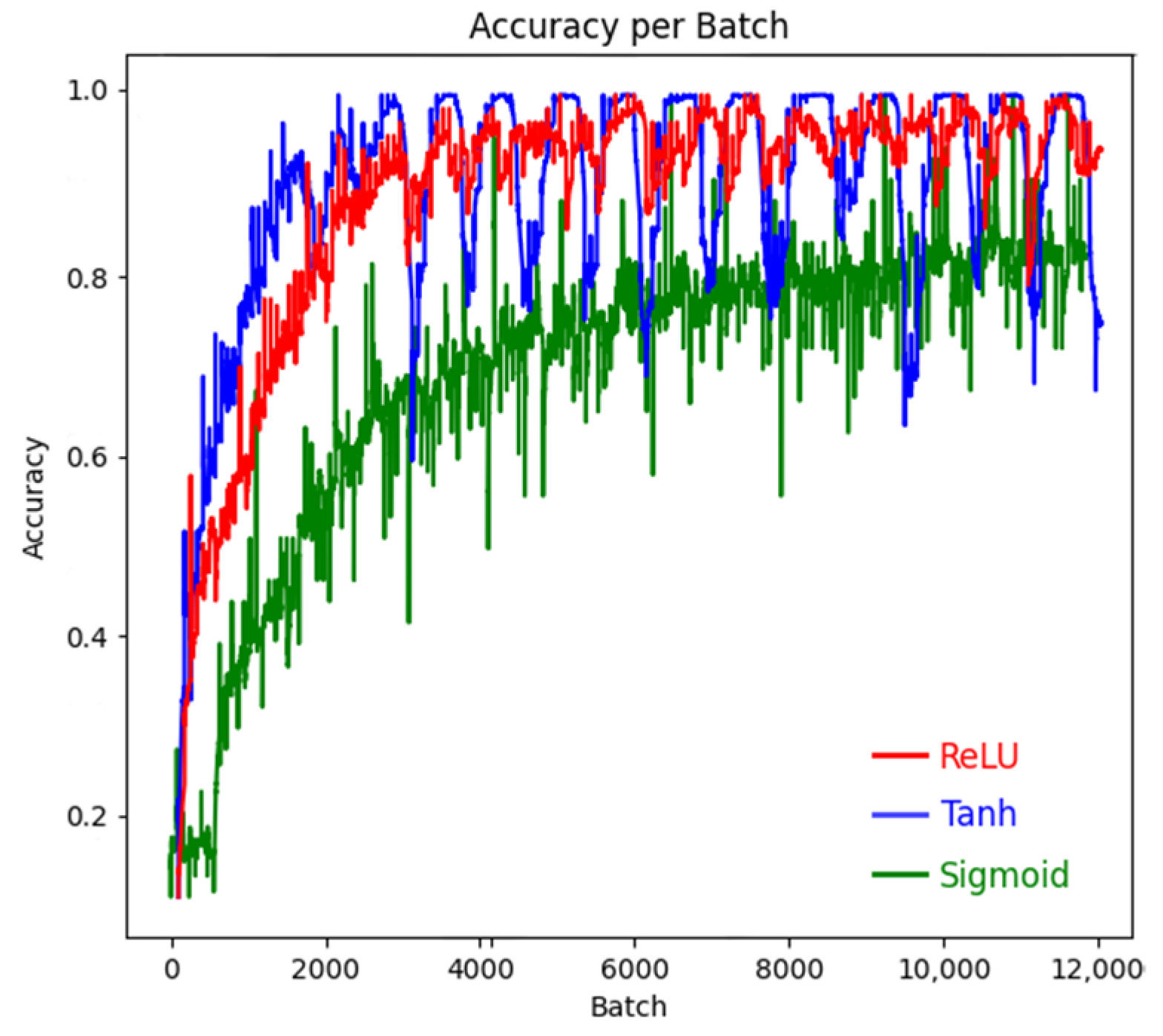
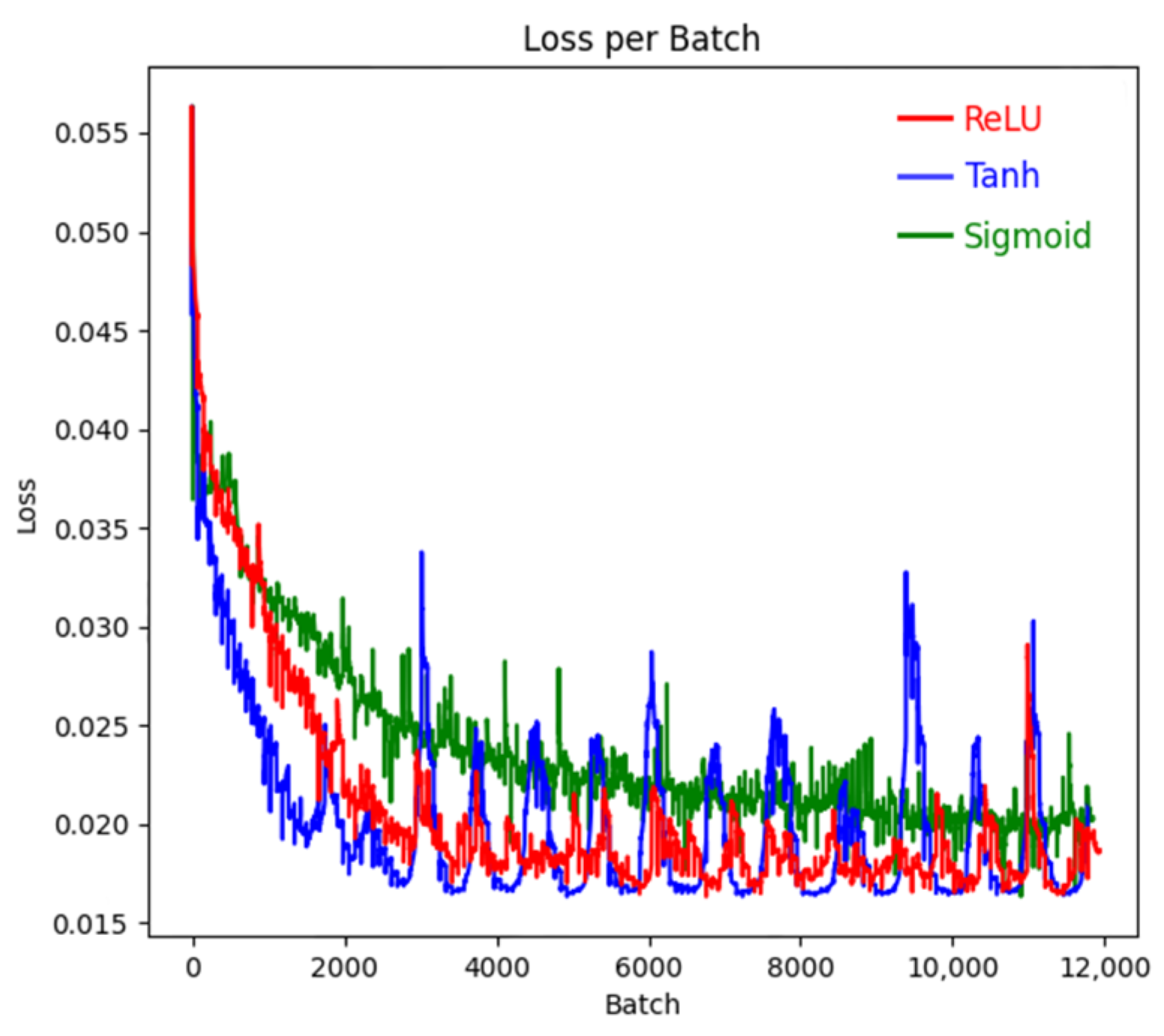
4.3. Classification by the CNN Model
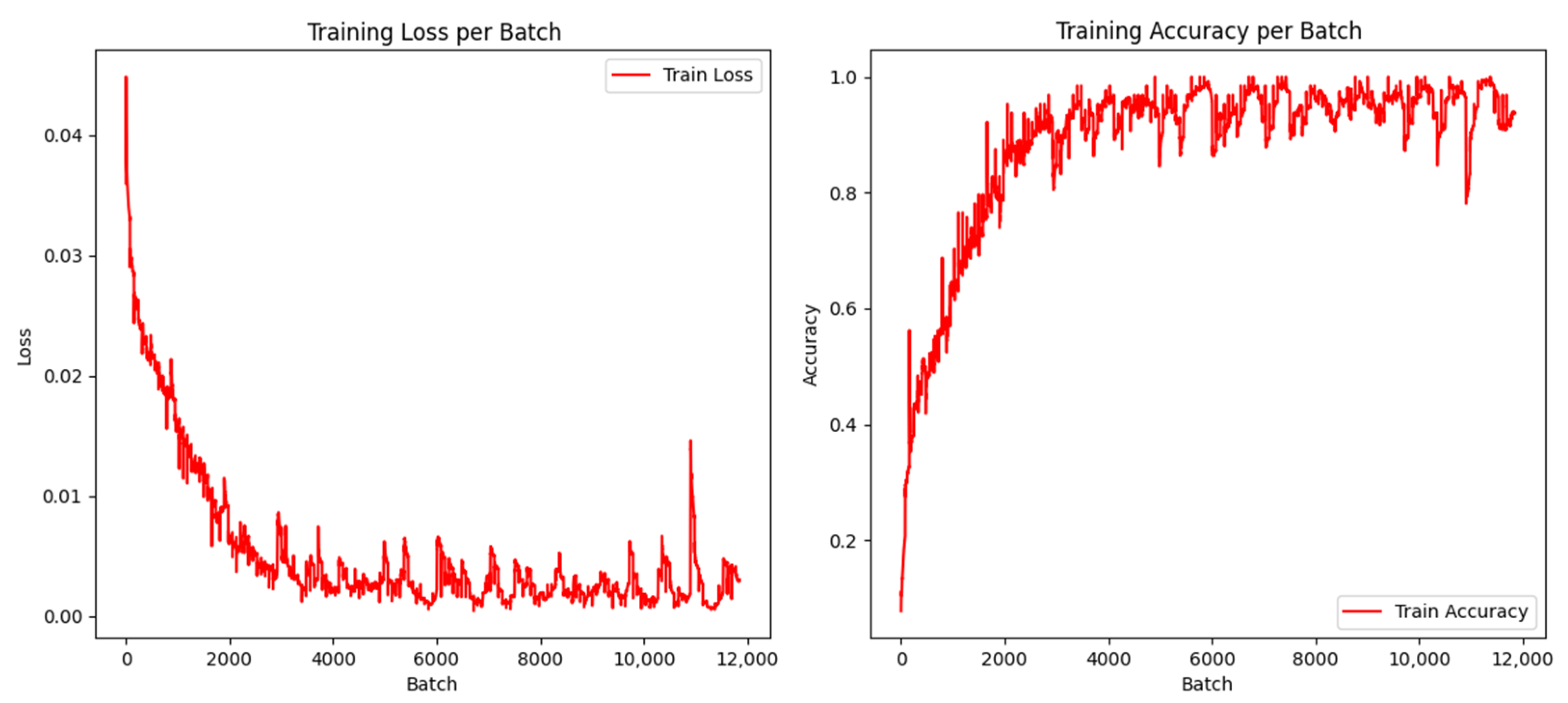
4.4. Classification by ResNet50 Model
4.5. Experimental Analysis
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, X.; Wang, Y.; Chen, Z.; Ma, B.; Zhang, Y. Analysis of welding process stability and weld quality by droplet transfer and explosion in MAG-laser hybrid welding process. J. Manuf. Process. 2018, 32, 522–529. [Google Scholar] [CrossRef]
- Gao, X.; Wen, Q.; Katayama, S. Analysis of high-power disk laser welding stability based on classification of plume and spatter characteristics. Trans. Nonferrous Met. Soc. China 2013, 23, 3748–3757. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; You, D.; Zhang, N. Data-driven detection of laser welding defects based on real-time spectrometer signals. IEEE Sens. J. 2019, 19, 9364–9373. [Google Scholar] [CrossRef]
- Wang, L.; Mohammadpour, M.; Yang, B.; Gao, X.; Lavoie, J.P.; Kleine, K.; Kovacevic, R. Monitoring of keyhole entrance and molten pool with quality analysis during adjustable ring mode laser welding. Appl. Opt. 2020, 59, 1576–1584. [Google Scholar] [CrossRef] [PubMed]
- Hawwat, S.; Shah, J.; Wang, H. Machine learning supported ultrasonic testing for characterization of cracks in polyethylene pipes. Measurement 2025, 240, 115609. [Google Scholar] [CrossRef]
- Chen, L.; Li, B.; Zhang, L.; Shang, Z. 3D positioning of defects for gas turbine blades based on digital radiographic projective imaging. NDT E Int. 2023, 133, 102751. [Google Scholar] [CrossRef]
- Gao, X.; Mo, L.; Xiao, Z.; Chen, X.; Katayama, S. Seam tracking based on Kalman filtering of micro-gap weld using magneto-optical image. Int. J. Adv. Manuf. Technol. 2016, 83, 21–32. [Google Scholar] [CrossRef]
- Gao, X.; Chen, Y.; You, D.; Xiao, Z.; Chen, X. Detection of micro gap weld joint by using magneto-optical imaging and Kalman filtering compensated with RBF neural network. Mech. Syst. Signal Process. 2017, 84, 570–583. [Google Scholar] [CrossRef]
- Gao, X.; Du, L.; Ma, N.; Zhou, X. Magneto-optical imaging characteristics of weld defects under alternating and rotating magnetic field excitation. Opt. Laser Technol. 2019, 112, 188–197. [Google Scholar] [CrossRef]
- Arakelyan, S.; Galstyan, O.; Lee, H.; Babajanyan, A.; Lee, J.H.; Friedman, B.; Lee, K. Direct current imaging using a magneto-optical sensor. Sens. Actuators A Phys. 2016, 238, 397–401. [Google Scholar] [CrossRef]
- Cacciola, M.; Megali, G.; Pellicano, D. Heuristic enhancement of magneto-optical images for NDE. EURASIP J. Adv. Signal Process. 2010, 2010, 44–55. [Google Scholar] [CrossRef]
- Li, Y.; Gao, X.; Zhang, Y.; You, D.; Zhang, N.; Wang, C.; Wang, C. Detection model of invisible weld defects by magneto-optical imaging at rotating magnetic field directions. Opt. Laser Technol. 2020, 121, 105772. [Google Scholar] [CrossRef]
- Gao, X.; Ma, N.; Du, L. Magneto-optical imaging characteristics of weld defects under alternating magnetic field excitation. Opt. Express 2018, 26, 9972–9983. [Google Scholar] [CrossRef] [PubMed]
- Su, G.; Qin, Y.; Xu, H.; Liang, J. Automatic real-time crack detection using lightweight deep learning models. Eng. Appl. Artif. Intell. 2024, 138, 109340. [Google Scholar] [CrossRef]
- Zhao, B.; Zhou, X.; Yang, G.; Wen, J.; Zhang, J.; Dou, J.; Li, G.; Chen, X.; Chen, B. High-resolution infrastructure defect detection dataset sourced by unmanned systems and validated with deep learning. Autom. Constr. 2024, 163, 105405. [Google Scholar] [CrossRef]
- Yu, H.; Deng, Y.; Guo, F. Real-time pavement surface crack detection based on lightweight semantic segmentation model. Transp. Geotech. 2024, 48, 101335. [Google Scholar] [CrossRef]
- Jin, G.S.; Oh, S.J.; Lee, Y.S.; Shin, S.C. Extracting weld bead shapes from radiographic testing images with U-Net. Appl. Sci. 2021, 11, 12051. [Google Scholar] [CrossRef]
- Golodov, V.A.; Maltseva, A.A. Approach to weld segmentation and defect classification in radiographic images of pipe welds. NDT E Int. 2022, 127, 102597. [Google Scholar] [CrossRef]
- Zapata, J.; Vilar, R.; Ruiz, R. Automatic inspection system of welding radiographic images based on ANN under a regularisation process. J. Nondestruct. Eval. 2012, 31, 34–45. [Google Scholar] [CrossRef]
- Malarvel, M.; Singh, H. An autonomous technique for weld defects detection and classification using multi-class support vector machine in X-radiography image. Optik 2021, 231, 166342. [Google Scholar] [CrossRef]
- Shen, Q.; Gao, J.; Li, C. Automatic classification of weld defects in radiographic image. Insight Non-Destr. Test. Cond. Monit. 2010, 52, 134–139. [Google Scholar] [CrossRef]
- Kumaresan, S.; Jai Aultrin, K.S.; Kumar, S.S.; Anand, M.D. Transfer learning with CNN for classification of weld defect. IEEE Access 2021, 9, 95097–95108. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Liu, Y.; Wang, P.; Lu, R.; Gooi, H.B. Deep learning based densely connected network for load Forecasting. IEEE Trans. Power Syst. 2021, 36, 2829–2840. [Google Scholar] [CrossRef]
- Singh, A.; Bruzzone, L. Mono- and Dual-Regulated Contractive-Expansive-Contractive deep convolutional networks for classification of Multispectral Remote sensing images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5513605. [Google Scholar] [CrossRef]
- Mohanasundari, L. Performance analysis of weld image classification using modified Resnet CNN architecture. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 2260–2266. [Google Scholar]
- Chinta, B.; Moorthi, M. EEG-dependent automatic speech recognition using deep residual encoder based VGG net CNN. Comput. Speech Lang. 2023, 79, 101477. [Google Scholar] [CrossRef]
- Slama, A.; Sahli, H.; Amri, Y.; Trabelsi, H. Res-Net-VGG19: Improved tumor segmentation using MR images based on Res-Net architecture and efficient VGG gliomas grading. Appl. Eng. Sci. 2023, 16, 100153. [Google Scholar] [CrossRef]
- Palma-Ramírez, D.; Ross-Veitía, B.D.; Font-Ariosa, P.; Espinel-Hernández, A.; Sanchez-Roca, A.; Carvajal-Fals, H.; Hernández-Herrera, H. Deep convolutional neural network for weld defect classification in radiographic images. Heliyon 2024, 10, e30590. [Google Scholar] [CrossRef]
- Yang, D.; Jiang, H.; Ai, S.; Yang, T.; Zhi, Z.; Jing, D.; Gao, J.; Yue, K.; Cheng, H.; Xu, Y. Detection method for weld defects in time-of-flight diffraction images based on multi-image fusion and feature hybrid enhancement. Eng. Appl. Artif. Intell. 2024, 138, 109442. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, K.; Pan, K.; Huang, W. Image defect classification of surface mount technology welding based on the improved ResNet model. J. Eng. Res. 2024, 12, 154–162. [Google Scholar] [CrossRef]
- Zhao, D.; Cai, W.; Cui, L. Adaptive thresholding and coordinate attention-based tree-inspired network for aero-engine bearing health monitoring under strong noise. Adv. Eng. Inform. 2024, 61, 102559. [Google Scholar] [CrossRef]
- Zhao, D.; Shao, D.; Cui, L. CTNet: A data-driven time-frequency technique for wind turbines fault diagnosis under time-varying speeds. ISA Trans. 2024, 154, 335–351. [Google Scholar] [CrossRef] [PubMed]
- Chandni; Sachdeva, M.; Kushwaha, A.K.S. Effective Brain Tumor Image Classification using Deep Learning. Natl. Acad. Sci. Lett. 2024, 47, 257–260. [Google Scholar] [CrossRef]
- He, X.; Wang, T.; Wu, K.; Liu, H. Automatic defects detection and classification of low carbon steel WAAM products using improved remanence/magneto-optical imaging and cost-sensitive convolutional neural network. Measurement 2020, 173, 108633. [Google Scholar] [CrossRef]
- Li, Y.; Gao, X.; Liu, J.; Zhang, Y.; Qu, M. Detection and classification of invisible weld defects by magneto-optical imaging under alternating magnetic field excitation. Sens. Actuators A Phys. 2024, 374, 115507. [Google Scholar] [CrossRef]
- Liu, Q.; Ye, G.; Gao, X.; Zhang, Y.; Gao, P.P. Magneto-optical imaging nondestructive testing of welding defects based on image fusion. NDT E Int. Indep. Nondestruct. Test. Eval. 2023, 138, 102887. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Wu, B.; Li, P.; Han, Z.; Zhang, C.; Liu, X. A novel sensor based on the composite mechanism of magnetic flux leakage and magnetic field disturbance for comprehensive inspection of defects with varying angles and width. NDT E Int. 2024, 145, 103131. [Google Scholar] [CrossRef]
- Vandendriessche, S.; Valev, V.K.; Verbiest, T. Faraday rotation and its dispersion in the visible region for saturated organic liquids. Phys. Chem. Chem. Phys. 2012, 14, 1860–1864. [Google Scholar] [CrossRef]
- Cheng, Y.; Deng, Y.; Bai, L.; Chen, K. Enhanced laser-based magneto-optic imaging system for nondestructive evaluation applications. IEEE Trans. Instrum. Meas. 2013, 62, 1192–1198. [Google Scholar] [CrossRef]
- Pradhan, K.; Patra, S. A semantic edge-aware parameter efficient image filtering technique. Comput. Graph. 2024, 124, 104068. [Google Scholar] [CrossRef]
- Zhang, C.; Gai, K.; Zhang, S. Matrix normal PCA for interpretable dimension reduction and graphical noise modeling. Pattern Recognit. 2024, 154, 110591. [Google Scholar] [CrossRef]
- Bisheh, H.; Amiri, G. Structural damage detection based on variational mode decomposition and kernel PCA-based support vector machine. Eng. Struct. 2023, 278, 115565. [Google Scholar] [CrossRef]
- Hu, D.; Liu, H.; Zhu, Y.; Sun, J.; Zhang, Z.; Yang, L.; Liu, Q.; Yang, B. Demand response-oriented virtual power plant evaluation based on AdaBoost and BP neural network. Energy Rep. 2023, 9, 922–931. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, J.; Shen, J.; Hu, Y.; Chen, S. A new DEM calibration method for wet and stick materials based on the BP neural network. Powder Technol. 2024, 448, 120228. [Google Scholar] [CrossRef]
- Hayati, R.; Munawar, A.A.; Lukitaningsih, E.; Earlia, N.; Karma, T. Combination of PCA with LDA and SVM classifiers: A model for determining the geographical origin of coconut in the coastal plantation. Aceh Prov. Indones. Case Stud. Chem. Environ. Eng. 2024, 9, 100552. [Google Scholar] [CrossRef]
- Zhang, G.; Carrasco, C.; Winsler, K.; Bahle, B.; Cong, F.; Luck, S. Assessing the effectiveness of spatial PCA on SVM-based decoding of EEG data. Neuro Image 2024, 293, 120625. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wu, J.; Shi, E.; Yu, S.; Gao, Y.; Li, L.C.; Kuo, L.R.; Pomeroy, M.J.; Liang, Z.J. MM-GLCM-CNN: A multi-scale and multi-level based GLCM-CNN for polyp classification. Comput. Med. Imaging Graph. 2023, 108, 102257. [Google Scholar] [CrossRef]
- Wang, J.J.; Sharma, A.K.; Liu, S.H.; Zhang, H.; Chen, W.; Lee, T.L. Prediction of vascular access stenosis by lightweight convolutional neural network using blood flow sound signals. Sensors 2024, 24, 5922. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, L.; Xu, C.; Chen, X.; Cui, Z. An attribution graph-based interpretable method for CNNs. Neural Netw. 2024, 179, 106597. [Google Scholar] [CrossRef]
- Mohajelin, F.; Sheykhivand, S.; Shabani, A.; Danishvar, M.; Danishvar, S.; Lahijan, L.Z. Automatic recognition of multiple emotional classes from EEG signals through the use of graph theory and convolutional neural networks. Sensors 2024, 24, 5883. [Google Scholar] [CrossRef]
- Xie, G.; Wang, L.; Williams, R.A.; Li, Y.; Zhang, P.; Gu, S. Segmentation of wood CT images for internal defects detection based on CNN: A comparative study. Comput. Electron. Agric. 2024, 224, 109244. [Google Scholar] [CrossRef]
- Vrbancic, G.; Podgorelec, V. Efficient ensemble for image-based identification of Pneumonia utilizing deep CNN and SGD with warm restarts. Expert Syst. Appl. 2022, 187, 115834. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.; Xu, J.; Zhao, Y.; Zhou, Y. Intelligent damage classification for tensile membrane structure based on continuous wavelet transform and improved ResNet50. Measurement 2024, 227, 114260. [Google Scholar] [CrossRef]
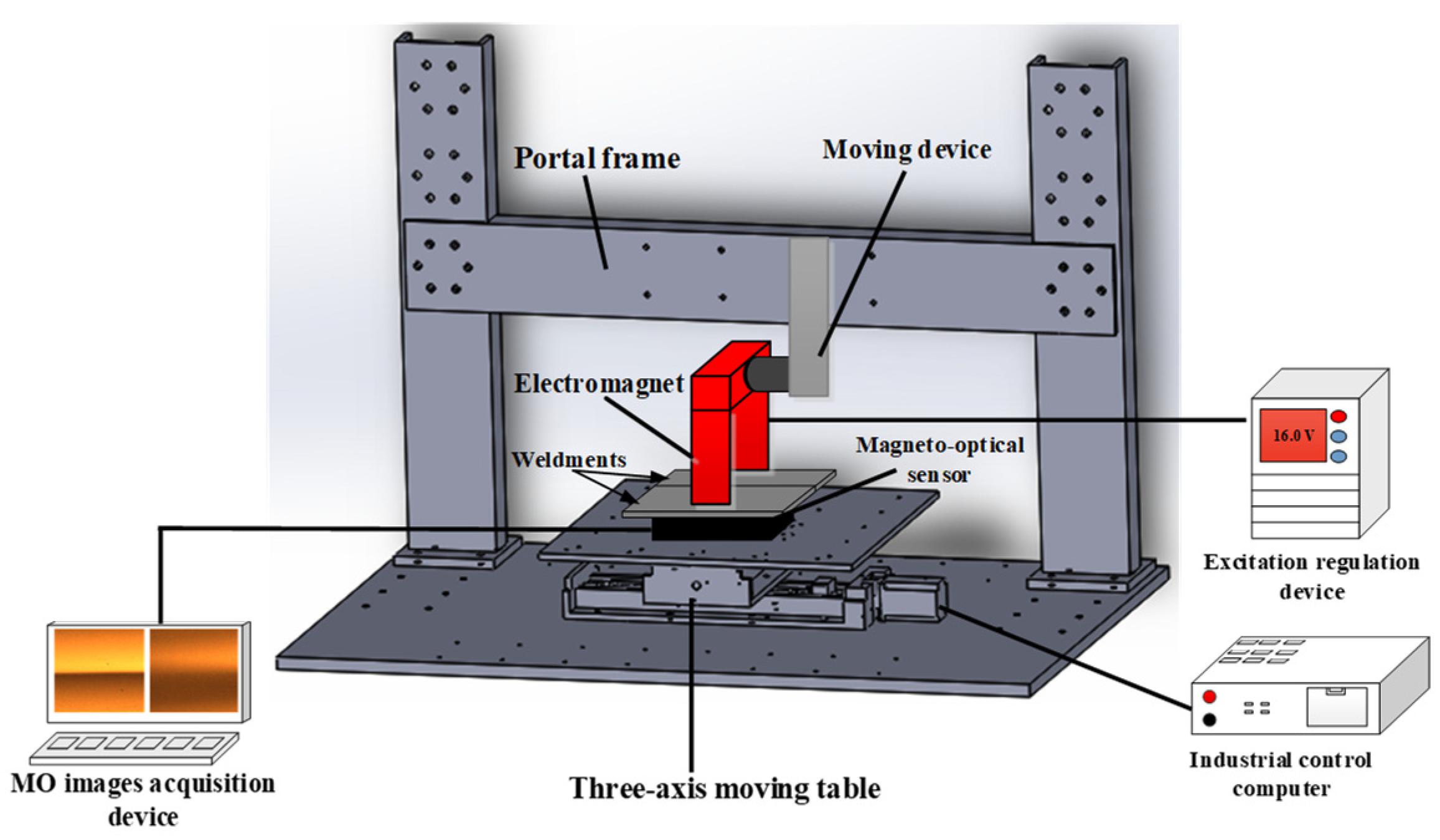

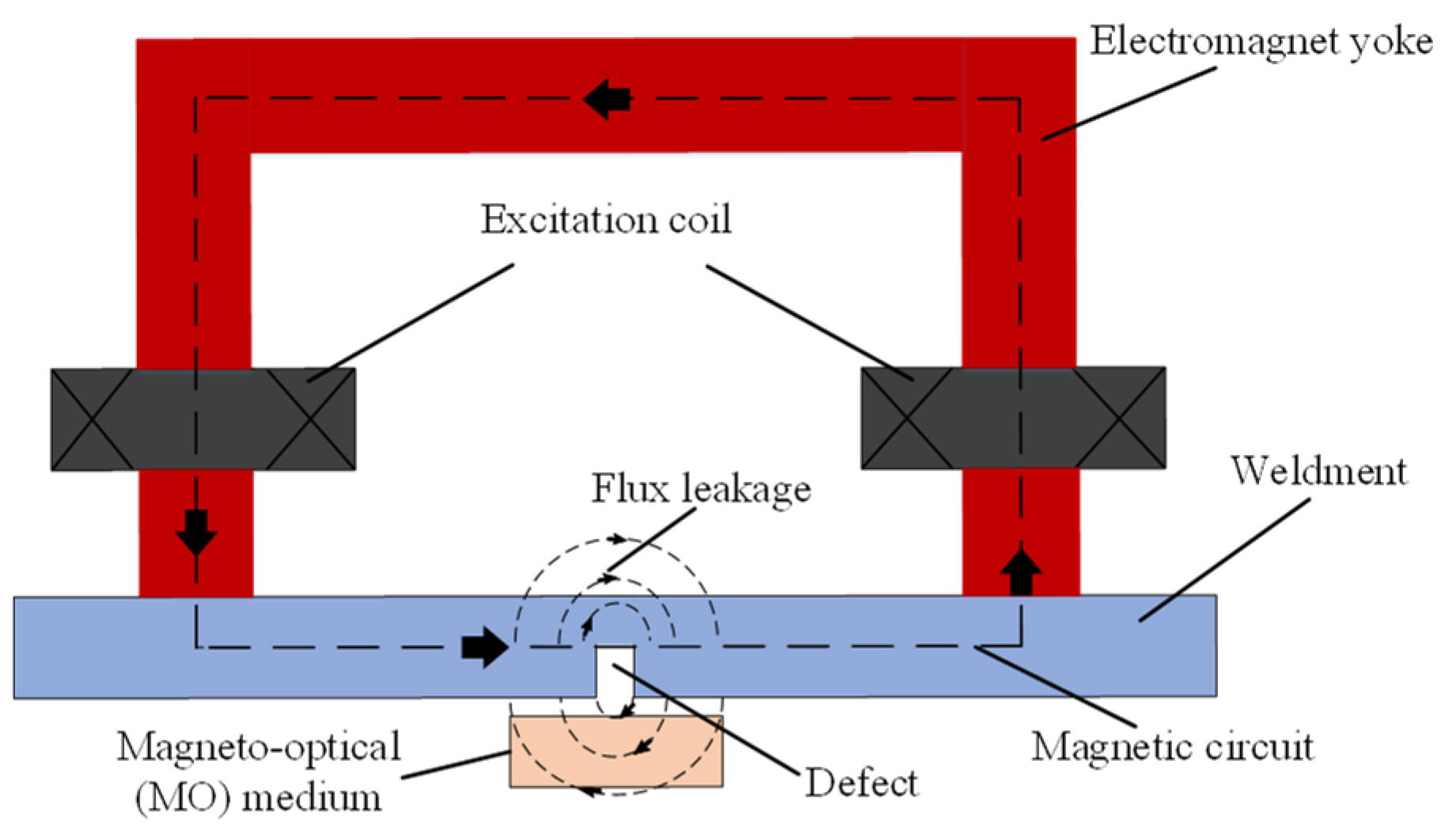










| Light Source Wavelength | Sampling Frequency | Maximum Resolution | Pixel Equivalent | Magnetic Field Range |
|---|---|---|---|---|
| 590 nm | [8, 100] fps | 2592 × 1944 pixel2 | 102 pixel/mm | [−2, 2] kA/m |
| Type | Filtering Result | MSE | PSNR (dB) | SSIM | Filtering Time (s) |
|---|---|---|---|---|---|
| Gaussian filtering |  | 0.39 | 52.18 | 0.9956 | 0.1009 |
| Bilateral filtering |  | 2.74 | 43.75 | 0.9656 | 0.8810 |
| Median filtering |  | 3.10 | 43.22 | 0.9684 | 0.0154 |
| Defects | Frame 1 | Frame 2 | Frame 3 |
|---|---|---|---|
| Pit |  | ||
| Crack | |||
| Lack of penetration | |||
| Gas pore | |||
| No defects | |||
| Defect Types | Number of Images | Train Samples | Test Samples | Recognition Result | Classification Accuracy/% |
|---|---|---|---|---|---|
| Crack | 250 | 200 | 50 | 48 | 96 |
| Pit | 250 | 200 | 50 | 46 | 92 |
| Lack of penetration | 250 | 200 | 50 | 45 | 90 |
| Gas pore | 250 | 200 | 50 | 39 | 78 |
| No defects | 250 | 200 | 50 | 49 | 98 |
| Total | 1250 | 1000 | 250 | 227 | 90.8 |
| Defect types | Number of Images | Train Samples | Test Samples | Recognition Result | Classification Accuracy/% |
|---|---|---|---|---|---|
| Crack | 250 | 200 | 50 | 43 | 86 |
| Pit | 250 | 200 | 50 | 46 | 92 |
| Lack of penetration | 250 | 200 | 50 | 47 | 94 |
| Gas pore | 250 | 200 | 50 | 44 | 88 |
| No defects | 250 | 200 | 50 | 49 | 98 |
| Total | 1250 | 1000 | 250 | 229 | 91.6 |
| Convolution Kernel Size | Accuracy Standard Deviation | Loss Value Standard Deviation | Training Set Accuracy % |
|---|---|---|---|
| 3 × 3 | 0.073 | 0.207 | 93.2 |
| 5 × 5 | 0.073 | 0.160 | 96.4 |
| 7 × 7 | 0.067 | 0.175 | 97.2 |
| 9 × 9 | 0.082 | 0.216 | 92.8 |
| 11 × 11 | 0.084 | 0.170 | 97.6 |
| Batch Size | Initial Learning Rate | Learning Rate Decay Factor | Number of Learning Rate Decay Steps | Number of Iterations |
|---|---|---|---|---|
| 32 | 0.0002 | 0.1 | 1 | 62 |
| Deep Learning Framework | CPU | RAM | GPU | Operating Environment | Programming Language |
|---|---|---|---|---|---|
| Pytorch2.1.1 | Intel(R)Core (TM)i7-10875 H | 16 GB | NVIDIA GeForceRTX 2060 | Anaconda 3 | Python3.11.5 |
| Layers | Types | Input Size | Filter Size | Number of Filters | Stride | Weights | Biases |
|---|---|---|---|---|---|---|---|
| I0 | Input Layer | 50 × 50 × 3 | — | — | — | — | — |
| C1 | Convolution Layer 1 | 50 × 50 × 3 | 7 × 7 × 3 | 32 | 1 | 7 × 7 × 3 × 32 | 1 × 1 × 32 |
| P2 | Pooling Layer 1 | 50 × 50 × 32 | 2 × 2 | — | 2 | — | — |
| C3 | Convolution Layer 2 | 25 × 25 × 32 | 3 × 3 × 32 | 64 | 1 | 3 × 3 × 32 × 64 | 1 × 1 × 64 |
| P4 | Pooling Layer 2 | 25 × 25 × 64 | 2 × 2 | — | 2 | — | — |
| C5 | Convolution Layer 3 | 12 × 12 × 64 | 3 × 3 × 64 | 128 | 1 | 3 × 3 × 64 × 128 | 1 × 1 × 128 |
| P6 | Pooling Layer 3 | 12 × 12 × 128 | 2 × 2 | — | 2 | — | — |
| C7 | Convolution Layer 4 | 6 × 6 × 128 | 3 × 3 × 128 | 256 | 1 | 3 × 3 × 128 × 256 | 1 × 1 × 256 |
| P8 | Pooling Layer 4 | 6 × 6 × 256 | 2 × 2 | — | 2 | — | — |
| C9 | Convolution Layer 5 | 3 × 3 × 256 | 3 × 3 × 256 | 512 | 1 | 3 × 3 × 256 × 512 | 1 × 1 × 512 |
| P10 | Pooling Layer 5 | 3 × 3 × 512 | 2 × 2 | — | 2 | — | — |
| F11 | Fully Connected Layer | 1 × 1 × 512 | — | — | — | 5 × 512 | 5 × 1 |
| S12 | Classification Layer | 1 × 1 × 5 | — | — | — | — | — |
| Defect Types | Number of Images | Train Samples | Valid Samples | Test Samples | Recognition Result | Classification Accuracy/% |
|---|---|---|---|---|---|---|
| Crack | 1000 | 800 | 100 | 100 | 97 | 97 |
| Pit | 1000 | 800 | 100 | 100 | 97 | 97 |
| Lack of penetration | 1000 | 800 | 100 | 100 | 100 | 100 |
| Gas pore | 1000 | 800 | 100 | 100 | 94 | 94 |
| No defects | 1000 | 800 | 100 | 100 | 98 | 98 |
| Total | 5000 | 4000 | 500 | 500 | 486 | 97.2 |
| Defect Types | Number of Images | Train Samples | Valid Samples | Test Samples | Recognition Result | Classification Accuracy/% |
|---|---|---|---|---|---|---|
| Crack | 1000 | 800 | 100 | 100 | 99 | 99 |
| Pit | 1000 | 800 | 100 | 100 | 98 | 98 |
| Lack of penetration | 1000 | 800 | 100 | 100 | 100 | 100 |
| Gas pore | 1000 | 800 | 100 | 100 | 98 | 98 |
| No defects | 1000 | 800 | 100 | 100 | 100 | 100 |
| Total | 5000 | 4000 | 500 | 500 | 495 | 99 |
| Methods | Params | FLOPS | Classification Accuracy/% | Complexity |
|---|---|---|---|---|
| PCA-BP | 6.12 × 103 | 6.17 × 103 | 90.8 | Low |
| PCA-SVM | 3.01 × 105 | 1.5 × 107 | 91.6 | Intermediate |
| CNN | 1.94 × 106 | 3.76 × 109 | 97.2 | High |
| ResNet50 | 2.35 × 107 | 1.34 × 1010 | 99 | Highest |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Gao, P.; Luo, Y.; Luo, X.; Xu, C.; Chen, J.; Zhang, Y.; Lin, G.; Xu, W. Automatic Detection and Classification of Natural Weld Defects Using Alternating Magneto-Optical Imaging and ResNet50. Sensors 2024, 24, 7649. https://doi.org/10.3390/s24237649
Li Y, Gao P, Luo Y, Luo X, Xu C, Chen J, Zhang Y, Lin G, Xu W. Automatic Detection and Classification of Natural Weld Defects Using Alternating Magneto-Optical Imaging and ResNet50. Sensors. 2024; 24(23):7649. https://doi.org/10.3390/s24237649
Chicago/Turabian StyleLi, Yanfeng, Pengyu Gao, Yongbiao Luo, Xianghan Luo, Chunmei Xu, Jiecheng Chen, Yanxi Zhang, Genxiang Lin, and Wei Xu. 2024. "Automatic Detection and Classification of Natural Weld Defects Using Alternating Magneto-Optical Imaging and ResNet50" Sensors 24, no. 23: 7649. https://doi.org/10.3390/s24237649
APA StyleLi, Y., Gao, P., Luo, Y., Luo, X., Xu, C., Chen, J., Zhang, Y., Lin, G., & Xu, W. (2024). Automatic Detection and Classification of Natural Weld Defects Using Alternating Magneto-Optical Imaging and ResNet50. Sensors, 24(23), 7649. https://doi.org/10.3390/s24237649







