Identification of Intrinsic Friction and Torque Ripple for a Robotic Joint with Integrated Torque Sensors with Application to Wheel-Bearing Characterization
Abstract
1. Introduction
1.1. Related Work
1.2. Wheel-Bearing Inspection
2. Sources of Torque Measurements in a Transmission System
2.1. Intrinsic Dynamics of Robot Actuators
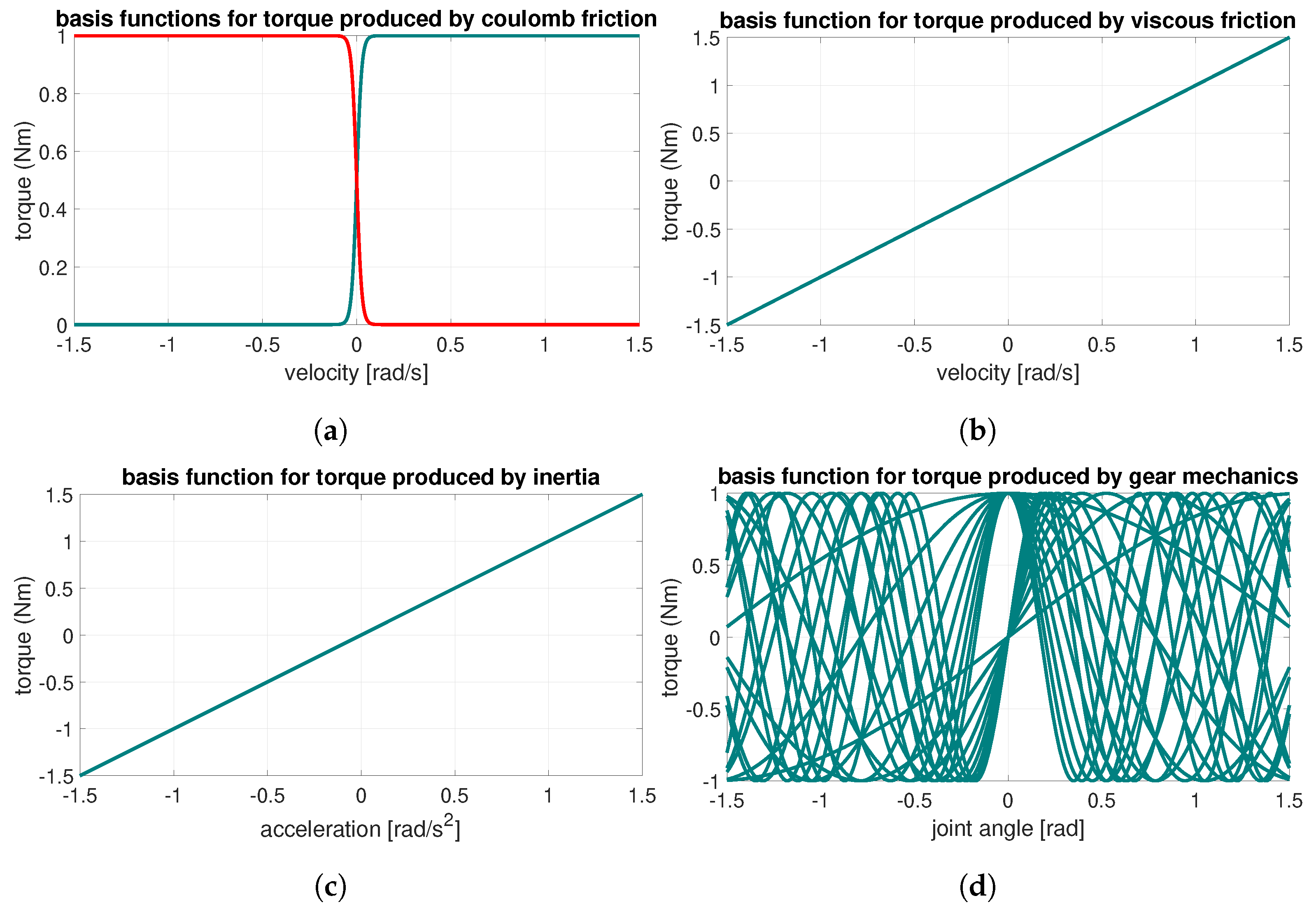
Selection of Basis Functions
- (a)
- Friction
- (b)
- Inertia
- (c)
- Ripple torques from harmonic drive
- (d)
- Torque offset
3. Experimental Validation of Intrinsic Dynamics Compensation
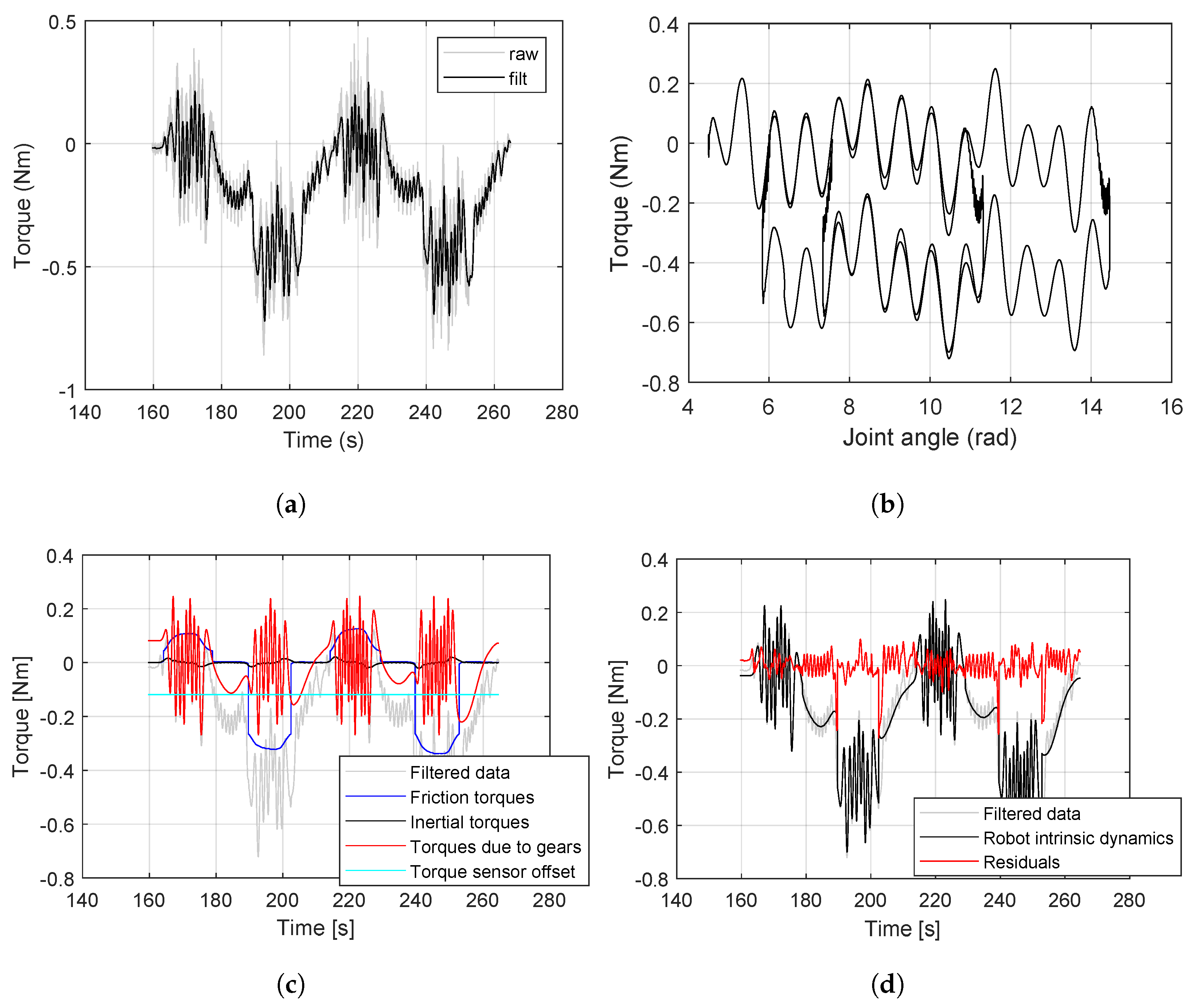
3.1. Experimental Protocol
3.1.1. No-Load Conditions
3.1.2. Measuring Wheel-Bearing Torques
4. Results
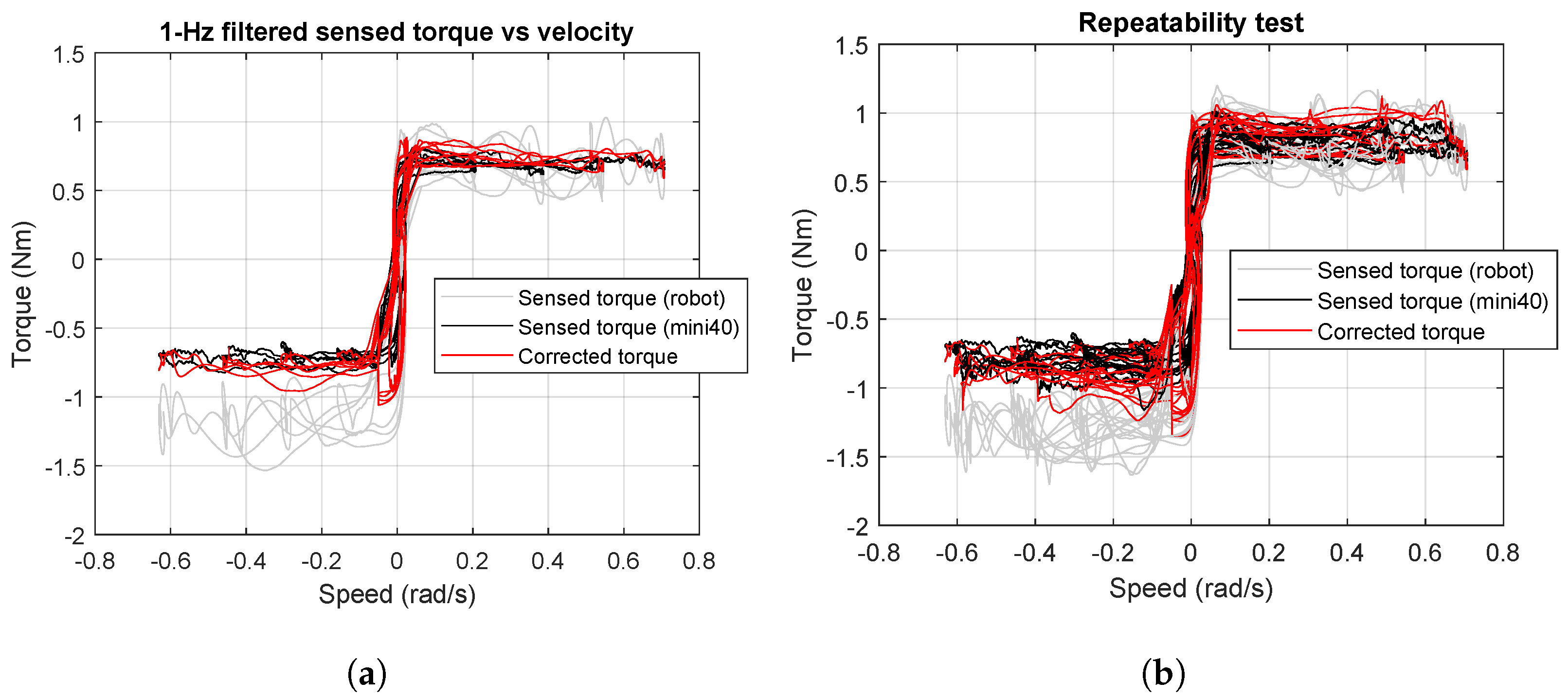
4.1. Validation with External Load Cell
4.2. Repeatability of Proposed Compensation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patil, S.; Vasu, V.; Srinadh, K.V.S. Advances and perspectives in collaborative robotics: A review of key technologies and emerging trends. Discov. Mech. Eng. 2023, 2, 13. [Google Scholar] [CrossRef]
- Keshvarparast, A.; Battini, D.; Battaia, O.; Pirayesh, A. Collaborative robots in manufacturing and assembly systems: Literature review and future research agenda. J. Intell. Manuf. 2024, 35, 2065–2118. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Chow, W.T.; Dhyan, S.B.; Zhang, B.; Han, B.S.; Wong, H.Y.A. Low-Cost Cable-Driven Robot Arm with Low-Inertia Movement and Long-Term Cable Durability. Robotics 2024, 13, 128. [Google Scholar] [CrossRef]
- Briquet-Kerestedjian, N. Impact Detection and Classification for Safe Physical Human-Robot Interaction Under Uncertainties. Ph.D. Thesis, Université Paris Saclay (COmUE), Paris, France, 2019. [Google Scholar]
- Min, J.-K.; Ahn, K.-H.; Park, H.-C.; Song, J.-B. A novel reactive-type joint torque sensor with high torsional stiffness for robot applications. Mechatronics 2019, 63, 102265. [Google Scholar] [CrossRef]
- Pástor, M.; Hagara, M.; Gašpár, Š.; Sapieta, M. Design and Implementation of a Low-Cost Torque Sensor for Manipulators. Appl. Sci. 2023, 13, 9406. [Google Scholar] [CrossRef]
- Li, P.; Nie, Z.; Li, Z.; Liu, X. Optimal Design of the Modular Joint Drive Train for Enhancing Cobot Load Capacity and Dynamic Performance. Chin. J. Mech. Eng. 2024, 37, 57. [Google Scholar] [CrossRef]
- Chen, S.; Luo, M.; He, F. A universal algorithm for sensorless collision detection of robot actuator faults. Adv. Mech. Eng. 2018, 10, 1687814017740710. [Google Scholar] [CrossRef]
- Zhang, X.; Tao, T.; Jiang, G.; Mei, X.; Zou, C. A Refined Dynamic Model of Harmonic Drive and Its Dynamic Response Analysis. Shock Vib. 2020, 2020, 1841724. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, W.; Gao, Y.; Li, Q.; Chen, Z.; Zhao, J. Disturbance Elimination for the Modular Joint Torque Sensor of a Collaborative Robot. Math. Probl. Eng. 2020, 2020, 2405134. [Google Scholar] [CrossRef]
- Taghirad, H.D.; Bélanger, P.R. Torque ripple and misalignment torque compensation for the built-in torque sensor of harmonic drive systems. IEEE Trans. Instrum. Meas. 1998, 47, 309–315. [Google Scholar] [CrossRef]
- Shi, Z.; Li, Y.; Liu, G. Adaptive torque estimation of robot joint with harmonic drive transmission. Mech. Syst. Signal Process. 2017, 96, 1–15. [Google Scholar] [CrossRef]
- Zhang, H.; Ahmad, S.; Liu, G. Torque estimation technique of robotic joint with harmonic drive transmission. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3034–3039. [Google Scholar]
- Zhang, H.; Ahmad, S.; Liu, G.; Member, S. Torque Estimation for Robotic Joint With Harmonic Drive Transmission Based on Position Measurements. IEEE Trans. Robot. 2015, 31, 322–330. [Google Scholar] [CrossRef]
- Yu, F.; Xiao, S.; Zhu, M.; Wang, Z. A novel method to improve the accuracy of torque estimation for robotic joint with harmonic drive transmission. Eng. Lett. 2018, 26, 455–460. [Google Scholar]
- Lessard, J.; Bigras, P.; Liu, Z.; Hazel, B. Characterization, modeling and vibration control of a flexible joint for a robotic system. JVC/J. Vib. Control. 2014, 20, 943–960. [Google Scholar] [CrossRef]
- Fanny, F.; Villani, L.; Siciliano, B. Variable impedance control of redundant manipulators for intuitive human—Robot physical interaction. IEEE Trans. Robot. 2015, 31, 850–863. [Google Scholar]
- Christian, O.; Mukherjee, R.; Nakamura, Y. Unified impedance and admittance control. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 554–561. [Google Scholar]
- Tegoeh, T.; Zhu, K.; Dailey, W.; Burdet, E.; Campolo, D. Multi-source micro-friction identification for a class of cable-driven robots with passive backbone. Mech. Syst. Signal Process. 2016, 80, 152–165. [Google Scholar]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turlapati, S.H.; Nguyen, V.P.; Gurnani, J.; Bin Ariffin, M.Z.; Kana, S.; Yee Wong, A.H.; Han, B.S.; Campolo, D. Identification of Intrinsic Friction and Torque Ripple for a Robotic Joint with Integrated Torque Sensors with Application to Wheel-Bearing Characterization. Sensors 2024, 24, 7465. https://doi.org/10.3390/s24237465
Turlapati SH, Nguyen VP, Gurnani J, Bin Ariffin MZ, Kana S, Yee Wong AH, Han BS, Campolo D. Identification of Intrinsic Friction and Torque Ripple for a Robotic Joint with Integrated Torque Sensors with Application to Wheel-Bearing Characterization. Sensors. 2024; 24(23):7465. https://doi.org/10.3390/s24237465
Chicago/Turabian StyleTurlapati, Sri Harsha, Van Pho Nguyen, Juhi Gurnani, Mohammad Zaidi Bin Ariffin, Sreekanth Kana, Alvin Hong Yee Wong, Boon Siew Han, and Domenico Campolo. 2024. "Identification of Intrinsic Friction and Torque Ripple for a Robotic Joint with Integrated Torque Sensors with Application to Wheel-Bearing Characterization" Sensors 24, no. 23: 7465. https://doi.org/10.3390/s24237465
APA StyleTurlapati, S. H., Nguyen, V. P., Gurnani, J., Bin Ariffin, M. Z., Kana, S., Yee Wong, A. H., Han, B. S., & Campolo, D. (2024). Identification of Intrinsic Friction and Torque Ripple for a Robotic Joint with Integrated Torque Sensors with Application to Wheel-Bearing Characterization. Sensors, 24(23), 7465. https://doi.org/10.3390/s24237465







