Speed of Light in Hollow-Core Photonic Bandgap Fiber Approaching That in Vacuum
Abstract
1. Introduction
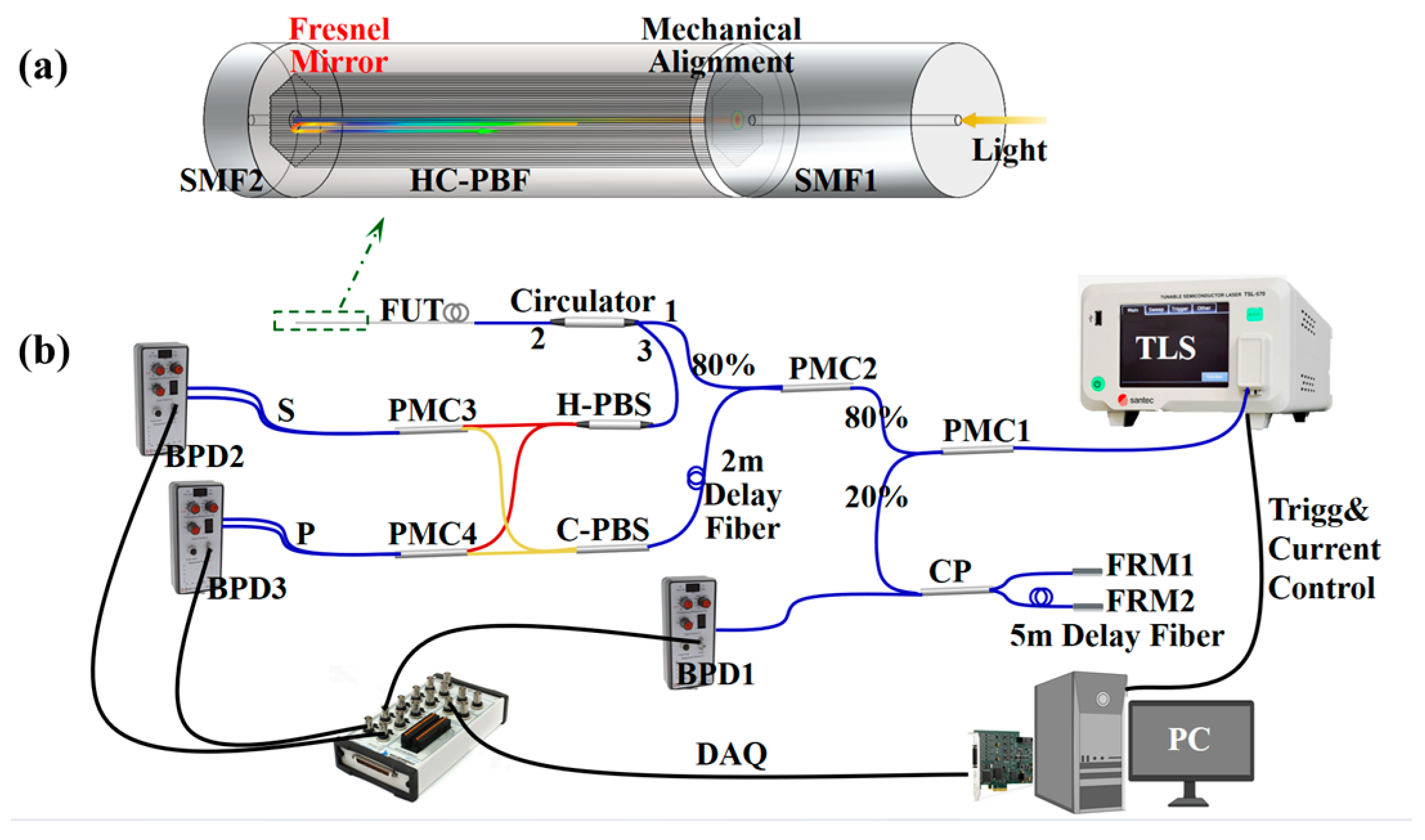
2. Principle and Experimental Setup
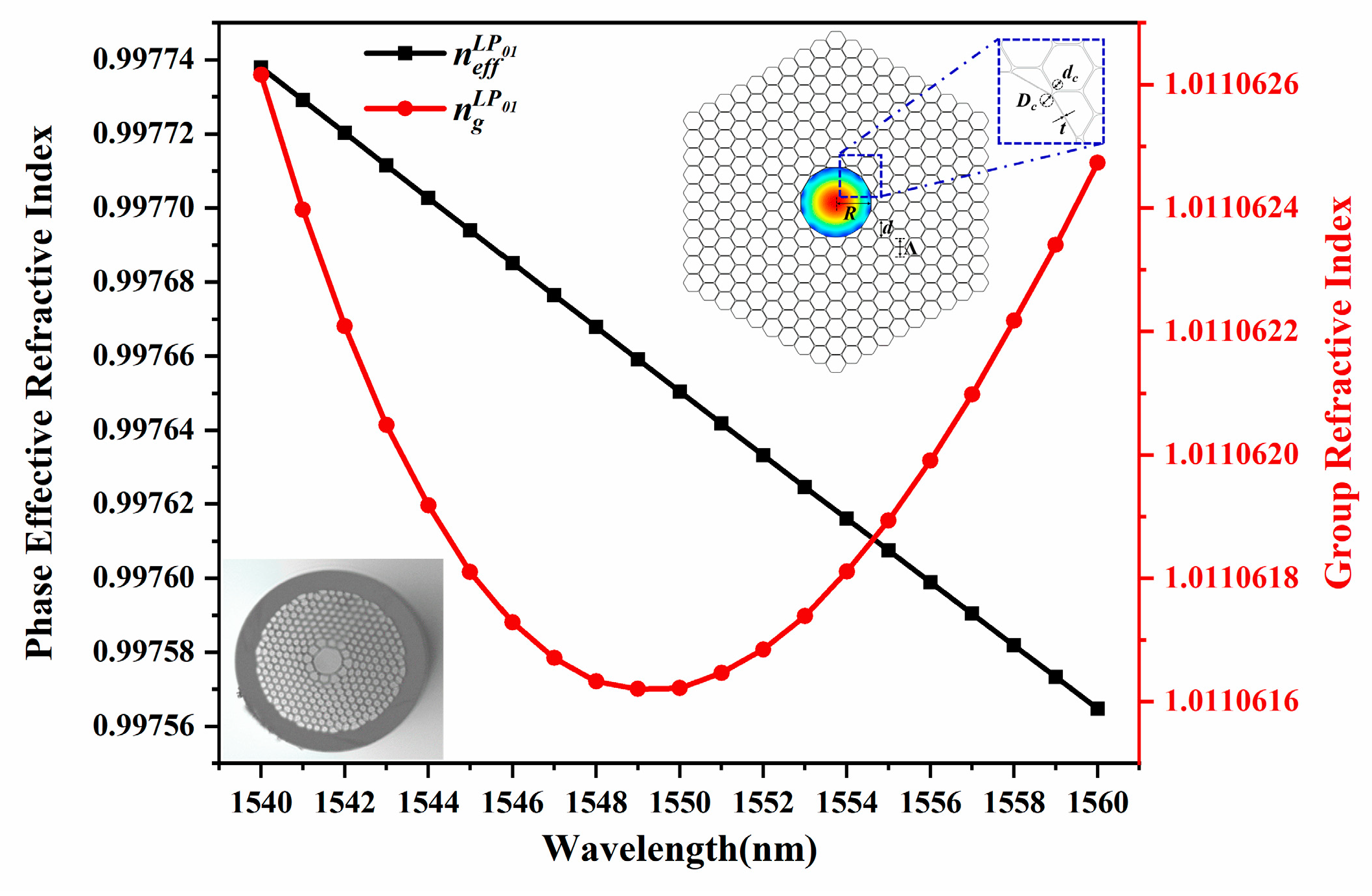
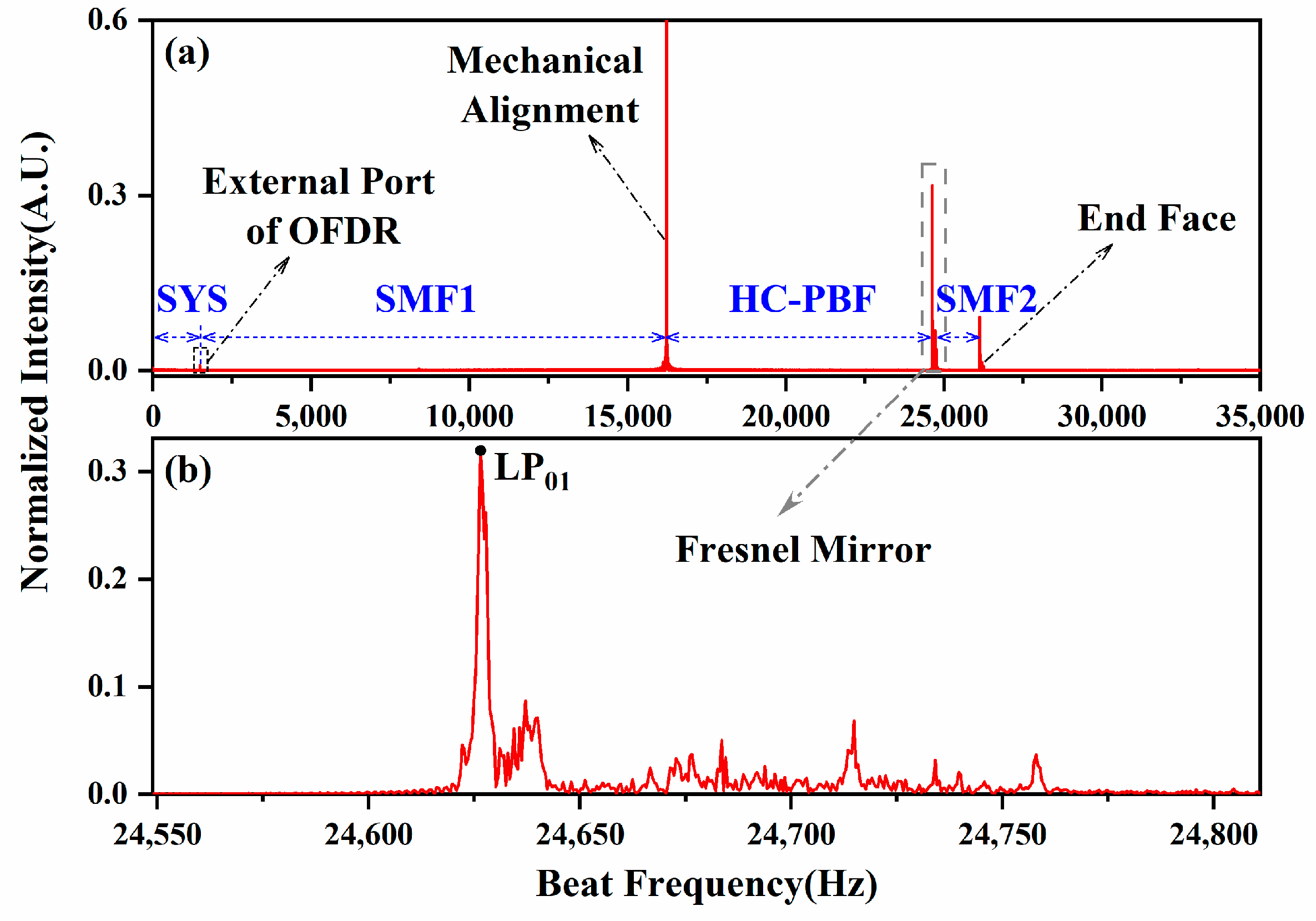
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Feng, Z.; Marpaung, D.; Fokoua, E.N.; Sakr, H.; Hayes, J.R.; Poletti, F.; Richardson, D.J.; Slavík, R. Low-loss microwave photonics links using hollow core fibres. Light. Sci. Appl. 2022, 11, 213. [Google Scholar] [CrossRef] [PubMed]
- Sakr, H.; Chen, Y.; Jasion, G.T.; Bradley, T.D.; Hayes, J.R.; Mulvad, H.C.H.; Davidson, I.A.; Fokoua, E.N.; Poletti, F. Hollow core optical fibres with comparable attenuation to silica fibres between 600 and 1100 nm. Nat. Commun. 2020, 11, 6030. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Wang, Y.; Ding, W.; Hong, Y.; Wang, P. Conquering the Rayleigh Scattering Limit of Silica Glass Fiber at Visible Wavelengths with a Hollow-Core Fiber Approach. Laser Photonics Rev. 2019, 14, 1900241. [Google Scholar] [CrossRef]
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Roberts, P.J.; Allan, D.C. Single-mode photonic band gap guidance of light in air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C. Photonic crystal fibres. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef]
- Poletti, F.; Wheeler, N.V.; Petrovich, M.N.; Baddela, N.; Fokoua, E.N.; Hayes, J.R.; Gray, D.R.; Li, Z.; Slavík, R.; Richardson, D.J. Towards high-capacity fibre-optic communications at the speed of light in vacuum. Nat. Photonics 2013, 7, 279–284. [Google Scholar] [CrossRef]
- Hong, Y.; Bradley, T.D.; Taengnoi, N.; Bottrill, K.R.H.; Hayes, J.R.; Jasion, G.T.; Poletti, F.; Petropoulos, P.; Richardson, D.J. Hollow-Core NANF for High-Speed Short-Reach Transmission in the S + C + L-Bands. J. Light. Technol. 2021, 39, 6167–6174. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Y.; Zhang, Y.; Cheng, T.; Wang, L.; Jiang, H. High-efficiency 6-hole structure anti-resonant hollow-core fiber 2.79 μm Cr, Er:YSGG high-energy pulse laser transmission system. Opt. Laser Technol. 2024, 175, 110743. [Google Scholar] [CrossRef]
- Fokoua, E.N.; Mousavi, S.A.; Jasion, G.T.; Richardson, D.J.; Poletti, F. Loss in hollow-core optical fibers: Mechanisms, scaling rules, and limits. Adv. Opt. Photon. 2023, 15, 1–85. [Google Scholar] [CrossRef]
- Osório, J.H.; Amrani, F.; Delahaye, F.; Dhaybi, A.; Vasko, K.; Melli, F.; Giovanardi, F.; Vandembroucq, D.; Tessier, G.; Vincetti, L.; et al. Hollow-core fibers with reduced surface roughness and ultralow loss in the short-wavelength range. Nat. Commun. 2023, 14, 1146. [Google Scholar] [CrossRef]
- Jasion, G.T.; Sakr, H.; Hayes, J.R.; Sandoghchi, S.R.; Hooper, L.; Fokoua, E.N.; Saljoghei, A.; Mulvad, H.C.; Alonso, M.; Taranta, A.; et al. 0.174 dB/km hollow core double nested antiresonant nodeless fiber (DNANF). In Proceedings of the 2022 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 10 March 2022; pp. 1–3. [Google Scholar]
- Danielmeyer, H.G.; Weber, H.P. Direct measurement of the group velocity of light. Phys. Rev. A 1971, 3, 1708. [Google Scholar] [CrossRef]
- Danielson, B.L. Precise length measurements in multimode optical fibers. Appl. Opt. 1991, 30, 3867–3872. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.; Du, J.; Sun, L.; Wang, C.; Zhu, Y.; Xu, K.; Chen, B.; He, Z. Low-Latency and High-Speed Hollow-Core Fiber Optical Interconnection at 2-Micron Waveband. J. Light. Technol. 2020, 38, 3874–3882. [Google Scholar] [CrossRef]
- Hong, Y.; Bottrill, K.R.H.; Bradley, T.D.; Sakr, H.; Jasion, G.T.; Harrington, K.; Poletti, F.; Petropoulos, P.; Richardson, D.J. Low-Latency WDM Intensity-Modulation and Direct-Detection Transmission over >100 km Distances in a Hollow Core Fiber. Laser Photonics Rev. 2021, 15, 2100102. [Google Scholar] [CrossRef]
- Kuschnerov, M.; Mangan, B.J.; Gong, K.; Sleiffer, V.A.J.M.; Herrmann, M.; Nicholson, J.W.; Fini, J.M.; Meng, L. Transmission of commercial low latency interfaces over hollow-core fiber. J. Light. Technol. 2016, 34, 314–320. [Google Scholar] [CrossRef]
- Cruz, J.L.; Barmenkov, Y.O.; Díez, A.; Andres, M.V. Measurement of phase and group refractive indices and dispersion of thermo-optic and strain-optic coefficients of optical fibers using weak fiber Bragg gratings. Appl. Opt. 2021, 60, 2824–2832. [Google Scholar] [CrossRef]
- Mori, K.; Morioka, T.; Saruwatari, M. Group velocity dispersion measurement using supercontinuum picosecond pulses generated in an optical fibre. Electron. Lett. 1993, 29, 987–989. [Google Scholar] [CrossRef]
- Arosa, Y.; Fuente, R.D.L. Refractive index spectroscopy and material dispersion in fused silica glass. Opt. Lett. 2020, 45, 4268–4271. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, S.; Wang, Y.; Ding, W.; Wang, X.; Wang, P. 7-cell hollow-core photonic bandgap fiber with broad spectral bandwidth and low loss. Opt. Express 2019, 27, 11608–11616. [Google Scholar] [CrossRef]
- Michaud-Belleau, V.; Fokoua, E.N.; Bradley, T.D.; Hayes, J.R.; Chen, Y.; Poletti, F.; Richardson, D.J.; Genest, J.; Slavik, R. Backscattering in antiresonant hollow-core fibers: Over 40 dB lower than in standard optical fibers. Optica 2021, 8, 216–219. [Google Scholar] [CrossRef]
- Luo, M.; Liu, J.; Tang, C.; Wang, X.; Lan, T.; Kan, B. 0.5 mm spatial resolution distributed fiber temperature and strain sensor with position-deviation compensation based on OFDR. Opt. Express 2019, 27, 35823–35829. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Luo, M.; Liu, J.; Gao, Q.; Li, C.; Guo, H.; Liu, Y.-G.; Ge, C. Observation and characterization of the high order modes in a six-mode fiber using an OFDR method. Opt. Express 2022, 30, 26341–26347. [Google Scholar] [CrossRef] [PubMed]
- Ahn, T.-J.; Kim, D.Y. High-resolution differential mode delay measurement for a multimode optical fiber using a modified optical frequency domain reflectometer. Opt. Express 2005, 13, 8256–8262. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Luo, M.; Liu, J.; Luan, N.; Xu, X.; Li, C.; He, Y. Group Birefringence Regulation and Measurement with Twin Zeros in a Selectively Infiltrated Microstructured Optical Fiber Based on OFDR. J. Light. Technol. 2022, 40, 308–312. [Google Scholar] [CrossRef]
- Meng, X.; Luo, M.; Liu, J.; Zhao, S.; Zhou, R. Birefringence characterization in a dual-hole microstructured optical fiber using an OFDR method. Appl. Opt. 2024, 63, 772–776. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Luo, M.; Liu, J.; Ma, J.; Hao, Y.; Liu, Y. Speed of Light in Hollow-Core Photonic Bandgap Fiber Approaching That in Vacuum. Sensors 2024, 24, 6954. https://doi.org/10.3390/s24216954
Cao X, Luo M, Liu J, Ma J, Hao Y, Liu Y. Speed of Light in Hollow-Core Photonic Bandgap Fiber Approaching That in Vacuum. Sensors. 2024; 24(21):6954. https://doi.org/10.3390/s24216954
Chicago/Turabian StyleCao, Xiaolu, Mingming Luo, Jianfei Liu, Jie Ma, Yundong Hao, and Yange Liu. 2024. "Speed of Light in Hollow-Core Photonic Bandgap Fiber Approaching That in Vacuum" Sensors 24, no. 21: 6954. https://doi.org/10.3390/s24216954
APA StyleCao, X., Luo, M., Liu, J., Ma, J., Hao, Y., & Liu, Y. (2024). Speed of Light in Hollow-Core Photonic Bandgap Fiber Approaching That in Vacuum. Sensors, 24(21), 6954. https://doi.org/10.3390/s24216954





