an-QNA: An Adaptive Nesterov Quasi-Newton Acceleration-Optimized CMOS LNA for 65 nm Automotive Radar Applications
Abstract
1. Introduction
Main Contributions
2. Proposed Methodology for Optimizing an LNA Circuit
2.1. Adaptive Nesterov Quasi-Newton Acceleration (an-QNA)
2.2. Modifications in an-QNA
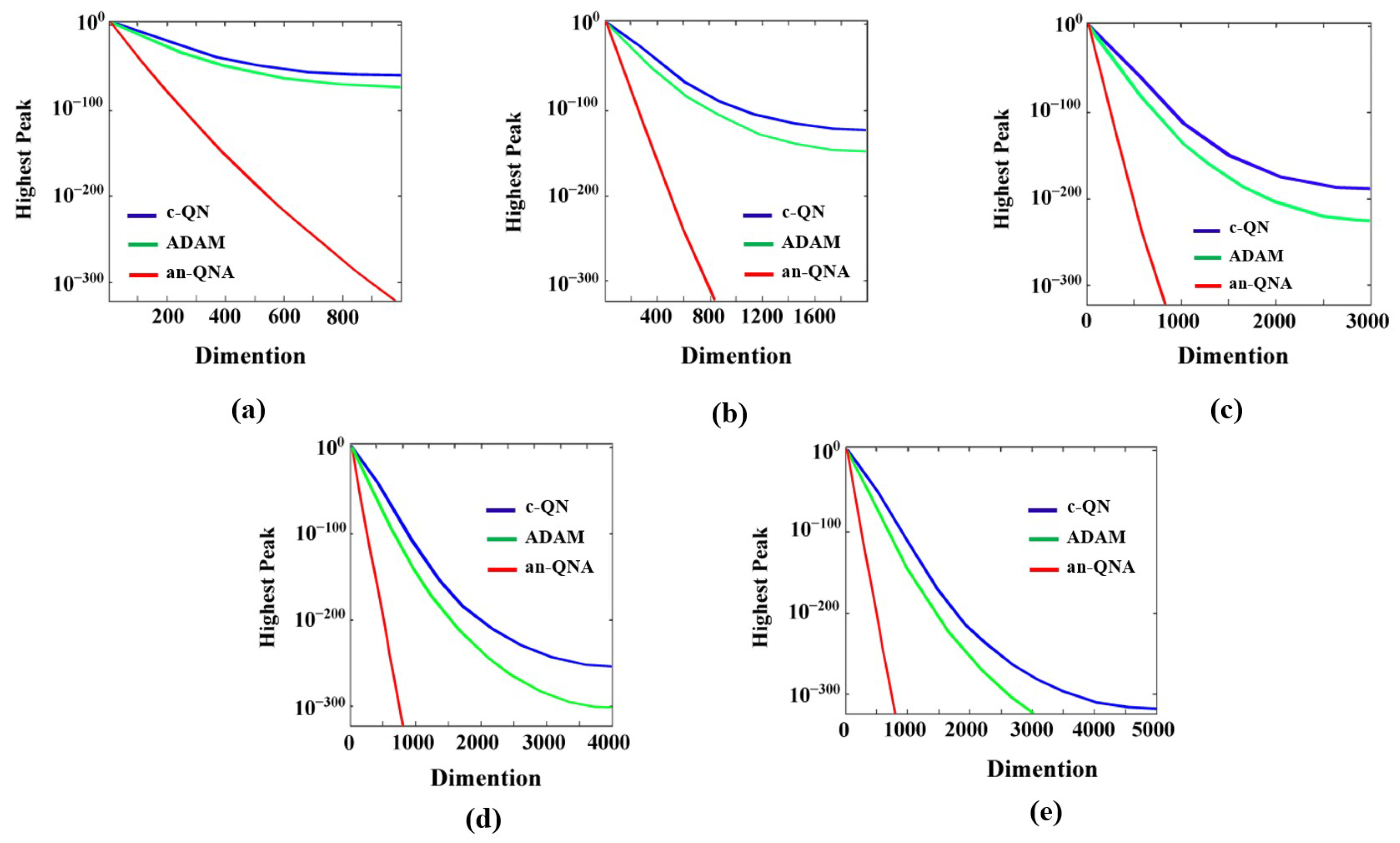
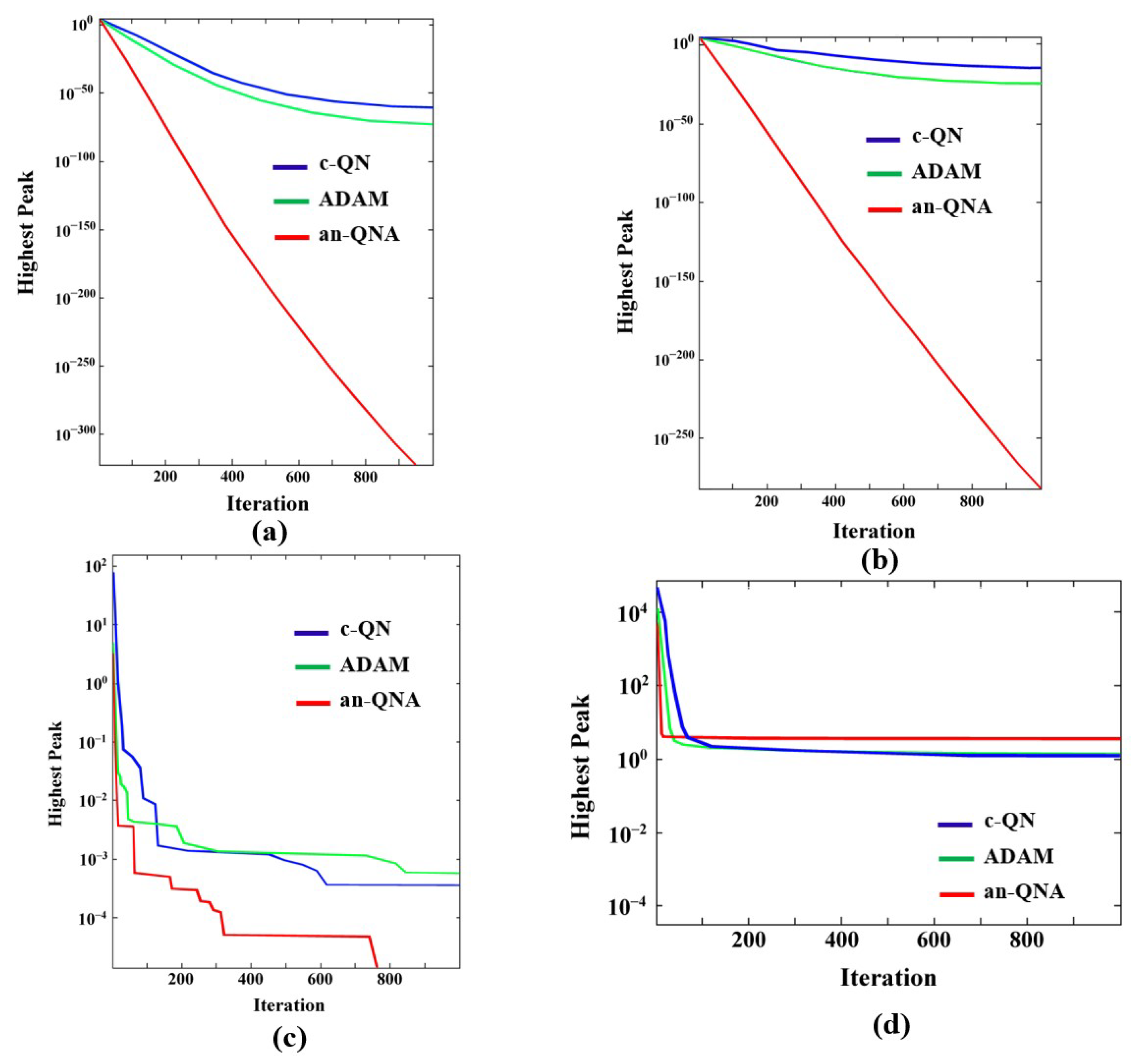
2.3. Convergence Performance Analysis of an-QNA
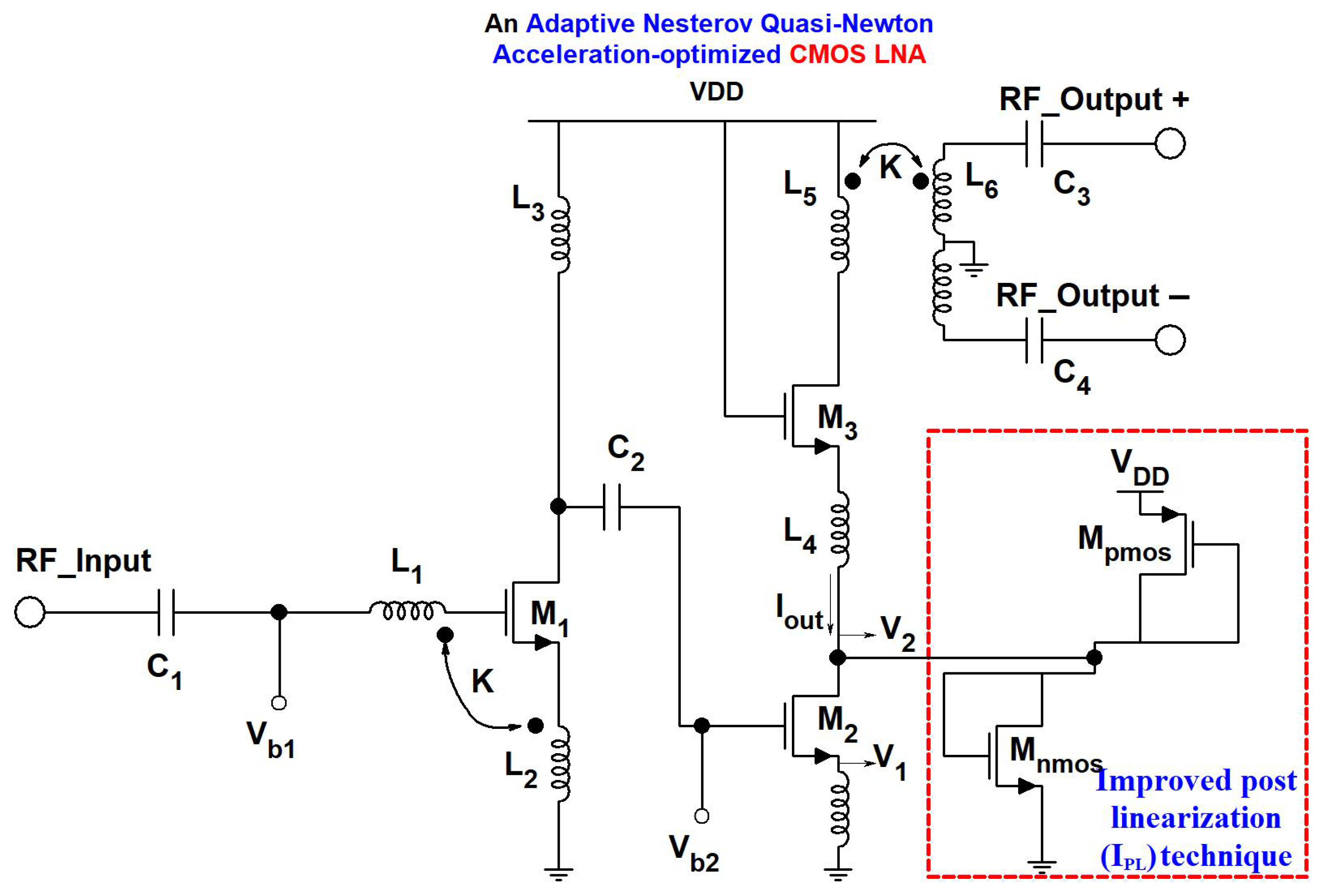
3. Proposed an-QNA Based LNA Circuit
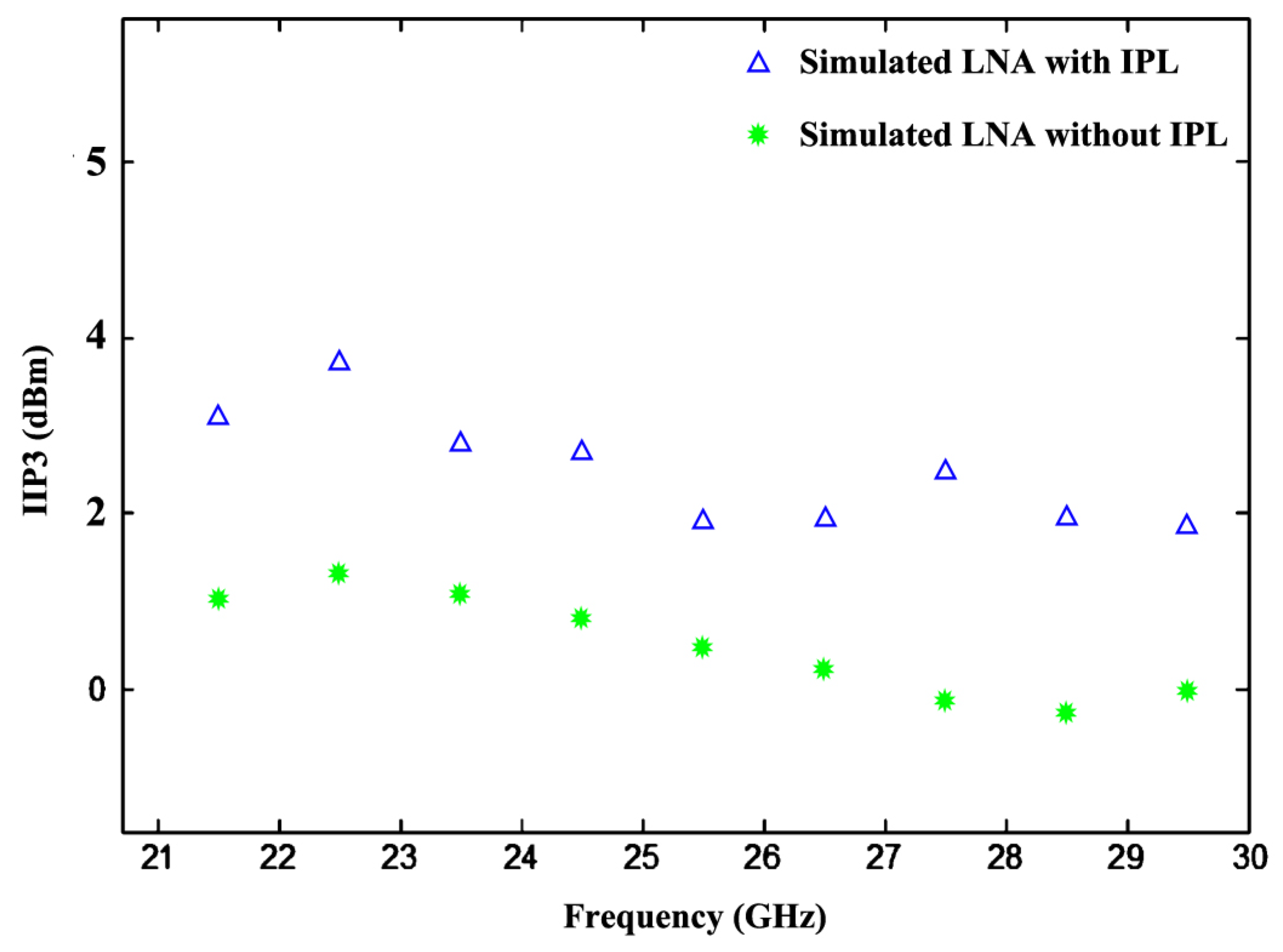
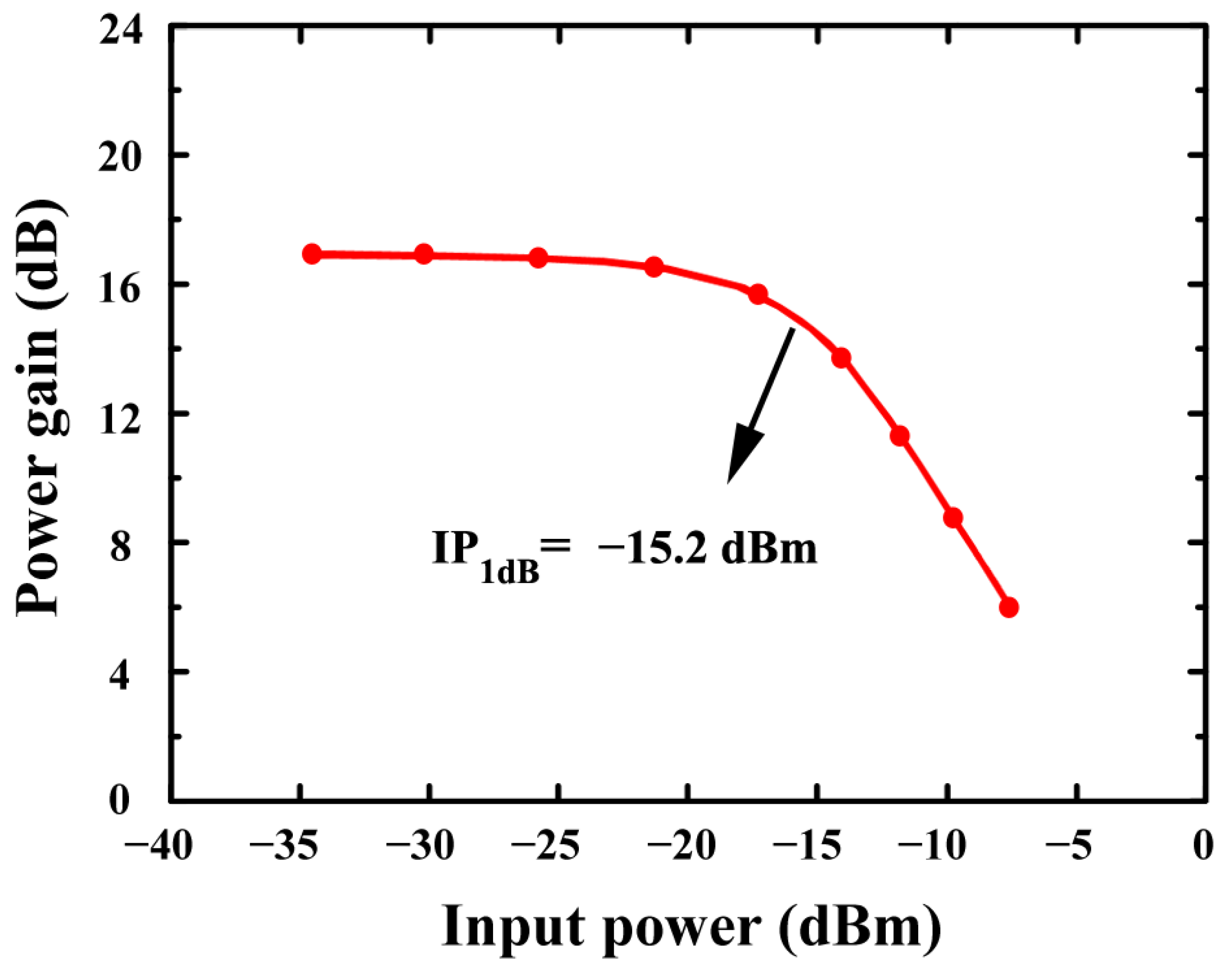
Linearity Analysis
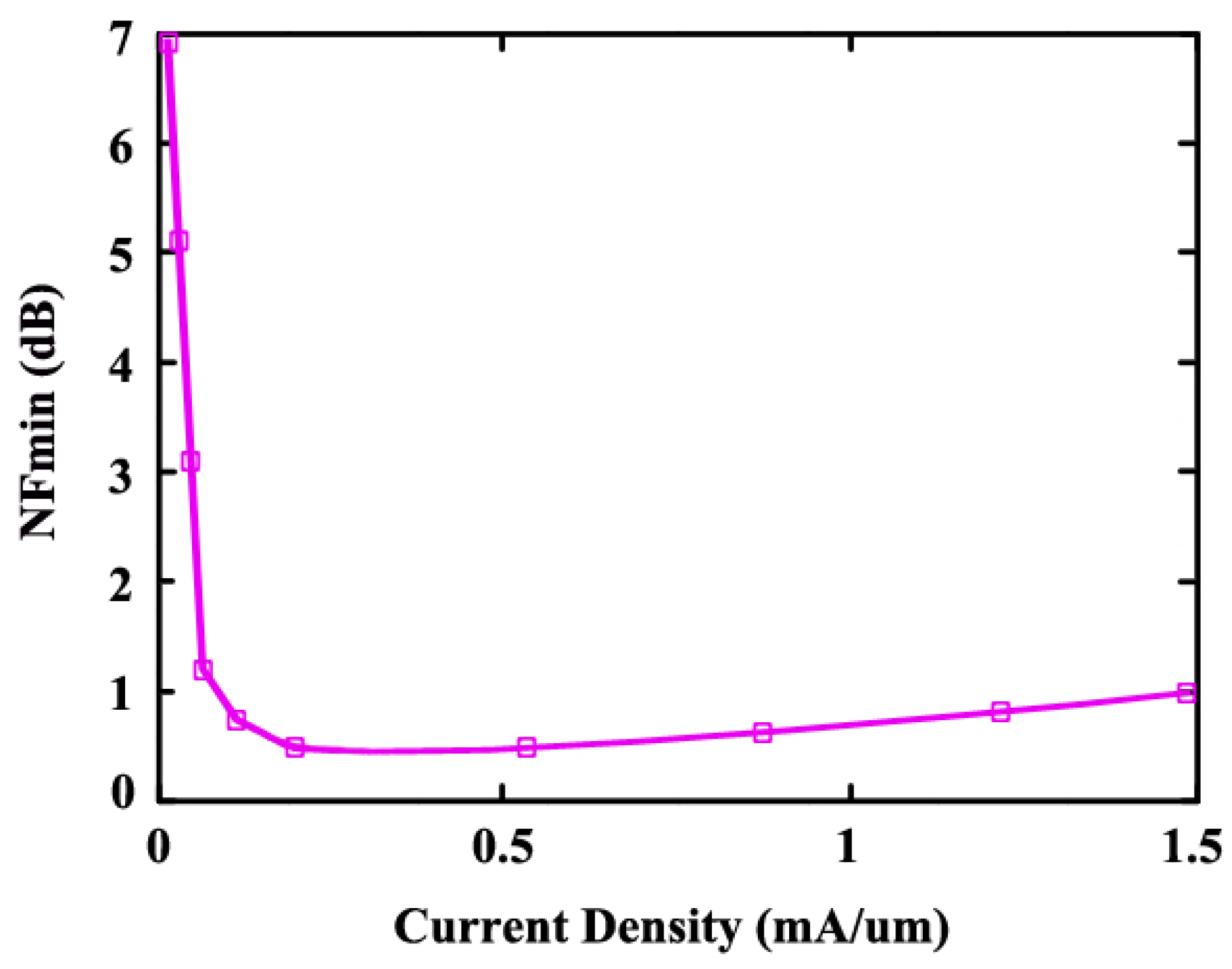
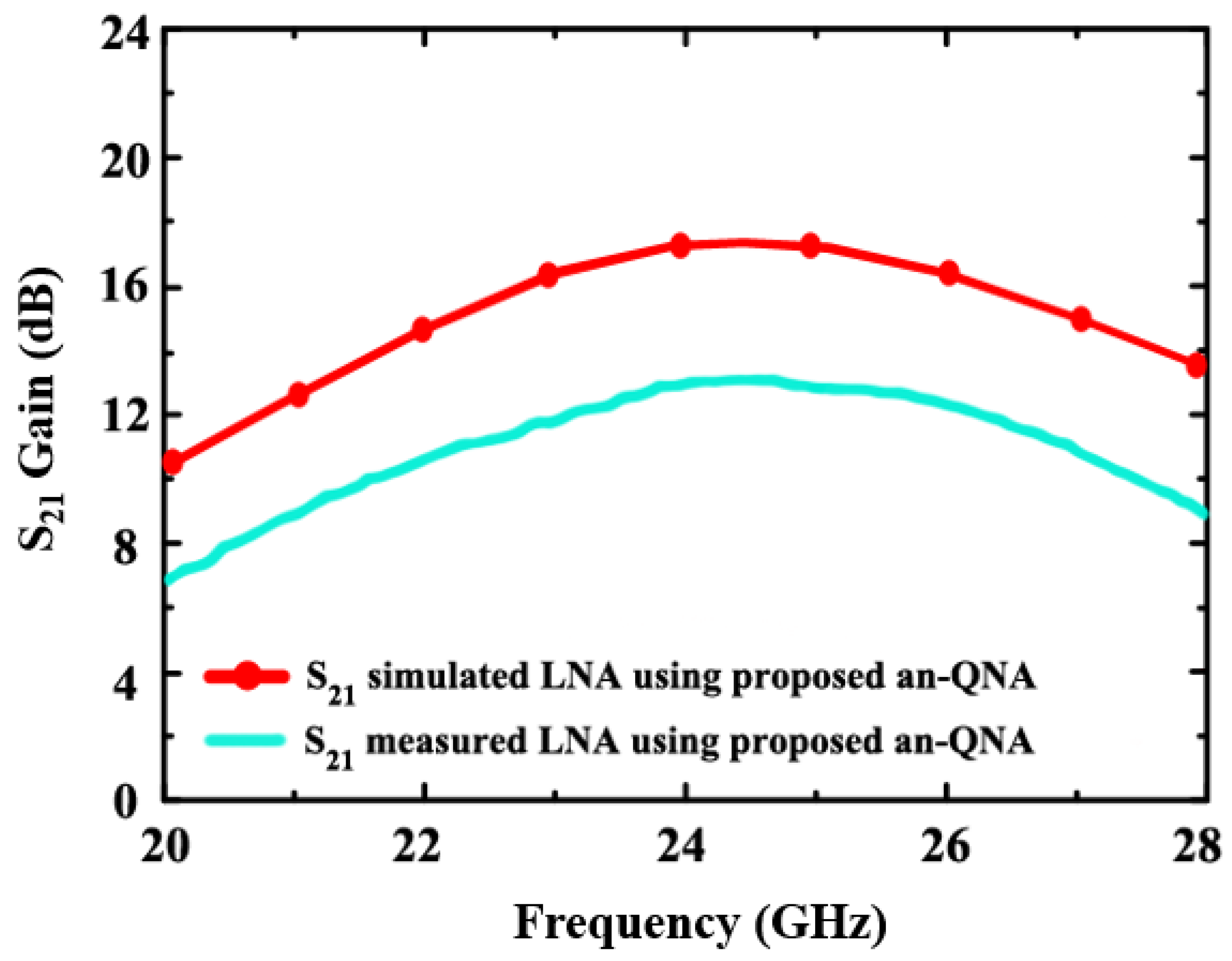
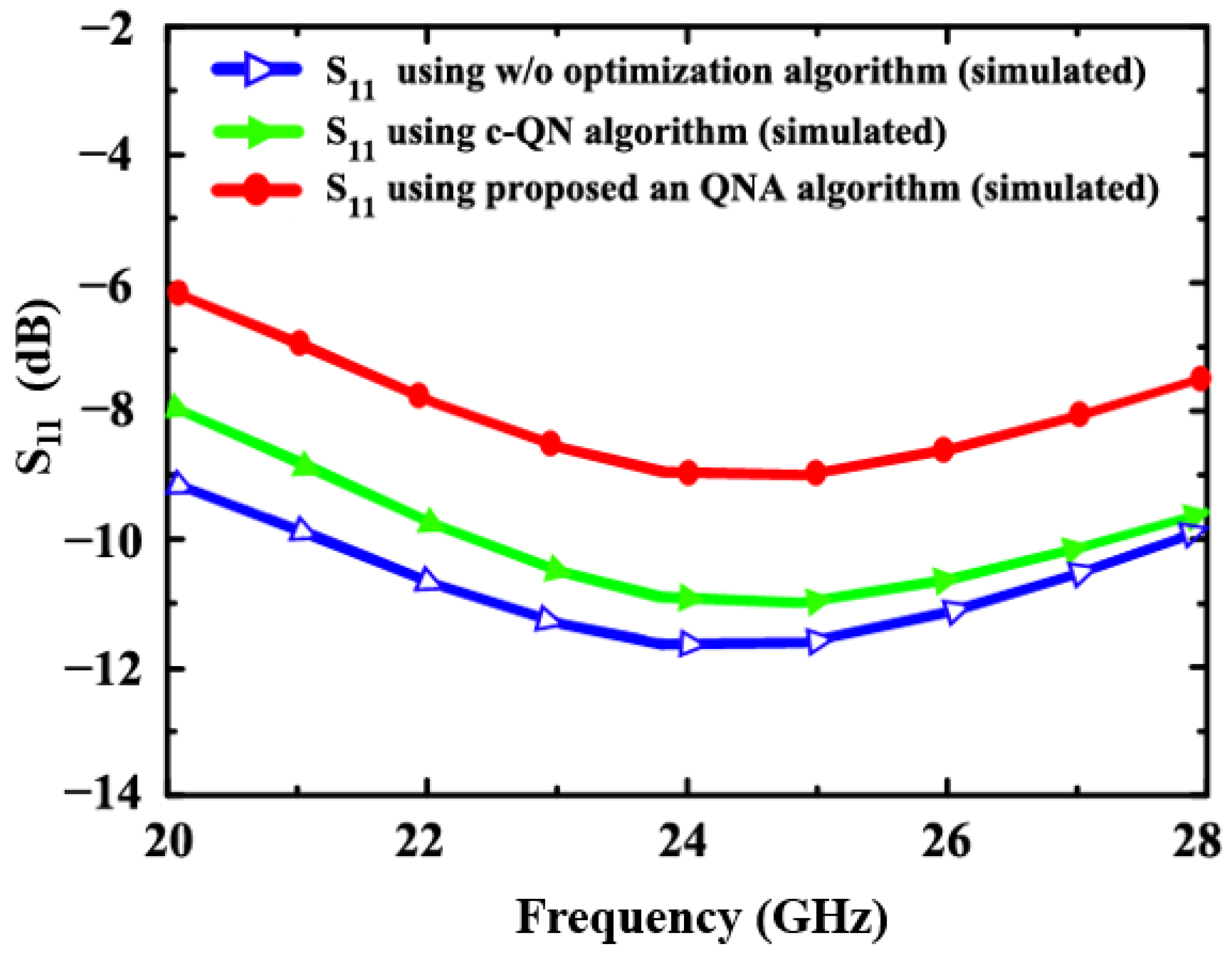
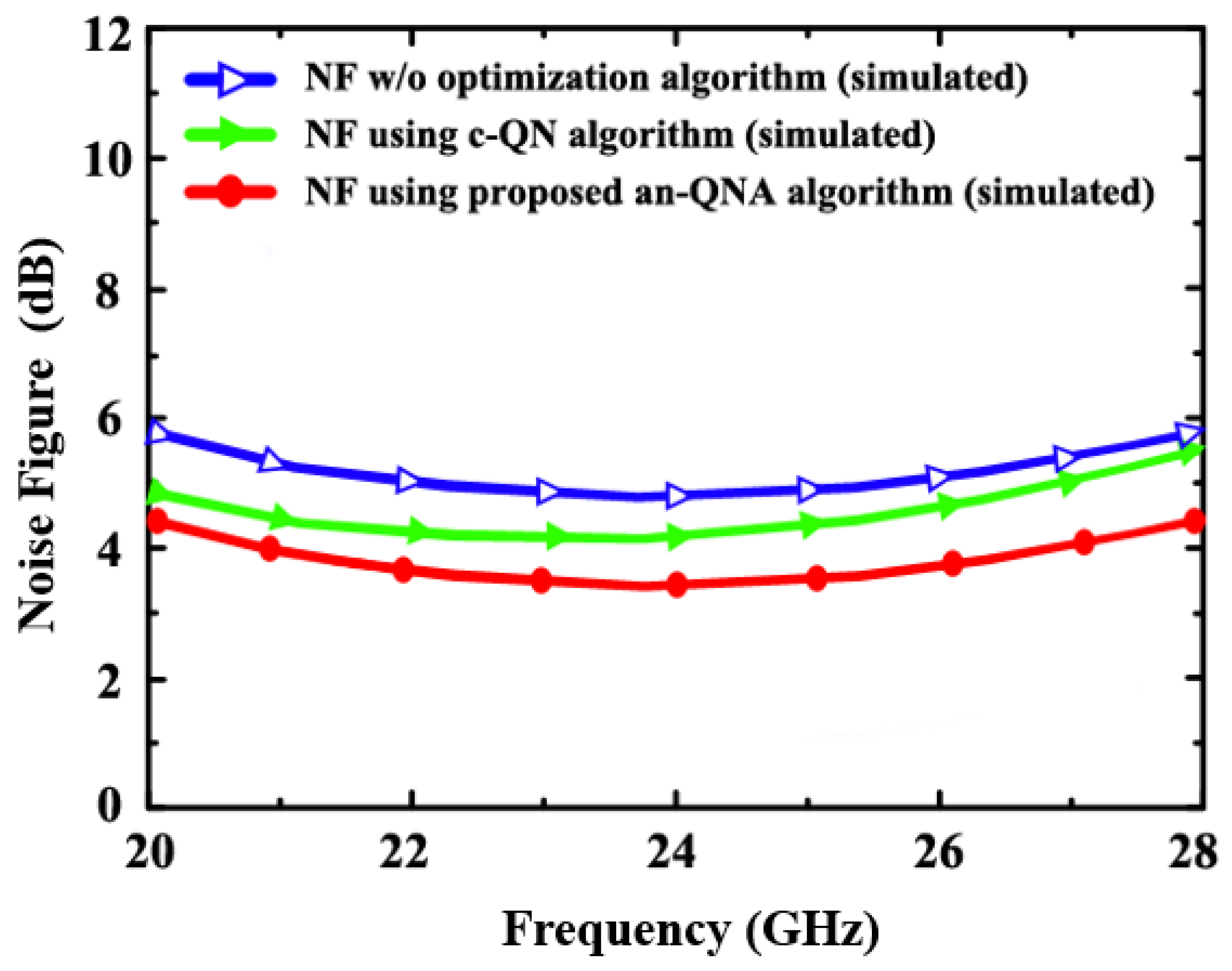
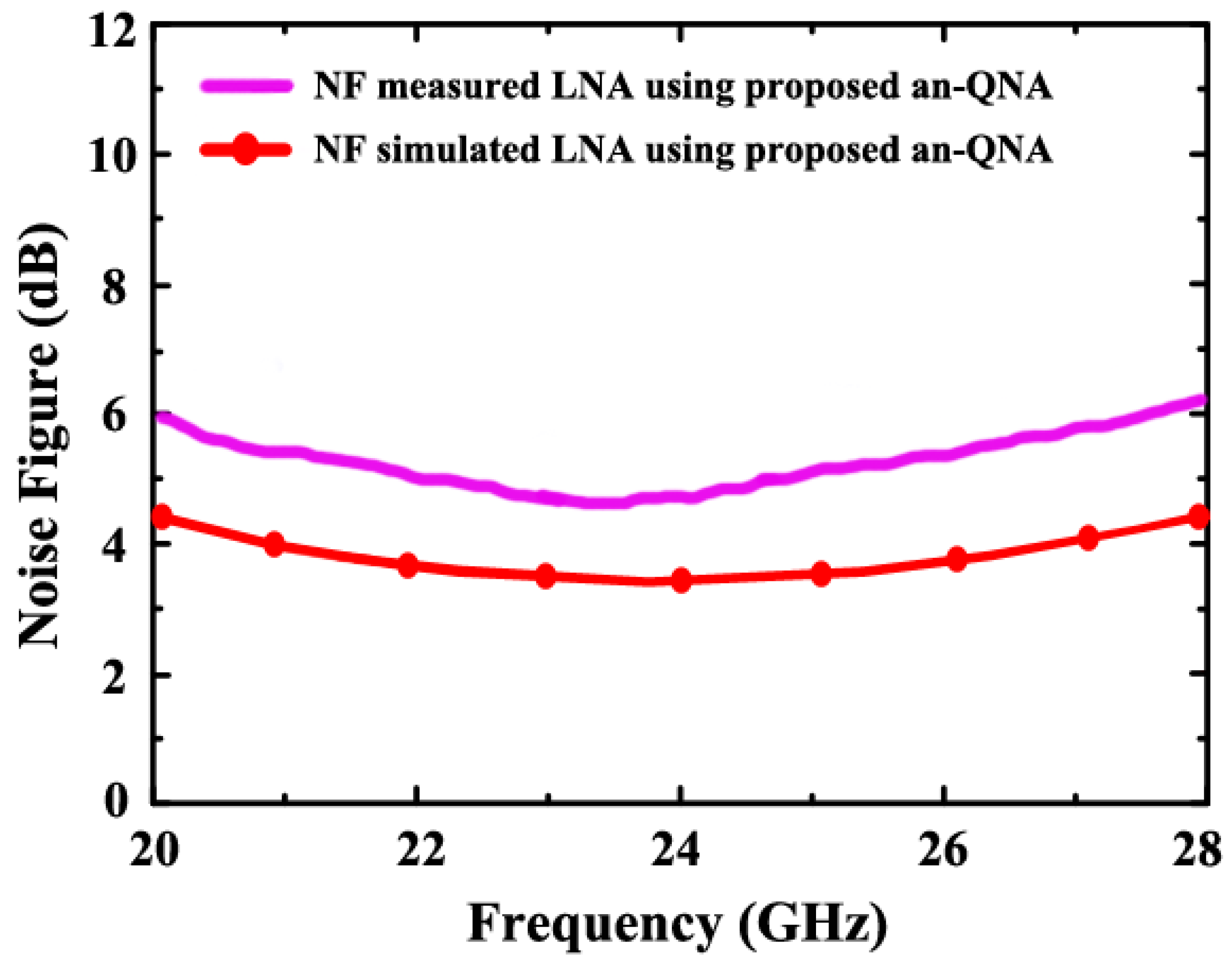
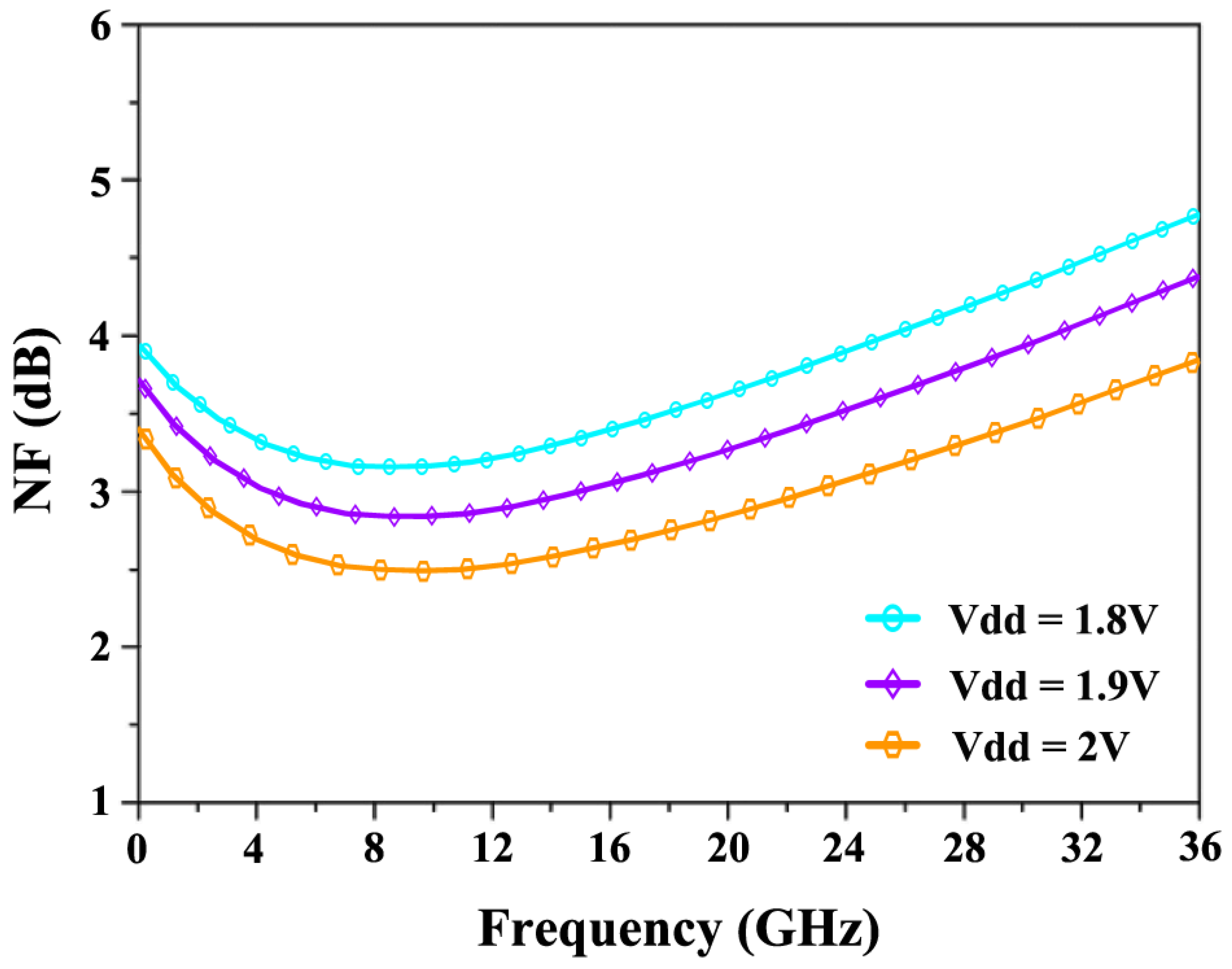
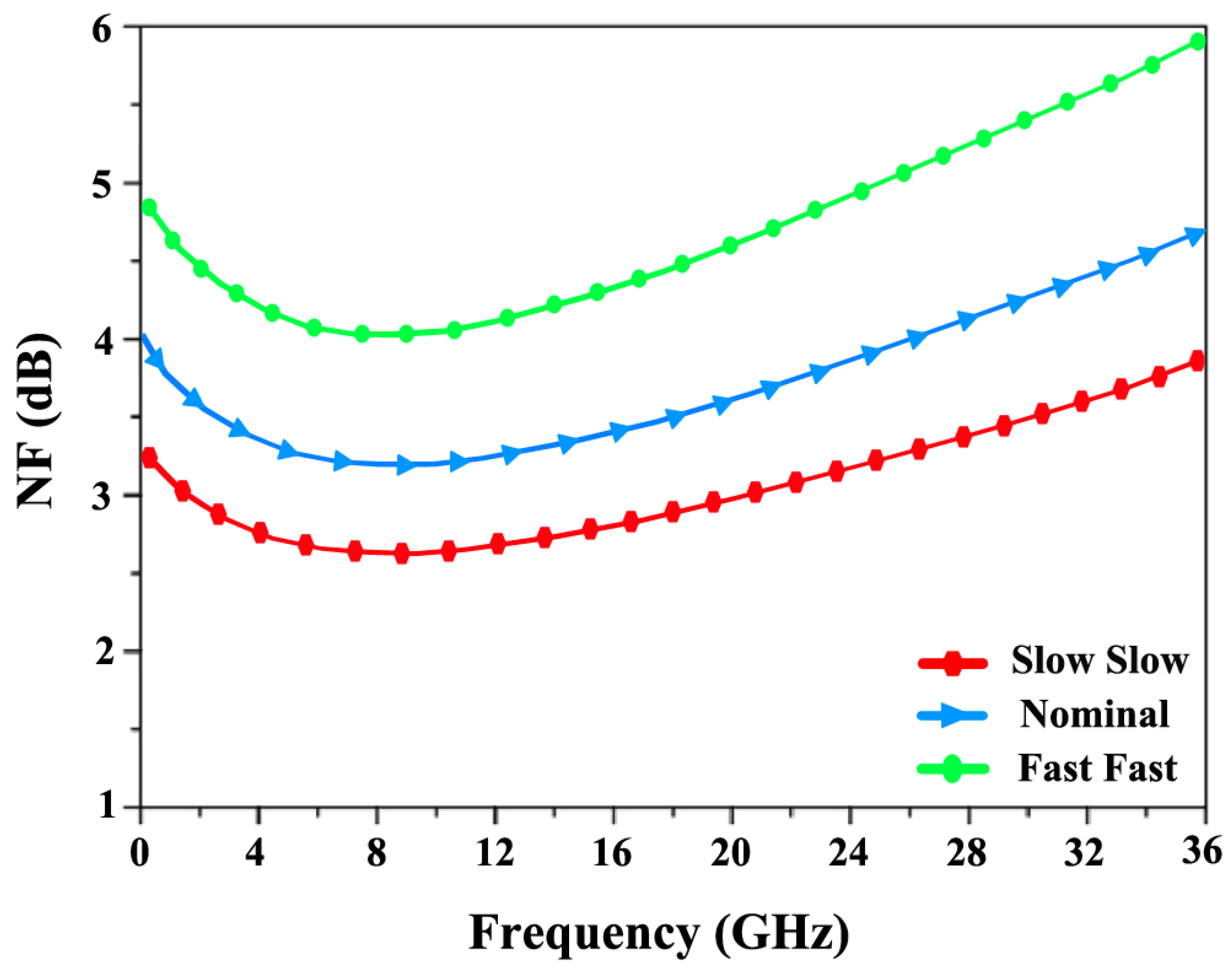
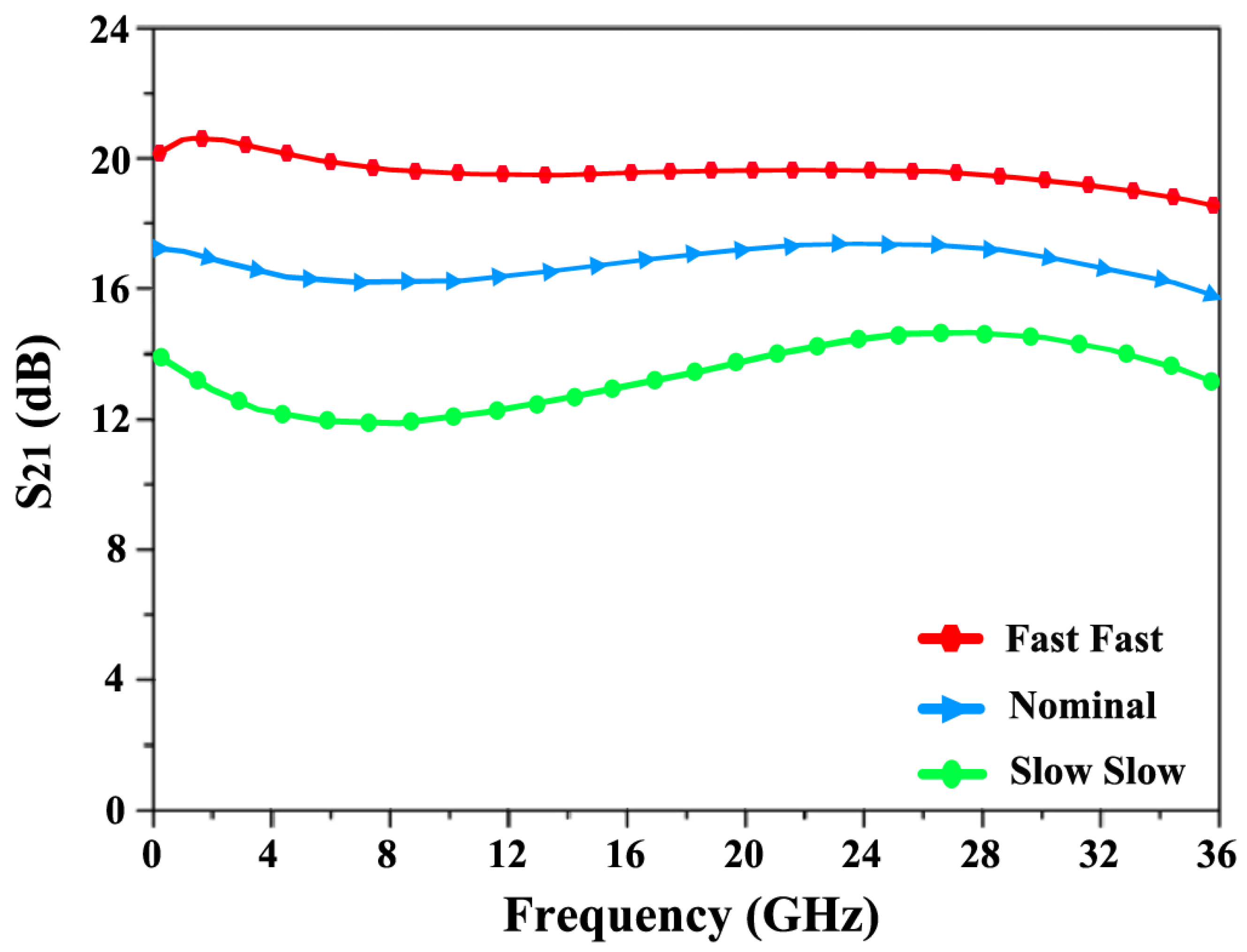
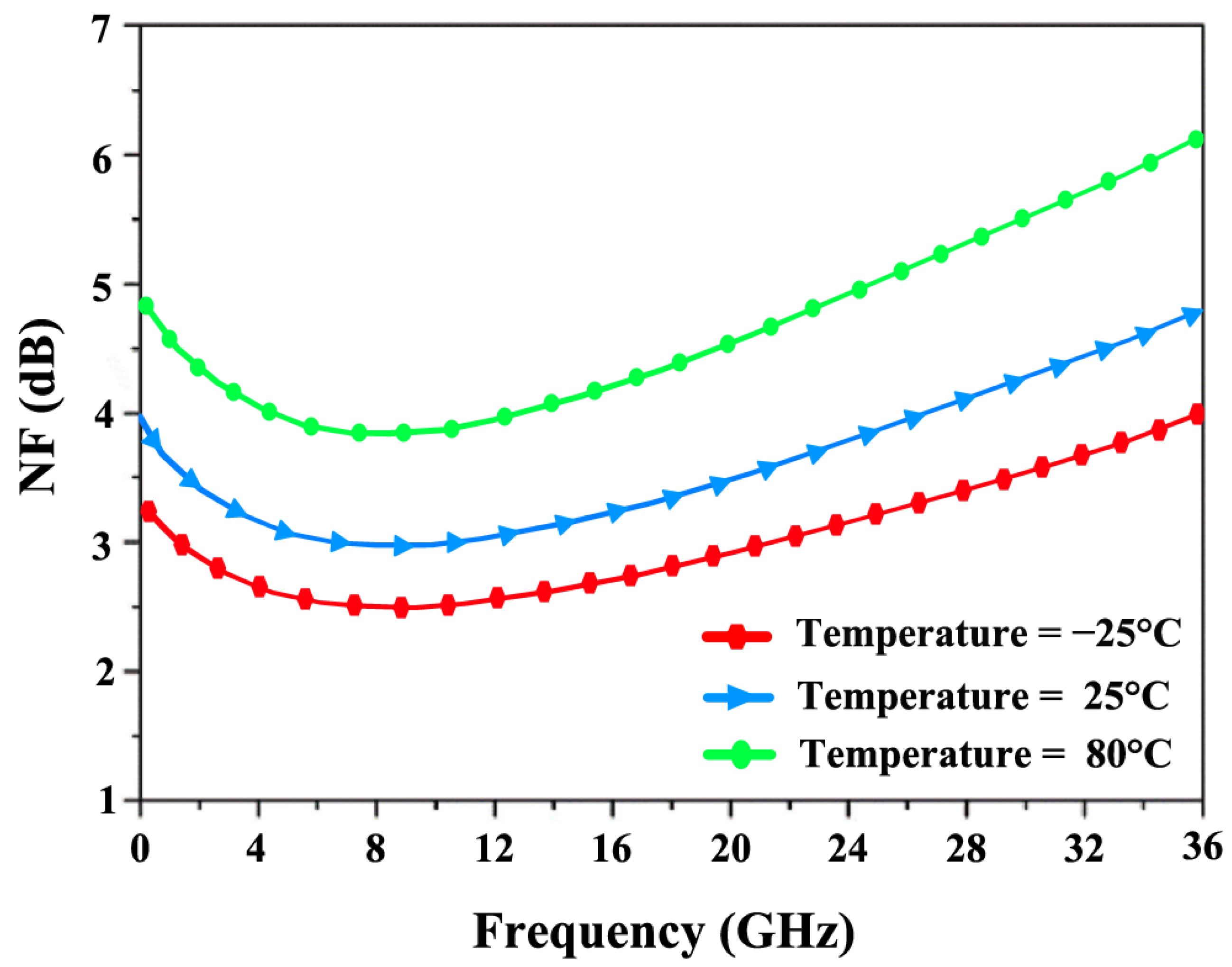
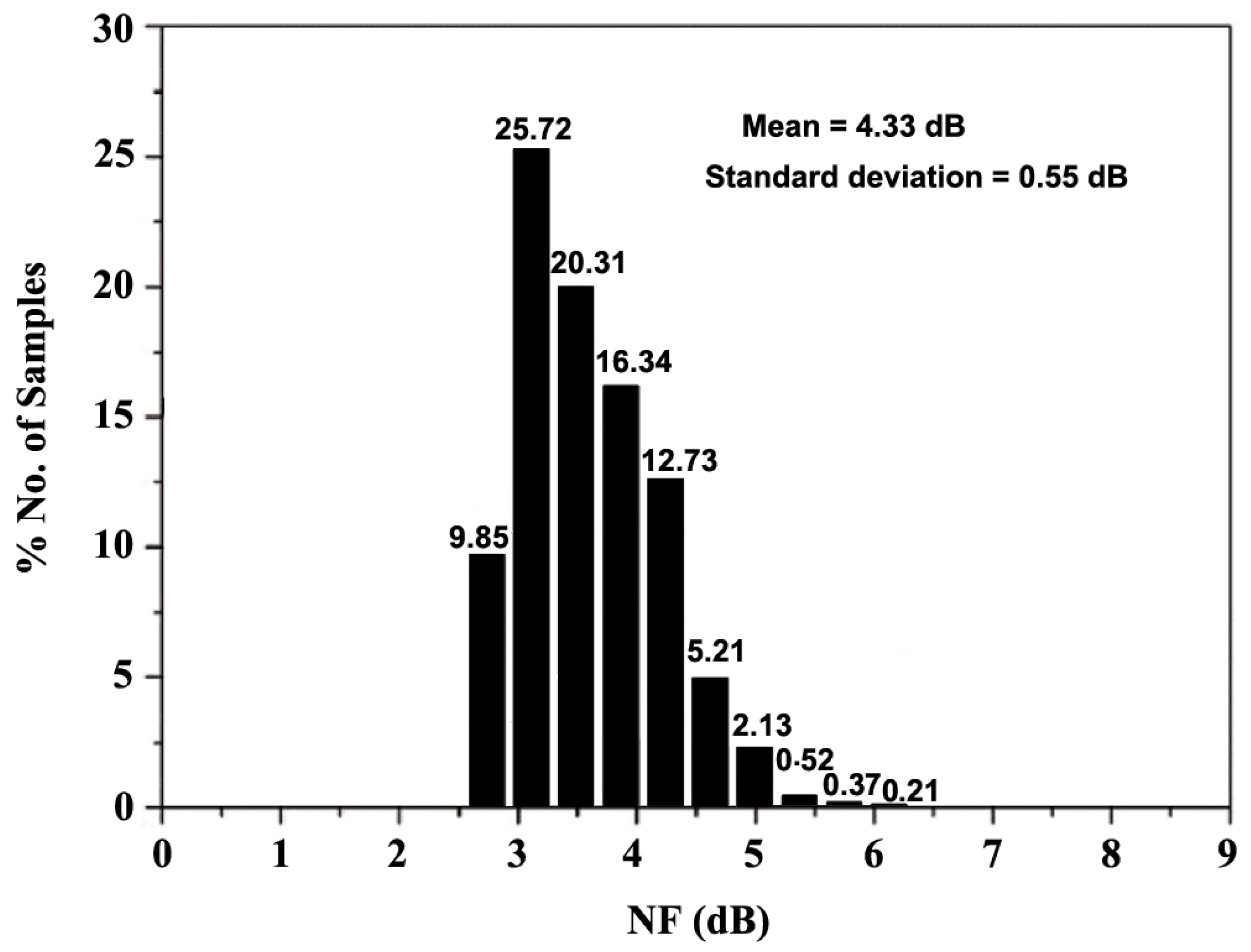
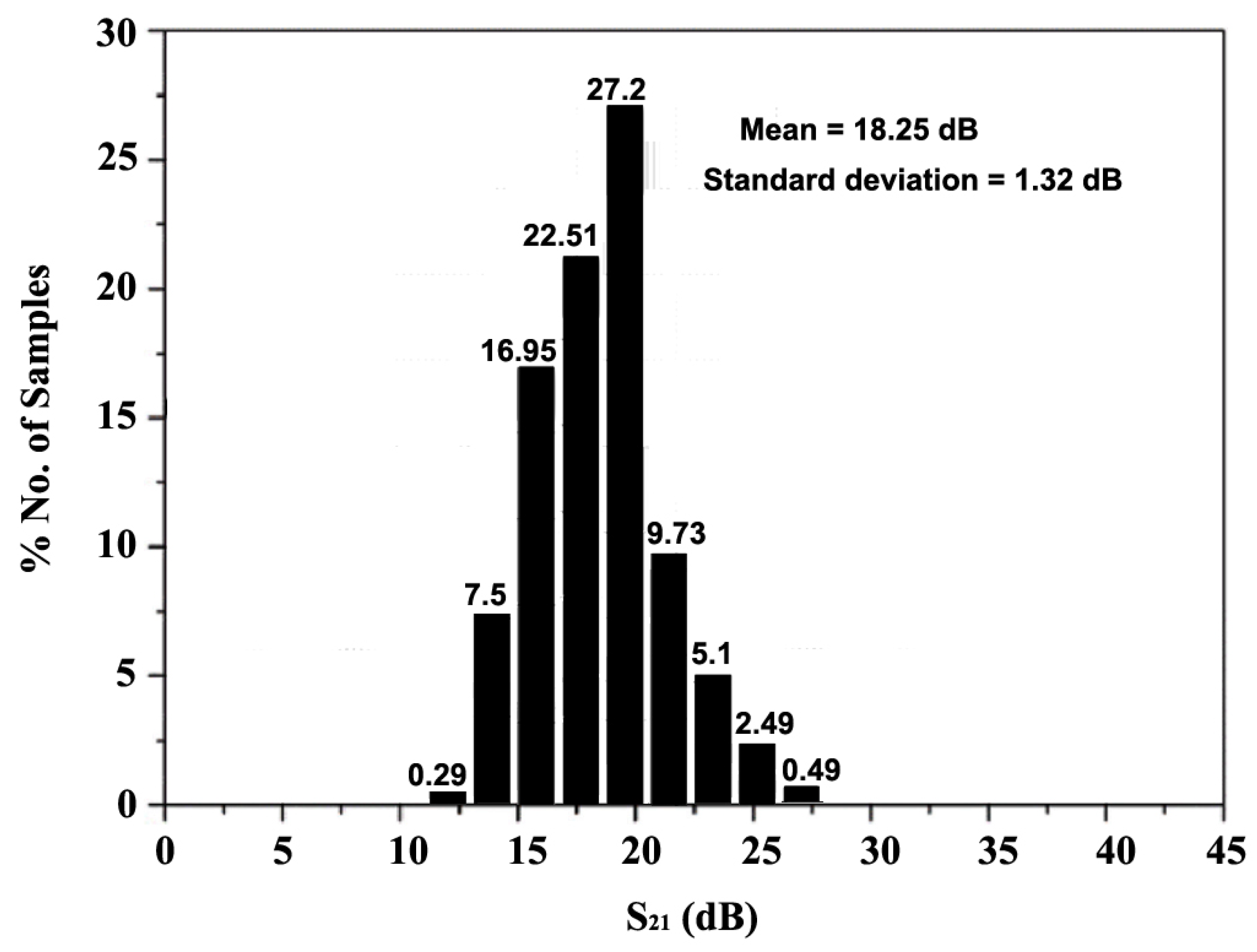
4. Results and Discussion
Layout Issues
5. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- As, D.E.; Yelten, M.B. A highly-linear, sub-mW LNA at 2.4 GHz in 40 nm CMOS process. Integration 2023, 88, 278–285. [Google Scholar]
- Lin, H.T.; Gao, L.; Li, H.Y.; Xu, J.X.; Zhang, X.Y. A 23.6–46.5 GHz LNA with 3 dB NF and 24 dB Gain Tuning Range in 28-nm CMOS Technology. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 71, 29–39. [Google Scholar] [CrossRef]
- Roobert, A.A.; Arunodhayamary, P.S.; Rani, D.G.N.; Venkatesh, M.; Julus, L.J. Design and analysis of 28 GHz CMOS low power LNA with 6.4 dB gain variability for 5G applications. Trans. Emerg. Telecommun. Technol. 2022, 33, e4486. [Google Scholar] [CrossRef]
- Kalra, D.; Srivastava, M. Design and optimization of variable gain LNA for IoT applications using meta-heuristics search algorithms. Microelectron. Eng. 2024, 286, 112125. [Google Scholar] [CrossRef]
- Kim, D.; Im, D. A reconfigurable balun-LNA and tunable filter with frequency-optimized harmonic rejection for sub-GHz and 2.4 GHz IoT receivers. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 3164–3176. [Google Scholar] [CrossRef]
- Pandey, R.J.; Raghava, N.S. Harmonic analysis of CMOS low noise amplifier with employing PMOS IMD technique for biosensor applications. Microsyst. Technol. 2023, 29, 875–898. [Google Scholar] [CrossRef]
- Deng, Z.; Zhou, J.; Qian, H.J.; Luo, X. A 22.9–38.2-GHz dual-path noise-canceling LNA with 2.65–4.62-dB NF in 28-nm CMOS. IEEE J. Solid-State Circuits 2021, 56, 3348–3359. [Google Scholar] [CrossRef]
- Seifi, Z.; Ghorbani, A.; Abdipour, A. Analysis and experimental study of radiative microwave pulses ef-fects on the nonlinear performance of a low-noise amplifier. IEEE Trans. Plasma Sci. 2021, 49, 1105–1114. [Google Scholar] [CrossRef]
- Shen, C.; Zhao, P.; Luo, X. On energy efficient uplink multi-user mimo with shared lna con-trol. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Ibragimov, A.M.; Mikhailov, M.N.; Smirnov, E.P. Reducing odd-order nonlinear distortions in a low noise amplifier. In Proceedings of the 2023 5th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 16–18 March 2023; Volume 5, pp. 1–5. [Google Scholar]
- Younis, A.T.; Abdo, E.A. Low noise amplifier (LNA) performance optimization using genetic algorithms (GAS). J. Eng. Sci. Technol. 2020, 15, 3122–3131. [Google Scholar]
- Bouali, H.; Benhala, B.; Guerbaoui, M. Multi-objective optimization of CMOS low noise amplifier through nature-inspired swarm intelligence. Bull. Electr. Eng. Inform. 2023, 12, 2824–2836. [Google Scholar] [CrossRef]
- Dheerai, R.; Hiranmayee, K.B.; Praveena, K.S.; Dhanaraj, A.B.; Mallikarjuna, B.; Bhargavi, K. A Study on LNA, PLL and BPF of Front-End Integrated RF Receiver for Wireless Applications. In Proceedings of the 2021 6th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 8–10 July 2021; pp. 977–982. [Google Scholar]
- Kalra, D.; Goyal, V.; Srivastava, M. LNA Parameters Optimization Using Firefly Algorithm. In Proceedings of the 2023 3rd International Conference on Advancement in Electronics & Communication Engineering (AECE), Ghaziabad, India, 23–24 November 2023; pp. 94–97. [Google Scholar]
- Abi, S.; Bouyghf, H.; Benhala, B.; Raihani, A. An optimal design of a short-channel RF low noise amplifier using a swarm intelligence technique. In Embedded Systems and Artificial Intelligence: Proceedings of the ESAI 2019, Fez, Morocco, 6–7 November 2019; Springer: Singapore, 2019; pp. 143–153. [Google Scholar]
- Bouali, H.; Benhala, B.; Bouyghf, H. Optimal Design of CMOS 0.18 µm Low Noise Amplifier using Multi-Objective Artificial Bee Colony Algorithm. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 69–75. [Google Scholar] [CrossRef]
- Thakker, R.A.; Baghini, M.S.; Patil, M.B. Low-power low-voltage analog circuit design using hierarchical particle swarm optimization. In Proceedings of the IEEE 22nd International Conference on VLSI Design 2009, New Delh, India, 5–9 January 2009; pp. 427–432. [Google Scholar]
- Fakhfakh, M.; Cooren, Y.; Sallem, A.; Loulou, M.; Siarry, P. Analog circuit design optimization through the particle swarm optimization technique. Analog. Integr. Circuits Signal Process. 2010, 63, 71–82. [Google Scholar] [CrossRef]
- Tulunay, G.; Balkir, S.A. synthesis tool for CMOS RF low noise amplifiers. IEEE Trans. CAD Integr. Circuits Syst. 2008, 21, 977–982. [Google Scholar] [CrossRef]
- Wen, W.; Yilong, L.; Jeffrey, S.F.; Yong, Z. Particle Swarm Optimization and Finite- Element Based Approach for Microwave Filter Design. IEEE Trans. Magn. 2005, 41, 1800–1803. [Google Scholar]
- Sad, C.; Michailidis, A.; Noulis, T.; Siozios, K. A Hybrid GA/ML-Based End-to-End Automated Methodology for Design Acceleration of Wireless Communications CMOS LNAs. Electronics 2023, 12, 2428. [Google Scholar] [CrossRef]
- Liao, T.; Zhang, L. Efficient parasitic-aware hybrid sizing methodology for analog and RF integrated circuits. Integration 2018, 62, 301–313. [Google Scholar] [CrossRef]
- Olenšek, J.; Bűrmen, Á.; Puhan, J.; Tuma, T. DESA: A new hybrid global optimization method and its application to analog integrated circuit sizing. J. Glob. Optim. 2009, 44, 53–77. [Google Scholar] [CrossRef]
- Li, Y. A simulation-based evolutionary approach to LNA circuit design optimization. Appl. Math. Comput. 2009, 209, 57–67. [Google Scholar] [CrossRef]
- Karkhanehchia, M.M.; Naderib, S.; Jafaria, F.; Majidifarc, S. Design and optimization of a very low noise amplifier using particle swarm optimization technique. Int. J. Eng. Technol. 2014, 2, 122–131. [Google Scholar]
- Shin, L.W.; Chin, N.S.; Marzuki, A. 5 GHz MMIC LNA design using particle swarm optimization. Inf. Manag. Bus. Rev. 2013, 5, 257–262. [Google Scholar]
- Papadimitriou, A.; Bucher, M. Multi-objective low-noise amplifier optimization using analytical model and genetic computation. Circuits Syst. Signal Process. 2017, 36, 4963–4993. [Google Scholar] [CrossRef]
- Khong, S.Z.; Nešić, D.; Manzie, C.; Tan, Y. Multidimensional global extremum seeking via the DIRECT optimisation algorithm. Automatica 2013, 49, 1970–1978. [Google Scholar] [CrossRef]
- Shams, M.; Rashedi, E.; Hakimi, A. Clustered-gravitational search algorithm and its application in parameter optimization of a low noise amplifier. Appl. Math. Comput. 2015, 258, 436–453. [Google Scholar] [CrossRef]
- Konstantopoulos, G.; Papathanasiou, K.; Samelis, A. Optimization of RF circuits by expert monitored genetic computation. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Island of Kos, Greece, 21–24 May 2006; pp. 5247–5250. [Google Scholar]
- Chen, H.-H.; Chen, M.-H.; Tsai, C.-Y. Optimization of low noise amplifier designs by genetic algorithms. In Proceedings of the International Symposium on Electromagnetic Theory (EMTS), Hiroshima, Japan, 20–23 May 2013; pp. 493–496. [Google Scholar]
- Dutta, A.; Dasgupta, K.; Bhattacharyya, T.K. Compact small signal modeling and PSO-based input matching of a packaged CMOS LNA in subthreshold region. Microelectron. J. 2007, 38, 1050–1056. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, Z.; Liu, H.; Zhao, C.; Wu, Y.; Kang, K. A 24 GHz enhanced neutralized cascode LNA with 4.7 dB NF and 19.8 dB gain. IEICE Electron. Express 2018, 15, 20180464. [Google Scholar] [CrossRef]
- Suganthi, K.; Malarvizhi, S. Millimeter wave CMOS minimum noise amplifier for automotive radars in the frequency band (60–66 GHZ). Clust. Comput. 2019, 22 (Suppl. 5), 11755–11764. [Google Scholar] [CrossRef]
- Zhang, H.; Sánchez-Sinencio, E. Linearization techniques for CMOS low noise amplifiers: A tutorial. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 58, 22–36. [Google Scholar] [CrossRef]
- Fan, X.; Sánchez-Sinencio, E.; Silva-Martinez, J. A 3 GHz–10 GHz common gate ultrawideband low noise amplifier. In Proceedings of the IEEE Midwest Symposium Circuits and Systems, Cincinnati, OH, USA, 7–10 August 2005; pp. 631–634. [Google Scholar]
- Shin, S.; Tsai, M.; Liu, R.; Lin, K.; Wang, H. A 24-GHz 3.9-dB NF low-noise amplifier using 0.18 CMOS technology. IEEE Microw. Wireless Compon. Lett. 2005, 15, 448–450. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, H.; Leenaerts, D.; Milosevic, D.; Baltus, P. A 29–37 GHz BiCMOS low-noise amplifier with 28.5 dB peak gain and 3.1–4.1 dB NF. In Proceedings of the 2018 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Philadelphia, PA, USA, 10–12 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 288–291. [Google Scholar]
- Hosseini, S.A.; Taheri, M.M.; Khosravi, R.; Moradi, G. A 27–31 GHz CMOS LNA for 5G Application via Improved Noise Cancellation Technique and Gain Boosting. Int. J. Smart Electr. Eng. 2022, 11, 21–26. [Google Scholar]
- Kumar, M.; Deolia, V.K. Performance analysis of low power LNA using particle swarm optimization for wide band application. AEU-Int. J. Electron. Commun. 2019, 111, 152897. [Google Scholar] [CrossRef]
- Kumar, R.; Talukdar, F.A.; Rajan, A.; Devi, A.; Raja, R. Parameter optimization of 5.5 GHz low noise amplifier using multi-objective Firefly Algorithm. Microsyst. Technol. 2020, 26, 3289–3297. [Google Scholar] [CrossRef]


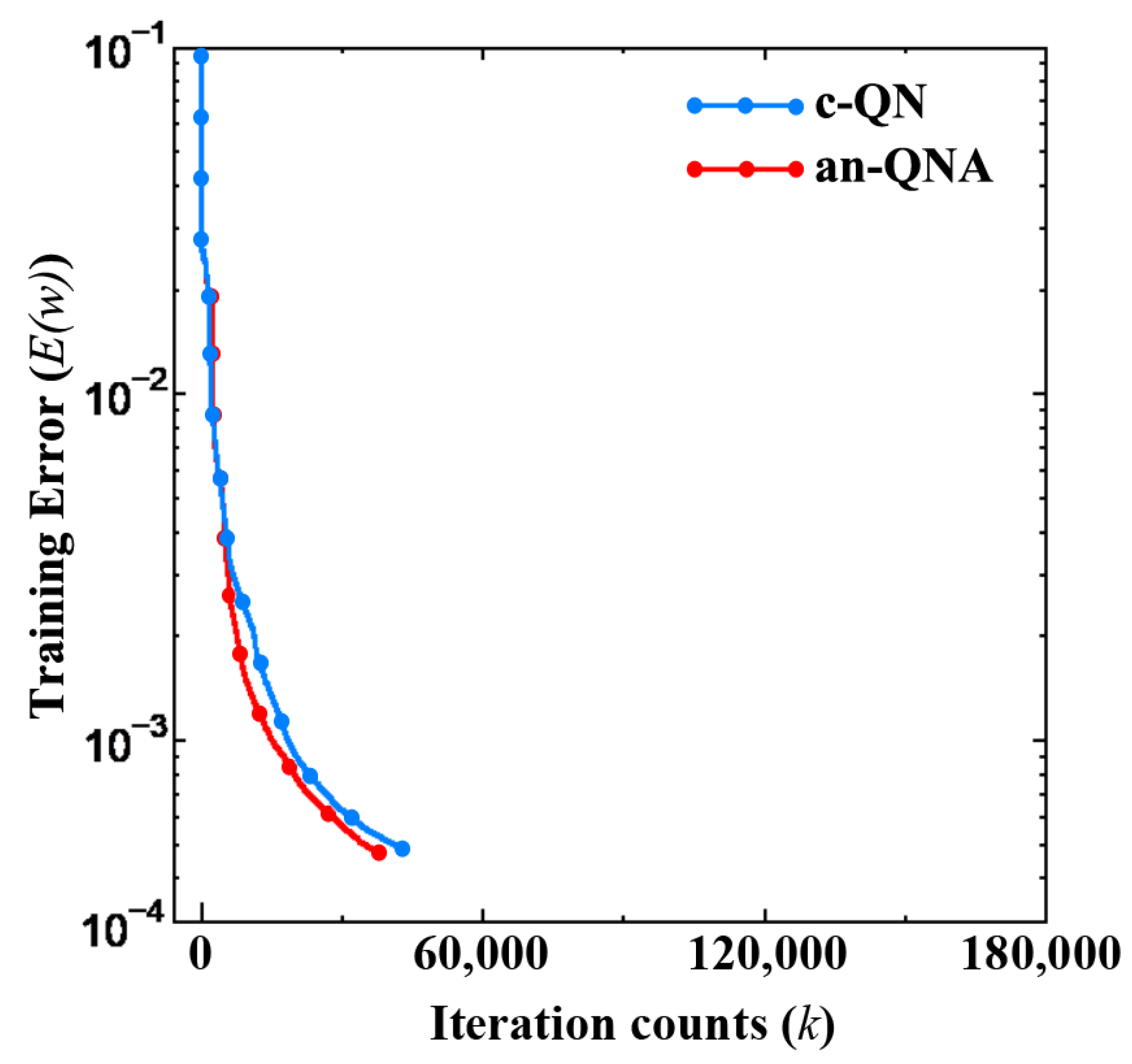
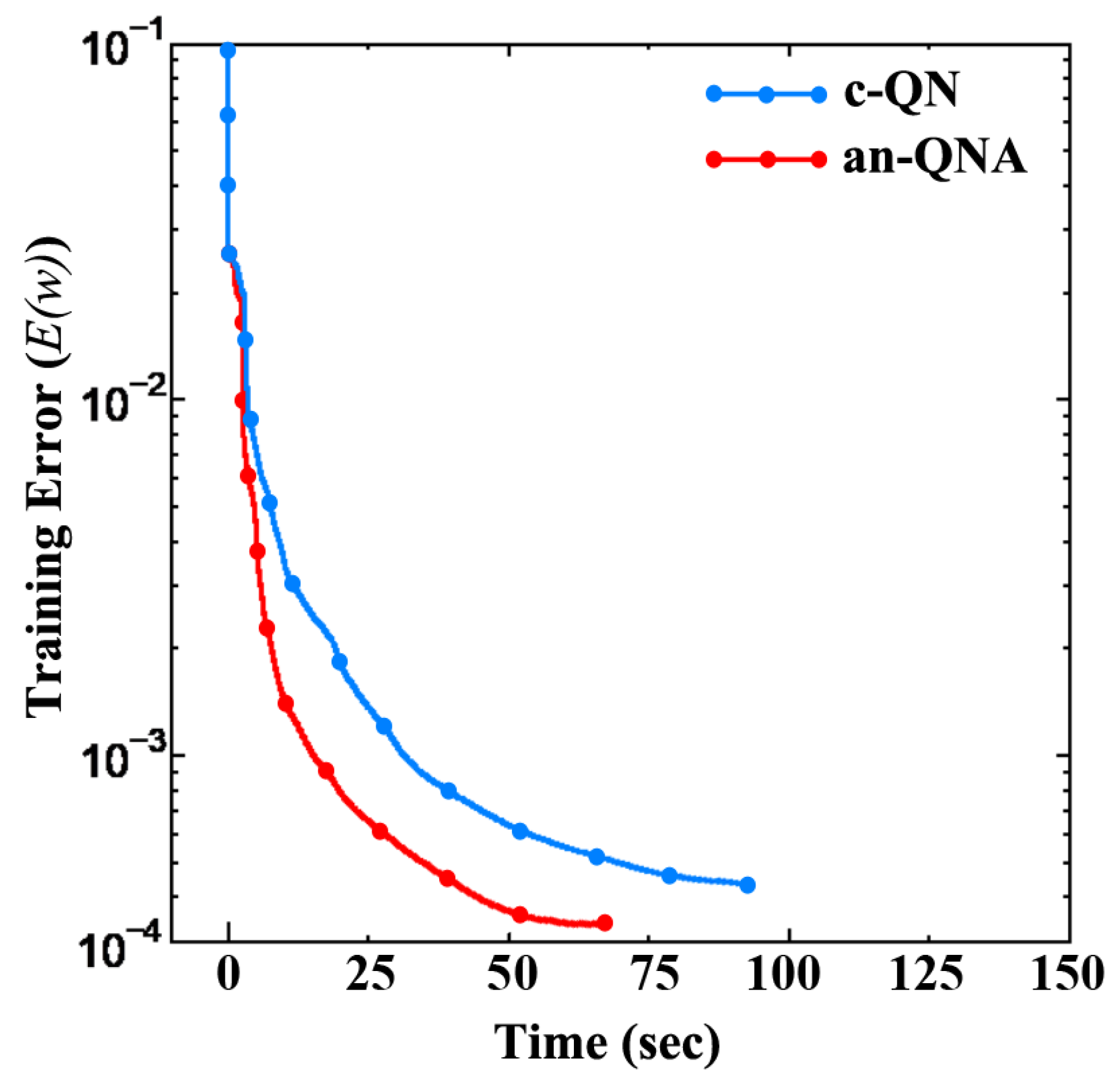









| Name of Algorithm | TrainingError Median/Ave/Best/Worst (w) (×10−3) | Iteration Counts (k) | Time (s) | TestError Median/Ave/Best/Worst (w) (×10−3) | Rate of Convergence (%) |
|---|---|---|---|---|---|
| c-QN | 0.75/0.76/0.62/0.91 | 41,828 | 95 | 0.640/0.901/0.534/2.01 | 75% |
| an-QNA | 0.57/0.51/0.32/0.65 | 35,561 | 65 | 0.798/1.14/0.591/2.15 | 100% |
| Function Name | Dimension | Range | Minimum Function (fmin) |
|---|---|---|---|
| Functionv1(unimodal) (y) | 30 | [−100, 100] | 0 |
| Functionv2(unimodal) (y) | 30 | [−100, 100] | 0 |
| Functionv3(unimodal) (y) | 30 | [−100, 100] | 0 |
| Functionv4(unimodal) (y) | 30 | [−1.28, 1.28] | 0 |
| Functionv5(multimodal) (y) | 30 | [−500, 500] | −418.9 × 5 |
| Functionv6(multimodal) (y) | 30 | [−32, 32] | 0 |
| Functionv7(multimodal) (y) | 30 | [−5.1, 5.1] | 0 |
| Functionv8(multimodal) (y) | 30 | [−600, 600] | 0 |
| c-QN | Minimum | Maximum | ||
| 6.16 × 10−61 | 5.8 × 104 | 215.8 | 2.5 × 103 | |
| 1.97 × 10−35 | 1.43 × 1012 | 1.43 × 109 | 4.52 × 1010 | |
| 3.3 × 10−15 | 1.8876 × 105 | 1.7745 × 103 | 1.0505 × 104 | |
| 2.6647 × 10−14 | 89.07 | 2.61 | 12.13 | |
| 27.11 | 2.1621 × 108 | 7.4518 × 105 | 1.0897 × 107 | |
| 1.2547 | 6.5240 × 104 | 335.9 | 3.4849 × 103 | |
| 3.61 × 10−4 | 92.21 | 0.49 | 5.80 |
| ADAM | Minimum | Maximum | ||
| 2.71 × 10−73 | 6.15 × 104 | 173.1716 | 2.53 × 103 | |
| 7.42 × 10−43 | 3.2669 × 109 | 3.2708 × 106 | 1.03 × 108 | |
| 2.52 × 10−25 | 1.1651 × 105 | 674.7361 | 5.80 × 103 | |
| 2.42 × 10−20 | 88.03 | 0.945 | 6.765 | |
| 27.16 | 2.30 × 108 | 6.71 × 105 | 9.98 × 106 | |
| 1.25 | 7.07 × 104 | 197.70 | 2.81 × 103 | |
| 5.791 × 10−4 | 80.65 | 0.133 | 2.668 |
| an-QNA | Minimum | Maximum | ||
| 0.00 | 7.10 × 104 | 125.5 | 2.4 × 103 | |
| 1.60 × 10−175 | 3.78 × 1013 | 1.27 × 1010 | 1.1956 × 1012 | |
| 1.2 × 10−282 | 6.174 × 104 | 1.2536 × 103 | 1.0787 × 104 | |
| 1.7 × 10−152 | 88.03 | 0.349 | 4.369 | |
| 27.10 | 2.30 × 108 | 3.5409 × 105 | 1.00 × 107 | |
| 3.87 | 7.07 × 104 | 123.81 | 2.5129 × 103 | |
| 1.41 × 10−5 | 80.652 | 0.202 | 4.97 |
| c-QN | Minimum | Maximum | ||
| −5.80 × 103 | −2.44 × 103 | −4.03 × 103 | 967.79 | |
| 5.68 × 10−14 | 458.78 | 10.78 | 48.011 | |
| 1.50 × 10−14 | 20.7623 | 0.412 | 2.276 | |
| 0.009 | 665.77 | 3.149 | 32.93 | |
| 0.03 | 5.520 × 108 | 1.57 × 106 | 2.49 × 107 | |
| 0.69 | 8.056 × 108 | 3.20 × 106 | 4.36 × 107 |
| ADAM | Minimum | Maximum | ||
| −4.8344 × 103 | −2.5399 × 103 | −3.3352 × 103 | 731.9012 | |
| 0 | 438.1148 | 4.9465 | 32.6783 | |
| 1.5099 × 10−14 | 20.7623 | 0.2497 | 1.7307 | |
| 0 | 527.3462 | 1.4174 | 20.4885 | |
| 0.0538 | 6.1414 × 108 | 1.1003 × 106 | 2.1982 × 107 | |
| 1.11284 | 9.0172 × 108 | 1.5261 × 106 | 3.2837 × 107 |
| an-QNA | Minimum | Maximum | ||
| −2.25 × 103 | −2.23 × 103 | −2.25 × 103 | 6.3372 | |
| 0 | 488.07 | 2.33 | 26.43 | |
| 1.4 × 10−15 | 20.8472 | 0.1045 | 1.1726 | |
| 0 | 555.03 | 0.959 | 18.93 | |
| 0.558 | 8.105 × 108 | 1.04 × 106 | 2.15 × 107 | |
| 0.193 | 9.23 × 108 | 1.103 × 106 | 2.9672 × 107 |
| Element | Dimension |
|---|---|
| M1 | 32 µm/65 nm |
| M2 | 54 µm/65 nm |
| M3 | 54 µm/65 nm |
| C1, C2, C3 | 1 pF, 4.2 pF, 1.2 pF |
| L1∼L3 | 1.3 nH, 1.5 nH, 170 pH |
| L4∼L6 | 1.5 nH, 1.8 nH, 154 pH |
| Distortion Sources | gm | gds | |||
|---|---|---|---|---|---|
| Methods of Linearization | Intrinsic 2nd Order | Intrinsic 3rd Order | 2nd-Order Interaction | Higher Order | |
| Feedback | ✓ | ✓ | ✓ | ||
| Harmonic termination | ✓ | ✓ | |||
| Optimal biasing | ✓ | ||||
| Feedforward | ✓ | ✓ | ✓ | ||
| Derivative superposition (DS) | ✓ | ||||
| Complementary DS | ✓ | ✓ | |||
| Differential DS | ✓ | ✓ | |||
| Modified DS | ✓ | ✓ | |||
| IM2 injection | ✓ | ✓ | |||
| Noise/distortion cancellation | ✓ | ✓ | ✓ | ||
| Post-Distortion | ✓ | ✓ | |||
| Ref. | Tech (nm) | VDD (V) | FrEquation (GHz) | S21 (dB) | NF (dB) | IP1dB | Power (mW) |
|---|---|---|---|---|---|---|---|
| [36] | 65 nm | 1.5 | 60 | 11.289 | 1.819 | N/A | 7.25 |
| [37] | 180 nm | N/A | 24 | 12.8 | 3.3 | N/A | 8 |
| [38] | 0.25 m BiCMOS | 1.8 | 16–43 | 10.5 | 2.5-4 | 1.8 (IIP3) | 24 |
| [39] | 0.13 m CMOS | 12 | 27–31 | 22.14 | 1.86 | −16 (IIP3) | 33.4 |
| [40] | 45 nm | N/A | 5.0–27.5 | 18.57 (PSO) | 2.4–3.1 | N/A | 1.6 |
| [41] | 180 nm | 1.8 | 5.5 | 22.15 (firefly) | 1.16 | −2.60 (IIP3) | N/A |
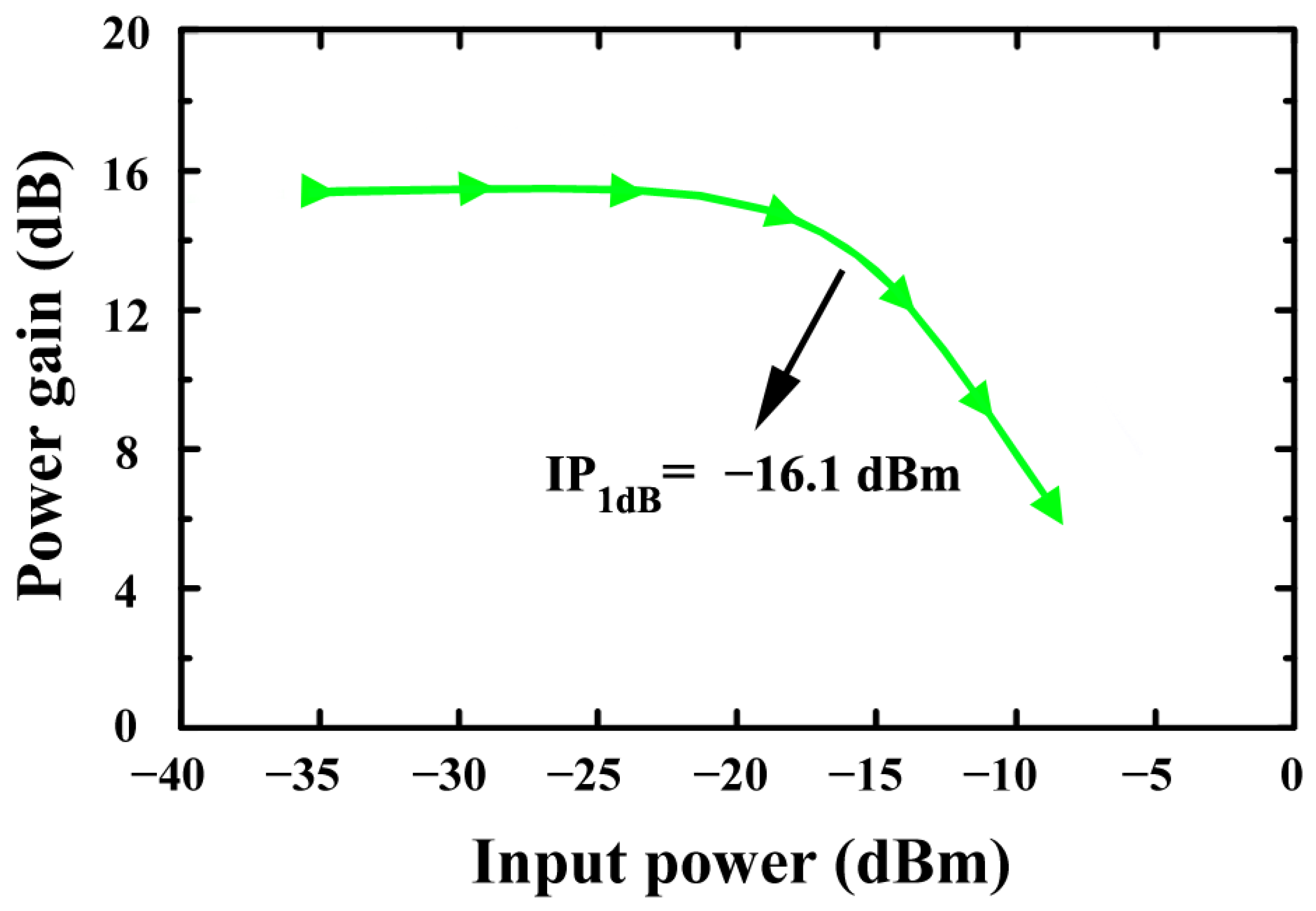
| [This Work] | 65 nm | 1.8 | 24 | 17.5/12.9 (sim./meas) (an-QNA) | 3.7/4.98 (sim./meas) (an-QNA) | −13.1/−17.8 (sim./meas) (an-QNA) | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aras, U.; Woo, L.S.; Delwar, T.S.; Siddique, A.; Jana, A.; Lee, Y.; Ryu, J.-Y. an-QNA: An Adaptive Nesterov Quasi-Newton Acceleration-Optimized CMOS LNA for 65 nm Automotive Radar Applications. Sensors 2024, 24, 6141. https://doi.org/10.3390/s24186141
Aras U, Woo LS, Delwar TS, Siddique A, Jana A, Lee Y, Ryu J-Y. an-QNA: An Adaptive Nesterov Quasi-Newton Acceleration-Optimized CMOS LNA for 65 nm Automotive Radar Applications. Sensors. 2024; 24(18):6141. https://doi.org/10.3390/s24186141
Chicago/Turabian StyleAras, Unal, Lee Sun Woo, Tahesin Samira Delwar, Abrar Siddique, Anindya Jana, Yangwon Lee, and Jee-Youl Ryu. 2024. "an-QNA: An Adaptive Nesterov Quasi-Newton Acceleration-Optimized CMOS LNA for 65 nm Automotive Radar Applications" Sensors 24, no. 18: 6141. https://doi.org/10.3390/s24186141
APA StyleAras, U., Woo, L. S., Delwar, T. S., Siddique, A., Jana, A., Lee, Y., & Ryu, J.-Y. (2024). an-QNA: An Adaptive Nesterov Quasi-Newton Acceleration-Optimized CMOS LNA for 65 nm Automotive Radar Applications. Sensors, 24(18), 6141. https://doi.org/10.3390/s24186141





