Generating Synthetic Health Sensor Data for Privacy-Preserving Wearable Stress Detection
Abstract
1. Introduction
- We achieve data generation models based on GANs that produce synthetic multimodal time-series sequences corresponding to available smartwatch health sensors. Each data point presents a moment of stress or non-stress and is labeled accordingly.
- Our models generate realistic data that are close to the original distribution, allowing us to effectively expand or replace publicly available, albeit limited, data collections for stress detection while keeping their characteristics and offering privacy guarantees.
- With our solutions for training stress detection models with synthetic data, we are able to improve on state-of-the-art results. Our private synthetic data generators for training DP-conform classifiers help us in applying DP with much better utility–privacy trade-offs and lead to higher performance than before. We give a quick overview regarding the improvements over related work in Table 1.
- Our approach enables applications for stress detection via smartwatches while safeguarding user privacy. By incorporating DP, we ensure that the generated health data can be leveraged freely, circumventing privacy concerns of basic anonymization. This facilitates the development and deployment of accurate models across diverse user groups and enhances research capabilities through increased data availability.
2. Background
2.1. Stress Detection from Physiological Measurements
2.2. Generative Adversarial Network
2.3. Differential Privacy
2.4. Differentially Private Stochastic Gradient Descent
3. Related Work
3.1. Synthetic Data for Stress Detection
3.2. Privacy of Synthetic Data
3.3. Stress Detection on WESAD Dataset
4. Methodology
4.1. Environment
4.2. Dataset Description
4.3. Data Preparation
4.4. Generative Models
- Time-series data: Instead of singular and individual input samples, we find continuous time-dependent data recorded over a specific time interval. Further, each data point is correlated to the rest of the sequence before and after it.
- Multimodal signal data: For each point in time, we find not a single sample but one each for all of our six signal modalities. Artificially generating this multimodality is further complicated by the fact that the modalities correlate to each other and to their labels.
- Class labels: Each sample also has a corresponding class label as stress or non-stress. This is solvable with standard GANs by training a separate GAN for each class, like when using the Time-series GAN (TimeGAN) [32]. However, with such individual models, some correlation between label and signal data might be lost.
4.4.1. Conditional GAN
4.4.2. DoppelGANger GAN
4.4.3. DP-CGAN
4.5. Synthetic Data Quality Evaluation
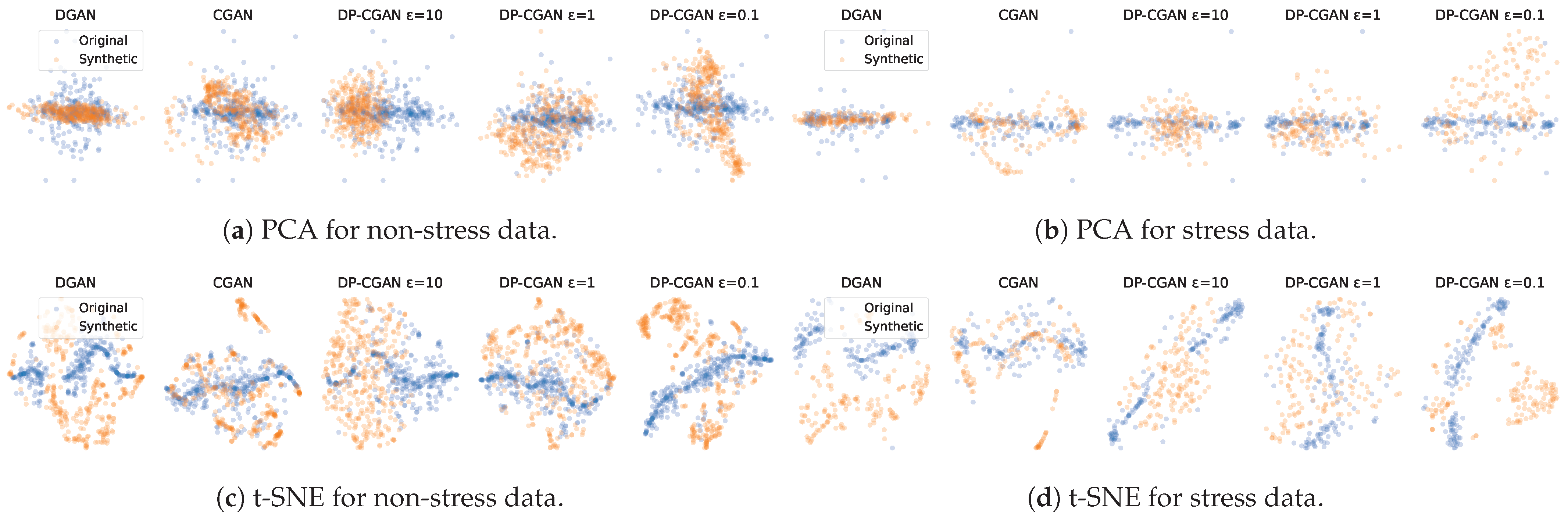
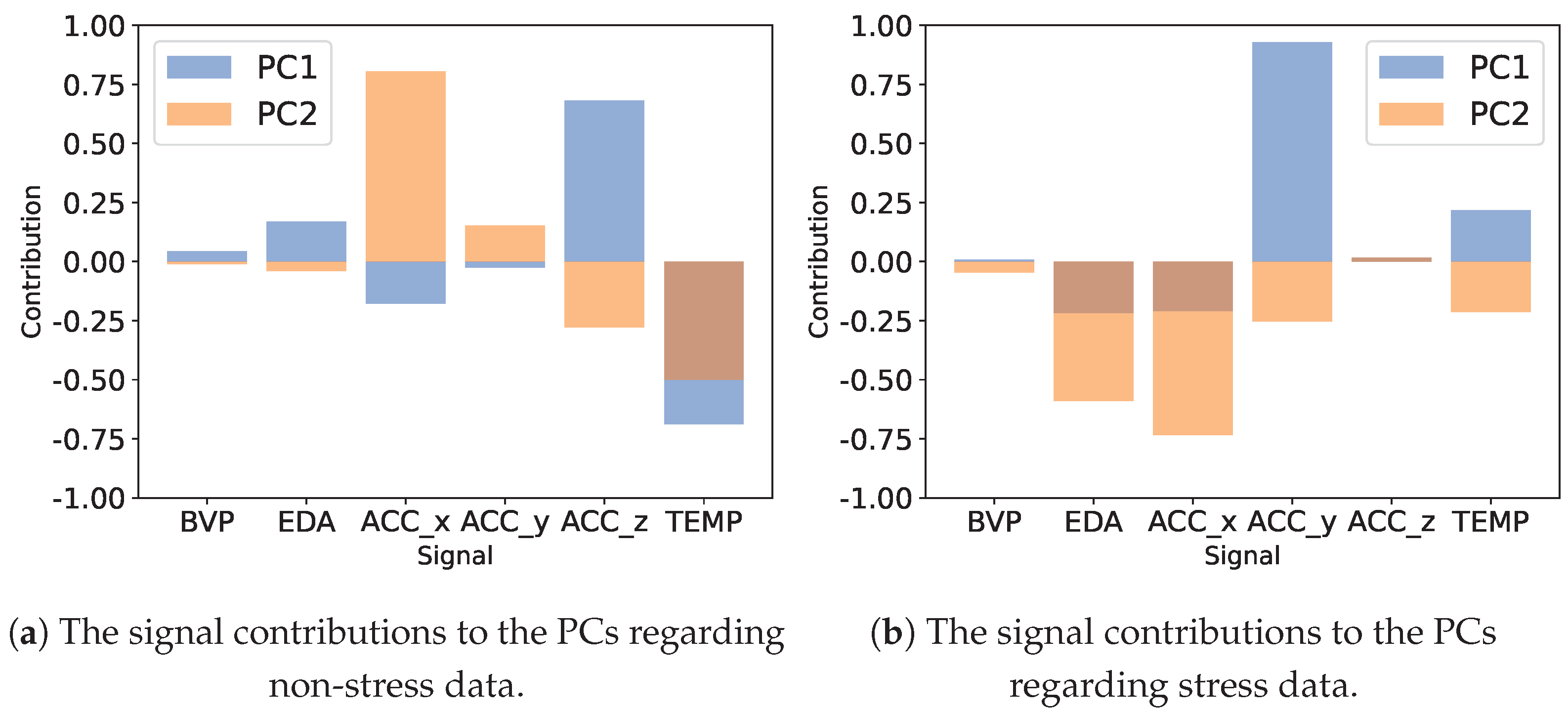
- Principal Component Analysis (PCA) [39]. As a statistical technique for simplifying and visualizing a dataset, PCA converts many correlated statistical variables into principal components to reduce the dimensional space. Generally, PCA is able to identify the principal components that identify the data while preserving their coarser structure. We restrict our analysis to calculating the first two PCs, which is a feasible representation since the major PCs capture most of the variance.
- t-Distributed Stochastic Neighbor Embedding (t-SNE) [40]. Another method for visualizing high-dimensional data is using t-SNE. Each data point is assigned a position in a two-dimensional space. This reduces the dimension while maintaining significant variance. Unlike PCA, it is less qualified at preserving the location of distant points, but can better represent the equality between nearby points.
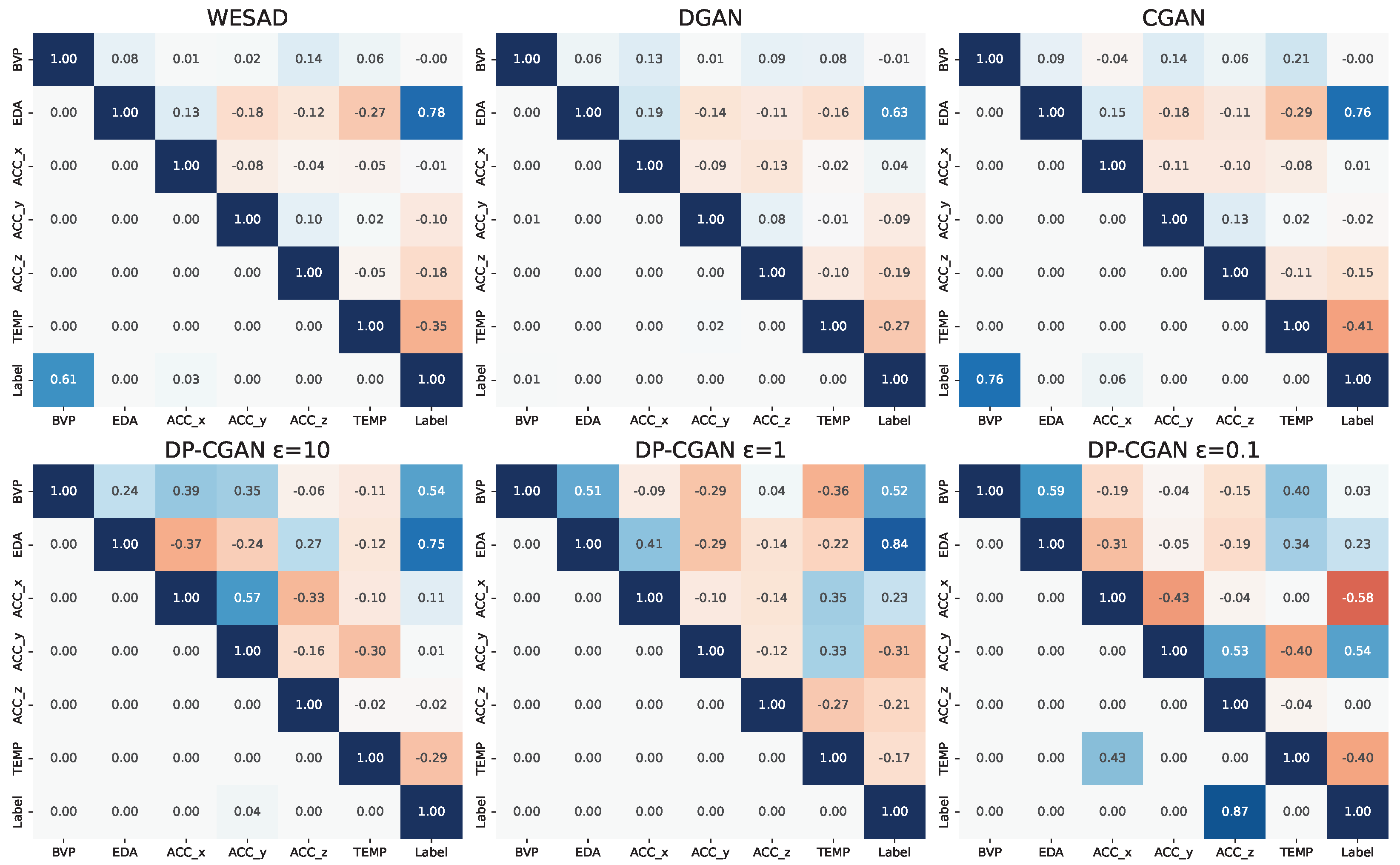
- Signal correlation and distribution. To validate the relationship between signal modalities and to their respective labels, we analyze the strength of the Pearson correlation coefficients [41] found inside the data. A successful GAN model should be able to output synthetic data with a similar correlation as the original training data. Even though correlation does not imply causation, the correlation between labels and signals can be essential to train classification models. Additionally, we calculate the corresponding p-values (probability values) [42] to our correlation coefficients to analyze if our findings are statistically significant. As a further analysis, we also take a look at the actual distribution of signal values to see if the GANs are able to replicate these statistics.
- Classifier Two-Sample Test (C2ST). To evaluate whether the generated data are overall comparable to real WESAD data, we employ a C2ST mostly as described by Lopez-Paz and Oquab [43]. The C2ST uses a classification model that is trained on a portion of both real and synthetic data, with the task of differentiating between the two classes. Afterward, the model is fed with a test set that again consists of real and synthetic samples in equal amounts. Now, if the synthetic data are close to the real data, the classifier would have a hard time correctly labeling the different samples, leaving it with a low accuracy result. In an optimal case, the classifier would label all given test samples as real and thus only achieve 0.5 of accuracy. This test method allows us to see if the generated data are indistinguishable from real data for a trained classifier. For our C2ST model, we decided on a Naive Bayes approach.
4.6. Use Case Specific Evaluation
- Train Synthetic Test Real (TSTR). The TSTR framework is commonly used in the synthetic data domain, which means that the classification model is trained on just the synthetic data and then evaluated on the real data for testing. We implement this concept by generating synthetic subject data in differing amounts, i.e., the number of subjects. We decide to first use the same size as the WESAD set of 15 subjects to simulate a synthetic replacement of the dataset. We then evaluate a larger synthetic set of 100 subjects. Complying with the LOSO method, the model is trained using the respective GAN model, leaving out the test subject on which it is then tested. The average overall subject results are then compared to the original WESAD LOSO result. Private TSTR models can use our already privatized DP-CGAN data in normal training.
- Synthetic Data Augmentation (AUGM). The AUGM strategy focuses on enlarging the original WESAD dataset with synthetic data. For each LOSO run of a WESAD subject, we combine the respective original training data and our LOSO-conform GAN data in differing amounts. As before in TSTR, we consider 15 and 100 synthetic subjects. Testing is also performed in the LOSO format. With this setup, we evaluate if adding more subjects, even though synthetic and of the same nature, helps the classification. Private training in this scenario takes the privatized DP-CGAN data but also has to consider the not-yet-private original WESAD data they are combined with. Therefore, the private AUGM models still undergo a DP-SGD training process to guarantee DP.
4.7. Stress Classifiers
4.7.1. Pre-Processing for Classification
4.7.2. Time-Series Classification Transformer
4.7.3. Convolutional Neural Network
4.7.4. Hybrid Convolutional Neural Network
4.8. Private Training
4.8.1. For Generative Models
4.8.2. For Classification Models
5. Results
5.1. Synthetic Data Quality Results
5.1.1. Two-Dimensional Visualization
5.1.2. Signal Correlation and Distribution
5.1.3. Indistinguishability
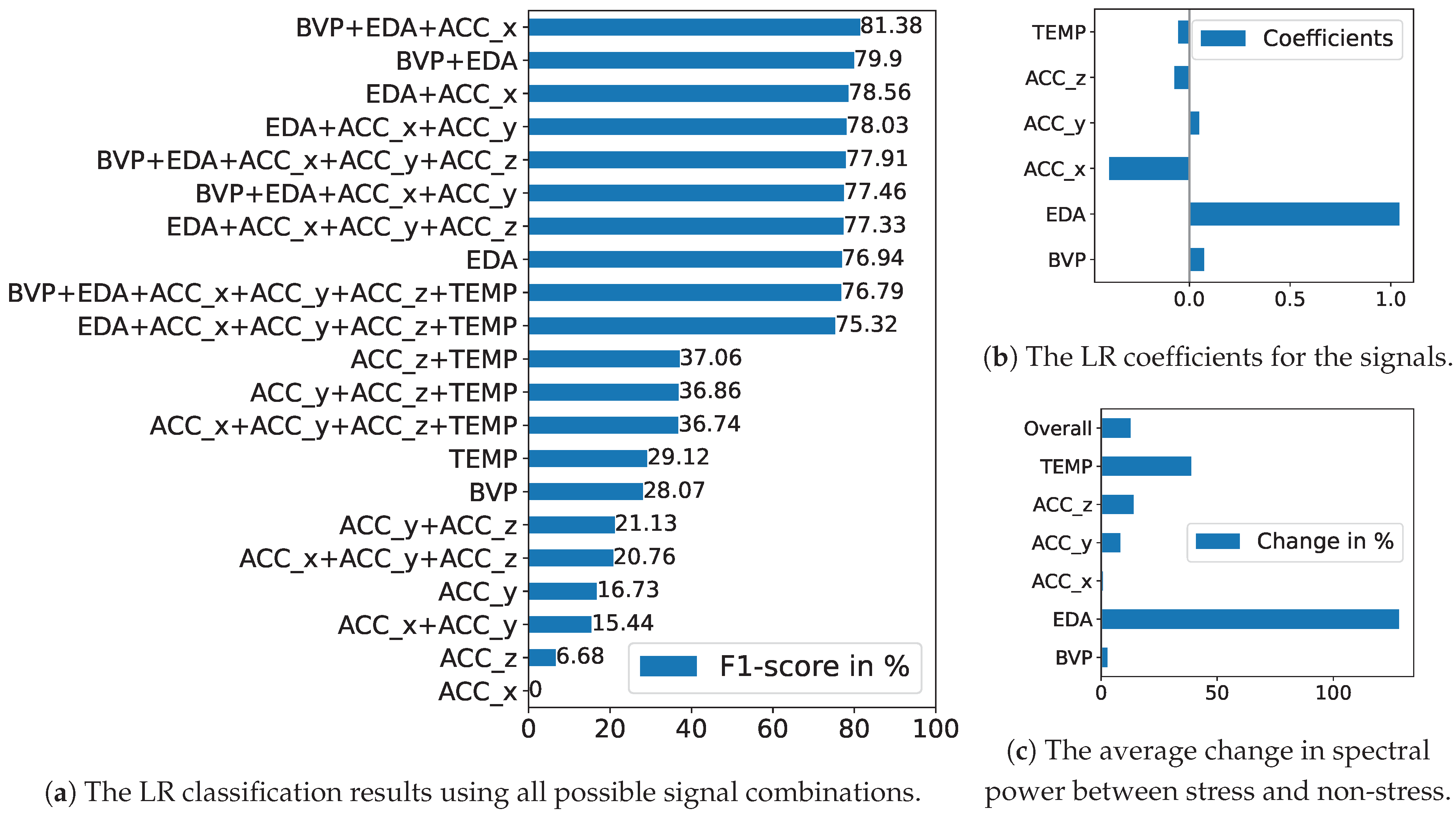
5.2. Stress Detection Use Case Results
5.2.1. Baseline Approach
5.2.2. Deep Learning Approach
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Expanded Results
Appendix A.1. Signal Distribution Plots
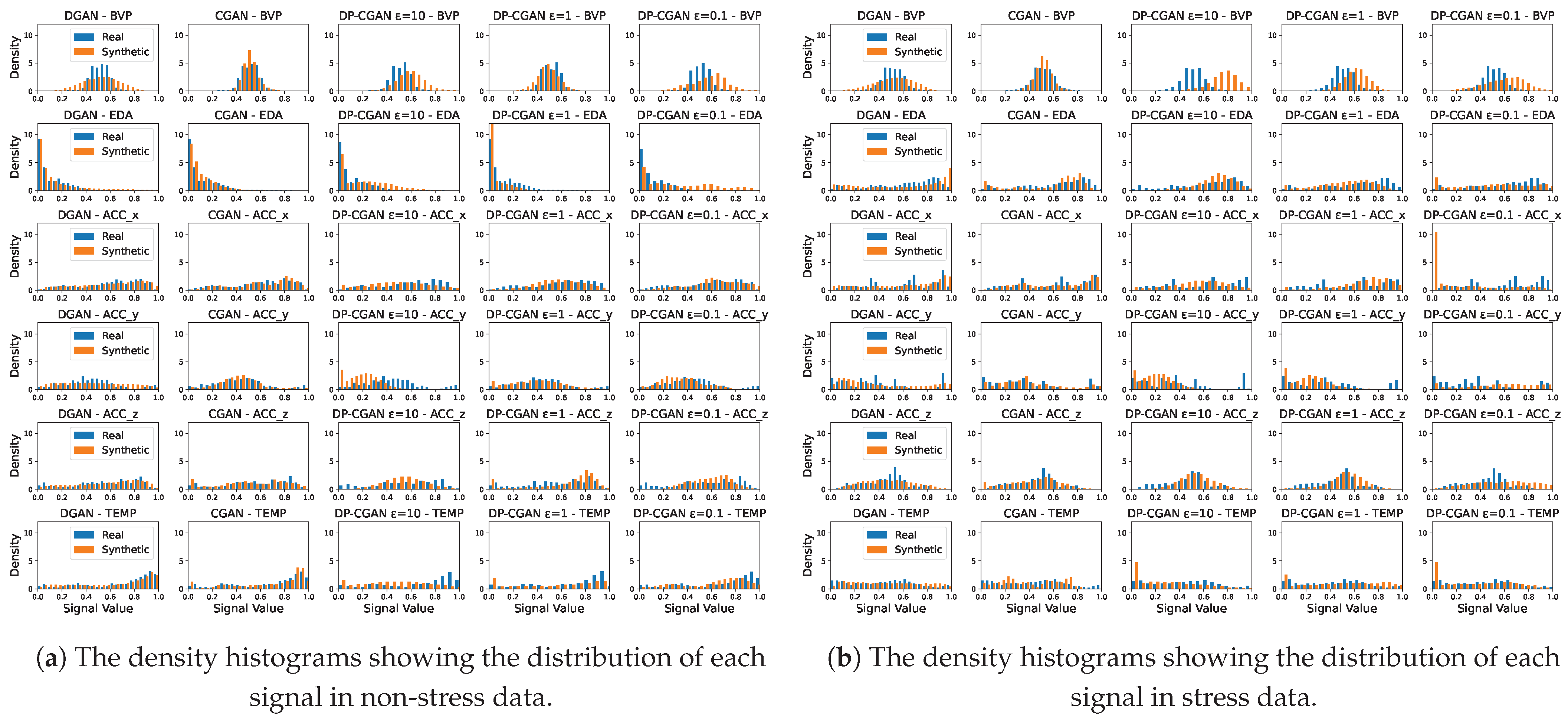
Appendix A.2. Per Subject LOSO Classification Results
| WESAD Subject | WESAD | CGAN | CGAN + WESAD | DP-CGAN | DP-CGAN | DP-CGAN |
|---|---|---|---|---|---|---|
| ID2 | 91.76 | 95.59 | 92.35 | 88.24 | 93.67 | 96.47 |
| ID3 | 74.04 | 70.00 | 77.65 | 65.39 | 61.86 | 66.57 |
| ID4 | 98.14 | 93.59 | 100.00 | 80.71 | 100.00 | 80.29 |
| ID5 | 97.15 | 96.29 | 97.43 | 100.00 | 100.00 | 86.57 |
| ID6 | 93.43 | 98.29 | 97.43 | 100.00 | 97.14 | 99.71 |
| ID7 | 90.12 | 92.29 | 91.43 | 97.14 | 84.26 | 86.86 |
| ID8 | 94.85 | 96.29 | 96.57 | 89.14 | 90.54 | 88.86 |
| ID9 | 97.14 | 97.71 | 98.86 | 100.00 | 97.14 | 90.96 |
| ID10 | 99.03 | 96.80 | 95.83 | 100.00 | 100.00 | 88.49 |
| ID11 | 79.84 | 83.77 | 90.43 | 73.58 | 79.89 | 78.89 |
| ID13 | 99.72 | 93.89 | 96.39 | 99.44 | 85.81 | 99.72 |
| ID14 | 54.46 | 74.88 | 77.22 | 69.44 | 61.00 | 57.22 |
| ID15 | 100.00 | 100.00 | 100.00 | 97.22 | 94.82 | 86.94 |
| ID16 | 96.73 | 89.17 | 95.00 | 95.13 | 91.18 | 71.94 |
| ID17 | 53.57 | 91.39 | 88.61 | 65.18 | 43.04 | 83.33 |
| Average | 88.00 | 91.33 | 93.01 | 88.04 | 85.36 | 84.19 |
References
- Giannakakis, G.; Grigoriadis, D.; Giannakaki, K.; Simantiraki, O.; Roniotis, A.; Tsiknakis, M. Review on psychological stress detection using biosignals. IEEE Trans. Affect. Comput. 2019, 13, 440–460. [Google Scholar] [CrossRef]
- Schmidt, P.; Reiss, A.; Dürichen, R.; Van Laerhoven, K. Wearable-based affect recognition—A review. Sensors 2019, 19, 4079. [Google Scholar] [CrossRef]
- Panicker, S.S.; Gayathri, P. A survey of machine learning techniques in physiology based mental stress detection systems. Biocybern. Biomed. Eng. 2019, 39, 444–469. [Google Scholar] [CrossRef]
- Perez, E.; Abdel-Ghaffar, S. (Google/Fitbit). How We Trained Fitbit’s Body Response Feature to Detect Stress. 2023. Available online: https://blog.google/products/fitbit/how-we-trained-fitbits-body-response-feature-to-detect-stress/ (accessed on 8 May 2024).
- Garmin Technology. Stress Tracking. 2023. Available online: https://www.garmin.com/en-US/garmin-technology/health-science/stress-tracking/ (accessed on 8 May 2024).
- Samsung Electronics. Measure Your Stress Level with Samsung Health. 2023. Available online: https://www.samsung.com/us/support/answer/ANS00080574/ (accessed on 8 May 2024).
- Narayanan, A.; Shmatikov, V. Robust de-anonymization of large sparse datasets. In Proceedings of the 2008 IEEE Symposium on Security and Privacy (SP), Oakland, CA, USA, 18–22 May 2008; pp. 111–125. [Google Scholar]
- Perez, A.J.; Zeadally, S. Privacy issues and solutions for consumer wearables. Professional 2017, 20, 46–56. [Google Scholar] [CrossRef]
- Jafarlou, S.; Rahmani, A.M.; Dutt, N.; Mousavi, S.R. ECG Biosignal Deidentification Using Conditional Generative Adversarial Networks. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Oakland, CA, USA, 18–22 May 2008; pp. 1366–1370. [Google Scholar]
- Lange, L.; Schreieder, T.; Christen, V.; Rahm, E. Privacy at Risk: Exploiting Similarities in Health Data for Identity Inference. arXiv 2023, arXiv:2308.08310. [Google Scholar]
- Saleheen, N.; Ullah, M.A.; Chakraborty, S.; Ones, D.S.; Srivastava, M.; Kumar, S. Wristprint: Characterizing user re-identification risks from wrist-worn accelerometry data. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, 15–19 November 2021; pp. 2807–2823. [Google Scholar]
- El Emam, K.; Jonker, E.; Arbuckle, L.; Malin, B. A systematic review of re-identification attacks on health data. PLoS ONE 2011, 6, e28071. [Google Scholar] [CrossRef]
- Chikwetu, L.; Miao, Y.; Woldetensae, M.K.; Bell, D.; Goldenholz, D.M.; Dunn, J. Does deidentification of data from wearable devices give us a false sense of security? A systematic review. Lancet Digit. Health 2023, 5, e239–e247. [Google Scholar] [CrossRef]
- Kokosi, T.; Harron, K. Synthetic data in medical research. BMJ Med. 2022, 1, e000167. [Google Scholar] [CrossRef] [PubMed]
- Javed, H.; Muqeet, H.A.; Javed, T.; Rehman, A.U.; Sadiq, R. Ethical Frameworks for Machine Learning in Sensitive Healthcare Applications. IEEE Access 2023, 12, 16233–16254. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 139–144. [Google Scholar] [CrossRef]
- Xie, L.; Lin, K.; Wang, S.; Wang, F.; Zhou, J. Differentially private generative adversarial network. arXiv 2018, arXiv:1802.06739. [Google Scholar]
- Lange, L.; Degenkolb, B.; Rahm, E. Privacy-Preserving Stress Detection Using Smartwatch Health Data. In Proceedings of the 4. Interdisciplinary Privacy & Security at Large Workshop, INFORMATIK 2023, Berlin, Germany, 26–29 September 2023. [Google Scholar]
- Schmidt, P.; Reiss, A.; Duerichen, R.; Marberger, C.; Van Laerhoven, K. Introducing wesad, a multimodal dataset for wearable stress and affect detection. In Proceedings of the 20th ACM International Conference on Multimodal Interaction, Boulder, CO, USA, 16–20 October 2018; pp. 400–408. [Google Scholar]
- Siirtola, P. Continuous stress detection using the sensors of commercial smartwatch. In Proceedings of the Adjunct Proceedings of the 2019 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2019 ACM International Symposium on Wearable Computers, London, UK, 9–13 September 2019; pp. 1198–1201. [Google Scholar]
- Gil-Martin, M.; San-Segundo, R.; Mateos, A.; Ferreiros-Lopez, J. Human stress detection with wearable sensors using convolutional neural networks. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 60–70. [Google Scholar] [CrossRef]
- Empatica Incorporated. E4 Wristband. 2020. Available online: http://www.empatica.com/research/e4/ (accessed on 8 May 2024).
- Nasr, M.; Songi, S.; Thakurta, A.; Papernot, N.; Carlin, N. Adversary instantiation: Lower bounds for differentially private machine learning. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 866–882. [Google Scholar]
- Carlini, N.; Liu, C.; Erlingsson, Ú.; Kos, J.; Song, D. The Secret Sharer: Evaluating and Testing Unintended Memorization in Neural Networks. In Proceedings of the 28th USENIX Security Symposium (USENIX Security 19), Santa Clara, CA, USA, 14–16 August 2019; pp. 267–284. [Google Scholar]
- Lange, L.; Schneider, M.; Christen, P.; Rahm, E. Privacy in Practice: Private COVID-19 Detection in X-Ray Images. In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023). SciTePress, Rome, Italy, 10–12 July 2023; pp. 624–633. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Ehrhart, M.; Resch, B.; Havas, C.; Niederseer, D. A Conditional GAN for Generating Time Series Data for Stress Detection in Wearable Physiological Sensor Data. Sensors 2022, 22, 5969. [Google Scholar] [CrossRef] [PubMed]
- Stadler, T.; Oprisanu, B.; Troncoso, C. Synthetic Data—Anonymisation Groundhog Day. In Proceedings of the 31st USENIX Security Symposium (USENIX Security 22), Boston, MA, USA, 10–12 August 2022; pp. 1451–1468. [Google Scholar]
- Torkzadehmahani, R.; Kairouz, P.; Paten, B. DP-CGAN: Differentially Private Synthetic Data and Label Generation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA; 2019; pp. 98–104. [Google Scholar] [CrossRef]
- Dzieżyc, M.; Gjoreski, M.; Kazienko, P.; Saganowski, S.; Gams, M. Can we ditch feature engineering? end-to-end deep learning for affect recognition from physiological sensor data. Sensors 2020, 20, 6535. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.; Jarrett, D.; Van der Schaar, M. Time-series generative adversarial networks. Adv. Neural Inf. Process. Syst. 2019, 32, 5508–5518. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-valued (medical) time series generation with recurrent conditional gans. arXiv 2017, arXiv:1706.02633. [Google Scholar]
- Wenzlitschke, N. Privacy-Preserving Smartwatch Health Data Generation For Stress Detection Using GANs. Master’s thesis, University Leipzig, Leipzig, Germany, 2023. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lin, Z.; Jain, A.; Wang, C.; Fanti, G.; Sekar, V. Using gans for sharing networked time series data: Challenges, initial promise, and open questions. In Proceedings of the ACM Internet Measurement Conference, Virtual Event, 27–29 October 2020; pp. 464–483. [Google Scholar]
- Liu, Y.; Peng, J.; James, J.; Wu, Y. PPGAN: Privacy-preserving generative adversarial network. In Proceedings of the 2019 IEEE 25Th International Conference on Parallel and Distributed Systems (ICPADS), Tianjin, China, 4–6 December 2019; pp. 985–989. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef]
- Schervish, M.J. P values: What they are and what they are not. Am. Stat. 1996, 50, 203–206. [Google Scholar] [CrossRef]
- Lopez-Paz, D.; Oquab, M. Revisiting classifier two-sample tests. arXiv 2016, arXiv:1610.06545. [Google Scholar]



| Reference | Model | Data | Accuracy | F1-Score | Privacy Budget |
|---|---|---|---|---|---|
| [20] | RF | WESAD | 87.12 | 84.11 | ∞ |
| [21] | LDA | WESAD | 87.40 | N/A | ∞ |
| [22] | CNN | WESAD | 92.70 | 92.55 | ∞ |
| [19] | TSCT | WESAD | 91.89 | 91.61 | ∞ |
| Ours | CNN-LSTM | CGAN + WESAD | 92.98 | 93.01 | ∞ |
| [19] | DP-TSCT | WESAD | 78.88 | 76.14 | 10 |
| Ours | CNN | DP-CGAN | 88.08 | 88.04 | 10 |
| [19] | DP-TSCT | WESAD | 78.16 | 71.26 | 1 |
| Ours | CNN | DP-CGAN | 85.46 | 85.36 | 1 |
| [19] | DP-TSCT | WESAD | 71.15 | 68.71 | 0.1 |
| Ours | CNN-LSTM | DP-CGAN | 84.16 | 84.19 | 0.1 |
| Signal | Frequency Range | Subwindow Length | # Inputs |
|---|---|---|---|
| ACC (x,y,z) | 0–30 Hz | 7 s | 210 |
| BVP | 0–7 Hz | 30 s | 210 |
| EDA | 0–7 Hz | 30 s | 210 |
| TEMP | 0–6 Hz | 35 s | 210 |
| WESAD (Unseen) | DGAN | CGAN | DP-CGAN | DP-CGAN | DP-CGAN | |
|---|---|---|---|---|---|---|
| Both | 0.59 | 0.93 | 0.61 | 0.93 | 0.77 | 0.75 |
| Stress | 0.72 | 0.94 | 0.77 | 1.00 | 0.90 | 0.85 |
| Non-stress | 0.70 | 0.90 | 0.71 | 0.99 | 0.83 | 0.91 |
| Strategy | Dataset (s) | Subject Counts | Privacy Budget | TSCT | CNN | CNN-LSTM |
|---|---|---|---|---|---|---|
| Original | WESAD | 15 | ∞ | 80.65 | 88.00 | 86.48 |
| TSTR | DGAN | 15 | ∞ | 80.60 | 85.89 | 85.33 |
| TSTR | CGAN | 15 | ∞ | 87.04 | 88.50 | 90.24 |
| TSTR | DGAN | 100 | ∞ | 73.90 | 84.46 | 79.31 |
| TSTR | CGAN | 100 | ∞ | 86.97 | 87.96 | 91.33 |
| AUGM | DGAN + WESAD | 15 + 15 | ∞ | 82.86 | 88.45 | 90.67 |
| AUGM | CGAN + WESAD | 15 + 15 | ∞ | 88.00 | 91.13 | 90.83 |
| AUGM | DGAN + WESAD | 100 + 15 | ∞ | 86.94 | 87.28 | 88.14 |
| AUGM | CGAN + WESAD | 100 + 15 | ∞ | 90.67 | 91.40 | 93.01 |
| Original | WESAD | 15 | 10 | 59.81 | 46.21 | 73.18 |
| TSTR | DP-CGAN | 15 | 10 | 87.55 | 88.04 | 84.84 |
| TSTR | DP-CGAN | 100 | 10 | 85.28 | 86.41 | 85.19 |
| AUGM | DP-CGAN + WESAD | 15 + 15 | 10 | 64.24 | 73.66 | 71.70 |
| AUGM | DP-CGAN + WESAD | 100 + 15 | 10 | 71.96 | 73.50 | 69.59 |
| Original | WESAD | 15 | 1 | 58.31 | 26.82 | 71.82 |
| TSTR | DP-CGAN | 15 | 1 | 82.90 | 85.36 | 78.07 |
| TSTR | DP-CGAN | 100 | 1 | 83.75 | 77.43 | 83.94 |
| AUGM | DP-CGAN + WESAD | 15 + 15 | 1 | 68.55 | 75.76 | 71.70 |
| AUGM | DP-CGAN + WESAD | 100 + 15 | 1 | 50.06 | 62.03 | 71.75 |
| Original | WESAD | 15 | 0.1 | 58.81 | 28.32 | 71.70 |
| TSTR | DP-CGAN | 15 | 0.1 | 76.27 | 81.35 | 76.53 |
| TSTR | DP-CGAN | 100 | 0.1 | 76.54 | 83.00 | 84.19 |
| AUGM | DP-CGAN + WESAD | 15 + 15 | 0.1 | 68.99 | 73.89 | 71.70 |
| AUGM | DP-CGAN + WESAD | 100 + 15 | 0.1 | 35.05 | 61.99 | 71.70 |
| WESAD Subject | WESAD | CGAN | CGAN + WESAD | DP-CGAN | DP-CGAN | DP-CGAN |
|---|---|---|---|---|---|---|
| ID14 | 54.46 | 74.88 | 77.22 | 69.44 | 61.00 | 57.22 |
| ID17 | 53.57 | 91.39 | 88.61 | 65.18 | 43.04 | 83.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lange, L.; Wenzlitschke, N.; Rahm, E. Generating Synthetic Health Sensor Data for Privacy-Preserving Wearable Stress Detection. Sensors 2024, 24, 3052. https://doi.org/10.3390/s24103052
Lange L, Wenzlitschke N, Rahm E. Generating Synthetic Health Sensor Data for Privacy-Preserving Wearable Stress Detection. Sensors. 2024; 24(10):3052. https://doi.org/10.3390/s24103052
Chicago/Turabian StyleLange, Lucas, Nils Wenzlitschke, and Erhard Rahm. 2024. "Generating Synthetic Health Sensor Data for Privacy-Preserving Wearable Stress Detection" Sensors 24, no. 10: 3052. https://doi.org/10.3390/s24103052
APA StyleLange, L., Wenzlitschke, N., & Rahm, E. (2024). Generating Synthetic Health Sensor Data for Privacy-Preserving Wearable Stress Detection. Sensors, 24(10), 3052. https://doi.org/10.3390/s24103052






