Hierarchical Multi-Objective Optimization for Dedicated Bus Punctuality and Supply–Demand Balance Control
Abstract
1. Introduction
2. Literature Review
2.1. Transit Signal Priority
2.2. Bus Speed Guidance
2.3. Bus Schedule Optimization
2.4. Summary
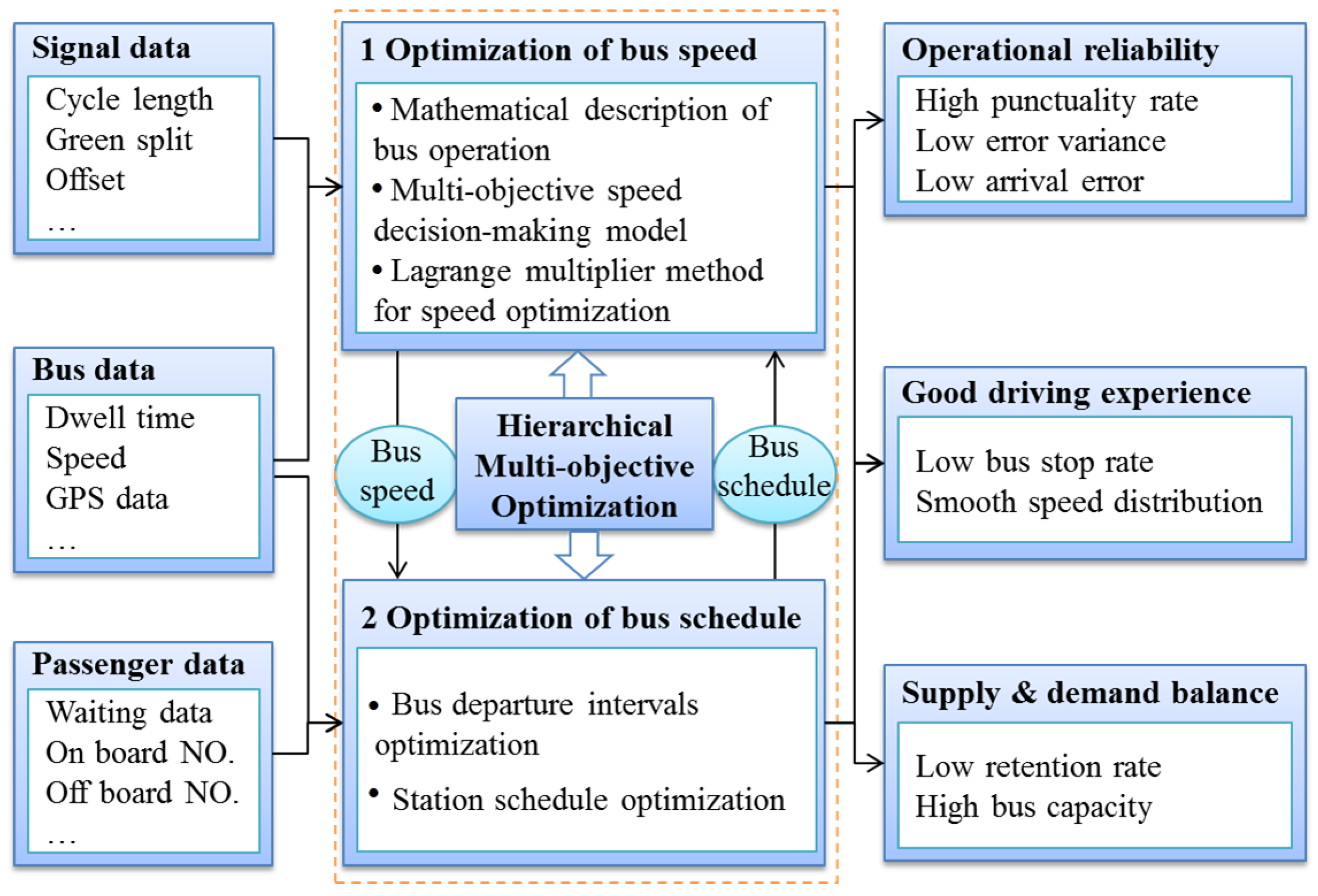
3. Outline of Research Framework
3.1. Assumptions
3.2. Research Framework
4. Optimization of Bus Speed
4.1. Mathematical Description of Bus Operation
4.2. Multi-Objective Speed-Decision-Making Model
4.3. Lagrange Multiplier Method for Speed Optimization
| Algorithm 1 Lagrangian multiplier method. |
| Input I: Guide speed of each section V Output I: Optimization results 1: According to (4), determine the first-level optimization goals and constraints: 3: Solve the speed combination : 6: Solve the speed combination : |
5. Optimization of Bus Schedule
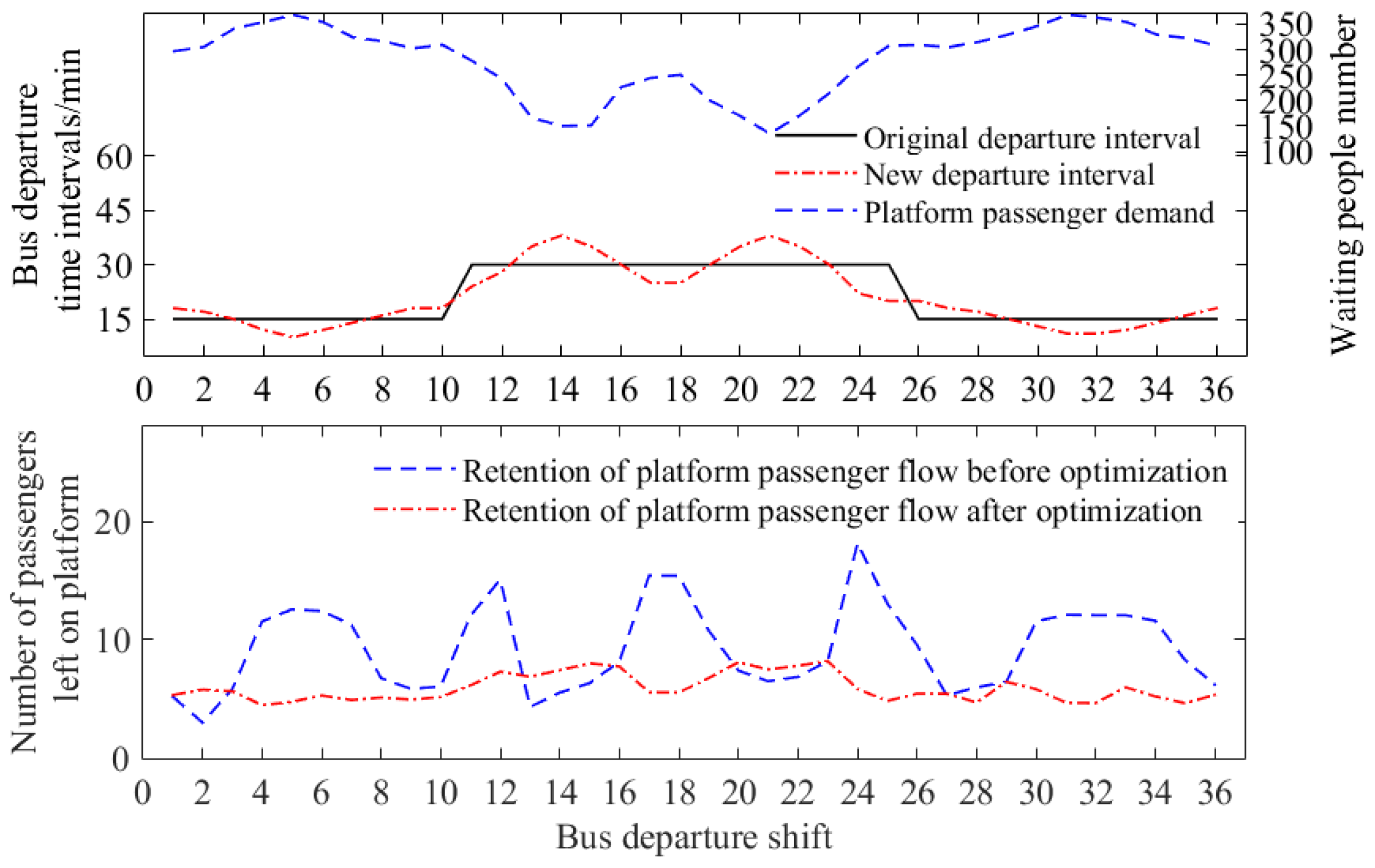
5.1. Bus Departure Intervals Optimization
| Algorithm 2 Genetic algorithm. |
| Input I: Output I: Optimal target values 1: need to be defined independently for optimization purposes, and can be obtained from (9). Moreover, the parameter constraints are 2: Determine the encoding method and use the real number encoding method. 3: Determine the individual evaluation method; the fitness function is (10). 4: Design a genetic operator, where the selection operation uses a proportional selection operator, the crossover operation uses a single point crossover operator, and the mutation operation uses a basic bit mutation operator. 5: Determine the operating parameters of genetic algorithm , population size , iteration number , crossover probability, and mutation probability . end |
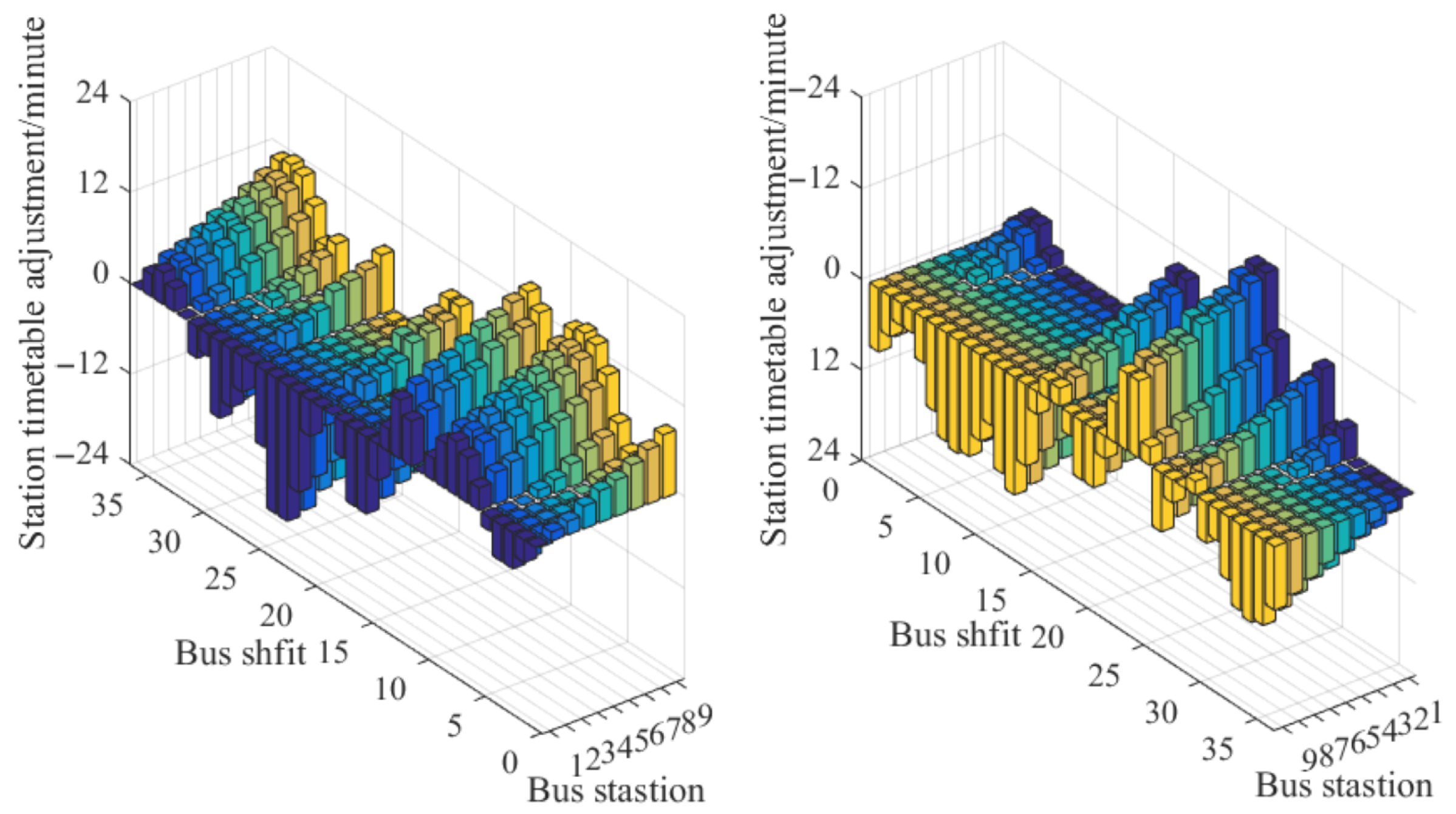
5.2. Station Schedule Optimization
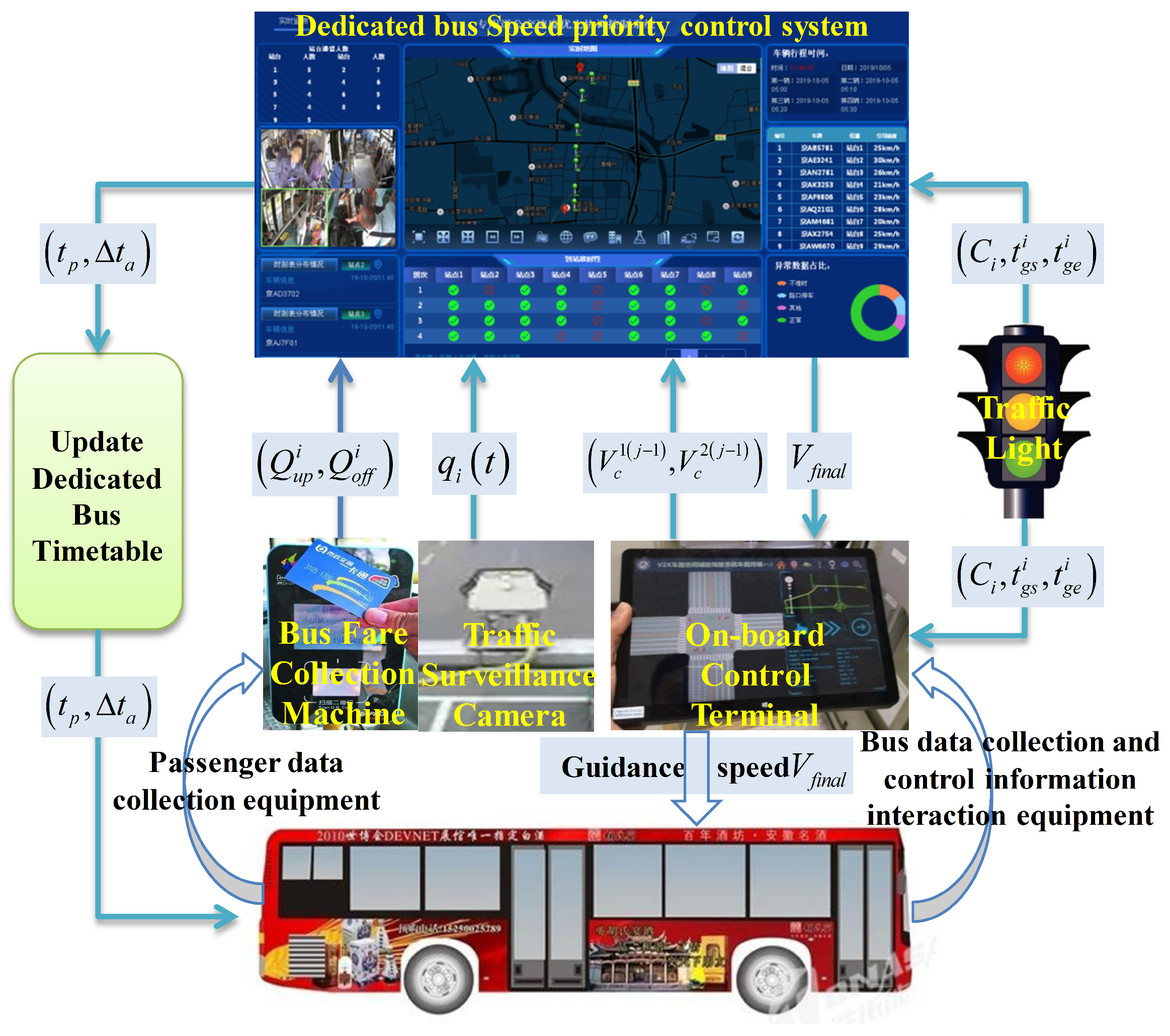
6. Evaluation
6.1. Introduction of Testing Scenario
6.2. Test Scheme Design
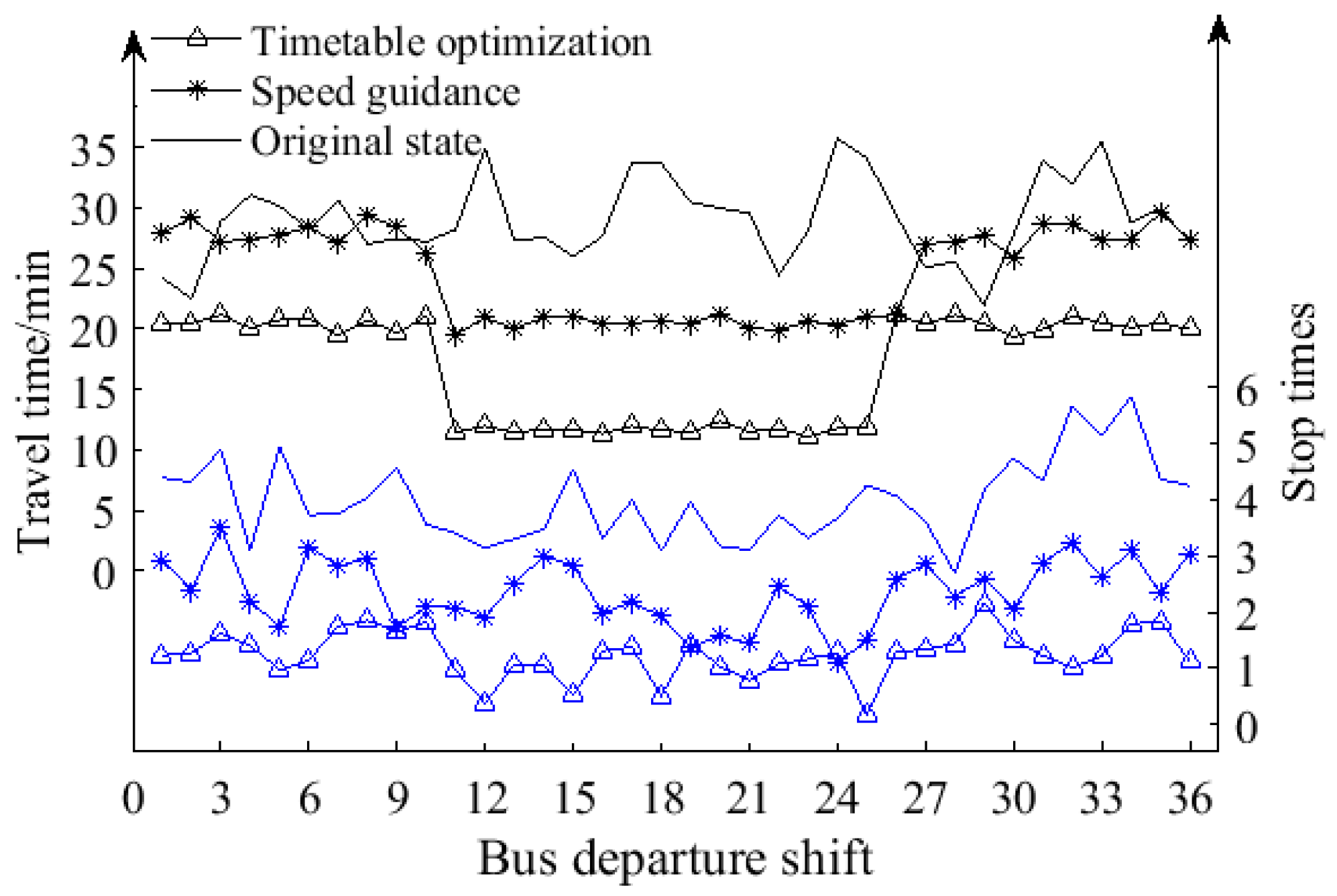
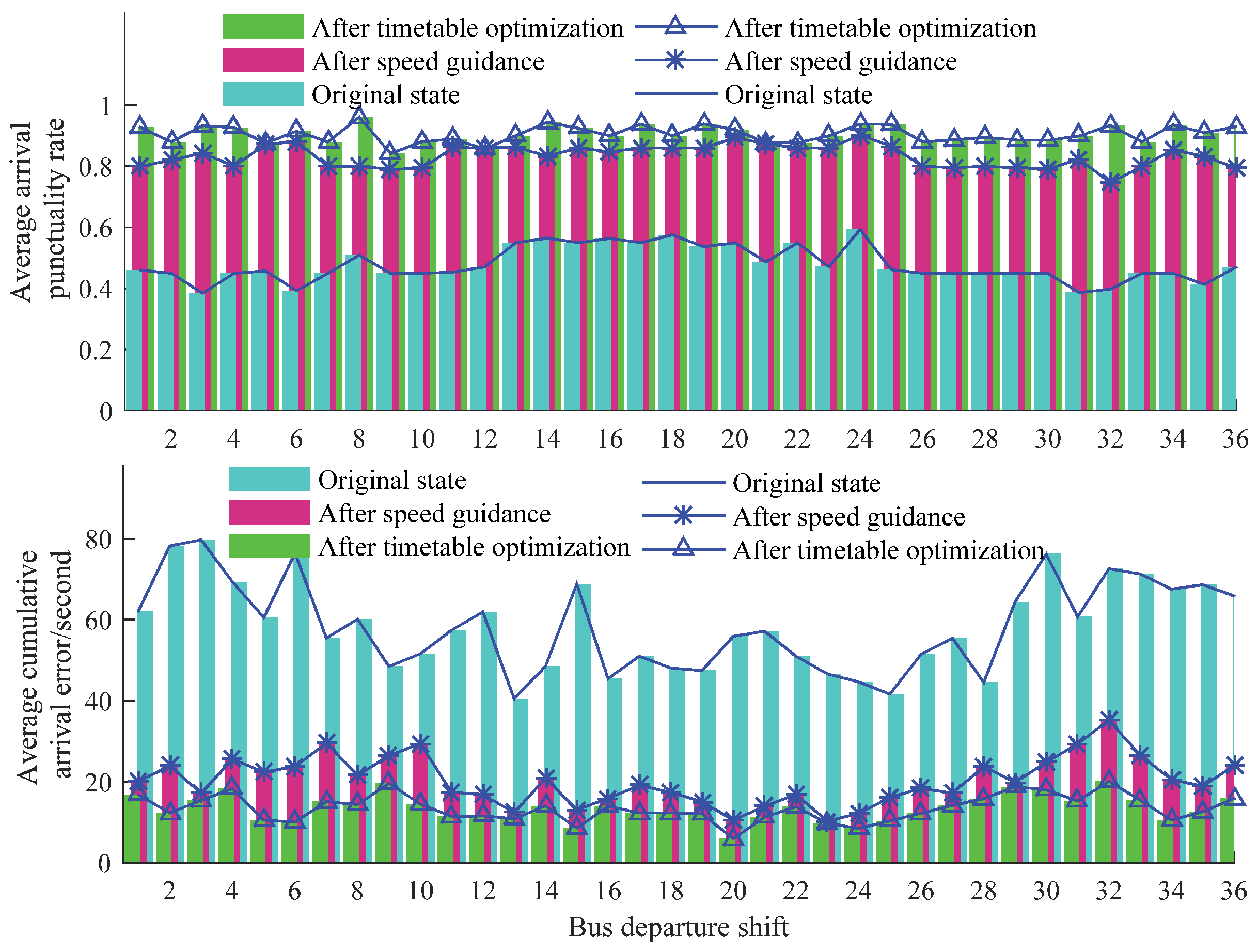
6.3. Analysis of Test Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TOD | transit-oriented development |
| ATSP | advanced transit signal priority |
| GPS | global positioning system |
References
- Ibraeva, A.; Correia, G.H.d.; Silva, C.; Antunes, A.P. Transit-oriented development: A review of research achievements and challenges. Transp. Res. Part A Policy Pract. 2020, 132, 110–130. [Google Scholar] [CrossRef]
- Xi, J.H.; Zhu, F.H.; Ye, P.J.; Lv, Y.S.; Tang, H.N.; Wang, F.Y. Hierarchical Mixed Deep Reinforcement Learning to Balance Vehicle Supply and Demand. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21861–21872. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, F.H.; Lv, Y.S.; Tan, C.; Liu, W.; Zhange, X.; Wang, F.Y. An adaptive graph learning algorithm for traffic prediction based on spatiotemporal neural networks. Transp. Res. Part C Emerg. Technol. 2022, 139, 1–17. [Google Scholar] [CrossRef]
- Zhu, F.H.; Lv, Y.S.; Chen, Y.Y.; Chen, S.C.; Wang, X.; Xiong, G.; Wang, F.Y. Parallel Transportation Systems: Toward IoT-Enabled Smart Urban Traffic Control and Management. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4063–4071. [Google Scholar] [CrossRef]
- Islam, T.; Vu, H.L.; Hoang, N.H.; Cricenti, A. A linear bus rapid transit with transit signal priority formulation. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 163–184. [Google Scholar] [CrossRef]
- Qiao, W.X.; Wang, D. A Transit Signal Priority Optimizing Model Based on Reliability. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 54–59, 67. [Google Scholar]
- Truong, L.T.; Currie, G.; Wallace, M.; Gruyter, C.D.; An, K. Coordinated Transit Signal Priority Model Considering Stochastic Bus Arrival Time. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1269–1277. [Google Scholar] [CrossRef]
- Li, J.L.; Liu, Y.G. Bus Priority Signal Control Considering Delays of Passengers and Pedestrians of Adjacent Intersections. J. Adv. Transp. 2020, 2020, 3935795. [Google Scholar] [CrossRef]
- He, H.T.; Guler, S.I.; Menendez, M. Adaptive control algorithm to provide bus priority with a pre-signal. Transp. Res. Part C 2016, 64, 28–44. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, Z.; Li, J. Shockwave-based queue length estimation method for pre-signals for bus priority. J. Transp. Eng. Part A Syst. 2018, 144, 150–162. [Google Scholar] [CrossRef]
- Shu, S.J.; Zhao, J.; Han, Y. Novel Design Method for Bus Approach Lanes with Bus Guidance and Priority Controls for Prioritizing Through and Left-Turn Buses. J. Adv. Transp. 2019, 2019, 2327876. [Google Scholar] [CrossRef]
- Chiara, C.; Fusco, G. A Simulation-Optimization Method for Signal Synchronization with Bus Priority and Driver Speed Advisory to Connected Vehicles. Transp. Res. Procedia 2020, 45, 890–897. [Google Scholar]
- Deng, Y.J.; Liu, X.H.; Hu, X.B. Reduce Bus Bunching with a Real-Time Speed Control Algorithm Considering Heterogeneous Roadway Conditions and Intersection Delays. J. Transp. Eng. Part A Syst. 2020, 146, 1–14. [Google Scholar] [CrossRef]
- Takashi, N. Effect of periodic inflow on speed-controlled shuttle bus. Phys. Stat. Mech. Its Appl. 2017, 469, 224–231. [Google Scholar]
- Yan, H.; Liu, R.K. Bus Speed Control Strategy and Algorithm Based on Real-time Information. J. Transp. Syst. Eng. Inf. Technol. 2018, 18, 61–68. [Google Scholar]
- Zhang, H.; Cui, H.; Shi, B. A Data-Driven Analysis for Operational Vehicle Performance of Public Transport Network. IEEE Access 2019, 7, 96404–96413. [Google Scholar] [CrossRef]
- Li, J.; Hu, J.; Zhang, Y. Optimal combinations and variable departure intervals for micro bus system. Tsinghua Sci. Technol. 2017, 22, 282–292. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Alesiani, F. Robust timetable optimization for bus lines subject to resource and regulatory constraints. Transp. Res. Part Logist. Transp. Rev. 2019, 128, 30–51. [Google Scholar] [CrossRef]
- Banerjee, D.; Smilowitz, K. Incorporating equity into the school bus scheduling problem. Transp. Res. Part Logist. Transp. Rev. 2019, 131, 228–246. [Google Scholar] [CrossRef]
- Teng, J.; Chen, T. Integrated Approach to Vehicle Scheduling and Bus Timetabling for an Electric Bus Line. J. Transp. Eng. Part A Syst. 2020, 146, 1–10. [Google Scholar] [CrossRef]
- Liu, Z.C.; Wu, N.Q.; Qiao, Y.; Li, Z.W. Performance Evaluation of Public Bus Transportation by Using DEA Models and Shannon Entropy: An Example from a Company in a Large City of China. IEEE/CAA J. Autom. Sin. 2021, 8, 779–795. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, Z.Y. Optimization Model for Public Transport Timetable with the Time Weight of Transfer Station. J. Transp. Eng. Inf. 2020, 18, 77–82+98. [Google Scholar]
- Bie, Y.M.; Liu, Z.Y.; Wang, H.Q. Integrating Bus Priority and Pre-signal Method at Signalized Intersection: Algorithm Development and Evaluation. J. Transp. Eng. Part A Syst. 2020, 146, 1–11. [Google Scholar] [CrossRef]
- Khaled, S.; Ghanim, M. Evaluation of Transit Signal Priority Implementation for Bus Transit along a Major Arterial Using Micro-simulation. Procedia Comput. Sci. 2018, 130, 82–89. [Google Scholar]
- Shang, H.Y.; Huang, H.J.; Wu, W.X. Bus timetabling considering passenger satisfaction: An empirical study in Beijing. Comput. Ind. Eng. 2019, 135, 1155–1166. [Google Scholar] [CrossRef]
- Ma, H.G.; Li, X.; Yu, H.T. Single bus line timetable optimization with big data: A case study in Beijing. Inf. Sci. 2020, 536, 53–66. [Google Scholar] [CrossRef]
- Rashidi, S.; Ranjitkar, P. Bus Dwell Time Modeling Using Gene Expression Programming. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 478–489. [Google Scholar] [CrossRef]
- Csaba, C.; Zsolt, S. Method for analysis and prediction of dwell times at stops in local bus transportation. Transport 2017, 32, 302–313. [Google Scholar]
- Liu, D.R.; Xu, Y.C.; Wei, Q.L.; Liu, X.L. Residential Energy Scheduling for Variable Weather Solar Energy Based on Adaptive Dynamic Programming. IEEE/CAA J. Autom. Sin. 2018, 5, 36–46. [Google Scholar] [CrossRef]
- Mahdavilayen, M.; Paquet, V.; He, Q. Using Microsimulation to Estimate Effects of Boarding Conditions on Bus Dwell Time and Schedule Adherence for Passengers with Mobility Limitations. J. Transp. Eng. Part A Syst. 2020, 146, 1–15. [Google Scholar] [CrossRef]
- Nie, J.W. Tight relaxations for polynomial optimization and Lagrange multiplier expressions. Math. Program. 2019, 178, 1–37. [Google Scholar] [CrossRef]
- Agrawal, N.; Kumar, A.; Bajaj, V. A New Design Approach for Nearly Linear Phase Stable IIR Filter using Fractional Derivative. IEEE/CAA J. Autom. Sin. 2020, 7, 527–538. [Google Scholar] [CrossRef]
- Choi, H.S.; Kim, J.G.; Doostan, A.; Park, K.C. Acceleration of uncertainty propagation through Lagrange multipliers in partitioned stochastic method. Comput. Methods Appl. Mech. Eng. 2020, 362, 1–27. [Google Scholar]
- Wu, W.T.; Liu, R.H.; Jin, W.Z. Stochastic bus schedule coordination considering demand assignment and rerouting of passengers. Transp. Res. Part B 2019, 121, 275–303. [Google Scholar] [CrossRef]
- Madhusudhanan, A.K.; Na, X.X. Effect of a Traffic Speed Based Cruise Control on an Electric Vehicle Performance and an Energy Consumption Model of an Electric Vehicle. IEEE/CAA J. Autom. Sin. 2020, 7, 386–394. [Google Scholar] [CrossRef]
- Deng, M.; Li, C.D. Dynamic Prediction Model of Bus Dwell Time under Different Station Conditions. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2019, 38, 105–109. [Google Scholar]

| NO. | Starting Point | Terminal | Distance (m) |
|---|---|---|---|
| 1 | Platform 1 | Intersection 1 | 260 |
| 2 | Intersection 1 | Platform 2 | 207 |
| 3 | Platform 2 | Intersection 2 | 280 |
| 4 | Intersection 2 | Platform 3 | 195 |
| 5 | Platform 3 | Intersection 3 | 167 |
| 6 | Intersection 3 | Platform 4 | 230 |
| 7 | Platform 4 | Intersection 4 | 170 |
| 8 | Intersection 4 | Platform 5 | 837 |
| 9 | Platform 5 | Intersection 5 | 203 |
| 10 | Intersection 5 | Platform 6 | 236 |
| 11 | Platform 6 | Intersection 6 | 120 |
| 12 | Intersection 6 | Platform 7 | 355 |
| 13 | Platform 7 | Intersection 7 | 295 |
| 14 | Intersection 7 | Platform 8 | 168 |
| 15 | Platform 8 | Intersection 8 | 108 |
| 16 | Intersection 8 | Platform 9 | 678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, C.; Zhu, F.; Xu, Y.; Liu, X.; Jiang, T. Hierarchical Multi-Objective Optimization for Dedicated Bus Punctuality and Supply–Demand Balance Control. Sensors 2023, 23, 4552. https://doi.org/10.3390/s23094552
Shang C, Zhu F, Xu Y, Liu X, Jiang T. Hierarchical Multi-Objective Optimization for Dedicated Bus Punctuality and Supply–Demand Balance Control. Sensors. 2023; 23(9):4552. https://doi.org/10.3390/s23094552
Chicago/Turabian StyleShang, Chunlin, Fenghua Zhu, Yancai Xu, Xiaoming Liu, and Tianhua Jiang. 2023. "Hierarchical Multi-Objective Optimization for Dedicated Bus Punctuality and Supply–Demand Balance Control" Sensors 23, no. 9: 4552. https://doi.org/10.3390/s23094552
APA StyleShang, C., Zhu, F., Xu, Y., Liu, X., & Jiang, T. (2023). Hierarchical Multi-Objective Optimization for Dedicated Bus Punctuality and Supply–Demand Balance Control. Sensors, 23(9), 4552. https://doi.org/10.3390/s23094552








