1. Introduction
Deep learning (DL) has swiftly emerged as an important subclass of machine learning (ML) offering break-neck speeds that are important for a variety of applications in diverse domains such as pattern recognition, image classification, computer vision, etc. [
1]. In order to reap the benefits of the deep learning models, tremendous costs need to be incurred though, owing to the requirements of such models to perform several complex and memory-access intensive operations [
2]. To accelerate the execution of such operations, deep neural networks (DNNs) rely on dedicated hardware accelerators that can speed-up the most critical computations while being much more energy-efficient compared to the host processors [
3]. Such networks are usually characterized by a plethora of multiply and add operations, and thus general matrix multiplication (GEMM) becomes an obvious choice to be accelerated in order to achieve the enormous processing abilities required for ML applications.
Systolic arrays (SAs), since originating in the 1980s, have found a renewed interest due to their crucial role in matrix multiplication acceleration. This is evident from some recent developments regarding DNN acceleration involving big market players such as Google, Nvidia, Samsung, etc. [
4,
5,
6]. A systolic array is a 2D arrangement of processing elements (PEs) arranged in a grid enabling the efficient execution of conventional algorithms, e.g., GEMM, performing single instruction multiple data (SIMD) types of operations [
7]. They have been readily adopted in a variety of ML accelerators based upon GEMM due to their properties such as regular structure, reconfigurability, scalability, etc. [
8].
The ability of ML accelerators to offer execution efficiency comes at the cost of their requirement of tremendous computing power, which necessitates them to be power efficient as well. While power efficiency is critical to both the cloud and edge aspects of modern artificial intelligence (AI) accelerators, its significance for the edge devices, i.e., within the sensors, cannot be overstated [
9]. Moreover, SAs, besides being used in ML accelerators at the cloud, have also found utility in several commercial edge devices (particularly owing to their regularity and enhanced data reuse causing reduced external memory accesses), e.g., the Tesla’s full self-driving chip (FSD) [
10] and Google’s edge TPU [
11] and have been actively researched to that effect as found in [
12,
13]. The power aspect of systolic array-based accelerators has been investigated in a variety of recent research articles, e.g., [
14,
15,
16], but the focus in all these works was to use various complex code optimizations to, e.g., either exploit the underlying embedded system hardware or to reduce memory-accesses. Additionally, sparse matrices are frequently encountered in a variety of ML applications, e.g., in recommender systems utilizing product usage data within a catalog, in natural language processing working with text documents and in computer vision involving image processing with monotonic images. Such cases result in the inefficient utilization of SAs because of the PEs having to do multiplication and accumulation (MAC) operations on zero-valued entries of the matrices that are not contributing to the ultimate result, thus resulting in wasted power due to idle PEs [
17,
18].
This work presents an approach to achieve power efficiency by exploiting fine-grained power gating (particularly for applications involving idle PEs) via the industry standard power-intent specification using a unified power format (UPF) while also utilizing logic-level design optimizations made to the systolic arrays through an open-source systolic array presented in [
19] as the baseline. Since the extent of computations performed by MAC operations of the PEs considering ML accelerators is well above 99%, it makes sense to target the MAC block inside the PE for various optimizations [
20]. UPF enables power-intent specifications distinctly as compared to the logic-level description of a digital design, thus enabling convenient power optimization by offering effective portability of power-intent description for a wide scope of commercial products throughout the whole cycle of the electronic system design [
21]. The logic-level optimizations involve decomposing the larger PE multiplier into multiple smaller sub-multipliers in addition to the multiplier carry propagation adders (CPAs) being replaced by carry save adders (CSAs) in each sub-multiplier as well as the PE.
The major contributions of this paper can be summarized as follows:
We apply power gating to the conventional systolic array (C-SA) Gemmini accelerator and observe its impact on the various performance parameters by using naive systolic array (N-SA) accelerator as the baseline.
Since the design mainly suffers from delay degradation due to the low power cells inserted and larger multiplier being used, we then propose a novel micro-architecture termed Power-Intent Systolic Array (PI-SA) utilizing a modified decomposed multiplier in the PEs with the sub-multiplier CPAs replaced by CSAs and power gating the PE multiplier that significantly improves the delay parameter in addition to giving a better mix of the other performance parameters in comparison to both the N-SA and the C-SA designs.
We perform an initial analysis for a 32-bit-wide accumulator, which is then followed by 16-bit- and 64-bit-wide designs, thus demonstrating the impact of precision scaling on the overall performance parameters.
The rest of the paper is organized as follows. The background information about the various technical aspects making the basis for this research work is presented in
Section 2. We present some relevant literature while also describing critical assessment of the published literature in light of our main theme in
Section 3. The proposed design is presented in detail in
Section 4. Our evaluation methodology and the results are presented in
Section 5. Finally, the work is concluded in
Section 6.
3. Related Work
Our work is mainly related to making micro-architectural changes to the systolic array to enable power-intent description, thus obtaining power optimized ML acceleration. The overall performance enhancement is thereafter achieved by decomposing the MAC multiplier into multiple sub-multipliers and making further modifications to these resulting sub-multipliers. We have thus categorized our literature review into three parts and then we critically analyze them in unison.
3.1. Low Power Accelerators
Various research activities have been found in the literature that are targeting power-efficient hardware accelerators for ML applications while focusing on different options to achieve power optimization. Ref. [
16] includes a comprehensive survey of various optimizations performed at the hardware architecture level to optimize the power consumption of DNNs. The authors present an overview of various architectures based on CPUs, GPUs, ASICs and FPGAs used for DNN acceleration and then present an overview of distinct work performed in optimizing each class of architecture. The work, however, only focuses on memory-access optimizations when considering ASIC-based accelerators.
Similarly, the authors in [
14] identify two aspects of ML accelerators that can be targeted for making them energy-efficient. These include factoring out various elements from the accelerator design and catering to inefficient memory transfers in such accelerators. The authors in this work target the latter while targeting a 65 nm process and comparing its performance with accelerators based on a multicore CPU and GPU. This shall, however, obviously include various complicated coding optimizations, e.g., by hard-coding activities such as loop tiling and memory partitioning to achieve the full capacity of these micro-architectural modifications.
The authors in [
27] utilize approximate computing via quantization in Convolutional Neural Networks (CNNs) to reduce the bit requirement of encoding the weights and inputs at each layer. This results in a loss of accuracy, but leads to energy efficiency when performing the implementation at 40nm technology while considering various CNN architectures for image classification. The same authors in [
28] utilize another approximate computing technique for CNNs termed as dynamic-voltage-accuracy-frequency-scaling (DVAFS) that dynamically scales the voltage and frequency based on accuracy requirements to considerably reduce the dynamic power consumption of the network. The results are supported by measurements made using Envision [
29], i.e., a CNN processor with 28nm technology implementation armed with the proposed DVAFS technique. The power efficiency in [
29] is again improved by dynamically varying the threshold voltage and hence the supply voltage to cater to varying precision requirements.
3.2. Re-Configurable Accelerators
In literature, different re-configurable MAC architectures are available for ML accelerators that are usually designed following either parallel or serial approaches [
30,
31,
32,
33] through bit-decomposition technique. Bit Fusion [
30] is one of the recent parallel re-configurable accelerators which can execute 8-bit × 8-bit, two 4-bit × 8-bit, four 4-bit × 4-bit, sixteen 2-bit × 2-bit, etc., multiplications in one clock cycle. However, Bit Fusion would incur a large area and energy overhead because it requires shift operations and heavy additions for re-configurability. In [
31], Mei et al. proposed a 2D symmetric scalable architecture, which used the array multiplier with sum-separate or sum-together modes. These two modes provide the same throughput with different precision (
-bit) at low area and power consumption costs. However, there is a trade-off in this design between input bandwidth and hardware utilization because the input bandwidth in the sum-together case remains the same in all the precision modes at the cost of a partly gated multiplier, even in the case of small precision such as 2-bit or 4-bit.
Similarly, serial approaches also gained attention in re-configurable architectures. In [
32], the authors introduced the Unified Neural Processing Unit (UNPU), in which the MAC receives weight inputs with 1-bit iterations, but the input activations are in parallel. Furthermore, right-shifting sequential multipliers have been used, as they require a smaller first stage adder to prevent carry propagation. BitBlade [
33] suggests an area-energy efficient accelerator based on Bit Fusion. To reduce the shifter and adder overheads of Bit Fusion, the PE is structured to have a bitwise summation. BitBlade sorts out the 2-bit × 2-bit multiplications that have the same amount of shifts from multiple PEs in [
30]. This makes all the BitBricks in each PE have the same number of shifts; hence, only one shifter is needed per PE. Additionally, the adder logic overhead is also reduced. In a nutshell, bit-serial approaches offer benefits in term of interconnections, area or power, but the throughput in such designs is very low.
3.3. Logic-Level Accelerators
Since the processing element is the core component and is replicated in systolic array-based accelerators, a few recent works presented the idea of breaking down the MAC logic in pre-processing and post-processing stages to factor out the replicated or redundant hardware [
34,
35,
36]. For example, in [
34], the authors suggested the FSA-based tensor processing, in which factorization of booth-encoding and hard multiple
of multiplicand
was proposed using radix-8 multiplier. Their designs show noteworthy improvement in large bit-widths (e.g., 16, 32, etc.) or big size SAs, while lesser improvements in small bit-widths (e.g., 8-bit) or small size of SAs. However, the most area and delay complexity in PEs MAC occur due to the carry propagation adder in the feedback loop of the accumulator. This bottleneck was remedied by the authors in [
35] that proposed factoring out CPA, thereby enabling the processing in a SA along with its arithmetic elements in an unconventional manner. While this resulted in a reduction in delay and the overall area, the power consumption increased significantly mainly due to an increased sequential area.
To summarize the related work, we have described several recent research works that are relevant but differently aligned as compared to the main theme of our work. While the two varieties of bit-decomposition, i.e., serial and parallel approaches, do offer some advantages, this is not without trading-off other parameters, e.g., area and power cost in parallel architectures versus delay cost in serial architectures. Furthermore, making logic-level modifications including the factoring out of the CPA offers area and latency gains at the cost of higher energy consumption. Various complex power optimization techniques, e.g., using approximate computing, have been identified as well that have been implemented standalone with no specific modifications made, e.g., to the multiplier structure or factoring. Moreover, utilizing approximate computing to achieve power optimization would result in a reduction in the overall design precision as well. These techniques are considerably different than what we are targeting in our proposed design, which are based on modified multiplier decomposition along with combining it with fine-grained power gating using a much simpler route of expressing power intent separately from the logic intent, thereby not having to rely on approximate computing to achieve power efficiency in ML accelerators.
4. Proposed Design
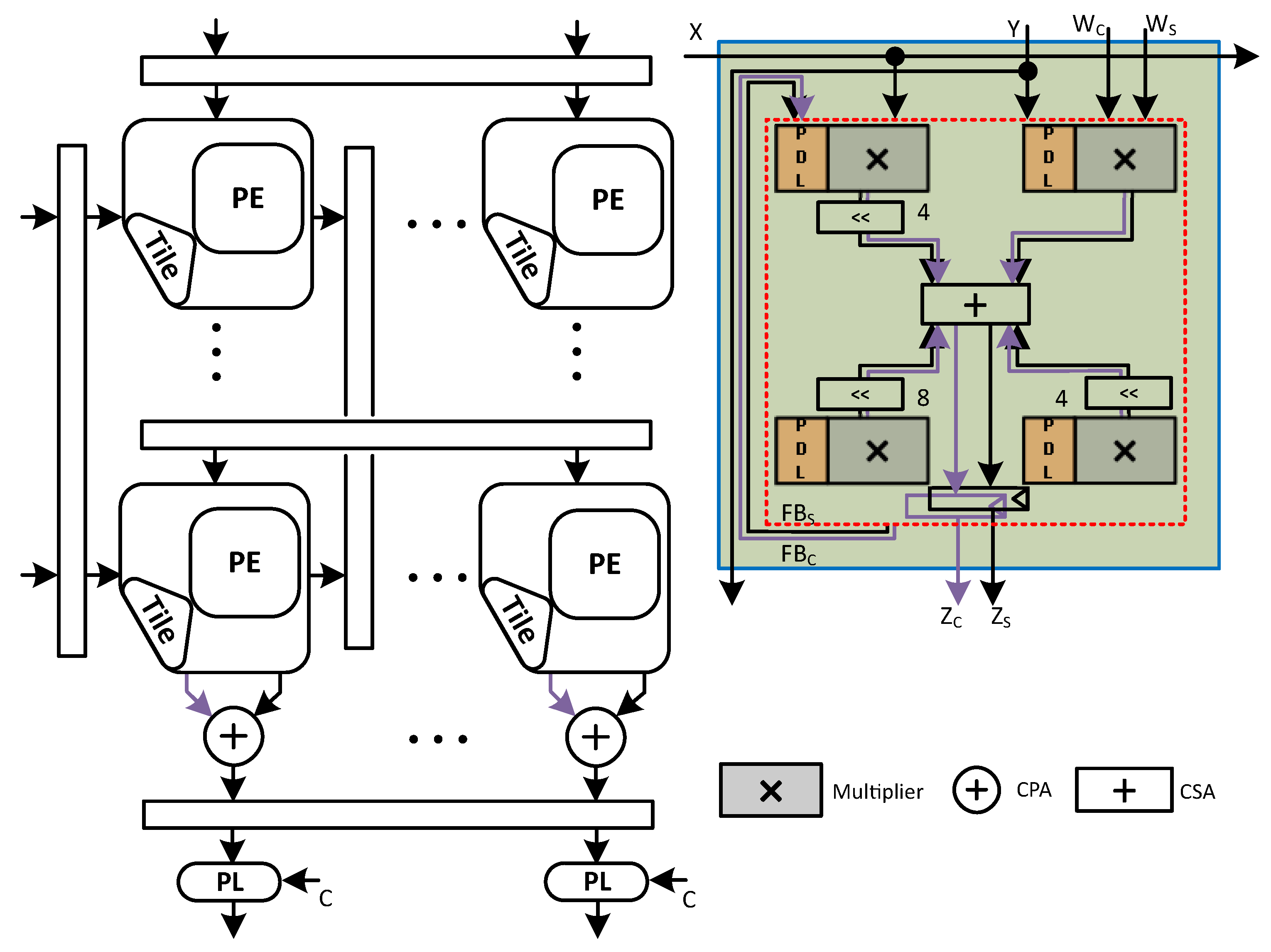
4.1. General Idea of the Proposed Design
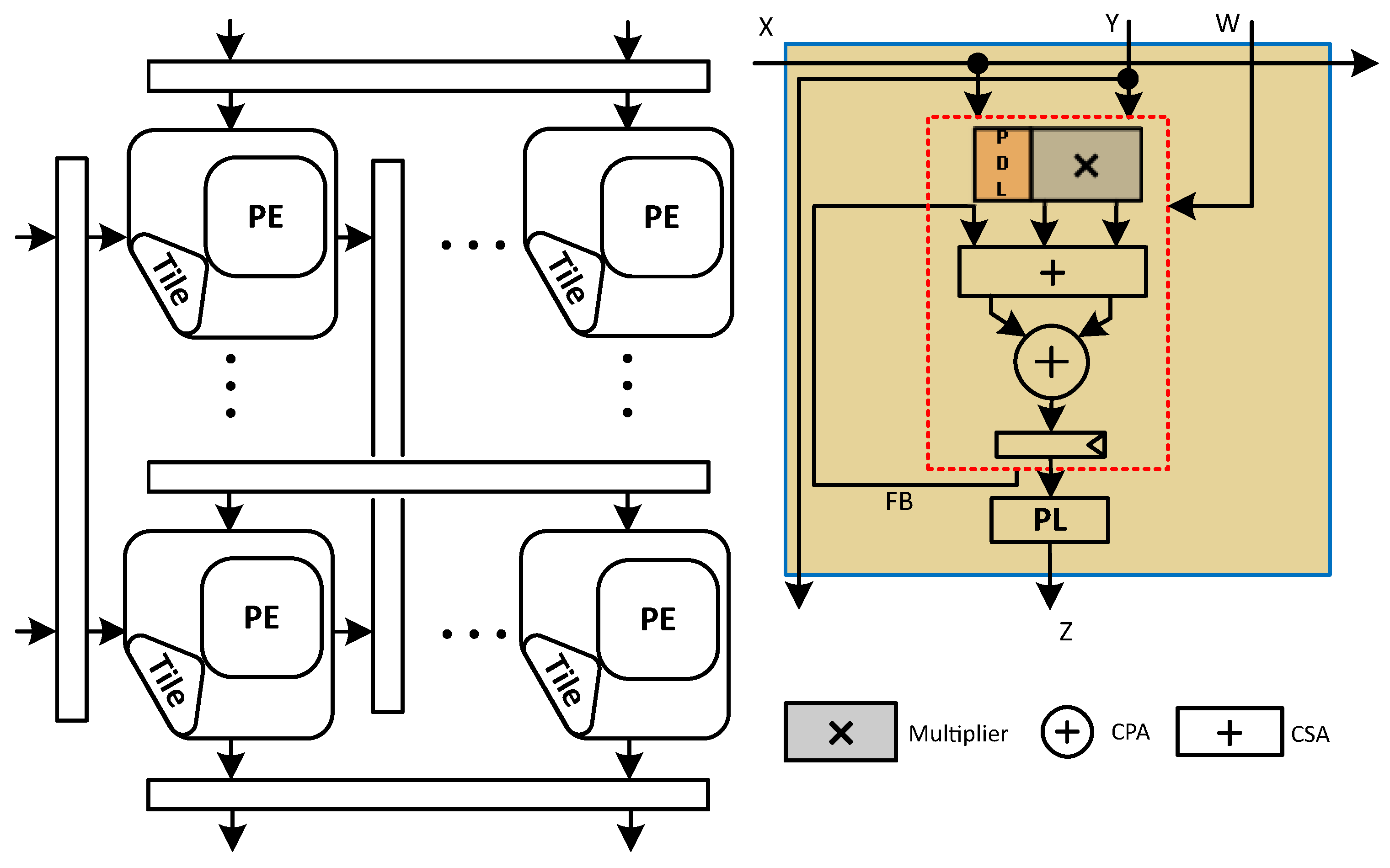
In this paper, a 2D N-SA Gemmini systolic array and its variants are implemented where PEs are connected in a mesh grid. The PEs contain MACs that receive two inputs (
X and
Y) to perform multiplication (
) and partial accumulation (
) on each clock cycle.
represents the partially accumulated value in the register, when the accumulation is complete,
represents the final accumulated product (i.e., dot product). Our assumption in this manuscript is for
and
to be binary representations while
and
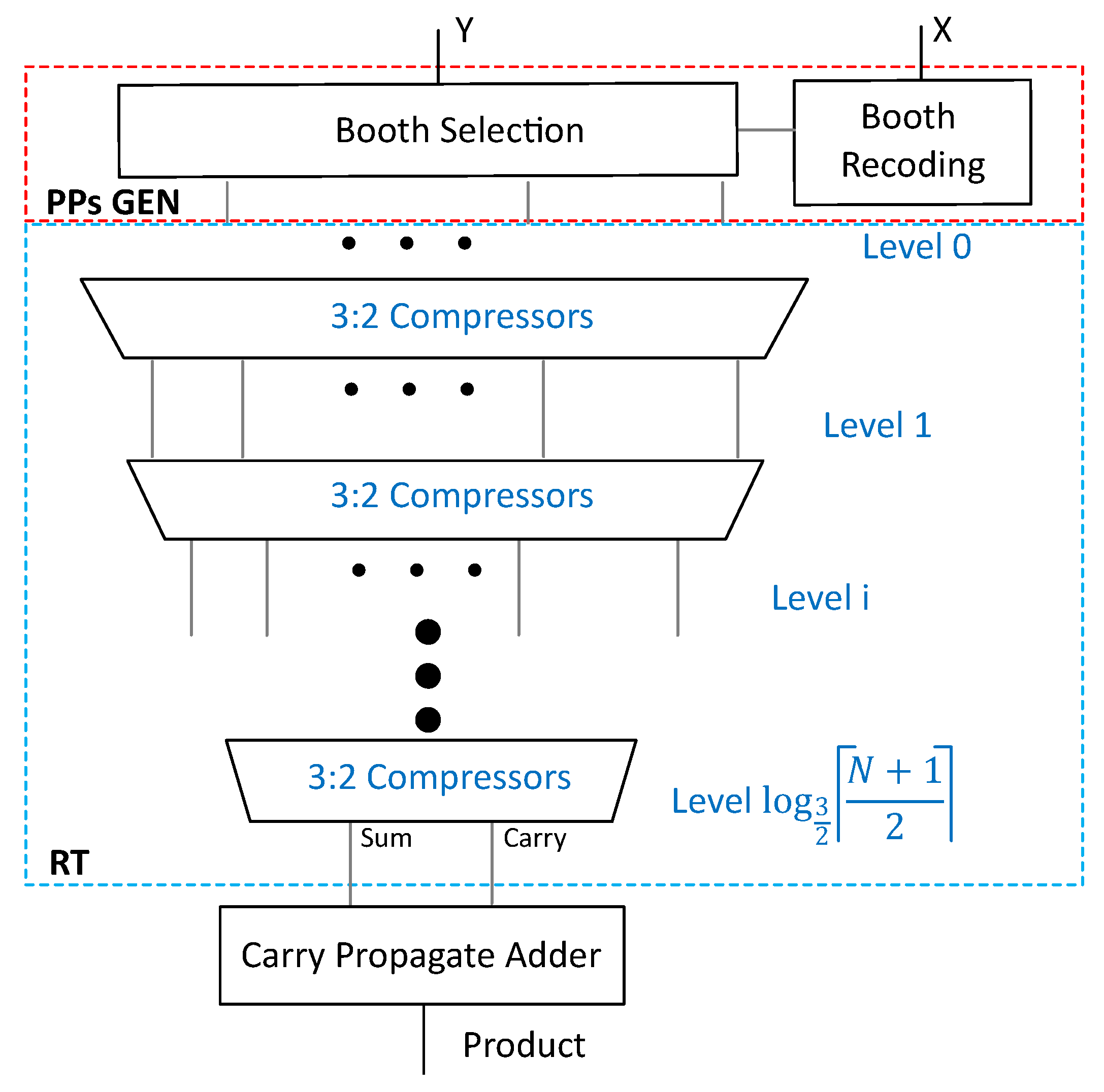
can have either binary or alternately redundant binary representations. The main components of a MAC block are the multiplier, the adder and an accumulator register, but critically, N-SA, as discussed previously, has two separate CPAs: one for the multiplier and the other for the accumulator. Nevertheless, a more practical MAC can be found in the literature, termed as a conventional systolic array (C-SA) design that utilizes a CSA to replace the multiplier CPA while the final accumulation is performed using a single CPA [
36]. A CSA compresses three inputs into two, termed as redundant binary representation (partial sum and shifted carry), without having to propagate the carry. A single CSA adds two XOR gate delays in its critical path [
23,
37].
Indeed, this design improves the area and delay in comparison to the N-SA, but the improvement in power is almost negligible, which is very necessary, especially for an edge-based ML workload. Moreover, most of the work in the literature for power improvement mainly deals with sparsity via using data compression and matrix packing algorithms to process the array mapping, thus ensuring a reduction in the quantity of zero values in the mapped arrays [
17]. The sparsity can alternately be exploited to power-off the processing element components (e.g., the multiplier and adders) to reduce the power consumption when the input bits are zero.
This can be performed via a non-conventional power gating approach that shuts-off the power to the different modules in the design through the PMU with low power cells, i.e., isolation (ISO) and retention (RET) cells being inserted. These cells are collectively termed as the Power Domain Logic (PDL) in this work. The power gating can be accomplished either by the common power format (CPF) standard endorsed by the Silicon Integration Initiative (Si2) or the essentially equivalent but more popular IEEE standard unified power format (UPF) from Accelera [
38,
39]. Both offer the additional advantage of expressing power intent separately from the logic-level design description, thus making the process of optimizing power more convenient by making minimal changes to the logic-level description of the design being power gated.
In ML accelerators, we can exploit the PDL in order to power-off the multiplier when either X or Y or both are zero. Therefore, initially the PDL was applied to the C-SA variant of Gemmini that improved the power efficiency quite substantially, though with a noticeable increase in the area, but due to the conventional nature of the C-SA structure and additional isolation/retention cells, the multiplier delay became very high, making it a dominant factor in the C-SA critical path delay.
In the systolic arrays with a power-intent description, we can actually benefit from the divide and conquer rule by dividing the large multipliers of the PEs into small sub-multipliers. It can help in two ways: (1) The power of sub-multipliers can be shut-off through PDL; (2) however, PDL shall always dominate the design critical path due to the additional delay incurred by the PDL cells. Since the PDL is applied at either the 8-bit multiplier (in C-SA) instance or the 4-bit sub-multiplier instance, so the design critical path would either be through the 8-bit multiplier or the 4-bit sub-multiplier. Thus, it is obvious that the four 4-bit sub-multipliers in parallel would give an advantage over a single 8-bit multiplier. To divide the large multiplier, bit-decomposition can be performed, which is widely used in re-configurable systolic array architectures. However, in conventional bit-decomposition-based multiplication, each multiplier contains a small CPA, which is still a bottleneck in the overall performance improvement. Therefore in this work, the bit-decomposed multiplication was restructured by replacing each sub-multiplier CPA with a CSA. We can thus term the proposed design with power-intent description and structurally redesigned decomposed multiplier as a power-intent systolic array (PI-SA) design. However, power saving through UPF comes at the cost of additional PDL circuitry, thereby resulting in an additional area cost that in turn is replicated in all the PEs of the SA, which can be offset by CPA factorization at the systolic array level [
35].
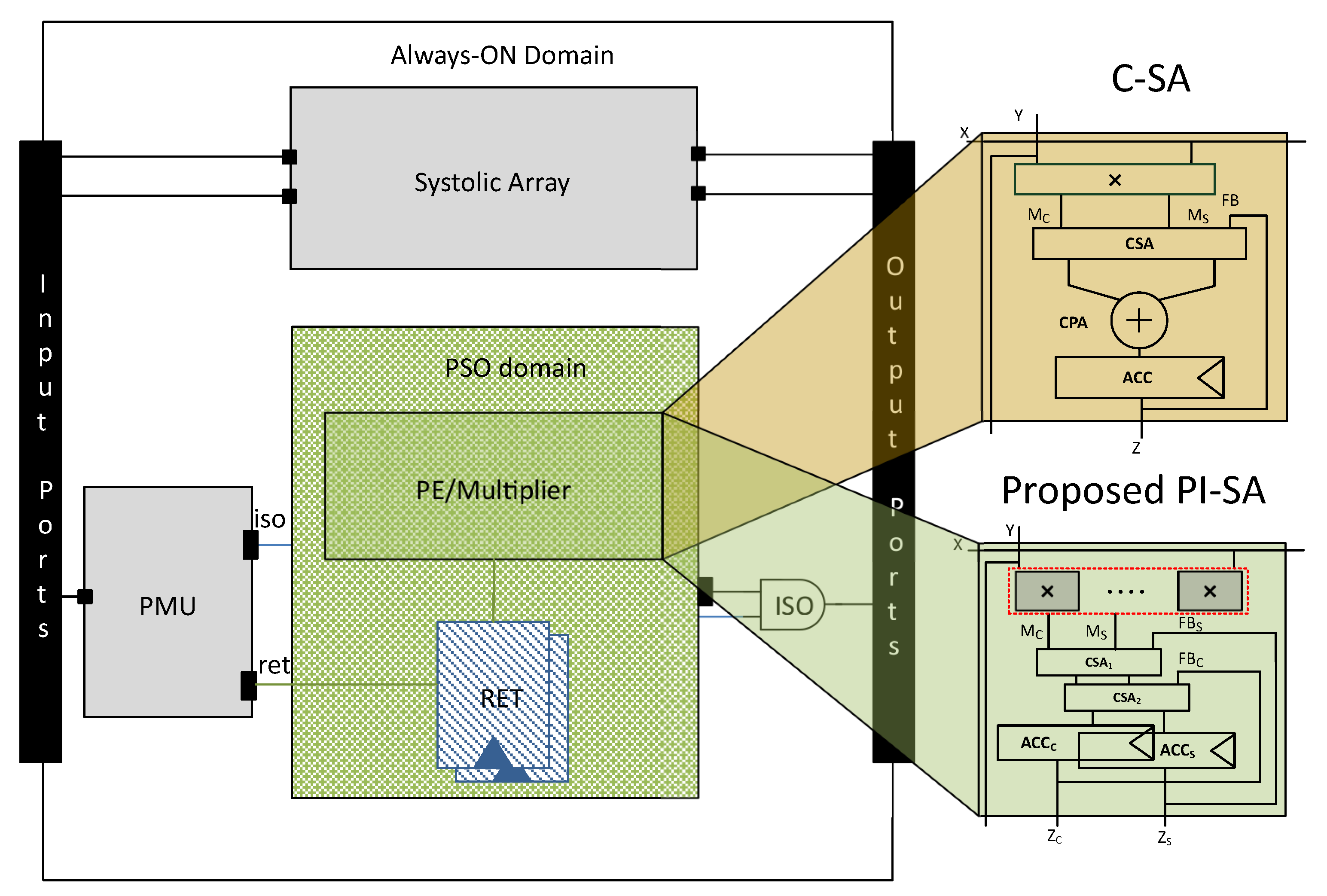
We have depicted a generalized view of the C-SA and the proposed PI-SA design (for simplicity, a single accumulator register is used in both SAs) along with the PMU and the relevant power domain representations in
Figure 3.
4.2. Multiplier Decomposition
Bit Fusion [
30] introduced the BitBricks concept through bit-decomposition of a large multiplier to accomplish re-configurable systolic array accelerators. BitBricks performs 2-bit × 2-bit multiplication and together with the bit decomposition concept, any variable length multiplication can be achieved.
For example, for an 8-bit × 8-bit bit-decomposition multiplication, the multiplier
and multiplicand
can be divided into four 4-bit groups, as shown in (
3).
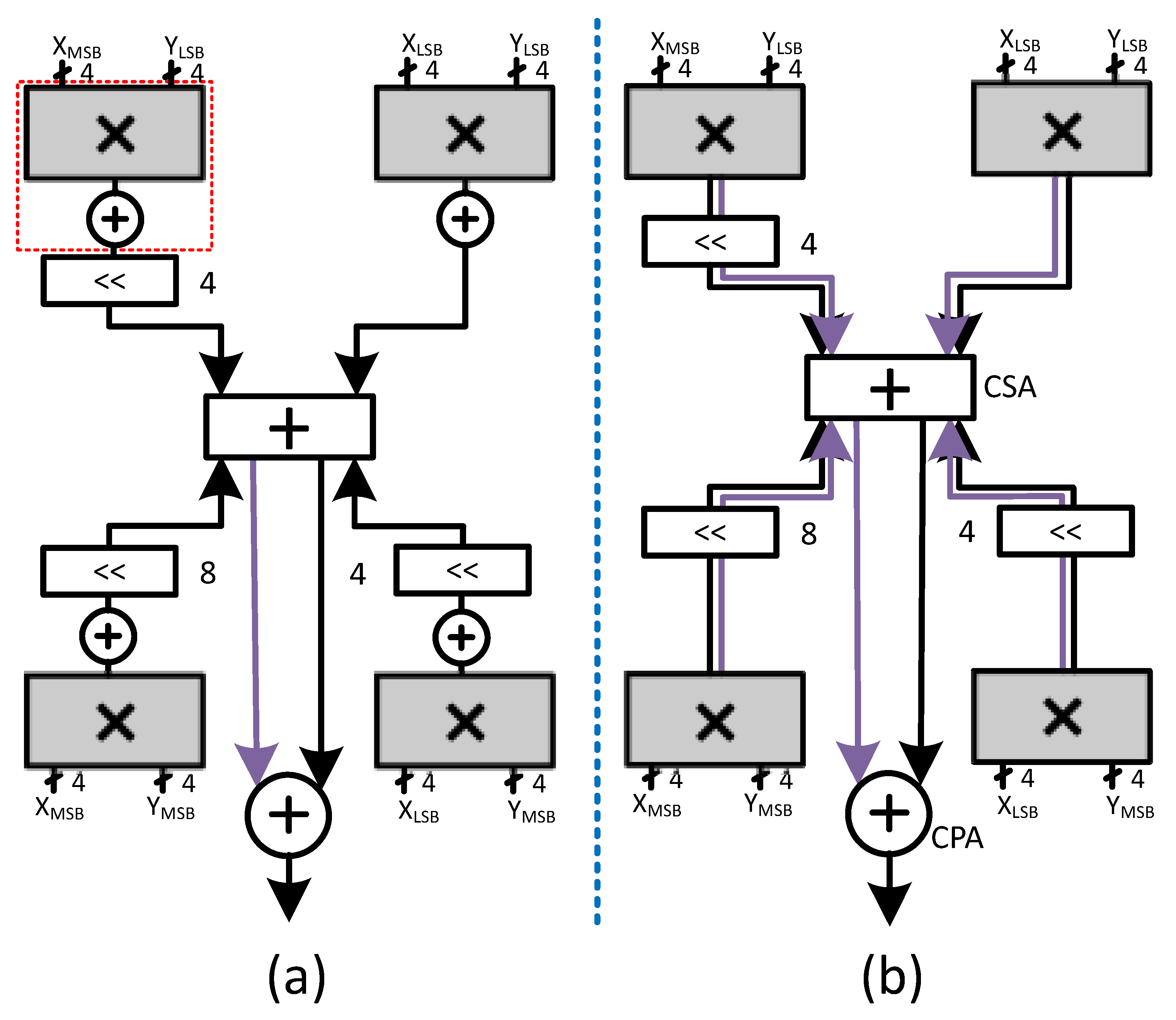
Using these four groups of 4-bits each, the decomposed multiplication can be performed in the following steps: (1) decomposed products generation, which can be accomplished through four 4-bit multipliers such as radix-2 or radix-4; (2) three decomposed products shifting through left shifters for correct alignment; (3) decomposed products reduction tree (e.g, Wallace Tree); and (4) the final addition of the last two partial products through carry propagation adder to obtain the product, as shown in
Figure 4a. We summarize the whole process generically in (
4).
Here,
n represents the bit-decomposition bit-width, or the number of bits in each group. Since the bit-decomposition requires a group of four multipliers, if we use the conventional radix-2 or radix-4 multiplier for each multiplication then, we would require four small 8-bit CPAs too inside each multiplier. Therefore, in a conventional bit-decomposed multiplication, (effectively BitBrick in [
30] or Radix-4), the carry propagation adder is replicated in each small multiplier thus, adding an additional area, delay and power cost. We can replace these CPAs inside each small multiplier with CSAs and put a single CPA at the output to obtain the final product. Indeed, this will make the interconnections and shifters logic cost double, but at the same time, we can get rid of the area, delay and power cost of using four CPAs.
Figure 4b shows the modified version of our bit-decomposed multiplier.
4.3. C-SA
A micro-architecture of an
power-intent Gemmini variant conventional systolic array (C-SA) is shown in
Figure 5, which performs multiplication on 8-bit signed inputs and accumulation with 32 bits.
Contrary to the N-SA, in C-SA MAC, we merged the multiplier (the structure-level 2’s complement signed radix-4 multiplier with complete sign extension is used) with the accumulator: Instead of using a CPA for the final addition of the two partial products, we used CSA with the third value, i.e.,
, stored in the accumulator register. As a result, we used just a single CPA to determine the final value, as explained in [
36].
Initially, we applied the PSO logic on each PE multiplier of the C-SA. Lets say,
are
systolic array inputs, where
are given at the left edge (in rows) and
at the top (in columns). If
is zero, then with the help of the retention cells, the previous outputs of the multipliers in the whole row of PEs, i.e.,
is retained and similarly isolation cells are also placed in a row-wise fashion. Similarly, if
, then the same logic is applied on the whole PE multipliers column-wise. We have represented it with a PDL block and highlighted it with orange color along with the multiplier in
Figure 5. Nevertheless, when
are both zero then, the whole row and whole column PE multipliers go into the PSO state. The algorithmic description of this whole procedure is shown in Algorithm 2, which shall in principle result in the
signal and subsequently the PDL according to the logic presented in the Algorithm 1.
| Algorithm 2: Generalized generation algorithm |
Input: Systolic Array Input signals , ; Output: PSO enable signal resulting in multiplier shutoff; if &&) then off; off; end else if ) then off; end else if ) then off; end |
In this way, the PDL consisting of state retention and isolation cells inserted through UPF saves power significantly. However, this improvement in C-SA is achieved at the cost of an increased delay of the multiplier due to the PDL, which makes it the critical path of the systolic array. As we used an 8-bit Radix-4 multiplier, so as per the equation
in
Section 2.1, the number of the total partial product equals:
. Thus, the multiplier delay can be reduced by decreasing the number of partial products, as explained in the subsequent section.
4.4. Proposed PI-SA Design
The micro-architecture of the proposed PI-SA design in Gemmini configuration with an output stationary dataflow is shown in
Figure 6. This design also utilizes an 8-bit multiplier and a 32-bit accumulator. The proposed design divides the 8-bit multiplier into four sub-multipliers (4-bit each) inside the PE MAC, using a bit-decomposition technique to reduce the partial products and a single CPA for the final product as explained in
Section 4.2 and shown in
Figure 4b.
Now that we have four 4-bit sub-multipliers, we can reduce the five partial products into partial products using radix-4 multipliers. This would then require the usage of only one CSA (3:2 compressor) for the last two partial products. On the contrary, in the case of a single 8-bit multiplier, we shall require three CSAs to reduce the five partial products to the final two partial products. In this way, the number of XOR gates in the reduction tree with the 4-bit sub-multiplier is reduced from six to two. Therefore, even though the PDL logic is added to each sub-multiplier (one per PD), with four of them functioning in parallel with no CPA, this sub-multiplier critical path would reduce considerably in comparison to a single multiplier (per PD) that constituted the critical path in the C-SA case. The addition of the final eight partial products (two from each sub-multiplier) thereafter is accomplished through CSAs placed outside the sub-multipliers.
Additionally, this bit-decomposition will increase the number of multiplier shut-off instances in general as compared to the C-SA design described in
Section 4.3. This is due to an increase in the PEs/multipliers/PDs in the proposed SA design as compared to the C-SA design as explained in the succeeding
Section 4.5. This increase in the multiplier shut-off instances can be demonstrated with the help of an example where only the
input of the SA equals zero in the case of C-SA. According to Algorithm 2, this shall result in the shutting-off of the row multipliers
. The consequence of the
input equaling zero would, however, be that the values of both the
and
inputs (ref. to Equation (
3)) to the bit-decomposed multipliers
(ref. to Equation (
4)) would be equal to zero. This shall, hence, result in shutting-off of four instances of sub-multipliers in PI-SA design for every single multiplier instance in the C-SA design. Additionally, for a C-SA multiplier to be shut-off, the whole 8-bit PE input needs to be zero, while in the case of PI-SA, two of the four sub-multipliers corresponding to each C-SA multiplier would be shut-off even with either the LSB or the MSB of any specific PE input equaling zero as indicated by Equation (
4).
Furthermore, because we divided a single 8-bit multiplier with 16-bit output into four 4-bit multipliers (working in parallel), each producing two 8-bit outputs in redundant binary representation (partial sum and shifted carry), the interconnections have been quadrupled (-bit instead of 16-bit) in comparison to a single multiplier. As a result, the PDL was increased along with the doubling of the shifters, thus, resulting in a degradation in the total area of the systolic array.
Moreover, since the sequential cells consume more power than the combinational cells, it led to a slight degradation in power improvement, but this can be accommodated since we already save enough power by increasing the opportunity of power gating the sub-multipliers as explained before. Lastly, as the effect of CPA factorization at SA level will also be added, so this new design provides handsome improvement in the overall area too, as explained in detail in the subsequent section.
4.5. Cost of Low Power Logic in the Systolic Arrays
The insertion of low power cells results in power optimization at the cost of additional low power logic in the form of isolation and state retention cells inserted in the switchable power domain. We have performed optimizations on the C-SA and the proposed PI-SA varieties of the test cases. Let
be the multiplier output register bitwidth per PE/PD in C-SA and
be the number of power domains in C-SA. The multiplier output register bitwidth per PE in the PI-SA design hence is
while, due to the multiplier decomposition, the number of power domains in this case is
. The number of low power isolation and retention cells (
) in each case can be represented mathematically by (
5).
Table 1 shows the number of power domains as well as the number of low power cells for each design test case in accordance with (
5).
6. Conclusions
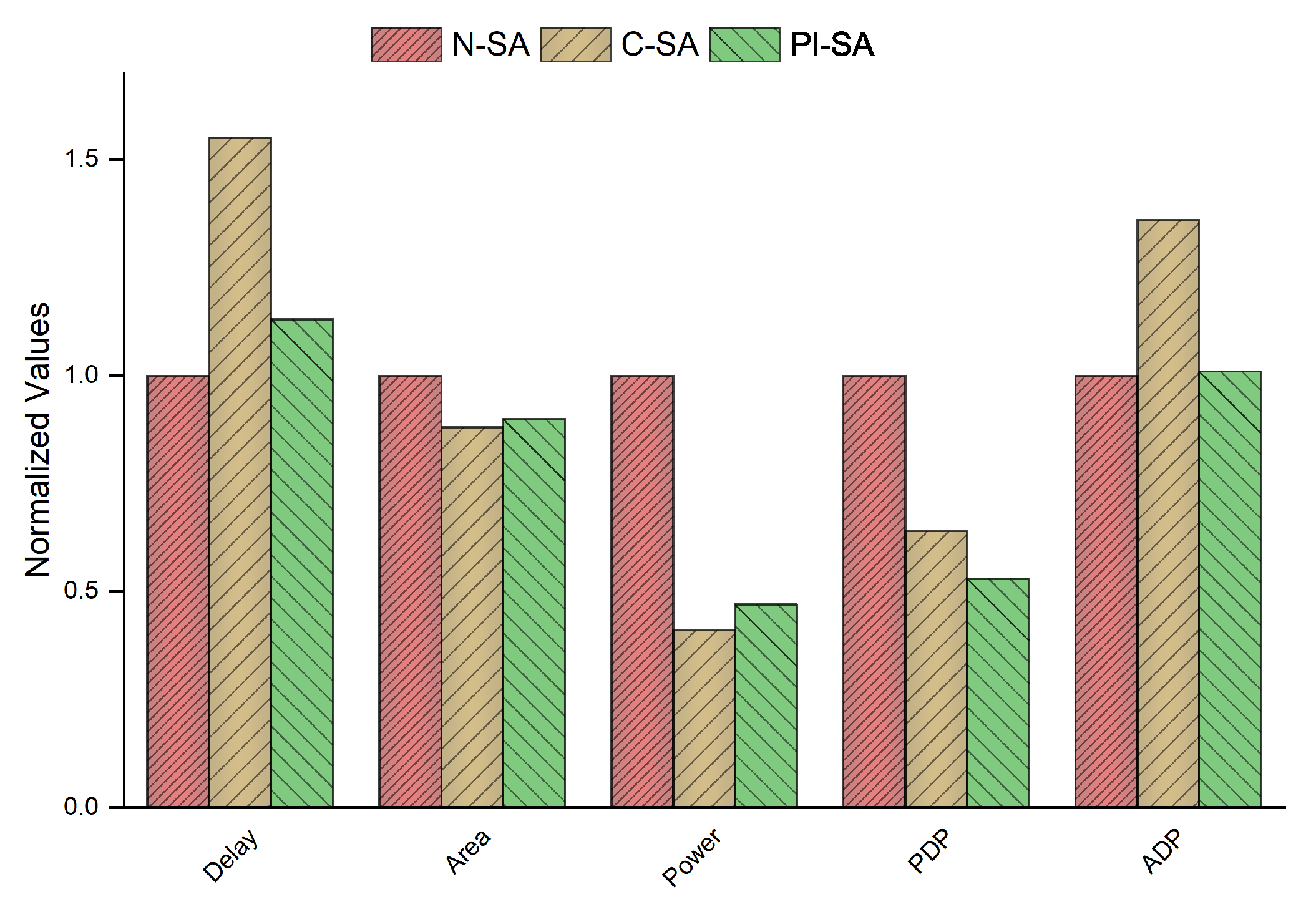
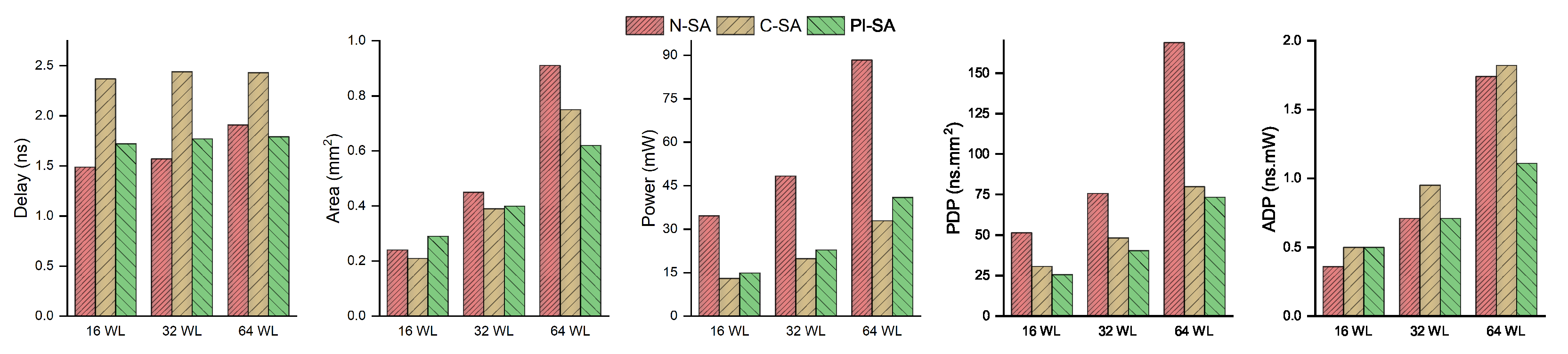
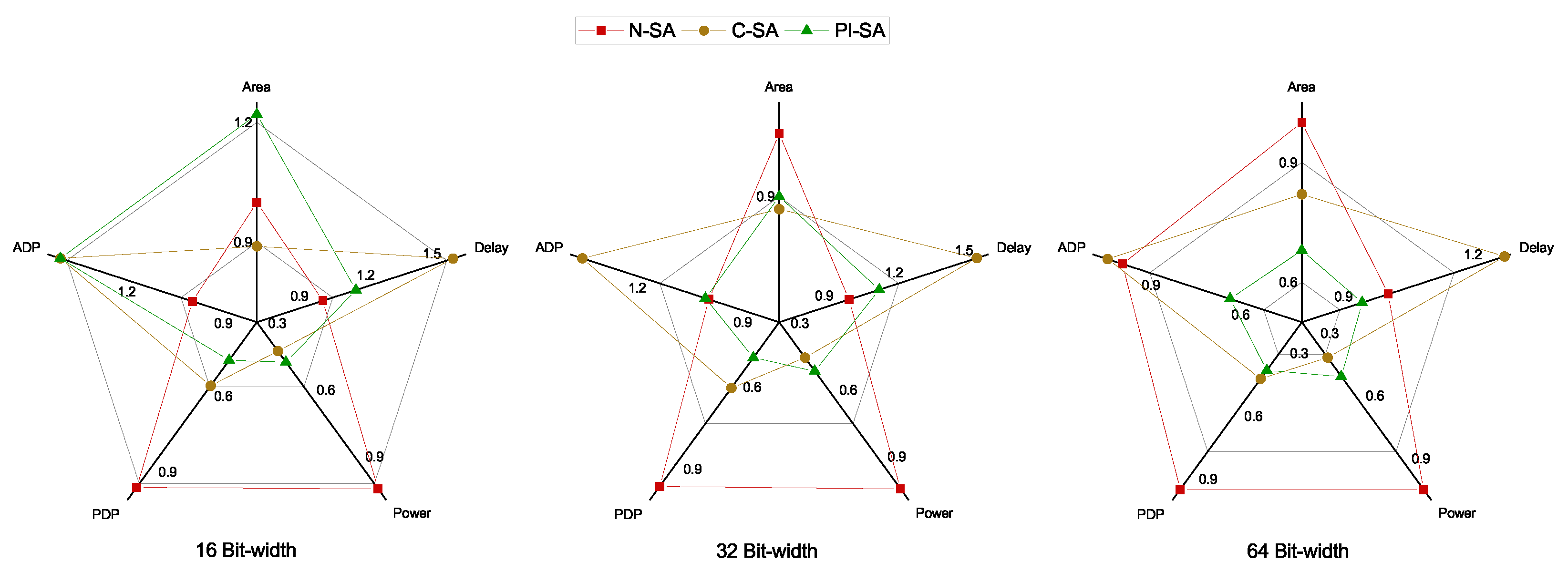
This manuscript presents our efforts in optimizing ML acceleration by utilizing the Gemmini SA micro-architecture as the baseline. In particular, our optimizations are based on introducing power-intent in the C-SA variant of the baseline design by using the UPF industrial standard, thus resulting in around 59% saving of the design power consumption. This, however, resulted in an increased delay by 55% in the C-SA design due to the additional power logic, which was further complimented by a single 8-bit multiplier dominating the design critical path. This was thereby remedied by proposing a novel PI-SA design with further micro-architectural modifications to divide the large 8-bit multiplier into four smaller 4-bit sub-multipliers, thus resulting in a smaller number of partial products and the corresponding delay reduction of more than 40% as compared to the C-SA. This was performed at a small area improvement cost of around 2% and power improvement cost of around 6% due to the additional sequential logic resulting from the doubling of the accumulator registers of the proposed PI-SA design in addition to the increased retention logic emanating from the increased power domains in the proposed design. The overall improvement in PDP and ADP, however, was quite profound in the proposed design as compared to the C-SA design when observed with respect to the N-SA design.
However, our further analysis considering higher precision with a wider 64-bit accumulator demonstrated a better performance of our proposed design with respect to all the performance parameters ranging from a minimum of 6% delay reduction to a maximum of around 57% performance improvement in the PDP performance as compared to the N-SA design. For future research, we intend to compliment this work with further macro-architectural power optimizations, e.g., to reduce frequent memory-accesses that are a major hurdle in the development of power-efficient edge AI devices.