Maintenance Cost Minimization for an Agricultural Harvesting Gripper
Abstract
1. Introduction
2. Proposed Harvesting Gripper
3. Materials and Methods
3.1. Cuckoo Search Algorithm
3.2. CBM Policy
- If the component failed during the last inspection interval, a failure replacement will be performed.
- If the Prest value obtained for the next time interval until the next inspection is greater than Pro, the decision maker will perform a preventive replacement of the monitored component. Otherwise, the scheduled inspections continue.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vu, Q.; Kuzov, M.; Ronzhin, A. Hierarchical classification of robotic grippers applied for agricultural object manipulations. MATEC Web Conf. 2018, 161, 03015. [Google Scholar] [CrossRef]
- Șerdean, M.; Șerdean, F.; Mândru, D. An Overview of Grippers in Agriculture Robotic Systems. In New Advances in Mechanisms, Mechanical Transmissions and Robotics; Mechanisms and Machine Science; Lovasz, E.C., Maniu, I., Doroftei, I., Ivanescu, M., Gruescu, C.M., Eds.; Springer: Cham, Switzerland, 2020; Volume 88, pp. 212–225. [Google Scholar]
- Ceccarelli, M.; Figliolini, G.; Ottaviano, E.; Mata, A.S.; Criado, E.J. Designing a robotic gripper for harvesting horticulture products. Robotica 2000, 18, 105–111. [Google Scholar] [CrossRef]
- Font, D.; Pallejà, T.; Tresanchez, M.; Runcan, D.; Moreno, J.J.; Martínez, D.; Teixidó, M.; Palacín, J. A Proposal for Automatic Fruit Harvesting by Combining a Low Cost Stereovision Camera and a Robotic Arm. Sensors 2014, 14, 11557–11579. [Google Scholar] [CrossRef] [PubMed]
- Hemming, J.; Bac, C.W.; van Tuijl, B.A.J.; Ruud, B.; Bontsema, J.; Pekkeriet, E. A robot for harvesting sweet-pepper in greenhouses. In Proceedings of the International Conference of Agricultural Engineering, Zurich, Switzerland, 6–10 July 2014. [Google Scholar]
- Zhao, D.-A.; Lv, J.D.; Ji, W.; Zhang, Y.; Chen, Y. Design and control of an apple harvesting robot. Biosyst. Eng. 2011, 110, 112–122. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, L.; Liu, C.; Huang, Y. Dual-arm Robot Design and Testing for Harvesting Tomato in Greenhouse. IFAC-PapersOnLine 2016, 49, 161–165. [Google Scholar] [CrossRef]
- Anderson, D. Oniqua Enterprise Analytics. Available online: http://www.plant-maintenance.com/articles/PMCostReduction.pdf (accessed on 14 March 2023).
- Durán, O.; Vergara, B. Maintenance Strategies Definition Based on Systemic Resilience Assessment: A Fuzzy Approach. Mathematics 2022, 10, 1677. [Google Scholar] [CrossRef]
- Gashi, M.; Gursch, H.; Hinterbichler, H.; Pichler, S.; Lindstaedt, S.; Thalmann, S. MEDEP: Maintenance Event Detection for Multivariate Time Series Based on the PELT Approach. Sensors 2022, 22, 2837. [Google Scholar] [CrossRef] [PubMed]
- Rykov, V.; Kochueva, O.; Rykov, Y. Preventive Maintenance of the k-out-of-n System with Respect to Cost-Type Criterion. Mathematics 2021, 9, 2798. [Google Scholar] [CrossRef]
- Kang, J.; Wang, Z.; Guedes Soares, C. Condition-Based Maintenance for Offshore Wind Turbines Based on Support Vector Machine. Energies 2020, 13, 3518. [Google Scholar] [CrossRef]
- Bucci, G.; Ciancetta, F.; Fioravanti, A.; Fiorucci, E.; Mari, S.; Silvestri, A. Online SFRA for Reliability of Power Systems: Characterization of a Batch of Healthy and Damaged Induction Motors for Predictive Maintenance. Sensors 2023, 23, 2583. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Wu, B.; Chen, M. Condition-based maintenance optimization considering improving prediction accuracy. J. Oper. Res. Soc. 2014, 65, 1412–1422. [Google Scholar] [CrossRef]
- Eti, M.; Ogaji, S.; Probert, S. Development and implementation of preventive-maintenance practices in nigerian industries. Appl. Energy 2006, 83, 1163–1179. [Google Scholar] [CrossRef]
- Zhong, S.; Gai, Z.; Yang, Y.; Zhao, Y.; Qi, Y.; Yang, Y.; Peng, Y. A contraction length feedback method for the McKibben pneumatic artificial muscle. Sens. Actuators A Phys. 2022, 334, 113321. [Google Scholar] [CrossRef]
- Soleymani, R.; Khajehsaeid, H. A mechanical model for McKibben pneumatic artificial muscles based on limiting chain extensibility and 3D application of the network alteration theories. Int. J. Solids Struct. 2020, 202, 620–630. [Google Scholar] [CrossRef]
- Serdean, M.; Besoiu, S.; Lungu, I.; Mandru, D. Robotic System Actuated by McKibben Artificial Muscles. Robot. Manag. 2011, 16, 37–42. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Tudose, L.; Rusu, F.; Tudose, C. Optimal design under uncertainty of bearing arrangements. Mech. Mach. Theory 2016, 98, 164–179. [Google Scholar] [CrossRef]
- Rusu, F. Optimizations under Uncertainty with Applications in Rolling Bearing Industry. Ph.D. Thesis, Technical University of Cluj-Napoca, Cluj-Napoca, Romania, 2014. [Google Scholar]
- Wu, B. Condition-Based Maintenance Optimization Using Data Driven Methods. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2013. [Google Scholar]



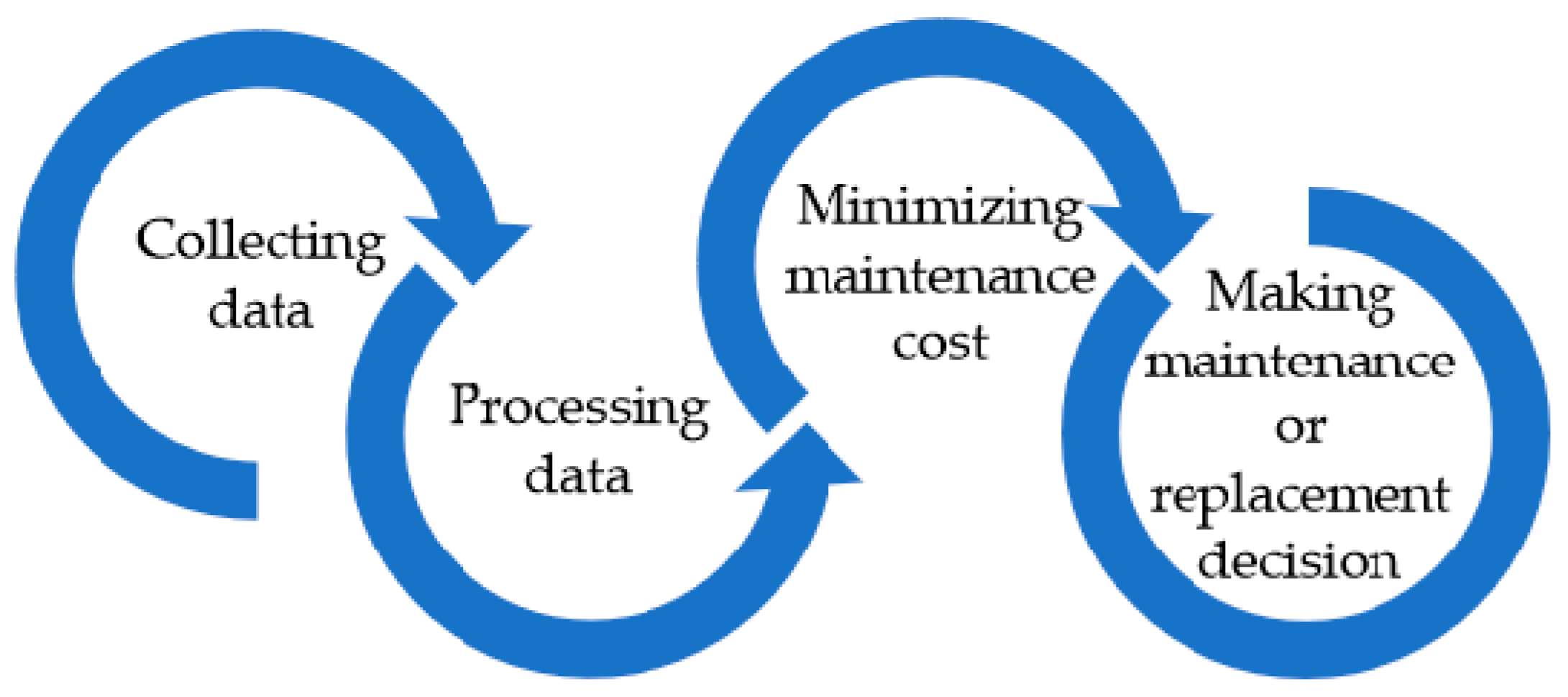


| Step 1 | Collect historical data relevant to the lifetime of the component |
| Step 2 | Build the surrogate model based on available historical data Obtain the prediction error based on tests using the surrogate model Determine the distribution of the component lifetime |
| Step 3 | Model the expected cost per unit of time in relation to a given failure probability Determine the optimal failure probability, Pro, that minimizes the expected cost |
| Step 4 | For each inspection point: If the component has failed Make failure replacement Else Calculate failure probability during next inspection interval Prest If Prest > Pro Make preventive replacement End if End if End for |
| No. | Optimal Failure Probability | Total Expected Cost per Time Unit [$/day] |
|---|---|---|
| 1 | 0.0546 | 0.3049 |
| 2 | 0.0538 | 0.3004 |
| 3 | 0.0543 | 0.3032 |
| Statistics | Optimal Failure Probability | Total Expected Cost per Time Unit [$/day] |
|---|---|---|
| Average | 0.0542 | 0.3028 |
| Variance | 1.6333 × 10−7 | 5.1633 × 10−6 |
| Standard deviation | 4.0415 × 10−4 | 0.023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Șerdean, F.M.; Șerdean, M.D.; Mândru, S.-D. Maintenance Cost Minimization for an Agricultural Harvesting Gripper. Sensors 2023, 23, 4103. https://doi.org/10.3390/s23084103
Șerdean FM, Șerdean MD, Mândru S-D. Maintenance Cost Minimization for an Agricultural Harvesting Gripper. Sensors. 2023; 23(8):4103. https://doi.org/10.3390/s23084103
Chicago/Turabian StyleȘerdean, Florina Maria, Mihai Dan Șerdean, and Silviu-Dan Mândru. 2023. "Maintenance Cost Minimization for an Agricultural Harvesting Gripper" Sensors 23, no. 8: 4103. https://doi.org/10.3390/s23084103
APA StyleȘerdean, F. M., Șerdean, M. D., & Mândru, S.-D. (2023). Maintenance Cost Minimization for an Agricultural Harvesting Gripper. Sensors, 23(8), 4103. https://doi.org/10.3390/s23084103







