Dynamic Compensation of a Piezoelectric Accelerometer Obtained through a General Probabilistic Approach †
Abstract
1. Introduction
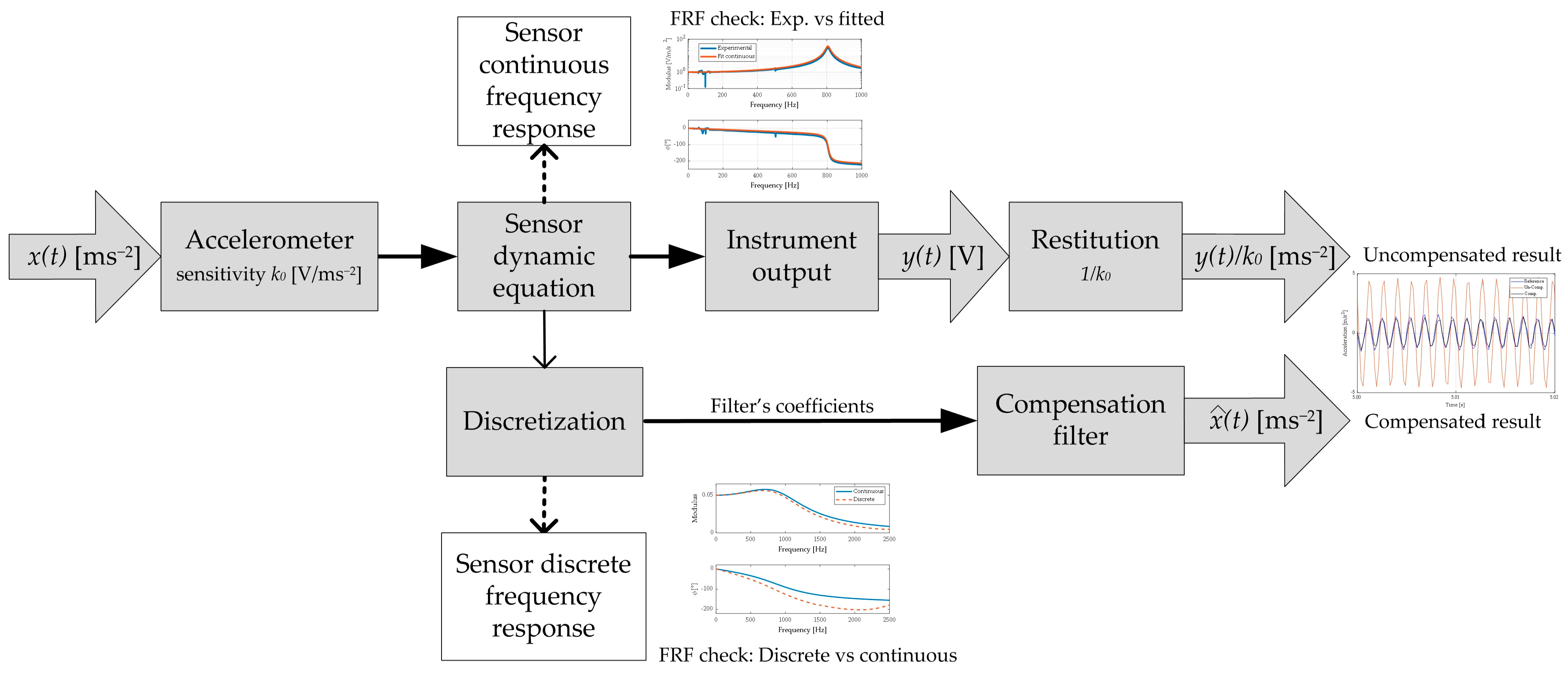
2. The Proposed Method
2.1. The Generic Modelling Framework
- for static measurement, based on a single observation, and are both scalar quantities;
- for static measurement, based on repeated observation, remains a scalar quantity, but becomes a vector, , with components;
- for direct dynamic measurement, where the goal is to measure the time history of some quantity, based on time-sampled observations, both and become vectors with components;
- for indirect dynamic measurement, where, for example, the final goal is to obtain a spectrum of the phenomenon, with, say, spectral lines, both and are still vectors, but , which is now the spectrum, has now components.
2.2. The Proposed Method
2.3. Overall View of the Method
3. Testing the Method by Simulation
3.1. Design of the Simulation Tests
- is the acceleration to be measured,
- (N) is the force detected by the piezoelectric transducer,
- (kg) is the seismic mass of the inertial sensor,
- (Hz) is its natural frequency, and
- is the damping factor.
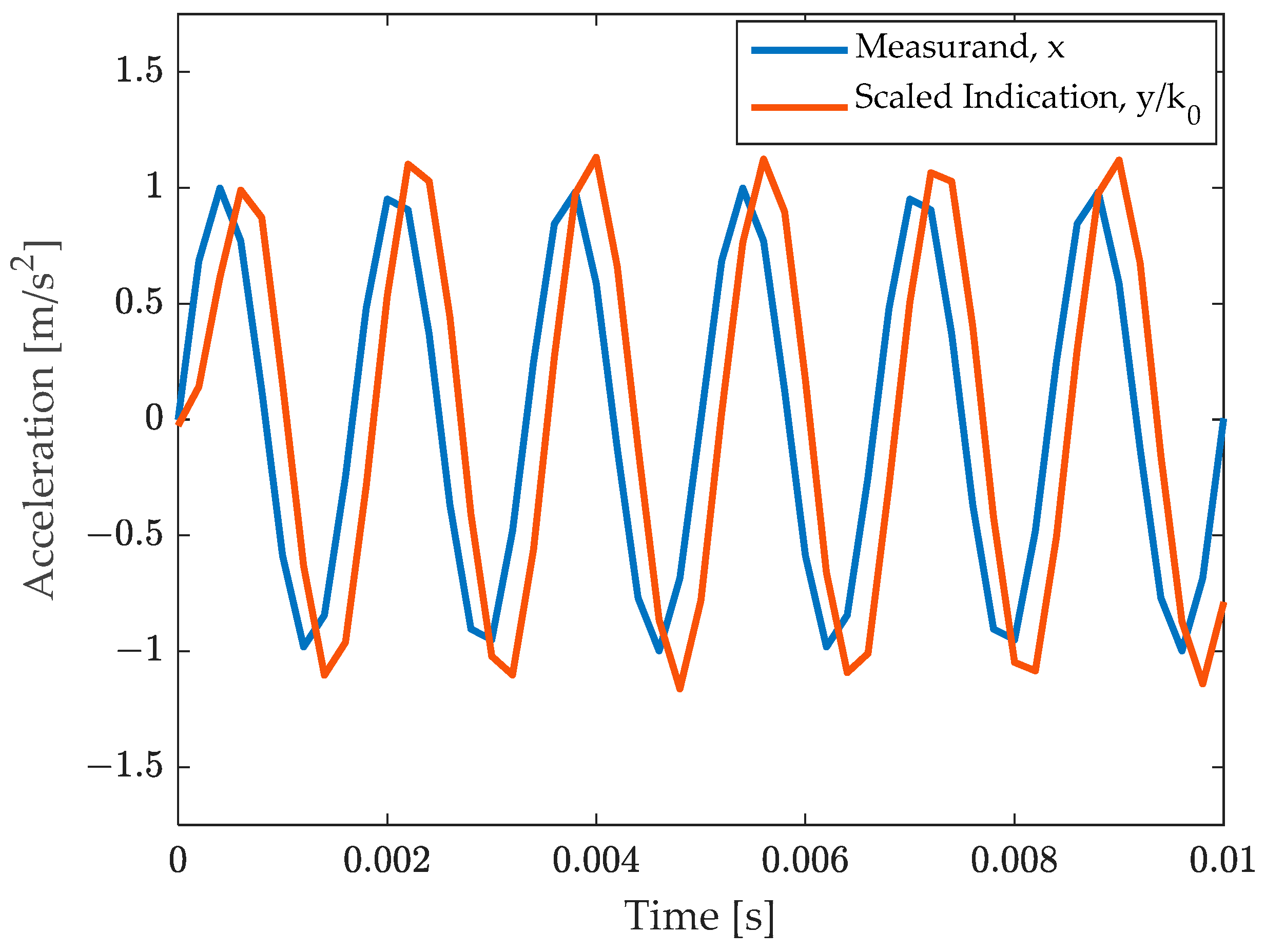
3.2. Simulated Periodic Phenomenon
- ,
- ,
- , and
- .
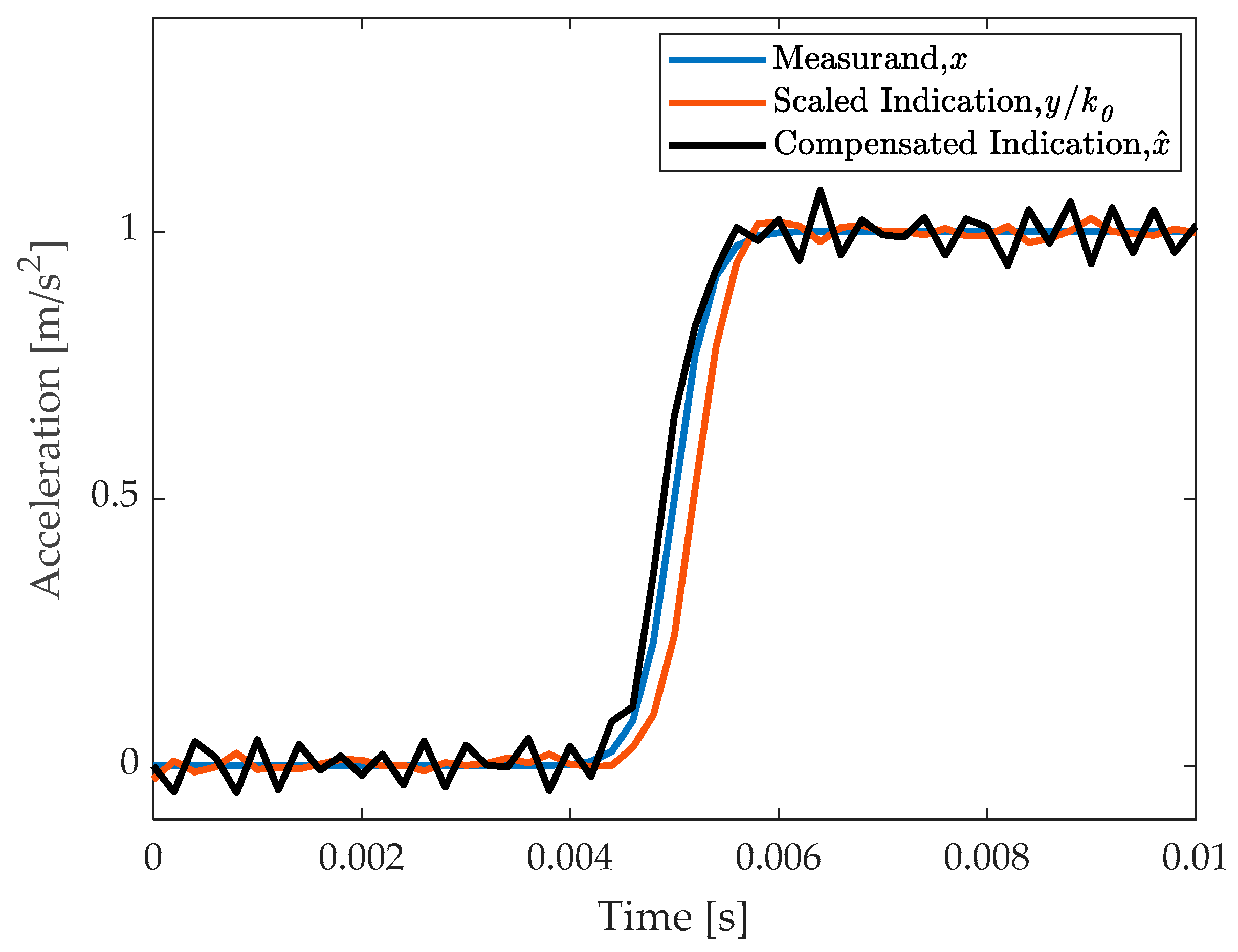
3.3. Simulated Step-like Phenomenon
- -
- Definition of the differential equation describing the dynamic behaviour of the measuring instrument, Equations (17) and (18), with its parameters;
- -
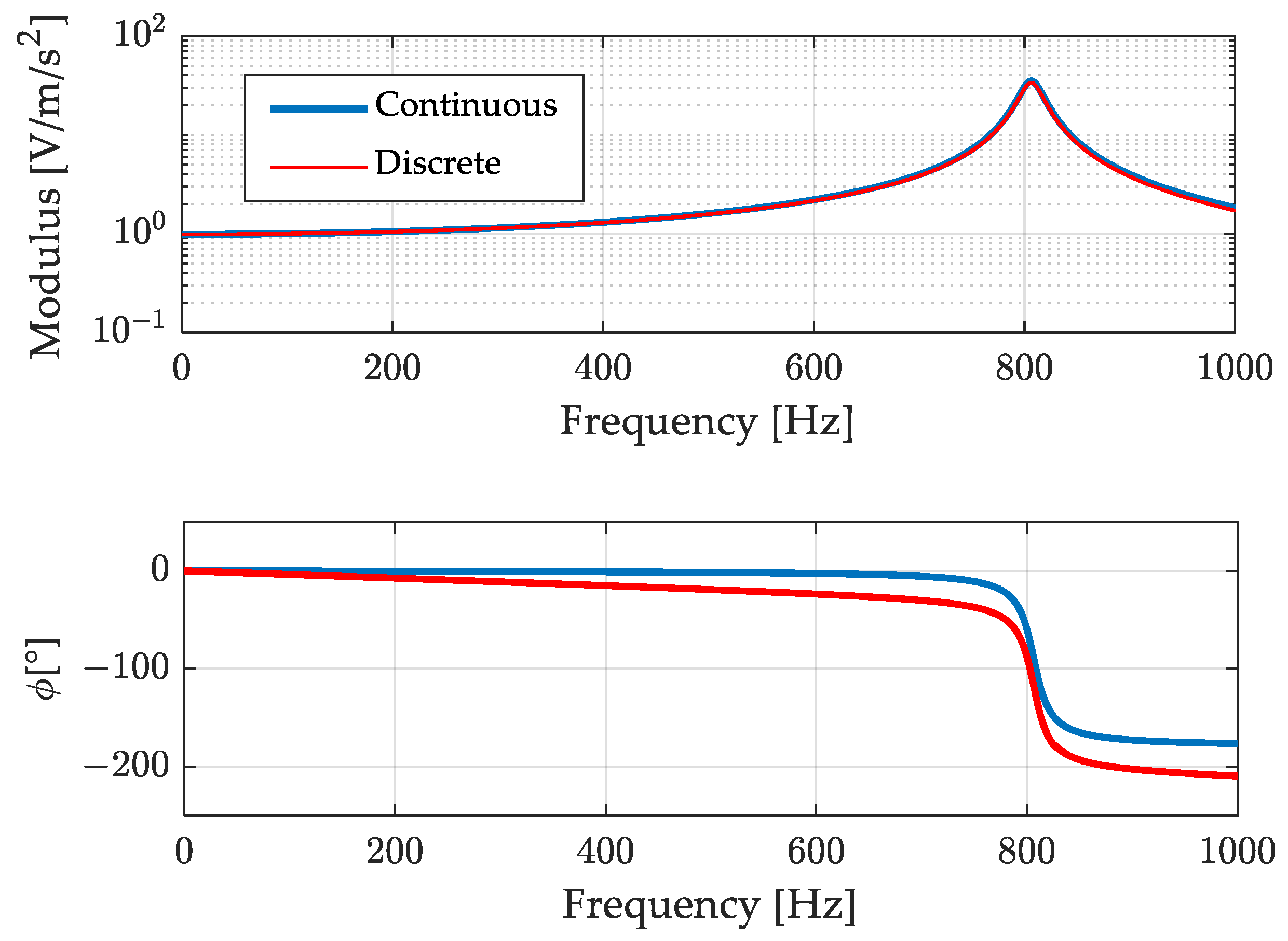
- Discretization of the continuous time equation (for example with zero hold method) to obtain a discrete time Equation (8);
- -
- Definition of the II order linear compensation filter from the discrete time equation coefficients (14);
- -
- Use the system for a dynamical measurement of a signal with proper sampling frequency, to obtain an array of readings ;
- -
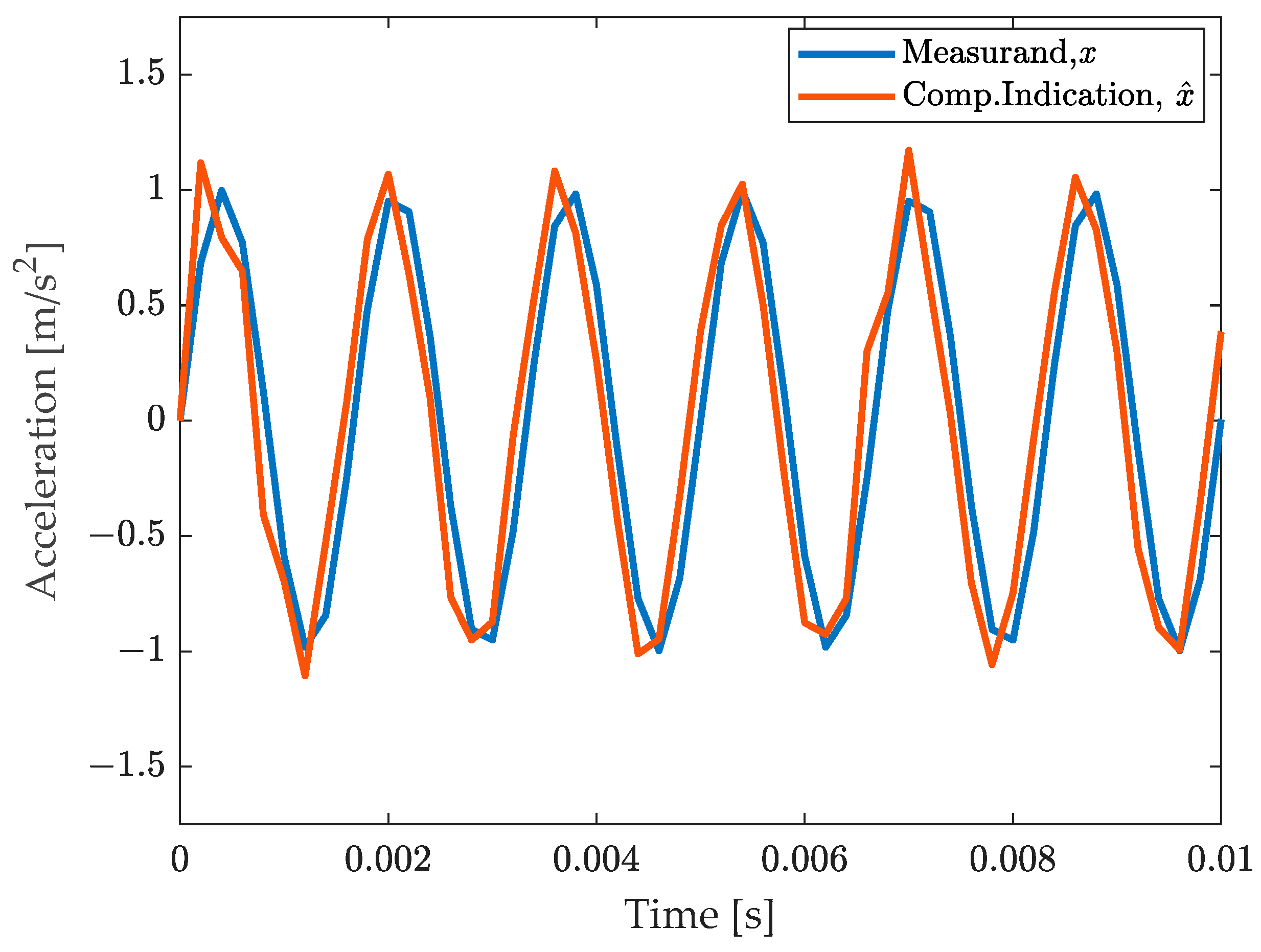
- Application of the compensation filter (14) to the readings to obtain the compensated measurement result .
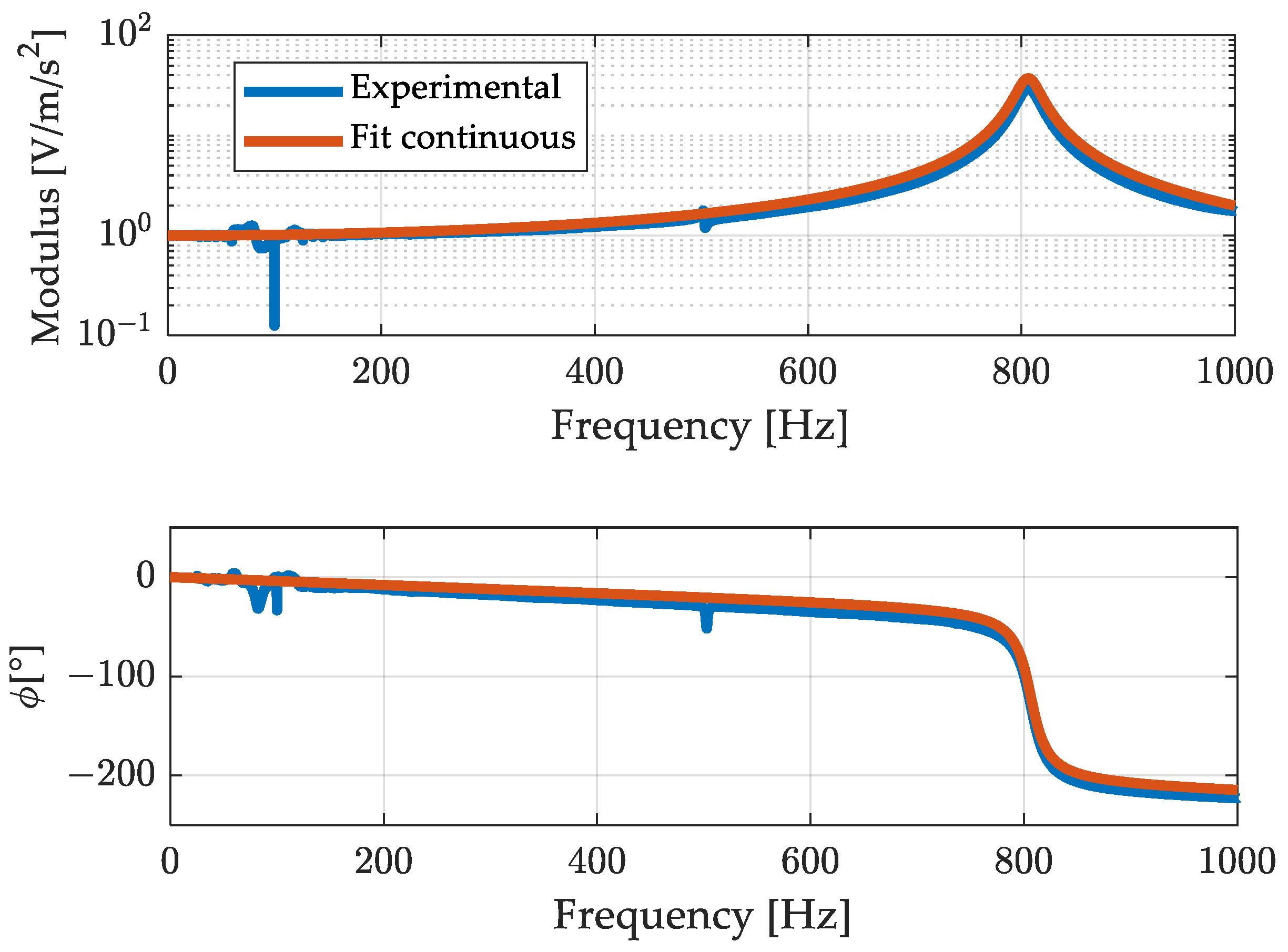
4. Experimental Validation of the Method
- Two mono-harmonic signals: a signal with one sinusoidal component with a frequency within the bandwidth of the accelerometer under test and the other having a frequency out of band and near the accelerometer resonant frequency (see Section 4.1);
- A bi-harmonic signal: a signal with two sinusoidal components, one with a frequency in band and the other with a frequency out of band (Section 4.2);
- A multicomponent signal including several in-band and out-of-band harmonic components (see Section 4.3).
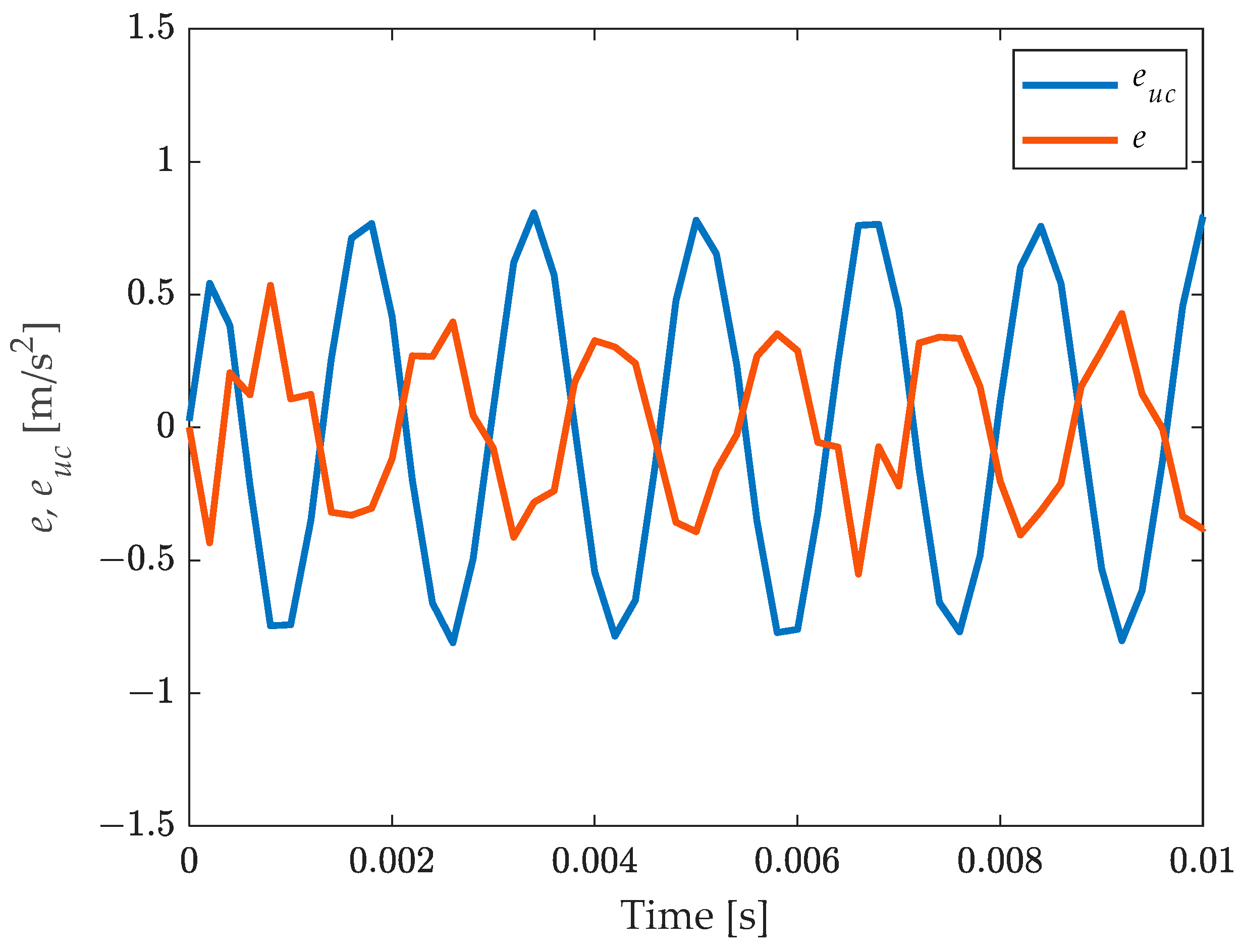
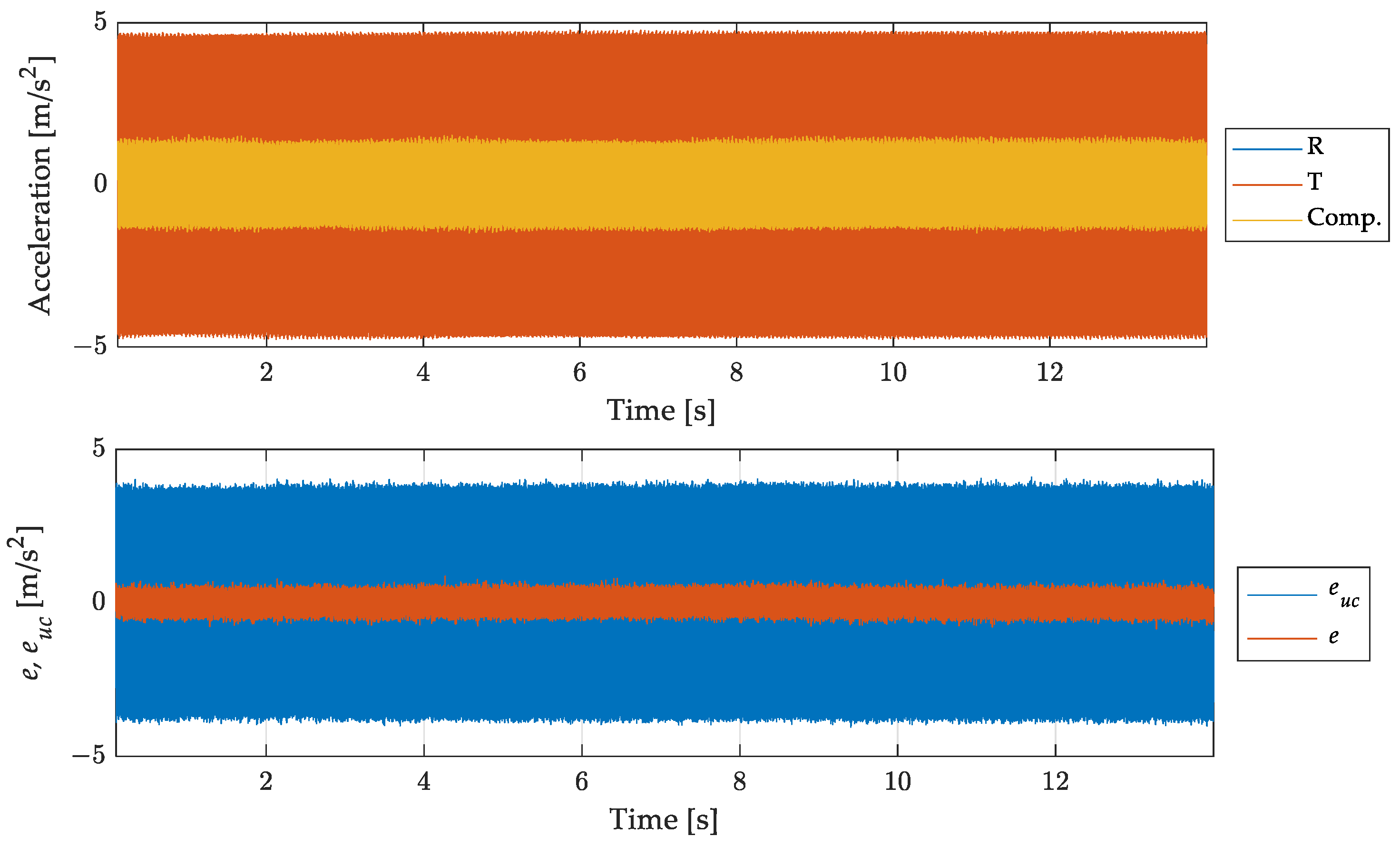
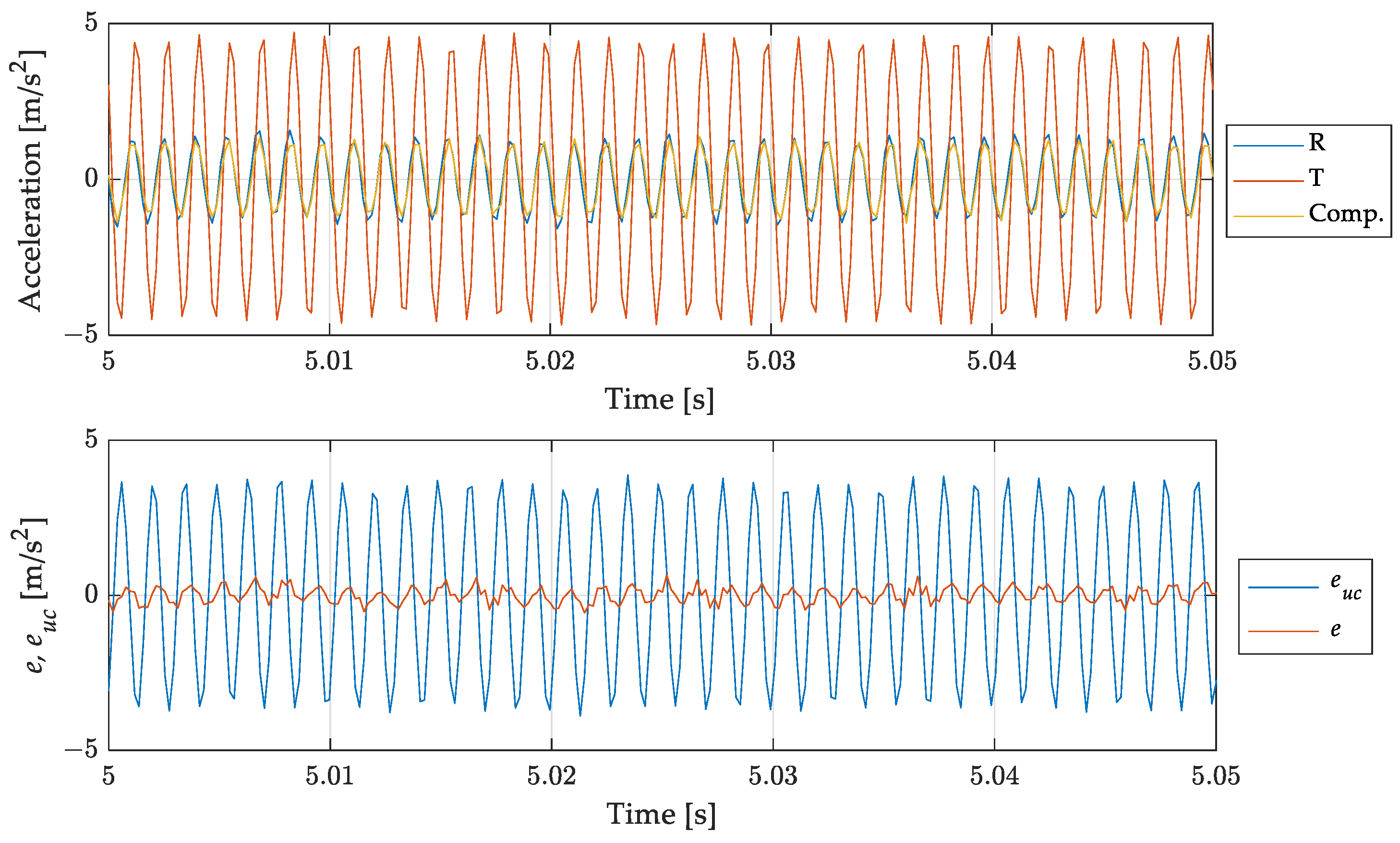
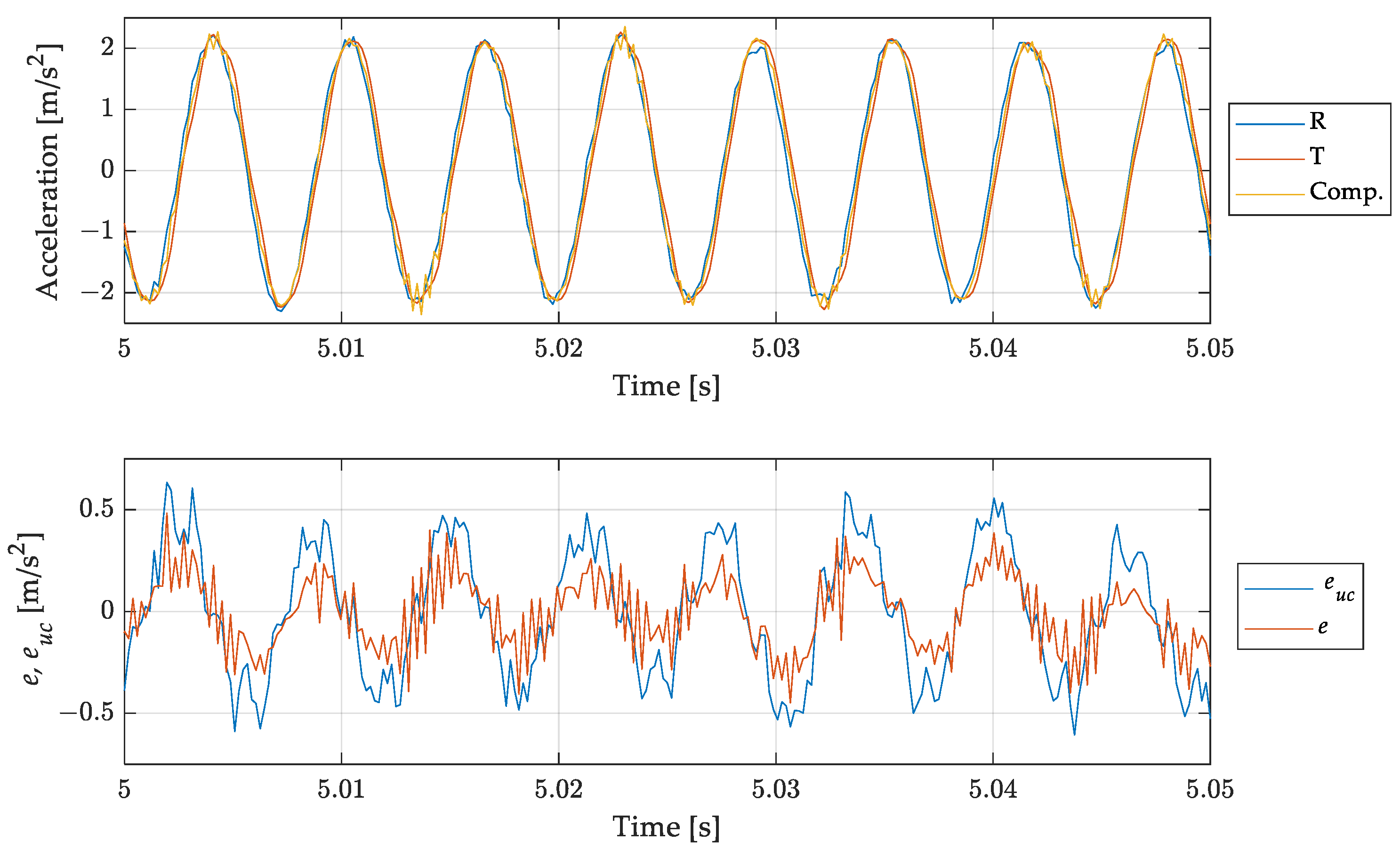
4.1. Test Case 1: Pure Sine (in Band and out of Band)
4.2. Test Case 2: Two Components Signal (out of Band + in Band)
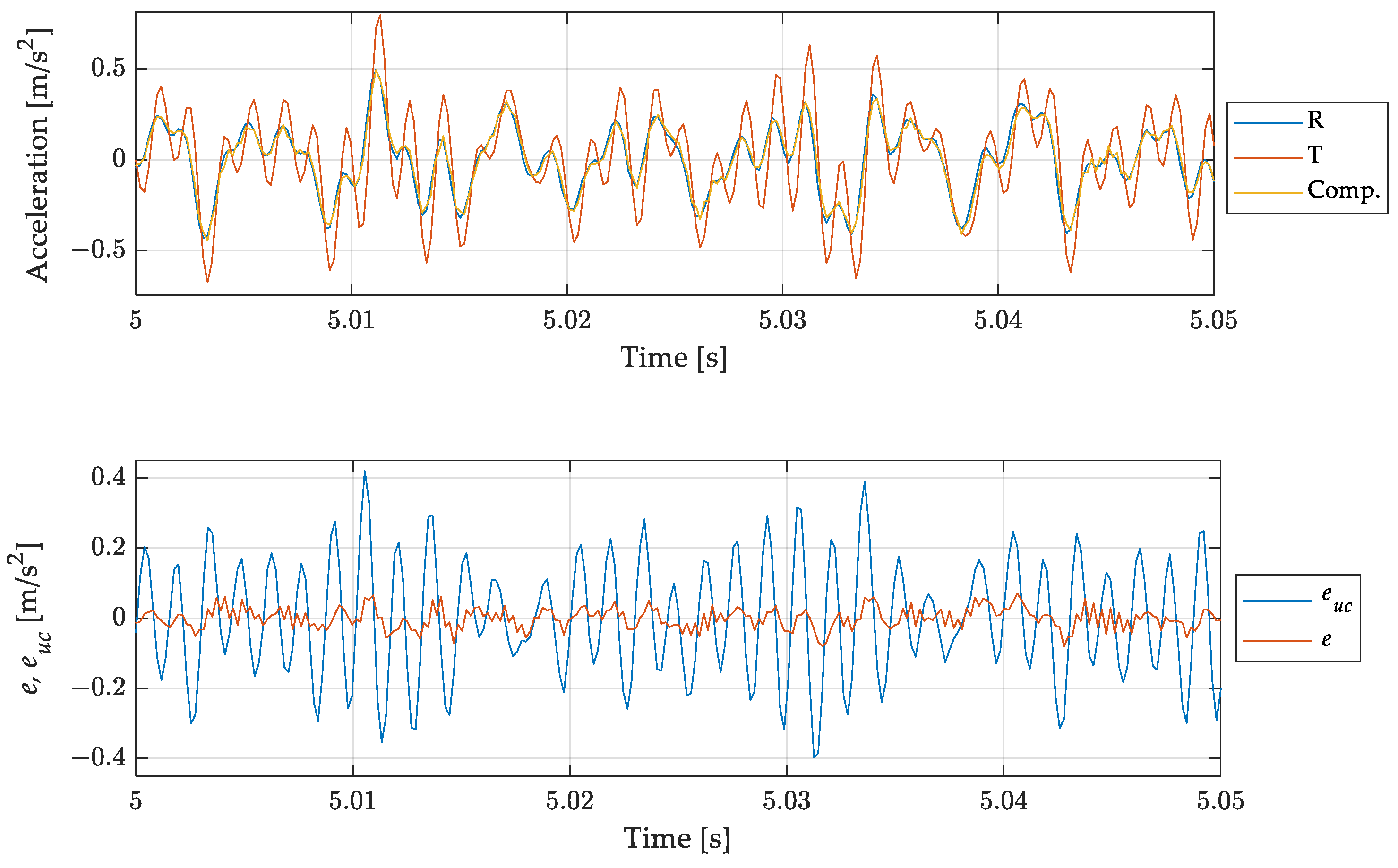
4.3. Test Case 3: Multicomponent
4.4. Result Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartoli, C.; Beug, M.F.; Bruns, T.; Elster, C.; Esward, T.J.; Klaus, L.; Knott, A.; Kobusch, M.; Saxholm, S.; Schlegel, C. Traceable dynamic measurement of mechanical quantities: Objectives and first results of this european project. Int. J. Metrol. Qual. Eng. 2012, 3, 127–135. [Google Scholar] [CrossRef]
- Hessling, J.P. Dynamic metrology. Meas. Sci. Technol. 2008, 19, 084008. [Google Scholar] [CrossRef]
- Sommer, K.D. Modelling of measurement, system theory, and uncertainty evaluation. In Data Modeling for Metrology and Testing in Measurement Science; Pavese, F., Forbes, A., Eds.; Birkhauser-Springer: Boston, MA, USA, 2009; pp. 275–298. [Google Scholar]
- Ruhm, K.H. Measurement plus observation—A new structure in metrology. Measurement 2018, 126, 421–432. [Google Scholar] [CrossRef]
- Ruhm, K.H. Dynamics and stability—A proposal for related terms in Metrology from a mathematical point of view. Measurement 2016, 79, 276–284. [Google Scholar] [CrossRef]
- Doebelin, E. Measurement Systems; Mc Graw Hill: New York, NY, USA, 1990. [Google Scholar]
- Hessling, J.P. A novel method of dynamic correction in the time domain. Meas. Sci. Technol. 2008, 19, 075101. [Google Scholar] [CrossRef]
- Eichstädt, S.; Elster, C.; Esward, T.J.; Hessling, J.P. Deconvolution filters for the analysis of dynamic measurement processes: A tutorial. Metrologia 2010, 47, 522–533. [Google Scholar] [CrossRef]
- Eichstädt, S.; Link, A.; Bruns, T.; Elster, C. On-line dynamic error compensation of accelerometers by uncertainty-optimal filtering. Measurement 2010, 43, 708–713. [Google Scholar] [CrossRef]
- Eichstädt, S.; Wilkens, V. Evaluation of uncertainty for regularized deconvolution: A case study in hydrophone measurements. J. Acoust. Soc. Am. 2017, 141, 4155–4167. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.-S.; Cheng, Z.-Y.; Gong, W.-C.; Yu, L.; Li, R.-J.; Huang, Q.-X. A novel dynamic compensation method for a contact probe based on Bayesian inversion. Measurement 2021, 186, 110143. [Google Scholar] [CrossRef]
- Yang, S.-L.; Yang, R.; Zha, F.-Y.; Liu, H.-D.; Liang, L.-P.; Xu, K.-J. Dynamic compensation method based on system identification and error-overrun mode correction for strain force sensor. Mech. Syst. Signal Process. 2020, 140, 106649. [Google Scholar] [CrossRef]
- Yang, F.; Kong, D.; Kong, L. Accurate measurement of high-frequency blast waves through dynamic compensation of miniature piezoelectric pressure sensors. Sens. Actuators A Phys. 2018, 280, 14–23. [Google Scholar] [CrossRef]
- Rossi, G.B. Toward an Interdisciplinary Probabilistic Theory of Measurement. IEEE Trans. Instrum. Meas. 2012, 61, 2095–2106. [Google Scholar] [CrossRef]
- Rossi, G.B. Measurement and Probability; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Rossi, G.B.; Crenna, F. A first-order probabilistic logic with application to measurement representations. Measurement 2016, 79, 251–259. [Google Scholar] [CrossRef]
- Rossi, G.B.; Crenna, F.; Berardengo, M. Probability theory as a logic for modelling the measurement process. In Proceedings of the IMEKO TC1+TC7+TC13+TC18 & MATHMET Joint Symposium “Cutting Edge Measurement Science for the Future”, ISEP, Porto, Portugal, 31 August–3 September 2022. [Google Scholar]
- Directive 2004/22/EC of the European Parliament and of the Council, Measuring Instrument Directive, 2004. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=CONSLEG:2004L0022:20091201:en:PDF (accessed on 1 March 2023).
- Crenna, F.; Rossi, G.B.; Bovio, L. Probabilistic measurement evaluation for the implementation of the Measuring Instrument Directive. Measurement 2009, 42, 1522–1531. [Google Scholar] [CrossRef]
- BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML 1993 Guide to the Expression of Uncertainty in Measurement; Corrected and Reprinted; ISO: Geneva, Switzerland, 1995; ISBN 92-67-10188.
- Rossi, G.B.; Crenna, F.; Palazzo, A. A Proposal for a More User-Oriented GUM. IEEE Trans. Instrum. Meas. 2019, 68, 1343–1352. [Google Scholar] [CrossRef]
- Rossi, G.B.; Crenna, F.; Palazzo, A. Probabilistic Framework for Dynamic Measurements for Markovian Models with a Uniform Prior for the Measurand. IEEE Trans. Instrum. Meas. 2019, 68, 4357–4367. [Google Scholar] [CrossRef]
- Rossi, G.B.; Crenna, F. Dynamic Compensation for a Second Order Measuring Device. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stocastic Processes, 2nd ed.; Mc Graw Hill: Singapore, 1984. [Google Scholar]
- Elster, C.; Link, A.; Bruns, T. Analysis of dynamic measurements and determination of time-dependent measurement uncertainty using a second-order model. Meas. Sci. Technol. 2007, 18, 3682–3687. [Google Scholar] [CrossRef]
- Kwakernaak, E.H.; Sivan, R. Linear Optimal Control Systems; Wiley-Interscience: New York, NY, USA, 1972. [Google Scholar]
- Brandt, A. Noise and Vibration Analysis—Signal Analysis and Experimental Procedures; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Kay, S.M. Modern Spectrum Estimation; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Research Studies Press Ltd.: Baldock, UK, 2000. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999; ISBN 0-13-656695-2. [Google Scholar]
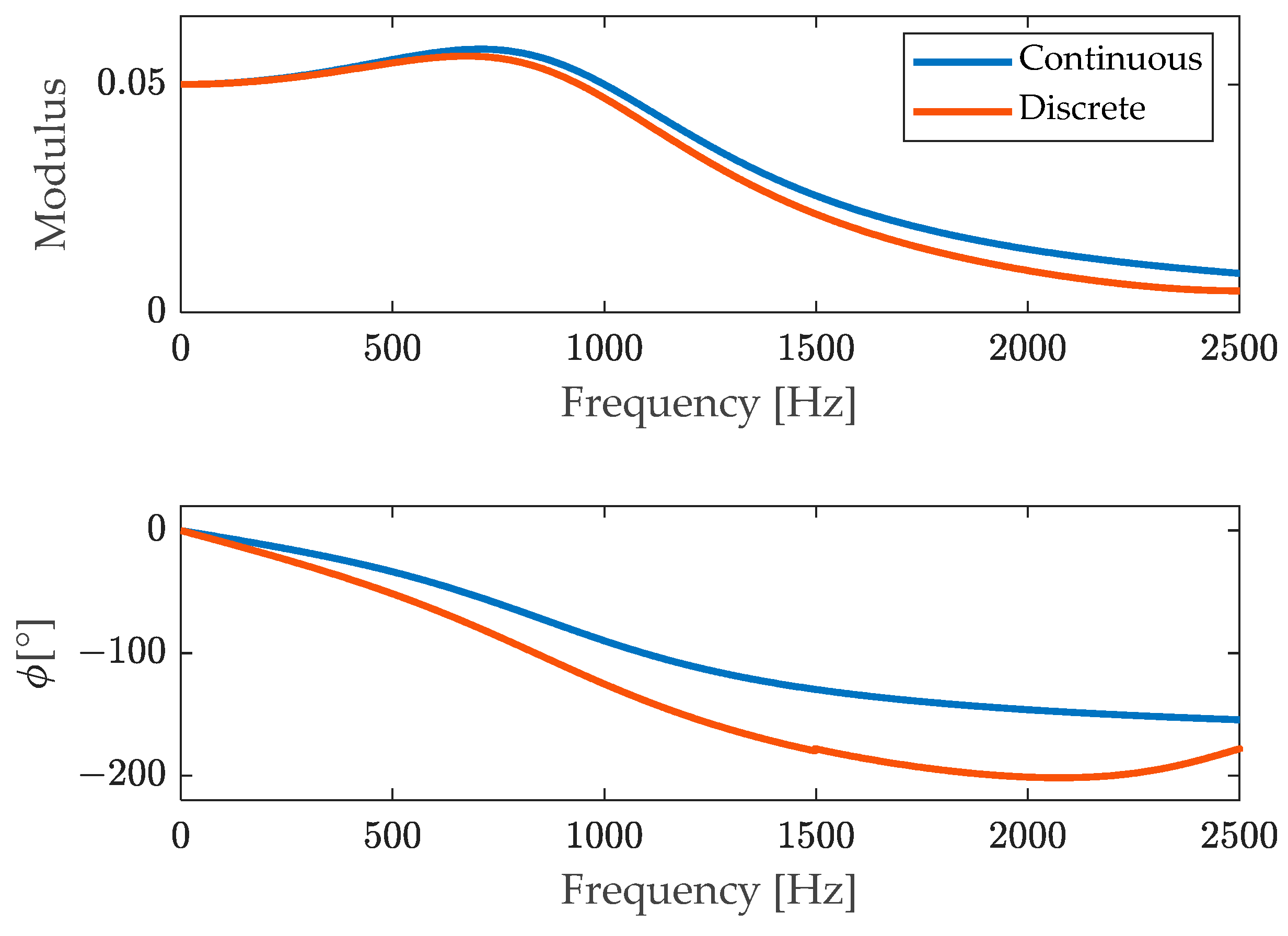


| PCB 333B30 (R) | PCB 393B31 (T) | |
|---|---|---|
| Mass (kg) | 0.004 | 0.635 |
| Sensitivity (mV/ms−2) | 10.2 | 1020 |
| ±5% bandwidth (Hz) | 0.5–3000 | 0.1–200 |
| Resonant frequency (kHz) | ≥40 | ≥0.7 |
| Multicomponent frequencies (Hz) | 160 | 170 | 180 | 200 | 300 | 350 | 400 | 600 | 650 | 700 | ||
| Accelerometer under test bandwidth and resonant frequency (Hz) | 0.07 | 200 | 806 |
| Test Case | (Equation (28)) % | (Equation (25)) % |
|---|---|---|
| 1a: mono-harmonic, out of band | 0.76 | 0.93 |
| 1b: mono-harmonic, in band | 20.30 | 35.14 |
| 2: bi-harmonic | 0.85 | 1.42 |
| 3: multi-harmonic | 1.86 | 3.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crenna, F.; Rossi, G.B.; Berardengo, M. Dynamic Compensation of a Piezoelectric Accelerometer Obtained through a General Probabilistic Approach. Sensors 2023, 23, 3950. https://doi.org/10.3390/s23083950
Crenna F, Rossi GB, Berardengo M. Dynamic Compensation of a Piezoelectric Accelerometer Obtained through a General Probabilistic Approach. Sensors. 2023; 23(8):3950. https://doi.org/10.3390/s23083950
Chicago/Turabian StyleCrenna, Francesco, Giovanni Battista Rossi, and Marta Berardengo. 2023. "Dynamic Compensation of a Piezoelectric Accelerometer Obtained through a General Probabilistic Approach" Sensors 23, no. 8: 3950. https://doi.org/10.3390/s23083950
APA StyleCrenna, F., Rossi, G. B., & Berardengo, M. (2023). Dynamic Compensation of a Piezoelectric Accelerometer Obtained through a General Probabilistic Approach. Sensors, 23(8), 3950. https://doi.org/10.3390/s23083950








