Low-Cost Turbidity Sensor to Determine Eutrophication in Water Bodies
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Proposal Description
3.1.1. Hardware Description
- Microcontroller board: This was used as the central processing unit of the system, responsible for executing the software that controls the sensor. We chose M5Stack [28], a prototyping board based on the ESP32 [29] microcontroller, which provides a range of analog and digital inputs and outputs. This board was chosen for the design of our sensor due to its several advantageous features. The M5Stack board offers a color display that can be used to display the results of the sensor, as well as three buttons for operating the sensor. Additionally, it includes an SD card reader which can be used to store the results of the sensor and a small battery that allows for use of the sensor without being connected to a power source. These features make M5Stack an ideal choice for the design of our sensor. One of the drawbacks of the M5Stack is that it only includes three analog inputs, which is why it has been necessary to add a demultiplexer.
- LED light source: This was used to project the beam of light required for the nephelometry or turbidimetry measurement. We used an infrared LED (950 nm) and RGB LED to generate different wavelengths. The IR light was selected because the commercial turbidimeter uses IR light. This is because this wavelength has low energy and, therefore, will be little absorbed by the substances in the environment. The RGB wavelengths were used because the sediment and algae have different colors. Therefore, the absorption and scattering of these lights were different. Accordingly, the light that arrived at the photoreceptors was different.
- Optical sensors: We used a photodiode (1612660) for infrared light and a light-dependent resistor (LDR) for visible light. These sensors were used in pairs at angles of 90 and 180 degrees depending on whether we were using either the nephelometry or turbidimetry method. Figure 1 shows the sensors nephelometry vs. turbidimetry.
- Auxiliary elements: In order to connect the sensors and actuators to the microcontroller and adapt the different signals, we needed different resistors, as shown in Figure 2. An amplification stage was also necessary in the 90-degree infrared sensor. All these components are shown in the schematic circuit. Since the resistors have been adjusted at various times, it was thought to be more efficient to assemble the prototype on a proto board. Once the final design was reached, we then mounted the equivalent PCB board.
- Signal adapter circuit: To connect the sensors and actuators to the microcontroller and adapt the different signals, we needed various resistors, as shown in the circuit schematic. An amplification stage was also necessary for the 90-degree infrared sensor, for which an operational amplifier with three adjustable resistors was utilized. The M5Stack only has 3 analog inputs, but our design required 4; 2 for the infrared light sensors at 90 and 180 degrees, and 2 for the visible light sensors. To overcome this issue, we added a multiplexer which can select up to sixteen inputs in one process.
- Sensor Enclosure: To protect the sensor and its components, we designed and 3D printed an enclosure for the sensor. Having a protective case for the sensor reduced the risk of cable disconnections that can occur when using a proto board, as well as protecting the components from water damage. Additionally, it allowed for the precise positioning of the LEDs. Figure 3 shows the sensor.
3.1.2. Software Functionality
| Algorithm 1: Master head algorithm. |
| Given: refresh_time, samples_number PHASE=[“IR180”,“IR90”,“R180”,“R90”,“G180”,“G90”,“B180”,“B90”,“NONE”] configure_graphical_output_UI() configure_pinMode_for_each_in_out() Repeat For Each phase In PHASE select_multiplexer_input(phase) turn_on_appropriate_LED(phase) For Each count In 1..samples_number value = read_analog_value() save_value(phase, count, value) // o data[phase,count] = value draw_value_UI(value) wait(refresh_time) End For obtain_mean_and_deviation(phase) End For check_alarm_system() save_phases_in_SD() Until button_C is pressed |
3.2. Test Bench
Methodology
4. Results
4.1. Selection of the Better Combination of Resistance
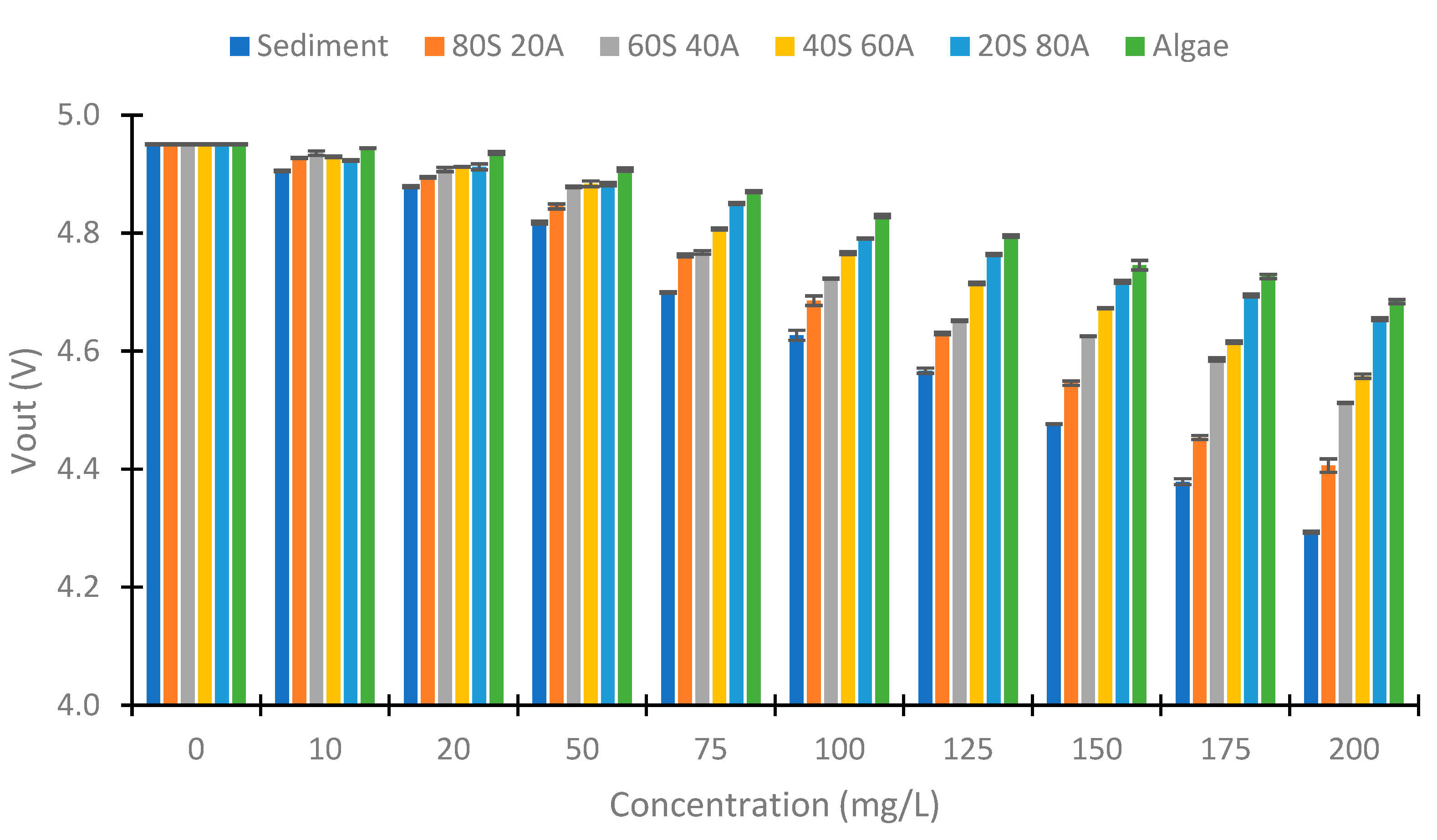
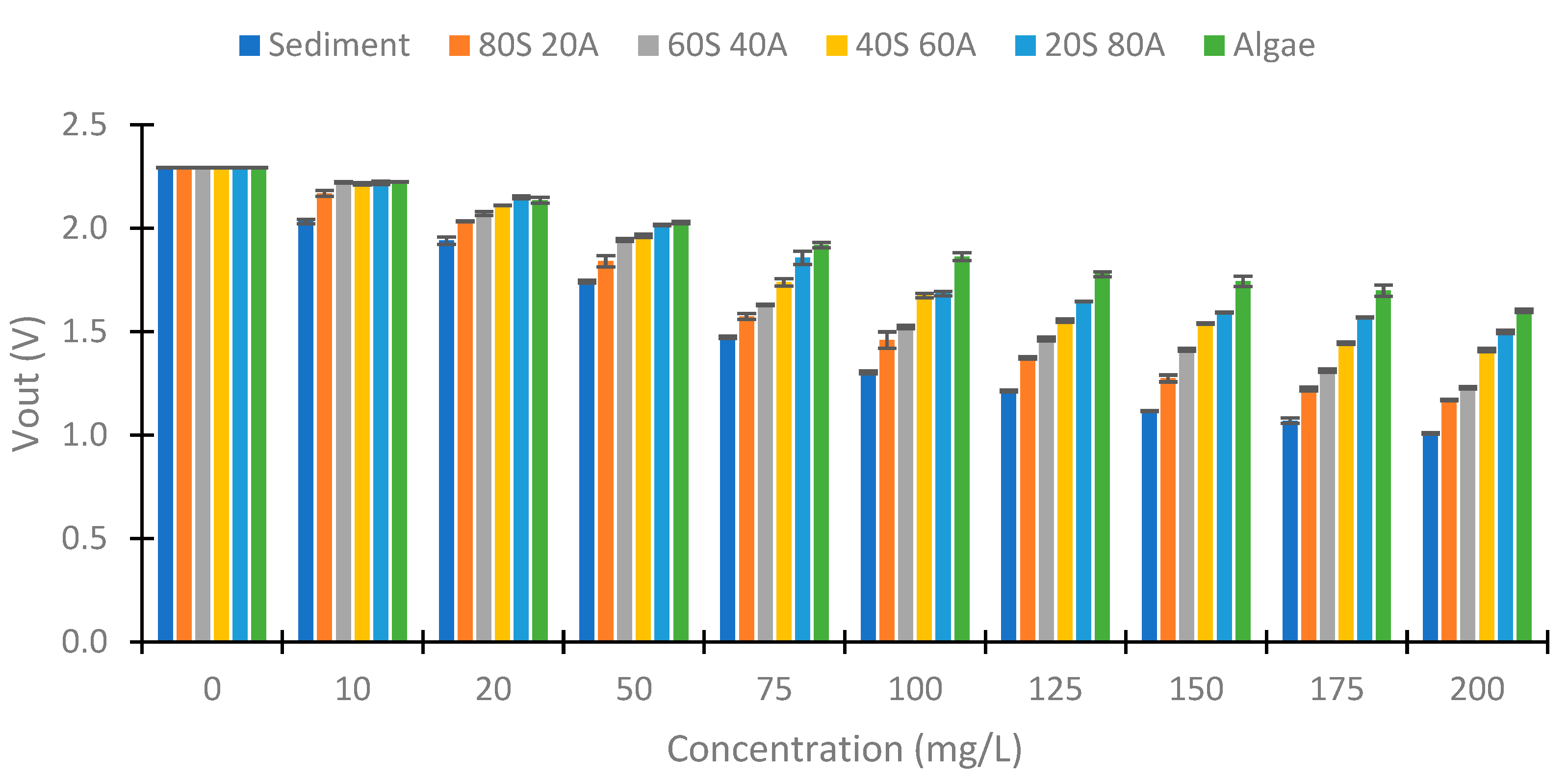
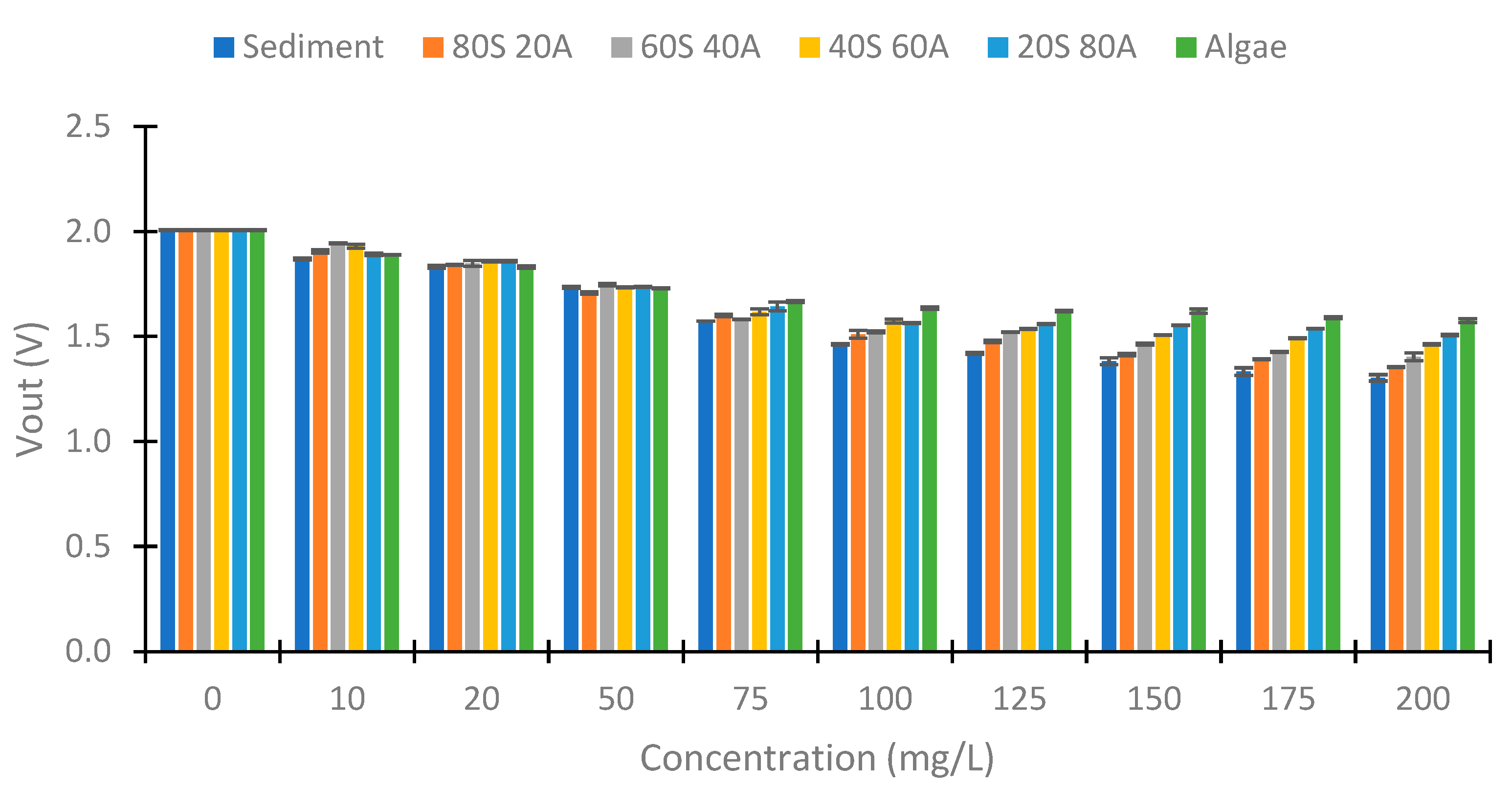
4.2. Turbidity of Samples
4.3. IR LED
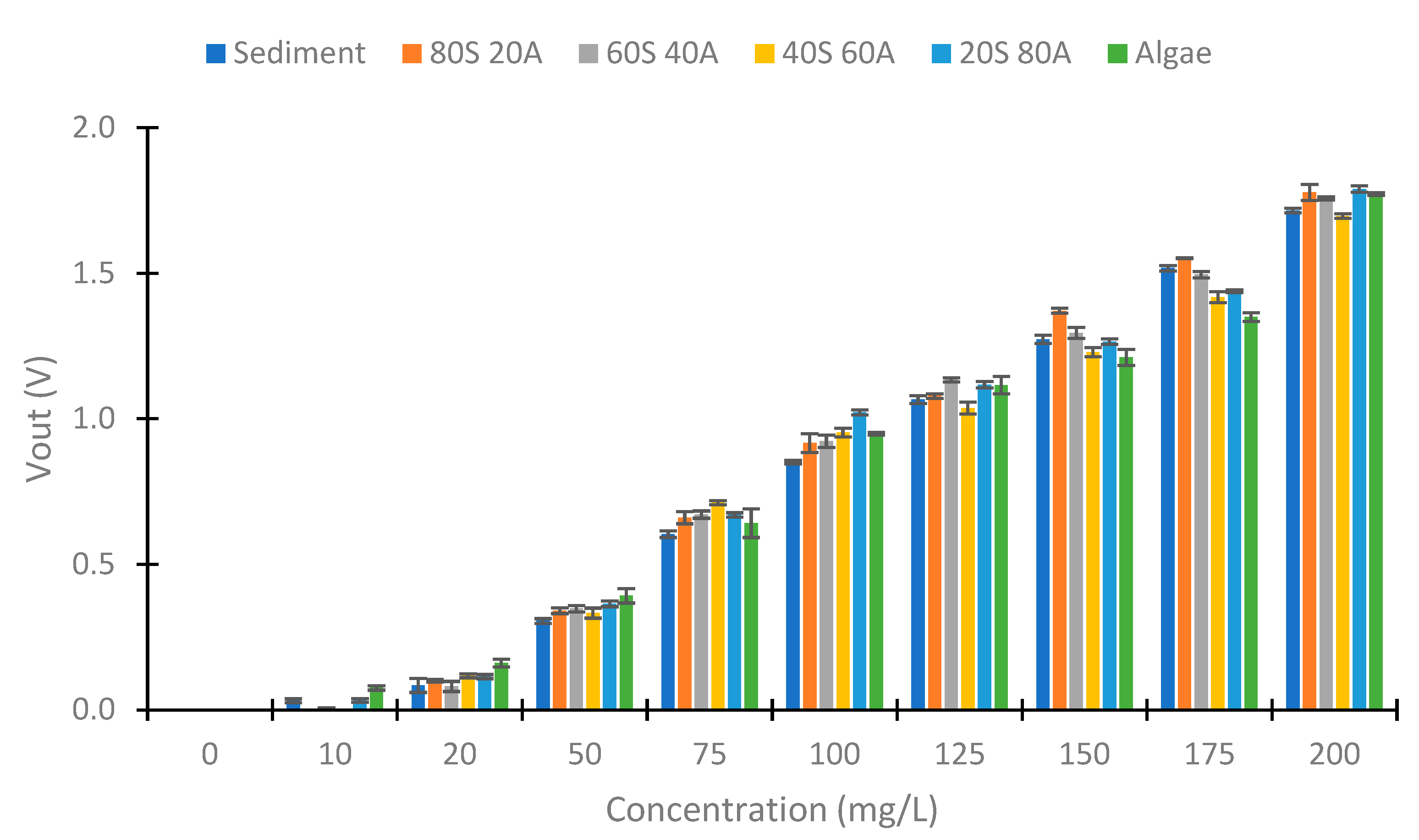
4.4. Use of Colour LEDs
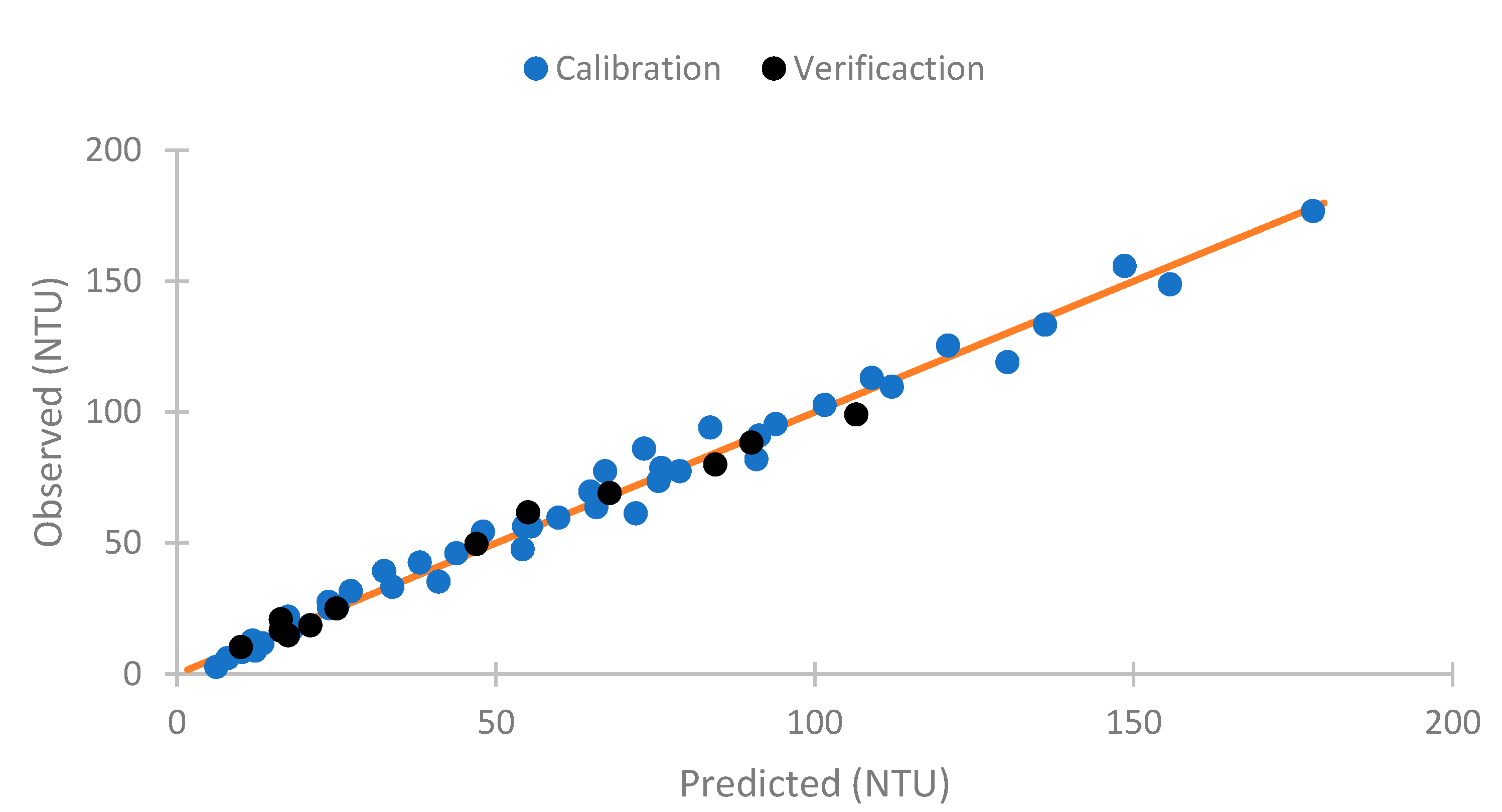
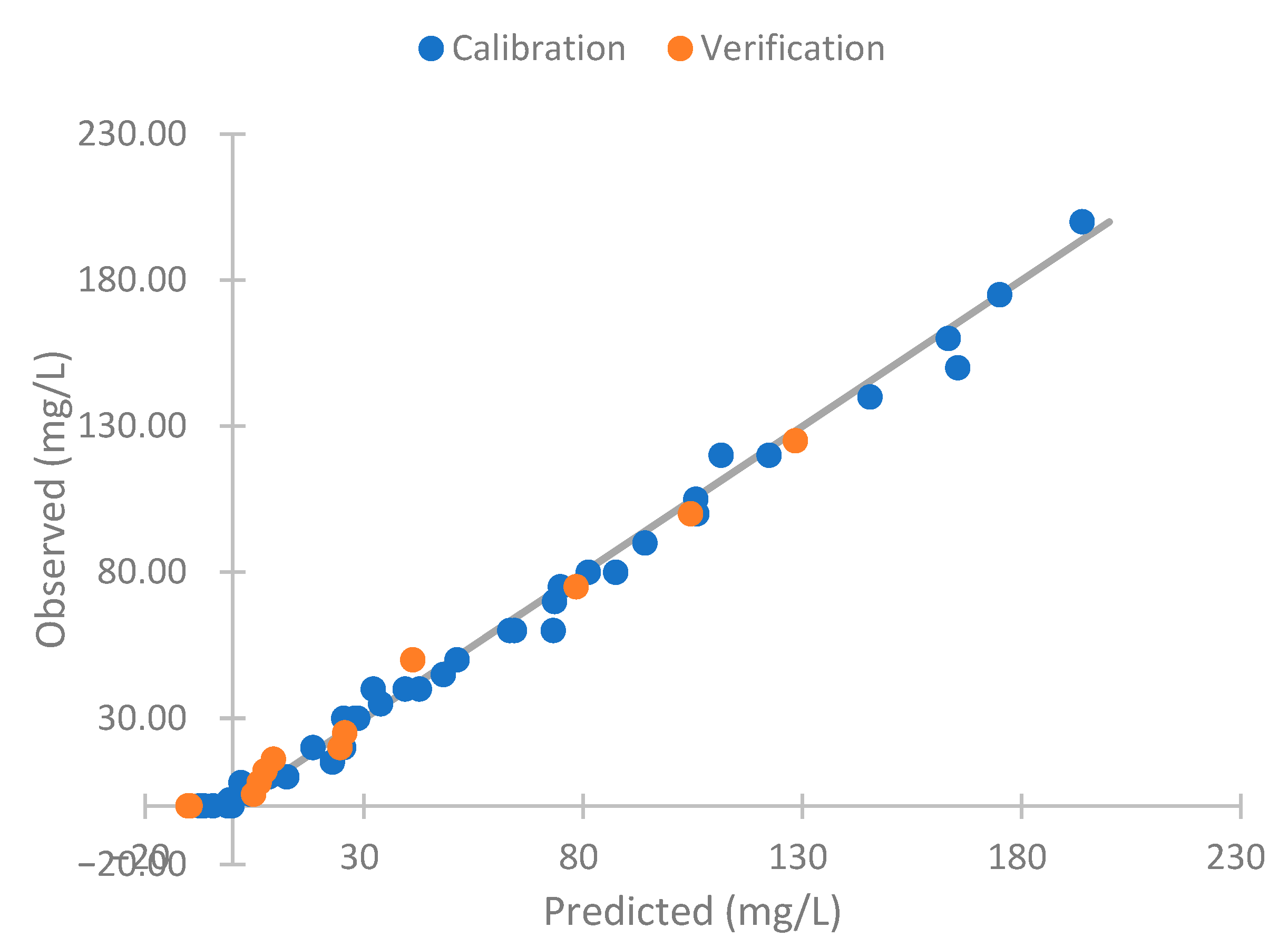
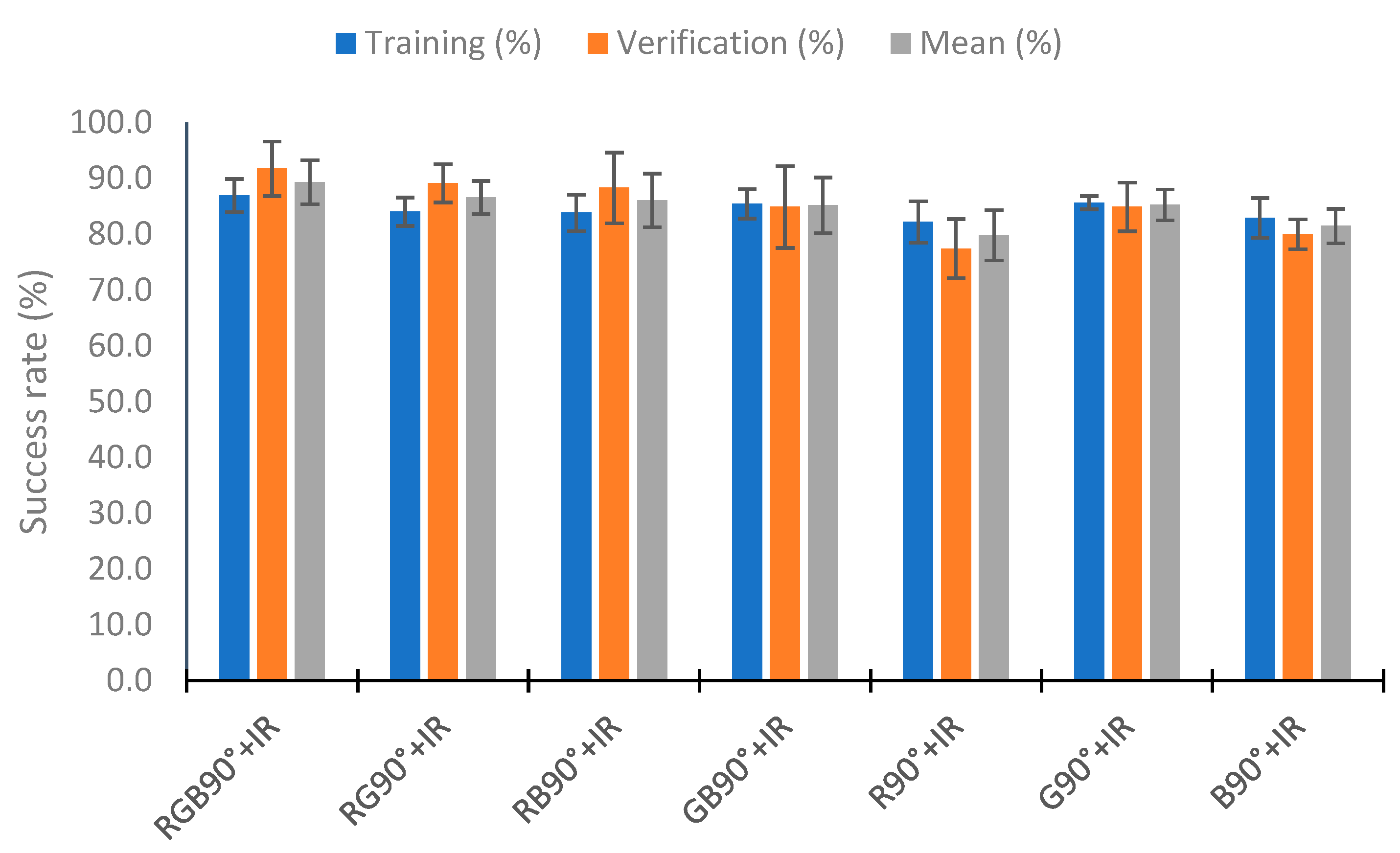
4.5. Use of Neural Network
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boyd, C.E. (Ed.) Chapter Suspended Solids, Color, Turbidity, and Light. In Water Quality: An Introduction; Springer: Berlin/Heidelberg, Germany, 2020; pp. 119–133. [Google Scholar]
- Shen, C.; Liao, Q.; Titi, H.H.; Li, J. Turbidity of Stormwater Runoff from Highway Construction Sites. J. Environ. Eng. 2018, 144, 04018061. [Google Scholar] [CrossRef]
- Pasika, S.; Gandla, S. Smart water quality monitoring system with cost-effective using IoT. Heliyon 2020, 6, e04096. [Google Scholar] [CrossRef]
- Adu-Manu, K.; Tapparello, C.; Heinzelman, W.; Katsriku, F.; Abdulai, J.D. Water quality monitoring using wireless sensor networks: Current trends and future research directions. ACM Trans. Sens. Netw. 2017, 13, 1–41. [Google Scholar] [CrossRef]
- Wang, Y.; Rajib, S.; Collins, C.; Grieve, B. Low-Cost Turbidity Sensor for Low-Power Wireless Monitoring of Fresh-Water Courses. IEEE Sens. J. 2018, 18, 4689–4696. [Google Scholar] [CrossRef]
- ISO 7027-1:2016. Water Quality—Determination of Turbidity—Part 1: Quantitative Methods. Available online: https://www.iso.org/standard/62801.html (accessed on 30 December 2022).
- O’Dell, J.W. Method 180.1 Determination of Turbidity by Nephelometry; Environmental Monitoring Systems Laboratory Office of Research and Development U.S. Environmental Protection Agency: Cincinnati, OH, USA, 1993. [Google Scholar]
- Fondriest Environmental, Inc. Fundamentals of Environmental Measurements: Measuring Turbidity, TSS, and Water Clarity. 2014. Available online: https://www.fondriest.com/environmental-measurements/measurements/measuring-water-quality/turbidity-sensors-meters-and-methods/ (accessed on 30 December 2022).
- Chanson, H.; Takeuchi, M.; Trevethan, M. Using turbidity and acoustic backscatter intensity as surrogate measures of suspended sediment concentration in a small subtropical estuary. J. Environ. Manag. 2008, 88, 1406–1416. [Google Scholar] [CrossRef]
- Bin Omar, A.F.; Bin MatJafri, M.Z. Turbidimeter Design and Analysis: A Review on Optical Fiber Sensors for the Measurement ofWater Turbidity. Sensors 2009, 9, 8311–8335. [Google Scholar] [CrossRef] [PubMed]
- Gillett, D.; Marchiori, A. A Low-Cost Continuous Turbidity Monitor. Sensors 2019, 19, 3039. [Google Scholar] [CrossRef]
- Zan, Z.; Qiu, X.; Guan, Y.; Zhang, E.; Liu, Q.; He, X.; Guo, G.; Li, C.; Yang, M. A novel low-cost turbidity sensor for in-situ extraction in TCM using spectral components of transmitted and scattered light. Measurement 2020, 160, 107838. [Google Scholar]
- Hakim, W.L.; Hasanah, L.; Mulyanti, B.; Aminudin, A. Characterization of turbidity water sensor SEN0189 on the changes of total suspended solids in the water. J. Phys. Conf. Ser. 2019, 1280, 022064. [Google Scholar] [CrossRef]
- Gavhane, P.M.; Sutrave, D.S.; Bachuwar, V.D.; Gothe, S.D.; Joshi, P.S. Smart Turbidity Monitoring and Data Acquisition using LabVIEW. J. Xi’an Shiyou Univ. 2019, 15, 22–30. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, L.; Bian, W.; Zhou, B.; Liang, D.; Li, J. Turbidity in combined sewer sewage: An identification of stormwater detention tanks. Int. J. Environ. Res. Public Health 2020, 17, 3053. [Google Scholar] [CrossRef] [PubMed]
- Parra, L.; Rocher, J.; Escrivá, J.; Lloret, J. Design and development of low cost smart turbidity sensor for water quality monitoring in fish farms. Aquac. Eng. 2018, 81, 10–18. [Google Scholar] [CrossRef]
- Parra, L.; Sendra, S.; Jimenez, J.M.; Lloret, J. Smart system to detect and track pollution in marine environments. In Proceedings of the 2015 IEEE International Conference on Communication Workshop, London, UK, 8–12 June 2015; pp. 1503–1508. [Google Scholar]
- Kirkey, W.D.; Bonner, J.S.; Fuller, C.B. Low-Cost Submersible Turbidity Sensors Using Low-Frequency Source Light Modulation. IEEE Sens. J. 2018, 18, 9151–9162. [Google Scholar] [CrossRef]
- Mylvaganaru, S.; Jakobsen, T. Turbidity sensor for underwater applications. In Proceedings of the IEEE Oceanic Engineering Society. OCEANS’98. Conference Proceedings (Cat. No.98CH36259), Nice, France, 28 September–1 October 1998. [Google Scholar] [CrossRef]
- Wei, J.; Qin, F.; Li, G.; Li, X.; Liu, X.; Dai, X. Chirp modulation enabled turbidity measurement for large scale monitoring of fresh water. Measurement 2021, 184, 109989. [Google Scholar] [CrossRef]
- Takaaki, A.B.E.; Mizugaki, S.; Toyabe, T.; Maruyama, M.; Murakami, Y.; Ishiya, T. High range turbidity monitoring in the Mu and Saru river basins: All-year monitoring of hydrology and suspended sediment transport in 2010. Int. J. Eros. Control Eng. 2012, 5, 70–79. [Google Scholar]
- Tyler, A.N.; Svab, E.; Preston, T.; Présing, M.; Kovács, W.A. Remote sensing of the water quality of shallow lakes: A mixture modelling approach to quantifying phytoplankton in water characterized by high-suspended sediment. Int. J. Remote Sens. 2006, 27, 1521–1537. [Google Scholar] [CrossRef]
- Yaser, M.; Priyanto, U.; Busalim, F. Measurement of Wastewater Turbidity Based on Total Dissolved Solids at Pancasila University. In Proceedings of the 2nd Faculty of Industrial Technology International Congress International Conference, Bandung, Indonesia, 28–30 January 2020. [Google Scholar]
- Hussain, I.; Ahamad, K.; Nath, P. Water turbidity sensing using a smartphone. RSC Adv. 2016, 6, 22374–22382. [Google Scholar] [CrossRef]
- Fay, C.D.; Nattestad, A. Advances in Optical Based Turbidity Sensing Using LED Photometry (PEDD). Sensors 2022, 22, 254. [Google Scholar] [CrossRef]
- Rocher, J.; Aldegheishem, A.; Alrajeh, N.; Lloret, J. Develop an Optical Sensor to Detect Pollution Incidents in Sewerage. IEEE Sens. J. 2022, 22, 24449–24457. [Google Scholar] [CrossRef]
- M5STACK. Available online: https://m5stack.com/ (accessed on 11 February 2023).
- Tang, Y.; Luo, Q.; Chen, Y.; Xu, K. All-Silicon Photoelectric Biosensor on Chip Based on Silicon Nitride Waveguide with Low Loss. Nanomaterials 2023, 13, 914. [Google Scholar] [CrossRef]
- ESP32. Available online: https://www.espressif.com/en/products/socs/esp32 (accessed on 11 February 2023).
- Lutron Datasheet TU-2016. Available online: https://www.sunwe.com.tw/lutron/TU-2016.pdf (accessed on 11 February 2023).
- RS online, Infrared Emitting Diode, 950 nm, GaAs. TSUS5400, TSUS5401, TSUS5402. Available online: https://docs.rs-online.com/f3b6/0900766b80e22d5c.pdf (accessed on 11 February 2023).
- Datasheet L-154A4SUREQBFZGEW. Available online: https://www.farnell.com/datasheets/3360919.pdf (accessed on 11 February 2023).
- RS online, “SFH 203”. Available online: https://docs.rs-online.com/9f58/0900766b816d8a09.pdf (accessed on 11 February 2023).
- Advanced Photonix NSL-19M51 Datasheet; Advanced Photonix. Available online: https://www.advancedphotonix.com/wp-content/uploads/2022/03/DS-NSL-19M51.pdf (accessed on 11 February 2023).
- Xu, K. Silicon Electro-Optic Micro-Modulator Fabricated in Standard CMOS Technology as Components for All Silicon Monolithic Integrated Optoelectronic Systems. J. Micromech. Microeng. 2021, 31, 054001. [Google Scholar] [CrossRef]
- Datarobot Nutonian. Available online: https://www.datarobot.com/nutonian/ (accessed on 11 February 2023).







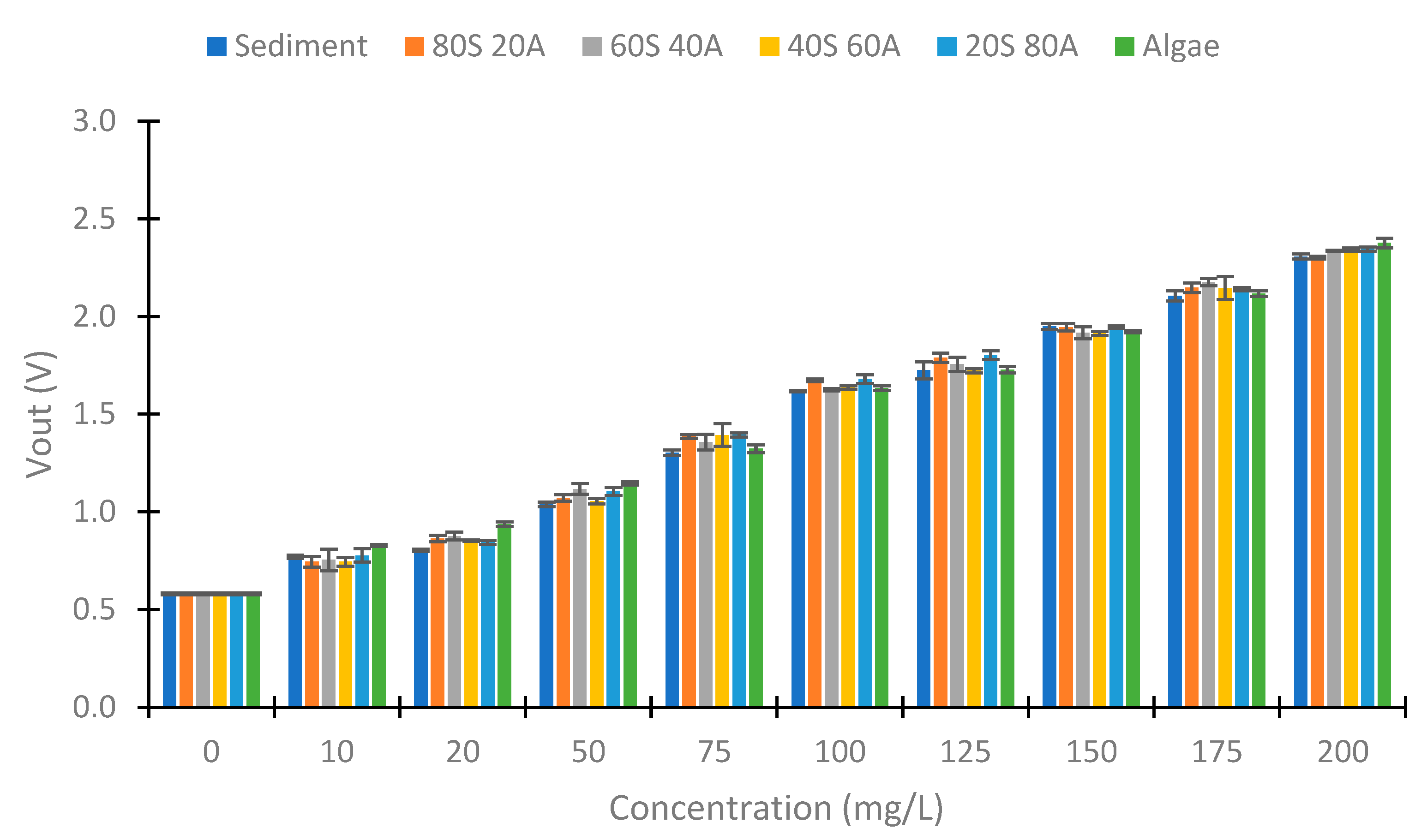









| Resistance LED (Ω) | 1200 | 560 | 220 | 150 | 100 | 68 | 33 |
| Intensity LED (mA) | 3.5 | 7.09 | 17.73 | 24.14 | 35.29 | 53 | 100 |
| Resistance photodiode (kΩ) | 100 | 330 | 1000 | 3000 | 8200 | 10,000 |
| Parameters | Red 180° | Red 90° | Green 180° | Green 90° | Blue 180° | Blue 90° |
|---|---|---|---|---|---|---|
| Resistance 0 mg/L (kΩ) | 1.04 | 16.25 | 0.72 | 16.61 | 1.09 | 27.12 |
| Resistance 100 mg/L (kΩ) | 1.24 | 84.70 | 0.97 | 40.71 | 1.53 | 65.70 |
| Optimal resistance (kΩ) | 1.14 | 37.10 | 0.84 | 26.00 | 1.29 | 42.21 |
| Voltage difference (V) | 0.153 | 1.280 | 0.245 | 0.707 | 0.280 | 0.685 |
| Select resistance (kΩ) | 1.20 | 33.00 | 1.20 | 33.00 | 1.20 | 33.00 |
| Voltage difference (V) | 0.145 | 1.276 | 0.238 | 0.698 | 0.280 | 0.674 |
| Equation (3) | Equation (4) | |||
|---|---|---|---|---|
| Absolute (mg/L) | Relative (%) | Absolute (mg/L) | Relative (%) | |
| Error calibration | 5.69 | 11.14 | 4.16 | 8.09 |
| Error verification | 3.90 | 11.84 | 3.79 | 11.40 |
| Equation (5) | Equation (6) | |||
|---|---|---|---|---|
| Absolute (mg/L) | Relative (%) | Absolute (mg/L) | Relative (%) | |
| Error calibration | 5.73 | 19.17 | 6.85 | 29.49 |
| Error verification | 6.78 | 30.58 | 8.62 | 53.33 |
| Equation G | Equation H | |||
|---|---|---|---|---|
| Absolute (mg/L) | Relative (%) | Absolute (mg/L) | Relative (%) | |
| Error calibration | 3.74 | 14.98 | 3.99 | 11.61 |
| Error verification | 4.95 | 17.95 | 5.63 | 25.53 |
| Absolute (mg/L) | Relative (%) | |
|---|---|---|
| Error calibration | 2.78 | 13.91 |
| Error verification | 3.20 | 17.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocher, J.; Jimenez, J.M.; Tomas, J.; Lloret, J. Low-Cost Turbidity Sensor to Determine Eutrophication in Water Bodies. Sensors 2023, 23, 3913. https://doi.org/10.3390/s23083913
Rocher J, Jimenez JM, Tomas J, Lloret J. Low-Cost Turbidity Sensor to Determine Eutrophication in Water Bodies. Sensors. 2023; 23(8):3913. https://doi.org/10.3390/s23083913
Chicago/Turabian StyleRocher, Javier, Jose M. Jimenez, Jesus Tomas, and Jaime Lloret. 2023. "Low-Cost Turbidity Sensor to Determine Eutrophication in Water Bodies" Sensors 23, no. 8: 3913. https://doi.org/10.3390/s23083913
APA StyleRocher, J., Jimenez, J. M., Tomas, J., & Lloret, J. (2023). Low-Cost Turbidity Sensor to Determine Eutrophication in Water Bodies. Sensors, 23(8), 3913. https://doi.org/10.3390/s23083913








