1. Introduction
In computer-aided manufacturing, Non-Uniform Rational B-Spline (NURBS) interpolation is used to generate a toolpath for the CNC machining of parts. Feedrate is an important parameter that needs to be carefully controlled during machining, as it affects not only the quality and accuracy of the machined part but also the tool life and the time required for machining. The feedrate of CNC machines is determined based on the NURBS curve and the cutting parameters such as spindle speed, depth of cut, and feed per tooth. However, the feedrate can fluctuate because of irregularities in the NURBS curve, which can result in unwanted effects such as tool vibration, chatter, and excessive tool wear. Therefore, minimizing feedrate fluctuations in the NURBS interpolation process is essential to attain high-precision and high-quality machined parts. Since NURBS curves are constructed piecewise using B-spline basis functions, the solution of curve trajectory points, the calculation of curve arc length, the derivation of NURBS curves, and the calculation of curvature surfaces have high computational loads. In particular, there is a nonlinear mapping relationship between the curve parameters and the arc length because of the segmented structure of the NURBS curve.
Nie et al. [
1] fully considered various constraints when planning the feedrate for the NURBS interpolator to improve the interpolation accuracy effectively. Liu et al. [
2] generated smooth instructions that satisfy all the specified kinematic requirements. Wang et al. [
3] introduced the pre-compensation-based theory to increase machining precision by lowering contour errors while maintaining federate. Cao et al. [
4] suggested a feedrate direct interpolator (FDI), which can effectively acquire potentially precise interpolation parameters without using rounding or compensation techniques. Li et al. [
5] employed the Sigmoid function for feedrate planning, considering both geometric and kinematic errors. Guo et al. [
6] presented a federate scheduling method to overcome the NURBS curvature changing along the trajectory. Hu et al. [
7] presented a brand-new feedrate scheduling approach based on an S-shape feedrate profile to improve interpolation accuracy. Wang et al. [
8] introduced the cosines theorem in the NURBS interpolation algorithm to minimize feedrate fluctuations. Sang et al. [
9] integrated morphological filtering with an S-shaped acc/dec profile for the NURBS interpolator in difficult regions. This resulted in more stable feedrates. Ji et al. [
10] corrected the estimated parameters iteratively to achieve smaller velocity fluctuations and lower computation load. Jiang et al. [
11] constrained the feedrate fluctuation by an iterative method. Zhao et al. [
12] generated the smooth feedrate profile by improving the feed correction polynomial to reduce fluctuations. Zhang et al. [
13] introduced a feedrate optimization method to achieve an ideal feedrate profile efficiently for the fastest machining efficiency. Ni et al. [
14] designed a novel feedrate scheduling approach that maintains the machining efficiency of interpolation while keeping high motion smoothness. To minimize fluctuations, Zhong et al. [
15] employed federate and acceleration lookahead operations. Ni et al. [
15] employed a two-way control strategy to maintain NURBS interpolation accuracy under round-off errors. Cho and Kim [
16] reduced the feedrate fluctuation using the compensation mechanism. Peng et al. [
17] presented the improved Adams–Moulton (IAM) method to attain minimal feedrate fluctuation. Huang and Zhu [
18] proposed a sinusoidal representation of the jerk profile for the parametric interpolator, thus making the feedrate profile more concise. These studies and analyses of the abovementioned literature indicate that direct interpolation of NURBS curves is a systematic project and obtaining high-speed and high-precision machining effects is essential.
Feedrate fluctuation during interpolation is unavoidable because of the improper mapping between the NURBS parameter and the arc length along the toolpath. The machining quality in NURBS interpolation is substantially influenced by feedrate fluctuation [
19]. Many strategies have been put up to eliminate feedrate fluctuation successfully. For instance, UI (uniform increment) method [
20] is the earliest direct approximation method. Although UI is the simplest method in this area, it may cause feedrate fluctuations. Taylor’s expansion (TE) based methods were widely utilized in the literature [
21,
22,
23,
24,
25]. However, the unavoidable rounding-off error will cause feedrate fluctuation. An improved Taylor’s expansion (TE) method [
26] was proposed to suppress feedrate fluctuation. The predictor–corrector interpolators (PCI) methods [
27,
28] can maintain feedrate fluctuations within specified tolerances after iteration while requiring variable iterations over successive sampling periods. Thus, the uncertain computation time caused by iteration is not conducive to interpolation stability and not suitable for high-speed real-time applications. Besides, there are remapping methods (RM) based on Hermite cubic splines [
29], cubic polynomials [
30], quintic splines [
31], and seventh-order polynomials [
32], which can reduce feedrate fluctuations. However, these methods require much storage space to store intermediate sub-polynomials and increase the computational load. Besides, the Steffensen-based iterative method [
33] was also employed to refine the estimated initial parameter to reduce the feedrate fluctuation. However, this method requires continuous iterative and repeated complex parameter calculations, causing issues such as time-consuming calculations and enormous difficulties. Some scholars have proposed an arc-length compensation method [
34], in which the command position is corrected by compensating for the arc and chord lengths in the parameter calculation process to reduce feedrate fluctuation. However, this method only considers the truncation error, and obtaining satisfactory results using the approximate method in the solution process is challenging. Super-resolution techniques [
35,
36] can be applied to the interpolated curves to enhance their resolution and improve their smoothness and curvature continuity. it is possible to improve the accuracy, precision, and overall quality of the interpolated curves, resulting in better performance and increased efficiency in various applications. However, super-resolution can bring a high computational load.
To improve the accuracy of NURBS interpolator systems and minimize feedrate fluctuations during CNC machining, a two-level parameter compensation strategy is proposed. The corresponding feedrate fluctuation methods are designed for different regions according to the curvature characteristics, which can greatly reduce the feedrate fluctuation rate on the premise of ensuring real-time performance. The first-level parameter compensation is employed in the non-curvature sensitive area to control the feedrate fluctuation of the interpolation. In the curvature-sensitive area, the second-level parameter compensation is adopted after the first-level parameter compensation to overcome the problem of large federate fluctuations caused by large curvature. This strategy raises the tolerated time load and cannot affect the interpolator’s real-time performance. It generally utilizes the fact that feedrate changes are more noticeable in the curvature-sensitive area.
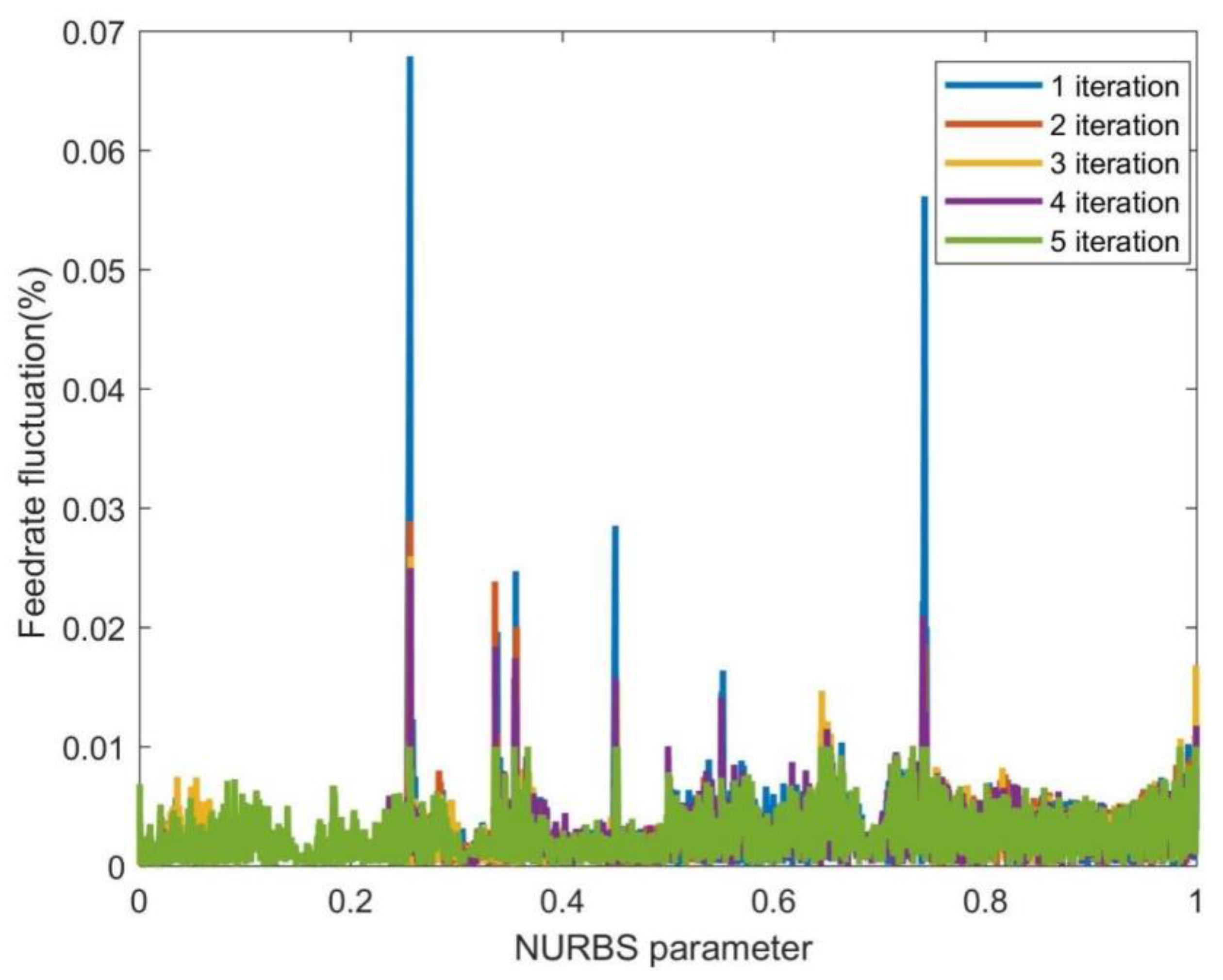
The novelty of the proposed two-level parameter compensation method lies in (1) proposing a two-level parameter compensation method specifically for NURBS interpolation to minimize feedrate fluctuation and improve machining quality, which utilizes the Taylor series expansion method in the first level and an iterative method without derivative calculations in the second level; (2) developing a novel approach for reducing feedrate fluctuation that considers the sensitivity of the curvature-sensitive areas, which can result in significant improvements in the quality of the final product; And (3) demonstrating the effectiveness of the proposed method through simulation studies and experiments, which show that the maximum feedrate fluctuation rate is below 0.01% with an average computational time of 360 us and that the proposed method outperforms other feedrate fluctuation elimination methods. Overall, the minimization of feedrate fluctuations is a novel contribution that can be applied to various applications, including those that require high precision and accuracy in motion control systems, such as 3D printing, CNC machining, and robotics.
The main contributions of this paper can be summarized as follows:
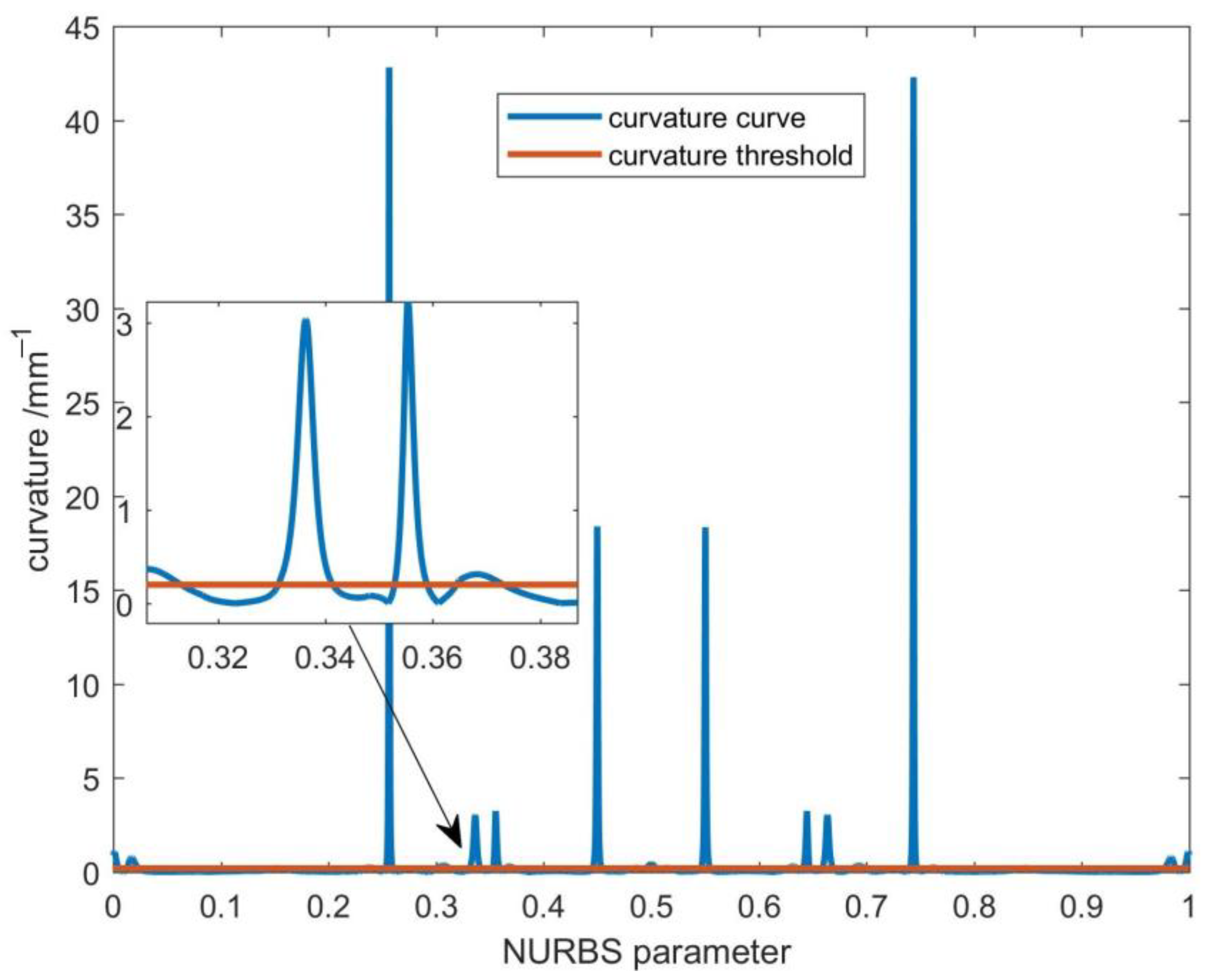
(1) We focused on the critical role of curvature in feedrate fluctuation, proposed the concept of the curvature-sensitive area, and divide the NURBS curve into curvature-sensitive areas and non-curvature-sensitive areas according to the curvature threshold to adapt to the curvature variations;
(2) A NURBS interpolator with minimum feedrate fluctuation based on two-level parameter compensation was proposed;
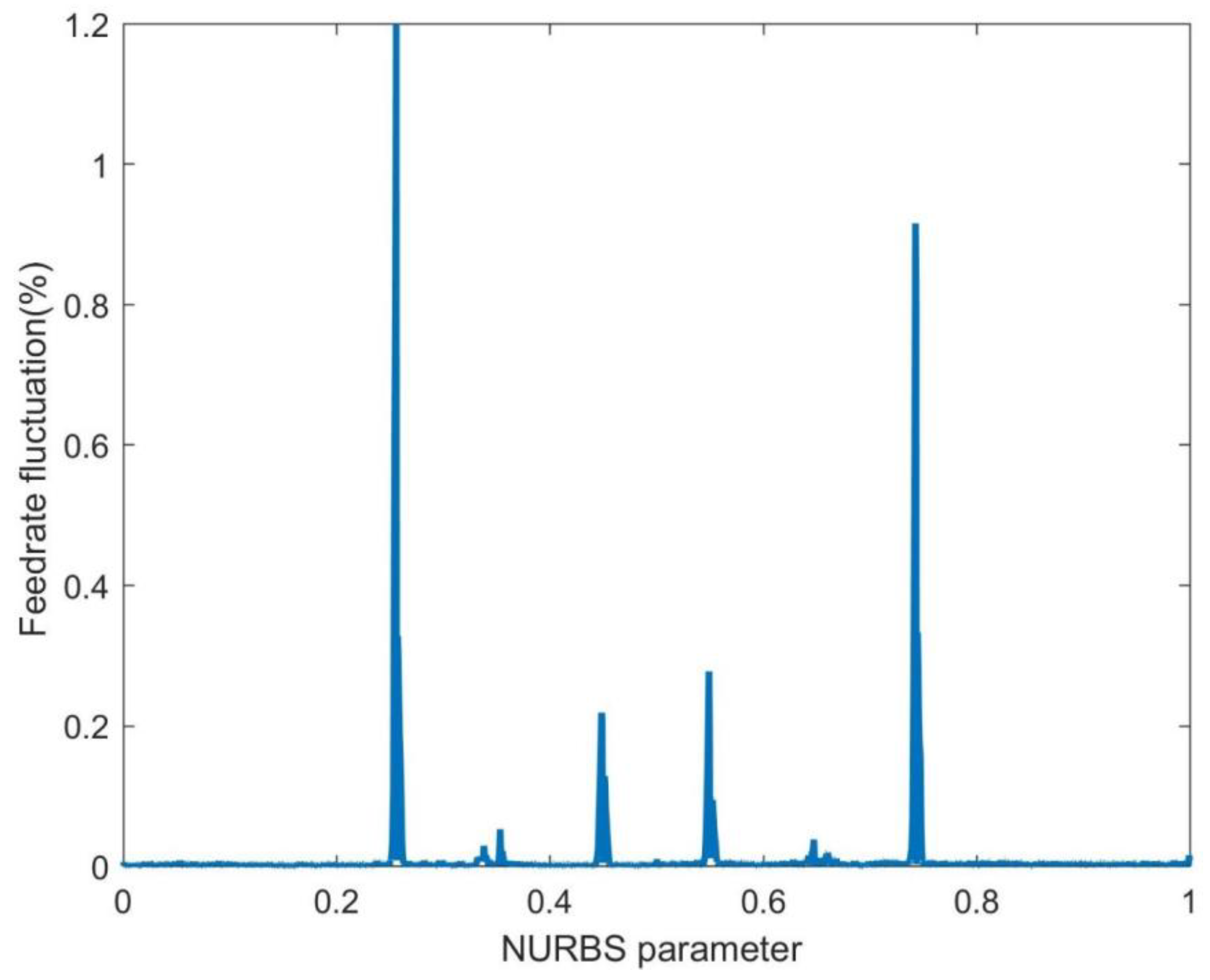
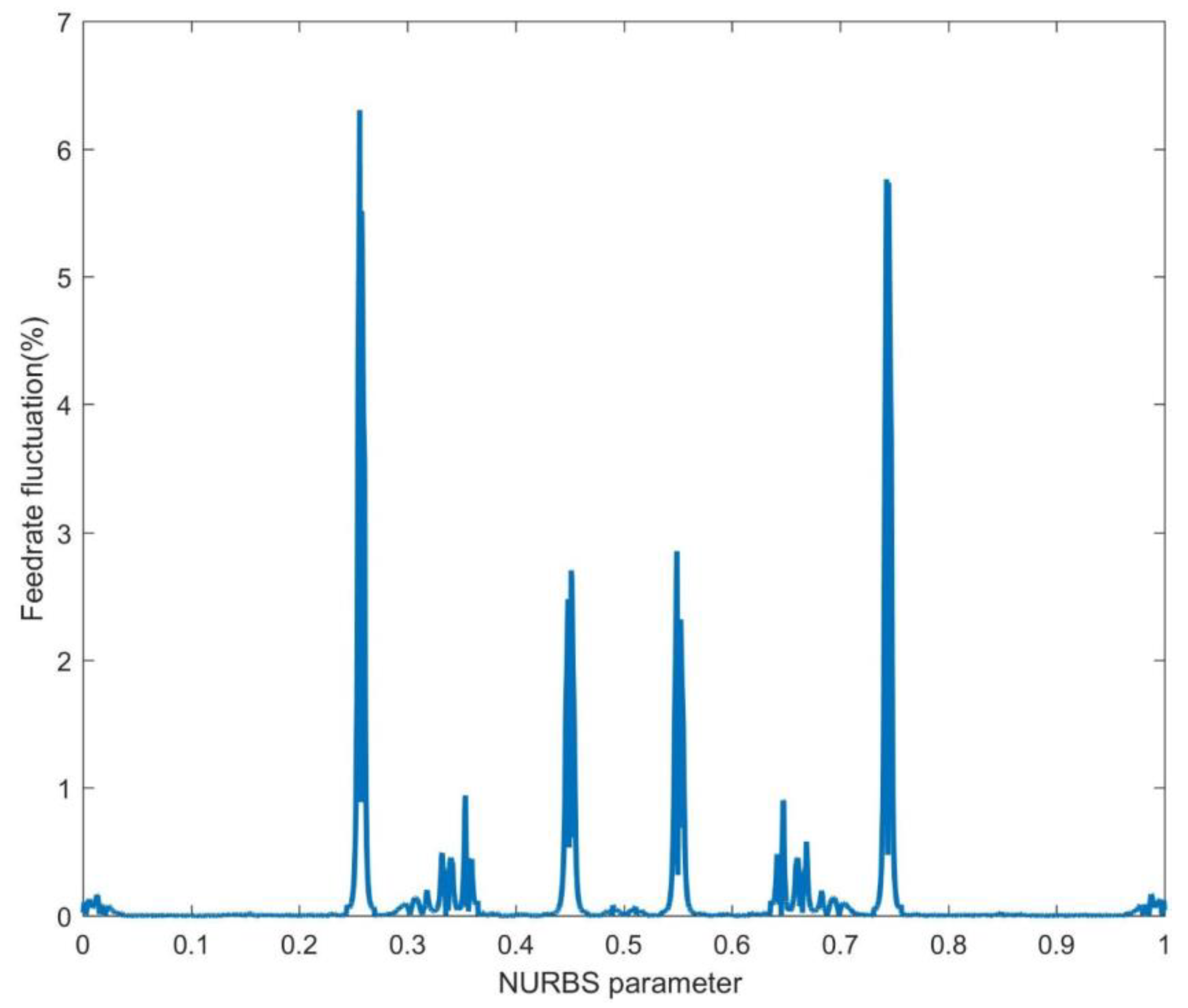
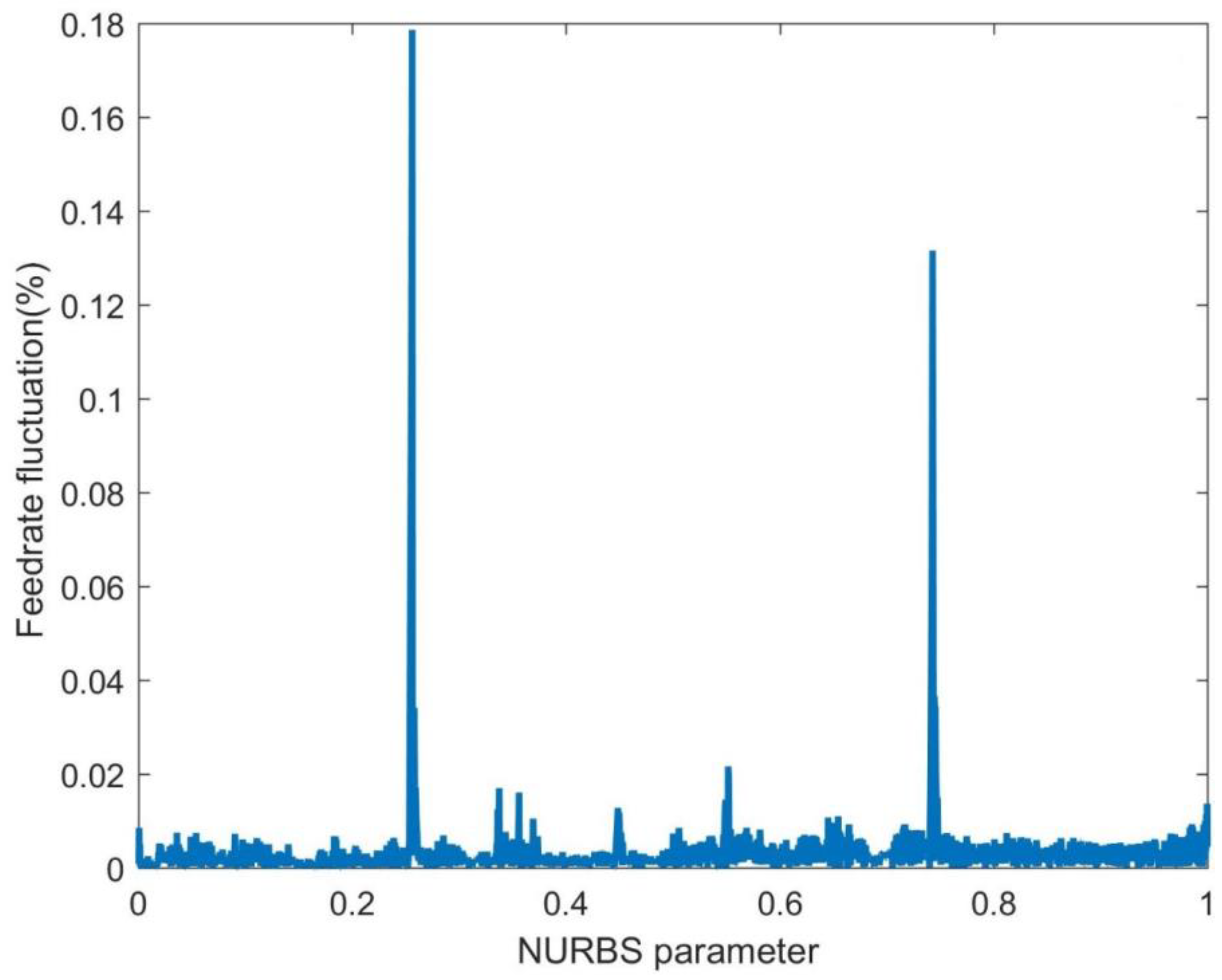
(3) The first-level parameter compensation based on Taylor series expansion was employed in the non-curvature-sensitive area; the second-level parameter compensation based on Secant method was employed in the curvature-sensitive area. Compared with the other four methods for eliminating feedrate fluctuation, the proposed method performed best and controlled the feedrate fluctuation within the standard range.
The remainder of this paper is structured as follows.
Section 2 introduces the NURBS interpolation and feedrate fluctuation.
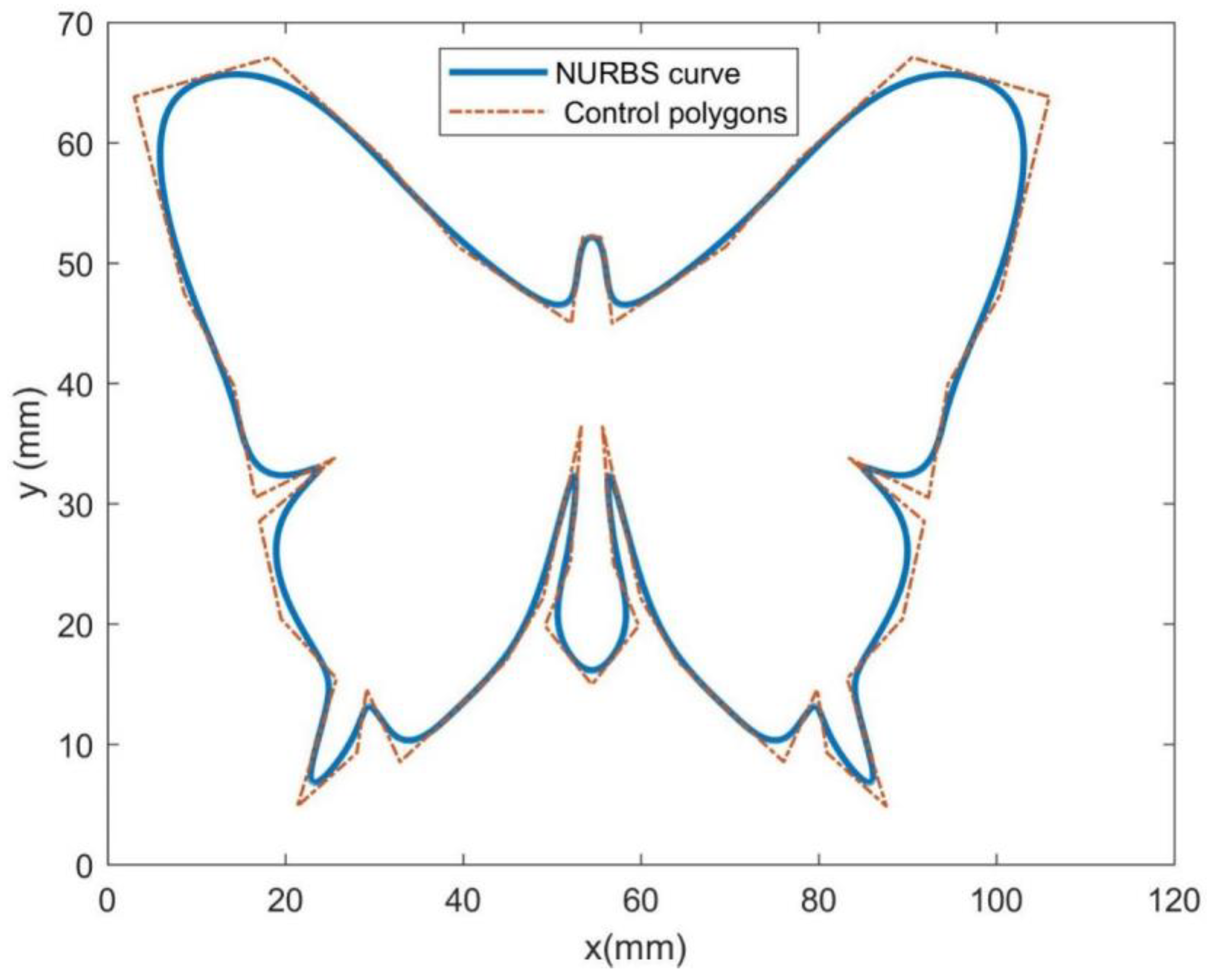
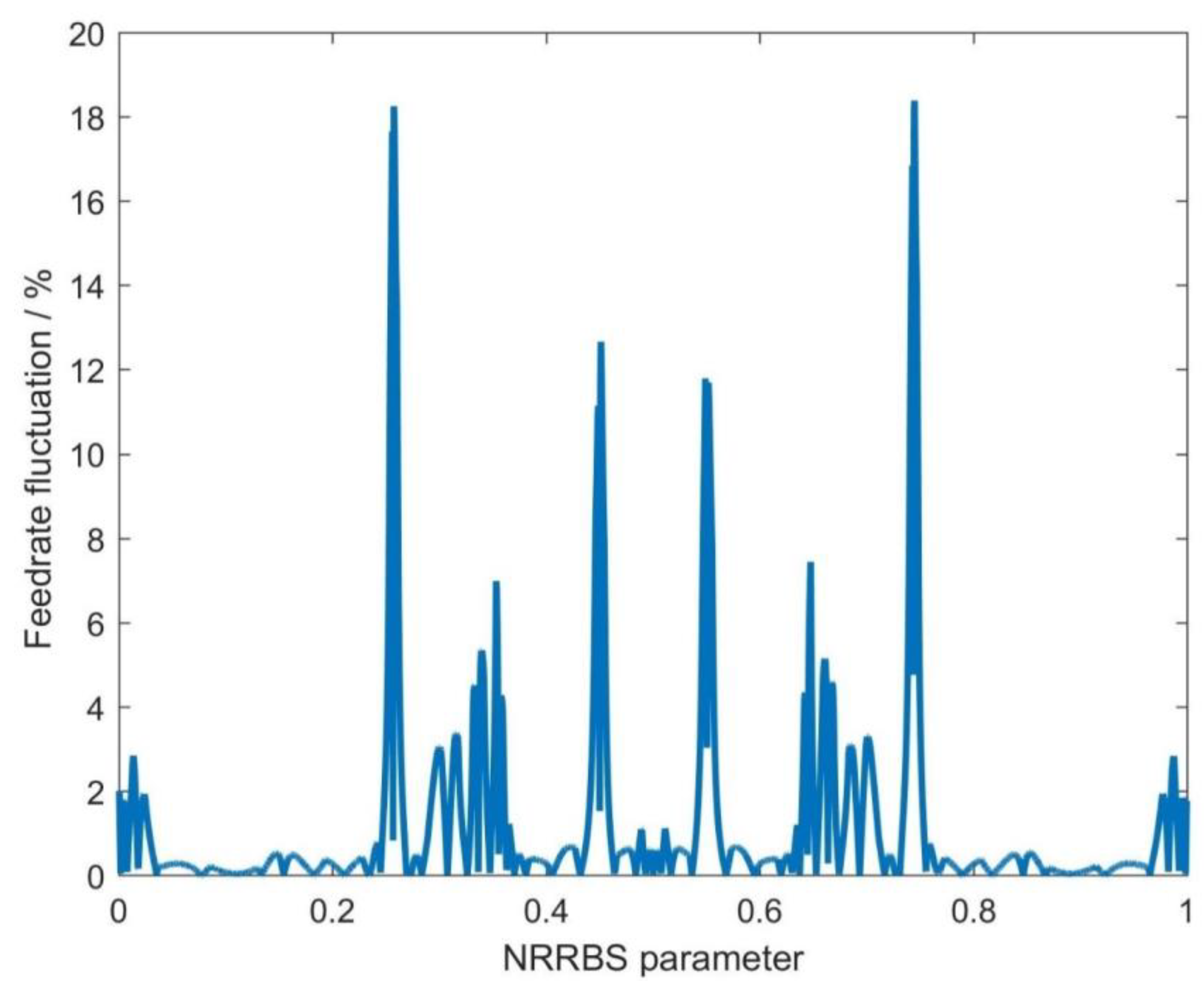
Section 3 describes the feedrate fluctuation elimination method based on the two-level parameter compensation. The simulation results of applying the suggested method on NURBS curves with a butterfly shape are presented in
Section 4. Finally, conclusions and future aspects are presented in
Section 5.
3. Two-Level Parameter Compensation
In this research, we aimed to address the issue of feedrate fluctuations that occur during NURBS interpolation. Such fluctuations can significantly impact the quality, accuracy, and efficiency of Computer Numerical Control (CNC) machining processes. Although various methods have been proposed in previous studies to reduce these fluctuations, most of them involve complex calculations and are not conducive to real-time and high-precision machining applications. Hence, we proposed a new two-level parameter compensation method that effectively minimizes feedrate fluctuations, considering the curvature-sensitive areas in the NURBS curve.
3.1. Feedrate Fluctuation Elimination Strategy
In order to balance efficiency and effectiveness, a two-level parameter compensation method is suggested to avoid feedrate fluctuations.
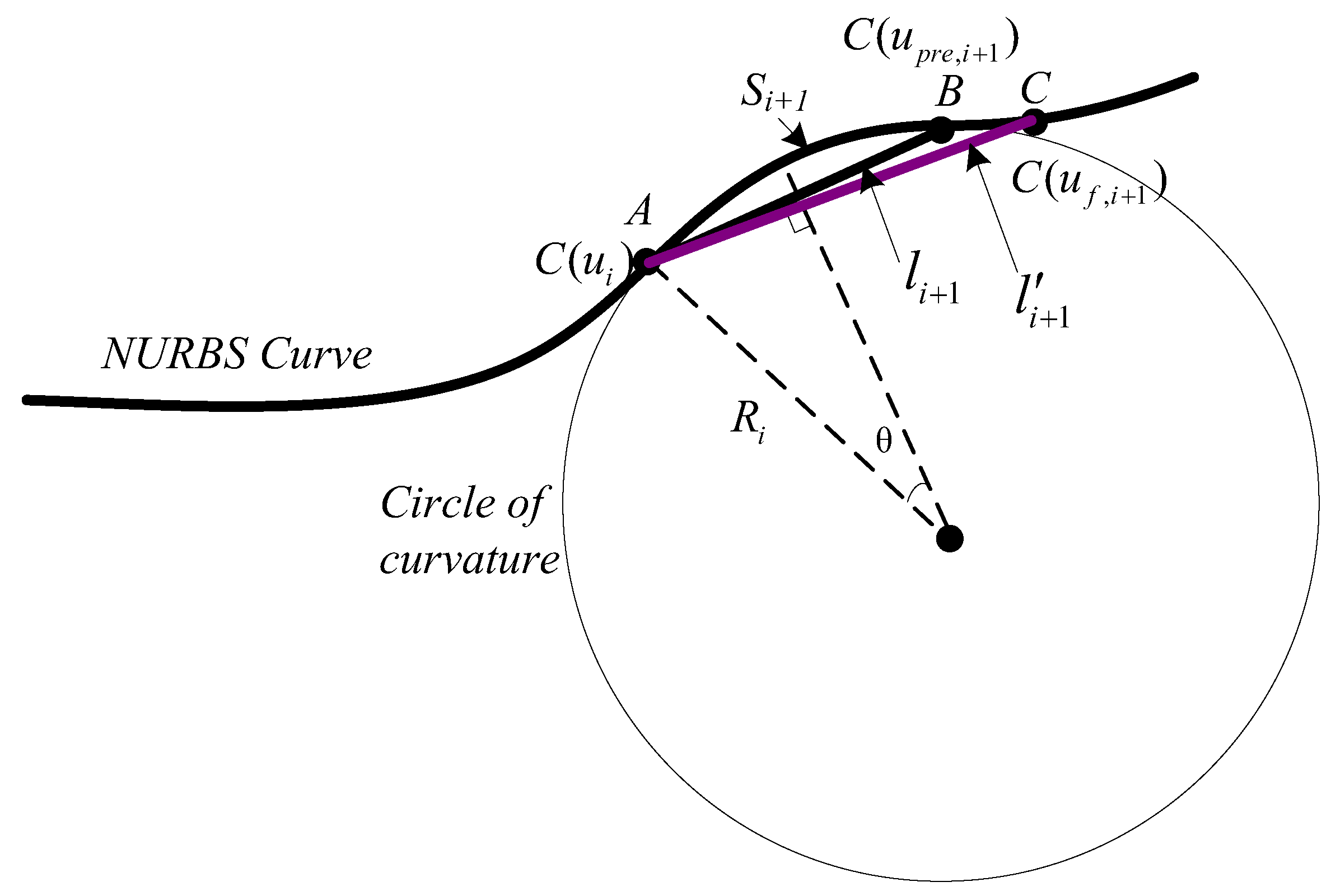
Figure 2 shows the schematic diagram of two-level parameter compensation for the (
i + 1)th interpolation point. Firstly, to address the federate fluctuation in non-curvature sensitive areas with low computational cost, first-level parameter compensation is performed. The compensation is achieved through the Taylor series expansion method, ensuring that the chord trajectory of the new interpolation point after compensation closely matches the original arc trajectory. Secondly, although the first-level parameter compensation reduces truncation error in curvature-sensitive areas, significant feedrate fluctuations can still occur. To further address this issue, second-level parameter compensation is performed using an iterative method that does not require derivative calculations.
As shown in
Figure 2, initially, parameters such as
and curvature
of the current interpolation point, command feedrate
F, the maximum chord error
, curvature threshold
, and the feedrate fluctuation tolerance
are input into the two-level parameter compensation module. Then, the first-level parameter compensation is performed. In this process, the adaptive velocity of the next interpolation point is calculated using the adaptive velocity approach described in Equation (5) and is restrained under the command feedrate constraint according to Equation (6). The estimated parameters
of the next interpolation point are obtained by using the FAM or SAM described in Equations (7) and (8). As the numerical approximation method is utilized to obtain the estimated parameters, there are inevitable discrepancies between these parameters and the actual ones. Consequently, the arc displacement along the curved path is inaccurately mapped to the spline parameters, leading to fluctuations in the federate. In this paper, we provided a theoretical derivation process for compensating for the problem of feedrate fluctuation caused by parameter estimation deviation. More details can be found in
Section 3.2. Therefore, we can obtain the parameter compensation step size
according to the method called first-level compensation in this paper. In this way, the first-level parameter compensation is completed and we can update the new predicted parameter through the formula
.
Greater curvature leads to more prominent fluctuation in feedrate. Even after eliminating the feedrate variation through the first-level parameter compensation in the curvature-sensitive area, there is still a pressing issue of substantial feedrate fluctuations. This paper presents a second-level parameter compensation method that is combined with curvature characteristics to address this problem. As shown in
Figure 2, after completing the first-level parameter compensation, it is important to check whether the next interpolation point is situated in the curvature-sensitive area. If the point is located in the non-curvature-sensitive area, the NURBS interpolator will proceed with the calculation process, which involves obtaining the interpolation position based on the parameters. Once this is done, the feed system will execute the interpolation action to complete the feed process. If the point falls within the curvature-sensitive area, then proceed to the second-level parameter compensation based on the Secant iteration method. First, initialize the parameters, including the number of iterations,
and
, etc. In each iteration, a new compensated parameter
is updated according to the formula
. Then, the estimated feedrate
is obtained by the ratio of the distance between two points
and
, which are the new compensated interpolation point and the previous interpolation point, to the interpolation period. After that, the new feedrate fluctuation is gained and is compared with the set fluctuation tolerance
. If the feedrate fluctuation is still higher than the set tolerance, the number of iterations k will update and the next update iteration process proceed. If the current parameter compensation results in the feedrate fluctuation being within the set tolerance and meets the accuracy condition, then, the second-level compensation will end. Next, the NURBS interpolator will solve the curve point coordinates and perform the feed motion. The specific process of second-level parameter compensation is detailed in
Section 3.3. After two-level parameter compensation, the feedrate fluctuation of the estimated point can be well eliminated, and the quality of the processed surface can be better guaranteed.
High curvature regions are the curve parts that exceed the curvature threshold in the second-level parameter compensation. The NURBS curve is firstly divided into low and high curvature regions by the curvature threshold. The curve’s curvature threshold is determined by considering dynamic limitations and geometric properties. Taking F as the maximum command feedrate, and
as the chord error tolerance, the curvature threshold can be determined from Equation (5) as
Then, the curve is divided into numerous sections based on the curvature threshold. The NURBS curve’s high and low-curvature areas are defined as the portion with curvature larger and less than the threshold, respectively. It can be seen from the curvature characteristics that when the interpolation point is located in the low curvature area, the feedrate fluctuation is slight, and only the first-level parameter compensation is required. In contrast, when the interpolation point is located in the high curvature area, the feedrate fluctuation is significant, and it is necessary to perform the second-level parameter compensation after the first-level parameter compensation.
3.2. The First-Level Parameter Compensation
The main factor causing feedrate fluctuation is that the synthesis trajectory is a short straight line instead of a circular arc. In order to make the chord trajectory of the new interpolation point after compensation as similar to the original arc trajectory as possible, the first-level parameter compensation was performed, as shown in
Figure 1, where C is the new point of point B after the first-level compensation.
The parameters of B and C were set as
. The parameter compensation incremental value of point B was set to
. Now, we have
where
is the predicted parameter of the next interpolation point by FAM or SAM.
Here, the first-order Taylor series expansion technique establishes a model between the interpolation point and the compensation value [
38].
where
is the first-order derivative of
.
After the first-level parameter compensation, it is assumed that there is no feedrate fluctuation, and
holds. This also means that the desired feedrate should equal the actual feedrate. It yields
Equation (23) can be rewritten by
By substituting (22) with (24), we obtain
The quadratic equation for Δ
ui+1 can be obtained by squaring both sides of Equation (25).
Then, it can be rewritten as
where
a,
b, and
c are listed as follows:
Two roots of Equation (27) can be obtained as
and
Since , one of the roots turns out to be close to zero, and the other root is . Therefore, the parameter compensation should be slight, and the parameter compensation is taken to be the value of .
3.3. The Second-Level Parameter Compensation
The FAM or SAM based on Taylor expansion employed in the first-level compensation has truncation errors, which cannot be ignored in high curvature areas, and will still cause feedrate fluctuations.
Suppose a point in the high curvature region with feedrate
. Assuming there are no feedrate fluctuations on this point, it just requires finding parameter
to satisfy
in Formula (31).
where
represents the difference between the linear distance of adjacent interpolation points and the actual interpolation trajectory length. When
equals 0, there is no feedrate fluctuation. The Secant method is introduced to solve (31), an iterative method without calculating the derivatives. Suppose the feedrate fluctuation tolerance is
ε. The pseudocode representation of the method is shown in Algorithm 1.
| Algorithm 1. Secant-Method Based Parameter Compensation |
| Input: , , , , |
Output:
1: initialize: Set k = 1, ,
2: do
3: |
4:
5: until
6: |
In Algorithm 1, the input parameters include parameter , the desired feedrate , the predicted parameter , the first-level parameter compensation , and the feedrate fluctuation tolerance . represents the parameter compensation of Equation (31) at the (k + 1)th iteration, and indicates the actual feedrate according to parameter . If the feedrate fluctuation is under the upper bound , then is set to the desired value.
3.4. The Order of Convergence for the Second-Level Parameter Compensation
Let
be an error in the
kth iteration approximation. The parameter compensations
and
can be written as
Substituting Equation (32) into Equation (31) and expanding with the Taylor series, we get
Since
, Equation (33) can be rewritten as
Now, the following formula can be obtained
The second-level iteration parameter compensation can be described as
Substituting Equations (34) and (35) into Equation (36) gives
Equation (37) can be rewritten as
By binomial theorem, Equation (38) can be rewritten as
Neglecting powers of
and
yields
If
p is the order of convergence of iterations, then
According to Equations (41) and (42), we have
From Equation (43), we have
From Equations (43) and (46), we can obtain
The roots of Equation (47) are
Taking the positive sign, we have .
The order of convergence of the second-level parameter compensation is 1.618, which is superlinear.