On the Advantages of Microwave Photonic Interrogation of Fiber-Based Sensors: A Noise Analysis
Abstract
1. Introduction
2. Sensor Evaluation in the Electrical Domain
2.1. Basic Concept
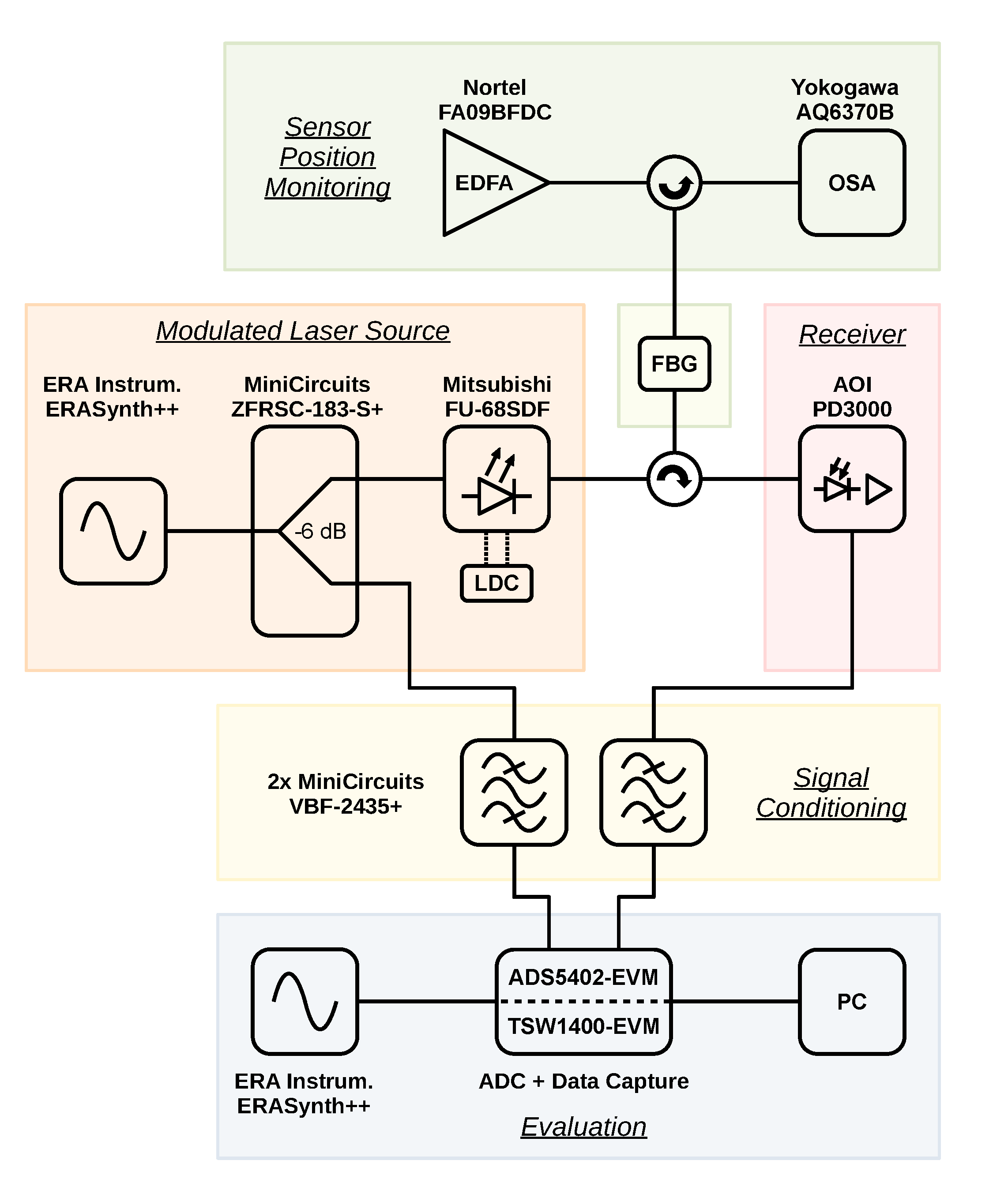
2.2. Experimental Setup
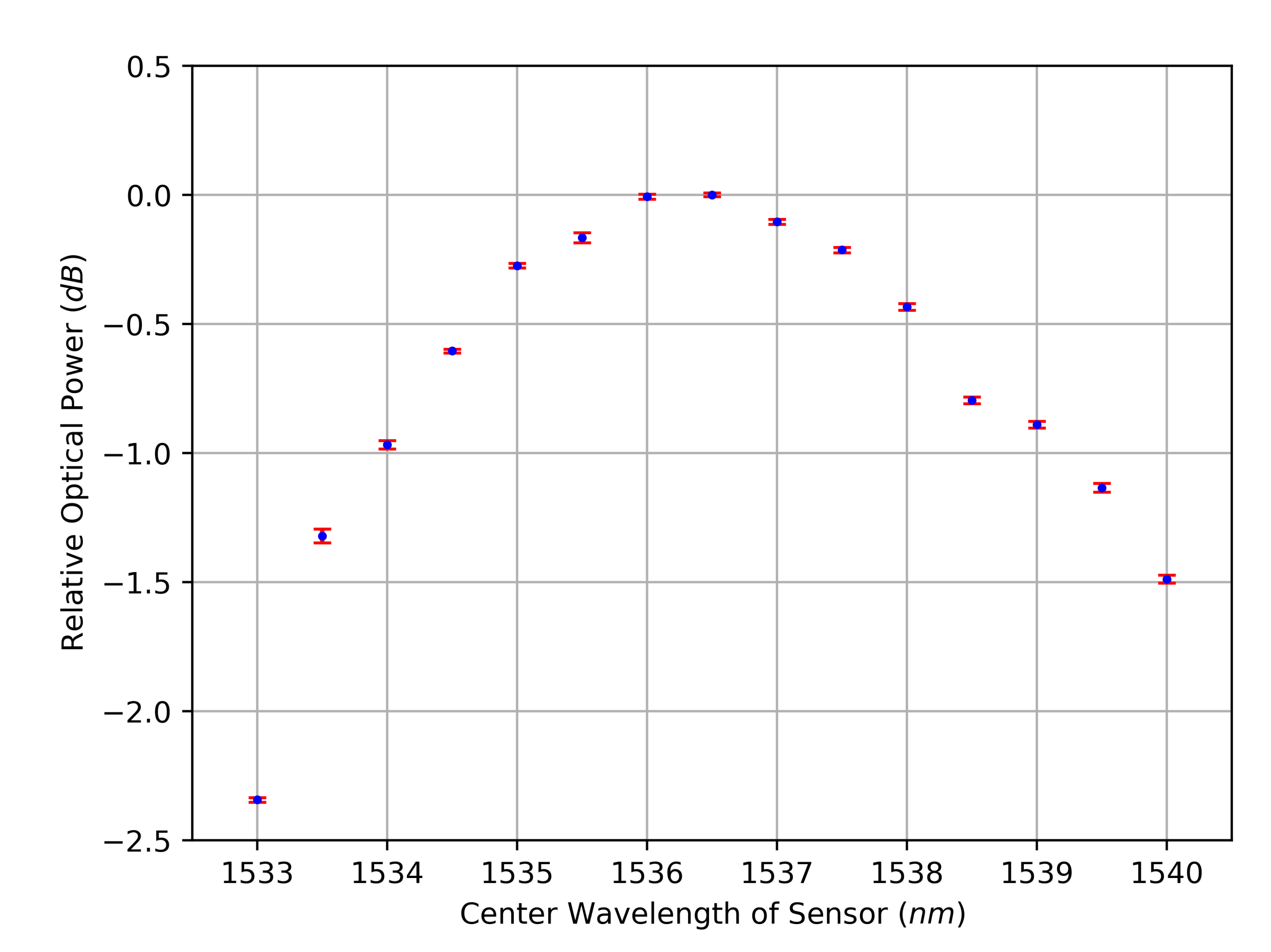
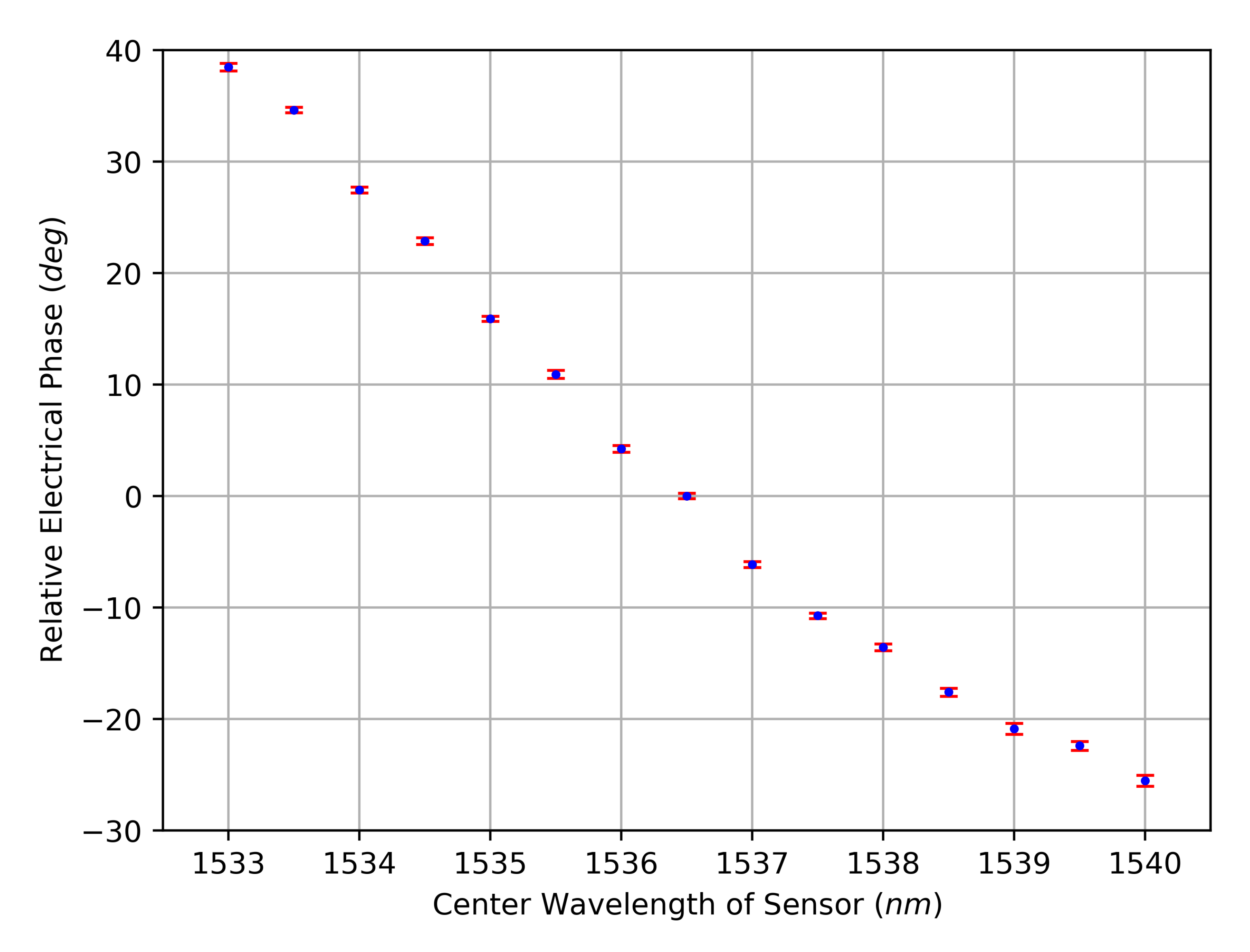
2.3. Derivation of the Characteristic Curves
2.4. Experimental Outcomes
3. Noise Analysis
3.1. Sources of Signal Degradation
3.1.1. Phase Noise of the Signal Generators
3.1.2. Phase Noise of the ADC
3.1.3. Quantization Noise
3.1.4. Johnson–Nyquist Noise
3.1.5. Relative Intensity Noise
3.1.6. Shot Noise
3.1.7. Further Influences
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADC | analog to digital converter |
| DFB | distributed feedback |
| DSB | double-sideband |
| EDFA | erbium-doped fiber amplifier |
| EVNA | electrical vector network analyzer |
| FBG | fiber Bragg grating |
| FWHM | full width at half minimum |
| LD | laser diode |
| LDC | laser diode controller |
| LSB | lower sideband |
| MWP | microwave photonics |
| OSA | optical spectrum analyzer |
| PC | personal computer |
| PD | photodiode |
| RF | radio frequency |
| RIN | relative intensity noise |
| RMS | root-mean-square |
| RoF | radio-over-fiber |
| SNR | signal-to-noise ratio |
| SSB | single-sideband |
| TLS | tuneable laser source |
| USB | upper sideband |
References
- Seeds, A.J.; Williams, K.J. Microwave Photonics. IEEE/OSA J. Light. Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonics. IEEE/OSA J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Capmany, J.; Mora, J.; Gasulla, I.; Sancho, J.; Lloret, J.; Sales, S. Microwave Photonic Signal Processing. IEEE/OSA J. Light. Technol. 2013, 31, 571–586. [Google Scholar] [CrossRef]
- Xu, K.; Wang, R.; Dai, Y.; Yin, F.; Li, J.; Ji, Y.; Lin, J. Microwave photonics: Radio-over-fiber links, systems, and applications. Photonics Res. 2014, 2, B54–B63. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.; Capmany, J. Integrated microwave photonics. Nat. Photonics 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonic Sensors. IEEE/OSA J. Light. Technol. 2021, 39, 3626–3637. [Google Scholar] [CrossRef]
- Zhou, D.; Dong, Y.; Yao, J. Truly Distributed and Ultra-Fast Microwave Photonic Fiber-Optic Sensor. IEEE/OSA J. Light. Technol. 2020, 38, 4150–4159. [Google Scholar] [CrossRef]
- Hervás, J.; Madrigal, J.; Barrera, D.; Sales, S. Multiplexing FBG sensors combining microwave photonics and phase modulation. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. Photonics-Based Broadband Microwave Measurement. IEEE/OSA J. Light. Technol. 2017, 35, 3498–3513. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonics for High-Resolution and High-Speed Interrogation of Fiber Bragg Grating Sensors. Fiber Integr. Opt. 2015, 34, 204–216. [Google Scholar] [CrossRef]
- Wang, G.; Liao, B.; Cao, Y.; Guo, T.; Feng, X.; Guan, B.O.; Yao, J. Microwave Photonic Interrogation of a High-Speed and High-Resolution Multipoint Refractive Index Sensor. IEEE/OSA J. Light. Technol. 2022, 40, 1245–1251. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, X.; Guo, T.; Ran, Y.; Feng, X.; Guan, B.O.; Yao, J. High-resolution and temperature-compensational HER2 antigen detection based on microwave photonic interrogation. Sens. Actuators B Chem. 2017, 245, 583–589. [Google Scholar] [CrossRef]
- Liu, W.; Fu, H.; Zhang, A.P.; He, S. Fiber Bragg Grating Based Wireless Sensor Module With Modulated Radio-Frequency Signal. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 358–360. [Google Scholar] [CrossRef]
- Hernández, R.; Loayssa, A.; Benito, D. On the use of single-sideband modulation for optical vector network analysis. In Proceedings of the MWP 2003 Proceedings: International Topical Meeting on Microwave Photonics, Budapest, Hungary, 10–12 September 2003; pp. 173–176. [Google Scholar] [CrossRef]
- Hernández, R.; Loayssa, A.; Benito, D. Optical vector network analysis based on single-sideband modulation. In Proceedings of the 16th Annual Meeting of the IEEE Lasers and Electro-Optics Society, Tucson, AZ, USA, 27–28 October 2003; Volume 2, pp. 909–910. [Google Scholar] [CrossRef]
- Erro, M.J.; Loayssa, A.; Taínta, S.; Hernández, R.; Benito, D.; Garde, M.J.; Muriel, M.A. Phase Reconstruction for the Frequency Response Measurement of FBGs. In Proceedings of the 2007 IEEE International Symposium on Intelligent Signal Processing, Alcala De Henares, Spain, 3–5 October 2007; pp. 1–3. [Google Scholar] [CrossRef]
- Erro, M.J.; Loayssa, A.; Taínta, S.; Hernández, R.; Benito, D.; Garde, M.J.; Muriel, M.A. On the Measurement of Fiber Bragg Grating’s Phase Responses and the Applicability of Phase Reconstruction Methods. IEEE Trans. Instrum. Meas. 2011, 60, 1416–1422. [Google Scholar] [CrossRef]
- Sartiano, D.; Hervás, J.; Madrigal, J.M.; Pérez-Galacho, D.; Sales, S. On the Use of Microwave Photonics Techniques for Novel Sensing Applications. In Proceedings of the 2019 21st International Conference on Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Sales, S.; Barrea, D.; Hervás, J.; Madrigal, J. Microwave Photonics for Optical Fiber Sensors. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Hervás, J.; Ricchiuti, A.L.; Li, W.; Zhu, N.H.; Fernández-Pousa, C.R.; Sales, S.; Li, M.; Capmany, J. Microwave Photonics for Optical Sensors. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 327–339. [Google Scholar] [CrossRef]
- Neumann, N.; Schuster, T.; Plettemeier, D. Novel approach for simultaneous wireless transmission and evaluation of optical sensors. In Advanced Sensor Systems and Applications VI; Liu, T., Jiang, S., Neumann, N., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2014; Volume 9274. [Google Scholar] [CrossRef]
- Schuster, T.; Neumann, N.; Plettemeier, D.; Körbitz, R.; Richter, A. A fiber-optic pH sensor with wireless Radio over Fiber read-out. In Proceedings of the 2015 IEEE SENSORS, Busan, Republic of Korea, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Nordmeyer, U.; Neumann, N.; Wang, X.; Thiel, T.; Kojucharow, K.; Plettemeier, D. Microwave based electrical read-out of optical sensors. In Proceedings of the 20. GMA/ITG-Fachtagung Sensoren und Messsysteme, Nürnberg, Germany, 25–26 June 2019; pp. 119–124. [Google Scholar] [CrossRef]
- Nordmeyer, U.; Neumann, N.; Wang, X.; Thiel, T.; Kojucharow, K.; Plettemeier, D. Application of microwave based electrical read-out of fiber Bragg gratings in thermometry. In Proceedings of the SMSI 2020—Sensors and Measurement Science International, Nürnberg, Germany, 20–25 June 2020; AMA Service: Wunstorf, Germany, 2020; pp. 181–182. [Google Scholar] [CrossRef]
- Nordmeyer, U.; Neumann, N.; Wang, X.; Thiel, T.; Kojucharow, K.; Plettemeier, D. Evaluation of optical fibre sensors in the electrical domain. J. Sens. Sens. Syst. 2020, 9, 199–208. [Google Scholar] [CrossRef]
- Nordmeyer, U.; Neumann, N.; Thiel, T.; Kojucharow, K.; Plettemeier, D. Using the Phase Response of Fiber Bragg Gratings for Measurement Applications. In Proceedings of the Sensors and Measuring Systems, 21. ITG/GMA-Symposium, Nuremberg, Germany, 10–11 May 2022; pp. 200–203. [Google Scholar]
- Texas Instruments Inc. Dual 12-Bit 800Msps Analog-to-Digital Converter, ADS5402 Datasheet (Rev. B); Texas Instruments Inc.: Dallas, TX, USA, 2014. [Google Scholar]
- Kester, W.; Analog Devices Inc. Data Conversion Handbook; Analog Devices Series; Elsevier Science: Amsterdam, The Netherlands, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nordmeyer, U.; Thiel, T.; Kojucharow, K.; Neumann, N. On the Advantages of Microwave Photonic Interrogation of Fiber-Based Sensors: A Noise Analysis. Sensors 2023, 23, 3746. https://doi.org/10.3390/s23073746
Nordmeyer U, Thiel T, Kojucharow K, Neumann N. On the Advantages of Microwave Photonic Interrogation of Fiber-Based Sensors: A Noise Analysis. Sensors. 2023; 23(7):3746. https://doi.org/10.3390/s23073746
Chicago/Turabian StyleNordmeyer, Ulrich, Torsten Thiel, Konstantin Kojucharow, and Niels Neumann. 2023. "On the Advantages of Microwave Photonic Interrogation of Fiber-Based Sensors: A Noise Analysis" Sensors 23, no. 7: 3746. https://doi.org/10.3390/s23073746
APA StyleNordmeyer, U., Thiel, T., Kojucharow, K., & Neumann, N. (2023). On the Advantages of Microwave Photonic Interrogation of Fiber-Based Sensors: A Noise Analysis. Sensors, 23(7), 3746. https://doi.org/10.3390/s23073746





