Kernel Estimation Using Total Variation Guided GAN for Image Super-Resolution
Abstract
1. Introduction
- The proposed method adopts a total variation map and uses it as a guide for the network to focus on the structural information of the image.
- Compared to previous methods, the proposed method is cost- and memory-efficient.
- We demonstrate that the proposed method exhibits superior performance, particularly in accurately estimating sizable and anisotropic kernels, compared to conventional methods.
2. Background
3. Proposed Method
3.1. Challenging Kernels and SR
3.2. Total Variation Weight Map
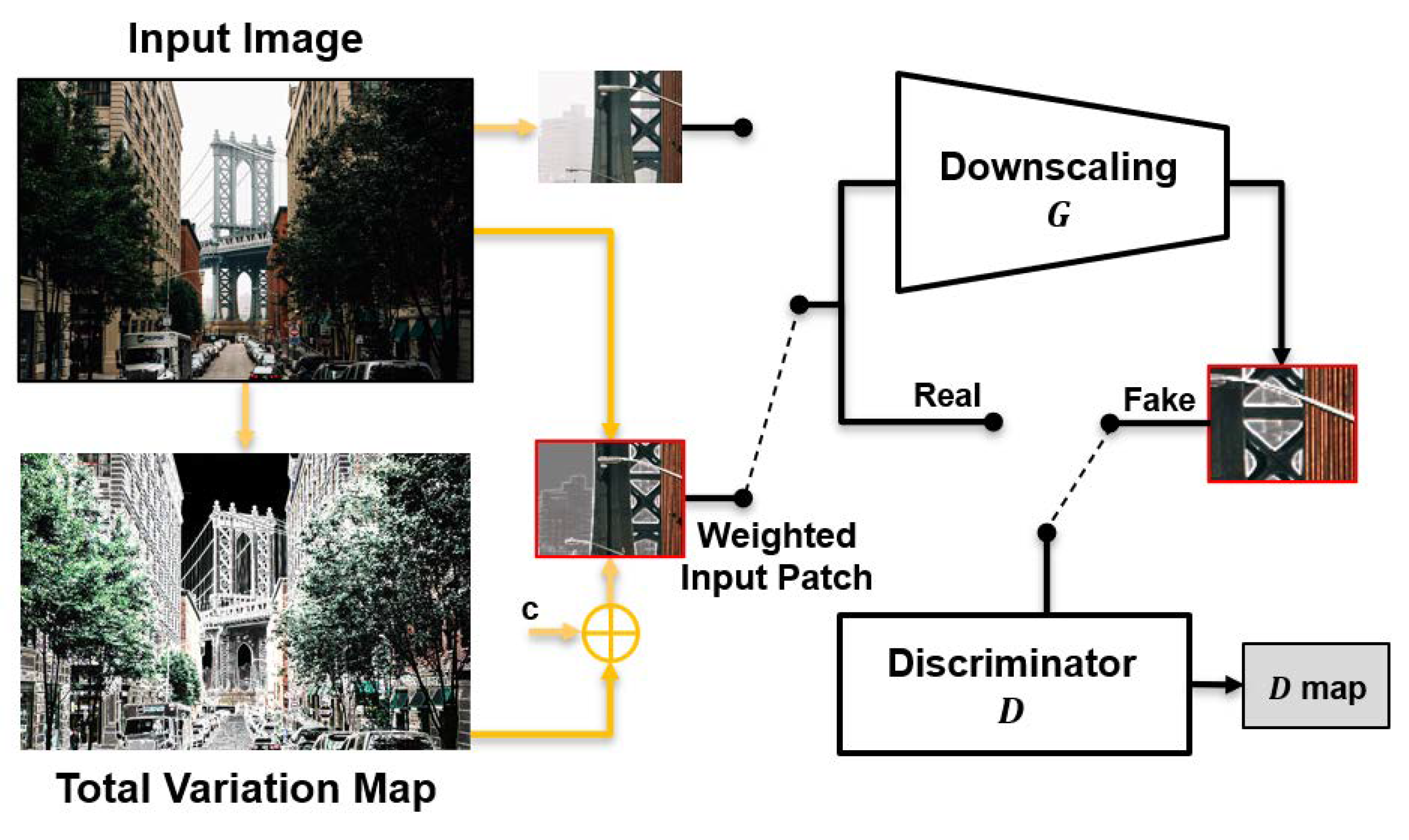
3.3. TVG-KernelGAN
4. Experimental Results
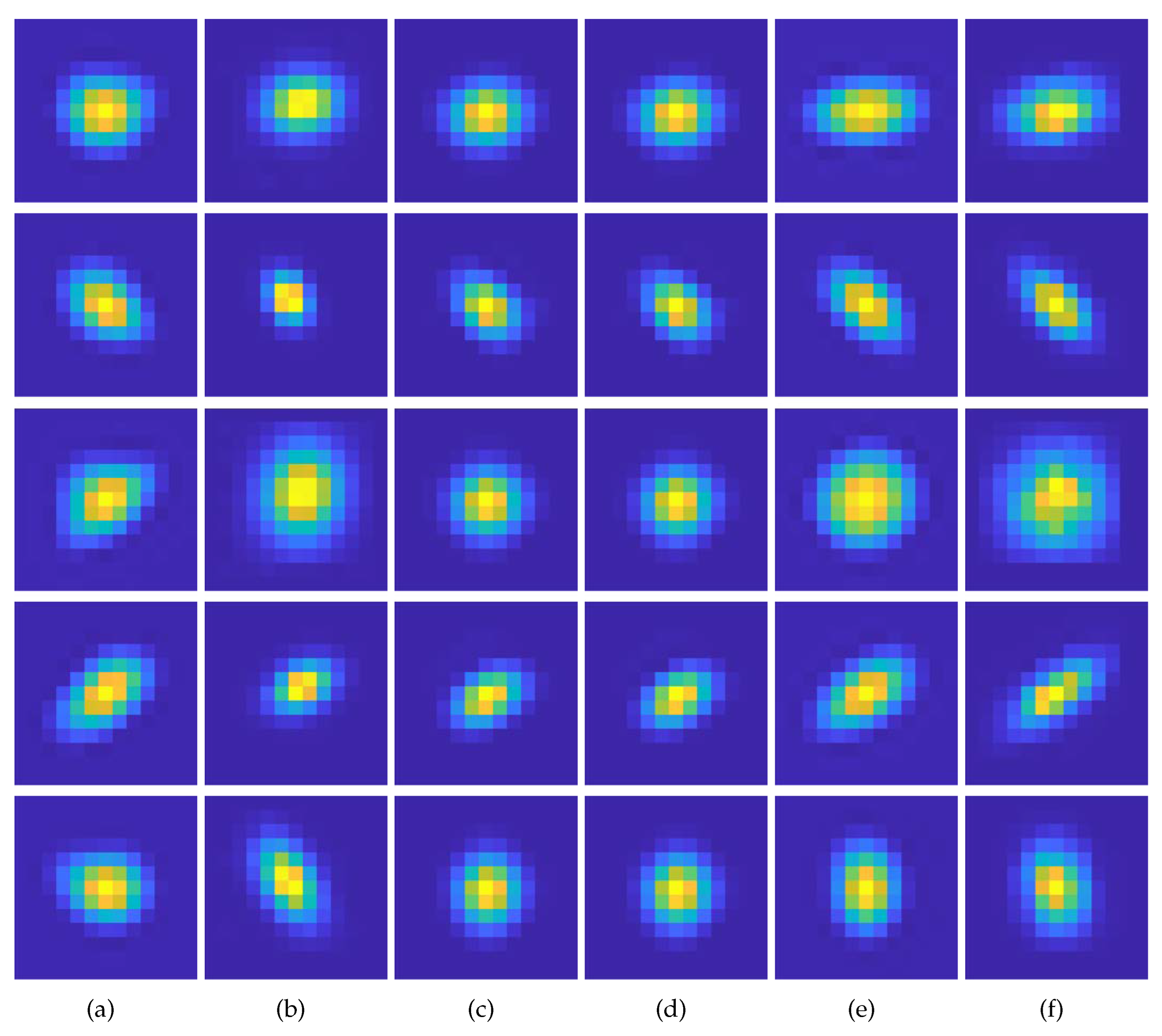
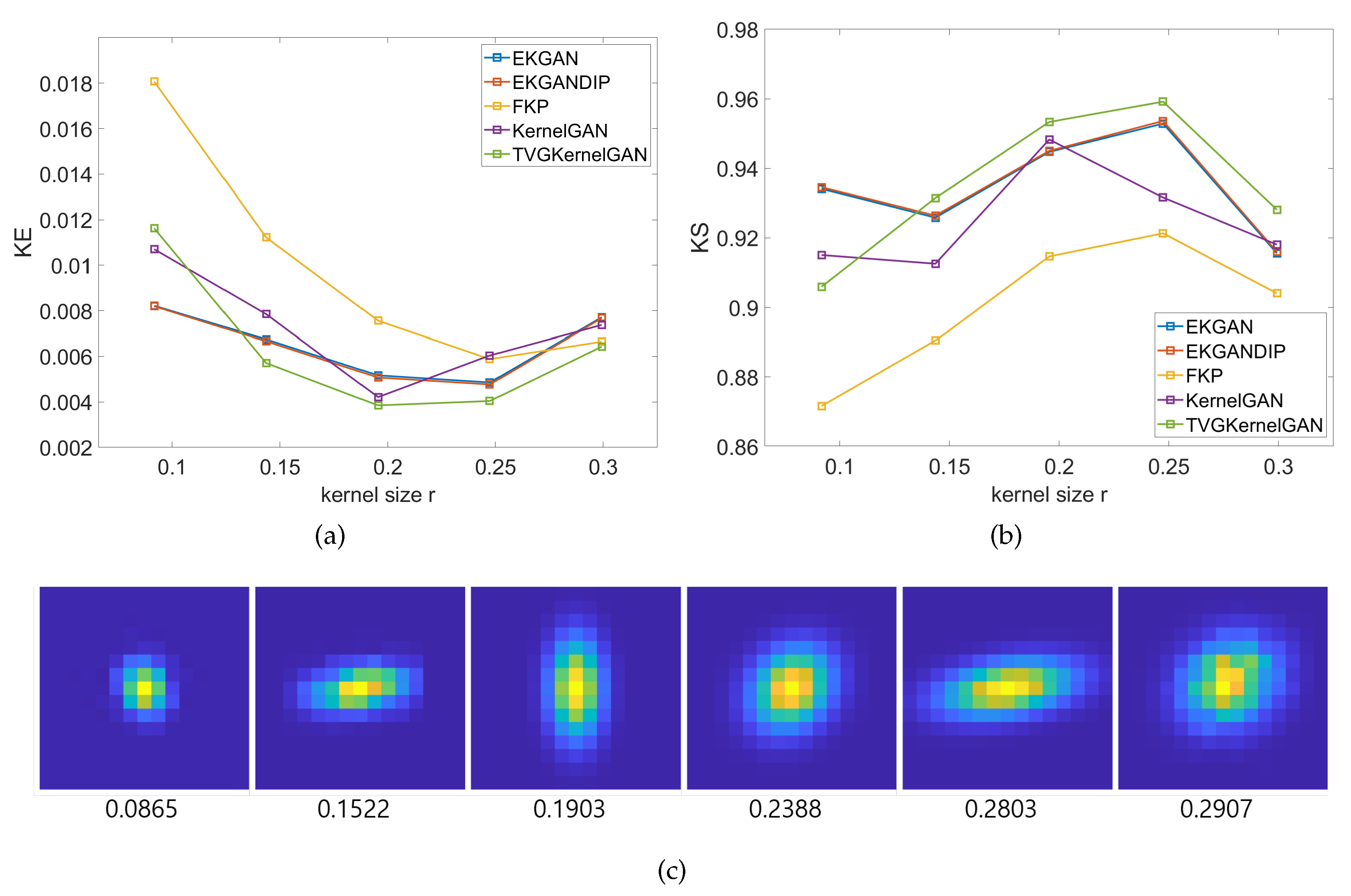
4.1. Kernel Estimation Results
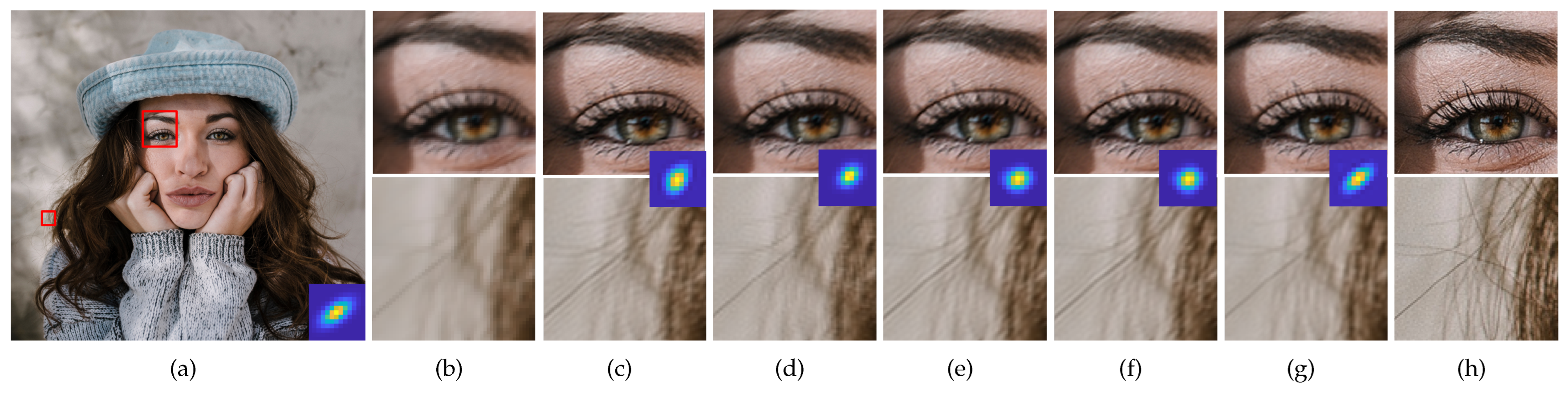
4.2. Non-Blind Super-Resolution Results
4.3. Memory and Cost Efficiency
4.4. Limitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef]
- Farsiu, S.; Robinson, M.D.; Elad, M.; Milanfar, P. Fast and robust multiframe super resolution. IEEE Trans. Image Process. 2004, 13, 1327–1344. [Google Scholar] [CrossRef] [PubMed]
- Hardie, R.C.; Barnard, K.J.; Bognar, J.G.; Armstrong, E.E.; Watson, E.A. High-resolution image reconstruction from a sequence of rotated and translated frames and its application to an infrared imaging system. Opt. Eng. 1998, 37, 247–260. [Google Scholar]
- Yuan, Q.; Zhang, L.; Shen, H. Multiframe super-resolution employing a spatially weighted total variation model. IEEE Trans. Circuits Syst. Video Technol. 2011, 22, 379–392. [Google Scholar] [CrossRef]
- Köhler, T.; Huang, X.; Schebesch, F.; Aichert, A.; Maier, A.; Hornegger, J. Robust multiframe super-resolution employing iteratively re-weighted minimization. IEEE Trans. Comput. Imaging 2016, 2, 42–58. [Google Scholar] [CrossRef]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 349–356. [Google Scholar]
- Michaeli, T.; Irani, M. Nonparametric Blind Super-resolution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Nice, France, 13 December 2013. [Google Scholar]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NA, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1664–1673. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. “zero-shot” super-resolution using deep internal learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3118–3126. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Ma, C.; Rao, Y.; Cheng, Y.; Chen, C.; Lu, J.; Zhou, J. Structure-preserving super resolution with gradient guidance. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7769–7778. [Google Scholar]
- Ji, X.; Cao, Y.; Tai, Y.; Wang, C.; Li, J.; Huang, F. Real-world super-resolution via kernel estimation and noise injection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 466–467. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Timofte, R. Unsupervised learning for real-world super-resolution. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3408–3416. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Timofte, R.; Fritsche, M.; Gu, S.; Purohit, K.; Kandula, P.; Suin, M.; Rajagoapalan, A.; Joon, N.H.; et al. Aim 2019 challenge on real-world image super-resolution: Methods and results. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3575–3583. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Timofte, R. Ntire 2020 challenge on real-world image super-resolution: Methods and results. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Nashville, TN, USA, 19–25 June 2020; pp. 494–495. [Google Scholar]
- Bell-Kligler, S.; Shocher, A.; Irani, M. Blind Super-Resolution Kernel Estimation using an Internal-GAN. In Proceedings of the Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Liang, J.; Zhang, K.; Gu, S.; Van Gool, L.; Timofte, R. Flow-based kernel prior with application to blind super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10601–10610. [Google Scholar]
- Kim, Y.; Ha, J.; Cho, Y.; Kim, J. Unsupervised Blur Kernel Estimation and Correction for Blind Super-Resolution. IEEE Access 2022, 10, 45179–45189. [Google Scholar] [CrossRef]
- Yamac, M.; Ataman, B.; Nawaz, A. KernelNet: A Blind Super-Resolution Kernel Estimation Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Nashville, TN, USA, 19–25 June 2021; pp. 453–462. [Google Scholar]
- Cho, S.; Lee, S. Fast Motion Deblurring. In Proceedings of the ACM SIGGRAPH Asia 2009 Papers, SIGGRAPH Asia ’09, Yokohama, Japan, 16–19 December 2009; Association for Computing Machinery: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Shan, Q.; Jia, J.; Agarwala, A. High-Quality Motion Deblurring from a Single Image. ACM Trans. Graph. 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9446–9454. [Google Scholar]
- Hu, Z.; Yang, M.H. Good Regions to Deblur. In Proceedings of the Computer Vision—ECCV 2012, Florence, Italy, 7–13 October 2012; Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 59–72. [Google Scholar]








| KernelGAN | FKP | E-KernelGAN | E-KernelGAN-DIP | TVG-KernelGAN | |||
|---|---|---|---|---|---|---|---|
| DIV2KRK | 0.0067 | 0.0072 | 0.0043 | 0.0043 | 0.0046 | ||
| 0.9294 | 0.9239 | 0.9574 | 0.9579 | 0.9543 | |||
| 0.00088 | 0.00080 | 0.00062 | 0.00062 | 0.00070 | |||
| 0.9537 | 0.9537 | 0.9698 | 0.9699 | 0.9680 | |||
| Flickr2KRK | 0.0087 | 0.0106 | 0.0081 | 0.0080 | 0.0077 | ||
| 0.8989 | 0.8833 | 0.9094 | 0.9100 | 0.9097 | |||
| 0.00111 | 0.00093 | 0.00090 | 0.00089 | 0.00089 | |||
| 0.9391 | 0.9392 | 0.9550 | 0.9550 | 0.9552 | |||
| DIV2KSK | 0.0051 | 0.0072 | 0.0058 | 0.0057 | 0.0043 | ||
| 0.9446 | 0.9138 | 0.9426 | 0.9431 | 0.9547 | |||
| 0.00088 | 0.00100 | 0.00083 | 0.00083 | 0.00074 | |||
| 0.9478 | 0.9419 | 0.9577 | 0.9579 | 0.9593 |
| Bicubic | KernelGAN | FKP | E-KernelGAN | E-KernelGAN-DIP | TVG-KernelGAN | GT | |||
|---|---|---|---|---|---|---|---|---|---|
| DIV2KRK | ZSSR | PSNR | 28.6953 | 28.7329 | 28.3635 | 29.3803 | 29.3544 | 29.0642 | 29.8799 |
| SSIM | 0.8035 | 0.8360 | 0.8413 | 0.8472 | 0.8470 | 0.8416 | 0.8656 | ||
| Equation (2) | PSNR | 28.6953 | 30.0237 | 28.9431 | 30.3637 | 30.3741 | 30.3425 | 31.5232 | |
| SSIM | 0.8035 | 0.8516 | 0.8329 | 0.8573 | 0.8576 | 0.8562 | 0.8801 | ||
| Flickr2KRK | ZSSR | PSNR | 28.0653 | 28.4859 | 27.5576 | 28.7836 | 28.7809 | 28.5700 | 29.4258 |
| SSIM | 0.7897 | 0.8230 | 0.8281 | 0.8297 | 0.8296 | 0.8281 | 0.8500 | ||
| Equation (2) | PSNR | 28.0653 | 29.2672 | 28.5526 | 29.3507 | 29.3542 | 29.2909 | 29.0367 | |
| SSIM | 0.7897 | 0.8385 | 0.8222 | 0.8404 | 0.8406 | 0.8406 | 0.8341 | ||
| DIV2KSK | ZSSR | PSNR | 24.5548 | 25.3626 | 24.7414 | 25.4244 | 25.4294 | 25.4313 | 26.2298 |
| SSIM | 0.6874 | 0.7507 | 0.7514 | 0.7499 | 0.7496 | 0.7529 | 0.7921 | ||
| Equation (2) | PSNR | 24.5548 | 25.9113 | 25.1470 | 25.7892 | 25.7525 | 25.9618 | 26.8826 | |
| SSIM | 0.6874 | 0.7608 | 0.7300 | 0.7566 | 0.7563 | 0.7629 | 0.7975 |
| KernelGAN | E-KernelGAN | E-KernelGAN-DIP | TVG-KernelGAN | |
|---|---|---|---|---|
| Network parameters | 181 k | 464 k | 2824 k | 181 k |
| Run-time | 57 s | 356 s | 930 s | 57 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Kim, H.; Kang, M.G. Kernel Estimation Using Total Variation Guided GAN for Image Super-Resolution. Sensors 2023, 23, 3734. https://doi.org/10.3390/s23073734
Park J, Kim H, Kang MG. Kernel Estimation Using Total Variation Guided GAN for Image Super-Resolution. Sensors. 2023; 23(7):3734. https://doi.org/10.3390/s23073734
Chicago/Turabian StylePark, Jongeun, Hansol Kim, and Moon Gi Kang. 2023. "Kernel Estimation Using Total Variation Guided GAN for Image Super-Resolution" Sensors 23, no. 7: 3734. https://doi.org/10.3390/s23073734
APA StylePark, J., Kim, H., & Kang, M. G. (2023). Kernel Estimation Using Total Variation Guided GAN for Image Super-Resolution. Sensors, 23(7), 3734. https://doi.org/10.3390/s23073734





