Design of Planar Differential Microphone Array Beampatterns with Controllable Mainlobe Beamwidth and Sidelobe Level
Abstract
1. Introduction
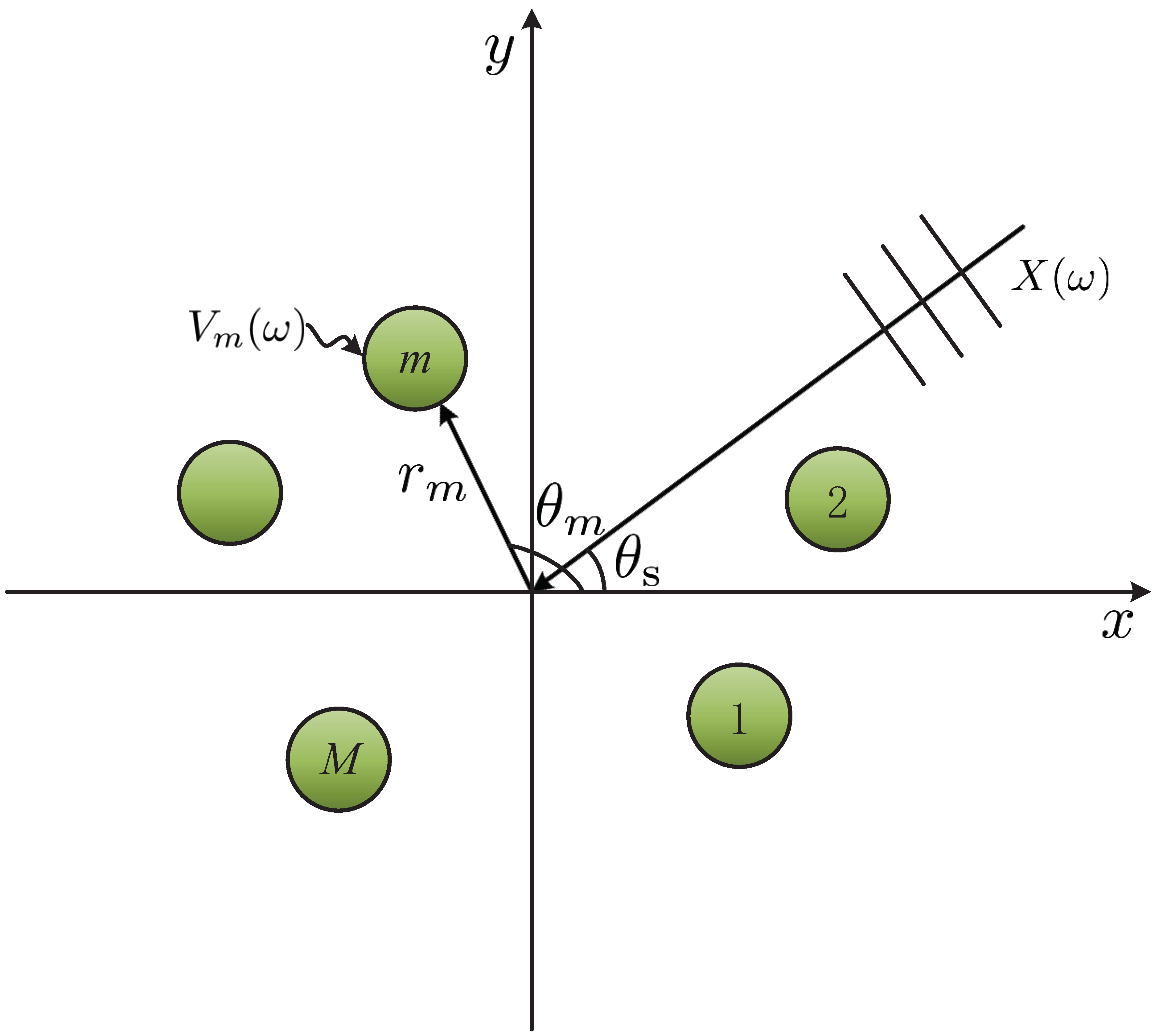
2. Signal Model, Problem Formulation and Performance Measures
- Spatially and temporally white Gaussian noise with identical variances at all sensors, which models microphones’ self-noise, nonuniform responses among the microphones, imperfections of the microphone positions, etc. In this scenario, , where is the identity matrix of size , and the resulting SNR gain is named as WNG, i.e.,So, the WNG evaluates the robust of the beamformer to some of the array imperfections. The maximum WNG that can be achieved by a beamforming filter is equal to M [40], i.e., . It can be obtained by the DS beamformer [40,54]:Note that indicates that there is white noise amplification.
- Spherical isotropic noise, which is characterized bywith , where is the spacing between the ith and jth microphones. In this case, the SNR gain is named DF:which quantifies how the beamformer performs in suppressing spatial directional noise, such as reverberation. The maximum DF that can be achieved by a beamformer with a given array is [40]which can be obtained by the so-called superdirective (hypercardioid) beamformer:
3. Beampattern Design
| Algorithm 1: Steps for designing the desired beampattern. |
1: Select the order, N, of the desired beampattern, , and choose the Chebyshev polynomial, , of the same order; 2: Set the ratio of the main lobe level to the sidelobe level, R, and determine according to (25), or set the main lobe beamwidth , and determine the parameter R according to (38) and then find ; 3: Change the scale by using the mapping function (28); |
4. DMA Design
4.1. Null Constrained Method
4.2. Least Square Method
4.3. Minimum Norm Solution
4.4. Combined Solution
4.5. Particular Case: Linear Microphone Array
5. Simulations
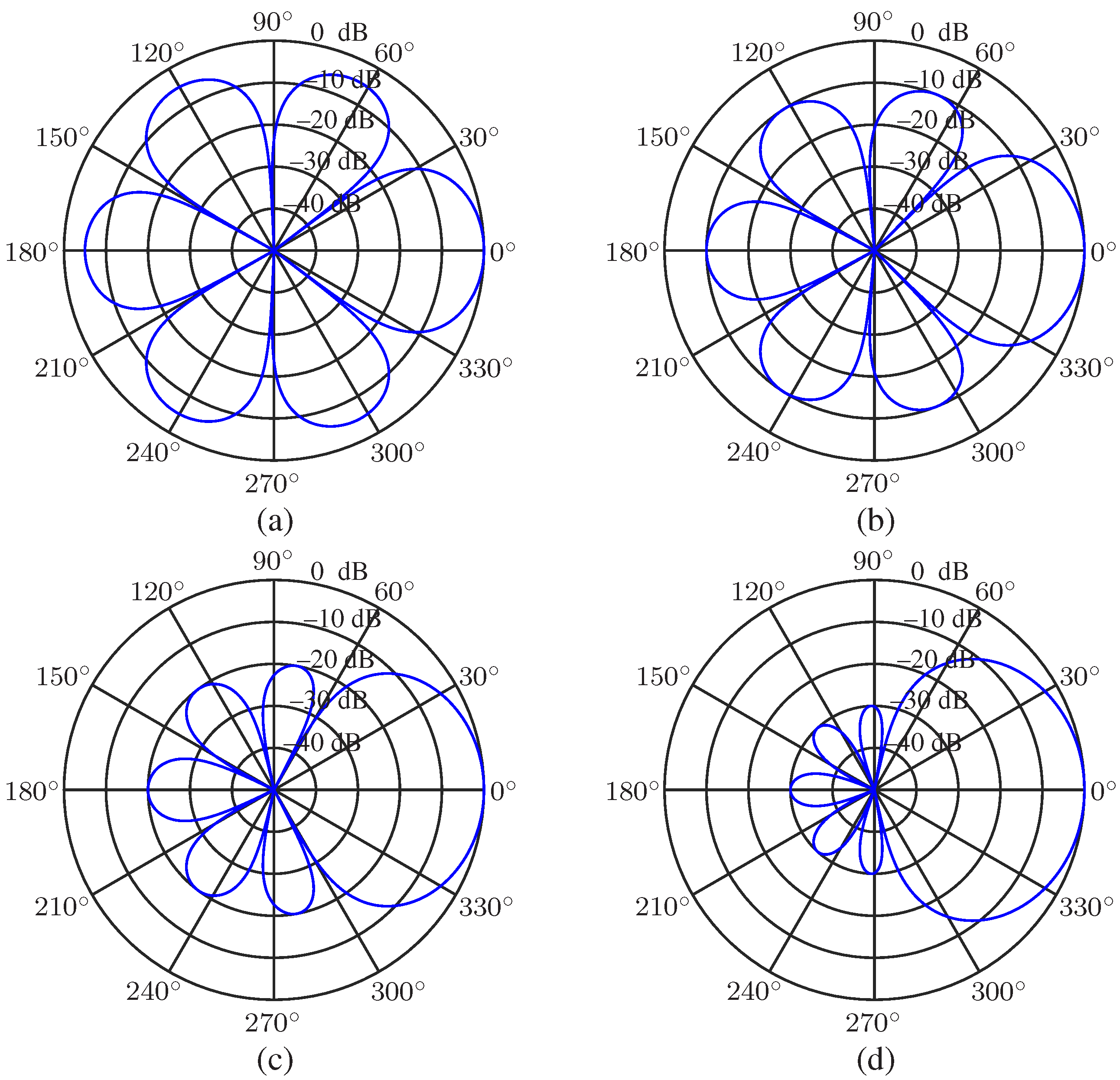
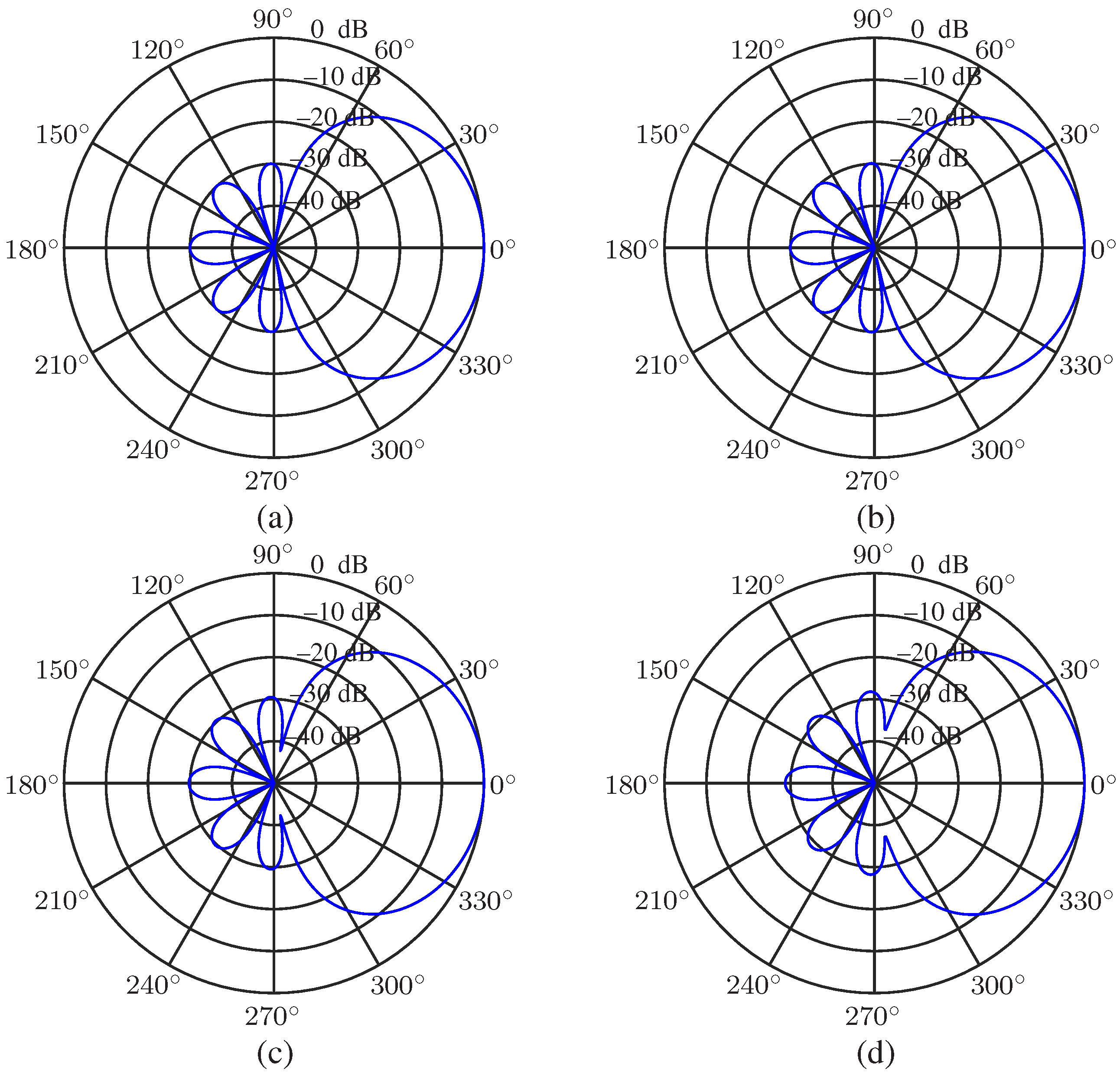
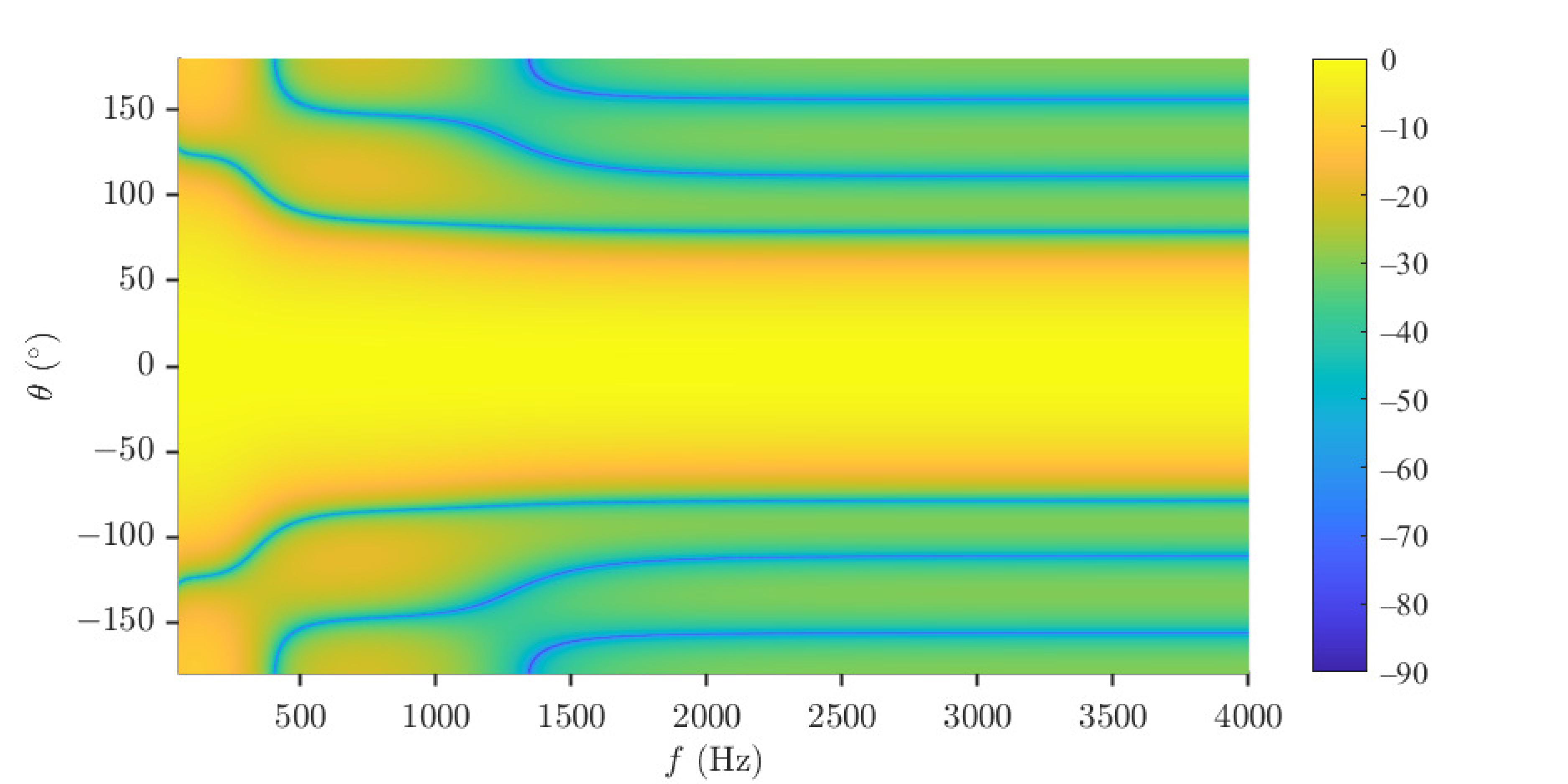
5.1. Desired Beampattern
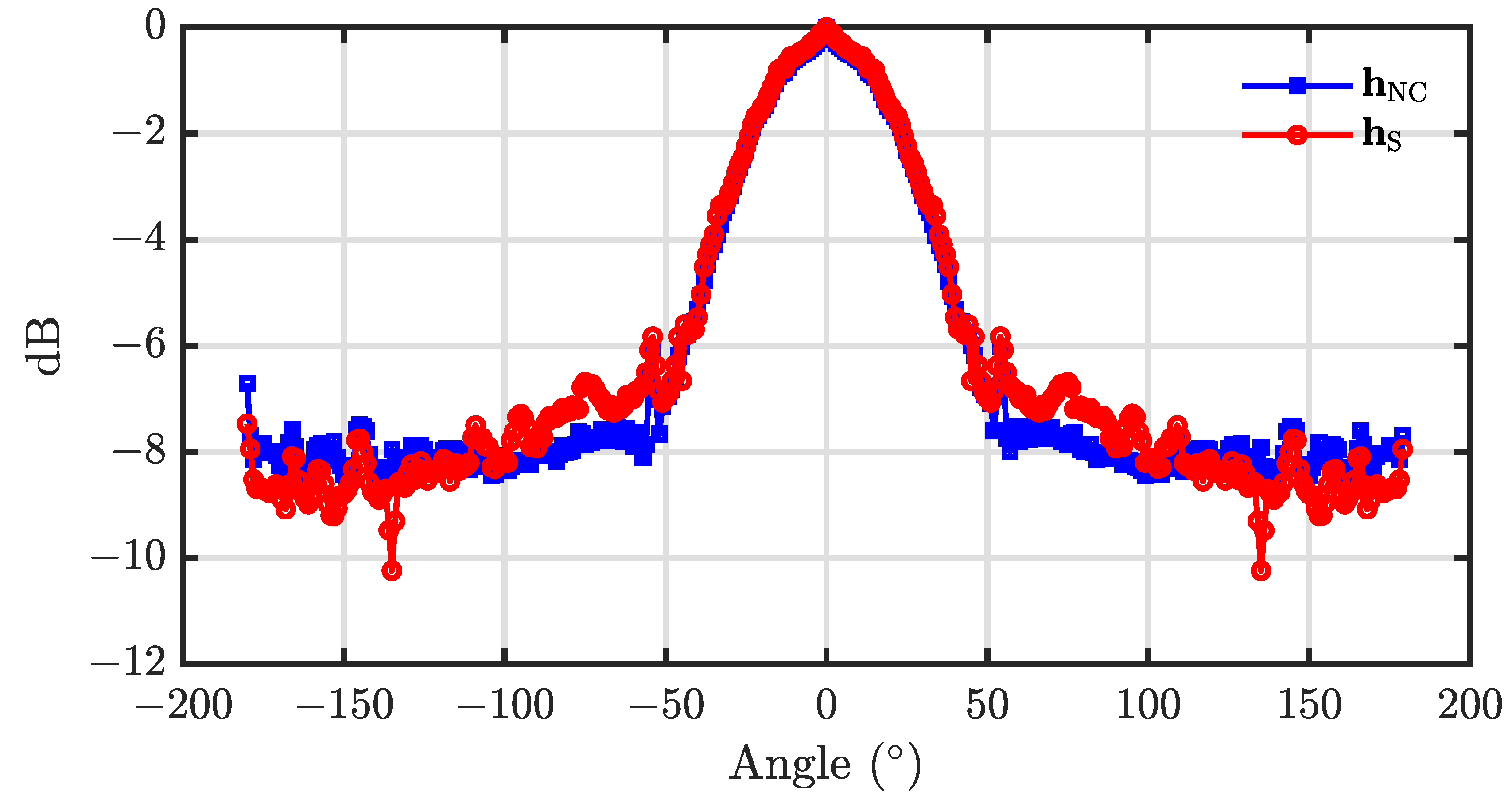
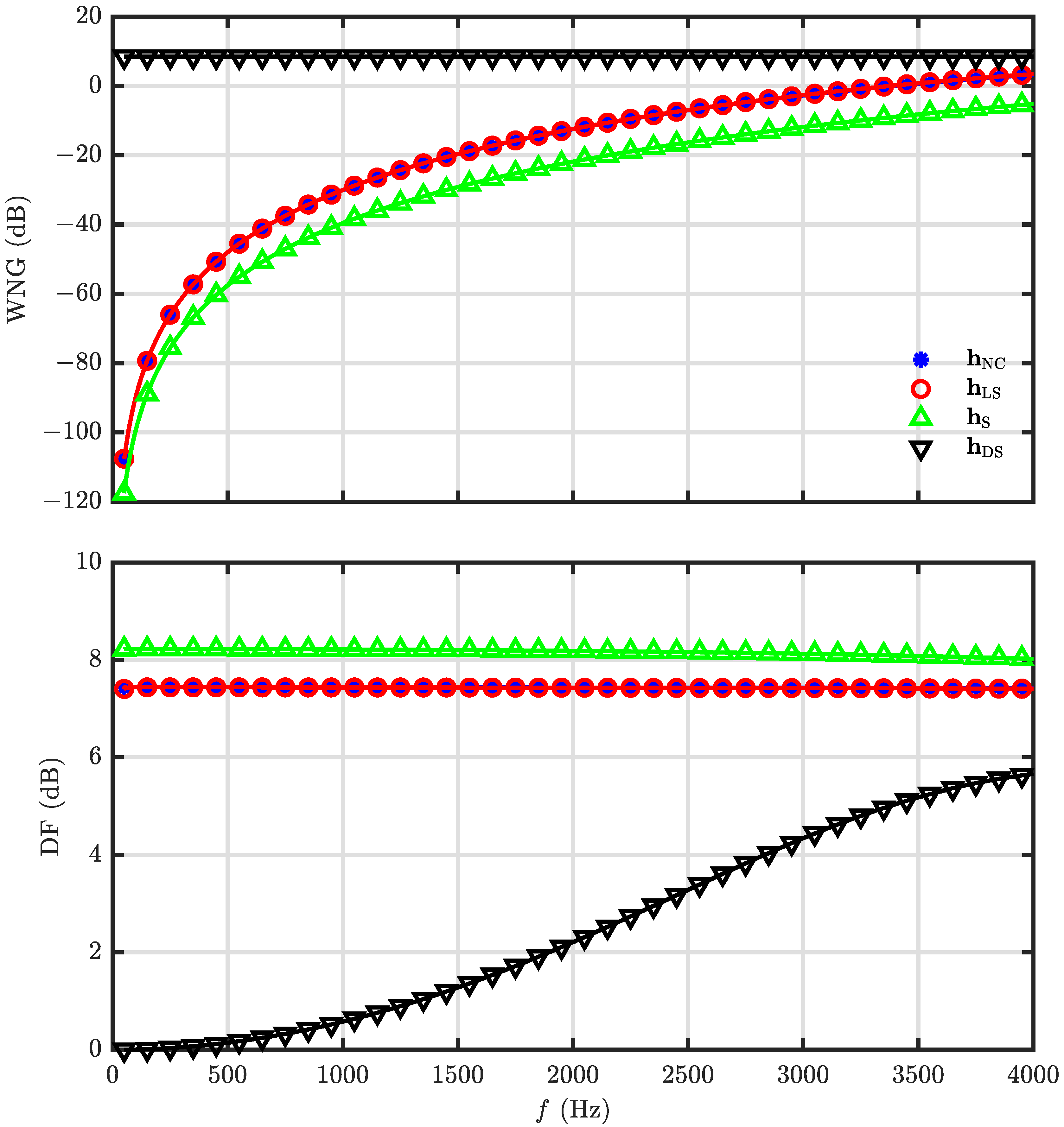
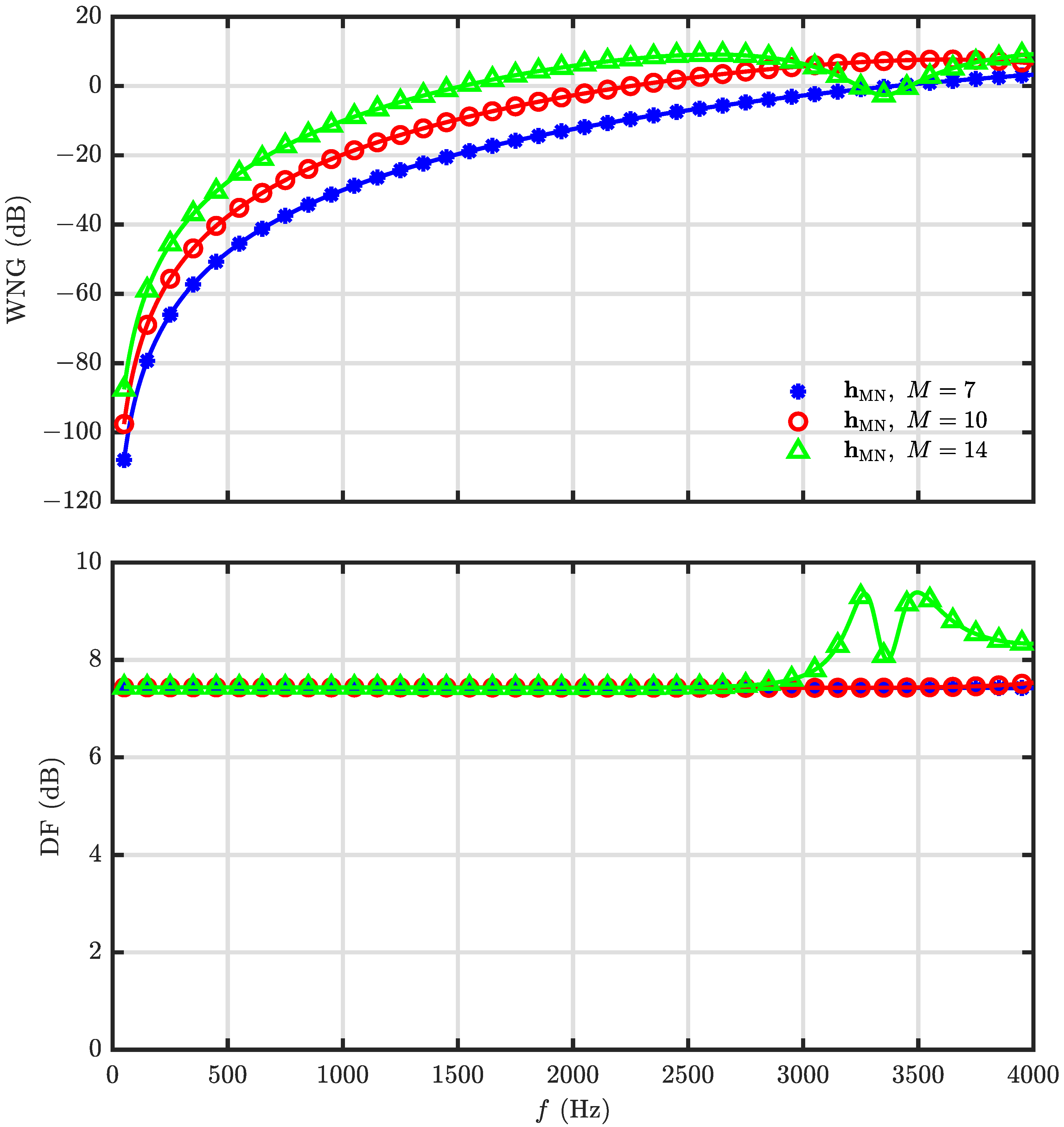
5.2. Performance of the Null Constrained and Least Square Beamformers
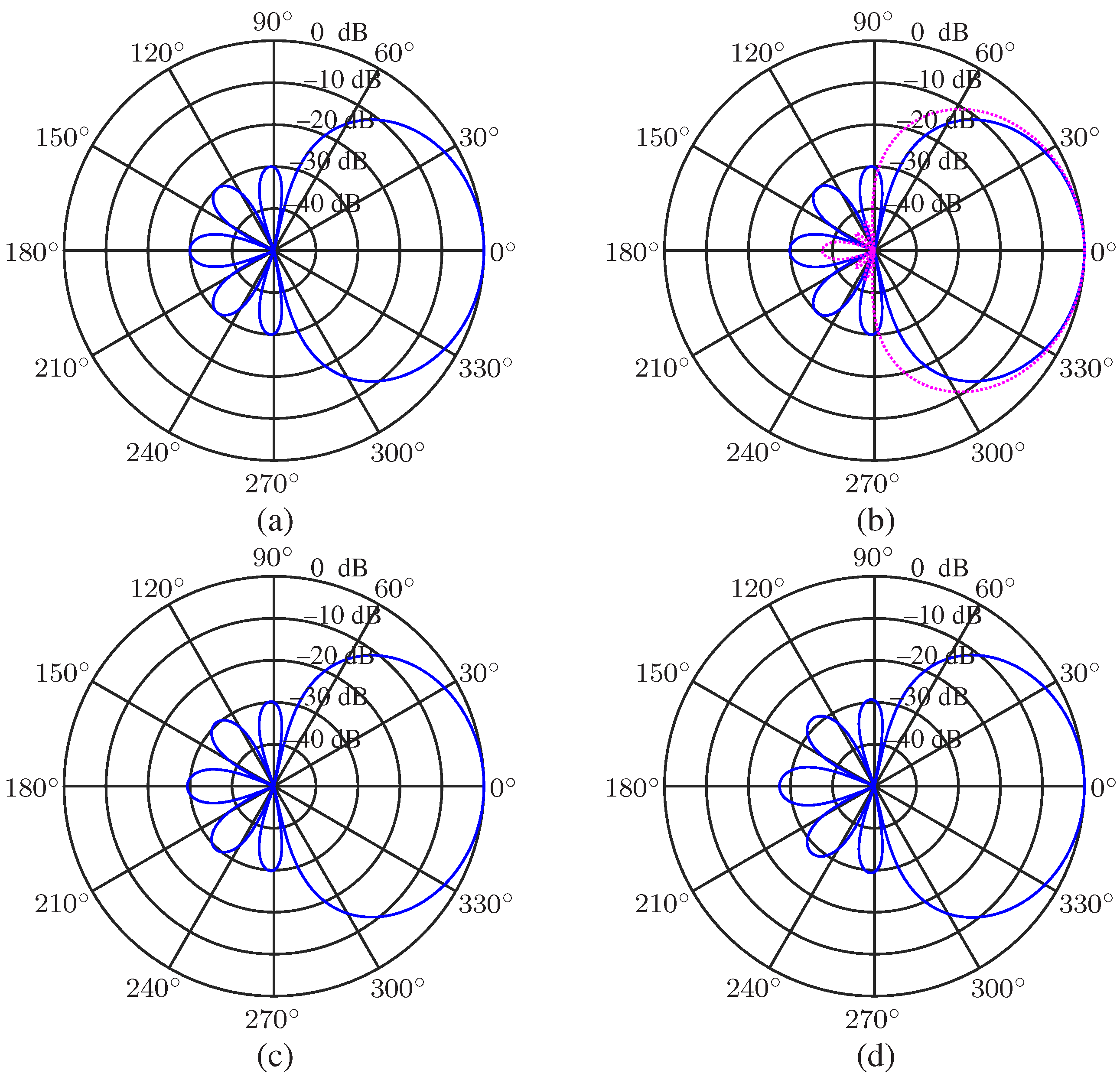
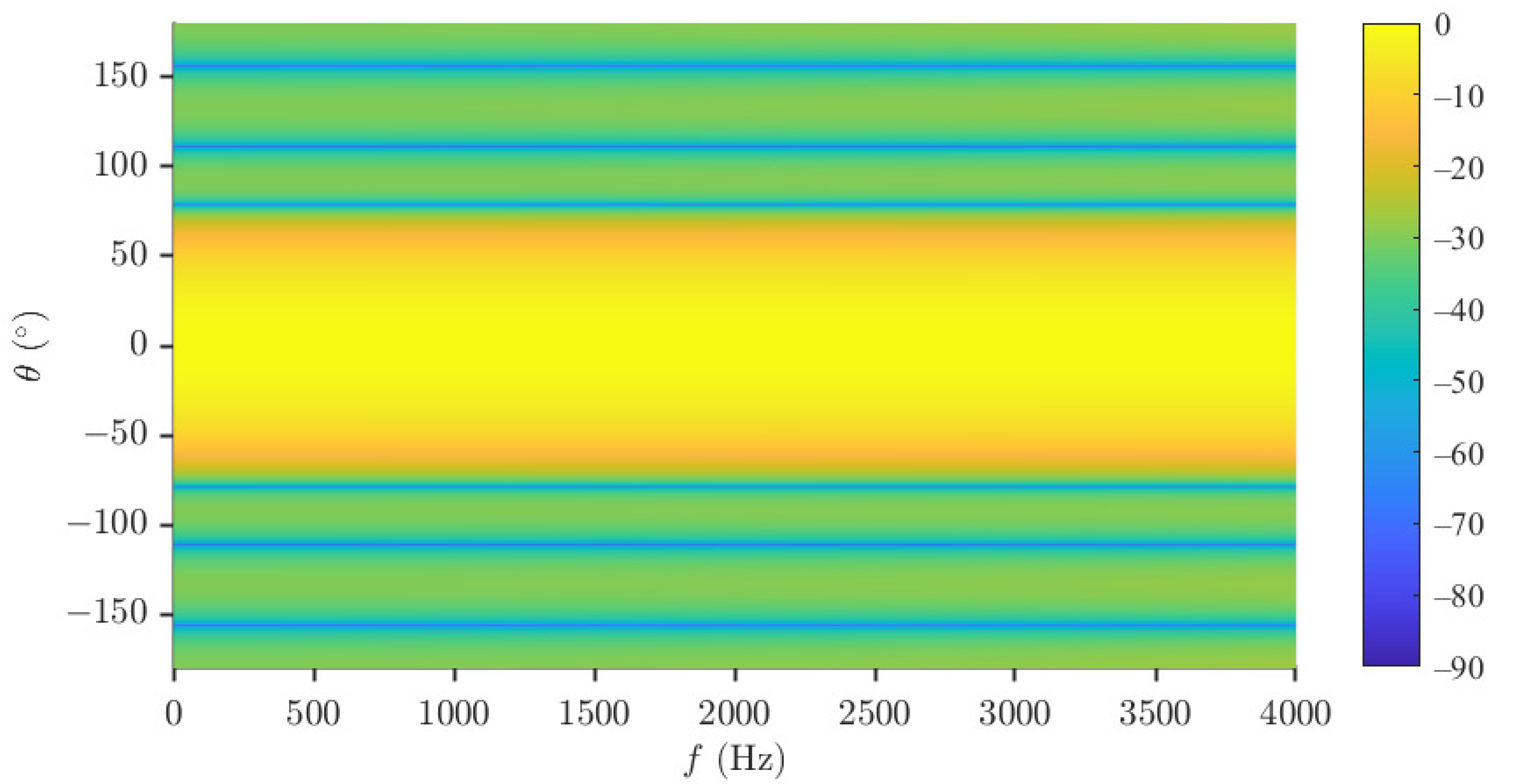
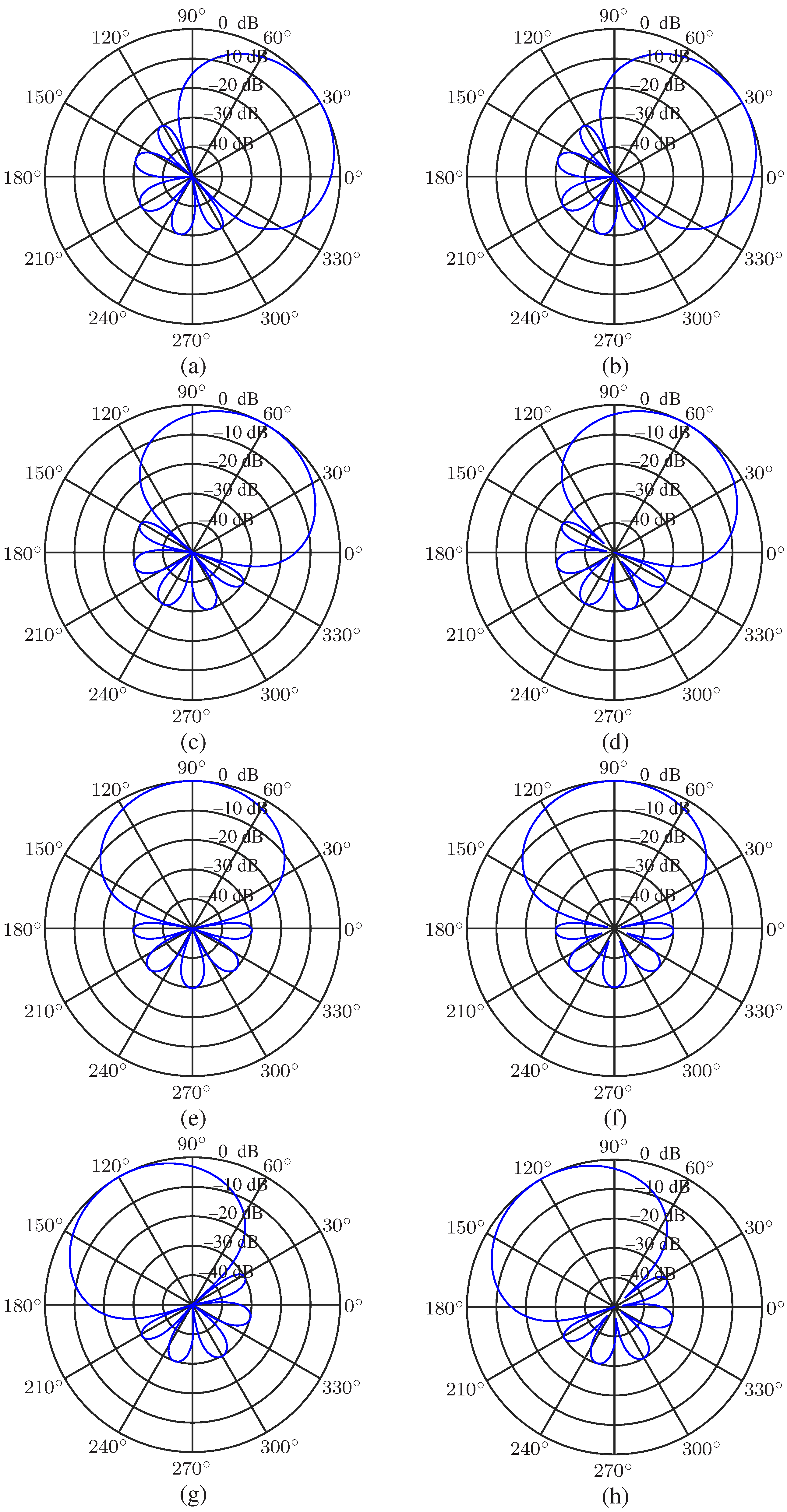
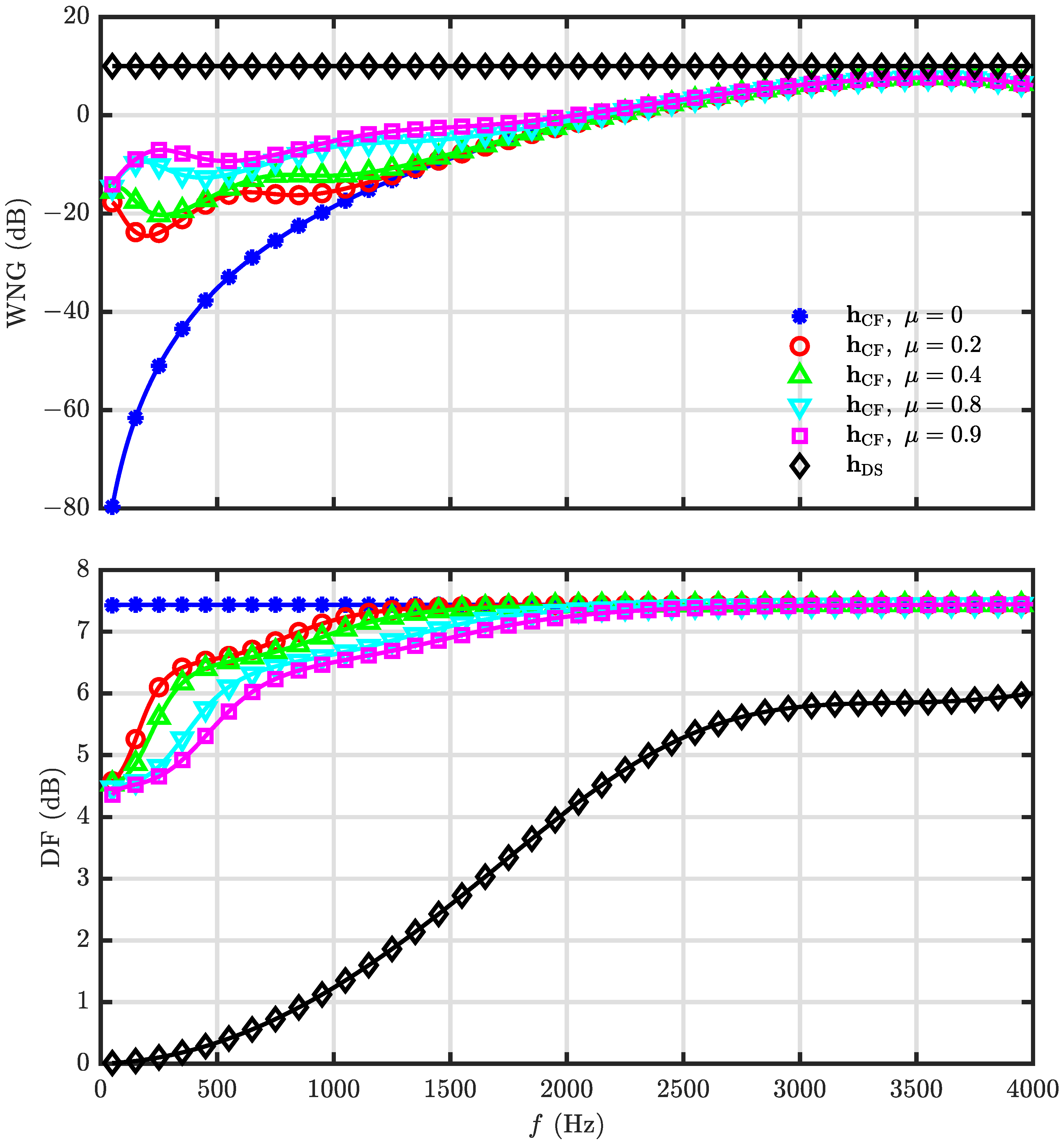
5.3. Performance of the Minimum Norm and Combined Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benesty, J.; Cohen, I.; Chen, J. Fundamentals of Signal Enhancement and Array Signal Processing; Wiley-IEEE Press: Hoboken, NJ, USA, 2017. [Google Scholar]
- Buchris, Y.; Cohen, I.; Benesty, J. On the design of time-domain differential microphone arrays. Appl. Acoust. 2019, 148, 212–222. [Google Scholar] [CrossRef]
- Hoshiba, K.; Washizaki, K.; Wakabayashi, M.; Ishiki, T.; Kumon, M.; Bando, Y.; Gabriel, D.; Nakadai, K.; Okuno, H.G. Design of UAV-embedded microphone array system for sound source localization in outdoor environments. Sensors 2017, 17, 2535. [Google Scholar] [CrossRef] [PubMed]
- Zu, X.; Guo, F.; Huang, J.; Zhao, Q.; Liu, H.; Li, B.; Yuan, X. Design of an acoustic target intrusion detection system based on small-aperture microphone array. Sensors 2017, 17, 514. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Guo, Q.; Chu, N.; Wang, R. Achieving 3D beamforming by non-synchronous microphone array measurements. Sensors 2020, 20, 7308. [Google Scholar] [CrossRef]
- Dehghan Firoozabadi, A.; Irarrazaval, P.; Adasme, P.; Zabala-Blanco, D.; Játiva, P.P.; Azurdia-Meza, C. 3D multiple sound source localization by proposed T-shaped circular distributed microphone arrays in combination with GEVD and adaptive GCC-PHAT/ML algorithms. Sensors 2022, 22, 1011. [Google Scholar] [CrossRef]
- Li, C.; Chen, C.; Gu, X. Acoustic-Based Rolling Bearing Fault Diagnosis Using a Co-Prime Circular Microphone Array. Sensors 2023, 23, 3050. [Google Scholar] [CrossRef]
- Prieur, F.; Rindal, O.M.H.; Austeng, A. Signal coherence and image amplitude with the filtered delay multiply and sum beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2018, 65, 1133–1140. [Google Scholar] [CrossRef]
- Lianghua, Y.; Yunfei, C.; Xiuyin, Z. Multibeam Antenna Based on Butler Matrix for 3G/LTE/5G/B5G Base Station Applications. ZTE Commun. 2020, 18, 12–18. [Google Scholar]
- Dong, W.; Fanggang, W.; Xiran, L.; Pu, Y.; Dajie, J. Orthogonal Time Frequency Space Modulation in Multiple-Antenna Systems. ZTE Commun. 2021, 19, 71–77. [Google Scholar]
- Sun, S.; Wen, G. Optimal Design of Wireless Power Transmission Systems Using Antenna Arrays. ZTE Commun. 2022, 20, 19–27. [Google Scholar]
- Doclo, S.; Moonen, M. Design of broadband beamformers robust against gain and phase errors in the microphone array characteristics. IEEE Trans. Signal Process. 2003, 51, 2511–2526. [Google Scholar] [CrossRef]
- Lin, T.; Cong, J.; Zhu, Y.; Zhang, J.; Letaief, K.B. Hybrid beamforming for millimeter wave systems using the MMSE criterion. IEEE Trans. Commun. 2019, 67, 3693–3708. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, W.; Zhang, X.; Zheng, W. Transformed nested array designed for DOA estimation of non-circular signals: Reduced sum-difference co-array redundancy perspective. IEEE Commun. Lett. 2020, 24, 1262–1265. [Google Scholar] [CrossRef]
- Patra, R.K.; Dhar, A.S. A novel nested array for real-valued sources exploiting array motion. IEEE Signal Process. Lett. 2021, 28, 1375–1379. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Zhou, H. Generalized nested array: Optimization for degrees of freedom and mutual coupling. IEEE Commun. Lett. 2018, 22, 1208–1211. [Google Scholar] [CrossRef]
- Yan, S. Robust time-domain broadband modal beamforming for circular arrays. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1783–1794. [Google Scholar] [CrossRef]
- Dougherty, R.P.; Bozak, R. Two-dimensional modal beamforming in wavenumber space for duct acoustics. In Proccedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 2805. [Google Scholar]
- Yadav, S.K.; George, N.V. Sparse distortionless modal beamforming for spherical microphone arrays. IEEE Signal Process. Lett. 2022, 29, 2068–2072. [Google Scholar] [CrossRef]
- Koyama, S.; Furuya, K.; Wakayama, K.; Shimauchi, S.; Saruwatari, H. Analytical approach to transforming filter design for sound field recording and reproduction using circular arrays with a spherical baffle. J. Acoust. Soc. Am. 2016, 139, 1024–1036. [Google Scholar] [CrossRef]
- Chen, X.; Benesty, J.; Huang, G.; Chen, J. On the robustness of the superdirective beamformer. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 838–849. [Google Scholar] [CrossRef]
- Trucco, A. The Statistics of Superdirective Beam Patterns. IEEE Trans. Signal Process. 2022, 70, 1959–1975. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Ma, Y.; He, Z. Robust high-order superdirectivity of circular sensor arrays. J. Acoust. Soc. Am. 2014, 136, 1712–1724. [Google Scholar] [CrossRef] [PubMed]
- Itzhak, G.; Benesty, J.; Cohen, I. Multistage approach for steerable differential beamforming with rectangular arrays. Speech Commun. 2022, 142, 61–76. [Google Scholar] [CrossRef]
- Cohen, I.; Benesty, J.; Chen, J. Differential Kronecker product beamforming. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 892–902. [Google Scholar] [CrossRef]
- Huang, W.; Feng, J. Differential Beamforming for Uniform Circular Array with Directional Microphones; INTERSPEECH: Brno, Czech Republic, 2020; pp. 71–75. [Google Scholar]
- Chen, J.; Benesty, J.; Pan, C. On the design and implementation of linear differential microphone arrays. J. Acoust. Soc. Am. 2014, 136, 3097–3113. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Chen, J.; Benesty, J. Theoretical Analysis of Differential Microphone Array Beamforming and an Improved Solution. IEEE Trans. Audio Speech Lang. Process. 2015, 23, 2093–2105. [Google Scholar] [CrossRef]
- Huang, G.; Benesty, J.; Chen, J. Fundamental approaches to robust differential beamforming with high directivity factors. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 3074–3088. [Google Scholar] [CrossRef]
- Weinberger, J.; Olson, H.F.; Massa, F. A Uni-Directional Ribbon Microphone. J. Acoust. Soc. Am. 1933, 5, 139–147. [Google Scholar] [CrossRef]
- Olson, H.F. Gradient microphones. J. Acoust. Soc. Am. 1946, 17, 192–198. [Google Scholar] [CrossRef]
- Elko, G.W.; Gay, S.L.; Benesty, J. Acoustic Signal Processing for Telecommunication; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Elko, G.W.; Meyer, J.; Benesty, J.; Sondhi, M.M.; Huang, Y. Springer Handbook of Speech Processing; Springer: Berlin, Germany, 2008. [Google Scholar]
- Abhayapala, T.D.; Gupta, A. Higher order differential-integral microphone arrays. J. Acoust. Soc. Am. 2010, 127, 227–233. [Google Scholar] [CrossRef]
- Buck, M. Aspects of first-order differential microphone arrays in the presence of sensor imperfections. Eur. Trans. Telecommun. 2002, 13, 115–122. [Google Scholar] [CrossRef]
- Ihle, M. Differential microphone arrays for spectral subtraction. In Proccedings of the International Workshop on Acoustic Echo and Noise Control (IWAENC), Kyoto, Japan, 8–11 September2003; pp. 259–262. [Google Scholar]
- De Sena, E.; Hacihabiboglu, H.; Cvetkovic, Z. On the design and implementation of higher order differential microphones. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 162–174. [Google Scholar] [CrossRef]
- Song, H.; Liu, J. First-order differential microphone array for robust speech enhancement. In Proccedings of the 2008 International Conference on Audio, Language and Image Processing, Shanghai, China, 7–9 July 2008; pp. 1461–1466. [Google Scholar]
- Elko, G.; Kubli, R.A.; Morgan, D.R.; West, J.E. Adjustable filter for differential microphones. J. Acoust. Soc. Am. 1995, 98, 1258. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J. Study and Design of Differential Microphone Arrays; Springer: Berlin, Germany, 2012. [Google Scholar]
- Benesty, J.; Chen, J.; Pan, C. Fundamentals of Differential Beamforming; Springer: Berlin, Germany, 2016. [Google Scholar]
- Borra, F.; Bernardini, A.; Antonacci, F.; Sarti, A. Efficient implementations of first-order steerable differential microphone arrays with arbitrary planar geometry. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 1755–1766. [Google Scholar] [CrossRef]
- Lovatello, J.; Bernardini, A.; Sarti, A. Steerable circular differential microphone arrays. In Proccedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 11–15. [Google Scholar]
- Pan, C.; Chen, J.; Benesty, J.; Shi, G. On the design of target beampatterns for differential microphone arrays. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1295–1307. [Google Scholar] [CrossRef]
- Dolph, C.L. A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level. Proc. IRE 1946, 34, 335–348. [Google Scholar] [CrossRef]
- Riblet, H. Discussion on a current distribution for broadside arrays which optimizes the relationship between beamwidth and side-lobe level. Proc. IRE 1947, 35, 489–492. [Google Scholar]
- Santhanakrishnan, T.; Rajesh, R.; Vijayan Pillai, S. An efficient destructive interference based on side lobe suppression method in sonar beamforming. Adv. Military Technol. 2021, 16, 107–120. [Google Scholar]
- Nusenu, S.Y.; Basit, A.; Asare, E. FDA transmit beamforming synthesis using Chebyshev window function technique to counteract deceptive electronic countermeasures signals. Prog. Electromag. Res. Lett. 2020, 90, 53–60. [Google Scholar] [CrossRef]
- Wang, S.; Lu, M.; Mei, J.; Cui, W. Deconvolved Beamforming Using the Chebyshev Weighting Method. J. Marine Sci. Appl. 2022, 21, 228–235. [Google Scholar] [CrossRef]
- Akkad, G.; Mansour, A.; ElHassan, B.; Le Roy, F.; Najem, M. Twiddle factor generation using chebyshev polynomials and hdl for frequency domain beamforming. In Applications in Electronics Pervading Industry, Environment and Society: APPLEPIES 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 153–165. [Google Scholar]
- Enache, F.; Deparateanu, D.; Enache, A.; Popescu, F. Sparse array antenna design based on dolph-chebyshev and genetic algorithms. In Proccedings of the 2016 8th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Ploiesti, Romania, 30 June–2 July 2016; pp. 1–4. [Google Scholar]
- Saputra, Y.P.; Oktafiani, F.; Wahyu, Y.; Munir, A. Side lobe suppression for X-band array antenna using Dolph-Chebyshev power distribution. In Proccedings of the 2016 22nd Asia-Pacific Conference on Communications (APCC), Yogyakarta, Indonesia, 25–27 August 2016; pp. 86–89. [Google Scholar]
- Khalaj-Amirhosseini, M.; Vecchi, G.; Pirinoli, P. Near-Chebyshev pattern for nonuniformly spaced arrays using zeros matching method. IEEE Trans. Antennas Propag. 2017, 65, 5155–5161. [Google Scholar] [CrossRef]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory, Part IV, Optimum Array Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Uzkov, A.I. An approach to the problem of optimum directive antenna design. In Comptes Rendus (Doklady) de l’Academie des Sciences de l’URSS; Academy of Sciences of the Soviet Union: Saint Petersburg, Russia, 1946; pp. 35–38. [Google Scholar]
- Cox, H.; Zeskind, R.M.; Kooij, T. Practical supergain. IEEE Trans. Acoust. Speech Signal Process. 1986, ASSP-34, 393–398. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Cohen, I. Design of Circular Differential Microphone Arrays; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964; Volume 55.
- Huang, G.; Benesty, J.; Chen, J. On the design of frequency-invariant beampatterns with uniform circular microphone arrays. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1140–1153. [Google Scholar] [CrossRef]
- Byun, J.; Park, Y.C.; Park, S.W. Continuously steerable second-order differential microphone arrays. J. Acoust. Soc. Am. 2018, 143, EL225–EL230. [Google Scholar] [CrossRef]
- Leng, X.; Chen, J.; Benesty, J. A New Method to Design Steerable First-Order Differential Beamformers. IEEE Signal Process. Lett. 2021, 28, 563–567. [Google Scholar] [CrossRef]
- Jin, J.; Huang, G.; Wang, X.; Chen, J.; Benesty, J.; Cohen, I. Steering study of linear differential microphone arrays. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 29, 158–170. [Google Scholar] [CrossRef]
- Wang, X.; Benesty, J.; Cohen, I.; Chen, J. Microphone array beamforming based on maximization of the front-to-Back ratio. J. Acoust. Soc. Am. 2018, 144, 3450–3464. [Google Scholar] [CrossRef]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-Room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Lehmanna, E.A.; Johansson, A.M. Prediction of energy decay in room impulse responses simulated with an image-Source model. J. Acoust. Soc. Am. 2008, 124, 269–277. [Google Scholar] [CrossRef]




| 0 | ||
| Beamformer | DSNR (dB) | DSRR (dB) |
|---|---|---|
| , | 5.14 | 4.89 |
| , | 8.24 | 4.74 |
| , | 14.24 | 4.39 |
| , | 15.81 | 4.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, M.; Zhao, Y.; Wang, J.; Tan, X. Design of Planar Differential Microphone Array Beampatterns with Controllable Mainlobe Beamwidth and Sidelobe Level. Sensors 2023, 23, 3733. https://doi.org/10.3390/s23073733
Wang X, Li M, Zhao Y, Wang J, Tan X. Design of Planar Differential Microphone Array Beampatterns with Controllable Mainlobe Beamwidth and Sidelobe Level. Sensors. 2023; 23(7):3733. https://doi.org/10.3390/s23073733
Chicago/Turabian StyleWang, Xianghui, Mei Li, Yingke Zhao, Jiao Wang, and Xin Tan. 2023. "Design of Planar Differential Microphone Array Beampatterns with Controllable Mainlobe Beamwidth and Sidelobe Level" Sensors 23, no. 7: 3733. https://doi.org/10.3390/s23073733
APA StyleWang, X., Li, M., Zhao, Y., Wang, J., & Tan, X. (2023). Design of Planar Differential Microphone Array Beampatterns with Controllable Mainlobe Beamwidth and Sidelobe Level. Sensors, 23(7), 3733. https://doi.org/10.3390/s23073733






