Advances in Multicore Fiber Interferometric Sensors
Abstract
1. Introduction
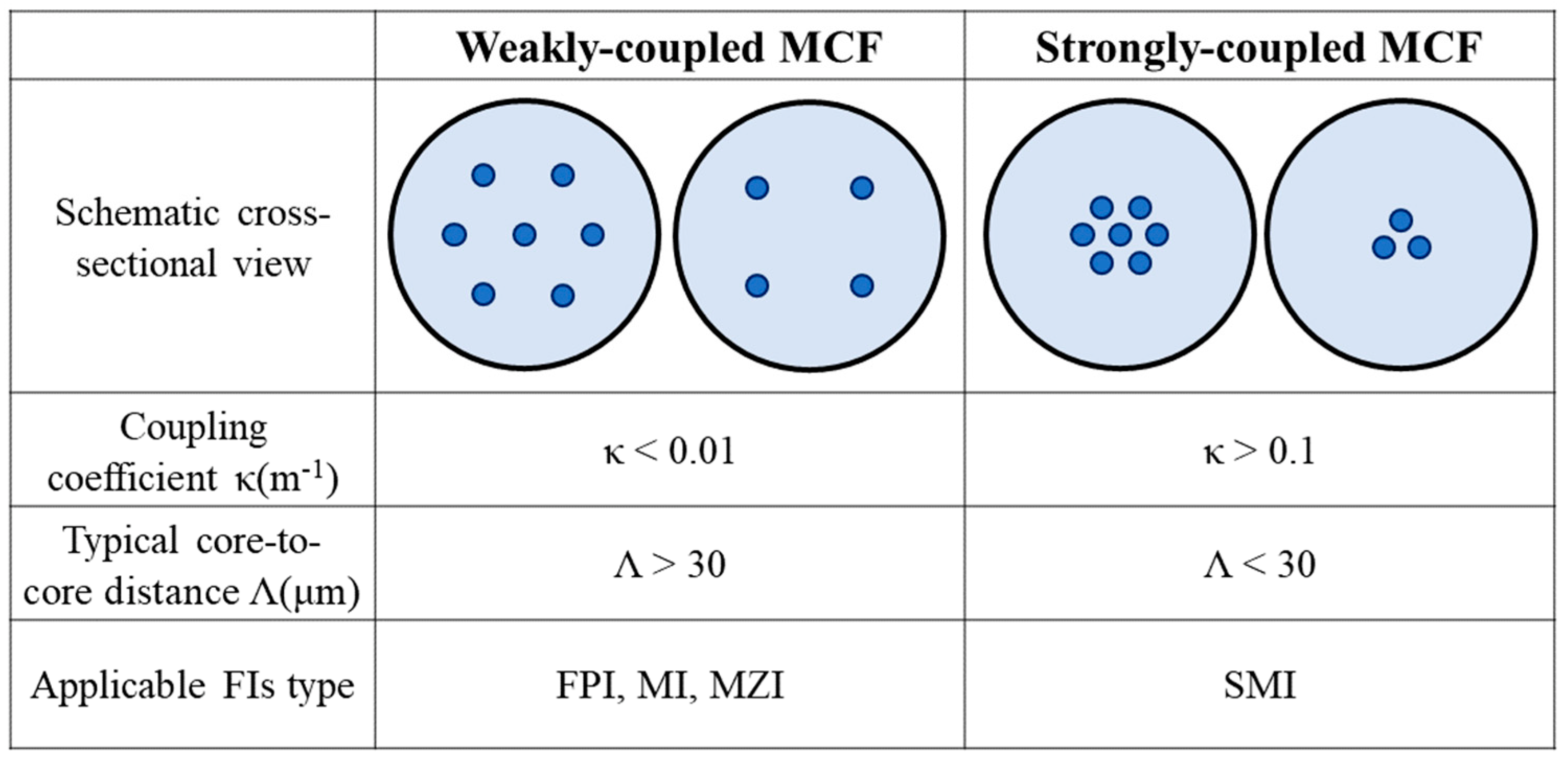
2. Multicore Fiber Interferometric Sensors
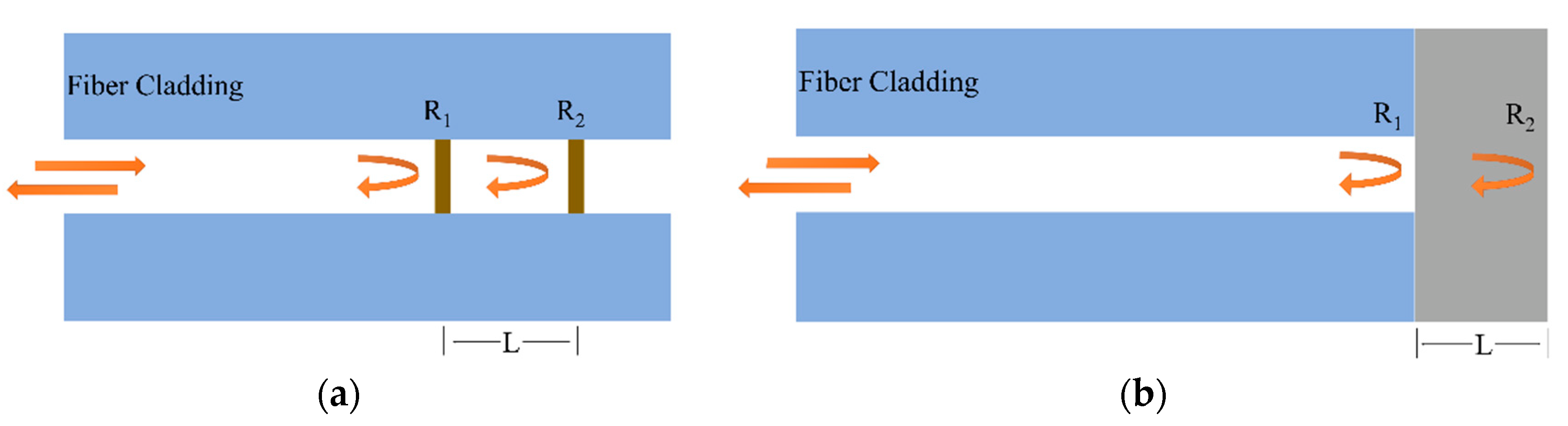
2.1. MCF-Based Fabry–Perot Interferometric Sensors
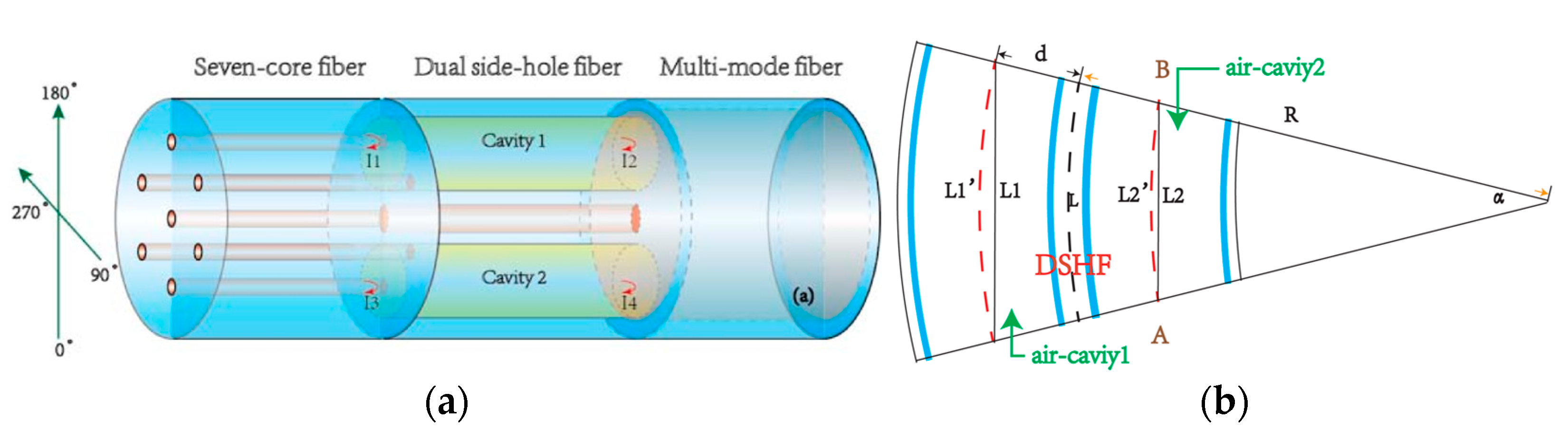
2.2. MCF-Based Michelson Interferometric Sensors
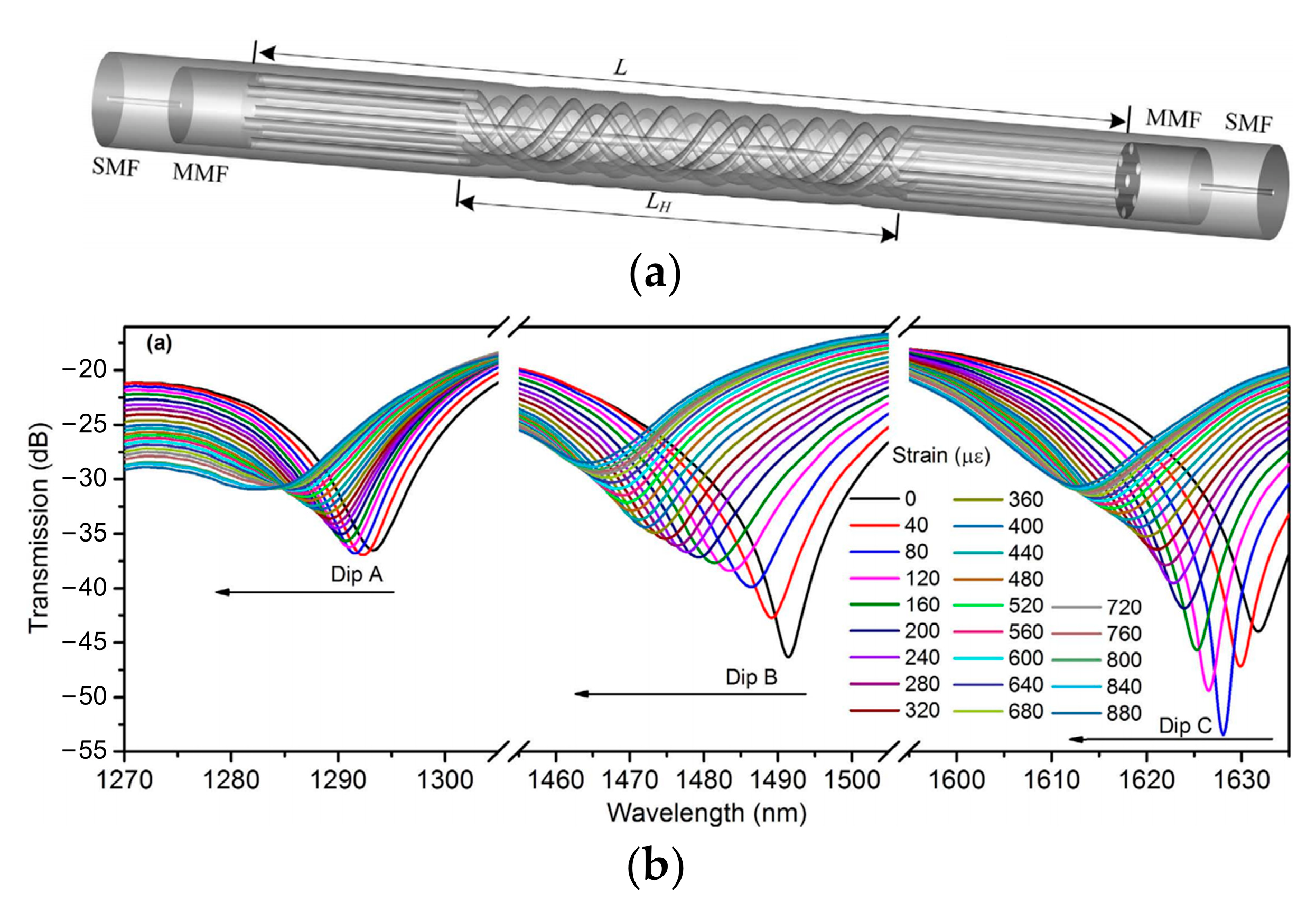
2.3. MCF-Based Mach–Zehnder Interferometric Sensors
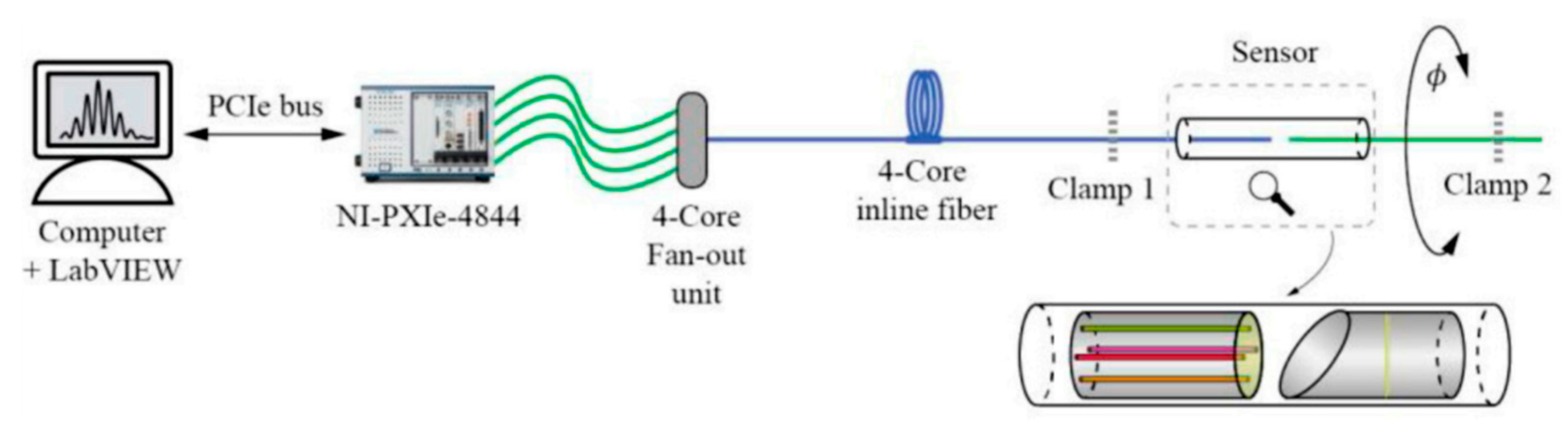
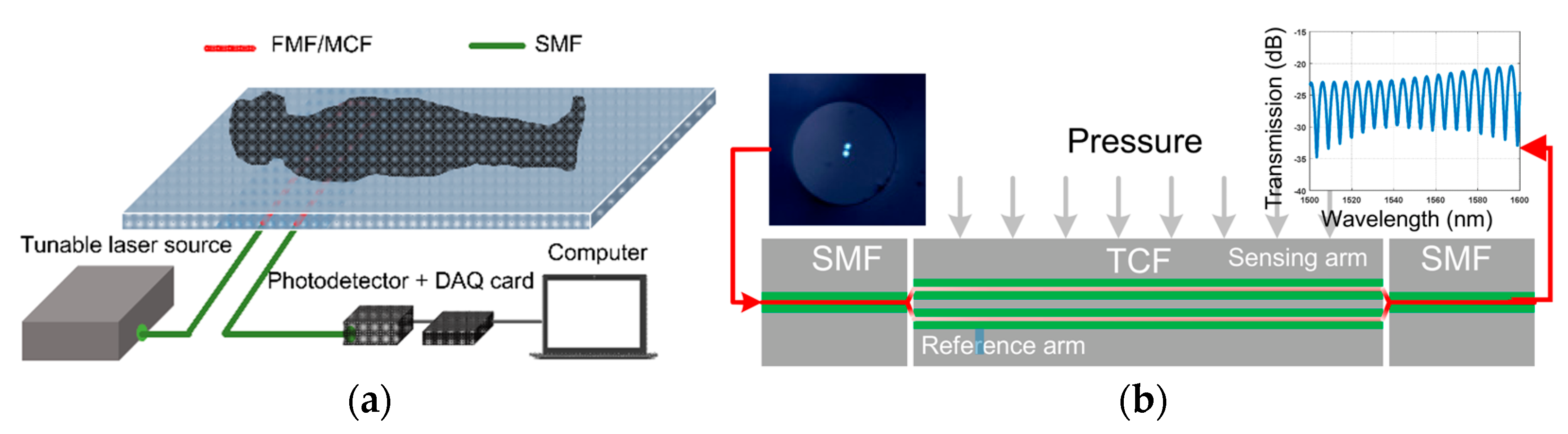
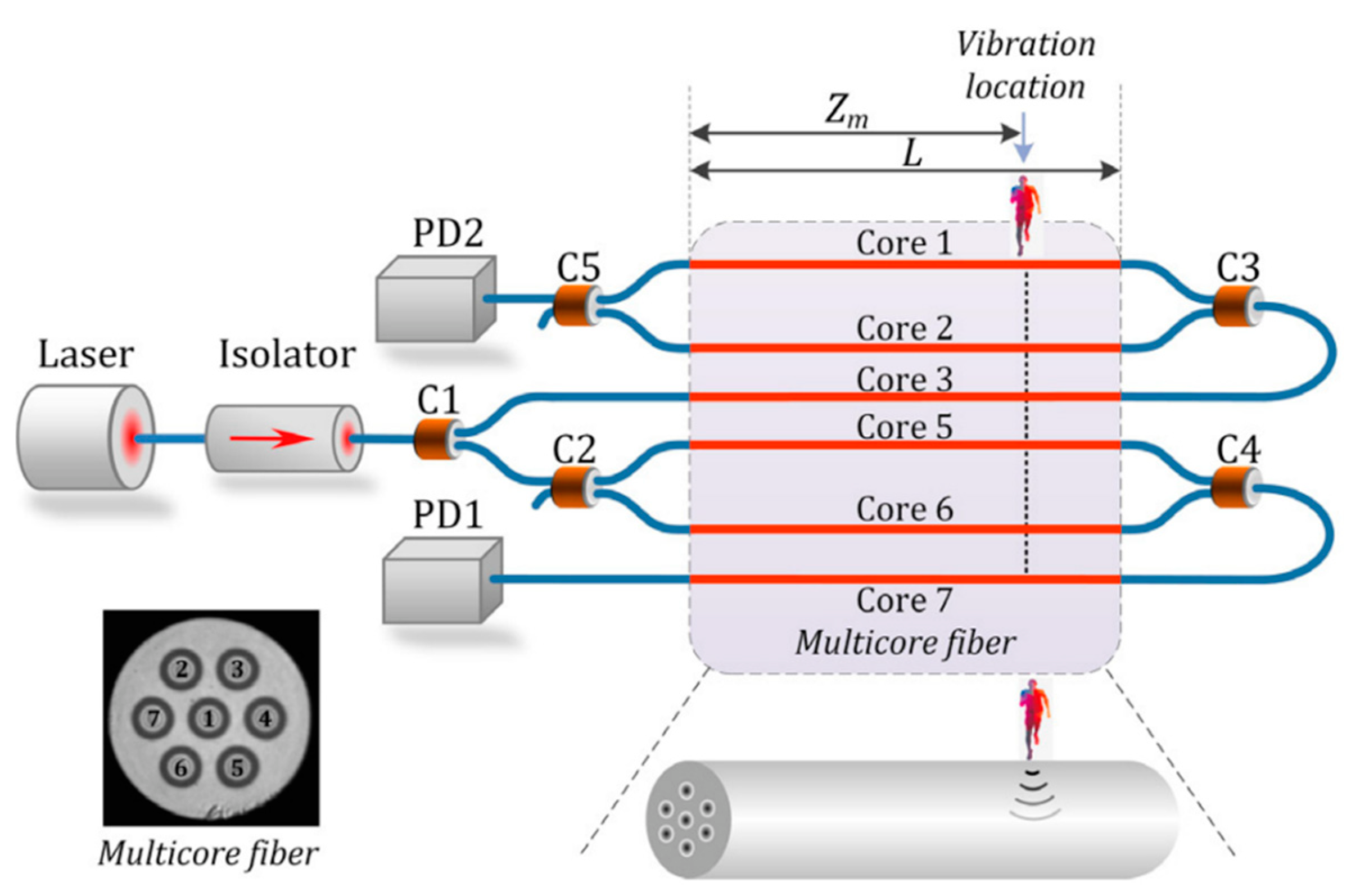
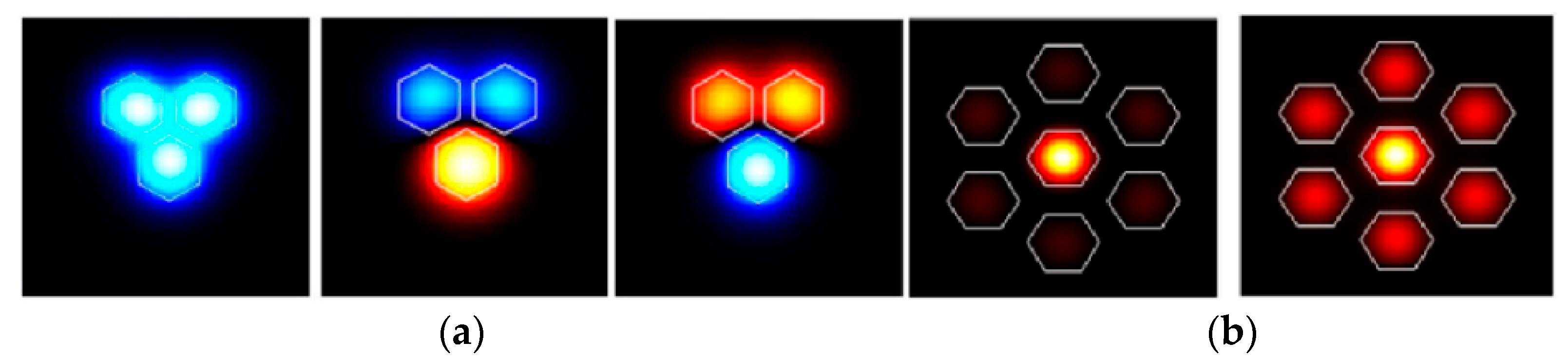
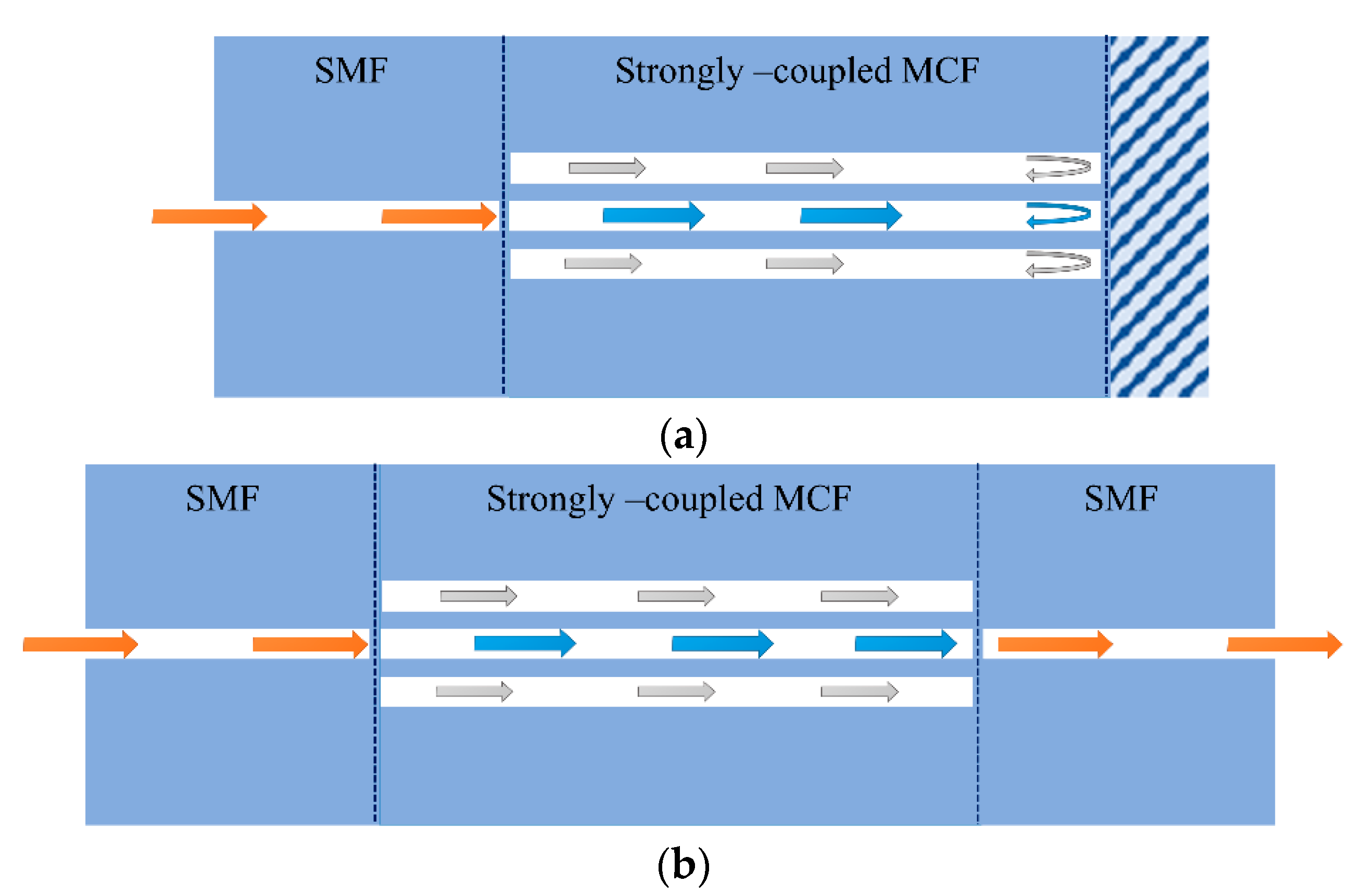
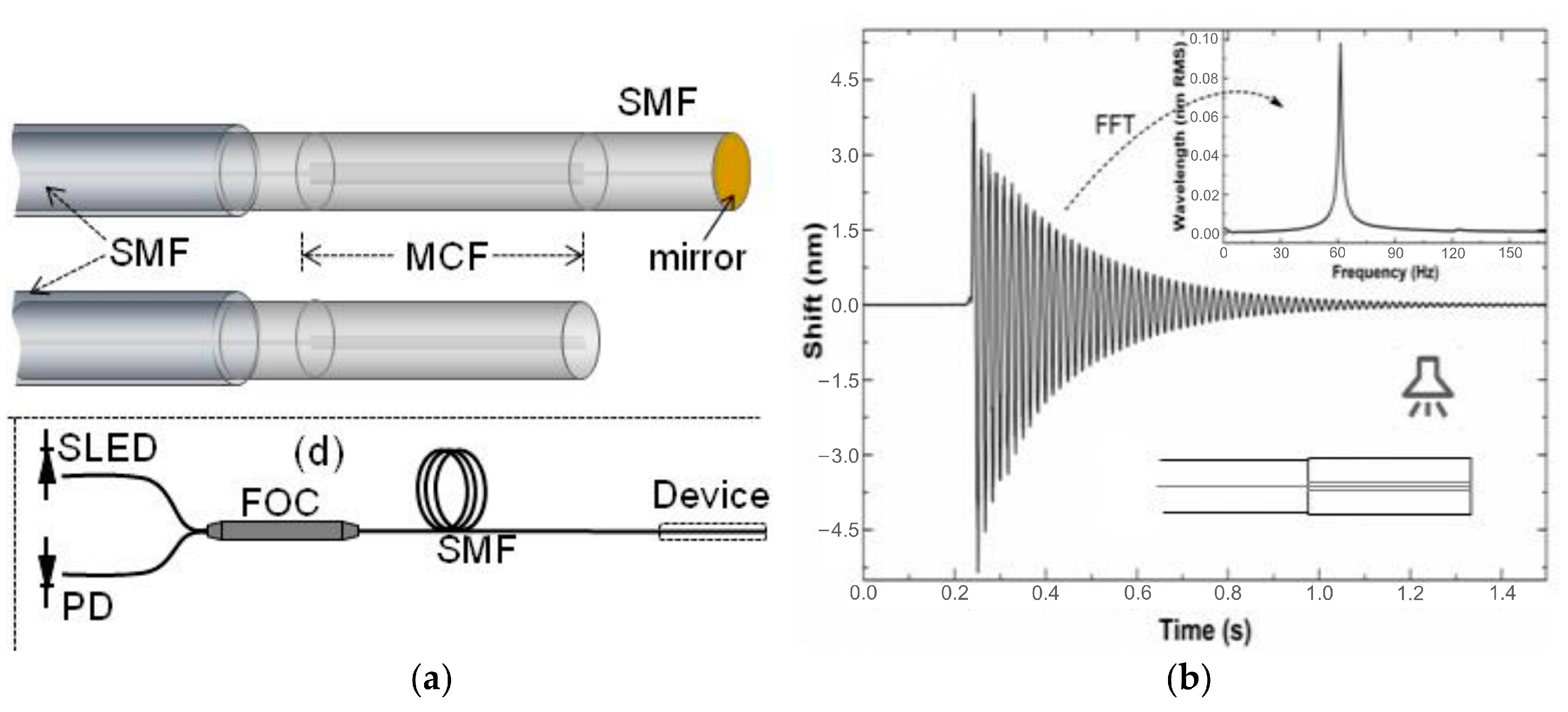
2.4. Supermode Interferometer-Based (SMI) Sensors
3. Discussion and Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Full Name |
| MCF | Multicore fiber |
| FPI | Fabry–Perot interferometer |
| MI | Michelson interferometer |
| MZI | Mach–Zehnder interferometer |
| SMI | Supermode interferometer |
| MFPI | MCF-based Fabry–Perot interferometer |
| MMI | MCF-based Michelson interferometers |
| MMZI | MCF-based Mach–Zehnder interferometer |
| SMF | Single-mode fiber |
| MMF | Multimode fiber |
| DCF | Dual-core fiber |
| TCF | Three-core fiber |
| SMS structure | SMF–MCF–SMF structure |
| SMF structure | SMF–MCF reflective structure |
| OPD | Optical path difference |
| FSR | Free spectrum range |
| FFT | Fast Fourier transform |
| PCF | Photonics crystal fiber |
References
- López-Higuera, J.M.; Cobo, L.R.; Incera, A.Q.; Cobo, A. Fiber optic sensors in structural health monitoring. J. Light. Technol. 2011, 29, 587–608. [Google Scholar] [CrossRef]
- Li, X.; Sun, Q.; Wo, J.; Zhang, M.; Liu, D. Hybrid TDM/WDM-based fiber-optic sensor network for perimeter intrusion detection. J. Light. Technol. 2011, 30, 1113–1120. [Google Scholar] [CrossRef]
- Daley, T.M.; Freifeld, B.M.; Ajo-Franklin, J.; Dou, S.; Pevzner, R.; Shulakova, V.; Kashikar, S.; Miller, D.E.; Goetz, J.; Henninges, J.; et al. Field testing of fiber-optic distributed acoustic sensing (DAS) for subsurface seismic monitoring. Lead. Edge 2013, 32, 699–706. [Google Scholar] [CrossRef]
- Inao, S.; Sato, T.; Sentsui, S.; Kuroha, T.; Nishimura, Y. Multicore optical fiber. In Proceedings of the 1979 Optical Fiber Communication Conference (OFC), Washington, DC, USA, 7 March 1979; p. WB1. [Google Scholar]
- Rugeland, P.; Margulis, W. Revisiting twin-core fiber sensors for high-temperature measurements. Appl. Opt. 2012, 51, 6227–6232. [Google Scholar] [CrossRef]
- Shao, M.; Han, L.; Sun, H.; Yin, X.; Qiao, X. A liquid refractive index sensor based on 3-core fiber Michelson interferometer. Opt. Commun. 2019, 453, 1–6. [Google Scholar] [CrossRef]
- Tan, F.; Liu, Z.; Tu, J.; Yu, C.; Lu, C.; Tam, H.-Y. Stable torsion sensor with tunable sensitivity and rotation direction discrimination based on a tapered Trench-Assisted Multi Core Fiber. In Proceedings of the 2018 Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 11–15 March 2018; p. W1K.6. [Google Scholar]
- Zhao, Z.; Soto, M.A.; Tang, M.; Thevenaz, L. Distributed shape sensing using Brillouin scattering in multi-core fibers. Opt. Express 2016, 24, 25211–25223. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, K.; Matsuo, S. Multicore fiber technology. J. Light. Technol. 2016, 34, 55–66. [Google Scholar] [CrossRef]
- Zhou, A.; Li, G.; Zhang, Y.; Wang, Y.; Guan, C.; Yang, J.; Yuan, L. Asymmetrical Twin-Core Fiber Based Michelson Interferometer for Refractive Index Sensing. J. Light. Technol. 2011, 29, 2985–2991. [Google Scholar] [CrossRef]
- Gander, M.; Macrae, D.; Galliot, E.; McBride, R.; Jones, J.; Blanchard, P.; Burnett, J.; Greenaway, A.; Inci, M. Two-axis bend measurement using multicore optical fibre. Opt. Commun. 2000, 182, 115–121. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, X.; Yuan, L. Four-core fiber-based bending sensor. Front. Optoelectron. China 2009, 1, 231–236. [Google Scholar] [CrossRef]
- Ouyang, Y.; Guo, H.; Ouyang, X.; Zhao, Y.; Zheng, Z.; Zhou, C.; Zhou, A. An In-Fiber Dual Air-Cavity Fabry–Perot Interferometer for Simultaneous Measurement of Strain and Directional Bend. IEEE Sens. J. 2017, 17, 3362–3366. [Google Scholar] [CrossRef]
- Ouyang, Y.; Xu, X.; Zhao, Y.; Zhou, A.; Yuan, L. Temperature Compensated Refractometer Based on Parallel Fiber Fabry–Pérot Interferometers. IEEE Photonics Technol. Lett. 2018, 30, 1262–1265. [Google Scholar] [CrossRef]
- Amorebieta, J.; Ortega-Gomez, A.; Durana, G.; Fernandez, R.; Antonio-Lopez, E.; Schulzgen, A.; Zubia, J.; Amezcua-Correa, R.; Villatoro, J. Compact omnidirectional multicore fiber-based vector bending sensor. Sci. Rep. 2021, 11, 5989. [Google Scholar] [CrossRef]
- Villatoro, J. Phase-shifted modal interferometers for high-accuracy optical fiber sensing. Opt. Lett. 2019, 45, 21–24. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.; Tang, M.; Fu, S.; Wang, L.; Guo, N.; Jin, C.; Tam, H.Y.; Lu, C. Robust in-fiber spatial interferometer using multicore fiber for vibration detection. Opt. Express 2018, 26, 29629–29637. [Google Scholar] [CrossRef] [PubMed]
- Villatoro, J.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Interferometer based on strongly coupled multi-core optical fiber for accurate vibration sensing. Opt. Express 2017, 25, 25734–25740. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Yang, J.; Liu, Z.; Sun, J. In-fiber integrated Michelson interferometer. Opt. Lett. 2006, 31, 2692–2694. [Google Scholar] [CrossRef]
- Amorebieta, J.; Ortega-Gomez, A.; Durana, G.; Fernandez, R.; Antonio-Lopez, E.; Schulzgen, A.; Zubia, J.; Amezcua-Correa, R.; Villatoro, J. Highly sensitive multicore fiber accelerometer for low frequency vibration sensing. Sci. Rep. 2020, 10, 16180. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Z.; Shum, P.P.; Shao, X.; Wang, R.; Dinh, X.Q.; Fu, S.; Tong, W.; Tang, M. Directional torsion and temperature discrimination based on a multicore fiber with a helical structure. Opt. Express 2018, 26, 544–551. [Google Scholar] [CrossRef]
- Yuan, L.; Yang, J.; Liu, Z. A Compact Fiber-Optic Flow Velocity Sensor Based on a Twin-Core Fiber Michelson Interferometer. IEEE Sens. J. 2008, 8, 1114–1117. [Google Scholar] [CrossRef]
- Tian, Y.; Chai, Q.; Tan, T.; Mu, B.; Liu, Q.; Liu, Y.; Ren, J.; Zhang, J.; Oh, K.; Lewis, E.; et al. Directional Bending Sensor Based on a Dual Side-Hole Fiber Mach–Zehnder Interferometer. IEEE Photonics Technol. Lett. 2018, 30, 375–378. [Google Scholar] [CrossRef]
- Wei, G.; Jiang, Q. Needle Shape Sensing with Fabry-Perot Interferometers. IEEE Sens. J. 2021, 21, 22720–22727. [Google Scholar] [CrossRef]
- Duan, L.; Zhang, P.; Tang, M.; Wang, R.; Zhao, Z.; Fu, S.; Gan, L.; Zhu, B.; Tong, W.; Liu, D.; et al. Heterogeneous all-solid multicore fiber based multipath Michelson interferometer for high temperature sensing. Opt. Express 2016, 24, 20210–20218. [Google Scholar] [CrossRef]
- Cheng, S.; Hu, W.; Ye, H.; Wu, L.; Li, Q.; Zhou, A.; Yang, M.; Zhao, Q.; Guo, D. Tapered multicore fiber interferometer for ultra-sensitive temperature sensing with thermo-optical materials. Opt. Express 2021, 29, 35765–35775. [Google Scholar] [CrossRef]
- Fu, H.; Wang, Q.; Ding, J.; Zhu, Y.; Zhang, M.; Yang, C.; Wang, S. Fe2O3 nanotube coating micro-fiber interferometer for ammonia detection. Sens. Actuators B 2020, 303, 127186. [Google Scholar] [CrossRef]
- Dong, J.T.; Cheng, C.H.; Wu, C.; Li, J.; Guan, B.O. Highly sensitive optofluidic refractive index sensor based on a seven-liquid-core Teflon-cladding fiber. Opt. Express 2020, 28, 26218–26227. [Google Scholar] [CrossRef]
- Guzman-Sepulveda, J.R.; Guzman-Cabrera, R.; Torres-Cisneros, M.; Sanchez-Mondragon, J.J.; May-Arrioja, D.A. A highly sensitive fiber optic sensor based on two-core fiber for refractive index measurement. Sensors 2013, 13, 14200–14213. [Google Scholar] [CrossRef]
- Cranch, G.A.; Flockhart, G.M.H.; MacPherson, W.N.; Barton, J.S.; Kirkendall, C.K. Ultra-high-sensitivity two-dimensional bend sensor. Electron. Lett. 2006, 42, 520–522. [Google Scholar] [CrossRef]
- Budinski, V.; Donlagic, D. Miniature Twist/Rotation Fabry Perot Sensor Based on a Four-Core Fiber. Proceedings 2018, 2, 1–5. [Google Scholar]
- Liu, G.; Sheng, Q.; Hou, W.; Han, M. Optical fiber vector flow sensor based on a silicon Fabry-Perot interferometer array. Opt. Lett. 2016, 41, 4629–4632. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Jiang, Z.; Fu, S.; Tang, M.; Tong, W.; Liu, D. Femtosecond laser enabled selective micro-holes drilling on the multicore-fiber facet for displacement sensor application. Opt. Express 2019, 27, 10777–10786. [Google Scholar] [CrossRef]
- Ma, X.; Liu, B.; Cai, Y.; Jia, D.; Fu, B.; Xu, L.; Ma, J. Suppression of reverberations at fiber tips for optical ultrasound sensing. Opt. Lett. 2020, 45, 2526–2529. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, A.; Guo, H.; Zhao, Y.; Yuan, L. Highly sensitive vector curvature sensor based on a triple-core fiber interferometer. OSA Contin. 2019, 2, 1953–1963. [Google Scholar] [CrossRef]
- Zhou, A.; Zhang, Y.; Li, G.; Yang, J.; Wang, Y.; Tian, F.; Yuan, L. Optical refractometer based on an asymmetrical twin-core fiber Michelson interferometer. Opt. Lett. 2011, 36, 3221–3223. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, F.; Dai, Y.; Wenbin, H.; Abbas, L.G.; Parveen, R.; Ashraf, M.A. A weakly coupled multi-core fibre-based Michelson interferometer composed of an in-fibre coupler. Opto-Electron. Rev. 2021, 29, 117–125. [Google Scholar]
- Shao, M.; Zhang, R.; Gao, H.; Liu, Y.; Qiao, X.; Lin, Y. A High-Sensitivity Low-Temperature Sensor Based on Michelson Interferometer in Seven-Core Fiber. IEEE Photonics Technol. Lett. 2021, 33, 1293–1296. [Google Scholar] [CrossRef]
- Bertholds, A.; Dandliker, R. Determination of the Individual Strain-Optic Coefficients in Single-Mode Optical Fibers. J. Light. Technol. 1988, 6, 17–20. [Google Scholar] [CrossRef]
- Qu, H.; Yan, G.F.; Skorobogatiy, M. Interferometric fiber-optic bending/nano-displacement sensor using plastic dual-core fiber. Opt. Lett. 2014, 39, 4835–4838. [Google Scholar] [CrossRef]
- Blanchard, P.M.; Burnett, J.G.; Erry, G.; Greenaway, A.H.; Harrison, P.; Mangan, B.; Knight, J.; Russell, P.S.J.; Gander, M.; McBride, R. Two-dimensional bend sensing with a single, multi-core optical fibre. Smart Mater. Struct. 2000, 9, 132–140. [Google Scholar] [CrossRef]
- Peng, F.; Yang, J.; Li, X.; Yuan, Y.; Wu, B.; Zhou, A.; Yuan, L. In-fiber integrated accelerometer. Opt. Lett. 2011, 36, 2056–2058. [Google Scholar] [CrossRef] [PubMed]
- Tan, F.; Lyu, W.; Chen, S.; Liu, Z.; Yu, C. Contactless vital signs monitoring based on few-mode and multi-core fibers. Opto-Electron. Adv. 2020, 3, 190034. [Google Scholar] [CrossRef]
- Zhao, J.; Jia, D.; Nie, A.; Zhang, H.; Liu, T. Compact Vectorial Transverse Force Sensor Based on Two-Modal Interference in a Few-Mode Seven-Core Fiber. J. Light. Technol. 2020, 38, 2046–2052. [Google Scholar] [CrossRef]
- Zhao, Z.; Shen, L.; Dang, Y.; Lu, C.; Tang, M. Enabling long range distributed vibration sensing using multicore fiber interferometers. Opt. Lett. 2021, 46, 3685–3688. [Google Scholar] [CrossRef] [PubMed]
- Coompson, J.; Colalillo, A.; Twigg, S.; Wynne, R. Multicore photonic crystal fiber thermal sensors. In Proceedings of the IEEE Sensors 2010 Conference, Waikoloa, HI, USA, 1–4 November 2010; pp. 853–855. [Google Scholar]
- Tang, Z.; Lou, S.; Wang, X.; Zhang, W.; Yan, S.; Xing, Z. Using Mode Coupling Mechanism in Symmetrical Triple-Core Photonic Crystal Fiber for High Performance Strain Sensing. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 4500707. [Google Scholar] [CrossRef]
- De, M.; Gangopadhyay, T.K.; Singh, V.K. Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview. Sensors 2019, 19, 464. [Google Scholar] [CrossRef] [PubMed]
- Pinto, A.M.; Lopez-Amo, M. Photonic crystal fibers for sensing applications. J. Sens. 2012, 2012, 1–21. [Google Scholar] [CrossRef]
- Arman, H.; Olyaee, S. Photonic bandgap fiber-based gas sensor with high sensitivity and high birefringence. J. Comput. Electron. 2022, 21, 1357–1364. [Google Scholar] [CrossRef]
- MacPherson, W.; Gander, M.; McBride, R.; Jones, J.; Blanchard, P.; Burnett, J.; Greenaway, A.; Mangan, B.; Birks, T.; Knight, J. Remotely addressed optical fibre curvature sensor using multicore photonic crystal fibre. Opt. Commun. 2001, 193, 97–104. [Google Scholar] [CrossRef]
- Zhao, Y.; Cai, L.; Li, X.-G. Temperature-Insensitive Optical Fiber Curvature Sensor Based on SMF-MMF-TCSMF-MMF-SMF Structure. IEEE Trans. Instrum. Meas. 2017, 66, 141–147. [Google Scholar] [CrossRef]
- Ding, L.; Li, Y.; Zhou, C.; Hu, M.; Xiong, Y.; Zeng, Z. In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending. Sensors 2019, 19, 205. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, X. Four-beam single fiber optic interferometer and its sensing characteristics. Sens. Actuators A 2007, 138, 9–15. [Google Scholar] [CrossRef]
- Li, C.; Ning, T.; Zhang, C.; Li, J.; Zhang, C.; Wen, X.; Lin, H.; Pei, L. All-fiber multipath Mach-Zehnder interferometer based on a four-core fiber for sensing applications. Sens. Actuators A 2016, 248, 148–154. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Li, H.; Feng, G.; Yang, J. In-Line Mach–Zehnder Interferometric Sensor Based on a Seven-Core Optical Fiber. IEEE Sens. J. 2017, 17, 100–104. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y. Optical fiber curvature sensor based on MMF-SCF-MMF structure. Opt. Fiber Technol. 2018, 43, 1–5. [Google Scholar] [CrossRef]
- Li, C.; Ning, T.; Li, J.; Zhang, C.; Zhang, C.; Lin, H.; Pei, L. Fiber-Optic Laser Sensor Based on All-Fiber Multipath Mach–Zehnder Interferometer. IEEE Photonics Technol. Lett. 2016, 28, 1908–1911. [Google Scholar] [CrossRef]
- Silva, R.; Ferreira, M.; Kobelke, J.; Schuster, K.; Frazão, O. Simultaneous measurement of curvature and strain using a suspended multicore fiber. Opt. Lett. 2011, 36, 3939–3941. [Google Scholar] [CrossRef]
- Zhou, R.; Qiao, X.; Wang, R.; Chen, F.; Ma, W. An Optical Fiber Sensor Based on Lateral-Offset Spliced Seven-Core Fiber for Bending and Stretching Strain Measurement. IEEE Sens. J. 2020, 20, 5915–5920. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Z.; Qiu, Y.; Kong, L.; Lin, H.; Jia, C.; Chen, H.; Li, H. Highly sensitive optical fiber curvature sensor based on a seven-core fiber with a twisted structure. Appl. Opt. 2019, 58, 8776–8784. [Google Scholar] [CrossRef]
- Ji, Y.; Sun, D.; Chen, Y.; Shi, Y.; Cao, J.; Zhang, G.; Han, Z.; Wang, C.; Zhu, X. A High Sensitivity Curvature Sensor Based on Microfiber Mach-Zehnder Interferometer with Tapered Seven-Core Fiber. IEEE Sens. J. 2021, 21, 24090–24097. [Google Scholar] [CrossRef]
- Harhira, A.; Santos, J.L.; Lapointe, J.; Culshaw, B.; López-Higuera, J.M.; Kashyap, R.; MacPherson, W.N. High sensitivity inline fiber Mach-Zehnder interferometer bend sensor using a twin core fiber. In Proceedings of the Fourth European Workshop on Optical Fibre Sensors, Porto, Portugal, 8–10 September 2010. [Google Scholar]
- Frazao, O.; Silva, S.F.O.; Viegas, J.; Baptista, J.M.; Santos, J.L.; Kobelke, J.; Schuster, K. All Fiber Mach–Zehnder Interferometer Based on Suspended Twin-Core Fiber. IEEE Photonics Technol. Lett. 2010, 22, 1300–1302. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Zhang, W.; Kong, L.; Li, Z.; Chen, G.; Yang, J.; Kang, X.; Yan, T. Two-dimensional microbend sensor based on the 2-core fiber with hump-shaped taper fiber structure. Opt. Fiber Technol. 2019, 52, 101948. [Google Scholar] [CrossRef]
- Yang, J.; Guan, C.; Zhang, J.; Wang, M.; Yang, M.; Zhu, Z.; Wang, P.; Yang, J.; Yuan, L. Low-temperature crosstalk and surrounding refractive index insensitive vector bending sensor based on hole-assistant dual-core fiber. Appl. Opt. 2019, 58, 6597–6603. [Google Scholar] [CrossRef] [PubMed]
- Yin, G.; Zhang, F.; Xu, B.; He, J.; Wang, Y. Intensity-modulated bend sensor by using a twin core fiber: Theoretical and experimental studies. Opt. Express 2020, 28, 14850–14858. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, W.; Chen, L.E.I.; Zhang, Y.; Geng, P.; Wang, B.; Yan, T.; Li, Y.; Hu, W. Bending Vector Sensor Based on the Multimode-2-Core-Multimode Fiber Structure. IEEE Photonics Technol. Lett. 2016, 28, 2066–2069. [Google Scholar] [CrossRef]
- Guan, C.; Zhong, X.; Mao, G.; Yuan, T.; Yang, J.; Yuan, L. In-Line Mach–Zehnder Interferometric Sensor Based on a Linear Five-Core Fiber. IEEE Photonics Technol. Lett. 2015, 27, 635–638. [Google Scholar] [CrossRef]
- Berghmans, F.; Mignani, A.G.; Gökbulut, B.; Inci, M.N. An interferometric vibration sensor based on a four-core optical fiber. In Proceedings of the Optical Sensing and Detection IV, Brussels, Belgium, 3–7 April 2016. [Google Scholar]
- Cai, L.; Pan, J.; Yue, P.; Zhong, N. Theoretical analysis and application of MTM fiber structure based low-frequency vibration sensor. Optik 2019, 195, 163161. [Google Scholar] [CrossRef]
- Tan, F.; Liu, Z.; Tu, J.; Yu, C.; Lu, C.; Tam, H.Y. Torsion sensor based on inter-core mode coupling in seven-core fiber. Opt. Express 2018, 26, 19835–19844. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, Y.; Du, B.; Wang, T.; Feng, D.; Jiang, B.; Yang, D. Strain-insensitive twist and temperature sensor based on seven-core fiber. Sens. Actuators A 2019, 290, 172–176. [Google Scholar] [CrossRef]
- Wang, X.; Qiao, X.; Yu, D.; Gao, H.; Fan, W. Fiber-optic sensor implanted with seven-core helical structure for measurement of tensile strain and extrusion bending. Opt. Eng. 2019, 58, 046111. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Z.; Shum, P.P.; Dinh, X.Q.; Low, C.W.; Xu, Z.; Wang, R.; Shao, X.; Fu, S.; Tong, W.; et al. Highly sensitive strain sensor based on helical structure combined with Mach-Zehnder interferometer in multicore fiber. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Zhan, X.; Liu, Y.; Tang, M.; Ma, L.; Wang, R.; Duan, L.; Gan, L.; Yang, C.; Tong, W.; Fu, S.; et al. Few-mode multicore fiber enabled integrated Mach-Zehnder interferometers for temperature and strain discrimination. Opt. Express 2018, 26, 15332–15342. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Wang, T.; Liu, C.; Feng, D.; Jiang, B.; Yang, D.; Zhao, J. Simultaneous measurement of refractive index and temperature with high sensitivity based on a multipath fiber Mach-Zehnder interferometer. Appl. Opt. 2019, 58, 4085–4090. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ning, T.; Li, J.; Zheng, J.; Gao, X.; Lin, H.; Pei, L. Etching twin core fiber for the temperature-independent refractive index sensing. J. Opt. 2018, 20, 045802. [Google Scholar] [CrossRef]
- Duan, S.; Liu, B.; Zhang, H.; Zhang, X.; Liu, H.; Wu, J.; Yao, Y. Intensity-interrogated refractive index sensor based on exposed-core multicore fiber Mach-Zehnder interferometer. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; p. SF3L.7. [Google Scholar]
- Al-Mashhadani, Z.A.A.; Navruz, I. Highly sensitive measurement of surrounding refractive index using tapered trench-assisted multicore fiber. Opt. Fiber Technol. 2019, 48, 76–83. [Google Scholar] [CrossRef]
- Shao, Z.; Qiao, X.; Rong, Q. Compact gas refractometer based on a tapered four-core fiber. Appl. Opt. 2018, 57, 10198–10206. [Google Scholar] [CrossRef]
- Guo, D.; Wu, L.; Yu, H.; Zhou, A.; Li, Q.; Mumtaz, F.; Du, C.; Hu, W. Tapered multicore fiber interferometer for refractive index sensing with graphene enhancement. Appl. Opt. 2020, 59, 3927–3932. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, J.; Feng, Q.; Zhang, X.; Liu, Y.; Han, Y. A Novel High Sensitivity Refractive Index Sensor Based on Multi-Core Micro/Nano Fiber. Photonic Sens. 2019, 9, 197–204. [Google Scholar] [CrossRef]
- Zhang, C.; Ning, T.; Li, J.; Pei, L.; Li, C.; Lin, H. Refractive index sensor based on tapered multicore fiber. Opt. Fiber Technol. 2017, 33, 71–76. [Google Scholar] [CrossRef]
- Cheng, P.; Yang, M.; Hu, W.; Guo, D.; Du, C.; Luo, X.; Mumtaz, F. Refractive index interferometer based on SMF-MMF-TMCF-SMF structure with low temperature sensitivity. Opt. Fiber Technol. 2020, 57, 102233. [Google Scholar] [CrossRef]
- Guzman-Sepulveda, J.R.; Ruiz-Perez, V.I.; Torres-Cisneros, M.; Sanchez-Mondragon, J.J.; May-Arrioja, D.A. Fiber Optic Sensor for High-Sensitivity Salinity Measurement. IEEE Photonics Technol. Lett. 2013, 25, 2323–2326. [Google Scholar] [CrossRef]
- Chunxia, Y.; Hui, D.; Wei, D.; Chaowei, X. Weakly-coupled multicore optical fiber taper-based high-temperature sensor. Sens. Actuators A 2018, 280, 139–144. [Google Scholar] [CrossRef]
- Mumtaz, F.; Cheng, P.; Li, C.; Cheng, S.; Du, C.; Yang, M.; Dai, Y.; Hu, W. A Design of Taper-Like Etched Multicore Fiber Refractive Index-Insensitive a Temperature Highly Sensitive Mach-Zehnder Interferometer. IEEE Sens. J. 2020, 20, 7074–7081. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Meng, F.; Lou, X.; Zhu, L. All-fiber MZI sensor based on seven-core fiber and fiber ball symmetrical structure. Opt. Lasers Eng. 2019, 112, 1–6. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, M.; Fu, S.; Liu, S.; Wei, H.; Cheng, Y.; Tong, W.; Shum, P.P.; Liu, D. All-solid multi-core fiber-based multipath Mach–Zehnder interferometer for temperature sensing. Appl. Phys. B Lasers Opt. 2013, 112, 491–497. [Google Scholar] [CrossRef]
- Yue, C.; Ding, H.; Liu, X. Magnetic-Field Measurement Based on Multicore Fiber Taper and Magnetic Fluid. IEEE Trans. Instrum. Meas. 2019, 68, 688–692. [Google Scholar] [CrossRef]
- Xia, C.; Bai, N.; Ozdur, I.; Zhuo, X.; Li, G. Supermodes for optical transmission. Opt. Express 2011, 19, 16653–16664. [Google Scholar] [CrossRef]
- Villatoro, J.; Van Newkirk, A.; Antonio-Lopez, E.; Zubia, J.; Schulzgen, A.; Amezcua-Correa, R. Ultrasensitive vector bending sensor based on multicore optical fiber. Opt. Lett. 2016, 41, 832–835. [Google Scholar] [CrossRef]
- Kalli, K.; Mendez, A.; Villatoro, J.; Antonio-Lopez, E.; Van Newkirk, A.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Supersensitive sensors based on multicore optical fibres. In Proceedings of the Micro-Structured and Specialty Optical Fibres IV, Prague, Czech Republic, 15–16 April 2015. [Google Scholar]
- Guzman-Sepulveda, J.R.; May-Arrioja, D.A. In-fiber directional coupler for high-sensitivity curvature measurement. Opt. Express 2013, 21, 11853–11861. [Google Scholar] [CrossRef]
- Salceda-Delgado, G.; Van Newkirk, A.; Antonio-Lopez, J.E.; Martinez-Rios, A.; Schulzgen, A.; Amezcua Correa, R. Compact fiber-optic curvature sensor based on super-mode interference in a seven-core fiber. Opt. Lett. 2015, 40, 1468–1471. [Google Scholar] [CrossRef]
- Van Newkirk, A.; Eznaveh, Z.S.; Antonio-Lopez, E.; Salceda-Delgado, G.; Schülzgen, A.; Amezcua-Correa, R. High temperature sensor based on supermode interference in multicore fiber. In Proceedings of the 2014 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 8–13 June 2014; p. SM2N.7. [Google Scholar]
- Antonio-Lopez, J.E.; Eznaveh, Z.S.; LiKamWa, P.; Schulzgen, A.; Amezcua-Correa, R. Multicore fiber sensor for high-temperature applications up to 1000 degrees C. Opt. Lett. 2014, 39, 4309–4312. [Google Scholar] [CrossRef]
- Wales, M.D.; Clark, P.; Thompson, K.; Wilson, Z.; Wilson, J.; Adams, C. Multicore fiber temperature sensor with fast response times. OSA Contin. 2018, 1, 764–771. [Google Scholar] [CrossRef]
- Amorebieta, J.; Ortega-Gomez, A.; Fernández, R.; Antonio-Lopez, E.; Schülzgen, A.; Zubia, J.; Amezcua-Correa, R.; Durana, G.; Villatoro, J. Sensitivity-optimized strongly coupled multicore fiber-based thermometer. Opt. Laser Technol. 2022, 145, 107532. [Google Scholar] [CrossRef]
- Amorebieta, J.; Durana, G.; Ortega-Gomez, A.; Fernandez, R.; Velasco, J.; Saez de Ocariz, I.; Zubia, J.; Antonio-Lopez, J.E.; Schulzgen, A.; Amezcua-Correa, R.; et al. Packaged Multi-Core Fiber Interferometer for High-Temperature Sensing. J. Light. Technol. 2019, 37, 2328–2334. [Google Scholar] [CrossRef]
- Antonio-Lopez, E.; Salceda-Delgado, G.; Van Newkirk, A.; Schülzgen, A.; Amezcua-Correa, R. Multiplexed high temperature sensor based on multicore fiber. In Proceedings of the Advanced Photonics, Barcelona, Spain, 27–31 July 2014 ; p. SeW4C. [Google Scholar]
- Cuando-Espitia, N.; Fuentes-Fuentes, M.A.; Velazquez-Benitez, A.; Amezcua, R.; Hernandez-Cordero, J.; May-Arrioja, D.A. Vernier effect using in-line highly coupled multicore fibers. Sci. Rep. 2021, 11, 18383. [Google Scholar] [CrossRef] [PubMed]
- Van Newkirk, A.; Antonio-Lopez, E.; Salceda-Delgado, G.; Amezcua-Correa, R.; Schulzgen, A. Optimization of multicore fiber for high-temperature sensing. Opt. Lett. 2014, 39, 4812–4815. [Google Scholar] [CrossRef]
- May-Arrioja, D.A.; Guzman-Sepulveda, J.R. Highly Sensitive Fiber Optic Refractive Index Sensor Using Multicore Coupled Structures. J. Light. Technol. 2017, 35, 2695–2701. [Google Scholar] [CrossRef]
- Flores-Bravo, J.A.; Fernandez, R.; Antonio Lopez, E.; Zubia, J.; Schulzgen, A.; Amezcua Correa, R.; Villatoro, J. Simultaneous Sensing of Refractive Index and Temperature with Supermode Interference. J. Light. Technol. 2021, 39, 7351–7357. [Google Scholar] [CrossRef]
- Vallés, J.A.; Benedicto, D. Optimized active multicore fiber bending sensor. Opt. Mater. 2019, 87, 53–57. [Google Scholar] [CrossRef]
- Capilla-Gonzalez, G.; May-Arrioja, D.A.; Lopez-Cortes, D.; Guzman-Sepulveda, J.R. Stress homogenization effect in multicore fiber optic bending sensors. Appl. Opt. 2017, 56, 2273–2279. [Google Scholar] [CrossRef]
- Newkirk, A.V.; Antonio-Lopez, J.E.; Velazquez-Benitez, A.; Albert, J.; Amezcua-Correa, R.; Schulzgen, A. Bending sensor combining multicore fiber with a mode-selective photonic lantern. Opt. Lett. 2015, 40, 5188–5191. [Google Scholar] [CrossRef]
- Salceda-Delgado, G.; Van-Newkirk, A.; Lopez, J.A.; Schülzgen, A.; Correa, R.A. Optical fiber curvature sensors based on single mode-7 core-single mode fiber structures. In Proceedings of the Advanced Photonics, Barcelona, Spain, 27–31 July 2014; p. SeW3C.2. [Google Scholar]
- Villatoro, J.; Amorebieta, J.; Ortega-Gomez, A.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Composed multicore fiber structure for direction-sensitive curvature monitoring. APL Photonics 2020, 5, 070801. [Google Scholar] [CrossRef]
- Arrizabalaga, O.; Sun, Q.; Beresna, M.; Lee, T.; Zubia, J.; Velasco Pascual, J.; Saez de Ocariz, I.; Schulzgen, A.; Antonio-Lopez, J.E.; Amezcua-Correa, R.; et al. High-performance vector bending and orientation distinguishing curvature sensor based on asymmetric coupled multi-core fibre. Sci. Rep. 2020, 10, 14058. [Google Scholar] [CrossRef] [PubMed]
- Villatoro, J.; Antonio-Lopez, E.; Schulzgen, A.; Amezcua-Correa, R. Miniature multicore optical fiber vibration sensor. Opt. Lett. 2017, 42, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Villatoro, J.; Flores-Bravo, J.; Arrospide, E.; Arrizabalaga, O.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Packaged Multi-core Fiber Interferometric Vibration Sensor. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; p. SM2K.6. [Google Scholar]
- Villatoro, J.; Arrizabalaga, O.; Antonio-Lopez, E.; Zubia, J.; de Ocáriz, I.S. Multicore fiber sensors. In Proceedings of the 2017 Optical Fiber Communication Conference (OFC), Los Angeles, CA, USA, 19–23 March 2017; p. Th3H.1. [Google Scholar]
- Villatoro, J.; Ortega-Gomez, A.; Zubia, J.; Antonio-Lopez, E.; Schülzgen, A.; Amezcua-Correa, R. Ultrasensitive vibration sensor based on an asymmetric multi-core optical fiber. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Lausanne, Switzerland, 24–28 September 2018. [Google Scholar]
- Villatoro, J.; Arrizabalaga, O.; Diez, M.; Arrospide, E.; Antonio-Lopez, E.; Zubia, J.; Schülzgen, A.; Amezcua-Correa, R. Simple Multi-core Optical Fiber Accelerometer. In Proceedings of the Advanced Photonics Congress Optical Sensors 2018, ETH, Zürich, Switzerland, 2–5 July 2018. [Google Scholar]
- Villatoro, J.; Arrizabalaga, O.; Durana, G.; Saez de Ocariz, I.; Antonio-Lopez, E.; Zubia, J.; Schulzgen, A.; Amezcua-Correa, R. Accurate strain sensing based on super-mode interference in strongly coupled multi-core optical fibres. Sci. Rep. 2017, 7, 4451. [Google Scholar] [CrossRef] [PubMed]
- Van Newkirk, A.; Antonio-Lopez, J.E.; Salceda-Delgado, G.; Piracha, M.U.; Amezcua-Correa, R.; Schulzgen, A. Multicore Fiber Sensors for Simultaneous Measurement of Force and Temperature. IEEE Photonics Technol. Lett. 2015, 27, 1523–1526. [Google Scholar] [CrossRef]




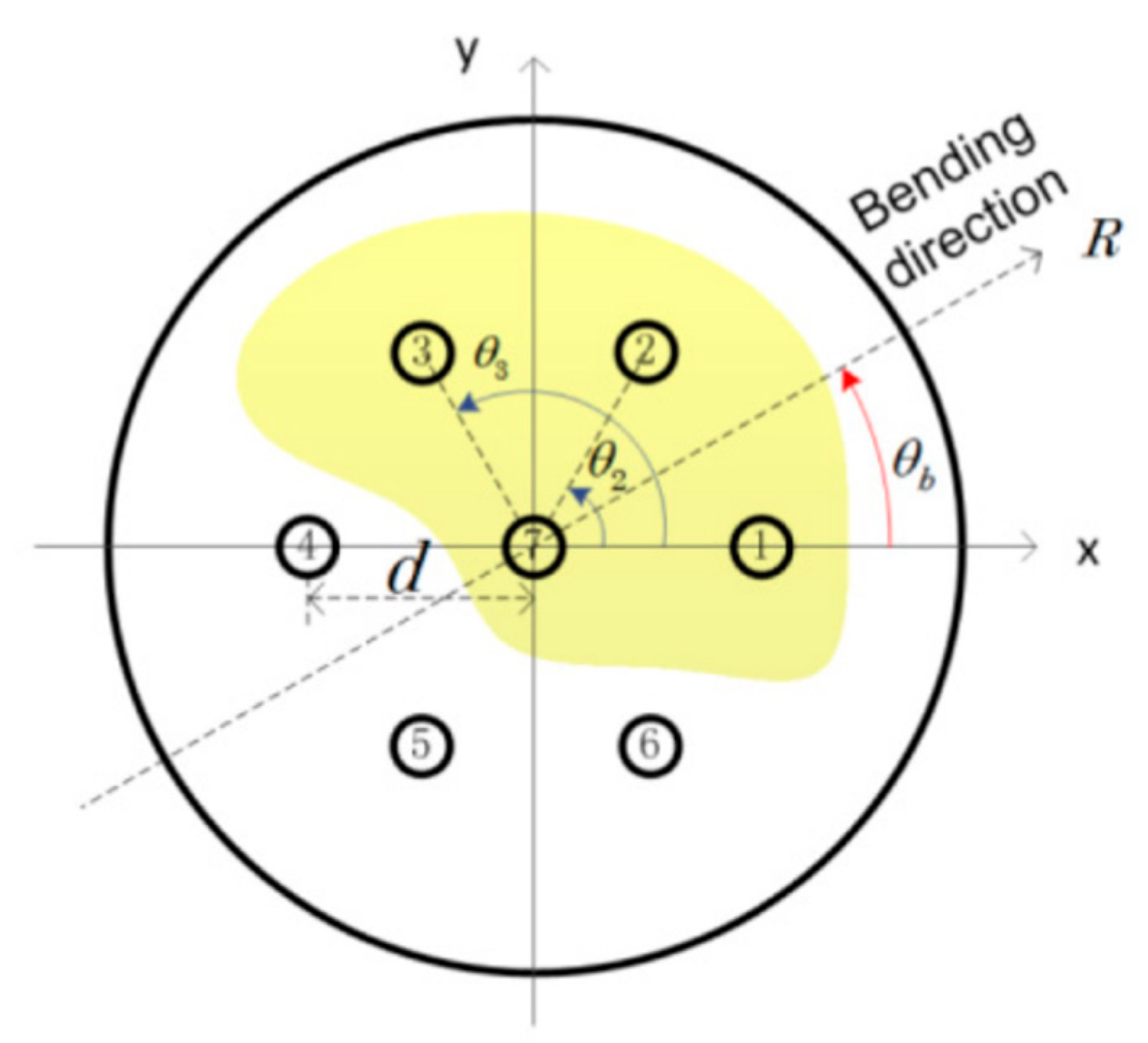
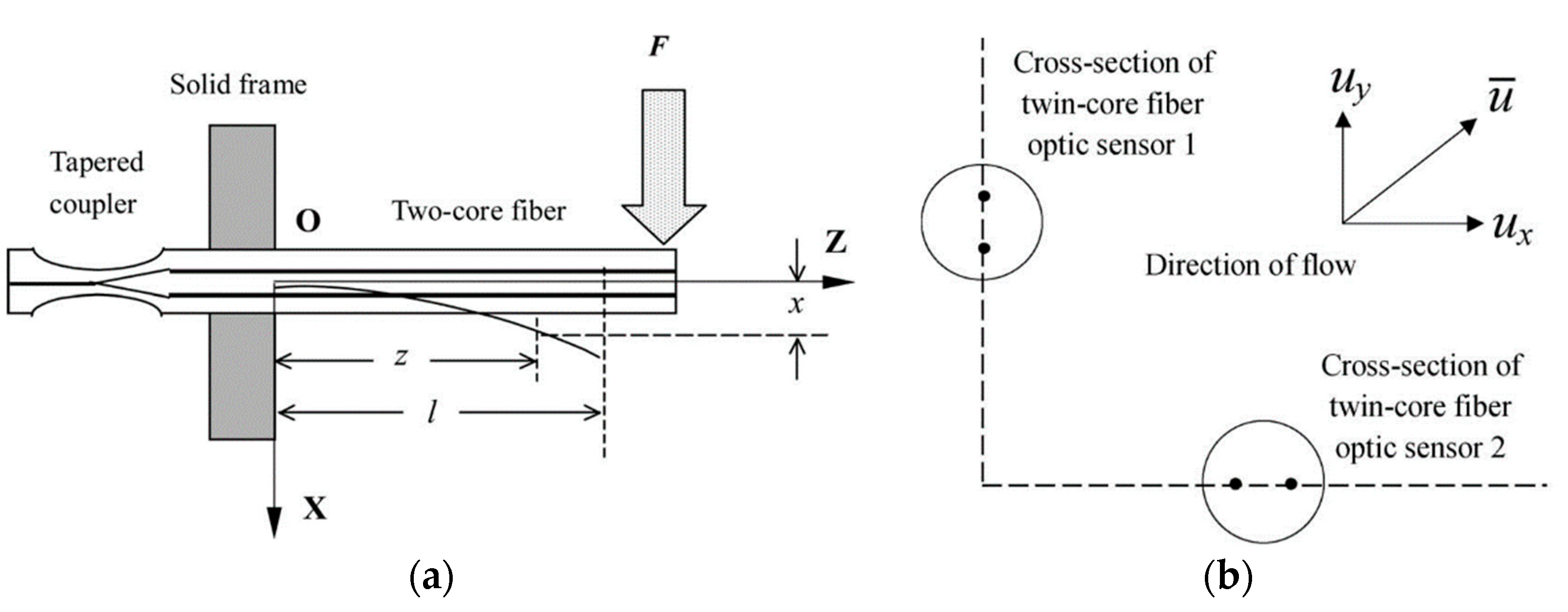

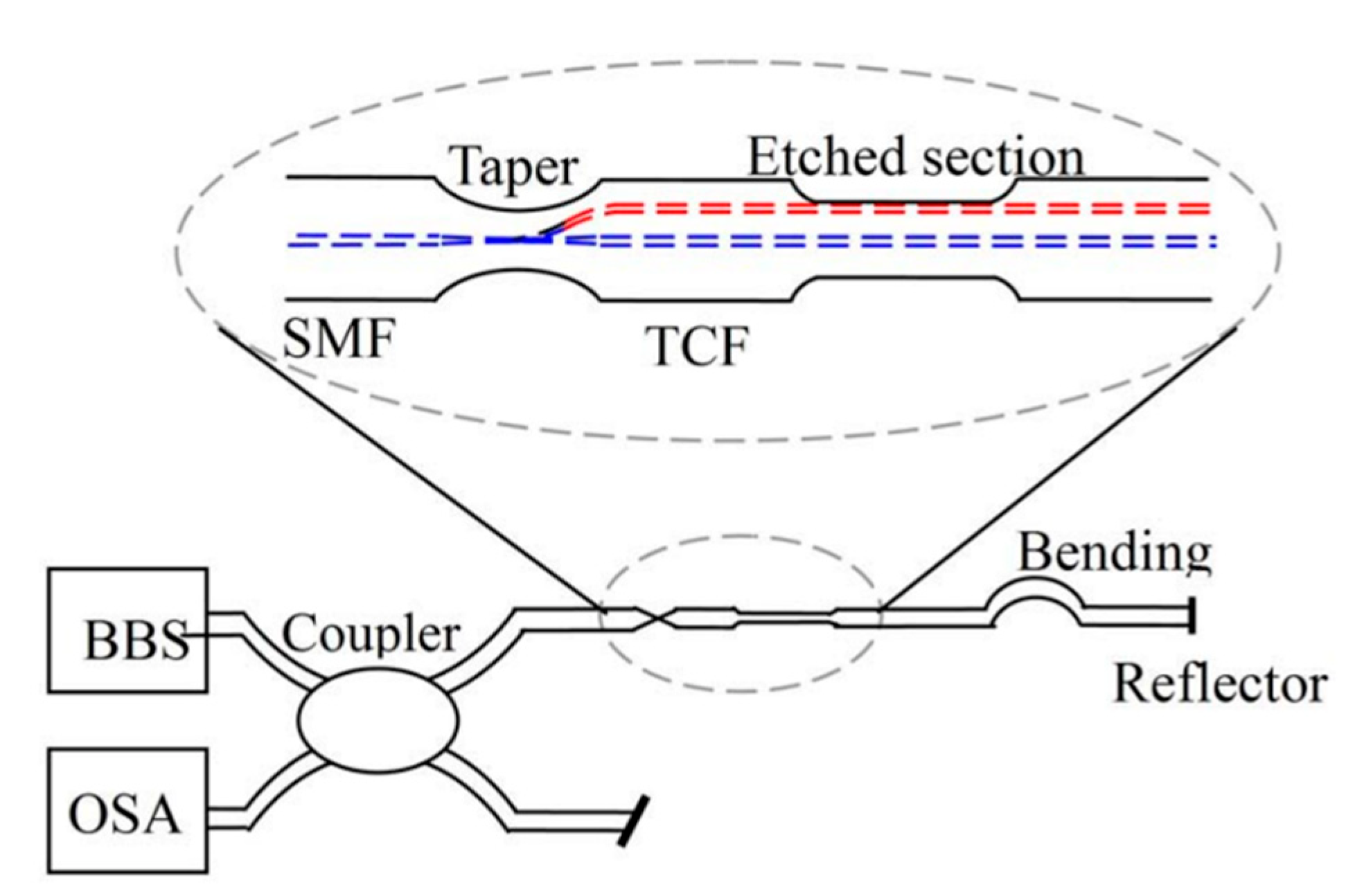

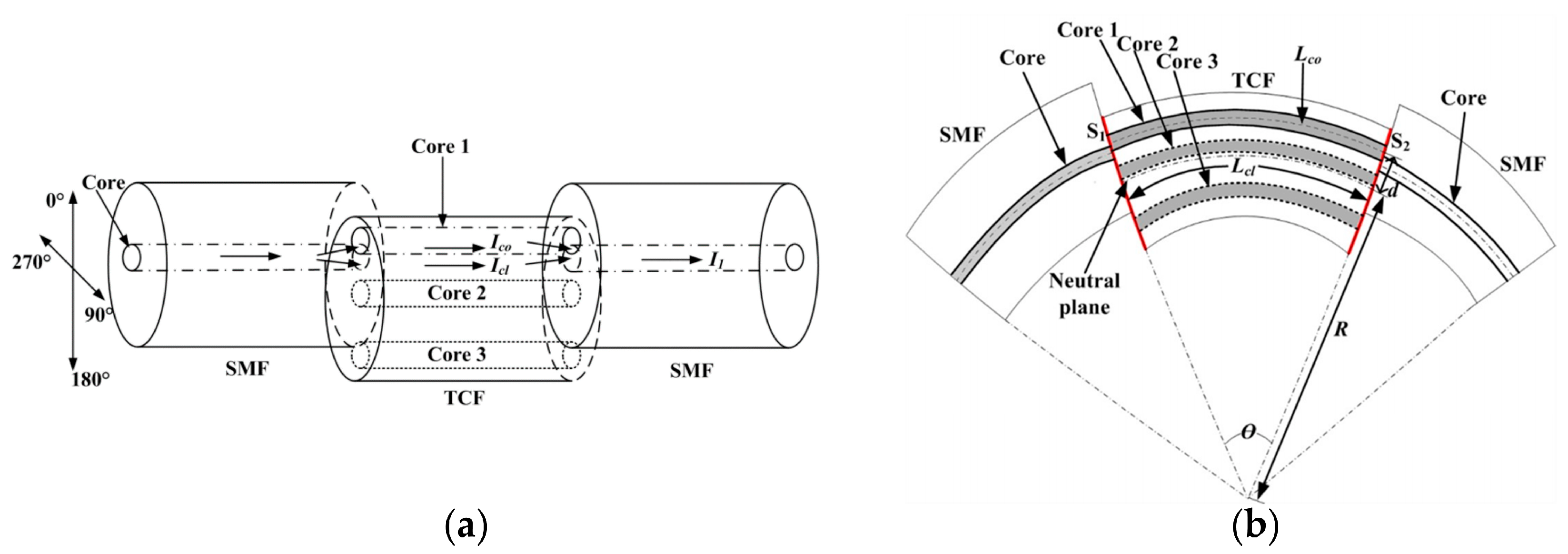


| Sensor Structure | Sensitivity (nm/m−1) | Applications | REF. |
|---|---|---|---|
| Four-core MCF MI | ― | Omnidirectional curvature sensing | [11] |
| Dual air-cavity FPI * | 242.5 pm/m−1 | Simultaneous measurement of strain and curvature | [13] |
| Asymmetrical three-core fiber SMI | 507 pm/° and 587 nW/° | Bending angle and direction sensing | [15] |
| Three parallel FPIs | ― * | 3D shape sensing in mini-invasive surgery | [24] |
| Tapered dual-core fiber MI * | ― | Flow velocity sensing | [22] |
| Tapered three-core fiber MI | −95.22 pm/m−1 | Curvature sensing | [35] |
| Plastic dual-core fiber MI | ― | Nano-displacement/curvature sensing | [40] |
| Three-core PCF MI | ― | Omnidirectional curvature sensing | [41] |
| MMF-coupled three-core fiber MZI * | −28.29 | Low-temperature crosstalk curvature measurement | [52] |
| Lateral offset-spliced three-core fiber MZI | −20.48 | Biomedical sensing equipment | [53] |
| MMF-coupled seven-core fiber MZI | 31.54 | Curvature measurement sensing | [56] |
| MMF-coupled seven-core fiber MZI | 41.46 | Temperature and curvature sensing | [57] |
| Four-core fiber MZI | 2.55 | Strain, refractive index, and curvature | [58] |
| Lateral offset-spliced seven-core fiber MZI | 25.96 | Strain and curvature sensing | [60] |
| Twisted seven-core fiber MZI | −25.16 | Structural health monitoring | [61] |
| Tapered seven-core fiber MZI | 174.03 nm/m−1 | Low-temperature crosstalk bending measurement | [62] |
| Dual-core fiber MZI | 1.52 | Large curvature measurement | [63] |
| Hump-shaped dual-core fiber MZI | −6.18 | Directional curvature measurement | [65] |
| Hole-assistant dual-core fiber MZI | −15.95 | Low-temperature/refractive index crosstalk vector-bending sensor | [66] |
| Asymmetrical dual-core fiber MZI | 12.98 | Directional curvature measurement | [68] |
| Asymmetrical three-core fiber SMI * | 4094 pm/° and 1.99 nm/m−1 | Bending angle and orientation sensing | [93] |
| Asymmetrical dual-core fiber SMI | −137.88 | Small curvature with high sensitivity | [95] |
| Seven-core fiber SMI | 3000 nm/mm−1 | Structural monitoring | [96] |
| Two asymmetrical three-core fiber SMIs | 4.66 dB/m−1 | Directional bending measurement and vibrations, force, pressure, etc. | [111] |
| Femtosecond laser-writing-modified seven-core fiber SMI | 1.4 nm/° and 17.5 nm/m−1 | Omnidirectional curvature and small bending angle measurement | [112] |
| Sensor Structure | Range | Applications | REF. |
|---|---|---|---|
| Phase-shifted modal interferometers | 1–1050 Hz | Various vibration measurements | [16] |
| MI* composed of seven-core fan-in coupler | 1 kHz–12 kHz | Long-distance vibration measurement | [17] |
| Seven-core fiber SMI | 2–2500 Hz | A variety of practical applications | [18] |
| Phase-shifted modal interferometers | 1 mHz–30 Hz/0.76 mg–29.64 mg (acceleration) | Accelerometers | [20] |
| Dual-core fiber MI | Below 500 Hz | Accelerometers | [42] |
| Dual-core fiber MZI*/Seven-core fiber MZI | Heartbeat rate (69–100 bpm)/respiration rate (9–12 bpm) | Contactless vital signs monitoring for healthcare | [43] |
| Two counter-propagating MZIs in a 38.5 km seven-core fiber | ― * | Long-distance distributed vibration location sensing | [45] |
| Four-core fiber MZI | Only demonstrated 100 Hz vibration sensing | Optical vibration sensor | [70] |
| Three-core fiber MZI | 1–20 Hz | Long-term monitoring of construction and mechanical structures | [71] |
| Seven-core fiber SMI * | 40–760 Hz in experiment and 50 Hz–25 KHz in theory | Diverse vibration sensing applications | [113] |
| Packaged seven-core fiber SMI | 30–240 Hz | Low-frequency vibration sensing | [114] |
| Seven-core fiber SMI | 60–290 Hz | Commercial vibration sensing applications | [115] |
| Three-core fiber SMI | 5–100 Hz | Low-frequency and low-amplitude seismic sensing | [116] |
| Seven-core fiber SMI | 5–50 Hz/0.00 g–0.04 g (acceleration) | Low-frequency accelerometers | [117] |
| Sensor Structure | Sensitivity (pm/°C) | Range (°C) | REF. |
|---|---|---|---|
| Seven-core fiber MI with spherical reflective structure | 165 | Up to 900 | [25] |
| Tapered seven-core fiber MZI with thermo-optical materials covered | Up to 25 nm/°C | 10–50 | [26] |
| Fiber-ball-coupled seven-core fiber MI * | 70.6 | 20–90 | [37] |
| Seven-core fiber MZI * | 59.02 | 22–55 | [57] |
| Lateral offset-fused seven-core few-mode fiber MZI | 223.6 | 20–60 | [76] |
| Tapered seven-core fiber MZI | 36.8 | Up to 1000 | [87] |
| Tapered seven-core fiber MZI | 89.19 | 24–130 | [88] |
| Seven-core fiber MZI coupled with fiber ball | 76.38 | 50–130 | [89] |
| Lateral offset-fused seven-core fiber MZI | 130.6 | 25–85 | [90] |
| Seven-core fiber SMI * | 48 | Up to 1000 | [97] |
| Seven-core fiber SMI | 52 | Up to 1000 | [98] |
| Reflective seven-core fiber SMI | 35 | 72–351 | [99] |
| Three-core fiber SMI | 29.426 | −25–900 | [100] |
| Sensor Structure | Sensitivity (nm/RIU) | Range (RIU) | REF. |
|---|---|---|---|
| Three-core fiber MI * | −151.56 dB/RIU | 1.3335–1.3720 | [6] |
| Cladding etched asymmetrical dual-core fiber MI | 270 | 1.34–1.38 | [10] |
| Parallel dual FPI * | 1096.9 | About 1.34–1.37 | [14] |
| Four-core fiber MZI * | 113.27 | 1.3353–1.3549 | [58] |
| Cladding etched asymmetrical dual-core fiber MZI | 3119 | 1.3160–1.3943 | [29] |
| Cladding etched seven-core fiber MZI | −1802.26 | 1.427–1.442 | [77] |
| Exposed-core seven-core fiber MZI | −287.252 dB/RIU | 1.3364–1.3679 | [79] |
| Tapered seven-core fiber MZI | 35089.28 | 1.4430–1.4442 | [80] |
| Tapered seven-core fiber MZI | 1280.94 dB/RIU | About 1.0005–1.0030 | [81] |
| Tapered seven-core fiber MZI with graphene-coating | 9194.6 | 1.4264–1.4278 | [82] |
| Tapered micro-three-core fiber MZI | 5815.50 | About 1.332–1.341 | [83] |
| Tapered four-core fiber MZI | 171.2 | 1.3448–1.3774 | [84] |
| Tapered seven-core fiber MZI | 1435.76 | 1.3330–1.3451 | [85] |
| Cladding etched seven-core fiber MZI | On the order of 104 | About 1.448–1.4476 | [105] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Zhao, Z.; Tang, M. Advances in Multicore Fiber Interferometric Sensors. Sensors 2023, 23, 3436. https://doi.org/10.3390/s23073436
Yao Y, Zhao Z, Tang M. Advances in Multicore Fiber Interferometric Sensors. Sensors. 2023; 23(7):3436. https://doi.org/10.3390/s23073436
Chicago/Turabian StyleYao, Yucheng, Zhiyong Zhao, and Ming Tang. 2023. "Advances in Multicore Fiber Interferometric Sensors" Sensors 23, no. 7: 3436. https://doi.org/10.3390/s23073436
APA StyleYao, Y., Zhao, Z., & Tang, M. (2023). Advances in Multicore Fiber Interferometric Sensors. Sensors, 23(7), 3436. https://doi.org/10.3390/s23073436








