Abstract
This paper addresses the simultaneous localization and guidance of two underwater hexapod robots under sea currents. This paper considers an underwater environment where there are no landmarks or features which can assist a robot’s localization. This article uses two underwater hexapod robots that move together while using each other as landmarks in the environment. While one robot moves, another robot extends its legs into the seabed and acts as a static landmark. A moving robot measures the relative position of another static robot, in order to estimate its position while it moves. Due to underwater currents, a robot cannot maintain its desired course. Moreover, there may be obstacles, such as underwater nets, that a robot needs to avoid. We thus develop a guidance strategy for avoiding obstacles, while estimating the perturbation due to the sea currents. As far as we know, this paper is novel in tackling simultaneous localization and guidance of underwater hexapod robots in environments with various obstacles. MATLAB simulations demonstrate that the proposed methods are effective in harsh environments where the sea current magnitude can change irregularly.
1. Introduction
In recent years, various autonomous unmanned robots have been developed for military, environmental and robotic research applications. Consider a scenario where autonomous underwater robots are deployed to approach a predefined goal while avoiding collision with obstacles, such as underwater nets. This scenario is feasible for a large variety of marine tasks, such as underwater construction, oceanographic surveys, coastal patrol, seabed and bathymetric data collection [1,2].
The localization of an underwater robot in deep water is not trivial, since the signal of Global Positioning Systems (GPS) cannot reach a robot in deep water. Doppler Velocity Logs (DVL) and Inertial Measurement Units (IMU) can be used to localize an underwater vehicle. However, the localization error using these sensors increases gradually as the travel distance of the robot increases [3]. This error integration is inevitable since the position estimation can be derived by integrating velocity measurements of DVL or integrating acceleration measurement of IMU twice. Moreover, DVL cannot be used for localization of a robot that crawls on the sea bottom.
Simultaneous localization and mapping (SLAM) was widely used to build a map of an unknown environment while simultaneously keeping track of an agent’s location within it. In SLAM, a robot keeps storing its trajectory, odometry information sequence, and observation information sequence. Then, graph-based optimization is used to update both the robot pose and the feature map, based on the stored information. As a robot explores a large outdoor environment, stored data increases and the computational load of the optimization increases. Therefore, the overall computational load of SLAM increases, as the robot travels a longer distance. It is thus argued that SLAM may not be preferred as a robot with small embedded computers explores a large outdoor environment, such as a seabed.
Various Visual-Inertial SLAM (VI-SLAM) methods [4,5,6] have been applied for robot localization. The authors of [7] review various papers on VI-SLAM. VI-SLAM applied both a camera and an IMU for robot localization [4,5]. VI-SLAM methods require the calculation of the 6-DOF transformation between the camera and the IMU. However, calculating this transformation is computationally expensive [8]. Any SLAM method requires that a robot can extract features, such as corners of the obstacles, from the environment [6,9,10,11].
Unknown underwater environments, where unknown sea currents exist in the deep sea, are considered in this paper. A hexapod robot [12] is utilized, which can extend its leg into the sea bottom. Once a hexapod robot extends its leg into the sea bottom, it can stay still while overcoming underwater currents. The hexapod robot in [12] mimics the design of crabs and lobsters that live in stormy waters but are still able to control their movements. This paper handles the localization of an underwater hexapod robot with small embedded computers, whose mission is to explore a large seabed. A practical scenario is considered, where it is difficult for an underwater robot to derive stable features of the underwater environment. For instance, it is common for an underwater robot’s vision sensors to have low visibility due to dust in water. In addition, an underwater robot on a flat sea floor has difficulty finding a stable feature to assist the robot’s localization. It may not be feasible to detect a stable feature since underwater currents can change the shape of the sea floor. In the case where there are no stable features in the environments, it is not feasible to use SLAM algorithms. It is thus argued that SLAM is not feasible, as a hexapod robot explores the seabed where underwater currents can easily change the seabed shape.
It is acknowledged that an Acoustic Doppler Current Profiler (ADCP) can be used to measure the velocity of underwater currents in real-time. However, ADCP cannot be used to measure motion perturbation due to underwater currents. Even in the case where the velocity of underwater currents can be measured, it is not trivial to estimate the complex interaction between the underwater currents and the maneuver of a hexapod robot on the sea bottom. This paper uses the Ultra-Short BaseLine (USBL) sensors for simultaneous estimation of both a robot’s pose and the motion perturbation due to underwater currents. Note that ADCP measures the velocity of currents, but it cannot measure the robot’s motion perturbation due to underwater currents.
This paper considers an underwater environment where there are no stable features that can assist a robot’s localization. Moreover, due to underwater currents, dead reckoning localization based on inertial navigation sensors results in a severe accumulation of localization errors. In order to avoid localization error accumulation due to underwater currents, this article introduces using two hexapod robots. These two robots move together while using each other as static landmarks in the environment. This implies that two robots move as one pair while a moving robot uses another robot as a static landmark for localization.
A moving robot measures the relative position of another static robot, in order to estimate its position while it moves. Here, relative position (bearing and range) measurements are feasible considering an underwater robot equipped with USBL sensors. To the best of our knowledge, this paper is novel in using relative position measurements for the cooperative localization of underwater hexapod robots.
This article proposes a stop–go policy, which iterates the following process. The moving robot sets a new waypoint and moves to reach the waypoint. While the moving robot travels, it calculates the relative position of the anchor robot using USBL sensor measurements and localizes itself. After the moving robot reaches the waypoint, the moving robot extends its legs into the sea bottom and is set as a new anchor robot. Then, the previous anchor robot becomes a new moving robot. The new moving robot approaches the anchor robot while localizing itself. Once the moving robot reaches the anchor robot, we iterate the process in this paragraph. Iterate this until the robots visit the goal point.
Due to underwater currents, a robot cannot maintain its desired course. Sea currents may perturb the robot’s maneuver significantly. Moreover, there may be obstacles, such as underwater nets, that a robot needs to avoid. For instance, the robot can use active sonar sensors to detect the relative position of underwater nets [13]. This manuscript thus develops a guidance strategy for avoiding obstacles, while estimating the motion perturbation due to underwater currents.
In summary, the novelties of this article are summarized as follows:
- As far as we know, this paper is novel in addressing a stop–go policy for simultaneous localization and guidance of underwater hexapod robots.
- This paper is novel in using relative position measurements for cooperative localization of underwater hexapod robots.
- This article develops a guidance strategy for avoiding obstacles while estimating the motion perturbation due to underwater currents.
The performance of the proposed cooperative localization methods is verified using MATLAB simulations. MATLAB simulations verify that the proposed localization methods are effective in that the current magnitude changes irregularly.
The remaining of this paper is organized as follows. Section 2 presents the literature review on cooperative localization and introduces the preliminary information of this paper. Section 3 presents several definitions and assumptions. Section 4 presents the cooperative localization based on the stop–go policy. Section 5 introduces MATLAB simulation results to demonstrate the performance of the proposed motion control with cooperative localization. Section 6 provides the conclusions.
2. Literature Review on Cooperative Localization
In order to improve the localization of two hexapod robots, the coordinated motion of the two robots is utilized. Coordinating multiple robots can be utilized in many tasks, such as sensor network building [14], exploration [15], intruder capture [16,17], rendezvous [18,19], formation control [20,21], or target tracking [22,23].
References [24,25] presented cooperative localization (CL) of a robot assisted by another autonomous vehicle, say Communication Navigation Aid (CNA), which can use GPS to localize itself. The CNA serves as a leader, and the robot serves as a follower. Reference [25] discussed the positioning performance indicators of different positioning methods in the case of different numbers of outliers in the measurement information. References [26,27] considered the case where the movement of a follower is constrained by the maneuver of a leader. In [27,28], the CNA localizes a robot by measuring the relative position (or distance) of the robot. However, the CNA must exist near the sea surface in order to use GPS.
In Ref. [29], surface buoys and anchor nodes were used for the localization of underwater sensor networks. Surface buoys are equipped with GPS to obtain their location estimates. In addition, anchor nodes are powerful nodes that can make direct contact with the surface buoys, and are capable of self-localization based on such contacts.
Our article considers cooperative navigation in the case where there are no CNAs or surface buoys. This is feasible as robots operate in the deep sea. This article considers a scenario where it is not possible to establish a communication link between the CNA (or surface buoys) and a hexapod robot at the sea bottom.
Several papers handled cooperative localization of underwater robots based on bearing-only [30,31] or range-only measurements [32]. References [33,34,35,36,37] considered multi-robot systems, such that every robot has sonar sensors to measure the time of arrival (TOA) of sound emitted from a transmitter. By processing sonar measurements of every robot, the robot team estimates the transmitter’s location. The authors of [38] handled how to place multiple sensors so as to yield the best-expected source location estimate. Reference [1] considered the case where a robot uses mutual range measurements for cooperative localization. Reference [1] validated their cooperative navigation procedure using experiments. However, [1] considered localization of a torpedo-shaped robot with propellers, thus [1] cannot be applied for localization of a hexapod robot.
In the literature, many location strategies were utilized for underwater localization [39,40]. Short-baseline (SBL) [41] or long-baseline (LBL) [40,42] can be used for locating an underwater robot. However, SBL requires that an acoustic pulse is transmitted by the transceiver and detected by the subsea transponder, which replies with its own acoustic pulse. LBL and SBL require that additional structures are built for underwater robot localization. Therefore, LBL and SBL are not suitable for underwater robots which explore unknown environments.
As far as we know, our manuscript is novel in using relative position measurements for cooperative localization of underwater hexapod robots. Note that relative position measurements are viable using USBL sensors. Relative position measurements are more desirable than bearing-only or range-only measurements since the relative position information can be measured directly.
3. Definitions and Assumptions
This paper considers two hexapod robots that move on a flat sea bottom. This article considers the problem of making two robots reach the goal while localizing themselves in environments with obstacles.
We address notations related to vectors and matrices. Let define the j-th element in a column vector, say . Let define a diagonal matrix where appear as diagonal elements in this order. Let define the inner product between two vectors, say and . Let denote the phase (or angle) of the complex number . Therefore, it is feasible that y or x in is zero. However, it is not possible that both x and y in are zeros.
Let define the estimation of a variable . Here, we use the hat operator to represent an estimation. The variance of is defined as . Here, + denotes the expected value (mean) of a random variable, say . Let define the variance of the estimate .
We consider two hexapod robots that move on a flat sea bottom. Hence, this paper considers the localization problem of a robot in 2D environments. We use an inertial reference frame whose origin is an arbitrary point on the flat sea bottom. The frame consists of two coordinates: one represents the position along the northern axis, and the other one is along the eastern axis. This frame is called the North-East (NE) reference frame.
In the NE reference frame, let , where , define the 2D position of the i-th robot. In other words, we need to derive while the i-th robot moves. Let , where , define the variance of the estimate .
This paper considers discrete-time systems. Let T define the sampling interval in discrete-time systems. In the NE reference frame, defines the 2D position of the i-th robot at sampling-stamp k. In addition, let denote the estimation of . Let present the localization error of the i-th robot at sampling-step k.
3.1. Horizontal Motion Model of a Hexapod Robot
One considers the horizontal motion of a robot in the NE reference frame. In the case where there is no sea current, the motion model of the i-th robot is
Here, , and . In addition, is the through-water speed of the i-th robot at sampling-stamp k, and defines the orientation direction of the i-th robot at sampling-stamp k, measured counterclockwise from the East direction. Furthermore, presents the orientation vector of the i-th robot. The simple dynamic model in (1) is commonly used in multi-robot systems [43,44,45,46,47,48,49].
It is acknowledged that the detailed inertial parameters of a hexapod robot are not considered in horizontal motion controls in (1). in (1) can be set as the input vector of the robot at sampling-stamp k.
Hexapod robots are omnidirectional vehicles [50]. Both sideways motion and rotational motion can be used to move according to the input vector [50]. References [50,51] discussed how to make the robot change foot placement based on an input vector in addition to controlling the position and orientation of the body.
Note that both and are not used in the localization process of underwater robots. These values are used to make a robot under underwater currents move towards its assigned waypoint.
In the NE reference frame, let denote the waypoint at sampling-stamp k. How to make the robot at sampling-stamp k move towards a waypoint is presented in Section 4.2. Since and are not used in the localization process, the error in measurements of and does not have an effect on the performance of the proposed localization scheme. The performance of the proposed localization scheme depends on the accuracy of sensors measuring the relative distance (bearing and range) between two robots.
In practice, there are sea currents in underwater environments. In the case where there are underwater currents, the motion model of the i-th robot is
This model is presented in [52]. In (2), defines the robot’s horizontal motion perturbation due to underwater currents. Since a robot crawls on the sea bottom, it is not trivial to estimate while the robot moves. How to estimate the horizontal motion perturbation is discussed in Section 4.2.
3.2. Relative Position Measurements between Two Robots
This paper uses the following stop–go policy. The proposed stop–go policy is as follows. During the maneuver of one moving robot, another robot stays still (extends legs into the sea bottom) and performs as the anchor robot. The moving robot struggles to move while being pushed by underwater currents.
During the maneuver of a moving robot, the anchor robot stands still. Assume that the anchor robot can stand still while extending its legs into the sea bottom. In this way, the anchor robot can resist severe underwater currents. The moving robot localizes itself by measuring the relative position of the anchor robot.
A moving robot uses USBL sensors for measuring the relative position (bearing and range) of the anchor robot. Let represent the maximum range of USBL sensors. Let represent the maximum communication range of a robot. Let . This implies that is the smaller value between and .
In the NE reference frame, let define the position of the anchor robot at sampling-stamp k. In the NE reference frame, let define the position of the moving robot at sampling-stamp k.
While the moving robot moves, it estimates its 2D position by measuring the relative position (bearing and range) of the anchor robot. Suppose that at each sampling-stamp k, the moving robot measures the bearing and range of the anchor robot.
The measurement model of a robot is as follows. Let for convenience. Moreover, let define the bearing measurement of the anchor robot with respect to the moving robot. The equation for is
Here, has a Gaussian distribution with mean 0 and standard deviation . In (3), recall that defines the j-th element in a column vector, say .
The moving robot measures the range of the anchor robot. As the range measurement, we have
Here, has a Gaussian distribution with mean 0 and standard deviation .
Let define the 2D estimate of the anchor robot at sampling-stamp k. In the NE reference frame, the 2D position of the moving robot can be localized as
Using (5), one gets as
Using partial derivatives of or with respect to and , one derives
Here,
3.3. Sinking Process of Two Hexapod Robots
Two hexapod robots are deployed from the sea surface. While the robots sink, their mutual distance may increase as time goes on, since the position of each robot is perturbed by underwater currents. It is desirable that the two robots are not too far from each other once they get to the sea bottom. Otherwise, two robots may not sense or communicate with each other after they get to the sea bottom.
We assume that each robot has depth sensors for measuring its depth. It is assumed that two robots are connected using a cable. The cable is used to avoid the case where the distance between the two robots gets too far while they fall to the sea bottom. In this way, the mutual distance between the two robots can be always shorter than the maximum length of the cable. It is assumed that the maximum length of the cable is shorter than . Recall that is the smaller value between and .
Initially, two robots settle down close to each other, using the cable. Since the maximum length of the cable is shorter than , the relative distance between the two robots is shorter than . Once two robots reach the sea bottom, the cable can be disconnected, since the cable is not used anymore. An entangled cable does not make problems, since the cable is disconnected after the robots reach the sea bottom.
While these robots fall to the sea bottom, the localization error of a robot increases due to underwater currents. This implies that a robot can be pushed by underwater currents while it falls to the sea bottom. However, its NE location estimate error can increase when it falls to the sea bottom.
At sampling-stamp 0, for two robots ( where ), one initializes the variance of each robot as
Here, is a positive definite diagonal matrix and is set considering the increase of localization error while each robot sinks. The localization approach in [3] can be used, in order to locate each robot while it sinks. However, in this case, the localization error increases gradually as the depth of the robot increases. can be considered as the initial covariance matrix in Kalman filters [53].
For instance, one can assume that underwater currents can push a robot by at most 5 m, while the robot falls for every 100 m. This implies that as a robot falls for m, underwater currents can push the robot by at most m. MATLAB simulations consider the case where the robot falls for 200 m until reaching the sea bottom. Here, a robot’s depth change can be measured using its depth sensor. In this case, the robot can have been pushed by at most 10 m. Thus, MATLAB simulations set the initial covariance matrix as .
3.4. The Summary of Assumptions
In summary, we use the following assumptions:
- A1
- The sea bottom is flat.
- A2
- A robot measures the relative position (bearing and range) of another robot using USBL sensors.
- A3
- The anchor robot can stand still while extending its legs into the sea bottom.
- A4
- While two robots fall to the sea bottom, they are connected using a cable, whose length is shorter than .
- A5
- A robot has active sonar sensors for detecting nearby obstacles.
- A6
- A robot has depth sensors for measuring its depth.
4. Cooperative Localization Based on the Stop–Go Policy
During the maneuver of a moving robot, the anchor robot stands still, while extending its legs into the sea bottom. In this way, the anchor robot can resist severe underwater currents. The moving robot localizes itself by measuring the relative position of the anchor robot.
The proposed stop–go policy iterates the following process. The moving robot sets a new waypoint and moves to reach the waypoint. While the moving robot travels, it calculates the relative position of the anchor robot using relative position measurements (USBL) and localizes itself. After the moving robot reaches the waypoint, the moving robot extends its legs into the sea bottom and is set as a new anchor robot. Then, the previous anchor robot becomes a new moving robot. The new moving robot approaches the anchor robot while localizing itself. Once the moving robot reaches the anchor robot, one iterates the process in this paragraph. Iterate this until the robots visit the goal point.
See Figure 1 for an illustration of the stop–go policy. In this figure, time elapses from top to bottom. In this figure, the movement of a moving robot is plotted with an arrow.
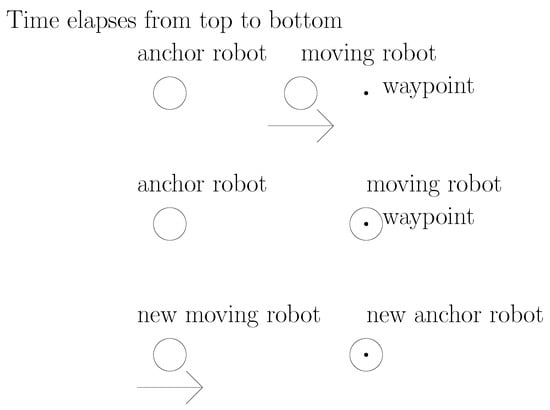
Figure 1.
An illustration of the stop–go policy. Time elapses from top to bottom. The movement of a moving robot is plotted with an arrow.
At the moment when a robot reaches the sea bottom, its position variance is initialized as . The position variance of each robot is updated using (6). As time goes on, the variance of each robot increases using (6). This is inevitable since there exists sensor measurement noise in the system (6).
4.1. Guidance Laws for a Moving Robot, While Avoiding Obstacles
Before a moving robot begins maneuvering at sampling-stamp k, the robot needs to determine a new waypoint to visit. The waypoint is set, so that heading towards the waypoint can make the robot approach the goal while avoiding obstacles. Let define the goal position defined in two dimensions (NE reference frame).
Once a waypoint is set, the robot begins moving toward the waypoint while overcoming underwater currents. Section 4.2 discusses how to make the robot move toward the waypoint.
To avoid collision with obstacles, the moving robot uses its active sonar sensors. The moving robot can use active sonar sensors to detect a point in obstacles. For instance, the moving robot can use active sonar sensors to detect the relative position of underwater nets [13]. Among all obstacle points, the moving robot detects the point, called the closestPnt, which is closest to the robot.
In the NE reference frame, let present the closestPnt at sampling-stamp k. Note that can be measured utilizing the horizontal range sensors, such as active sonar sensors, with maximum sensing range . Let be defined as .
Let define the separation threshold between the moving robot and an obstacle boundary (the boundary of an obstacle). Since an obstacle boundary is detected utilizing active sonar sensors of the moving robot, is required.
Suppose that the moving robot is sufficiently far from an obstacle. Then, the robot moves towards the goal. In other words, if , then the moving robot at sampling-stamp k sets the waypoint, , as
Let define the sampling-stamp such that
and that
At sampling-stamp , the moving robot begins following the obstacle boundary.
Suppose that we want to make the moving robot follow the obstacle, while the obstacle is to the right of the robot. Then, the moving robot sets its waypoint as
Here,
is the matrix presenting radians rotation. In (13), is multiplied so that the moving robot’s orientation vector is normal to .
Suppose that we want to make the moving robot follow the obstacle, while the obstacle is to the left of the robot. Then, the moving robot sets its waypoint as
Note that in (15) is in the opposite direction from in (13). We can set the waypoint considering the relative position of the goal with respect to the robot. In the case where
is met, then the moving robot sets its waypoint as . Otherwise, the moving robot sets its waypoint as .
It is desirable that the robot moves toward the goal if possible. Recall that is the sampling-stamp when the moving robot begins following the obstacle. While the moving robot follows the obstacle boundary under (13) or (15), it detects the moment when both
and
are satisfied. This implies that the obstacle boundary, which the moving robot has been following, is opposite to the goal direction. At this moment, the robot begins moving toward the goal using (10), since the robot does not have to keep following the obstacle boundary.
As the line-of-sight between the robot and the goal point is not blocked by an obstacle, the waypoint is set as (10). In this manner, the robot can move towards the goal while avoiding collision with an obstacle.
If the waypoint is set by the moving robot under (10), (13), or (15), then the robot needs to move towards . Due to underwater currents, it is not trivial to make the robot at sampling-stamp k move towards . In other words, due to underwater currents, heading toward the waypoint does not necessarily make the robot move toward the waypoint. How to make the robot under underwater currents move towards the waypoint is presented in Section 4.2.
Figure 2 illustrates concepts used in the guidance controls. The triangle centered at shows the attitude of the moving robot. In Figure 2, is depicted on the obstacle boundary. In addition, is plotted as an arrow emanating from . Suppose that the robot heads towards in this figure. Due to underwater currents, the robot moves towards instead of .
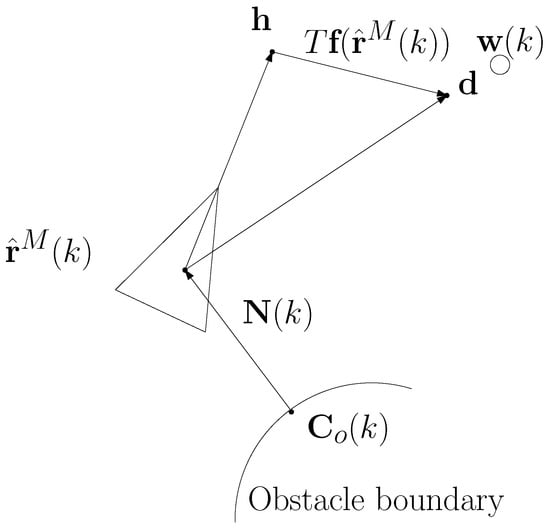
Figure 2.
An illustration of concepts used in the guidance controls. The triangle centered at shows the attitude of the moving robot. In this figure, is depicted on the obstacle boundary. In addition, is plotted as an arrow emanating from . Suppose that the robot heads towards in this figure. Due to underwater currents, the robot moves towards instead of . This implies that the robot moves towards the waypoint , which is depicted as a circle.
4.2. Make the Robot under Underwater Currents Move towards the Waypoint
Due to underwater currents, heading toward the waypoint does not necessarily make the robot move toward the waypoint. In order to move towards the waypoint, the moving robot estimates the horizontal motion perturbation due to underwater currents.
While the robot moves, it localizes itself utilizing (5). Based on the localization result , the robot’s motion perturbation due to underwater currents is estimated in real-time.
One next presents how to estimate the horizontal motion perturbation due to underwater currents which apply to the moving robot. Suppose the robot moves with speed and with orientation at sampling-stamp k. Then, in the NE reference frame, the predicted position of the robot at sampling-stamp is
Using (2), we get
However, accessing or is not feasible due to sensor noise. At each sampling-stamp, is estimated by measuring the relative position of the anchor robot. In other words, is derived utilizing (5).
By replacing in (20) by , one gets
Note that the accuracy of this perturbation estimation depends on the accuracy of location estimation since in (20) was replaced by .
Next, the variance of the perturbation estimation is derived. Using (22), one gets
Here, one used the fact that , since the anchor robot does not move at all. Recall that (7) can be used to derive .
In underwater environments, the magnetic field may be distorted, which leads to inaccurate measurements of . In addition, there may be an error in the estimation of through-water speed . Therefore, in (23) is not zero. in (23) can be estimated utilizing extensive experiments.
Once the horizontal motion perturbation due to underwater currents is estimated utilizing (22), then the estimated perturbation is further used to make the robot at sampling-stamp k move towards the waypoint . Recall that at each sampling-stamp k, the waypoint is set using (10), (13), or (15). Since one desires that the robot moves towards the waypoint , the desired position of the robot at sampling-stamp is
Here, where
Figure 2 illustrates the concepts. In Figure 2, the waypoint is depicted as a circle. The robot sets its heading point as
In Figure 2, the triangle centered at shows the attitude of the robot in the case where the robot sets its heading point as . However, due to underwater currents, the robot moves towards instead of . This implies that the robot moves towards .
As depicted on Figure 2, the orientation direction of the moving robot is set as
Moreover, the robot’s speed is changed to . In this manner, the robot can move towards considering the motion perturbation due to underwater currents.
5. Simulations
This section verifies the effectiveness of the proposed approach utilizing MATLAB simulations. Since we consider a flat sea bottom, one considers localization of a robot in the NE reference frame. Initially, one robot is at (35,35), and the other robot is at (40,40) meters. m, and m. In addition, one sets s.
We verify the robustness of the proposed strategy by setting noise parameters as follows: m, and degrees. These sensor specifications are available using USBL sensors.
The initial covariance matrix is set as . The simulation ends when a robot reaches the goal .
Recall that in (20) defines the perturbation on the robots’ position due to underwater currents. It is not trivial to simulate the complex interaction between the underwater currents and the motion of a hexapod robot on the sea bottom. In addition, it is not trivial to simulate the complex interaction between underwater currents and obstacles, such as underwater nets. We simulate the perturbation vector field in a rectangular 2D workspace with size 1200 × 1200 m.
This section simulates scenarios where the underwater currents change irregularly. One discusses how to generate the irregular perturbation vector field. Let (m) denote the side length of the rectangular workspace. Since exists inside the rectangular workspace, and exist in the interval . Let (m/s) denote the maximum flow speed. The function is calculated using the following equations.
Here, indicates the noise strength in the flow field. In addition, indicates a Gaussian noise with zero mean and variance 1. We use in simulations. Due to the noise term , a distinct perturbation vector field is generated whenever one runs a scenario simulation. Blue arrows in the following figures (Figures 3, 4, 7, 10 and 13) show the perturbation vector field that is irregularly generated in the environment.
Note that the maximum perturbation speed must be slower than the speed of a moving robot. Otherwise, it is impossible to make a moving robot overcome underwater currents. (2) is used to simulate the motion of a robot under underwater currents. In MATLAB simulations, the speed of a moving robot is m/s, which is faster than the maximum perturbation speed.
Figure 3 depicts the overview of the simulation environment. The origin of the rectangular workspace is located at the left bottom corner of the workspace. Blue arrows show the perturbation vector field in the environment. In addition, obstacle boundaries are depicted in red.
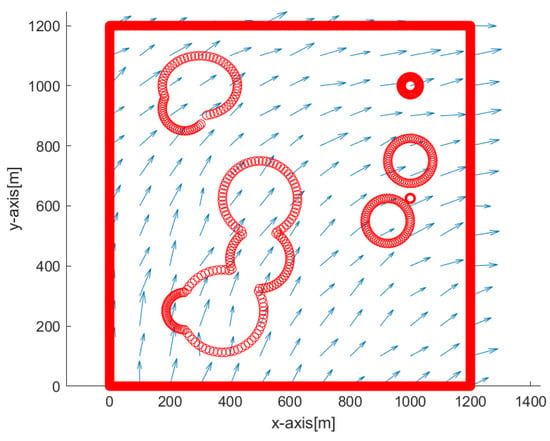
Figure 3.
The origin of the rectangular workspace is located at the left bottom corner of the workspace. Blue arrows show the perturbation vector field that is irregularly generated in the environment. Obstacle boundaries are depicted with red circles.
5.1. Scenario 1
This subsection simulates the case where the goal is located at (80,80) meters. Figure 4 presents the simulation result in the environment of Figure 3. Figure 4 is the enlarged figure of Figure 3. In Figure 4, the path of one robot is depicted with blue asterisks, and that of another robot is depicted with green asterisks. See that both robots move towards the goal while overcoming underwater currents. The path of one robot overlaps with that of another robot since both robots visit identical waypoints sequentially. Red dotted arrows in the figure show the perturbation vector field estimated at the anchor robot’s position. It is acknowledged that the perturbation direction is not estimated accurately. This is due to the fact that the true robot position is not available due to sensor noise in the system. Equation (23) presents the variance in the perturbation velocity estimation.
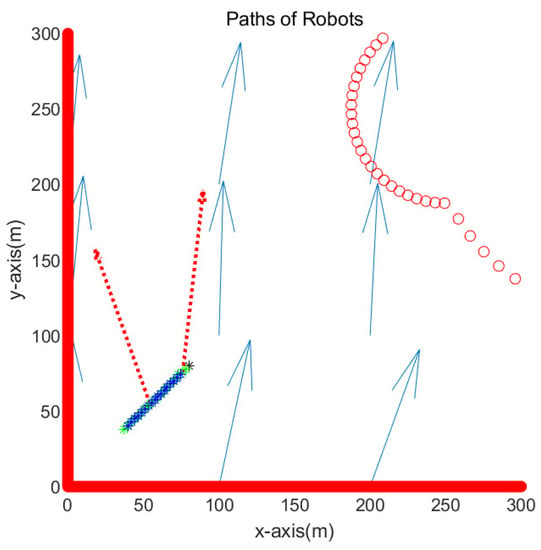
Figure 4.
Scenario 1. The path of one robot is depicted with blue asterisks, and that of another robot is depicted with green asterisks. Red dotted arrows show the perturbation vector field estimated at the robot’s position.
Figure 5 presents the localization error with respect to sampling-stamp k. Here, is an estimate of the true position . Under underwater currents, dead reckoning localization based on inertial navigation sensors results in the accumulation of localization errors. Figure 5 shows that the error accumulation under the stop–go policy is not severe. Note that sensor noise specifications ( m, and degrees) are used, which are available using USBL sensors.
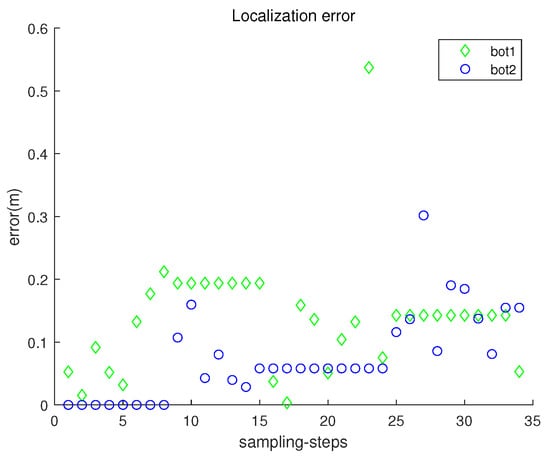
Figure 5.
Scenario 1. The localization error with respect to sampling-stamp k.
The orientation direction of the i-th robot at sampling-stamp k is in (2). Let represent , and let represent . Figure 6 plots both and of each robot at each sampling-stamp k. While a robot is settled down, its and are set as zeros. See that the orientation of a moving robot changes according to the estimated underwater currents.
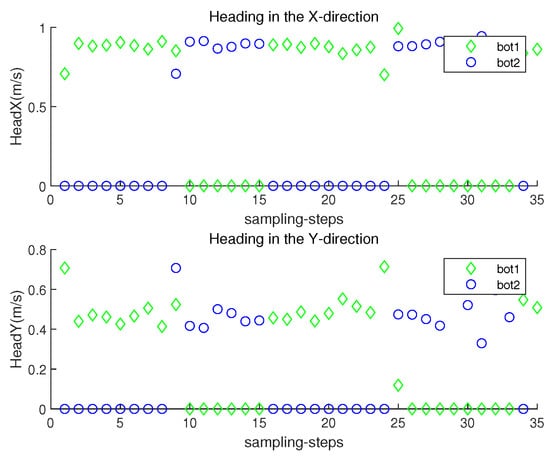
Figure 6.
Scenario 1. and with respect to sampling-stamps.
Comparison with Dead Reckoning Localization Methods
For comparison, we run Scenario 1 using dead reckoning localization methods. For all , in (2) is set as . Note that (2) is used to simulate the motion of a robot under underwater currents. In MATLAB simulations, the speed of a moving robot is m/s. A robot cannot move towards the goal, due to the perturbation of underwater currents. See term in (2).
Figure 7 presents the simulation result in the environment of Figure 3. Figure 7 is the enlarged figure of Figure 3. In Figure 7, the path of one robot is depicted with blue asterisks, and that of another robot is depicted with green asterisks. See that both robots cannot reach the goal, which is marked with a black asterisk. Therefore, the simulations end when 700 s (70 sampling-stamps) elapse.
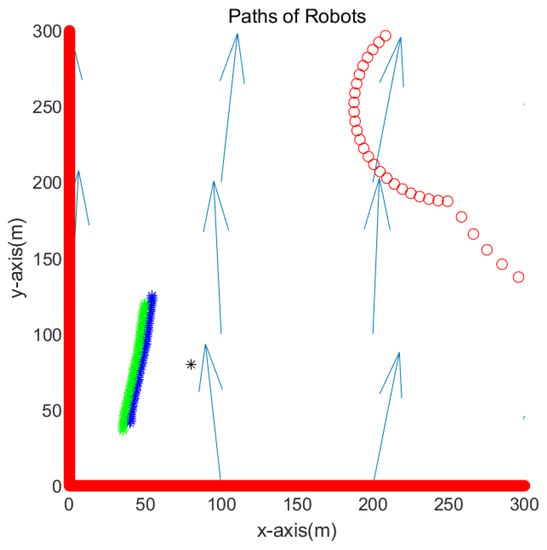
Figure 7.
Scenario 1. Dead reckoning localization methods are used. The path of one robot is depicted with blue asterisks, and that of another robot is depicted with green asterisks. The goal is marked with a black asterisk.
Figure 8 depicts the localization error with respect to sampling-stamp k. Under underwater currents, dead reckoning localization based on inertial navigation sensors results in a severe accumulation of localization errors. Figure 9 plots both and with respect to sampling-stamps. See that the orientation of a moving robot does not change as time goes on. Since the perturbation direction is not considered, a robot does not head toward the goal.
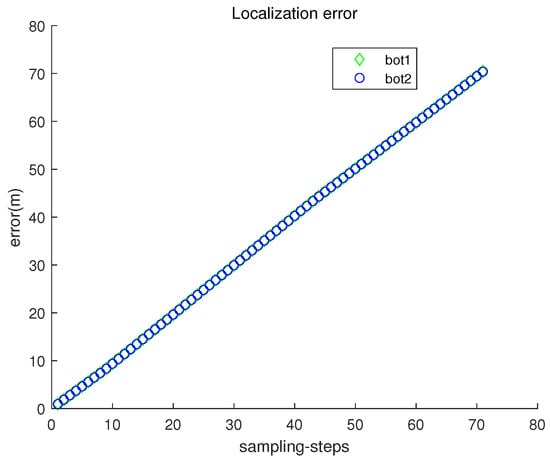
Figure 8.
The localization error with respect to sampling-stamp k (dead reckoning strategy in Scenario 1).
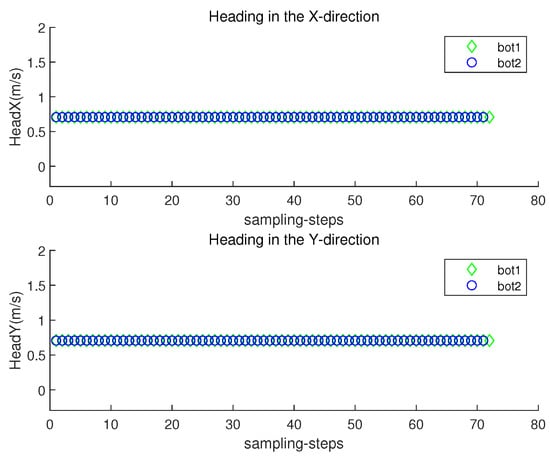
Figure 9.
and with respect to sampling-stamps (dead reckoning strategy in Scenario 1).
5.2. Scenario 2
We verify the robustness of the proposed strategy in complex environments with various obstacles. We simulate the case where the goal is located at (1100,900) meters. Figure 10 presents the simulation result. The path of one robot overlaps with that of another robot since both robots visit identical waypoints sequentially. See that two robots approach the goal while avoiding obstacles. Red dotted arrows in the figure show the perturbation vector field estimated at the anchor robot’s position. It is acknowledged that the perturbation direction is not estimated accurately, since the true robot position is not available due to sensor noise in the system. Note that sensor noise specifications ( m, and degrees) are used, which are available using USBL sensors.
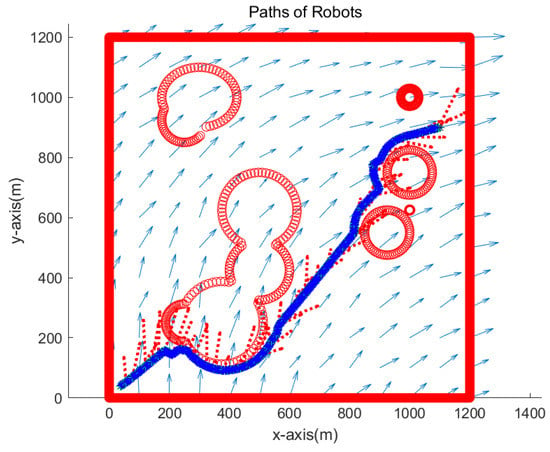
Figure 10.
Scenario 2. The path of one robot is depicted with blue asterisks, and that of another robot is depicted with green asterisks. Red dotted arrows show the perturbation vector field estimated at the anchor robot’s position.
Figure 11 presents the localization error with respect to sampling-stamp k. See that the localization error remains a small value at all sampling-stamps. Figure 12 plots both and with respect to sampling-stamps. While a robot is settled down, its and are set as zeros. The orientation of a moving robot changes according to the estimated perturbation due to underwater currents.
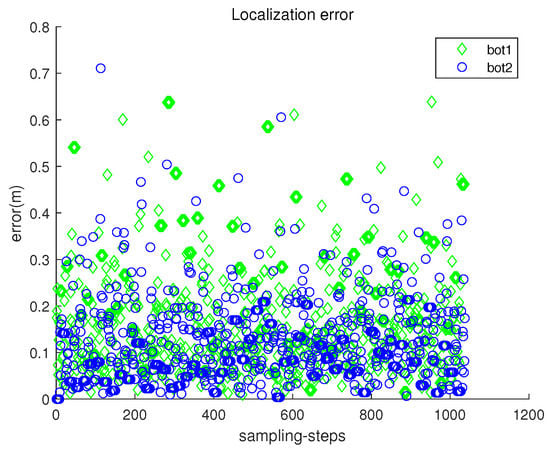
Figure 11.
Scenario 2. The localization error with respect to sampling-stamp k.
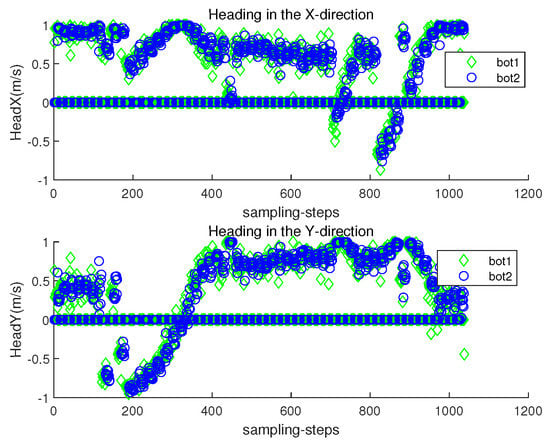
Figure 12.
Scenario 2. and with respect to sampling-stamps.
5.3. Scenario 3
We verify the robustness of the proposed strategy in complex environments with large perturbation noise. Recall that the perturbation vector field was generated by adding Gaussian noise with zero mean and standard deviation to the noiseless perturbation vector. In Scenario 3, the perturbation vector field was generated by adding Gaussian noise with zero mean and standard deviation to the noiseless perturbation vector.
We simulate the case where the goal is located at (1100,900) meters. Figure 13 depicts the simulation result. The path of one robot overlaps with that of another robot since both robots visit identical waypoints sequentially. See that two robots approach the goal while avoiding obstacles. It is acknowledged that the perturbation direction is not estimated accurately, since the true robot position is not accessible due to sensor noise in the system.
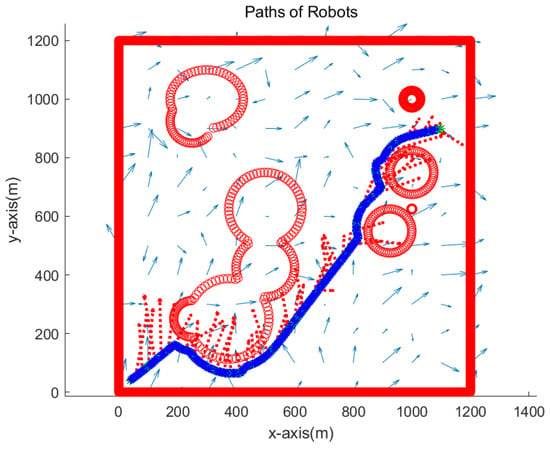
Figure 13.
Scenario 3. In Scenario 3, the perturbation vector field was generated by adding Gaussian noise with zero mean and standard deviation of 0.05 to the noiseless perturbation vector. The path of one robot is depicted with blue asterisks, and that of another robot is depicted with green asterisks. See that two robots approach the goal while avoiding obstacles.
Figure 14 presents the localization error with respect to sampling-stamp k. See that the localization error remains a small value at all sampling-stamps. The localization error in Scenario 3 is comparable to that in Scenario 2 (Figure 11), which verifies the robustness of the proposed location scheme.
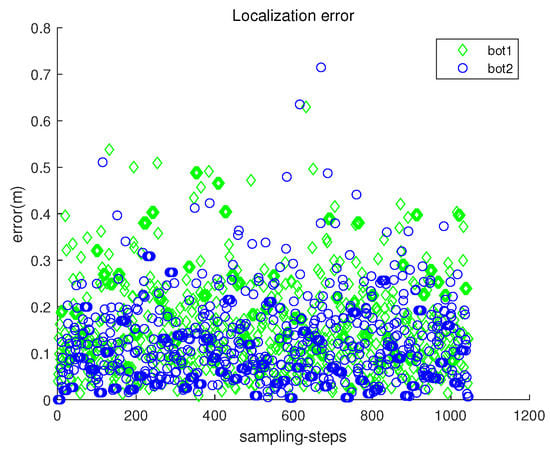
Figure 14.
Scenario 3. The localization error with respect to sampling-stamp k. The localization error in Scenario 3 is comparable to that in Scenario 2 (Figure 11), which verifies the robustness of the proposed location scheme.
Figure 15 plots both and with respect to sampling-stamps. While a robot is settled down, its and are set as zeros. The orientation of a moving robot changes according to the estimated perturbation due to underwater currents.
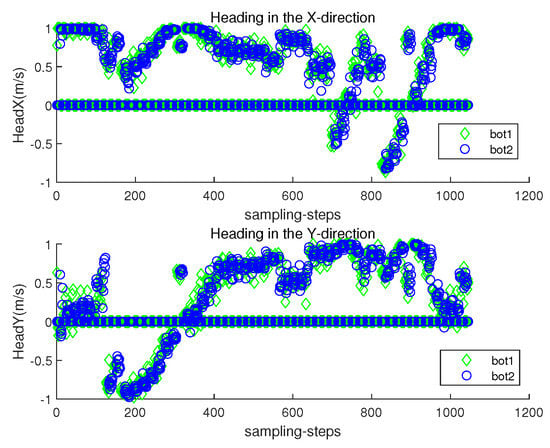
Figure 15.
Scenario 3. and with respect to sampling-stamps.
6. Conclusions
This paper considers underwater environments where there are no stable landmarks or features which can assist a robot’s localization. Furthermore, due to underwater currents, dead reckoning localization based on inertial navigation sensors results in a severe accumulation of localization errors.
This paper proposes novel cooperative localization schemes of two underwater hexapod robots together with a guidance strategy for avoiding obstacles under underwater currents. As for cooperation localization, the stop–go policy is developed to avoid the accumulation of localization errors due to the conventional dead reckoning approach based on inertial navigation sensors.
The estimation of motion perturbation due to underwater currents is taken into account while developing the guidance strategy for avoiding obstacles. The effectiveness of the proposed stop–go policy and guidance strategy is verified using MATLAB simulations. MATLAB simulations demonstrate that the proposed schemes are effective in that the current magnitude changes irregularly.
Since the proposed algorithms are simple, the computational load of our algorithms is very low. In addition, the algorithms can be applied for simultaneous localization and guidance for aerial vehicles or ground vehicles in environments with no landmarks or features. In the future, the effectiveness of the proposed methods will be verified using underwater experiments with real hexapod robots.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (Grant Number: 2022R1A2C1091682). This research was supported by the faculty research fund of Sejong university in 2023.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Allotta, B.; Caiti, A.; Costanzi, R.; Di Corato, F.; Fenucci, D.; Monni1, N.; Pugi, L.; Ridolfi, A. Cooperative navigation of AUVs via acoustic communication networking: Field experience with the Typhoon vehicles. Auton. Robot. 2016, 40, 1229–1244. [Google Scholar] [CrossRef]
- Kim, T.S.; Jang, I.S.; Shin, C.J.; Lee, M.K. Underwater construction robot for rubble leveling on the seabed for port construction. In Proceedings of the 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014), Bucheon-city, Republic of Korea, 22–25 October 2014; pp. 1657–1661. [Google Scholar]
- Allotta, B.; Costanzi, R.; Fanelli, F.; Monni, N.; Paolucci, L.; Ridolfi, A. Sea currents estimation during AUV navigation using Unscented Kalman Filter. IFAC-PapersOnLine 2017, 50, 13668–13673. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, H.; Li, M.; You, S. A Review of Visual-Inertial Simultaneous Localization and Mapping from Filtering-Based and Optimization-Based Perspectives. Robotics 2018, 7, 45. [Google Scholar] [CrossRef]
- Lynen, S.; Zeisl, B.; Aiger, D.; Bosse, M.; Hesch, J.; Pollefeys, M.; Siegwart, R.; Sattler, T. Large-scale, real-time visual–inertial localization revisited. Int. J. Robot. Res. 2020, 39, 1061–1084. [Google Scholar] [CrossRef]
- Kramer, A.; Kasper, M.; Heckman, C. VI-SLAM for Subterranean Environments. In Field and Service Robotics; Ishigami, G., Yoshida, K., Eds.; Springer Singapore: Singapore, 2021; pp. 159–172. [Google Scholar]
- Zhang, S.; Zhao, S.; An, D.; Liu, J.; Wang, H.; Feng, Y.; Li, D.; Zhao, R. Visual SLAM for underwater vehicles: A survey. Comput. Sci. Rev. 2022, 46, 100510. [Google Scholar] [CrossRef]
- Kelly, J.; Sukhatme, G.S. Visual-inertial simultaneous localization, mapping and sensor-to-sensor self-calibration. In Proceedings of the 2009 IEEE International Symposium on Computational Intelligence in Robotics and Automation (CIRA), Daejeon, Republic of Korea, 15–18 December 2009; pp. 360–368. [Google Scholar]
- Joshi, B.; Xanthidis, M.; Rahman, S.; Rekleitis, I. High Definition, Inexpensive, Underwater Mapping. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 1113–1121. [Google Scholar]
- Gao, H.; Zhang, X.; Wen, J.; Yuan, J.; Fang, Y. Autonomous Indoor Exploration Via Polygon Map Construction and Graph-Based SLAM Using Directional Endpoint Features. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1531–1542. [Google Scholar] [CrossRef]
- Donoso, F.; Austin, K.; McAree, P. Three new Iterative Closest Point variant-methods that improve scan matching for surface mining terrain. Robot. Auton. Syst. 2017, 95, 117–128. [Google Scholar] [CrossRef]
- Jun, B.H.; Shim, H.; Kim, B.; Park, J.Y.; Baek, H.; Yoo, S.; Lee, P.M. Development of seabed walking robot CR200. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–14 June 2013; pp. 1–5. [Google Scholar]
- Qin, R.; Zhao, X.; Zhu, W.; Yang, Q.; He, B.; Li, G.; Yan, T. Multiple Receptive Field Network (MRF-Net) for Autonomous Underwater Vehicle Fishing Net Detection Using Forward-Looking Sonar Images. Sensors 2021, 21, 1933. [Google Scholar] [CrossRef]
- Kim, J. Multirobot Exploration While Building Power-Efficient Sensor Networks in Three Dimensions. IEEE Trans. Cybern. 2018, 49, 2771–2778. [Google Scholar] [CrossRef]
- Janchiv, A.; Batsaikhan, D.; Kim, B.; Lee, W.G.; Lee, S.G. Time-efficient and complete coverage path planning based on flow networks for multi-robots. Int. J. Control. Autom. Syst. 2013, 11, 369–376. [Google Scholar] [CrossRef]
- Kim, J. Three-dimensional multi-robot control to chase a target while not being observed. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419829667. [Google Scholar] [CrossRef]
- Kim, J. Three-dimensional discrete-time controller to intercept a targeted UAV using a capture net towed by multiple aerial robots. IET Radar Sonar Navig. 2019, 13, 682–688. [Google Scholar] [CrossRef]
- Cortés, J.; Martínez, S.; Bullo, F. Robust rendezvous for mobile autonomous agents via proximity graphs in arbitrary dimensions. IEEE Trans. Autom. Control 2006, 51, 1289–1298. [Google Scholar] [CrossRef]
- Park, H.; Hutchinson, S. A distributed optimal strategy for rendezvous of multi-robots with random node failures. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1155–1160. [Google Scholar]
- Flocchinia, P.; Prencipeb, G.; Santoroc, N.; Widmayerd, P. Gathering of asynchronous robots with limited visibility. Theor. Comput. Sci. 2005, 337, 147–168. [Google Scholar] [CrossRef]
- Peng, J.; Akella, S. Coordinating Multiple Robots with Kinodynamic Constraints Along Specified Paths. Int. J. Robot. Res. 2005, 24, 295–310. [Google Scholar] [CrossRef]
- Kim, J. Tracking Controllers to Chase a Target Using Multiple Autonomous Underwater Vehicles Measuring the Sound Emitted From the Target. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4579–4587. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, W.; Yu, L. A Bank of Decentralized Extended Information Filters for Target Tracking in Event-Triggered WSNs. IEEE Trans. Syst. Man Cybern. Syst. 2019, 50, 3281–3289. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Peng, Z.; Cui, J.; Fiondella, L. Suave: Swarm underwater autonomous vehicle localization. In Proceedings of the IEEE INFOCOM 2014—IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 64–72. [Google Scholar]
- Xu, B.; Li, S.; Razzaqi, A.A.; Zhang, J. Cooperative Localization in Harsh Underwater Environment Based on the MC-ANFIS. IEEE Access 2019, 7, 55407–55421. [Google Scholar] [CrossRef]
- Cao, Y.; Ren, W.; Egerstedt, M. Distributed Containment Control with Multiple Stationary or Dynamic Leaders in Fixed and Switching Directed Networks. Automatica 2012, 48, 1586–1597. [Google Scholar] [CrossRef]
- Bahr, A.; Leonard, J.J.; Fallon, M.F. Cooperative Localization for Autonomous Underwater Vehicles. Int. J. Robot. Res. 2009, 28, 714–728. [Google Scholar] [CrossRef]
- Chen, Q.; You, K.; Song, S. Cooperative localization for autonomous underwater vehicles using parallel projection. In Proceedings of the 2017 13th IEEE International Conference on Control Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; pp. 788–793. [Google Scholar]
- Zhou, Z.; Peng, Z.; Cui, J.; Shi, Z.; Bagtzoglou, A. Scalable Localization with Mobility Prediction for Underwater Sensor Networks. IEEE Trans. Mob. Comput. 2011, 10, 335–348. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, B.M.; Lee, T.H. Optimal placement of bearing-only sensors for target localization. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 5108–5113. [Google Scholar]
- Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Sensor Networks for Optimal Target Localization with Bearings-Only Measurements in Constrained Three-Dimensional Scenarios. Sensors 2013, 13, 10386–10417. [Google Scholar] [CrossRef] [PubMed]
- Bayat, M.; Crasta, N.; Aguiar, A.P.; Pascoal, A.M. Range-Based Underwater Vehicle Localization in the Presence of Unknown Ocean Currents: Theory and Experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 122–139. [Google Scholar] [CrossRef]
- Guarato, F.; Laudan, V.; Windmill, J.F.C. Ultrasonic sonar system for target localization with one emitter and four receivers: Ultrasonic 3D localization. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Crasta, N.; Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Multiple autonomous surface vehicle motion planning for cooperative range-based underwater target localization. Annu. Rev. Control 2018, 46, 326–342. [Google Scholar] [CrossRef]
- Ferreira, B.M.; Matos, A.C.; Campos, H.S.; Cruz, N.A. Localization of a sound source: Optimal positioning of sensors carried on autonomous surface vehicles. In Proceedings of the 2013 OCEANS-San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–8. [Google Scholar]
- Martinez, S.; Bullo, F. Optimal sensor placement and motion coordination for target tracking. Automatica 2006, 42, 661–668. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Optimal Sensor Placement for Multiple Target Positioning with Range-Only Measurements in Two-Dimensional Scenarios. Sensors 2013, 13, 10674–10710. [Google Scholar] [CrossRef]
- Isaacs, J.T.; Klein, D.J.; Hespanha, J.P. Optimal sensor placement for time difference of arrival localization. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 7878–7884. [Google Scholar]
- Gonzalez-Garcia, J.; Gomez-Espinosa, A.; Cuan-Urquizo, E.; Garcia-Valdovinos, L.G.; Salgado-Jimenez, T.; Cabello, J.A.E. Autonomous Underwater Vehicles: Localization, Navigation, and Communication for Collaborative Missions. Appl. Sci. 2020, 10, 1256. [Google Scholar] [CrossRef]
- Allotta, B.; Costanzi, R.; Meli, E.; Pugi, L.; Ridolfi, A.; Vettori, G. Cooperative localization of a team of AUVs by a tetrahedral configuration. Robot. Auton. Syst. 2014, 62, 1228–1237. [Google Scholar] [CrossRef]
- Almeida, J.; Matias, B.; Ferreira, A.; Almeida, C.; Martins, A.; Silva, E. Underwater Localization System Combining iUSBL with Dynamic SBL in VAMOS Trials. Sensors 2020, 20, 4710. [Google Scholar] [CrossRef]
- Han, Y.; Zheng, C.; Sun, D. Accurate underwater localization using LBL positioning system. In Proceedings of the OCEANS 2015-MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–4. [Google Scholar]
- Garcia de Marina, H.; Cao, M.; Jayawardhana, B. Controlling Rigid Formations of Mobile Agents Under Inconsistent Measurements. IEEE Trans. Robot. 2015, 31, 31–39. [Google Scholar] [CrossRef]
- Krick, L.; Broucke, M.E.; Francis, B.A. Stabilization of infinitesimally rigid formations of multi-robot networks. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 477–482. [Google Scholar]
- Paley, D.A.; Zhang, F.; Leonard, N.E. Cooperative Control for Ocean Sampling: The Glider Coordinated Control System. IEEE Trans. Control Syst. Technol. 2008, 16, 735–744. [Google Scholar] [CrossRef]
- Ji, M.; Egerstedt, M. Distributed Coordination Control of Multiagent Systems While Preserving Connectedness. IEEE Trans. Robot. 2007, 23, 693–703. [Google Scholar] [CrossRef]
- Kim, J. Constructing 3D Underwater Sensor Networks without Sensing Holes Utilizing Heterogeneous Underwater Robots. Appl. Sci. 2021, 11, 4293. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S. Motion control of multiple autonomous ships to approach a target without being detected. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418763184. [Google Scholar] [CrossRef]
- Luo, S.; Kim, J.; Parasuraman, R.; Bae, J.H.; Matson, E.T.; Min, B.C. Multi-robot rendezvous based on bearing-aided hierarchical tracking of network topology. Ad Hoc Netw. 2019, 86, 131–143. [Google Scholar] [CrossRef]
- Bjelonic, M.; Kottege, N.; Homberger, T.; Borges, P.; Beckerle, P.; Chli, M. Weaver: Hexapod robot for autonomous navigation on unstructured terrain. J. Field Robot. 2018, 35, 1063–1079. [Google Scholar] [CrossRef]
- Sahin, F.; Stevenson, B. Modeling and dynamic control for a hexapod robot. In Proceedings of the 2015 10th System of Systems Engineering Conference (SoSE), San Antonio, TX, USA, 17–20 May 2015; pp. 304–309. [Google Scholar]
- Chang, D.; Wu, W.; Edwards, C.R.; Zhang, F. Motion Tomography: Mapping Flow Fields Using Autonomous Underwater Vehicles. Int. J. Robot. Res. 2017, 36, 320–336. [Google Scholar] [CrossRef]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House Radar Library: Boston, MA, USA, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).