Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review
Abstract
1. Introduction
1.1. Review Objectives and Research Strategy
1.2. Content of the Article
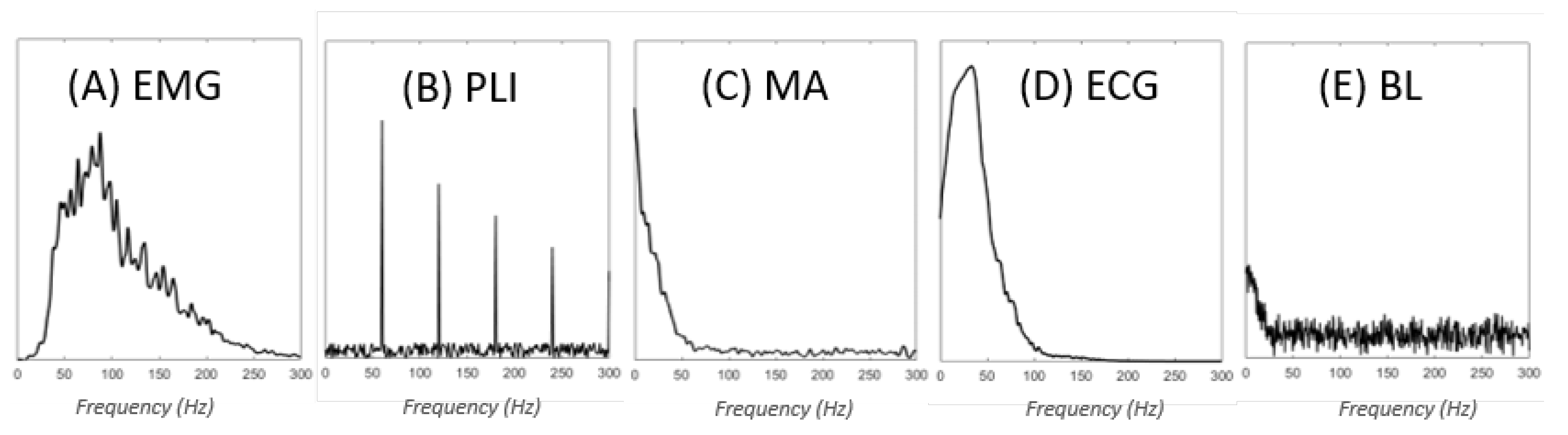
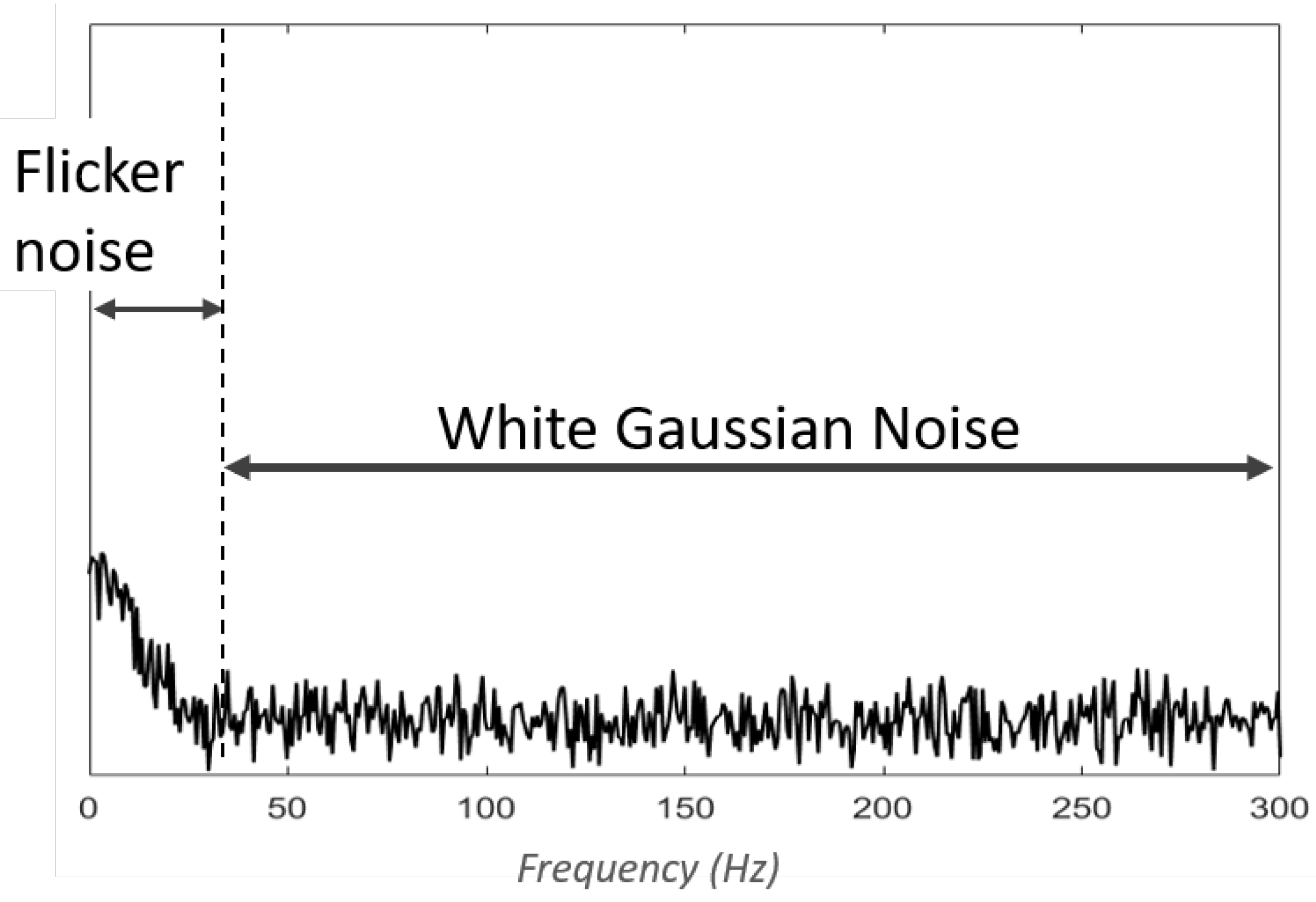
2. Contaminant Types
Other Terminology Considerations
3. Contaminant Reduction Methods
3.1. Conventional Digital Filters
3.2. Gating and Clipping Methods
3.3. Subtraction Methods in the Time Domain
3.3.1. Estimation of PLI Using the Regression Method on a Reference Signal
3.3.2. Estimation of PLI Using Spectral Analysis on a Reference Signal
3.3.3. Estimation of PLI Using the Least Squares Algorithm on the Signal Itself
3.3.4. Template Estimation of the ECG Interference Signal
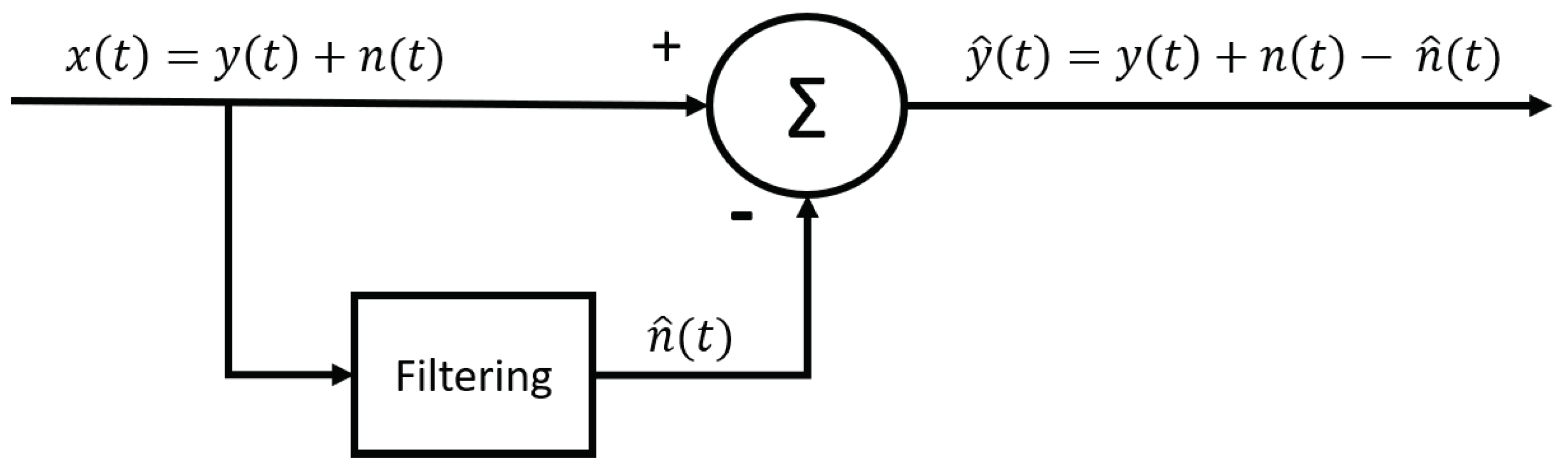
3.3.5. Adaptive Estimation of the Interference Signal by Means of Filtering the Raw Signal
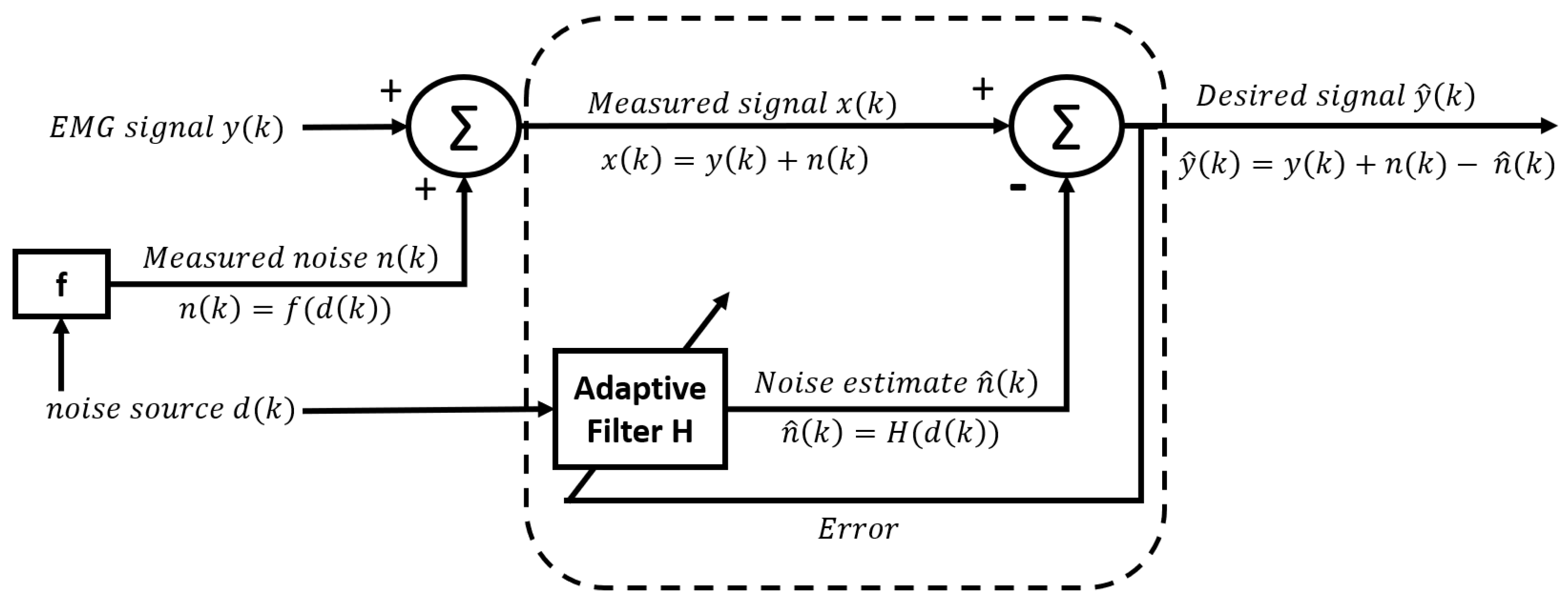
3.3.6. Adaptive Noise Canceller (ANC)
3.3.7. Nonlinear ANC
3.4. Denoising Methods after Signal Decomposition
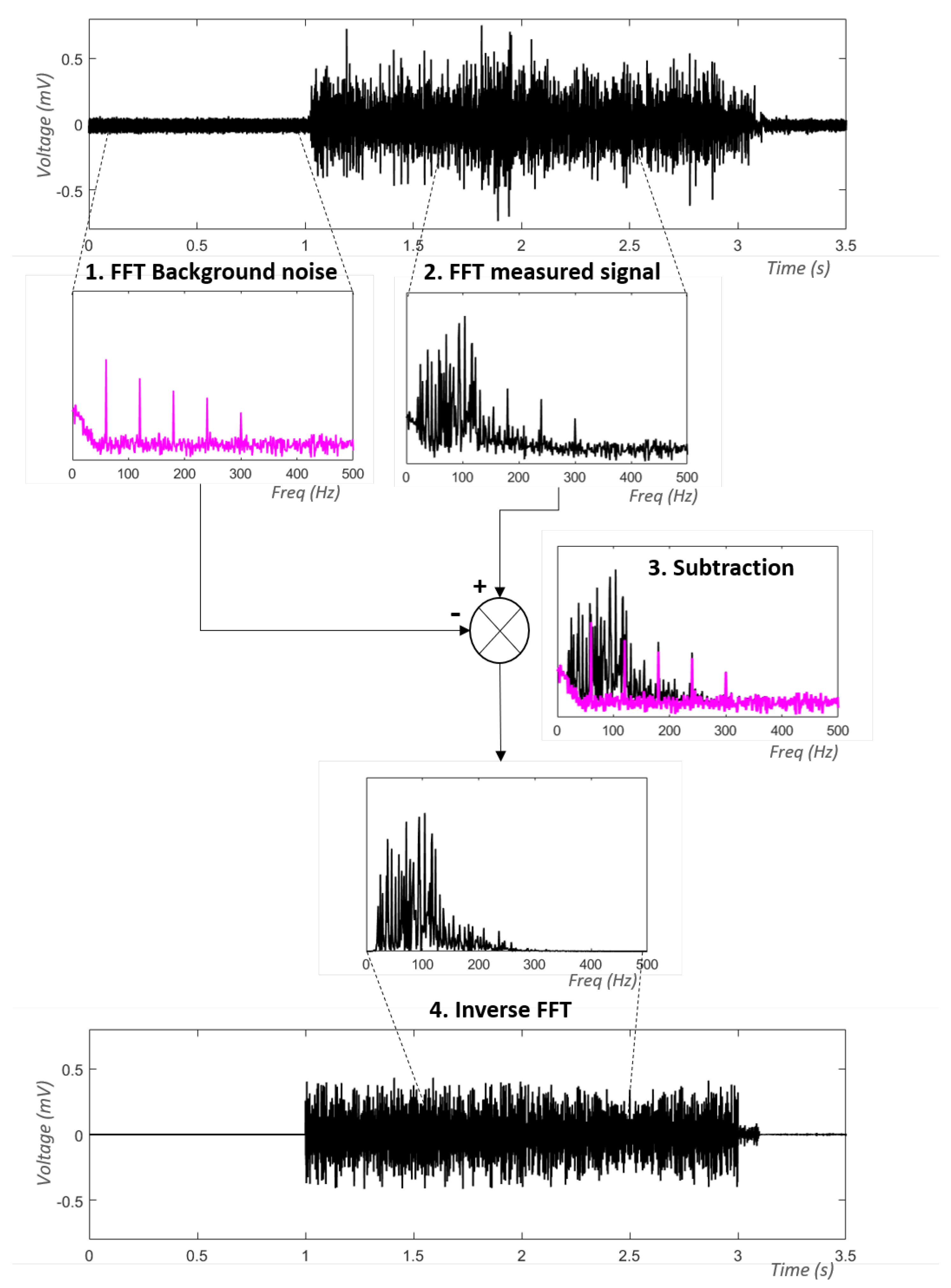
3.4.1. Decomposition Methods after Fourier Decomposition
3.4.2. Denoising Methods after Wavelet Decomposition
3.4.3. Denoising after Empirical Mode Decomposition (EMD)
3.4.4. Denoising after Variational Mode Decomposition (VMD)
3.5. Combining Methods and Hybrid Methods
3.5.1. Wavelet-ICA and EMD-ICA
3.5.2. Wavelet-Adaptive
3.5.3. Wavelet-Wiener and FFT-Wiener
4. Performance Evaluation
5. Discussion
5.1. Contaminant Type to Be Eliminated
5.2. Possibility to Be Used in Real-Time
5.3. Adaptivity of the Methods
5.4. Complementarity of the Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANC | Adaptive noise canceller |
| ANFIS | Adaptive neuro fuzzy inference system |
| BL | Baseline noise |
| BN | Background noise |
| BPN | Back propagation network |
| BSS | Blind source separation |
| BW | Baseline wander |
| CCA | Canonical correlation analysis |
| CCN | Cascade correlation network |
| CEEMD | Complementary ensemble empirical mode decomposition |
| CWT | Continuous wavelet transform |
| DCT | Discrete cosine transform |
| DPR | Maximum drop in power density |
| DWT | Discrete wavelet transform |
| ECG | Electrocardiographic signal |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical mode decomposition |
| EMG | Electromyography |
| ESAIC | Event-synchronous adaptive interference canceller |
| FIR | Finite impulse response |
| FT | Fourier transform |
| HD-EMG | High-dimension Electromyography |
| ICA | Independent component analysis |
| IMFs | Intrinsic mode functions |
| IT | Interval thresholding |
| IWT | Inverse wavelet transform |
| LMS | Least mean squares |
| MA | Motion artifacts |
| PCA | Principal component analysis |
| PLI | Power-line interference |
| RLS | Recursive least square |
| SCICA | Single channel independent component analysis |
| sEMG | Surface Electromyography |
| SER | Signal-to-ECG ratio |
| SIT | Soft interval thresholding |
| SMR | Signal-to-motion artifact ratio |
| SNR | Signal-to-noise ratio |
| SPR | Signal-to-powerline ratio |
| SWT | Stationary wavelet transform |
| VMD | Variational mode decomposition |
| VMFs | Variational mode functions |
| WGN | White Gaussian noise |
| WPT | Wavelet packet transform |
| WT | Wavelet transform |
References
- Chan, B.; Saad, I.; Bolong, N.; Siew, K.E. A Review of Surface EMG in Clinical Rehabilitation Care Systems Design. In Proceedings of the 2021 IEEE 19th Student Conference on Research and Development (SCOReD), Kota Kinabalu, Malaysia, 23–25 November 2021; pp. 371–376. [Google Scholar] [CrossRef]
- Rozaqi, L.; Nugroho, A.; Sanjaya, K.H.; Simbolon, A.I. Design of Analog and Digital Filter of Electromyography. In Proceedings of the 2019 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Serpong, Indonesia, 23–24 October 2019; IEEE: New York, NY, USA; pp. 186–192. [Google Scholar] [CrossRef]
- Corvini, G.; D’Anna, C.; Conforto, S. Estimation of mean and median frequency from synthetic sEMG signals: Effects of different spectral shapes and noise on estimation methods. Biomed. Signal Process. Control 2022, 73, 103420. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, D.; Sheng, X.; Zhu, X. Quantification and solutions of arm movements effect on sEMG pattern recognition. Biomed. Signal Process. Control 2014, 13, 189–197. [Google Scholar] [CrossRef]
- Maier, J.; Naber, A.; Ortiz-Catalan, M. Improved Prosthetic Control Based on Myoelectric Pattern Recognition via Wavelet-Based De-Noising. IEEE Trans. Neural. Syst. Rehabil. Eng. 2018, 26, 506–514. [Google Scholar] [CrossRef]
- Merletti, R.; Cerone, G.L. Tutorial. Surface EMG detection, conditioning and pre-processing: Best practices. J. Electromyogr. Kinesiol. 2020, 54, 102440. [Google Scholar] [CrossRef]
- Andrade, A.O.; Nasuto, S.; Kyberd, P.; Sweeney-Reed, C.M.; Van Kanijn, F.R. EMG signal filtering based on Empirical Mode Decomposition. Biomed. Signal Process. Control 2006, 1, 44–55. [Google Scholar] [CrossRef]
- Fraser, G.D.; Chan, A.D.; Green, J.R.; Macisaac, D.T. Automated biosignal quality analysis for electromyography using a one-class support vector machine. IEEE Trans. Instrum. Meas. 2014, 63, 2919–2930. [Google Scholar] [CrossRef]
- McCool, P.; Fraser, G.D.; Chan, A.D.; Petropoulakis, L.; Soraghan, J.J. Identification of contaminant type in surface electromyography (EMG) signals. IEEE Trans. Neural. Syst. Rehabil. Eng. 2014, 22, 774–783. [Google Scholar] [CrossRef]
- De Luca, C.J.; Donald Gilmore, L.; Kuznetsov, M.; Roy, S.H. Filtering the surface EMG signal: Movement artifact and baseline noise contamination. J. Biomech. 2010, 43, 1573–1579. [Google Scholar] [CrossRef]
- Huigen, E.; Peper, A.; Grimbergen, C.A. Investigation into the origin of the noise of surface electrodes. Med. Biol. Eng. Comput. 2002, 40, 332–338. [Google Scholar] [CrossRef]
- Drake, J.D.; Callaghan, J.P. Elimination of electrocardiogram contamination from electromyogram signals: An evaluation of currently used removal techniques. J. Electromyogr. Kinesiol. 2006, 16, 175–187. [Google Scholar] [CrossRef]
- Webster, J.G. Reducing Motion Artifacts and Interference in Biopotential Recording. IEEE Trans. Biomed. Eng. 1984, BME-31, 823–826. [Google Scholar] [CrossRef]
- Naik, G.R. Computational Intelligence in Electromyography Analysis: A Perspective on Current Applications and Future Challenges; InTech: London, UK, 2012. [Google Scholar]
- De Talhouet, H.; Webster, J.G. The origin of skin-stretch-caused motion artifacts under electrodes. Physiol. Meas. 1996, 17, 81. [Google Scholar] [CrossRef]
- Clancy, E.A.; Morin, E.L.; Merletti, R. Sampling, noise-reduction and amplitude estimation issues in surface electromyography. J. Electromyogr. Kinesiol. 2002, 12, 1–16. [Google Scholar] [CrossRef]
- Baratta, R.V.; Solomonow, M.; Zhou, B.H.; Zhu, M. Methods to reduce the variability of EMG power spectrum estimates. J. Electromyogr. Kinesiol. 1998, 8, 279–285. [Google Scholar] [CrossRef]
- Zivanovic, M.; Niegowski, M.; Lecumberri, P.; Gómez, M. A low-rank matrix factorization approach for joint harmonic and baseline noise suppression in biopotential signals. Comput. Methods Programs Biomed. 2017, 141, 59–71. [Google Scholar] [CrossRef]
- Vijayvargiya, A.; Gupta, V.; Kumar, R.; Dey, N.; Tavares, J.M.R. A hybrid WD-EEMD sEMG feature extraction technique for lower limb activity recognition. IEEE Sens. J. 2021, 21, 20431–20439. [Google Scholar] [CrossRef]
- Winter, D.A.; Rau, G.; Kadefors, R.; Broman, H.; De Luca, C. Units, terms and standards in the reporting of EMG research. ISEK 1980, 97. [Google Scholar]
- Merletti, R.; Di Torino, P. Standards for reporting EMG data. J. Electromyogr. Kinesiol. 1999, 9, 3–4. [Google Scholar]
- Stegeman, D.; Hermens, H. Standards for surface electromyography: The European project Surface EMG for non-invasive assessment of muscles (SENIAM). Enschede Roessingh Res. Dev. 2007, 10, 8–12. [Google Scholar]
- Van Boxtel, A. Optimal signal bandwidth for the recording of surface EMG activity of facial, jaw, oral, and neck muscles. J. Psychophysiol. 2001, 38, 22–34. [Google Scholar] [CrossRef]
- Clancy, E.A.; Farry, K.A. Adaptive whitening of the electromyogram to improve amplitude estimation. IEEE. Trans. Biomed. Eng. 2000, 47, 709–719. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, G.; Jiang, G.; Chen, D.; Liu, H. Surface EMG data aggregation processing for intelligent prosthetic action recognition. Neural. Comput. Appl. 2020, 32, 16795–16806. [Google Scholar] [CrossRef]
- Yacoub, S.; Raoof, K. Noise removal from surface respiratory EMG signal. Int. J. Comput. Sci. Eng. 2008, 2, 226–233. [Google Scholar] [CrossRef]
- Schweitzer, T.; Fitzgerald, J.; Bowden, J.; Lynne-Davies, P. Spectral analysis of human inspiratory diaphragmatic electromyograms. J. Appl. Physiol. 1979, 46, 152–165. [Google Scholar] [CrossRef]
- Redfern, M.S.; Hughes, R.E.; Chaffin, D.B. High-pass filtering to remove electrocardiographic interference from torso EMG recordings. Clin. Biomech. 1993, 8, 44–48. [Google Scholar] [CrossRef]
- Reaz, M.B.I.; Hussain, M.S.; Mohd-Yasin, F. Techniques of EMG signal analysis: Detection, processing, classification and applications. Biol. Proced. Online 2006, 8, 11–35. [Google Scholar] [CrossRef]
- Zhou, P.; Lock, B.; Kuiken, T.A. Real time ECG artifact removal for myoelectric prosthesis control. Physiol. Meas. 2007, 28, 397. [Google Scholar] [CrossRef]
- Rhou, B.; Sawan, M.; Desilets, T.; Bellemare, F. Real-time filtering technique to remove ECG interference from recorded esophageal EMG. In Proceedings of the 2008 IEEE Biomedical Circuits and Systems Conference, Baltimore, MD, USA, 20–22 November 2008; IEEE: New York, NY, USA; pp. 21–24. [Google Scholar] [CrossRef]
- Beck, T.W.; DeFreitas, J.M.; Cramer, J.T.; Stout, J.R. A comparison of adaptive and notch filtering for removing electromagnetic noise from monopolar surface electromyographic signals. Physiol. Meas. 2009, 30, 353–361. [Google Scholar] [CrossRef]
- Galiana-Merino, J.J.; Ruiz-Fernandez, D.; Martinez-Espla, J.J. Power line interference filtering on surface electromyography based on the stationary wavelet packet transform. Comput. Methods Programs Biomed. 2013, 111, 338–346. [Google Scholar] [CrossRef]
- Zivanovic, M.; Gonzalez-Izal, M. Simultaneous powerline interference and baseline wander removal from ECG and EMG signals by sinusoidal modeling. Med. Eng. Phys. 2013, 35, 1431–1441. [Google Scholar] [CrossRef]
- Fraser, G.D.; Chan, A.D.; Green, J.R.; Abser, N.; MacIsaac, D. CleanEMG—Power line interference estimation in sEMG using an adaptive least squares algorithm. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 1–3 September 2011; IEEE: New York, NY, USA, 2011; pp. 7941–7944. [Google Scholar] [CrossRef]
- Bloch, R. Subtraction of electrocardiographic signal from respiratory electromyogram. J. Appl. Physiol. 1983, 55, 619–623. [Google Scholar] [CrossRef] [PubMed]
- Levine, S.; Gillen, J.; Weiser, P.; Gillen, M.; Kwatny, E. Description and validation of an ECG removal procedure for EMGdi power spectrum analysis. J. Appl. Physiol. 1986, 60, 1073–1081. [Google Scholar] [CrossRef] [PubMed]
- Bartolo, A.; Dzwonczyk, R.; Roberts, O.; Goldman, E. Description and validation of a technique for the removal of ECG contamination from diaphragmatic EMG signal. Med. Biol. Eng. Comput. 1996, 34, 76–81. [Google Scholar] [CrossRef]
- Junior, J.D.C.; de Seixas, J.M.; de Sá Miranda, A.F.M.L. A template subtraction method for reducing electrocardiographic artifacts in EMG signals of low intensity. Biomed. Signal Process. Control 2019, 47, 380–386. [Google Scholar] [CrossRef]
- Jonkman, A.H.; Juffermans, R.; Doorduin, J.; Heunks, L.M.; Harlaar, J. Estimated ECG Subtraction method for removing ECG artifacts in esophageal recordings of diaphragm EMG. Biomed. Signal Process. Control 2021, 69, 102861. [Google Scholar] [CrossRef]
- Sbrollini, A.; Agostinelli, A.; Morettini, M.; Verdini, F.; Nardo, F.D.; Fioretti, S.; Burattini, L. Separation of superimposed electrocardiographic and electromyographic signals. In EMBEC & NBC 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 518–521. [Google Scholar] [CrossRef]
- Conforto, S.; D’Alessio, T. Optimal rejection of artifacts in the processing of surface EMG signals for movement analysis. In Computer Methods in Biomechanics & Biomedical Engineering–2; CRC Press: Boca Raton, FL, USA, 2020; pp. 799–805. [Google Scholar]
- Conforto, S.; D’Alessio, T.; Pignatelli, S. Optimal rejection of movement artefacts from myoelectric signals by means of a wavelet filtering procedure. J. Electromyogr. Kinesiol. 1999, 9, 47–57. [Google Scholar] [CrossRef]
- Fraser, G.D.; Chan, A.D.; Green, J.R.; MacIsaac, D. Detection of ADC clipping, quantization noise, and amplifier saturation in surface electromyography. In Proceedings of the MeMeA 2012—2012 IEEE Symposium on Medical Measurements and Applications, Budapest, Hungary, 18–19 May 2012; pp. 162–166. [Google Scholar] [CrossRef]
- Marker, R.J.; Maluf, K.S. Effects of electrocardiography contamination and comparison of ECG removal methods on upper trapezius electromyography recordings. J. Electromyogr. Kinesiol. 2014, 24, 902–909. [Google Scholar] [CrossRef]
- Widrow, B.; Glover, J.R.; McCool, J.M.; Kaunitz, J.; Williams, C.S.; Hearn, R.H.; Zeidler, J.R.; Dong, J.E.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE 1975, 63, 1692–1716. [Google Scholar] [CrossRef]
- Akkiraju, P.; Reddy, D. Adaptive cancellation technique in processing myoelectric activity of respiratory muscles. IEEE Trans. Biomed. Eng. 1992, 39, 652–655. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Lin, Z.; Ramahi, M.; Mittal, R. Adaptive cancellation of ECG artifacts in the diaphragm electromyographic signals obtained through intraoesophageal electrodes during swallowing and inspiration. Neurogastroenterol. Motil. 1994, 6, 279–288. [Google Scholar] [CrossRef]
- Zhou, P.; Kuiken, T.A. Eliminating cardiac contamination from myoelectric control signals developed by targeted muscle reinnervation. Physiol. Meas. 2006, 27, 1311. [Google Scholar] [CrossRef]
- Xu, L.; Peri, E.; Vullings, R.; Rabotti, C.; Van Dijk, J.P.; Mischi, M. Comparative review of the algorithms for removal of electrocardiographic interference from trunk electromyography. Sensors 2020, 20, 4890. [Google Scholar] [CrossRef]
- Lu, G.; Brittain, J.S.; Holland, P.; Yianni, J.; Green, A.L.; Stein, J.F.; Aziz, T.Z.; Wang, S. Removing ECG noise from surface EMG signals using adaptive filtering. Neurosci. Lett. 2009, 462, 14–19. [Google Scholar] [CrossRef]
- Marque, C.; Bisch, C.; Dantas, R.; Elayoubi, S.; Brosse, V.; Perot, C. Adaptive filtering for ECG rejection from surface EMG recordings. J. Electromyogr. Kinesiol. 2005, 15, 310–315. [Google Scholar] [CrossRef] [PubMed]
- Ortolan, R.L.; Mori, R.N.; Pereira, R.R.; Cabral, C.M.; Pereira, J.C.; Cliquet, A. Evaluation of adaptive/nonadaptive filtering and wavelet transform techniques for noise reduction in EMG mobile acquisition equipment. IEEE Trans. Neural. Syst. Rehabil. Eng. 2003, 11, 60–69. [Google Scholar] [CrossRef]
- Costa, M.H.; Tavares, M.C. Removing harmonic power line interference from biopotential signals in low cost acquisition systems. Comput. Biol. Med. 2009, 39, 519–526. [Google Scholar] [CrossRef]
- Malboubi, M.; Razzazi, F.; Aliyari, S.M. Elimination of power line noise from EMG signals using an efficient adaptive Laguerre filter. In Proceedings of the ICSES 2010 International Conference on Signals and Electronic Circuits, Gliwice, Poland, 7–10 September 2010; IEEE: New York, NY, USA, 2010; pp. 49–52. [Google Scholar]
- Deng, Y.; Wolf, W.; Schnell, R.; Appel, U. New aspects to event-synchronous cancellation of ECG interference: An application of the method in diaphragmatic EMG signals. IEEE Trans. Biomed. Eng. 2000, 47, 1177–1184. [Google Scholar] [CrossRef] [PubMed]
- Vijila, C.K.S.; Kumar, C.E.S. Interference cancellation in EMG signal Using ANFIS. Int. J. Recent Trends Eng. Res. 2009, 2, 244. [Google Scholar]
- Abbaspour, S.; Fallah, A.; Lindén, M.; Gholamhosseini, H. A novel approach for removing ECG interferences from surface EMG signals using a combined ANFIS and wavelet. J. Electromyogr. Kinesiol. 2016, 26, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Lin, Z.; Yin, F. Removal of ECG contamination from diaphragmatic EMG by nonlinear filtering. Nonlinear Anal. Theory Methods Appl. 2005, 63, 745–753. [Google Scholar] [CrossRef]
- Chen, S.; Luo, Z.; Hua, T. Research on AR-AKF Model Denoising of the EMG Signal. Comput. Math. Methods Med. 2021, 2021, 940950. [Google Scholar] [CrossRef]
- Kim, M.; Moon, Y.; Hunt, J.; McKenzie, K.A.; Horin, A.; McGuire, M.; Kim, K.; Hargrove, L.J.; Jayaraman, A. A Novel Technique to Reject Artifact Components for Surface EMG Signals Recorded During Walking With Transcutaneous Spinal Cord Stimulation: A Pilot Study. Front. Hum. Neurosci. 2021, 15, 660583. [Google Scholar] [CrossRef] [PubMed]
- Aschero, G.; Gizdulich, P. Denoising of surface EMG with a modified Wiener filtering approach. J. Electromyogr. Kinesiol. 2010, 20, 366–373. [Google Scholar] [CrossRef]
- Djellatou, M.E.F.; Nougarou, F.; Massicotte, D. Enhanced FBLMS algorithm for ECG and noise removal from sEMG signals. In Proceedings of the 2013 18th International Conference on Digital Signal Processing (DSP), Corfu, Greece, 1–3 July 2013; IEEE: New York, NY, USA, 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Shin, H.S.; Lee, C.; Lee, M. Ideal filtering approach on DCT domain for biomedical signals: Index blocked DCT filtering method (IB-DCTFM). J. Med. Syst. 2010, 34, 741–753. [Google Scholar] [CrossRef]
- Mewett, D.T.; Nazeran, H.; Reynolds, K.J. Removing power line noise from recorded EMG. In Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey, 25–28 October 2001; IEEE: New York, NY, USA, 2001; Volume 3, pp. 2190–2193. [Google Scholar]
- Allen, D.P. A frequency domain Hampel filter for blind rejection of sinusoidal interference from electromyograms. J. Neurosci. Methods 2009, 177, 303–310. [Google Scholar] [CrossRef]
- Wei, G.; Tian, F.; Tang, G.; Wang, C. A wavelet-based method to predict muscle forces from surface electromyography signals in weightlifting. J. Bionic Eng. 2012, 9, 48–58. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Phinyomark, A.; Phukpattaranont, P.; Limsakul, C. The usefulness of wavelet transform to reduce noise in the SEMG signal. In EMG Methods for Evaluating Muscle and Nerve Function; BoD–Books on Demand: Norderstedt, Germany, 2012; pp. 107–132. [Google Scholar]
- Jamaluddin, F.N.; Ahmad, S.A.; Noor, S.B.M.; Hassan, W.Z.W.; Yaacob, A.; Adam, Y. Estimation of wavelet threshold value for surface EMG baseline removal. In Proceedings of the 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 4–8 December 2016; IEEE: New York, NY, USA, 2016; pp. 102–105. [Google Scholar] [CrossRef]
- Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. EMG denoising estimation based on adaptive wavelet thresholding for multifunction myoelectric control. In Proceedings of the 2009 Innovative Technologies in Intelligent Systems and Industrial Applications, Kuala Lumpur, Malaysia, 25–26 July 2009; IEEE: New York, NY, USA, 2009; pp. 171–176. [Google Scholar] [CrossRef]
- Limem, M.; Hamdi, M.A. Uterine Electromyography signals denoising using discrete wavelet transform. In Proceedings of the 2015 International Conference on Advances in Biomedical Engineering (ICABME), Beirut, Lebanon, 16–18 September 2015; IEEE: New York, NY, USA, 2015; pp. 101–103. [Google Scholar] [CrossRef]
- Jiang, C.F.; Kuo, S.L. A comparative study of wavelet denoising of surface electromyographic signals. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: New York, NY, USA, 2007; pp. 1868–1871. [Google Scholar] [CrossRef]
- Rampp, S.; Prell, J.; Thielemann, H.; Posch, S.; Strauss, C.; Romstöck, J. Baseline correction of intraoperative electromyography using discrete wavelet transform. J. Clin. Monit. Comput. 2007, 21, 219–226. [Google Scholar] [CrossRef]
- Phinyomark, A. Optimal Wavelet Functions in Wavelet Denoising for Multifunction Myoelectric Control. Trans. Electr. Eng. Electron. Commun. 2010, 8. [Google Scholar]
- Abbas, B.; Farooq, O.; Uzzaman, Y.; Khan, A.A.; Vyas, A. Enhancing classification accuracy of wrist movement by denoising sEMG signals. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; IEEE: New York, NY, USA, 2013; pp. 5762–5764. [Google Scholar] [CrossRef]
- Bartolomeo, L.; Zecca, M.; Sessa, S.; Lin, Z.; Mukaeda, Y.; Ishii, H.; Takanishi, A. Baseline adaptive wavelet thresholding technique for sEMG denoising. In Proceedings of the American institute of Physics (AIP), Chandigarh, India, 23–26 February 2011; American Institute of Physics: College Park, MD, USA, 2011; Volume 1371, pp. 205–214. [Google Scholar]
- Schimmack, M.; Mercorelli, P. Noise detection for biosignals using an orthogonal wavelet packet tree denoising algorithm. Int. J. Electron. Telecommun. 2016, 62, 15–21. [Google Scholar] [CrossRef]
- Petersen, E.; Sauer, J.; Graßhoff, J.; Rostalski, P. Removing cardiac artifacts from single-channel respiratory electromyograms. IEEE Access 2020, 8, 30905–30917. [Google Scholar] [CrossRef]
- Amirmazlaghani, M.; Amindavar, H. EMG signal denoising via Bayesian wavelet shrinkage based on GARCH modeling. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; IEEE: New York, NY, USA, 2009; pp. 469–472. [Google Scholar] [CrossRef]
- Slim, Y.; Raoof, K. Removal of ECG interference from surface respiratory electromyography. IRBM 2010, 31, 209–220. [Google Scholar] [CrossRef]
- Sharma, T.; Veer, K. Comparative study of wavelet denoising in myoelectric control applications. J. Med. Eng. Technol. 2016, 40, 80–86. [Google Scholar] [CrossRef]
- Gradolewski, D.; Tojza, P.M.; Jaworski, J.; Ambroziak, D.; Redlarski, G.; Krawczuk, M. Arm EMG wavelet-based denoising system. In Mechatronics-Ideas for Industrial Application; Springer: Berlin/Heidelberg, Germany, 2015; pp. 289–296. [Google Scholar] [CrossRef]
- Strazza, A.; Verdini, F.; Mengarelli, A.; Cardarelli, S.; Tigrini, A.; Fioretti, S.; Di Nardo, F. Wavelet Analysis-Based Reconstruction for sEMG Signal Denoising. In Proceedings of the Mediterranean Conference on Medical, Biological Engineering and Computing, Coimbra, Portugal, 26–28 September 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 245–252. [Google Scholar] [CrossRef]
- Chowdhury, R.; Reaz, M.; Ali, M.; Bakar, A.; Chellappan, K.; Chang, T. Surface Electromyography Signal Processing and Classification Techniques. Sensors 2013, 13, 12431–12466. [Google Scholar] [CrossRef]
- Guang-ying, Y.; Zhi-zeng, L. Surface electromyography disposal based on the method of wavelet de-noising and power spectrum. In Proceedings of the 2004 International Conference on Intelligent Mechatronics and Automation, Chengdu, China, 26–31 August 2004; IEEE: New York, NY, USA, 2004; pp. 896–900. [Google Scholar] [CrossRef]
- Guo, X.; Yang, P.; Li, Y.; Yan, W.L. The SEMG analysis for the lower limb prosthesis using wavelet transformation. In Proceedings of the The 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; IEEE: New York, NY, USA, 2004; Volume 1, pp. 341–344. [Google Scholar] [CrossRef]
- Qingju, Z.; Zhizeng, L. Wavelet de-noising of electromyography. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; IEEE: New York, NY, USA, 2006; pp. 1553–1558. [Google Scholar]
- Jiang, D.; Li, G.F.; Sun, Y.; Jiang, G.Z.; Kong, J.Y.; Xu, S. Pretreatment of sEMG using wavelet threshold method. In Proceedings of the 2018 International Conference on Machine Learning and Cybernetics (ICMLC), Chengdu, China, 15–18 July 2018; IEEE: New York, NY, USA, 2018; Volume 2, pp. 638–643. [Google Scholar] [CrossRef]
- Wang, H.P.; Bi, Z.Y.; Fan, W.J.; Zhou, Y.X.; Zhou, Y.X.; Li, F.; Wang, K.; Lü, X.Y.; Wang, Z.G. Real-Time Artifact Removal System for Surface EMG Processing during Ten-Fold Frequency Electrical Stimulation. IEEE Access 2021, 9, 68320–68331. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Phinyomark, A.; Phukpattaranont, P.; Limsakul, C. Wavelet-based denoising algorithm for robust EMG pattern recognition. Fluct. Noise Lett. 2011, 10, 157–167. [Google Scholar] [CrossRef]
- Zhan, C.; Yeung, L.F.; Yang, Z. A wavelet-based adaptive filter for removing ECG interference in EMGdi signals. J. Electromyogr. Kinesiol. 2010, 20, 542–549. [Google Scholar] [CrossRef]
- Sobahi, N. Denoising of EMG signals based on wavelet transform. Asia-SAME Trans. Eng. Sci. 2011, 1, 17–23. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Pilkar, R.; Yarossi, M.; Ramanujam, A.; Rajagopalan, V.; Bayram, M.B.; Mitchell, M.; Canton, S.; Forrest, G. Application of empirical mode decomposition combined with notch filtering for interpretation of surface electromyograms during functional electrical stimulation. IEEE Trans. Neural. Syst. Rehabil. Eng. 2016, 25, 1268–1277. [Google Scholar] [CrossRef]
- Naji, M.; Firoozabadi, M.; Kahrizi, S. The Application of Empirical Mode Decomposition in Elimination of ECG contamination from EMG signals. In Proceedings of the 2011 18th Iranian Conference of Biomedical Engineering (ICBME), Tehran, Iran, 14–16 December 2011; IEEE: New York, NY, USA, 2011; pp. 77–80. [Google Scholar] [CrossRef]
- Kopsinis, Y.; McLaughlin, S. Development of EMD-based denoising methods inspired by wavelet thresholding. IEEE Trans. Signal Process 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Ashraf, H.; Waris, A.; Gilani, S.O.; Tariq, M.U.; Alquhayz, H. Threshold parameters selection for empirical mode decomposition-based EMG signal denoising. Intell. Autom. Soft Comput. 2021, 27, 799–815. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, P. Filtering of surface EMG using ensemble empirical mode decomposition. Med. Eng. Phys. 2013, 35, 537–542. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Sun, Z.; Xi, X.; Yuan, C.; Yang, Y.; Hua, X. Surface electromyography signal denoising via EEMD and improved wavelet thresholds. Math. Biosci. Eng. 2020, 17, 6945–6962. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Xi, X.; Zhang, Y.; Zhao, Y.; She, Q.; Luo, Z. Denoising of surface electromyogram based on complementary ensemble empirical mode decomposition and improved interval thresholding. Rev. Sci. Instrum. 2019, 90, 035003. [Google Scholar] [CrossRef]
- Damasevicius, R.; Vasiljevas, M.; Martisius, I.; Jusas, V.; Birvinskas, D.; Wozniak, M. BoostEMD: An extension of EMD method and its application for denoising of EMG signals. Elektron. Ir. Elektrotechnika 2015, 21, 57–61. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, D.; Guo, X.; Wang, Y. VMD-based denoising methods for surface electromyography signals. J. Neural Eng. 2019, 16, 056017. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Ma, S.; Lv, B.; Lin, C.; Sheng, X.; Zhu, X. EMG signal filtering based on variational mode decomposition and sub-band thresholding. IEEE J. Biomed. Health Inform. 2020, 25, 47–58. [Google Scholar] [CrossRef]
- Cao, X.R.; Liu, R.w. General approach to blind source separation. IEEE Trans. Signal Process. 1996, 44, 562–571. [Google Scholar]
- Azzerboni, B.; Carpentieri, M.; La Foresta, F.; Morabito, F. Neural-ICA and wavelet transform for artifacts removal in surface EMG. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; IEEE: New York, NY, USA, 2004; Volume 4, pp. 3223–3228. [Google Scholar] [CrossRef]
- Taelman, J.; Van Huffel, S.; Spaepen, A. Wavelet-independent component analysis to remove electrocardiography contamination in surface electromyography. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: New York, NY, USA, 2007; pp. 682–685. [Google Scholar]
- von Tscharner, V.; Eskofier, B.; Federolf, P. Removal of the electrocardiogram signal from surface EMG recordings using non-linearly scaled wavelets. J. Electromyogr. Kinesiol. 2011, 21, 683–688. [Google Scholar] [CrossRef]
- Abbaspour, S.; Lindén, M.; Gholamhosseini, H. ECG Artifact Removal from Surface EMG Signal Using an Automated Method Based on Wavelet-ICA. In Proceedings of the Phealth 2015 Proceedings Of The 12th International Conference On Wearable Micro And Nano Technologies For Personalized Health, Västerås, Sweden, 2–4 June 2015; pp. 91–97. [Google Scholar]
- Mijović, B.; De Vos, M.; Gligorijević, I.; Taelman, J.; Van Huffel, S. Source separation from single-channel recordings by combining empirical-mode decomposition and independent component analysis. IEEE Trans. Biomed. Eng. 2010, 57, 2188–2196. [Google Scholar] [CrossRef]
- Wang, F.; Qiao, X.y. Removal of Motion Noise from Surface-electromyography Signal Using Wavelet Adaptive Filter. In Proceedings of the 2016 3rd International Conference on Materials Engineering, Manufacturing Technology and Control, Taiyuan, China, 27–28 February 2016; Atlantis Press: Amsterdam, The Netherlands, 2016; pp. 1270–1274. [Google Scholar] [CrossRef]
- Liu, J.; Ying, D.; Zhou, P. Wiener filtering of surface EMG with a priori SNR estimation toward myoelectric control for neurological injury patients. Med. Eng. Phys. 2014, 36, 1711–1715. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Phys. A Stat. Mech. Appl. 2014, 400, 159–167. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boyer, M.; Bouyer, L.; Roy, J.-S.; Campeau-Lecours, A. Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review. Sensors 2023, 23, 2927. https://doi.org/10.3390/s23062927
Boyer M, Bouyer L, Roy J-S, Campeau-Lecours A. Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review. Sensors. 2023; 23(6):2927. https://doi.org/10.3390/s23062927
Chicago/Turabian StyleBoyer, Marianne, Laurent Bouyer, Jean-Sébastien Roy, and Alexandre Campeau-Lecours. 2023. "Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review" Sensors 23, no. 6: 2927. https://doi.org/10.3390/s23062927
APA StyleBoyer, M., Bouyer, L., Roy, J.-S., & Campeau-Lecours, A. (2023). Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review. Sensors, 23(6), 2927. https://doi.org/10.3390/s23062927






