A Modified Keystone-Based Forward-Looking Arc Array Synthetic Aperture Radar 3D Imaging Method
Abstract
1. Introduction
2. Arc Array Synthetic Aperture Radar (AA-SAR)
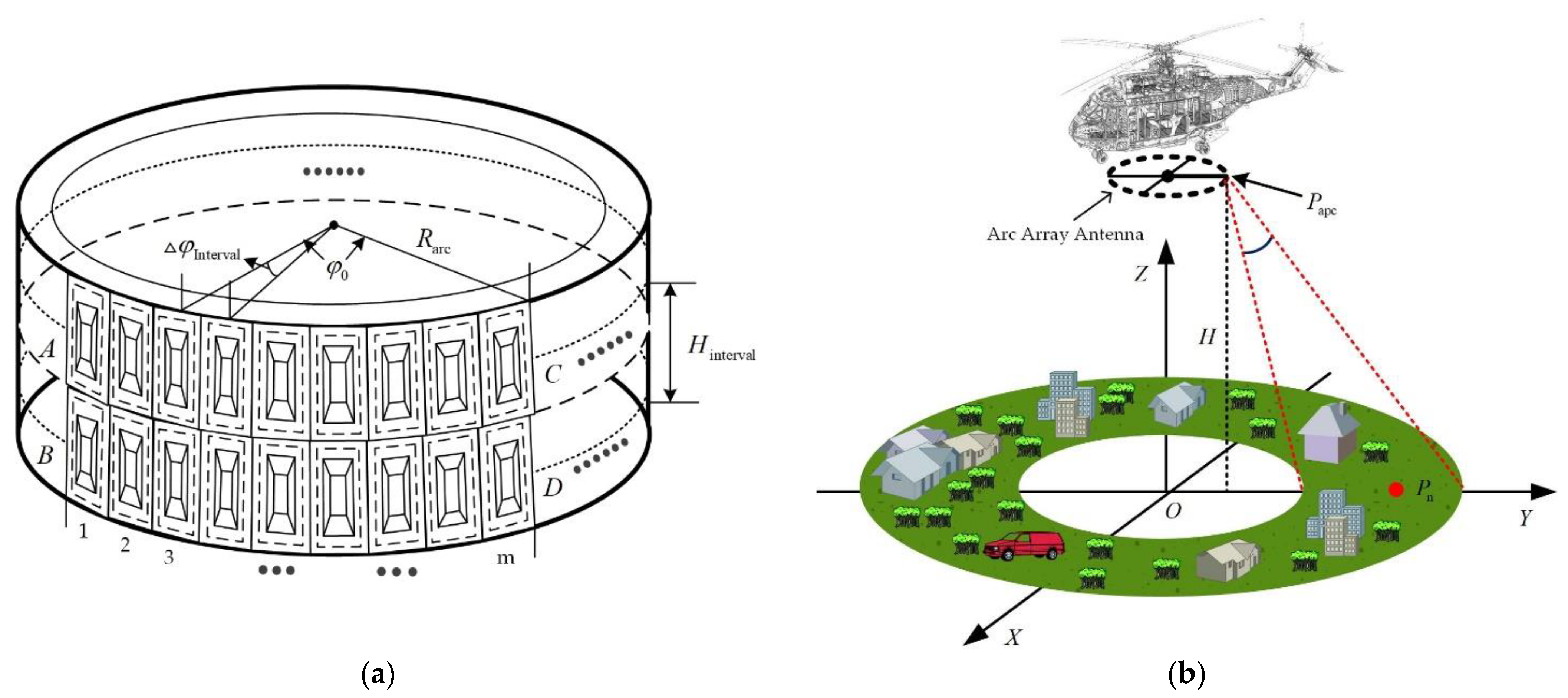
2.1. Imaging Geometry
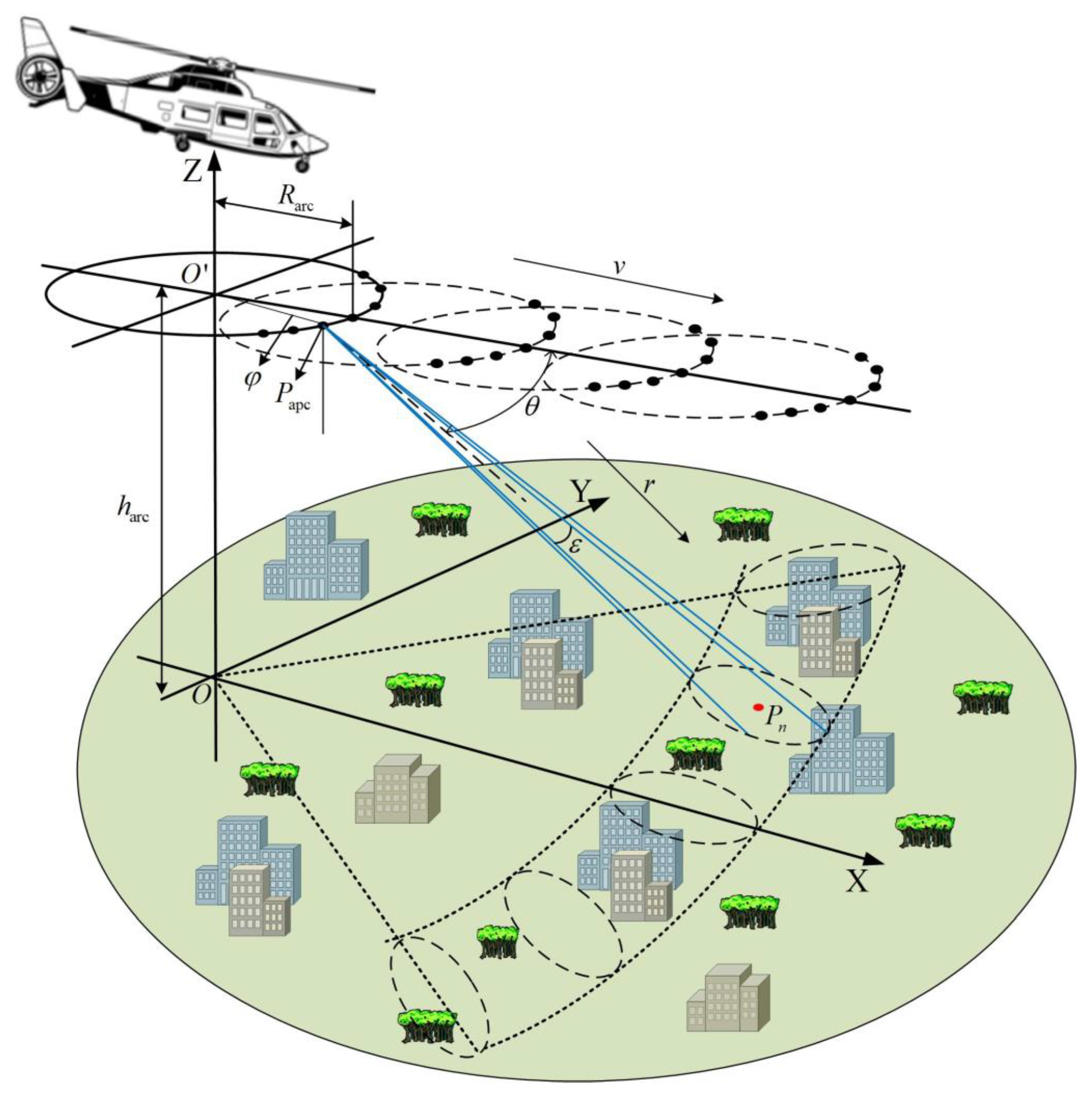
2.2. Platform Observation Geometry in Forward Mode
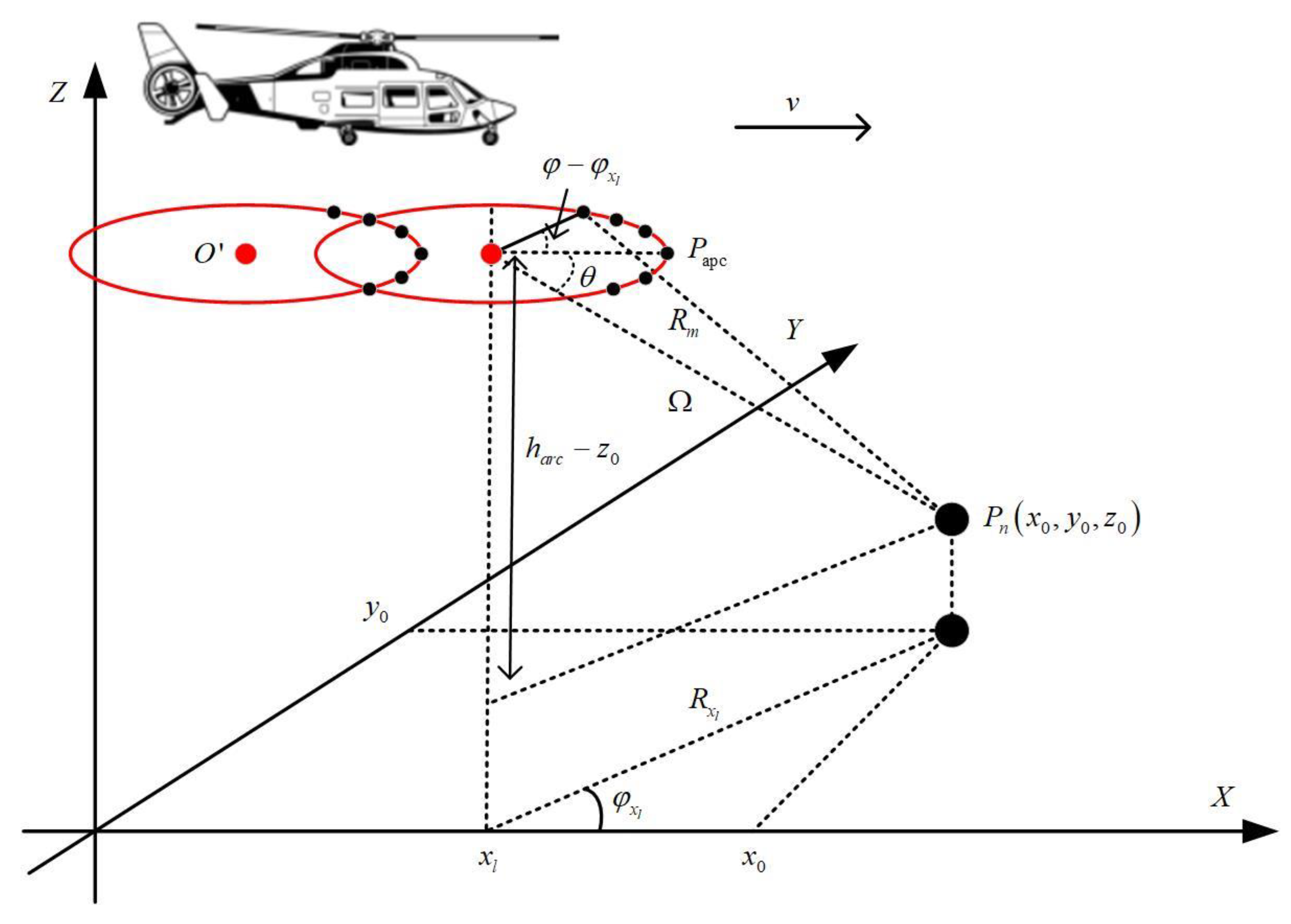
3. Analysis of Change in the Azimuth Angle
3.1. Echo Signal Model
3.2. Target Azimuth Analysis
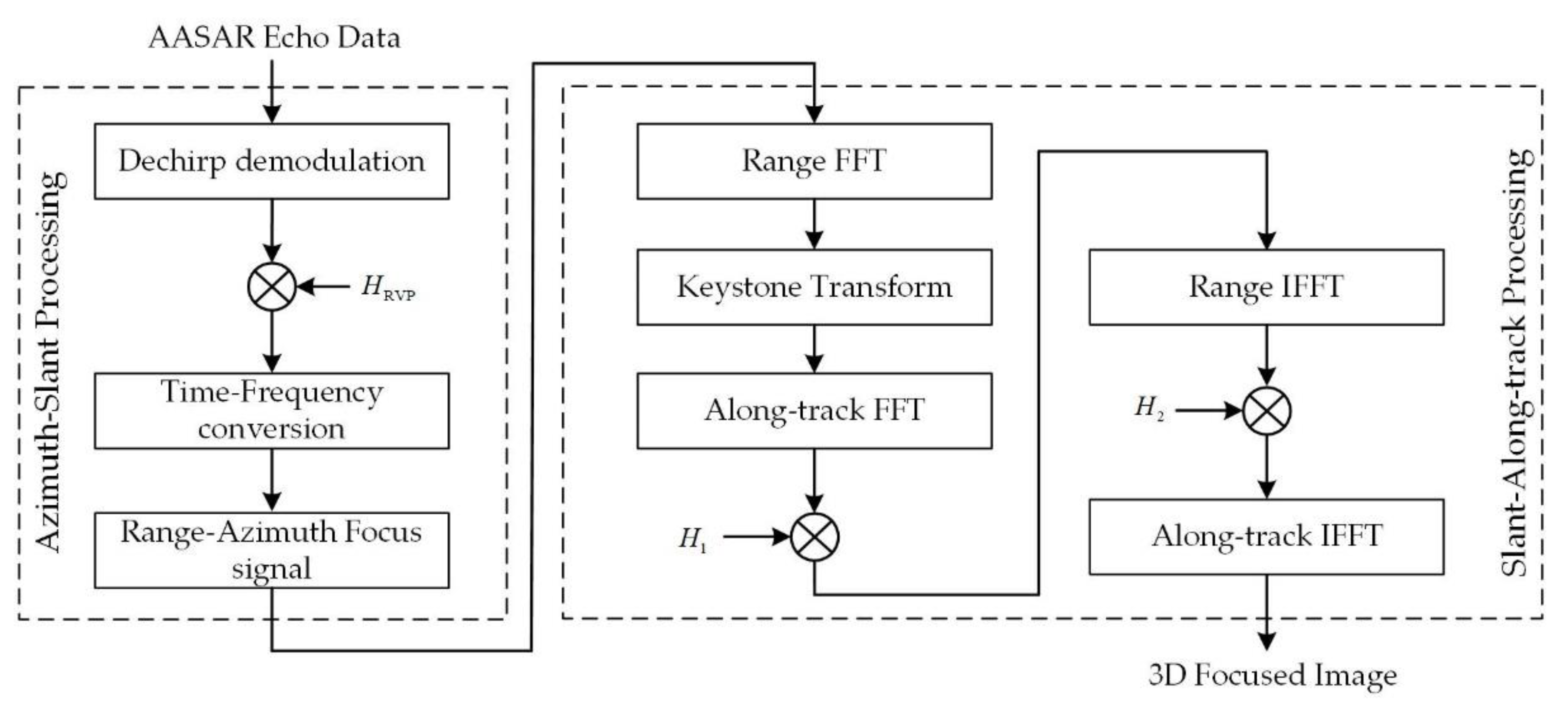
4. Arc Array SAR 3D Imaging Algorithm
4.1. Azimuth–Slant Range Processing
4.2. Improved Transformation Based on Keystone
5. Numerical Simulation Experiments
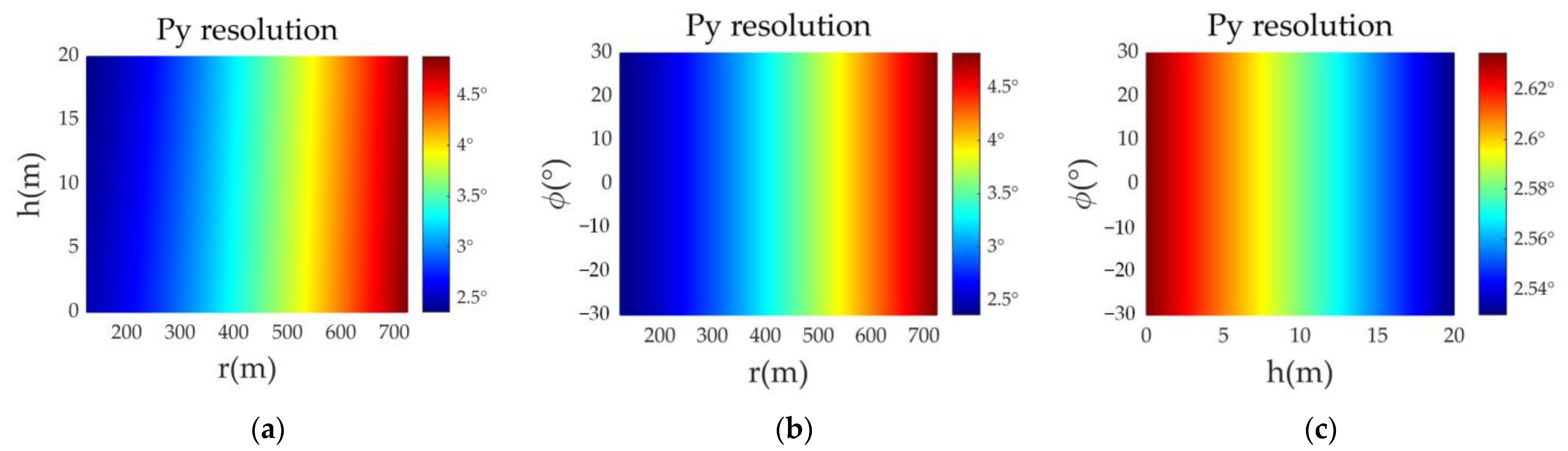
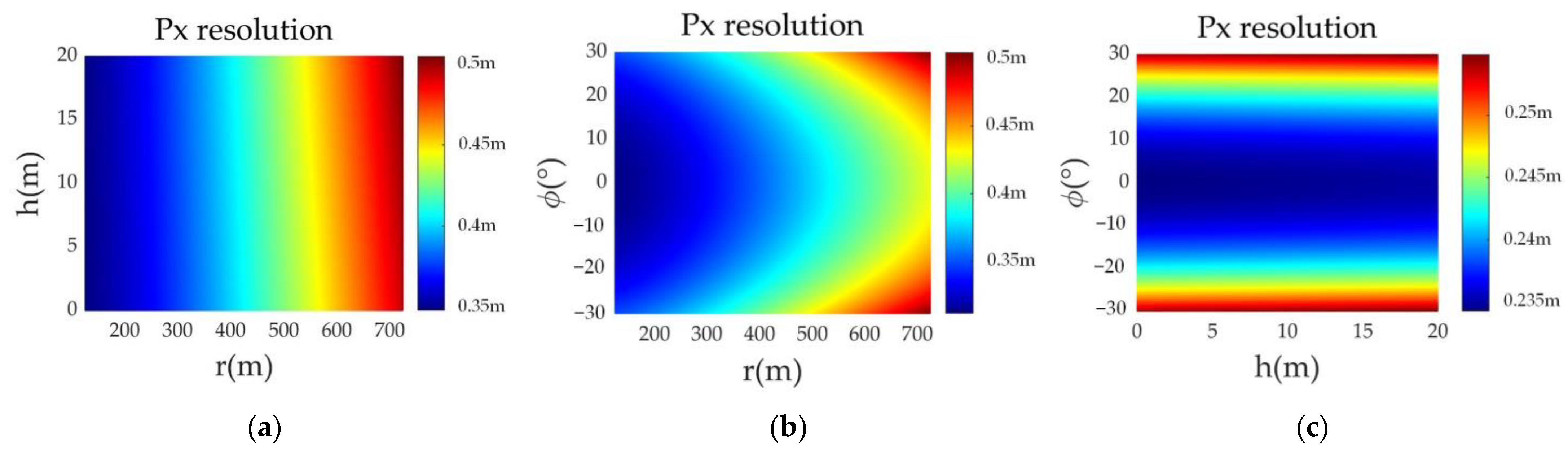
5.1. Spatial Resolution Analysis
5.1.1. Azimuth Resolution
5.1.2. Along-Track Resolution
5.1.3. Height-Wise Resolution
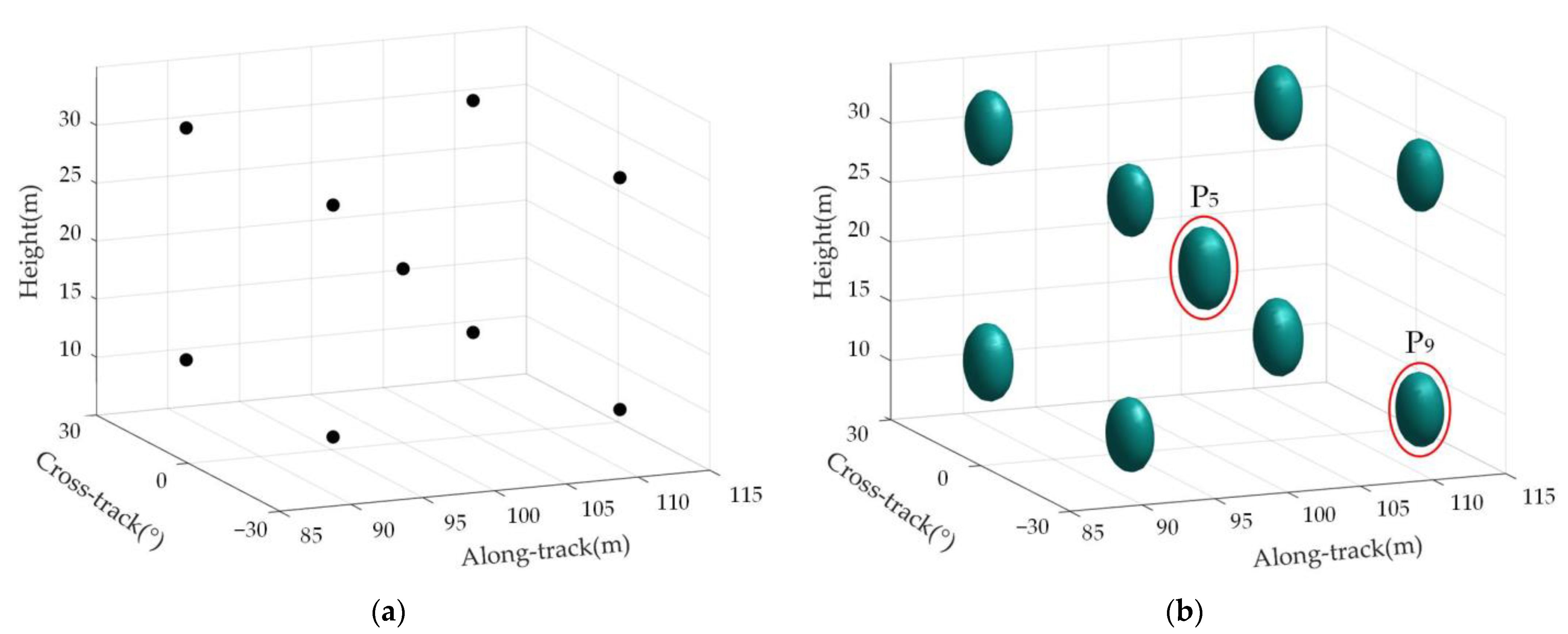
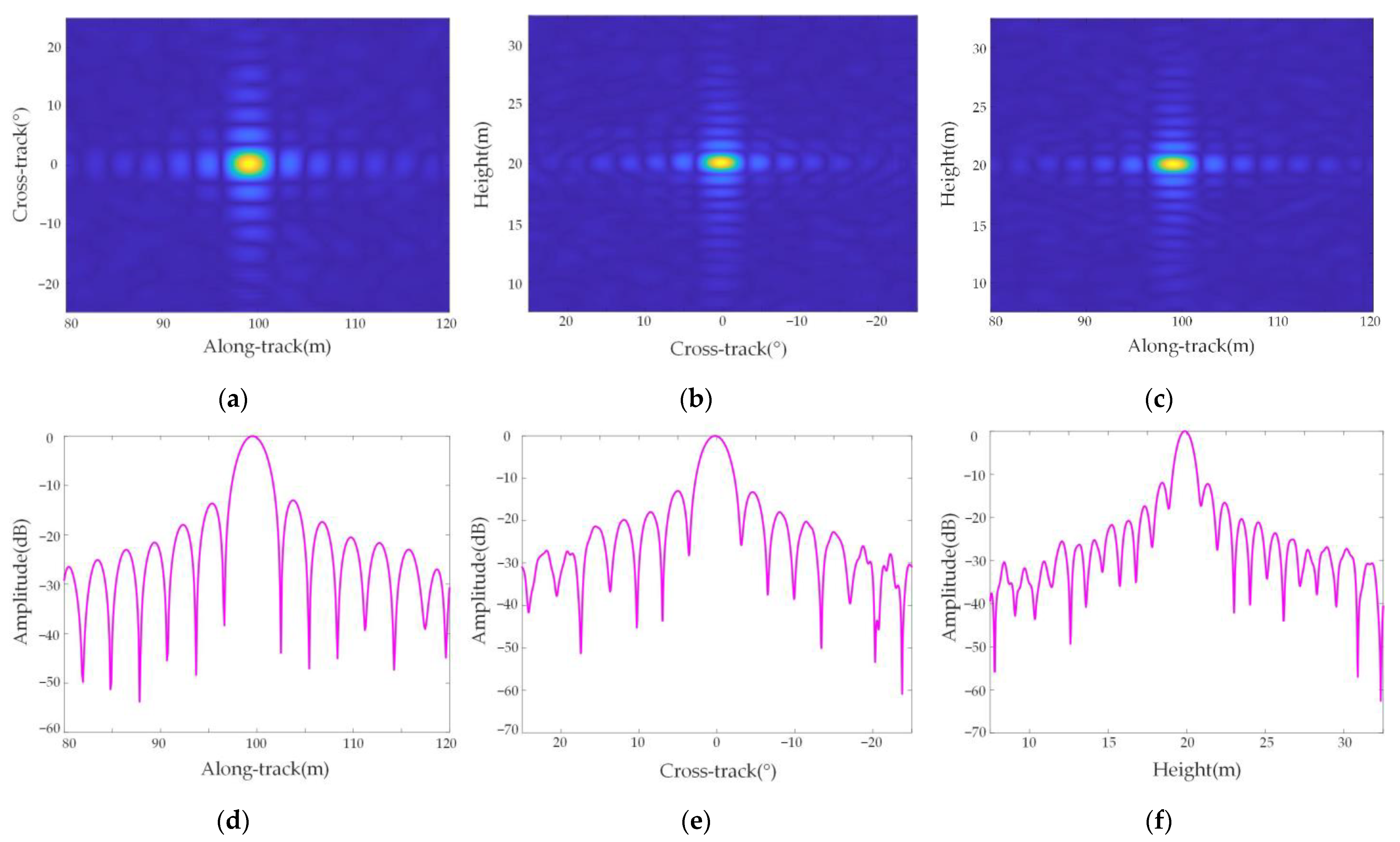
5.2. Point Target Imaging Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, J.R.; Cumming, I.G.; Deane, R.A. The digital processing of Seasat synthetic aperture radar data. In Proceedings of the International Radar Conference, Arlington, VA, USA, 28–30 April 1980. [Google Scholar]
- Mahafza, B.R.; Elsherbeni, A. MATLAB Simulations for Radar Systems Design; Taylor and Francis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Sun, L.; Li, C. A High-Resolution, Wide-Swath SAR Imaging System Based on Tandem SAR Satellites. Sensors 2022, 22, 7747. [Google Scholar] [CrossRef]
- Cao, Y.; Guo, S.; Jiang, S.; Zhou, X.; Wang, X.; Luo, Y.; Yu, Z.; Zhang, Z.; Deng, Y. Parallel Optimisation and Implementation of a Real-Time Back Projection (BP) Algorithm for SAR Based on FPGA. Sensors 2022, 22, 2292. [Google Scholar] [CrossRef] [PubMed]
- Drozdowicz, J.; Samczynski, P. Drone-Based 3D Synthetic Aperture Radar Imaging with Trajectory Optimization. Sensors 2022, 22, 6990. [Google Scholar] [CrossRef]
- Li, L.; Zhang, F.; Shao, Y.; Wei, Q.; Huang, Q.; Jiao, Y. Airborne SAR Radiometric Calibration Based on Improved Sliding Window Integral Method. Sensors 2022, 22, 320. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, R.; Liu, H.; Guo, J.; Wang, Y.; Zhang, J. Research on Configuration Constraints of Airborne Bistatic SARs. Sensors 2022, 22, 6534. [Google Scholar] [CrossRef]
- Huang, P.; Hao, L.; Tan, W.; Xu, W.; Qi, Y. An Adjusted Frequency-Domain Algorithm for Arc Array Bistatic SAR Data with One-Moving Transmitter. Sensors 2022, 22, 4725. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.; Li, K.; Xu, W.; Tan, W.; Gao, Z.; Li, Y. Focusing Arc-Array Bistatic Synthetic Aperture Radar Data Based on Keystone Transform. Electronics 2019, 8, 1389. [Google Scholar] [CrossRef]
- Huang, Z.; Sun, J.; Tan, W.; Huang, P.; Han, K. Investigation of Wavenumber Domain Imaging Algorithm for Ground-Based Arc Array SAR. Sensors 2017, 17, 2950. [Google Scholar] [CrossRef]
- Manzoni, M.; Tebaldini, S.; Monti-Guarnieri, A.V.; Prati, C.M.; Russo, I. A Comparison of Processing Schemes for Automotive MIMO SAR Imaging. Remote Sens. 2022, 14, 4696. [Google Scholar] [CrossRef]
- Wang, H.; Li, K.; Zhang, J.; Hong, L.; Chi, H. Monitoring and Analysis of Ground Surface Settlement in Mining Clusters by SBAS-InSAR Technology. Sensors 2022, 22, 3711. [Google Scholar] [CrossRef]
- Wang, L.; Li, S.; Teng, C.; Jiang, C.; Li, J.; Li, Z.; Huang, J. Automatic-Detection Method for Mining Subsidence Basins Based on InSAR and CNN-AFSA-SVM. Sustainability 2022, 14, 13898. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, G.Z. Novel Approach for InSAR Sensors Imaging via Gradient-Based Algorithm for the Sparse Signal Reconstruction. IEEE Sens. J. 2018, 18, 2385–2394. [Google Scholar] [CrossRef]
- Martín-del-Campo-Becerra, G.D.; Reigber, A.; Nannini, M.; Hensley, S. Single-Look SAR Tomography of Urban Areas. Remote Sens. 2020, 12, 2555. [Google Scholar] [CrossRef]
- Lu, H.; Sun, J.; Wang, J.; Wang, C. A Novel Phase Compensation Method for Urban 3D Reconstruction Using SAR Tomography. Remote Sens. 2022, 14, 4071. [Google Scholar] [CrossRef]
- Liu, K.; Liao, M.; Timo, B. High Resolution 3D Tomographic SAR with Compressive Sensing. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 1456–1459. [Google Scholar]
- Yang, L.; Zhang, F.; Zhang, Z.; Chen, L.; Wang, D.; Yang, Y.; Li, Z. Elevation Resolution Enhancement Method Using Non-Ideal Linear Motion Error of Airborne Array TomoSAR. Remote Sens. 2022, 14, 2891. [Google Scholar] [CrossRef]
- Ren, X.; Yang, R. Study on Three-Dimensional Imaging Algorithm for Airborne Forward-Looking SAR. J. Electron. Inf. Technol. 2010, 32, 1361–1365. [Google Scholar]
- Peng, X.; Wang, Y.; Tan, W.; Hong, W.; Wu, Y. Airborne Downward-looking MIMO 3D-SAR Imaging Algorithm Based on Cross-track Thinned Array. J. Electron. Inf. Technol. 2012, 34, 943–949. [Google Scholar]
- Li, D.; Liao, G.; Xu, Q.; Wang, W. High resolution imaging algorithm for helicopter-borne rotating synthetic aperture radar. Syst. Eng. Electron. 2013, 35, 1389–1395. [Google Scholar]
- Li, W.J.; Liao, G.S.; Zhu, S.Q.; Xu, J.W. A Novel Helicopter-Borne RoSAR Imaging Algorithm Based on the Azimuth Chirp z transform. IEEE Geosci. Remote Sens. Lett. 2019, 16, 226–230. [Google Scholar] [CrossRef]
- Bai, B.; Ding, Y.; Li, X.; Liu, Y. A Radar Detection Method of Plasma-Sheath-Covered Target Based on the Improved Keystone Algorithm. Remote Sens. 2022, 14, 4869. [Google Scholar] [CrossRef]
- Wu, J.; Li, Z.; Huang, Y.; Yang, J.; Yang, H.; Liu, Q.H. Focusing Bistatic Forward-Looking SAR With Stationary Transmitter Based on Keystone Transform and Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2014, 11, 148–152. [Google Scholar] [CrossRef]
- Liang, M.; Su, W.; Gu, H. Focusing High-Resolution High Forward-Looking Bistatic SAR with Nonequal Platform Velocities Based on Keystone Transform and Modified Nonlinear Chirp Scaling Algorithm. IEEE Sens. J. 2019, 19, 901–908. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, R. Research of chirp scaling imaging algorithm for air-borne forward-looking SAR. J. Electron. Inf. Technol. 2008, 30, 228–232. [Google Scholar] [CrossRef]
- Krieger, G.; Mittermayer, J.; Wendler, M.; Witte, F.; Moreira, A. SIREV—Sector Imaging Radar for Enhanced Vision. In Proceedings of the 2nd International Symposium on Image and Signal Processing and Analysis, Pula, Croatia, 19–21 June 2001; Volume 2001. [Google Scholar]
- Vu, V.; Pettersson, M. Doppler and Cross-range Resolutions in Bistatic Forward-looking SAR Imaging. In Proceedings of the 2015 IEEE International Radar Conference (Radarcon), Arlington, VA, USA, 10–15 May 2015; IEEE: Piscataway, NJ, USA; pp. 72–76. [Google Scholar]
- Ruliang, Y.; Lulu, T.; Xiaozhen, R. Research of three-dimensional imaging processing for airborne forward-looking SAR. In Proceedings of the International Radar Conference, Guilin, China, 20–22 April 2009; p. 347. [Google Scholar]



| Symbol | Definition | Value |
|---|---|---|
| Carrier Frequency | 35.5 GHz | |
| Signal Bandwidth | 800 MHz | |
| Arc Array Radius | 0.6 m | |
| Array Beamwidth (−3 dB) | 56° | |
| Elevation Beamwidth (−3 dB) | 30° | |
| Carrier Platform Height | 500 m | |
| Platform Pitch Angle | 60° | |
| Platform Forward Speed | 40 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Huang, P.; Xu, W.; Tan, W.; Qi, Y. A Modified Keystone-Based Forward-Looking Arc Array Synthetic Aperture Radar 3D Imaging Method. Sensors 2023, 23, 2674. https://doi.org/10.3390/s23052674
Zhu X, Huang P, Xu W, Tan W, Qi Y. A Modified Keystone-Based Forward-Looking Arc Array Synthetic Aperture Radar 3D Imaging Method. Sensors. 2023; 23(5):2674. https://doi.org/10.3390/s23052674
Chicago/Turabian StyleZhu, Xiaofan, Pingping Huang, Wei Xu, Weixian Tan, and Yaolong Qi. 2023. "A Modified Keystone-Based Forward-Looking Arc Array Synthetic Aperture Radar 3D Imaging Method" Sensors 23, no. 5: 2674. https://doi.org/10.3390/s23052674
APA StyleZhu, X., Huang, P., Xu, W., Tan, W., & Qi, Y. (2023). A Modified Keystone-Based Forward-Looking Arc Array Synthetic Aperture Radar 3D Imaging Method. Sensors, 23(5), 2674. https://doi.org/10.3390/s23052674






