A Novel Approach for Simulation of Automotive Radar Sensors Designed for Systematic Support of Vehicle Development
Abstract
1. Introduction
- Operational Models (OMs): Generic sensor models can be easily and rapidly parameterised without knowledge of the specific perception sensor technology. Usually, the perception concept can be derived by focusing only on some typical geometric sensor properties such as field of view (FOV), detection range, etc.
- Functional Models (FMs): Stochastic, phenomenological, and data-driven modelling techniques are considered for subsequent investigations after the concept phase. In contrast to OMs, FMs require more detailed information about the sensor technology under consideration, but typically do not address the internal function of the HW/SW components of a real sensor. The functional representation of radar detection resulting in an object list can be modelled by the simulation of a simplified antenna pattern and the uncertainty of real sensors.
- Technical Models (TMs): Tailor-made sensor models for over-the-air (OTA) radar target stimulator test benches that support X-in-the-loop methods in the vehicle engineering process. A radar point target can be stimulated to validate basic sensor functionality such as bus communication. State-of-the-art OTA test benches require a reduced object list with position, distance, speed, and signal strength to generate a radar signature.
- Individual Models (IMs): Physics-based models for verification of sensor components and perception algorithms. Technology- and HW-specific parameters as well as detailed technical information of sensors are required for qualitative performance analysis. IMs are the most accurate models at the cost of high computational effort and real-time capability. Reliable modelling is only possible with the expertise of sensor suppliers.
- To the authors’ knowledge, this is the first time that the asynchronous output data streams of two automotive radar sensors of the same type, but with different configurations in terms of output processing level, have been recorded synchronously and analysed by projecting them onto each other in order to identify sensor-specific phenomena.
- The modelling approach is semi-physical by incorporating the characteristics of the directional antenna, the propagation factor, and some backscattering properties into the radar equation. In addition, physical effects such as Doppler and µDoppler, derived from measurements with the real radar sensors, have also been incorporated. By using these effects, a much more realistic radial velocity simulation can be achieved. The proposed model synthesises the radar point cloud and radar cross-section (RCS) taking into account the subsequent detection algorithms.
- As the required input from the sensor system supplier is limited to public information from datasheets and access to the radar point cloud, an extensive driving scenario catalogue was defined and performed to derive critical sensor characteristics and parameters. An off-line analysis tool was then developed to synchronously overlay ground truth information and all asynchronous sensor outputs.
- The model is, in real time, capable and ready for implementation on different X-in-the-loop test benches, for example, for over-the-air radar simulation test benches.
- The model is intentionally prepared to be used over the overall development process ranging from the concept phase to future virtual vehicle homologation.
2. Related Work
3. Model Development Procedure
- Physical modeling where possible, otherwise mathematical approximation based on experimental data.
- Systematic modular structure in which the modules are connected via defined interfaces.
- Sufficient fidelity to reality or to the respective vehicle development phase to support the safety validation. Component testing that is the responsibility of system and component suppliers is not addressed.
- Implementation in commercial ADAS testing software.
- Real-time performance for X-in-the-loop testing.
3.1. Development of a Suitable Measurement Setup
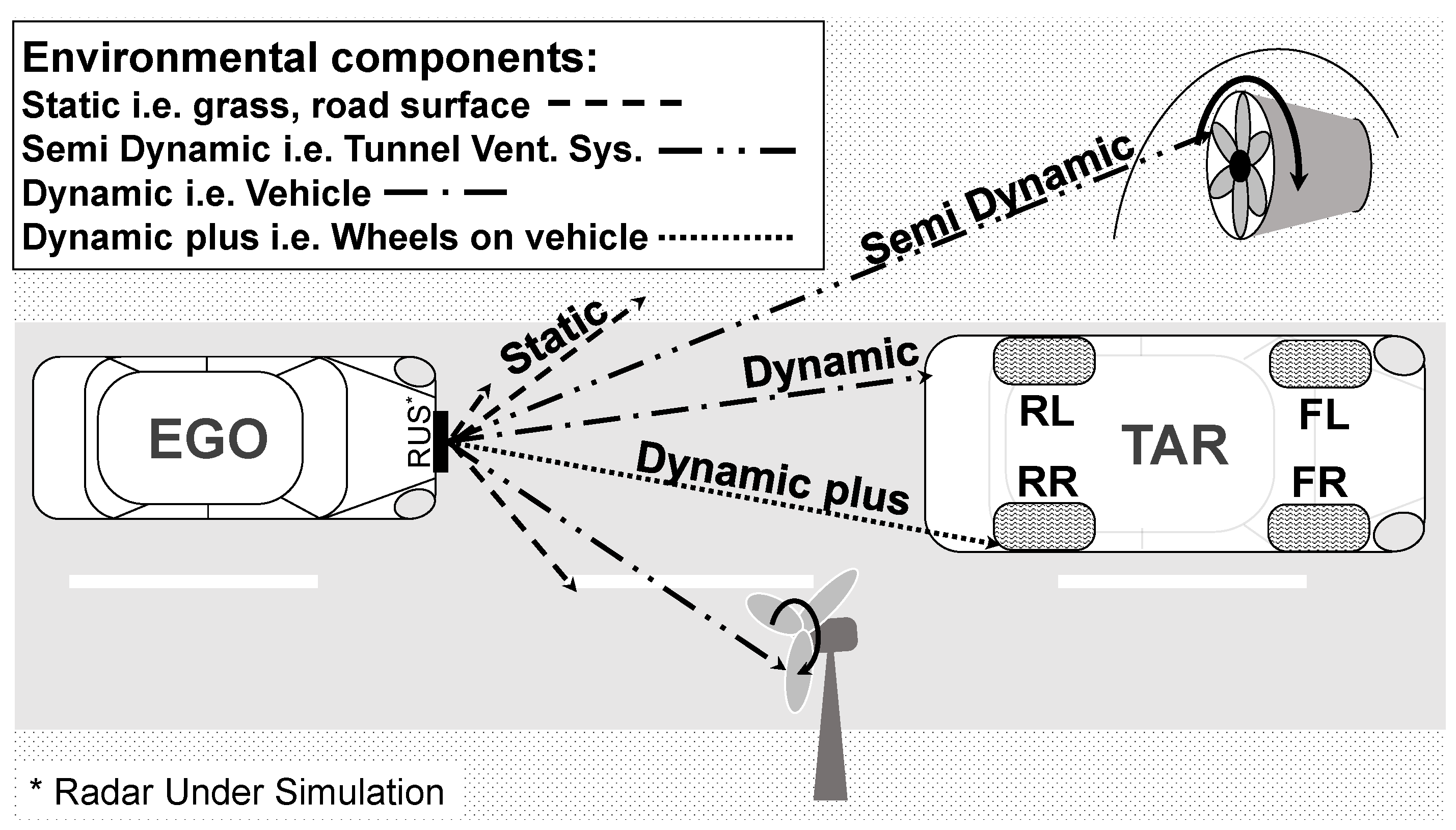
3.2. Identifying Radar Perception-Related Phenomena
- i
- Radar detections can be assigned to distinct areas within the gate window.
- ii
- The characteristic fluctuation pattern of the measured RCS value [43].
- iii
- Detection of occluded targets.
- iv
- The micro-Doppler effect [44] on rotating wheels.
- v
- The effect of a rapid change in the relative acceleration (jerk).
- vi
- The sensor’s FOV, resolution, and separability as specified in the data-sheet [45].
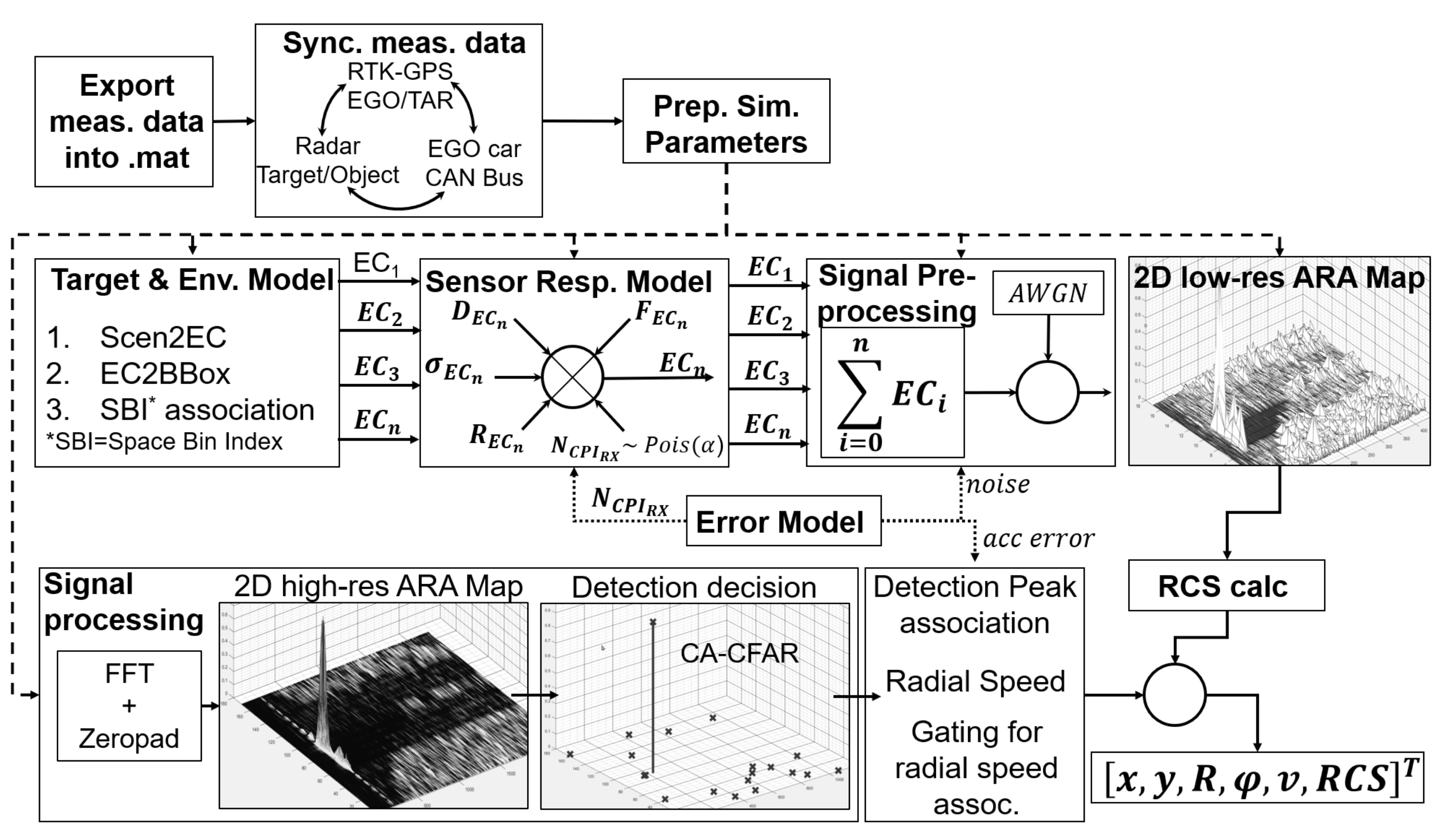
3.3. Radar Sensor Model
3.3.1. Simulation Input
3.3.2. Targets and Environment Model
3.3.3. Sensor Response Model
- Amplitude weighting as a function of distance. In radar theory, the power of the received signal is expected to be proportional to the fourth power of the distance to the scatterer or target. Due to the many simplifications applied for the simulation, this rule does not fit our radar link budget [46] (p. 102) compared to the real sensor output, so we introduced a new amplitude weighting function in the form of an exponential decay. The new exponential amplitude decay is still the function of the range and can be expressed by definition as follows:where is the minimum detection range of the radar under simulation (RUS), is the rate constant and if it is less than zero, it represents a decay.
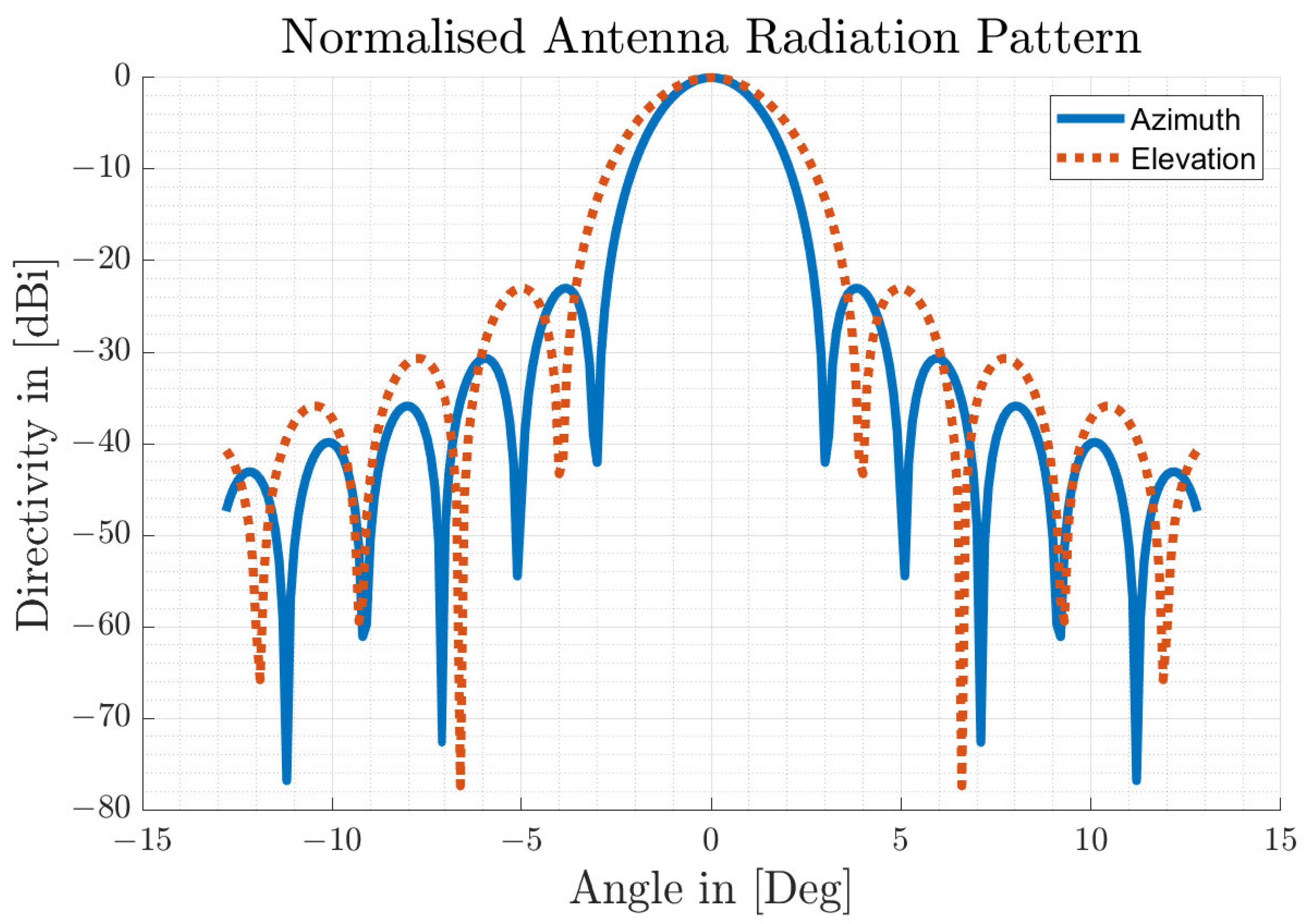
- 3D Antenna Characteristic The antenna is the coupler that transforms the EM waves of the propagating channel into current for the RF electronic components in receive mode, and vice versa in transmit mode of the radar sensor. Radar antennas are characterised by their directivity, which can be described by the antenna pattern. The ARS-308 industrial radar sensor is designed with a unique mechanically scanning antenna concept, which is a improvement of the folded parabolic antenna [50]. A prototype of a high-resolution imaging radar sensor for automotive applications with a similar narrow beam antenna concept was presented by the authors in [41]. They achieved a half-power (3 dB) beam-width of 1.6 degrees in azimuth and 4.2 degrees in elevation. According to [51] (p. 279), in order to achieve an operational antenna performance with an asymmetrical beam width and a low sidelobe level, different types of aperture antennas can be considered. In particular, a good result can be obtained for two-dimensional planar arrays in the form of a rectangular radiating surface [52] (p. 316) with cosine-weighted aperture irradiances. Certain aperture distributions (e.g., Hamming or Taylor) have a lower first sidelobe, but cosine shaping is appropriate for the modelling approach introduced here [51] (p. 232). Accordingly, the 1-D normalised antenna pattern for the cosine aperture distribution over one angular direction or plane of a rectangular aperture is calculated as follows:where the phase distribution is given by
- Propagation factor
3.3.4. Signal Processing
3.3.5. Error Model
3.4. Implementation in Matlab
4. Results
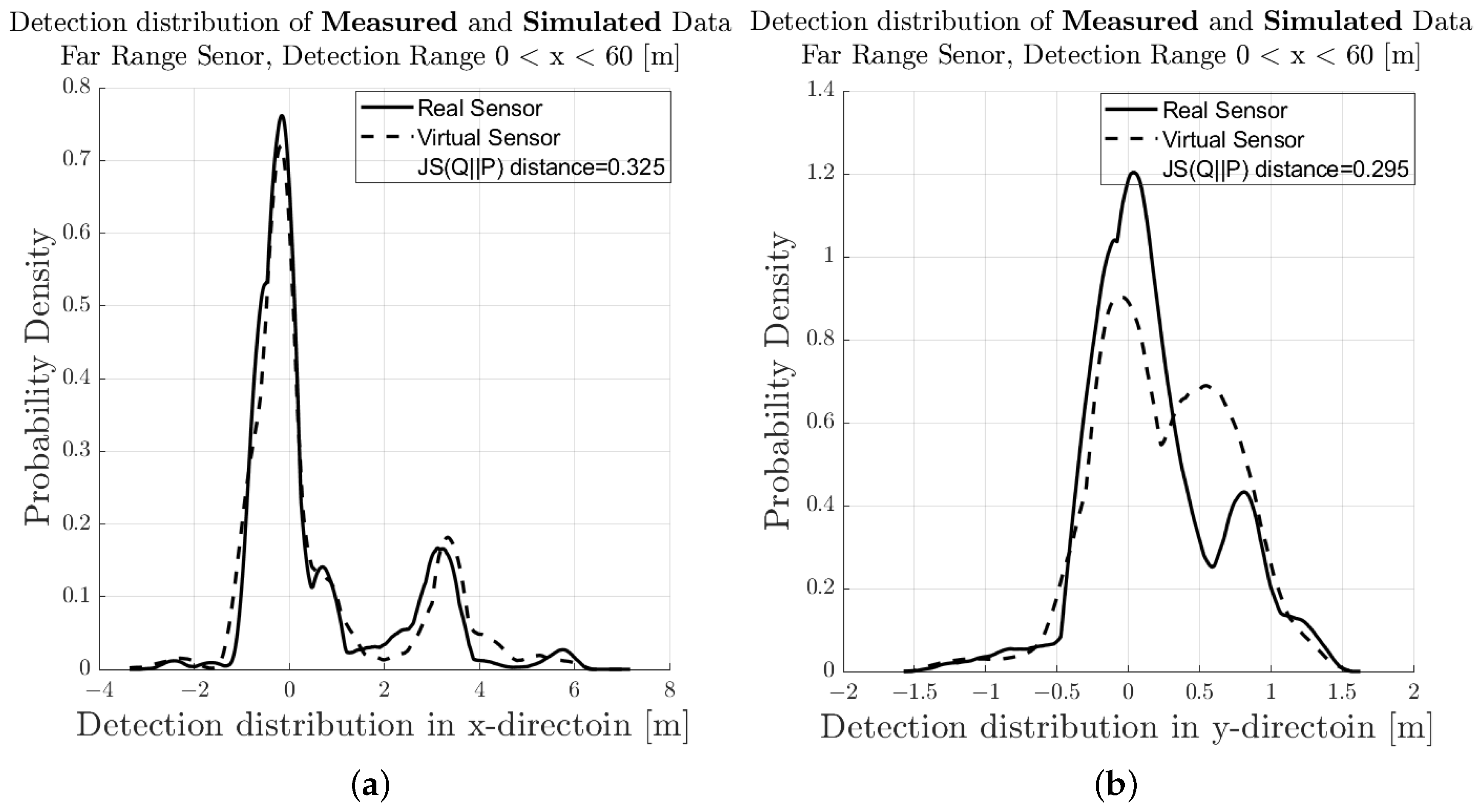
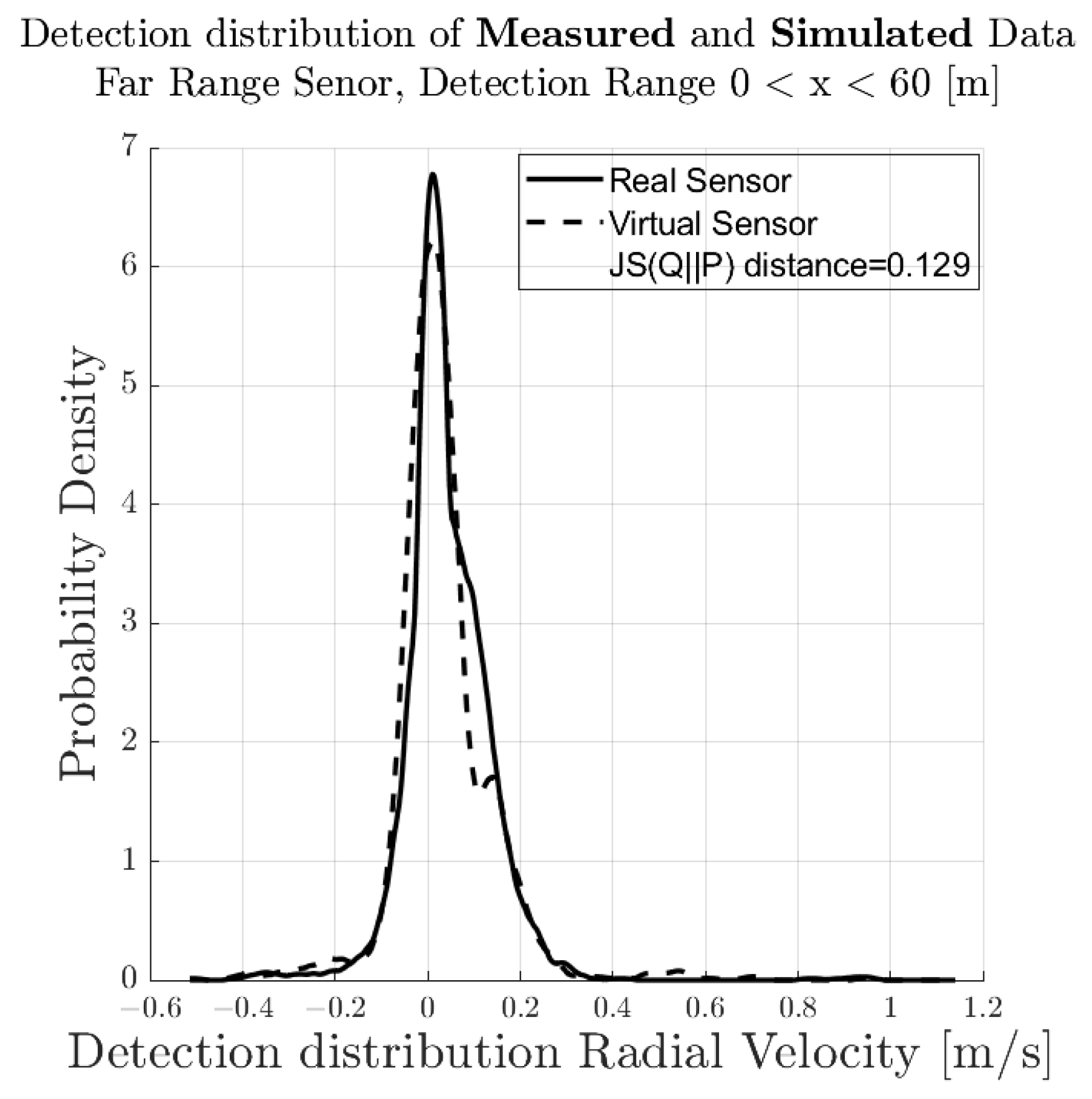
4.1. Evaluation of Modelling Approach
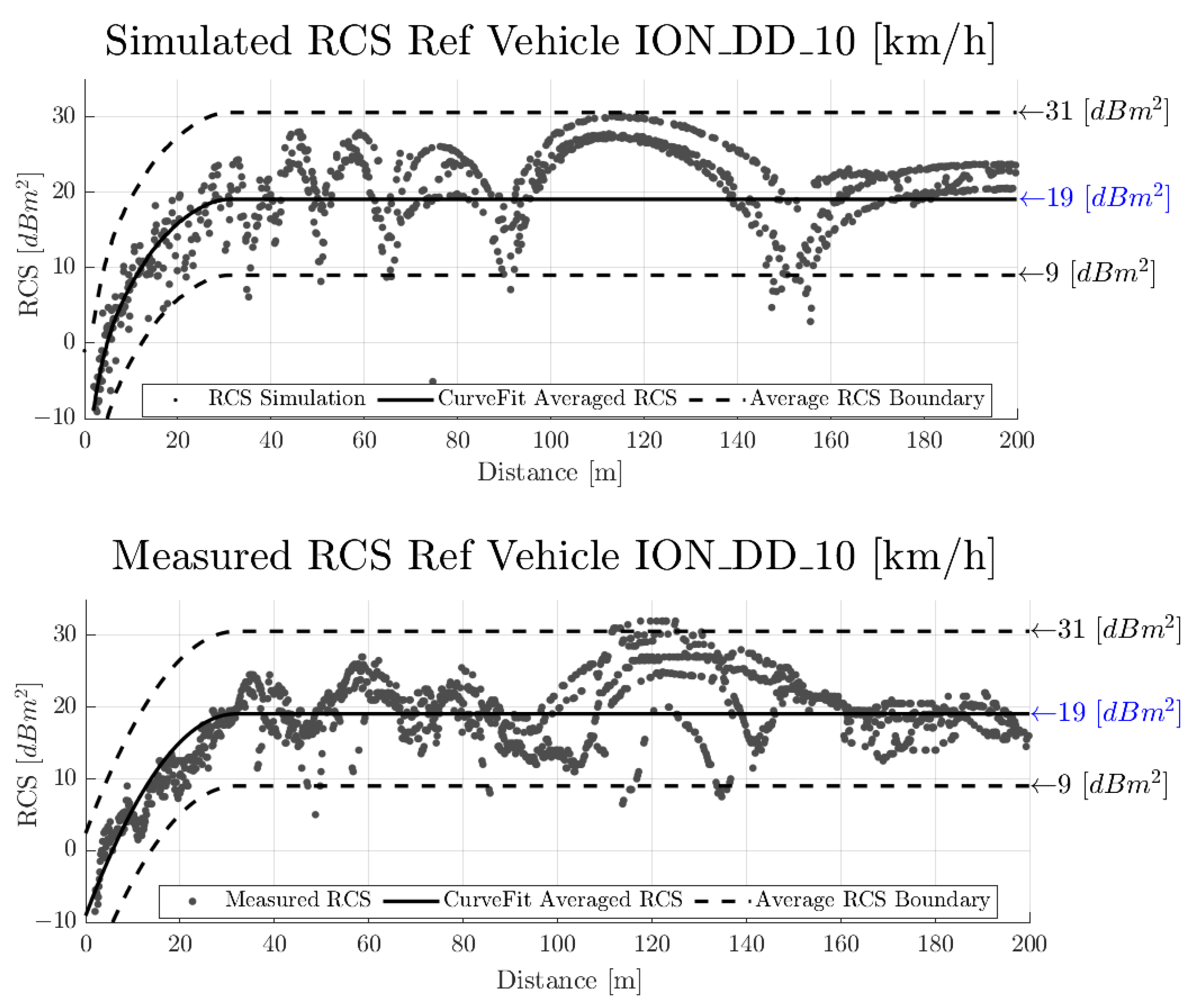
4.2. Performance Assessment—Radar Cross-Section
5. Discussion and Conclusion
5.1. Comparison of Measurement and Simulation
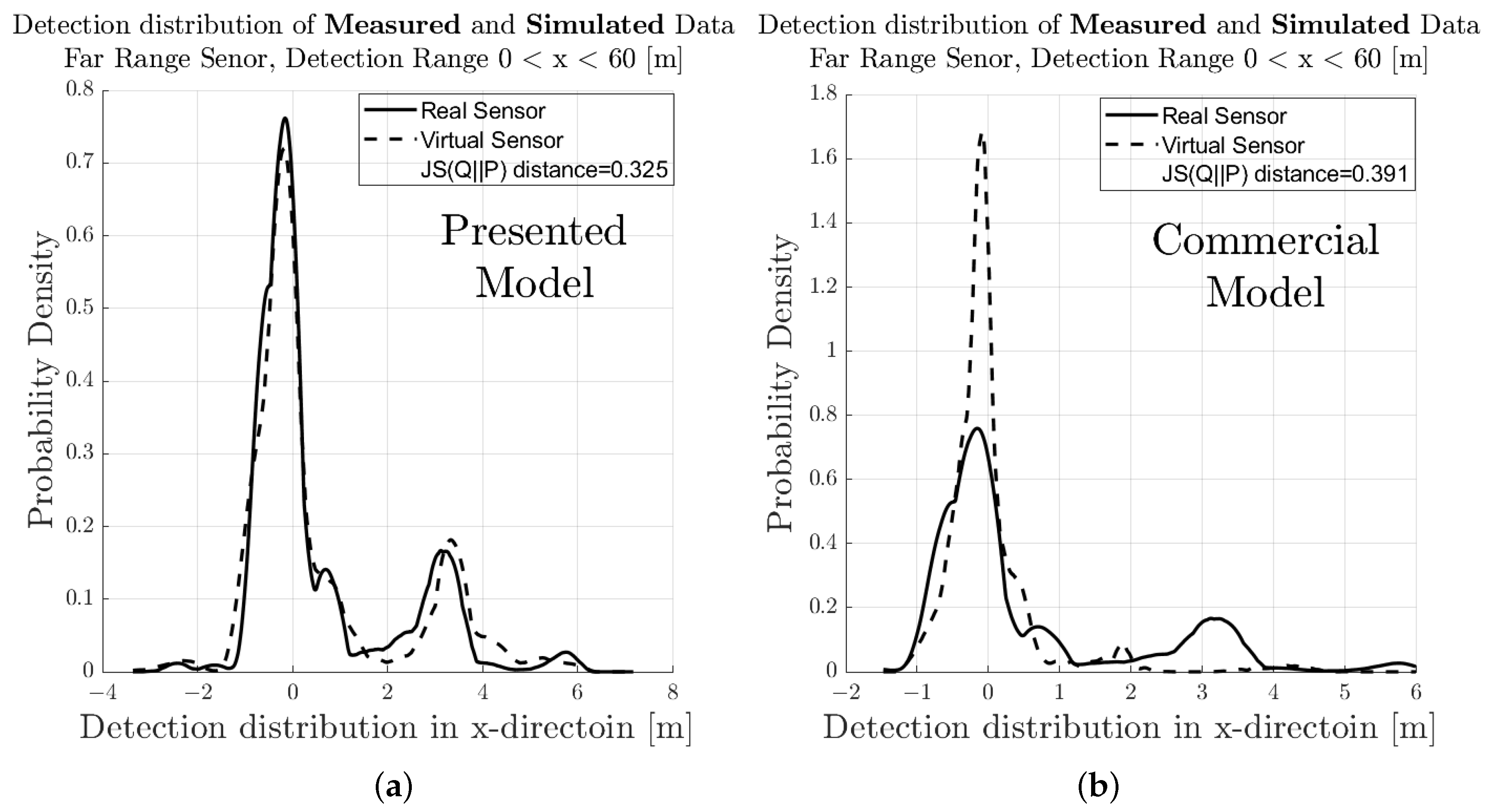
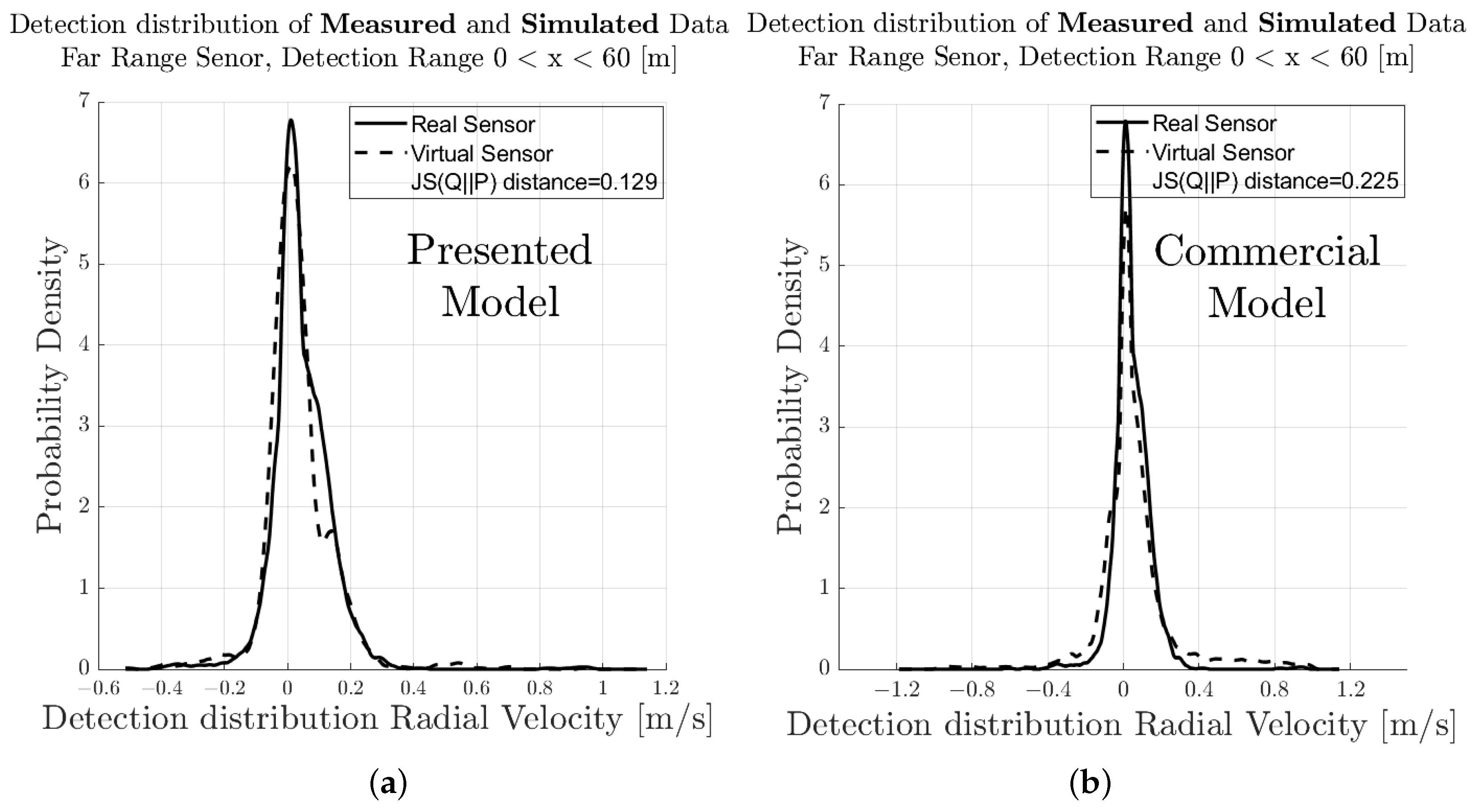
5.2. Comparison to Commercial Applications
5.3. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADAS | Advanced Driver Assistance Systems |
| AD | Automated Driving |
| ADF | Automated Driving Functions |
| ARA | Amplitude Range Azimuth |
| ARS-308 | Continental Automotive Radar of Series 308 |
| CAN | Controller Area Network |
| CA | Cell Averaging |
| CFAR | Continuous False Alarm Rate |
| DC | Detection Classes |
| DGT-SMV | Dynamic Ground Truth—Sensor Model Validation |
| DFM | Doppler Frequency Migration |
| DL | Deep Learning |
| CPI | Coherent Process Interval |
| EuroNCAP | European New Car Assessment Program |
| EC | Environment Components |
| FFT | Fast Fourier Transformation |
| FM | Functional Model |
| FMCW | Frequency Modulated Continuous Wave (Radar) |
| FOV | Field of View |
| GT | Ground Truth |
| HAR | Human Activity Recognition |
| HW/SW | Hardware/Software |
| IM | Individual Model |
| JSD | Jensen–Shannon Divergence |
| LTI | Linear Time Invariant System |
| LOS | Line Of Sight |
| ML | Machine Learning |
| RA | Range Azimuth |
| RCS | Radar Cross-Section |
| RF | Radio Frequency |
| RNN | Recurrent Neural Network |
| RT | Ray Tracing |
| RTK–GPS | Real-Time Kinematics–Global Positioning System |
| RUS | Radar Under Simulation |
| Rx/Tx | Receiver/Transmitter |
| SAE | Society of Automotive Engineers |
| SB | Space Bin |
| SBI | Space Bin Indicator |
| SNR | Signal-to-Noise Ratio |
| TM | Technical Model |
| OEM | Original Equipment Manufacturer, i.e., Vehicles Manufacturer |
| OM | Operational Model |
| OS-CFAR | Ordered Statistic Continuous False Alarm Rate |
| OTA | Over-the-Air (Radar Target Simulators) |
| Probability Density Function | |
| V&V | Validation (of intended use) and Verification (of requirements) |
References
- Kalra, N.; Paddock, S.M. Driving to Safety: How Many Miles of Driving Would It Take to Demonstrate Autonomous Vehicle Reliability? Transp. Res. Part A Policy Pract. 2016, 2016, 182–193. [Google Scholar] [CrossRef]
- Magosi, Z.F.; Li, H.; Rosenberger, P.; Wan, L.; Eichberger, A. A Survey on Modelling of Automotive Radar Sensors for Virtual Test and Validation of Automated Driving. Sensors 2022, 22, 5693. [Google Scholar] [CrossRef] [PubMed]
- Hartstern, M.; Rack, V.; Kaboli, M.; Stork, W. Simulation-based Evaluation of Automotive Sensor Setups for Environmental Perception in Early Development Stages. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 858–864. [Google Scholar] [CrossRef]
- Hanke, T.; Schaermann, A.; Matthias, G.; Konstantin, W.; Hirsenkorn, N.; Rauch, A.; Schneider, S.A. Generation and validation of virtual point cloud data for automated driving systems. In Proceedings of the 20th International Conference on Intelligent Transportation Systems, Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Linnhoff, C.; Rosenberger, P.; Holder, M.F.; Cianciaruso, N.; Winner, H. Highly Parameterizable and Generic Perception Sensor Model Architecture. In Automatisiertes Fahren 2020; Bertram, T., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; pp. 195–206. [Google Scholar] [CrossRef]
- Rosique, F.; Navarro, P.J.; Fernández, C.; Padilla, A. A Systematic Review of Perception System and Simulators for Autonomous Vehicles Research. Sensors 2019, 19, 648. [Google Scholar] [CrossRef]
- Muckenhuber, S.; Museljic, E.; Stettinger, G. Performance evaluation of a state-of-the-art automotive radar and corresponding modelling approaches based on a large labeled dataset. J. Intell. Transp. Syst. 2021, 26, 1–20. [Google Scholar] [CrossRef]
- Hanke, T.; Hirsenkorn, N.; Dehlink, B.; Rauch, A.; Rasshofer, R.; Biebl, E. Generic architecture for simulation of ADAS sensors. In Proceedings of the 2015 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 125–130. [Google Scholar] [CrossRef]
- Jun, Z.; Kai, Y.; Xuecai, D.; Zhangu, W.; Huainan, Z.; Chunguang, D. New modeling method of millimeter-wave radar considering target radar echo intensity. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2857–2870. [Google Scholar] [CrossRef]
- Bernsteiner, S.; Magosi, Z.; Lindvai-Soos, D.; Eichberger, A. Radar Sensor Model for the Virtual Development Process. ATZelektronik Worldw. 2015, 10, 46–52. [Google Scholar] [CrossRef]
- Thieling, J.; Frese, S.; RoBmann, J. Scalable and Physical Radar Sensor Simulation for Interacting Digital Twins. IEEE Sens. J. 2021, 21, 3184–3192. [Google Scholar] [CrossRef]
- Schuesler, C.; Hoffmann, M.; Braunig, J.; Ullmann, I.; Ebelt, R.; Vossiek, M. A Realistic Radar Ray Tracing Simulator for Large MIMO-Arrays in Automotive Environments. IEEE J. Microwaves 2021, 1, 962–974. [Google Scholar] [CrossRef]
- Dudek, M.; Wahl, R.; Kissinger, D.; Weigel, R.; Fischer, G. Millimeter wave FMCW radar system simulations including a 3D ray tracing channel simulator. In Proceedings of the 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 7–10 December 2010; pp. 1665–1668. [Google Scholar]
- Chipengo, U. Full Physics Simulation Study of Guardrail Radar-Returns for 77 GHz Automotive Radar Systems. IEEE Access 2018, 6, 70053–70060. [Google Scholar] [CrossRef]
- Zhu, L.; He, D.; Ai, B.; Zhong, Z.; Zhu, F.; Wang, Z. Measurement and Ray-Tracing Simulation for Millimeter-Wave Automotive Radar. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 582–587. [Google Scholar] [CrossRef]
- Maier, F.M.; Makkapati, V.P.; Horn, M. Environment perception simulation for radar stimulation in automated driving function testing. E I Elektrotechnik Und Informationstechnik 2018, 135, 309–315. [Google Scholar] [CrossRef]
- Maier, M.; Makkapati, V.P.; Horn, M. Adapting Phong into a Simulation for Stimulation of Automotive Radar Sensors. In Proceedings of the 2018 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Munich, Germany, 15–17 April 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Holder, M.F.; Makkapati, V.P.; Rosenberger, P.; D’hondt, T.; Slavik, Z.; Maier, F.M.; Schreiber, H.; Magosi, Z.; Winner, H.; Bringmann, O.; et al. Measurements revealing Challenges in Radar Sensor Modeling for Virtual Validation of Autonomous Driving. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- Hirsenkorn, N., Subkowski, P., Hanke, T., Schaermann, A., Rauch, A., Rasshofer, R., Biebl, E., Eds.; A ray launching approach for modeling an FMCW radar system. In Proceedings of the 18th International Radar Symposium IRS 2017, Prague, Czech Republic, 28–30 June 2017. [Google Scholar]
- Martin, M.Y.; Winberg, S.L.; Gaffar, M.Y.A.; Macleod, D. The Design and Implementation of a Ray-tracing Algorithm for Signal-level Pulsed Radar Simulation Using the NVIDIA® OptiXTM Engine. J. Commun. 2022, 17, 761–768. [Google Scholar] [CrossRef]
- Holder, M.; Linnhoff, C.; Rosenberger, P.; Winner, H. (Eds.) The Fourier Tracing Approach for Modeling Automotive Radar Sensors. In Proceedings of the 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019.
- Schubert, R.; Mattern, N.; Bours, R. Simulation of Sensor Models for the Evaluation of Advanced Driver Assistance Systems. ATZelektronik Worldw. 2014, 9, 26–29. [Google Scholar] [CrossRef]
- Li, H.; Kanuric, T.; Eichberger, A. Automotive Radar Modeling for Virtual Simulation Based on Mixture Density Network. IEEE Sens. J. 2022; Early Access. [Google Scholar] [CrossRef]
- Owaki, T.; Machida, T. Hybrid Physics-Based and Data-Driven Approach to Estimate the Radar Cross-Section of Vehicles. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Hirsenkorn, N.; Hanke, T.; Rauch, A.; Dehlink, B.; Rasshofer, R.; Biebl, E. A non-parametric approach for modeling sensor behavior. In Proceedings of the 2015 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 131–136. [Google Scholar] [CrossRef]
- Hirsenkorn, N.; Hanke, T.; Rauch, A.; Dehlink, B.; Rasshofer, R.; Biebl, E. Virtual sensor models for real-time applications. Adv. Radio Sci. 2016, 14, 31–37. [Google Scholar] [CrossRef][Green Version]
- Choi, W.Y.; Yang, J.H.; Chung, C.C. Data-Driven Object Vehicle Estimation by Radar Accuracy Modeling with Weighted Interpolation. Sensors 2021, 21, 2317. [Google Scholar] [CrossRef] [PubMed]
- Moujahid, A.; Tantaoui, M.E.; Hina, M.D.; Soukane, A.; Ortalda, A.; ElKhadimi, A.; Ramdane-Cherif, A. Machine learning techniques in ADAS: A review. In Proceedings of the 2018 International Conference on Advances in Computing and Communication Engineering (ICACCE), Paris, France, 22–23 June 2018; pp. 235–242. [Google Scholar]
- Sligar, A.P. Machine Learning-Based Radar Perception for Autonomous Vehicles Using Full Physics Simulation. IEEE Access 2020, 8, 51470–51476. [Google Scholar] [CrossRef]
- Rathi, A.; Deb, D.; Sarath Babu, N.; Mamgain, R. Two-level Classification of Radar Targets Using Machine Learning. In Smart Trends in Computing and Communications; Smart Innovation, Systems and Technologies Series; Zhang, Y.D., Mandal, J.K., So-In, C., Thakur, N.V., Eds.; Springer: Singapore, 2020; Volume 165, pp. 231–242. [Google Scholar] [CrossRef]
- Abeynayake, C.; Son, V.; Shovon, M.; Yokohama, H. Machine learning based automatic target recognition algorithm applicable to ground penetrating radar data. In Proceedings of the Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXIV, Baltimore, MD, USA, 15–17 April 2019; Bishop, S.S., Isaacs, J.C., Eds.; SPIE: Baltimore, MA, USA, 2019; p. 1101202. [Google Scholar] [CrossRef]
- Carrera, E.V.; Lara, F.; Ortiz, M.; Tinoco, A.; León, R. Target detection using radar processors based on machine learning. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Shinde, P.P.; Shah, S. A review of machine learning and deep learning applications. In Proceedings of the 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 16–18 August 2018; pp. 1–6. [Google Scholar]
- Chen, K.; Yao, L.; Zhang, D.; Wang, X.; Chang, X.; Nie, F. A Semisupervised Recurrent Convolutional Attention Model for Human Activity Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1747–1756. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Yao, L.; Chen, K.; Wang, S.; Chang, X.; Liu, Y. Making sense of spatio-temporal preserving representations for EEG-based human intention recognition. IEEE Trans. Cybern. 2019, 50, 3033–3044. [Google Scholar] [CrossRef]
- Arefnezhad, S.; Hamet, J.; Eichberger, A.; Frühwirth, M.; Ischebeck, A.; Koglbauer, I.V.; Moser, M.; Yousefi, A. Driver drowsiness estimation using EEG signals with a dynamical encoder–decoder modeling framework. Sci. Rep. 2022, 12, 1–18. [Google Scholar]
- Song, Y.; Wang, Y.; Li, Y. Radar data simulation using deep generative networks. J. Eng. 2019, 2019, 6699–6702. [Google Scholar] [CrossRef]
- Slavik, Z.; Mishra, K.V. Phenomenological Modeling of Millimeter-Wave Automotive Radar. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Schuler, K.; Becker, D.; Wiesbeck, W. Extraction of Virtual Scattering Centers of Vehicles by Ray-Tracing Simulations. IEEE Trans. Antennas Propag. 2008, 56, 3543–3551. [Google Scholar] [CrossRef]
- Lutz, S.; Ellenrieder, D.; Walter, T.; Weigel, R. On fast chirp modulations and compressed sensing for automotive radar applications. In Proceedings of the 2014 15th International Radar Symposium (IRS), Gdansk, Poland, 16–18 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Schneider, R.; Wenger, J. High resolution radar for automobile applications. In Advances in Radio Science; Copernicus Publications: Göttingen, Germany, 2003; pp. 105–111. [Google Scholar] [CrossRef]
- Magosi, Z.F.; Wellershaus, C.; Tihanyi, V.R.; Luley, P.; Eichberger, A. Evaluation Methodology for Physical Radar Perception Sensor Models Based on On-Road Measurements for the Testing and Validation of Automated Driving. Energies 2022, 15, 2545. [Google Scholar] [CrossRef]
- EuroNCAP. Technical Bulletin TB025 Global Vehicle Target Specification v1.0. 2018. Available online: https://cdn.euroncap.com/media/39159/tb-025-global-vehicle-target-specification-for-euro-ncap-v10.pdf (accessed on 3 February 2022).
- Li, Y.; Du, L.; Liu, H. Hierarchical Classification of Moving Vehicles Based on Empirical Mode Decomposition of Micro-Doppler Signatures. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3001–3013. [Google Scholar] [CrossRef]
- Continental Engineering Services GmbH. ARS 308-2C/-21; Standardized ARS Interface; Technical Documentation; Continental Engineering Services GmbH: Frankfurt am Main, Germany, 2012. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Rabe, H. Bildgebende Verfahren zur Steigerung der Ausfallsicherheit Radarbasierter Füllstandsmesssysteme. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hanover, Germany, 2013. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, L.J.; Chizhik, D.; Valenzuela, R.A. Spatial Diversity in Radars—Models and Detection Performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Koks, D. How to Create and Manipulate Radar Range-Doppler Plots: DSTO–TN–1386. Available online: https://apps.dtic.mil/sti/pdfs/ADA615308.pdf (accessed on 3 February 2023).
- Waldschmidt, C.; Hasch, J.; Menzel, W. Automotive Radar—From First Efforts to Future Systems. IEEE J. Microwaves 2021, 1, 135–148. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to Radar Systems, 3rd ed.; McGraw-Hill Electrical Engineering Series; McGraw-Hill: Boston, MA, USA, 2007. [Google Scholar]
- Richards, M.A.; Scheer, J.A.; Holm, W.A. Principles of Modern Radar; First Published 2010, Reprinted with Corrections 2015 ed.; SciTech Publ: Raleigh, NC, USA, 2015; Volume 1. [Google Scholar] [CrossRef]
- Slocumb, B.J.; Macumber, D.L. Surveillance radar range-bearing centroid processing, part II: Merged measurements. In Proceedings SPIE 6236, Signal and Data Processing of Small Targets 2006; Drummond, O.E., Ed.; SPIE: Bellingham, WA, USA, 2006; p. 623604. [Google Scholar] [CrossRef]
- Rohling, H. Radar CFAR Thresholding in Clutter and Multiple Target Situations. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 608–621. [Google Scholar] [CrossRef]
- Herrmann, M.; Schön, H. Efficient Sensor Development Using Raw Signal Interfaces. In Fahrerassistenzsysteme 2018; Bertram, T., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2019; pp. 30–39. [Google Scholar] [CrossRef]
- Wellershaus, C. Performance Assesment of a Physical Sensor Model for Automated Driving. Master’s Thesis, Graz University of Technolgy, Graz, Austria, 2021. [Google Scholar]






| Modules | Classifies as | Execution Time (s) | Speed of Execution |
|---|---|---|---|
| ① | OM | 29.35 | ∼5.4 × RT (Real-Time) |
| ① + ② | TM | 40.12 | ∼4.0 × RT |
| ① + ② + ③ | FM | 114.67 | ∼1.4 × RT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magosi, Z.F.; Eichberger, A. A Novel Approach for Simulation of Automotive Radar Sensors Designed for Systematic Support of Vehicle Development. Sensors 2023, 23, 3227. https://doi.org/10.3390/s23063227
Magosi ZF, Eichberger A. A Novel Approach for Simulation of Automotive Radar Sensors Designed for Systematic Support of Vehicle Development. Sensors. 2023; 23(6):3227. https://doi.org/10.3390/s23063227
Chicago/Turabian StyleMagosi, Zoltan Ferenc, and Arno Eichberger. 2023. "A Novel Approach for Simulation of Automotive Radar Sensors Designed for Systematic Support of Vehicle Development" Sensors 23, no. 6: 3227. https://doi.org/10.3390/s23063227
APA StyleMagosi, Z. F., & Eichberger, A. (2023). A Novel Approach for Simulation of Automotive Radar Sensors Designed for Systematic Support of Vehicle Development. Sensors, 23(6), 3227. https://doi.org/10.3390/s23063227







