A Novel Transformer-Based IMU Self-Calibration Approach through On-Board RGB Camera for UAV Flight Stabilization
Abstract
1. Introduction
2. Related Work
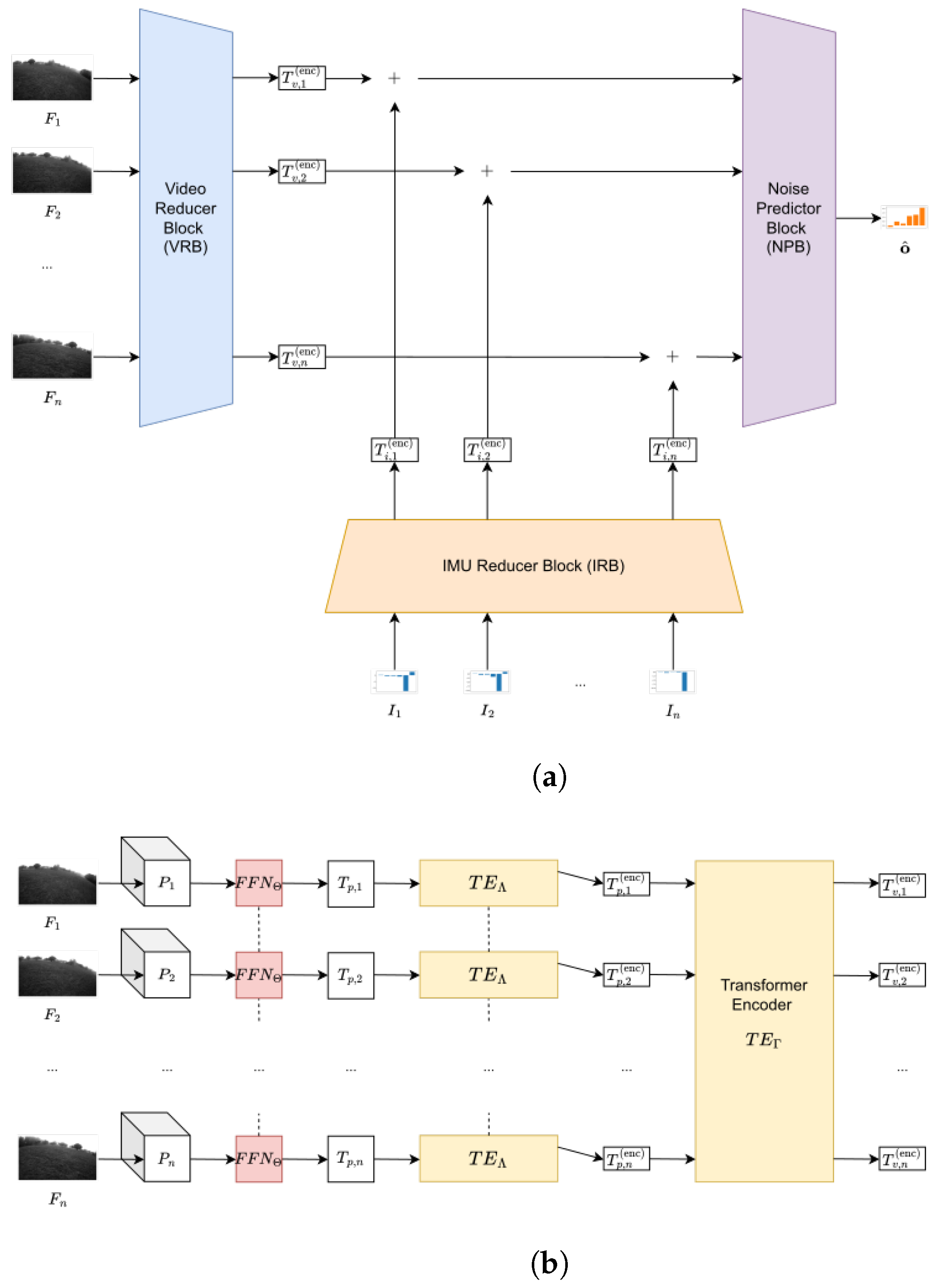
3. Proposed Method
3.1. Video Reducer Block
3.2. IMU Reducer Block
3.3. Noise Predictor Block
3.4. Training Strategy
4. Experiments and Discussion
4.1. Datasets
4.2. Metrics
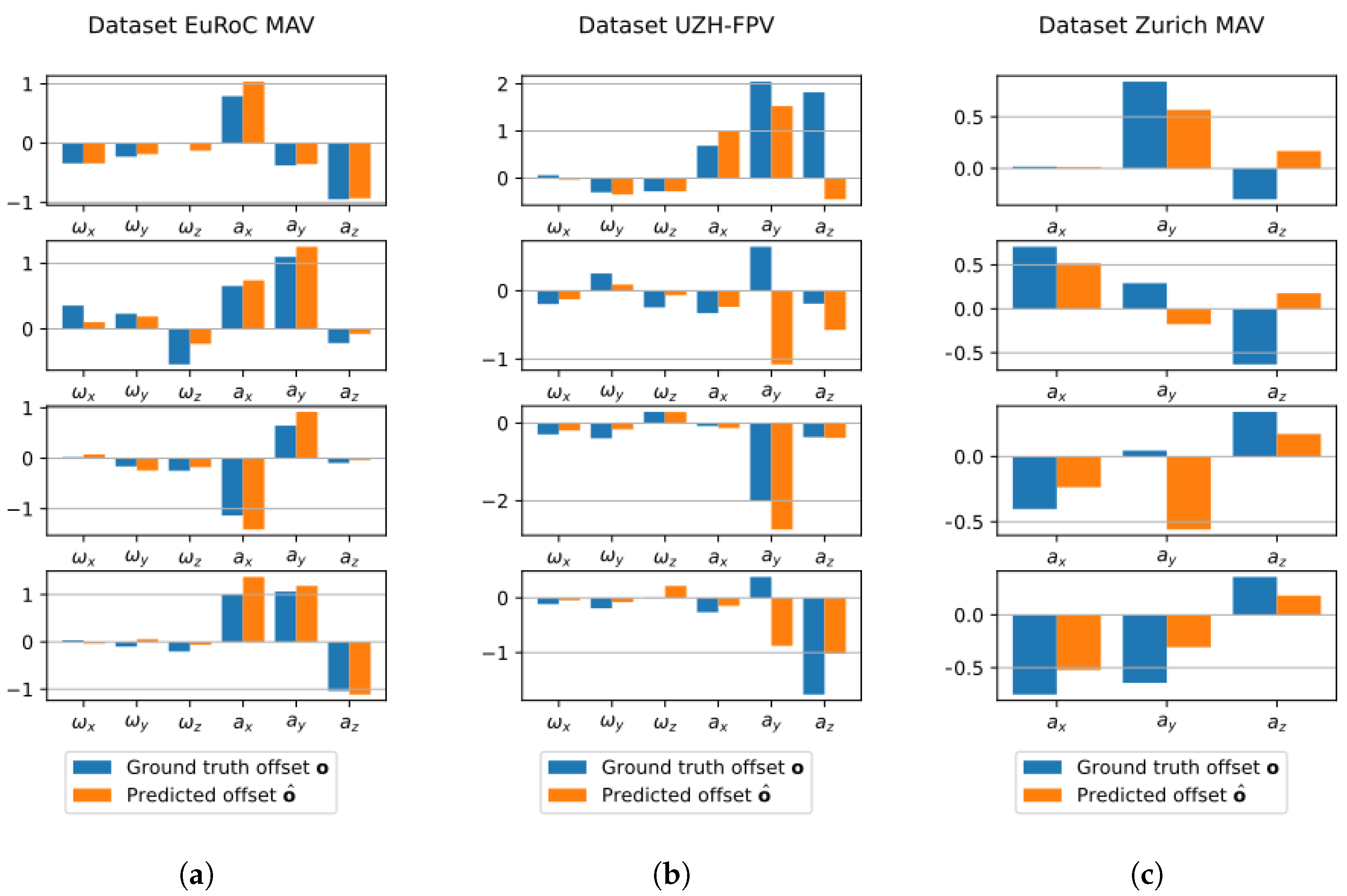
4.3. Results and Discussion
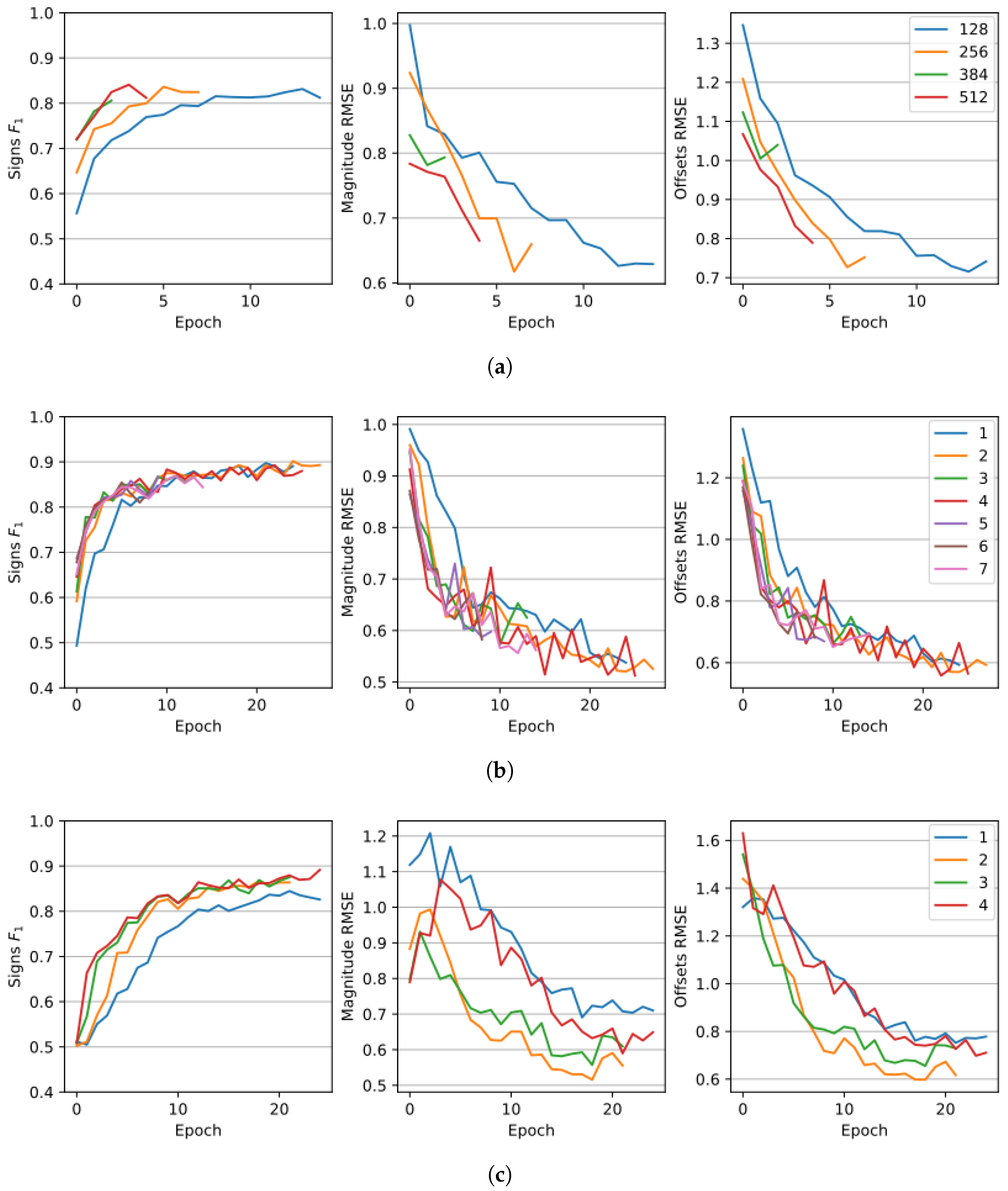
4.4. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LOO | Leave One Out validation |
| UAV | Unmanned Aerial Vehicle |
| MAV | Micro Aerial Vehicle |
| LIDAR | Light Detection And Ranging |
| FPV | First Person View |
| GPS | Global Positioning System |
| RGB | Red, Green, and Blue channels |
| HD | High Definition |
| IMU | Inertial Measurement Unit |
| TP | True Positive |
| FP | False Positive |
| FN | False Negative |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| FFN | Feed-Forward Network |
| CNN | Convolutional Neural Network |
| MHA | Multi-Head Attention |
| TE | Transformer Encoder |
| TD | Transformer Decoder |
| VRB | Video Reducer Block |
| IRB | IMU Reducer Block |
| NPB | Noise Predictor Block |
References
- Bonin-Font, F.; Ortiz, A.; Oliver, G. Visual Navigation for Mobile Robots: A Survey. J. Intell. Robot. Syst. 2008, 53, 263. [Google Scholar] [CrossRef]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- de Ponte Müller, F. Survey on Ranging Sensors and Cooperative Techniques for Relative Positioning of Vehicles. Sensors 2017, 17, 271. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Ta, X.; Xiao, R.; Wei, Y.; An, D.; Li, D. Survey of underwater robot positioning navigation. Appl. Ocean. Res. 2019, 90, 101845. [Google Scholar] [CrossRef]
- Tariq, Z.B.; Cheema, D.M.; Kamran, M.Z.; Naqvi, I.H. Non-GPS Positioning Systems: A Survey. ACM Comput. Surv. 2017, 50, 1–34. [Google Scholar] [CrossRef]
- Bajaj, R.; Ranaweera, S.; Agrawal, D. GPS: Location-tracking technology. Computer 2002, 35, 92–94. [Google Scholar] [CrossRef]
- Yuan, Q.; Chen, I.M. Localization and velocity tracking of human via 3 IMU sensors. Sens. Actuators A Phys. 2014, 212, 25–33. [Google Scholar] [CrossRef]
- Marsico, M.D.; Mecca, A. Biometric walk recognizer. Multimed. Tools Appl. 2017, 76, 4713–4745. [Google Scholar] [CrossRef]
- Steven Eyobu, O.; Han, D. Feature Representation and Data Augmentation for Human Activity Classification Based on Wearable IMU Sensor Data Using a Deep LSTM Neural Network. Sensors 2018, 18, 2892. [Google Scholar] [CrossRef]
- Avola, D.; Cinque, L.; Del Bimbo, A.; Marini, M.R. MIFTel: A multimodal interactive framework based on temporal logic rules. Multimed. Tools Appl. 2020, 79, 13533–13558. [Google Scholar] [CrossRef]
- Avola, D.; Cinque, L.; Fagioli, A.; Foresti, G.L.; Pannone, D.; Piciarelli, C. Automatic estimation of optimal UAV flight parameters for real-time wide areas monitoring. Multimed. Tools Appl. 2021, 80, 25009–25031. [Google Scholar] [CrossRef]
- Avola, D.; Cinque, L.; Foresti, G.L.; Martinel, N.; Pannone, D.; Piciarelli, C. A UAV Video Dataset for Mosaicking and Change Detection from Low-Altitude Flights. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 2139–2149. [Google Scholar] [CrossRef]
- Conforti, M.; Mercuri, M.; Borrelli, L. Morphological changes detection of a large earthflow using archived images, lidar-derived dtm, and uav-based remote sensing. Remote Sens. 2020, 13, 120. [Google Scholar] [CrossRef]
- Avola, D.; Cannistraci, I.; Cascio, M.; Cinque, L.; Diko, A.; Fagioli, A.; Foresti, G.L.; Lanzino, R.; Mancini, M.; Mecca, A.; et al. A Novel GAN-Based Anomaly Detection and Localization Method for Aerial Video Surveillance at Low Altitude. Remote Sens. 2022, 14, 4110. [Google Scholar] [CrossRef]
- Hamdi, S.; Bouindour, S.; Snoussi, H.; Wang, T.; Abid, M. End-to-end deep one-class learning for anomaly detection in uav video stream. J. Imaging 2021, 7, 90. [Google Scholar] [CrossRef] [PubMed]
- Avola, D.; Cinque, L.; Di Mambro, A.; Diko, A.; Fagioli, A.; Foresti, G.L.; Marini, M.R.; Mecca, A.; Pannone, D. Low-Altitude Aerial Video Surveillance via One-Class SVM Anomaly Detection from Textural Features in UAV Images. Information 2022, 13, 2. [Google Scholar] [CrossRef]
- Avola, D.; Cinque, L.; Diko, A.; Fagioli, A.; Foresti, G.L.; Mecca, A.; Pannone, D.; Piciarelli, C. MS-Faster R-CNN: Multi-Stream Backbone for Improved Faster R-CNN Object Detection and Aerial Tracking from UAV Images. Remote Sens. 2021, 13, 1670. [Google Scholar] [CrossRef]
- Örnhag, M.V.; Persson, P.; Wadenbäck, M.; Åström, K.; Heyden, A. Trust Your IMU: Consequences of Ignoring the IMU Drift. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, New Orleans, LA, USA, 19–20 June 2022; pp. 4468–4477. [Google Scholar] [CrossRef]
- Couturier, A.; Akhloufi, M.A. A review on absolute visual localization for UAV. Robot. Auton. Syst. 2021, 135, 103666. [Google Scholar] [CrossRef]
- Munaye, Y.Y.; Lin, H.P.; Adege, A.B.; Tarekegn, G.B. UAV Positioning for Throughput Maximization Using Deep Learning Approaches. Sensors 2019, 19, 2775. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1 (Long and Short Papers), pp. 4171–4186. [Google Scholar] [CrossRef]
- Zaheer, M.; Guruganesh, G.; Dubey, K.A.; Ainslie, J.; Alberti, C.; Ontanon, S.; Pham, P.; Ravula, A.; Wang, Q.; Yang, L.; et al. Big Bird: Transformers for Longer Sequences. Adv. Neural Inf. Process. Syst. 2020, 33, 17283–17297. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 10–17 October 2021; pp. 9992–10002. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Liu, C.; Shuai, B.; Zhu, Y.; Brattoli, B.; Chen, H.; Marsic, I.; Tighe, J. VidTr: Video Transformer without Convolutions. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 10–17 October 2021; pp. 13557–13567. [Google Scholar] [CrossRef]
- Kolesnikov, A.; Dosovitskiy, A.; Weissenborn, D.; Heigold, G.; Uszkoreit, J.; Beyer, L.; Minderer, M.; Dehghani, M.; Houlsby, N.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2010, arXiv:2010.11929. [Google Scholar]
- Baevski, A.; Zhou, Y.; Mohamed, A.; Auli, M. wav2vec 2.0: A Framework for Self-Supervised Learning of Speech Representations. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Association for Computing Machinery: New York, NY, USA, 2020; Volume 33, pp. 12449–12460. [Google Scholar] [CrossRef]
- Xing, D.; Evangeliou, N.; Tsoukalas, A.; Tzes, A. Siamese Transformer Pyramid Networks for Real-Time UAV Tracking. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–6 July 2022; pp. 1898–1907. [Google Scholar] [CrossRef]
- Ye, J.; Fu, C.; Cao, Z.; An, S.; Zheng, G.; Li, B. Tracker Meets Night: A Transformer Enhancer for UAV Tracking. IEEE Robot. Autom. Lett. 2022, 7, 3866–3873. [Google Scholar] [CrossRef]
- Ghali, R.; Akhloufi, M.A.; Mseddi, W.S. Deep Learning and Transformer Approaches for UAV-Based Wildfire Detection and Segmentation. Sensors 2022, 22, 1977. [Google Scholar] [CrossRef] [PubMed]
- Parcollet, T.; Ravanelli, M. The Energy and Carbon Footprint of Training End-to-End Speech Recognizers. 2021. Available online: https://hal.science/hal-03190119/ (accessed on 22 December 2022).
- Xiao, Y.; Ruan, X.; Chai, J.; Zhang, X.; Zhu, X. Online IMU Self-Calibration for Visual-Inertial Systems. Sensors 2019, 19, 1624. [Google Scholar] [CrossRef]
- Henawy, J.; Li, Z.; Yau, W.Y.; Seet, G. Accurate IMU Factor Using Switched Linear Systems for VIO. IEEE Trans. Ind. Electron. 2021, 68, 7199–7208. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan North Campus long-term vision and lidar dataset. Int. J. Robot. Res. 2016, 35, 1023–1035. [Google Scholar] [CrossRef]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. [Google Scholar] [CrossRef]
- Pfrommer, B.; Sanket, N.; Daniilidis, K.; Cleveland, J. PennCOSYVIO: A challenging Visual Inertial Odometry benchmark. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3847–3854. [Google Scholar] [CrossRef]
- Majdik, A.L.; Till, C.; Scaramuzza, D. The Zurich urban micro aerial vehicle dataset. Int. J. Robot. Res. 2017, 36, 269–273. [Google Scholar] [CrossRef]
- Schubert, D.; Goll, T.; Demmel, N.; Usenko, V.; Stückler, J.; Cremers, D. The TUM VI Benchmark for Evaluating Visual-Inertial Odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1680–1687. [Google Scholar] [CrossRef]
- Qiu, D.; Li, S.; Wang, T.; Ye, Q.; Li, R.; Ding, K.; Xu, H. A high-precision calibration approach for Camera-IMU pose parameters with adaptive constraints of multiple error equations. Measurement 2020, 153, 107402. [Google Scholar] [CrossRef]
- Lee, Y.; Yoon, J.; Yang, H.; Kim, C.; Lee, D. Camera-GPS-IMU sensor fusion for autonomous flying. In Proceedings of the 2016 Eighth International Conference on Ubiquitous and Future Networks (ICUFN), Vienna, Austria, 5–8 July 2016; pp. 85–88. [Google Scholar] [CrossRef]
- Ren, C.; Liu, Q.; Fu, T. A Novel Self-Calibration Method for MIMU. IEEE Sens. J. 2015, 15, 5416–5422. [Google Scholar] [CrossRef]
- Hausman, K.; Weiss, S.; Brockers, R.; Matthies, L.; Sukhatme, G.S. Self-calibrating multi-sensor fusion with probabilistic measurement validation for seamless sensor switching on a UAV. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4289–4296. [Google Scholar] [CrossRef]
- Huang, B.; Feng, P.; Zhang, J.; Yu, D.; Wu, Z. A Novel Positioning Module and Fusion Algorithm for Unmanned Aerial Vehicle Monitoring. IEEE Sens. J. 2021, 21, 23006–23023. [Google Scholar] [CrossRef]
- Sanjukumar, N.; Koundinya, P.N.; Rajalakshmi, P. Novel technique for Multi Sensor Calibration of a UAV. In Proceedings of the 2020 IEEE International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 2–4 October 2020; pp. 778–782. [Google Scholar] [CrossRef]
- Li, M.; Yu, H.; Zheng, X.; Mourikis, A.I. High-fidelity sensor modeling and self-calibration in vision-aided inertial navigation. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 409–416. [Google Scholar] [CrossRef]
- Hwangbo, M.; Kim, J.S.; Kanade, T. IMU Self-Calibration Using Factorization. IEEE Trans. Robot. 2013, 29, 493–507. [Google Scholar] [CrossRef]
- Wu, Y.; Goodall, C.; El-Sheimy, N. Self-calibration for IMU/odometer land navigation: Simulation and test results. In Proceedings of the 2010 International Technical Meeting of The Institute of Navigation, Portland, OR, USA, 21–24 September 2010; pp. 839–849. [Google Scholar]
- Yang, Y.; Geneva, P.; Zuo, X.; Huang, G. Online Self-Calibration for Visual-Inertial Navigation Systems: Models, Analysis and Degeneracy. arXiv 2022, arXiv:2201.09170. [Google Scholar]
- Huang, F.; Wang, Z.; Xing, L.; Gao, C. A MEMS IMU Gyroscope Calibration Method Based on Deep Learning. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Mahdi, A.E.; Azouz, A.; Abdalla, A.; Abosekeen, A. IMU-Error Estimation and Cancellation Using ANFIS for Improved UAV Navigation. In Proceedings of the 2022 13th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 29–31 March 2022; pp. 120–124. [Google Scholar] [CrossRef]
- Buchanan, R.; Agrawal, V.; Camurri, M.; Dellaert, F.; Fallon, M. Deep IMU Bias Inference for Robust Visual-Inertial Odometry with Factor Graphs. IEEE Robot. Autom. Lett. 2023, 8, 41–48. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Steinbrener, J.; Brommer, C.; Jantos, T.; Fornasier, A.; Weiss, S. Improved State Propagation through AI-based Pre-processing and Down-sampling of High-Speed Inertial Data. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 6084–6090. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training Very Deep Networks. Adv. Neural Inf. Process. Syst. 2015, 9, 2377–2385. [Google Scholar]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-Attention with Relative Position Representations. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 2–4 June 2018; Volume 2 (Short Papers), pp. 464–468. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR (Poster), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Delmerico, J.; Cieslewski, T.; Rebecq, H.; Faessler, M.; Scaramuzza, D. Are We Ready for Autonomous Drone Racing? The UZH-FPV Drone Racing Dataset. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 6713–6719. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Jana, P.; Tiwari, M. 2—Lean terms in apparel manufacturing. In Lean Tools in Apparel Manufacturing; Jana, P., Tiwari, M., Eds.; The Textile Institute Book Series; Woodhead Publishing: Sawston, UK, 2021; pp. 17–45. [Google Scholar] [CrossRef]


| Window Size | Signs | Offsets RMSE |
|---|---|---|
| 2 | 87.4% | 0.686 |
| 4 | 87.9% | 0.616 |
| 6 | 87.4% | 0.532 |
| 8 | 90.1% | 0.563 |
| 10 | 91.8% | 0.495 |
| Parameter | Value |
|---|---|
| Dropout | |
| Hidden size (d) | 256 |
| Attention heads | 8 |
| Layers | 2 |
| Noise multiplier () | |
| Patches size () | |
| Batch size | |
| Activation function () | Rectified Linear Unit: |
| Learning rate |
| Dataset | Validation Type | Number of Trials | Batch Size |
| EuRoC MAV [37] | LOO | 11 | 16 |
| UZH-FPV [65] | LOO | 28 | 16 |
| Zurich MAV [39] | 10-fold | 10 | 8 |
| Dataset | Epochs per Trial | Time per Trial | Time per Every Trial |
| EuRoC MAV [37] | 17.5 | ||
| UZH-FPV [65] | 13.6 | ||
| Zurich MAV [39] | 4.7 | ||
| Dataset | Batches per Training Epoch | Time per Training Step | Time per Training Epoch |
| EuRoC MAV [37] | 69 | ||
| UZH-FPV [65] | 133 | ||
| Zurich MAV [39] | 300 | ||
| Dataset | Batches per Validation Epoch | Time per Validation Step | Time per Validation Epoch |
| EuRoC MAV [37] | 10 | ||
| UZH-FPV [65] | 3 | ||
| Zurich MAV [39] | 33 |
| Dataset | Validation | Signs | Magnitude RMSE | Offsets RMSE |
|---|---|---|---|---|
| EuRoC MAV [37] | LOO | 94.59%/1.55% | 0.177/0.044 | 0.193/0.062 |
| UZH-FPV [65] | LOO | 89.61%/3.57% | 0.454/0.164 | 0.502/0.203 |
| Zurich MAV [39] | 10-fold | 73.79%/3.84% | 0.273/0.038 | 0.360/0.049 |
| Parameter | Value | Signs | Magnitude RMSE | Offsets RMSE |
|---|---|---|---|---|
| Dropout | 0% | 80.62% | 0.631 | 0.750 |
| Dropout | 1% | 80.53% | 0.635 | 0.749 |
| Dropout | 5% | 78.29% | 0.662 | 0.792 |
| Dropout | 10% | 72.30% | 0.741 | 0.932 |
| Dropout | 20% | 70.51% | 0.776 | 0.986 |
| Hidden size | 128 | 78.51% | 0.720 | 0.862 |
| Hidden size | 256 | 79.67% | 0.733 | 0.862 |
| Hidden size | 384 | 79.39% | 0.788 | 1.022 |
| Hidden size | 512 | 81.21% | 0.728 | 0.883 |
| Attention heads | 4 | 79.04% | 0.663 | 0.793 |
| Attention heads | 8 | 77.99% | 0.684 | 0.818 |
| Layers | 1 | 83.51% | 0.669 | 0.780 |
| Layers | 2 | 85.79% | 0.610 | 0.706 |
| Layers | 3 | 83.82% | 0.661 | 0.789 |
| Layers | 4 | 85.66% | 0.602 | 0.699 |
| Layers | 5 | 82.17% | 0.667 | 0.786 |
| Layers | 6 | 81.55% | 0.673 | 0.778 |
| Layers | 7 | 83.22% | 0.637 | 0.755 |
| Noise multiplier | 74.83% | 0.879 | 0.968 | |
| Noise multiplier | 78.49% | 0.665 | 0.809 | |
| Noise multiplier | 80.76% | 0.690 | 0.839 | |
| Noise multiplier | 82.52% | 0.800 | 0.946 | |
| Patches size | 59.97% | 0.919 | 1.276 | |
| Patches size | 73.89% | 0.750 | 0.929 | |
| Patches size | 76.85% | 0.697 | 0.841 | |
| Patches size | 72.04% | 0.787 | 0.976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avola, D.; Cinque, L.; Foresti, G.L.; Lanzino, R.; Marini, M.R.; Mecca, A.; Scarcello, F. A Novel Transformer-Based IMU Self-Calibration Approach through On-Board RGB Camera for UAV Flight Stabilization. Sensors 2023, 23, 2655. https://doi.org/10.3390/s23052655
Avola D, Cinque L, Foresti GL, Lanzino R, Marini MR, Mecca A, Scarcello F. A Novel Transformer-Based IMU Self-Calibration Approach through On-Board RGB Camera for UAV Flight Stabilization. Sensors. 2023; 23(5):2655. https://doi.org/10.3390/s23052655
Chicago/Turabian StyleAvola, Danilo, Luigi Cinque, Gian Luca Foresti, Romeo Lanzino, Marco Raoul Marini, Alessio Mecca, and Francesco Scarcello. 2023. "A Novel Transformer-Based IMU Self-Calibration Approach through On-Board RGB Camera for UAV Flight Stabilization" Sensors 23, no. 5: 2655. https://doi.org/10.3390/s23052655
APA StyleAvola, D., Cinque, L., Foresti, G. L., Lanzino, R., Marini, M. R., Mecca, A., & Scarcello, F. (2023). A Novel Transformer-Based IMU Self-Calibration Approach through On-Board RGB Camera for UAV Flight Stabilization. Sensors, 23(5), 2655. https://doi.org/10.3390/s23052655










