A High-Linearity Closed-Loop Capacitive Micro-Accelerometer Based on Ring-Diode Capacitance Detection
Abstract
:1. Introduction
2. Measurement and Control Scheme of Capacitive Accelerometer
2.1. Analysis of Working Principle of Capacitive Accelerometer
2.2. Closed-Loop Detection and Control Scheme
2.3. Closed-Loop Capacitive Accelerometer
3. Systems Analysis
3.1. Derivation of Accurate Model of Ring-Diode Capacitance Detection Circuit
3.2. Derivation of Closed-Loop Control Scheme
3.2.1. Control the Middle Electrode Voltage Only
3.2.2. Control the Voltage of One Side Electrode Only
3.2.3. Control the Voltage of Top and Bottom Electrodes Simultaneously (Control Scheme Used in This Paper)
4. Implementation and Test Results
4.1. Test Environment Construction
4.2. Test Results
4.2.1. Open-Loop Test
4.2.2. Closed-Loop Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sethuramalingam, T.K.; Vimalajuliet, A. Design of MEMS based capacitive accelerometer. In Proceedings of the 2010 International Conference on Mechanical and Electrical Technology, Singapore, 10–12 September 2010. [Google Scholar] [CrossRef]
- Brunthaler, J.; Grabski, P.; Sturm, V.; Lubowski, W.; Efrosinin, D. On the Problem of State Recognition in Injection Molding Based on Accelerometer Data Sets. Sensors 2022, 22, 6165. [Google Scholar] [CrossRef] [PubMed]
- Ghazali, M.H.M.; Rahiman, W. An Investigation of the Reliability of Different Types of Sensors in the Real-Time Vibration-Based Anomaly Inspection in Drone. Sensors 2022, 22, 6015. [Google Scholar] [CrossRef] [PubMed]
- Merdassi, A.; Yang, P.; Chodavarapu, V.P. A Wafer Level Vacuum Encapsulated Capacitive Accelerometer Fabricated in an Unmodified Commercial MEMS Process. Sensors 2015, 15, 7349–7359. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zhu, R.; Lin, Y. Analysis and compensation for nonlinearity of sandwich MEMS capacitive accelerometer induced by fabrication process error. Microelectron. Eng. 2022, 252, 111672. [Google Scholar] [CrossRef]
- Lin, R.; Huang, S.; Duan, Q. A MEMS Capacitance Accelerometer Readout Circuit with Ring-Diode Detection. In Proceedings of the 2021 4th ICEDME, Guangzhou, China, 19–21 March 2021. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R. Ring-diode capacitance detection circuit characteristics. J. Tsinghua Univ. 2021, 61, 653–658. [Google Scholar] [CrossRef]
- Zwahlen, P.; Balmain, D.; Habibi, S. Open-loop and closed-loop high-end accelerometer platforms for high demanding applications. In Proceedings of the 2016 IEEE/ION PLANS, Savannah, GA, USA, 11–14 April 2016; pp. 932–937. [Google Scholar] [CrossRef]
- Marjoux, D.; Ullah, P.; Frantz-Rodriguez, N. Silicon MEMS by Safran—Navigation grade accelerometer ready for mass production. In Proceedings of the 2020 DGON ISS, Braunschweig, Germany, 15–16 September 2020; pp. 1–18. [Google Scholar] [CrossRef]
- Grinberg, B.; Feingold, A.; Koenigsberg, L. Closed-loop MEMS accelerometer: From design to production. In Proceedings of the 2016 DGON ISS, Karlsruhe, Germany, 20–21 September 2016; pp. 1–16. [Google Scholar] [CrossRef]
- Filipe, A.; Gaff, V.; Unrau, W. High performance MEMS accelerometer and gyro with a unique SMD and digital interface. In Proceedings of the 2021 DGON ISS, Braunschweig, Germany, 29–30 September 2021; pp. 1–19. [Google Scholar] [CrossRef]
- Wan, C.; Dong, J.; Liu, Y.; Zhao, C. Nonlinearity of a Closed-Loop Micro-accelerometer. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1260–1265. [Google Scholar] [CrossRef]
- Langfelder, G.; Bestetti, M.; Gadola, M. Silicon MEMS Inertial Sensors Evolution over a Quarter Century. J. Micromech. Microeng. 2021, 31, 084002. [Google Scholar] [CrossRef]
- Benmessaoud, M.; Nasreddine, M.M. Optimization of MEMS capacitive accelerometer. Microsyst. Technol. 2013, 19, 713–720. [Google Scholar] [CrossRef]
- Stauffer, J.-M.; Dietrich, O.; Dutoit, B. RS9000, a novel MEMS accelerometer family for Mil/Aerospace and safety critical applications. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Feingold, A.; Grinberg, B. In-plane Βulk-Micromachining fabrication of high dynamic range tactical grade open loop and closed loop MEMS accelerometers. In Proceedings of the 2015 IEEE SENSORS, Busan, Korea, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Gonseth, S.; Rudolf, F.; Eichenberger, C. Miniaturized high-performance MEMS accelerometer detector. CEAS Space 2015, 7, 263–270. [Google Scholar] [CrossRef]
- Deppe, O.; Dorner, G.; König, S. MEMS and FOG Technologies for Tactical and Navigation Grade Inertial Sensors—Recent Improvements and Comparison. Sensors 2017, 17, 567. [Google Scholar] [CrossRef] [PubMed]
- Grinberg, B.; Feingold, A.; Furman, L. High precision open-loop and closed-loop MEMS accelerometers with wide sensing range. In Proceedings of the 2016 IEEE/ION PLANS, Savannah, GA, USA, 11–14 April 2016; pp. 924–931. [Google Scholar] [CrossRef]
- Shi, Z.; Jefimovs, K.; Romano, L.; Stampanoni, M. Towards the Fabrication of High-Aspect-Ratio Silicon Gratings by Deep Reactive Ion Etching. Micromachines 2020, 11, 864. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Liu, Y.; Dong, J. The optimization of drive and sense circuit in silicon micro-machined resonant accelerometer. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 2058–2063. [Google Scholar] [CrossRef]
- Xiao, P.; Liu, L.; Wang, X.B. Non-linearity analysis of a capacitance detector diodes circuit for closed-loop micro-silicon accelerometer. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 5601–5604. [Google Scholar] [CrossRef]
- Henrion, W.; DiSanza, L.; Ip, M. Wide dynamic range direct accelerometer. In Proceedings of the IEEE 4th Technical Digest on Solid-State Sensor and Actuator Workshop, Hilton Head Island, Hilton Head, SC, USA, 4–7 June 1990; pp. 153–157. [Google Scholar] [CrossRef]
- Dong, Y.; Zwahlen, P.; Nguyen, A.M. Ultra-high precision MEMS accelerometer. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 695–698. [Google Scholar] [CrossRef]
- Closed Loop Accelerometer MAXL-CL-3030—Physical Logic. Available online: https://physical-logic.com/closed-loop-accelerometers/maxl-cl-3030/ (accessed on 1 December 2022).
- Terzioglu, Y.; Alper, S.E.; Azgin, K. A capacitive MEMS accelerometer readout with concurrent detection and feedback using discrete components. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 12–15. [Google Scholar] [CrossRef]
- Chu, Y.; Dong, J.; Chi, B.; Liu, Y. A Novel Digital Closed Loop MEMS Accelerometer Utilizing a Charge Pump. Sensors 2016, 16, 389. [Google Scholar] [CrossRef] [PubMed]
- Xianshan, D.; Qinwen, H.; Wei, X. Research on temperature characteristic of parasitic capacitance in MEMS capacitive accelerometer. Sens. Actuator A Phys. 2019, 285, 581–587. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, M.; Zhang, T. Linearity analysis of closed-loop capacitive accelerometer due to distance mismatch between plates and the influence of compensation capacitor array. Sci. China Inf. Sci. 2014, 57, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Zhou, X.; Wu, J. A MEMS accelerometer with double-sided symmetrical folded-beams on single wafer. In Proceedings of the 12th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, NEMS 2017, Los Angeles, CA, USA, 9–12 April 2017; pp. 194–197. [Google Scholar] [CrossRef]


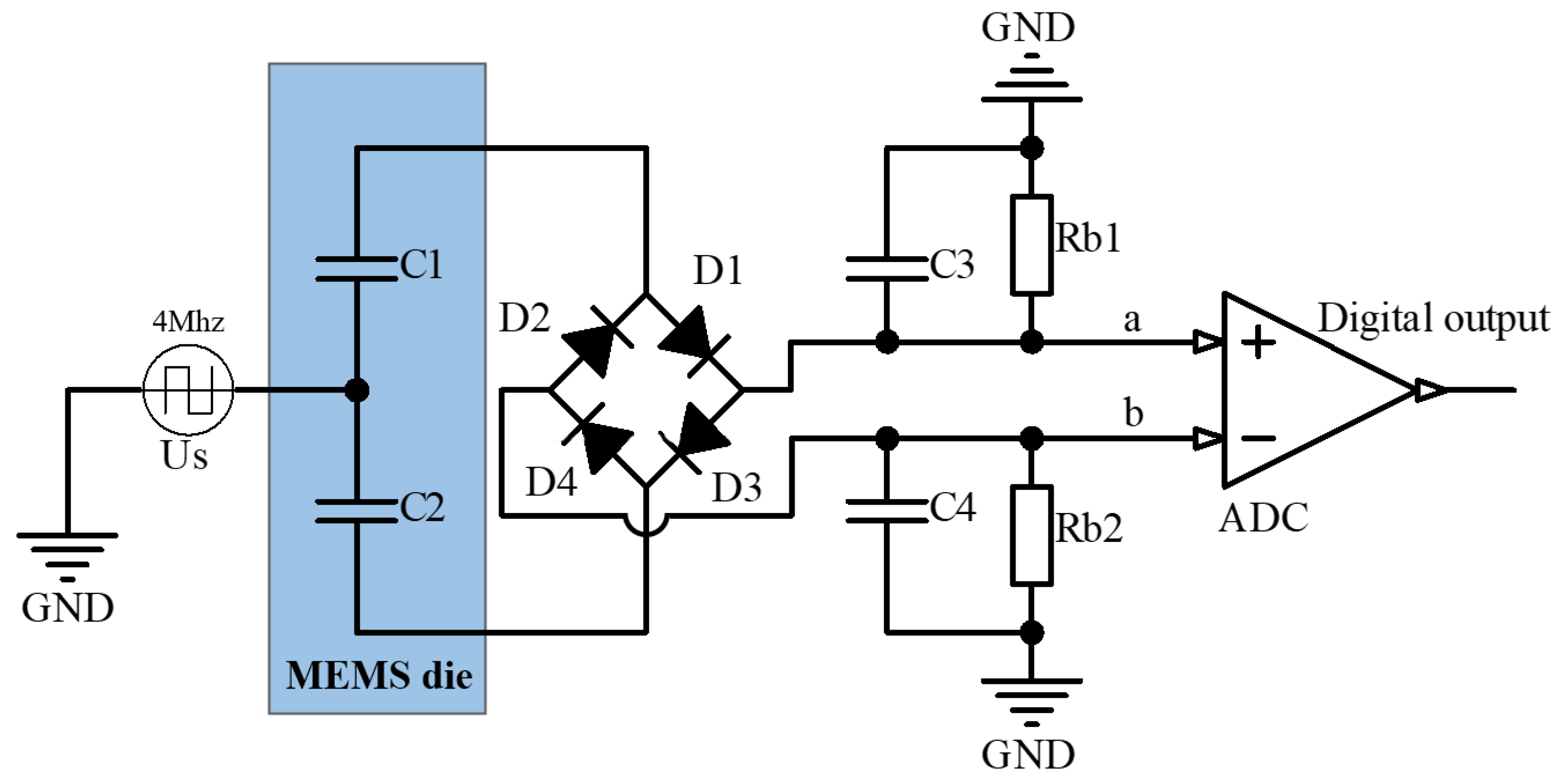

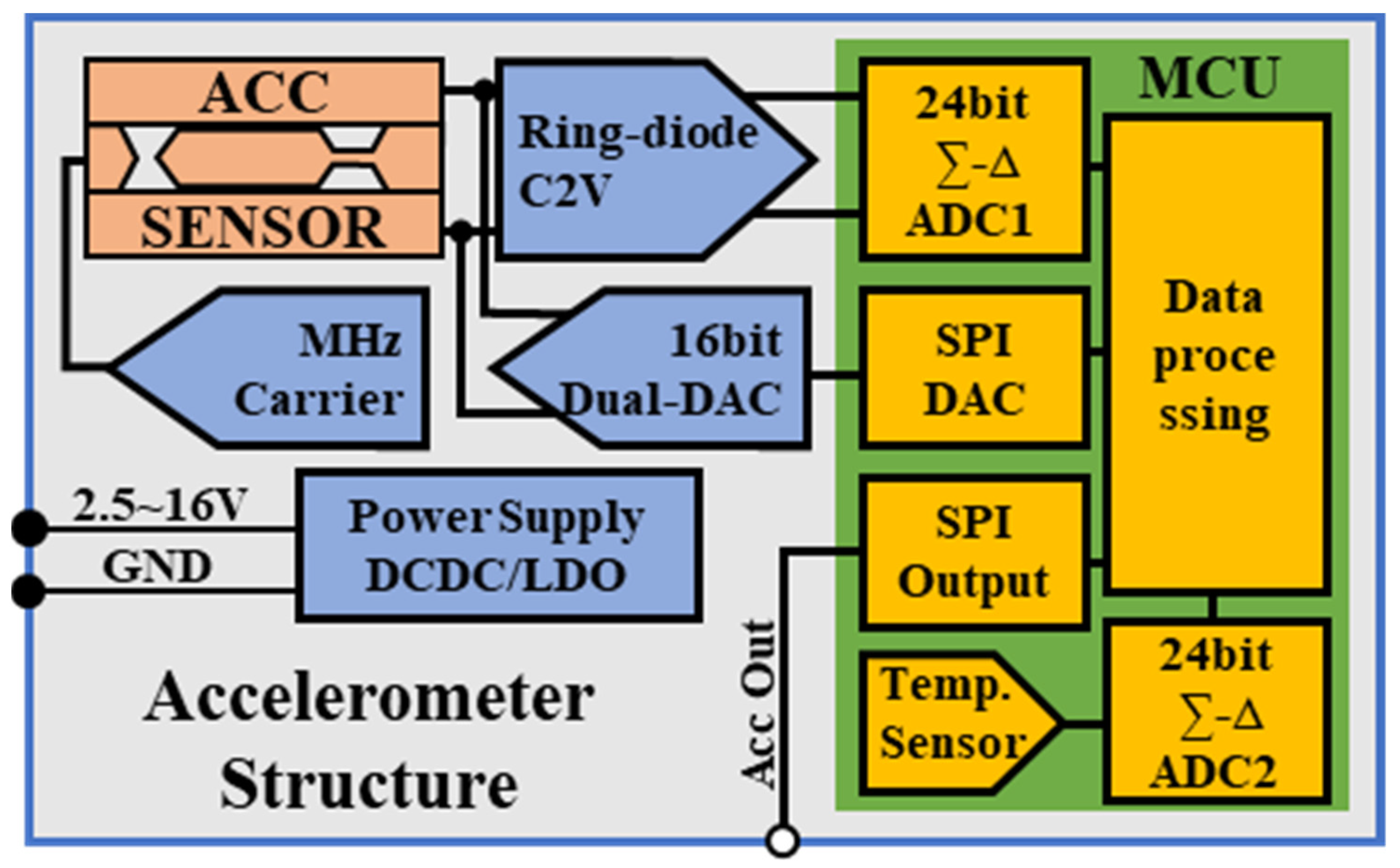


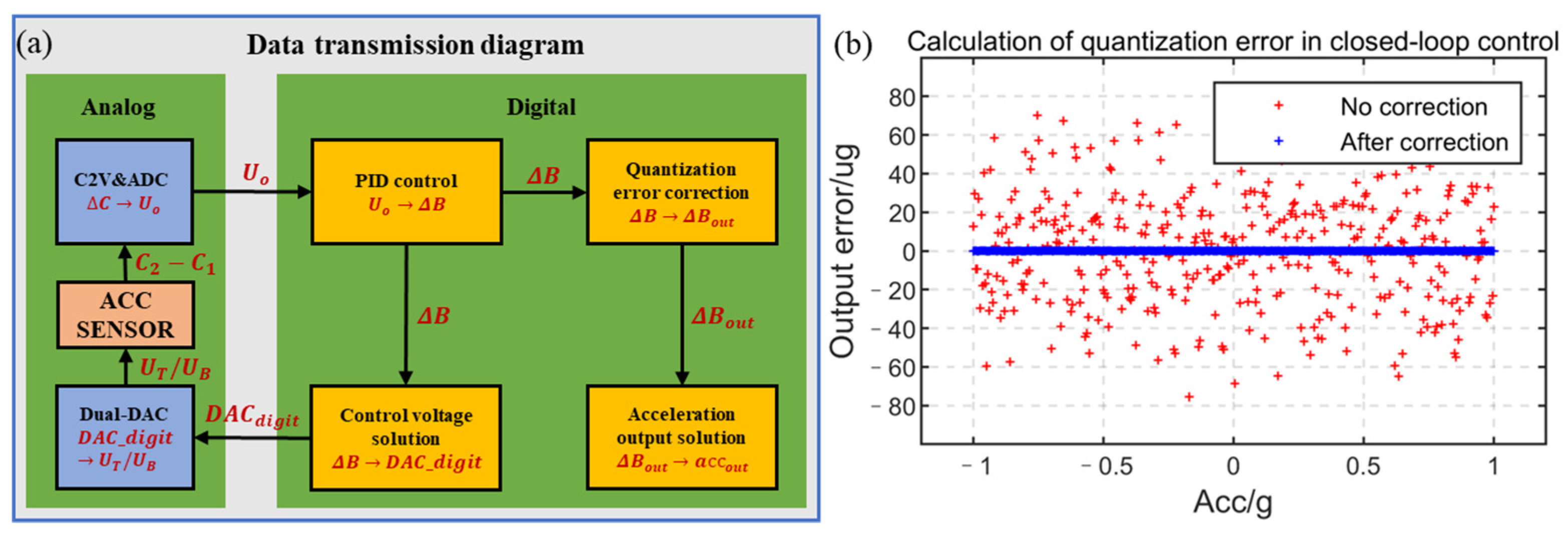
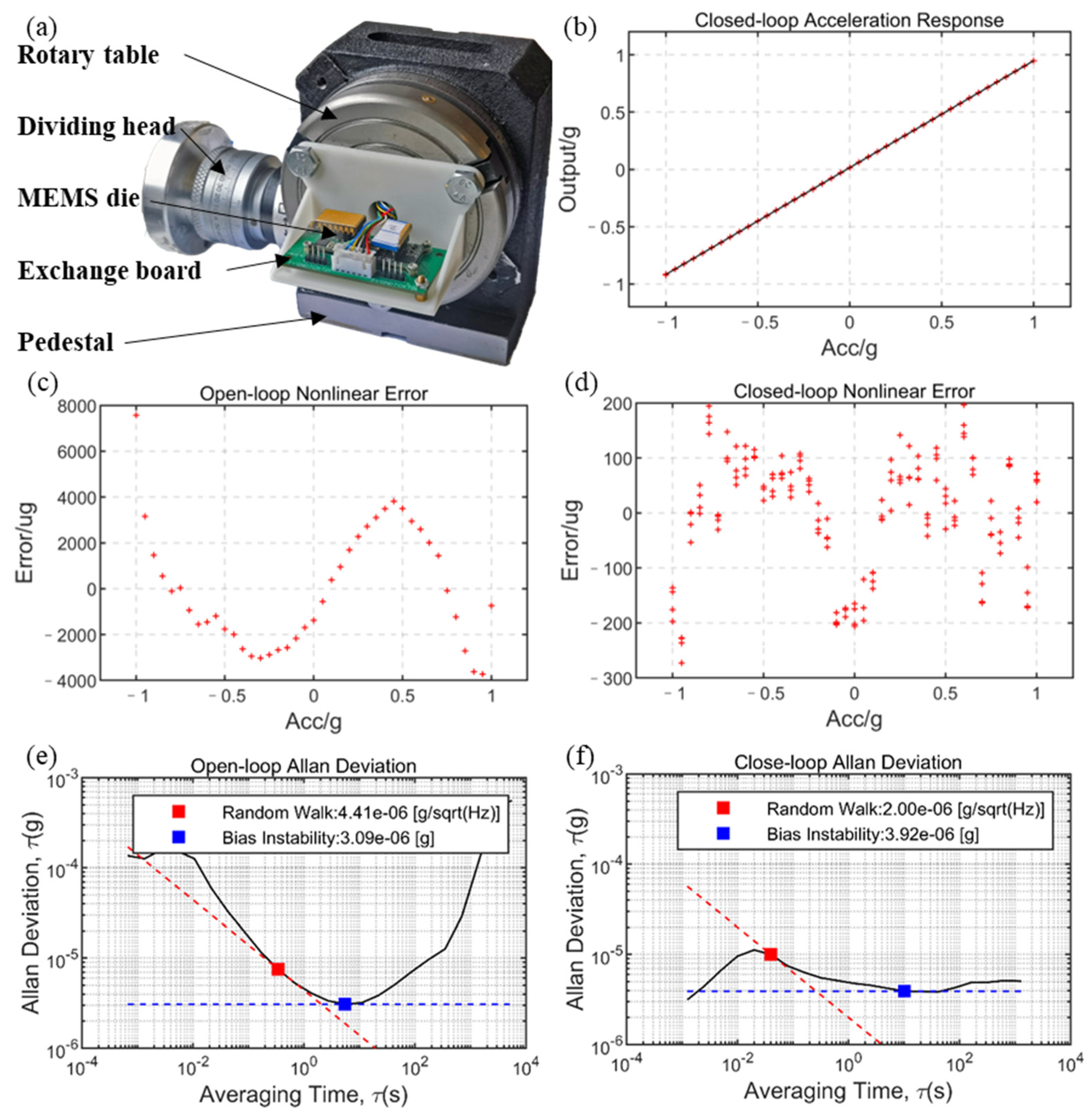
| Element | Value/Model |
|---|---|
| C1, C2 | ≈32 pF |
| C3, C4, C5, C6 | 1 nF |
| R1, R2 | 100 kΩ |
| Rb1, Rb2 | 20 kΩ |
| D1, D2, D3, D4 | HSMS-2829 |
| MCU | MSP430I2040 |
| DAC | DAC80502 |
| Performance | Value |
|---|---|
| Full-scale | ±2 g |
| Non-linearity (IEEE) | 130 ppm |
| Short-term bias stability | 10.5 µg (1 s average) |
| Bias instability | 3.92 µg (10 s) |
| Short-term repeatability | 12.74 µg |
| Scale factor repeatability | 11.61 ppm |
| Output mode | SPI/UART |
| Supply voltage (VDD) | 2.5~16 V |
| Power consumption | 150 mW |
| Size | 22 × 23 mm2 |
| Parameter | Yunus [26] 2014 | Chu [27] 2016 | Dong [28] 2019 | Huang [29] 2014 | Li [30] 2017 | Dong [28] 2019 | This work |
|---|---|---|---|---|---|---|---|
| Structure | Comb-finger structure | Parallel-plate structure | |||||
| Non-linearity | 1500 ppm | 2220 ppm | <2000 ppm | 2000 ppm | 500 ppm | <5000 ppm | 130 ppm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Q.; Tang, B. A High-Linearity Closed-Loop Capacitive Micro-Accelerometer Based on Ring-Diode Capacitance Detection. Sensors 2023, 23, 1568. https://doi.org/10.3390/s23031568
Tao Q, Tang B. A High-Linearity Closed-Loop Capacitive Micro-Accelerometer Based on Ring-Diode Capacitance Detection. Sensors. 2023; 23(3):1568. https://doi.org/10.3390/s23031568
Chicago/Turabian StyleTao, Qi, and Bin Tang. 2023. "A High-Linearity Closed-Loop Capacitive Micro-Accelerometer Based on Ring-Diode Capacitance Detection" Sensors 23, no. 3: 1568. https://doi.org/10.3390/s23031568
APA StyleTao, Q., & Tang, B. (2023). A High-Linearity Closed-Loop Capacitive Micro-Accelerometer Based on Ring-Diode Capacitance Detection. Sensors, 23(3), 1568. https://doi.org/10.3390/s23031568






