Deep Learning of GNSS Acquisition
Abstract
:1. Introduction
2. GNSS Signal Model and Acquisition
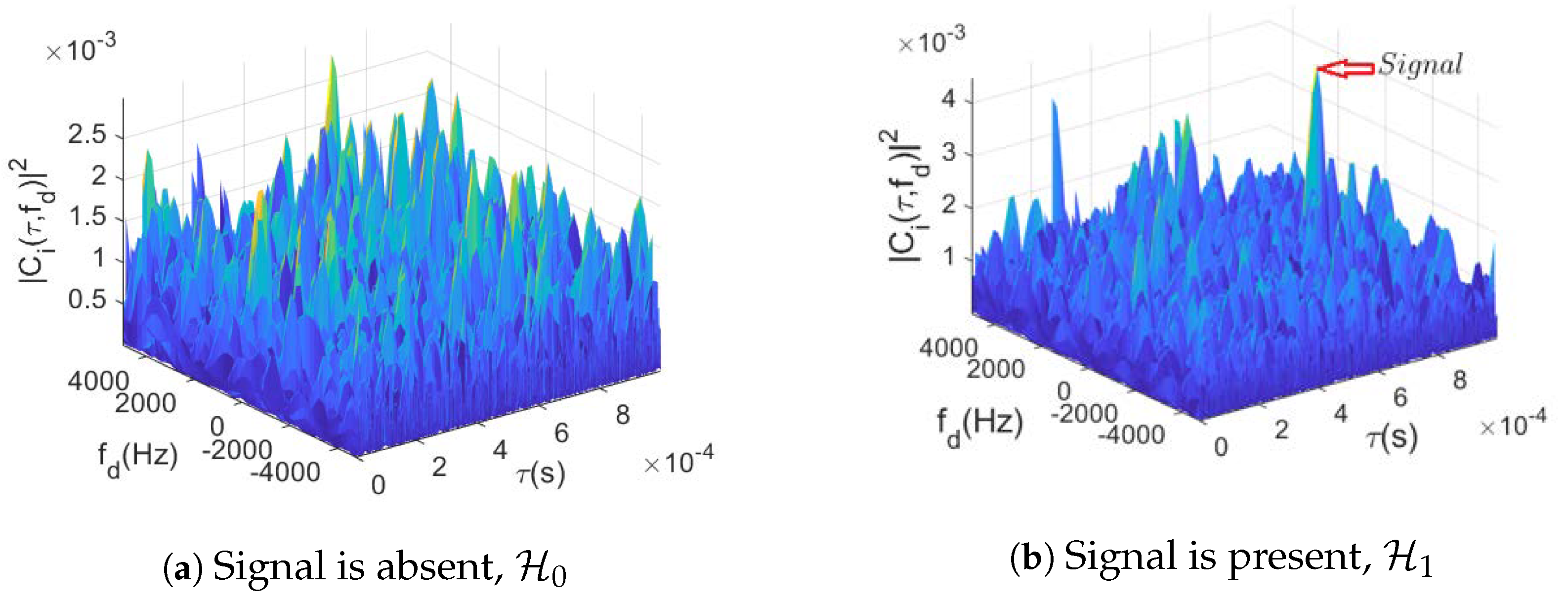
2.1. CAF Evaluation
- Maximum: This strategy evaluates the CAF all over the search space , such that each cell corresponds to a CAF value at the corresponding delay/Doppler pair. The overall maximum value of the ambiguity function is then selected and compared with the threshold , if the maximum’s value is greater than , the satellite is considered acquired, with the estimated code delay and Doppler frequency corresponding to those of the maximum’s cell.
- Serial: In this strategy, the ambiguity function is evaluated serially cell by cell. In each cell, when the ambiguity function (9) is computed, it is immediately compared with the threshold. If the value exceeds the threshold, the acquisition process stops, and the value of the estimated code delay and Doppler frequency are matched to those from the cell under the test. This strategy has the benefit of reducing the number of CAF evaluations, at the expense of some performance degradation.
- Hybrid: This strategy evaluates the ambiguity function row by row (or column by column), and at the end of each row (column), the values of the computed ambiguity functions are compared with the threshold. As soon as the maximum value in the current row (column) exceeds the threshold, the acquisition process stops, and the estimated code delay and Doppler frequency are set to the corresponding cell. This strategy brings in a balance between the two approaches above.
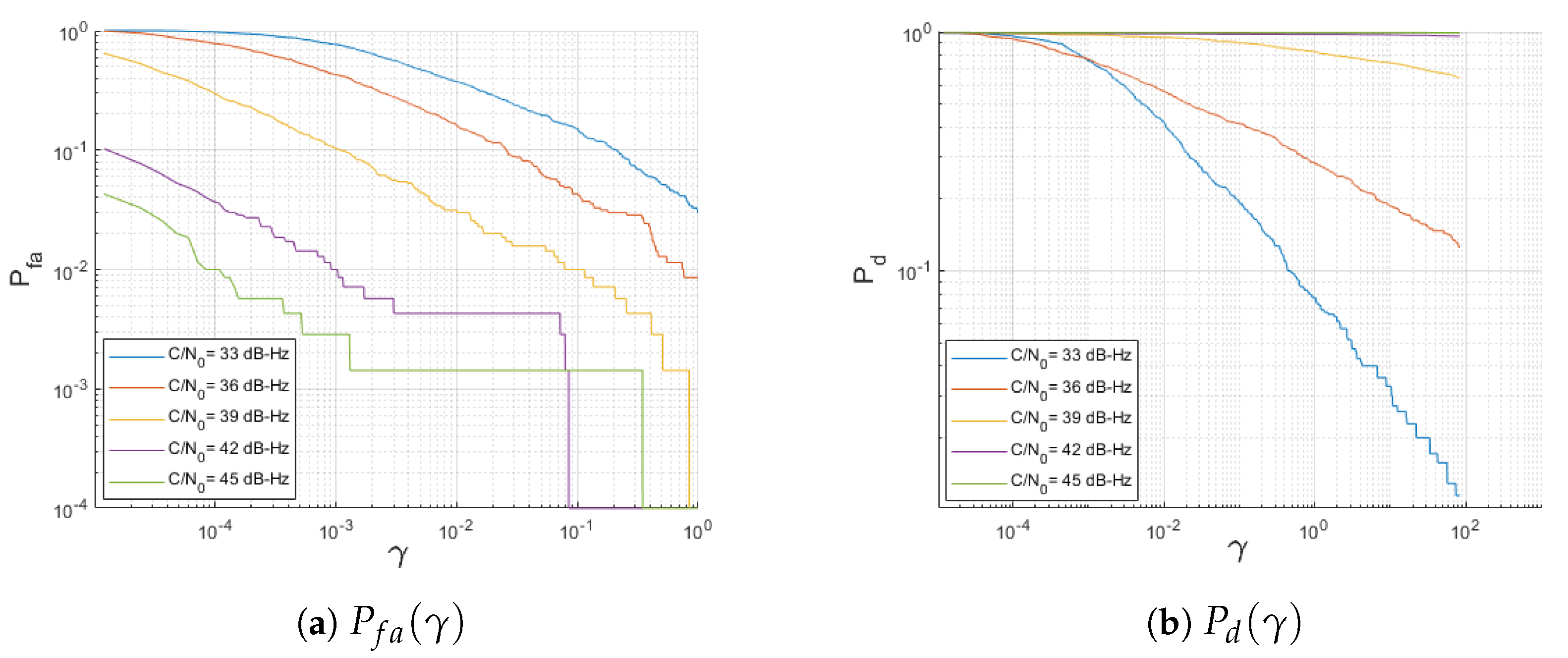
2.2. Benchmark Performance Using the Receiver Operating Characteristic Function
3. Deep Learning Method for GNSS Acquisition
3.1. Data-Driven, Physics-Based Signal Acquisition
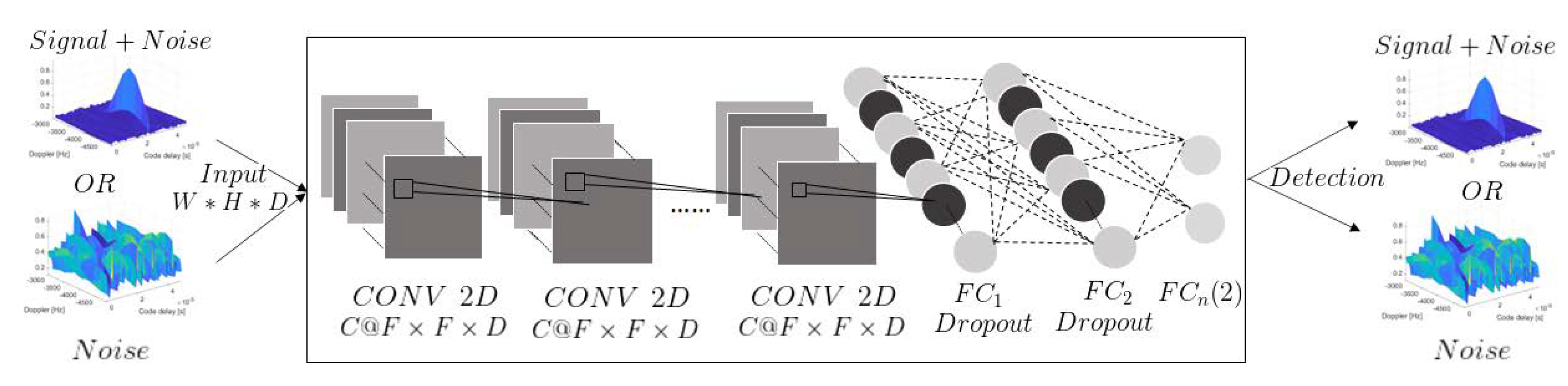
3.2. Model Structure
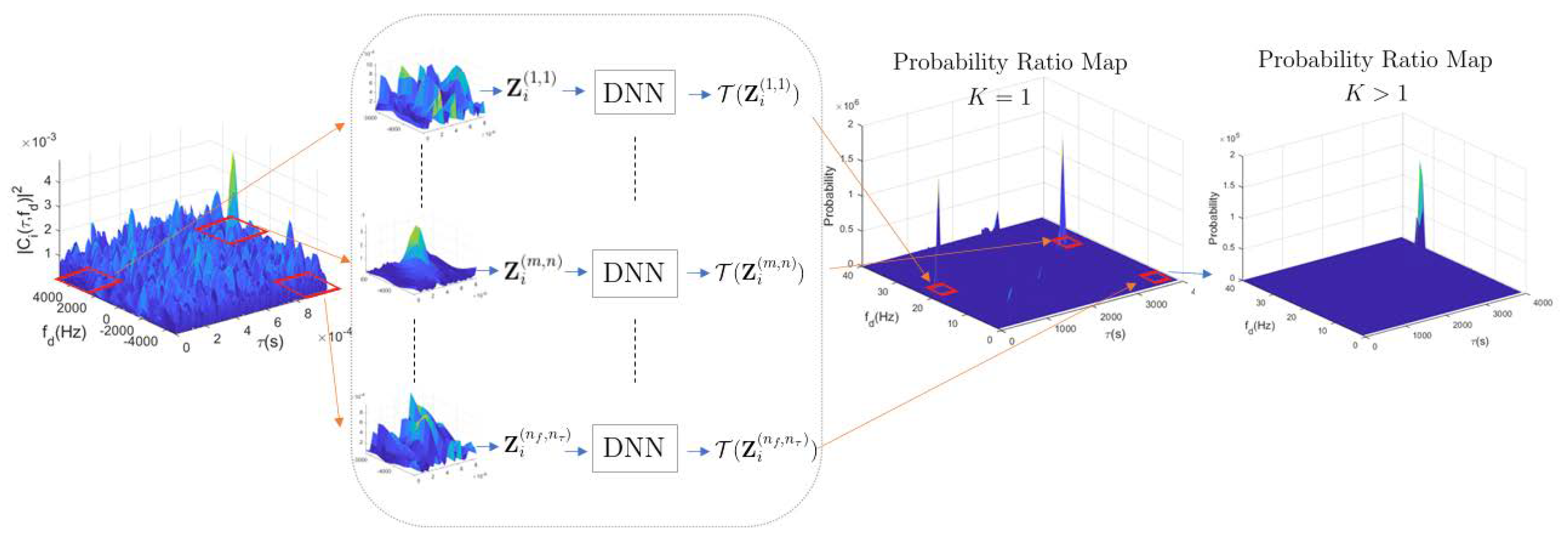
3.3. Noncoherent Integration through Fusion of Classifiers
4. Model Training
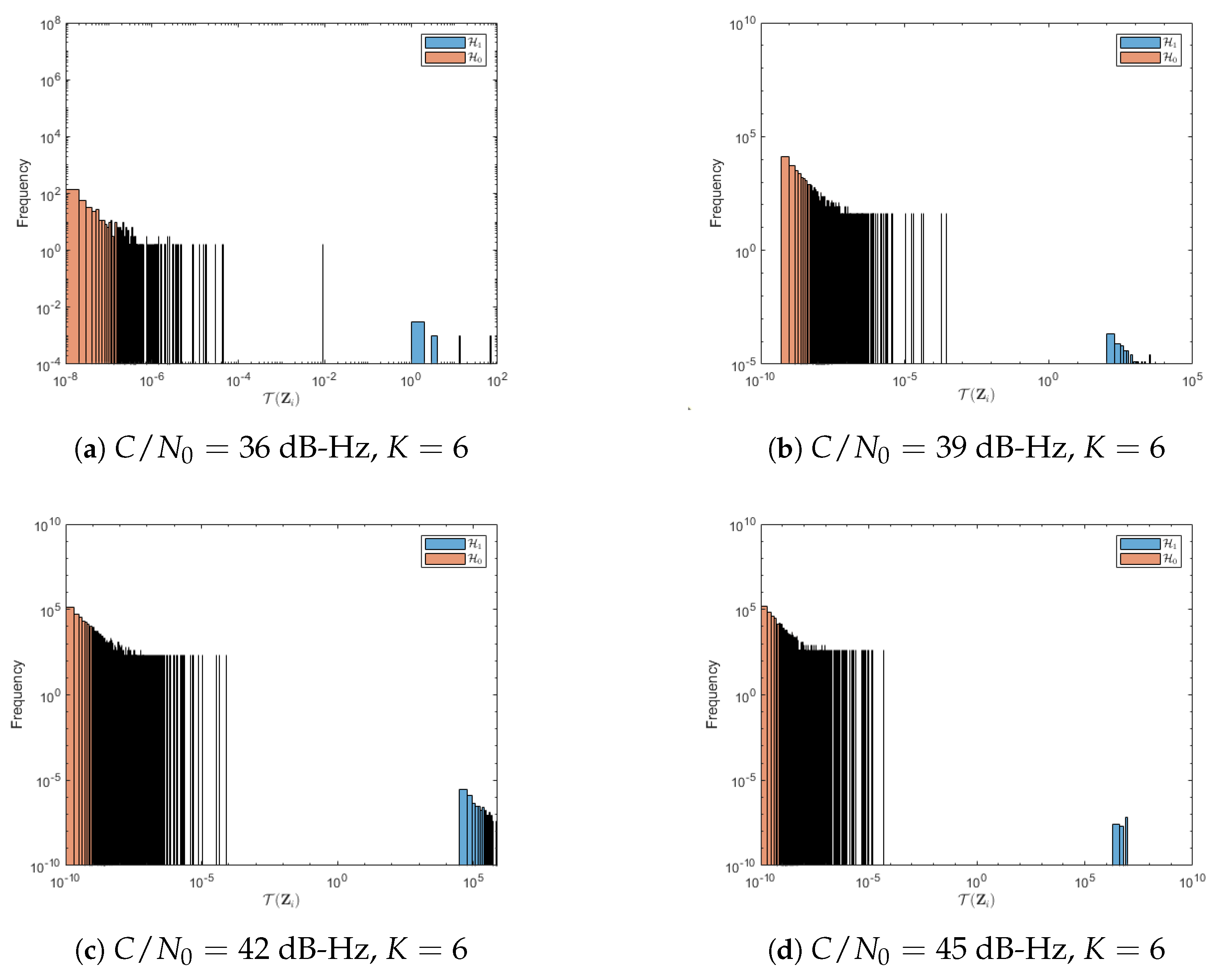
5. Results
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Dardari, D.; Falletti, E.; Luise, M. Satellite and Terrestrial Radio Positioning Techniques: A Signal Processing Perspective; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Dardari, D.; Closas, P.; Djurić, P.M. Indoor tracking: Theory, methods, and technologies. IEEE Trans. Veh. Technol. 2015, 64, 1263–1278. [Google Scholar] [CrossRef]
- Williams, N.; Darian, P.B.; Wu, G.; Closas, P.; Barth, M. Impact of Positioning Uncertainty on Connected and Automated Vehicle Applications. SAE Int. J. Connect. Autom. Veh. 2022, 6. [Google Scholar] [CrossRef]
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Kassas, Z.M.; Closas, P.; Gross, J. Navigation systems panel report navigation systems for autonomous and semi-autonomous vehicles: Current trends and future challenges. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 82–84. [Google Scholar] [CrossRef]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Tsui, J.B. Fundamentals of Global Positioning System Receivers: A Software Approach; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 173. [Google Scholar]
- Borio, D. A Statistical Theory for GNSS Signal Acquisition. Ph.D. Thesis, Polytecnico di Torino, Turin, Italy, 2008. [Google Scholar]
- Mathis, H.; Flammant, P.; Thiel, A. An analytic way to optimize the detector of a post-correlation FFT acquisition algorithm. Quadrature 2003, 1000, 1. [Google Scholar]
- Whalen, A. Detection of Signals in Noise; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Lehner, A.; Steingass, A. A novel channel model for land mobile satellite navigation. In Proceedings of the Institute of Navigation Conference ION GNSS, Long Beach, CA, USA, 13–16 September 2005; pp. 13–16. [Google Scholar]
- Borio, D.; Closas, P. A fresh look at GNSS anti-jamming. Inside GNSS 2017, 12, 54–61. [Google Scholar]
- Borio, D. Robust signal processing for GNSS. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 150–158. [Google Scholar] [CrossRef]
- Borio, D. Myriad Non-Linearity for GNSS Robust Signal Processing. IET Radar Sonar Navig. 2017, 11, 1467–1476. [Google Scholar] [CrossRef]
- Borio, D.; Closas, P. Complex Signum Non-Linearity for Robust GNSS Signal Mitigation. IET Radar Sonar Navig. 2018, 12. [Google Scholar] [CrossRef]
- Borio, D.; Li, H.; Closas, P. Huber’s Non-Linearity for GNSS Interference Mitigation. Sensors 2018, 18, 2217. [Google Scholar] [CrossRef]
- Borio, D.; Closas, P. Robust Transform Domain Signal Processing for GNSS. Navigation 2019. [Google Scholar] [CrossRef]
- Li, H.; Borio, D.; Closas, P. Dual-Domain Robust GNSS Interference Mitigation. In Proceedings of the International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Borio, D.; Gioia, C. GNSS interference mitigation: A measurement and position domain assessment. Navig. J. Inst. Navig. 2021, 68, 93–114. [Google Scholar] [CrossRef]
- Borhani-Darian, P.; Closas, P. Deep Neural Network Approach to GNSS Signal Acquisition. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1214–1223. [Google Scholar]
- Azari, B.; Cheng, H.; Soltani, N.; Li, H.; Li, Y.; Belgiovine, M.; Imbiriba, T.; D’Oro, S.; Melodia, T.; Wang, Y.; et al. Automated deep learning-based wide-band receiver. Comput. Netw. 2022, 218, 109367. [Google Scholar] [CrossRef]
- Dampf, J.; Pany, T.; Bär, W.; Winkel, J.; Stöber, C.; Fürlinger, K.; Closas, P.; Garcia-Molina, J. More than we ever dreamed possible: Processor technology for GNSS software receivers in the year 2015. Inside GNSS 2015, 10, 62–72. [Google Scholar]
- Siemuri, A.; Kuusniemi, H.; Elmusrati, M.; Välisuo, P.; Shamsuzzoha, A. Machine Learning Utilization in GNSS—Use Cases, Challenges and Future Applications. In Proceedings of the 2021 International Conference on Localization and GNSS (ICL-GNSS), Tampere, Finland, 1–3 June 2021; pp. 1–6. [Google Scholar]
- Abdallah, A.A.; Kassas, Z.M. Deep learning-aided spatial discrimination for multipath mitigation. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1324–1335. [Google Scholar]
- Zhang, G.; Xu, P.; Xu, H.; Hsu, L.T. Prediction on the Urban GNSS Measurement Uncertainty Based on Deep Learning Networks With Long Short-Term Memory. IEEE Sens. J. 2021, 21, 20563–20577. [Google Scholar] [CrossRef]
- Huang, P.; Rizos, C.; Roberts, C. Satellite selection with an end-to-end deep learning network. GPS Solut. 2018, 22, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Borhani-Darian, P.; Wu, P.; Closas, P. Deep Learning of GNSS Signal Correlation. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), St. Louis, MO, USA, 21–25 September 2020; pp. 2836–2847. [Google Scholar]
- Savas, C.; Dovis, F. Multipath Detection based on K-means Clustering. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3801–3811. [Google Scholar]
- Suzuki, T.; Kusama, K.; Amano, Y. NLOS Multipath Detection using Convolutional Neural Network. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), St. Louis, MO, USA, 21–25 September 2020; pp. 2989–3000. [Google Scholar]
- Munin, E.; Blais, A.; Couellan, N. Convolutional neural network for multipath detection in GNSS receivers. In Proceedings of the 2020 International Conference on Artificial Intelligence and Data Analytics for Air Transportation (AIDA-AT), Singapore, 3–4 February 2020; pp. 1–10. [Google Scholar]
- Caparra, G.; Zoccarato, P.; Melman, F. Machine Learning Correction for Improved PVT Accuracy. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 3392–3401. [Google Scholar]
- Manesh, M.R.; Kenney, J.; Hu, W.C.; Devabhaktuni, V.K.; Kaabouch, N. Detection of GPS spoofing attacks on unmanned aerial systems. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–6. [Google Scholar]
- Borhani-Darian, P.; Li, H.; Wu, P.; Closas, P. Deep Neural Network Approach to Detect GNSS Spoofing Attacks. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), Portland, OR, USA, 20–23 April 2020; pp. 3241–3252. [Google Scholar]
- Tohidi, S.; Mosavi, M.R. Effective detection of GNSS spoofing attack Using A multi-layer perceptron neural network classifier trained by PSO. In Proceedings of the 2020 25th International Computer Conference, Computer Society of Iran (CSICC), Tehran, Iran, 1–2 January 2020; pp. 1–5. [Google Scholar]
- Calvo-Palomino, R.; Bhattacharya, A.; Bovet, G.; Giustiniano, D. Short: LSTM-based GNSS Spoofing Detection Using Low-cost Spectrum Sensors. In Proceedings of the 2020 IEEE 21st International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Cork, Ireland, 31 August–3 September 2020; pp. 273–276. [Google Scholar]
- Semanjski, S.; Muls, A.; Semanjski, I.; De Wilde, W. Use and validation of supervised machine learning approach for detection of GNSS signal spoofing. In Proceedings of the 2019 International Conference on Localization and GNSS (ICL-GNSS), Nuremberg, Germany, 4–6 June 2019; pp. 1–6. [Google Scholar]
- Morales Ferre, R.; de la Fuente, A.; Lohan, E.S. Jammer classification in GNSS bands via machine learning algorithms. Sensors 2019, 19, 4841. [Google Scholar] [CrossRef]
- Louis, A.; Raimondi, M. Neural Network based Evil WaveForms Detection. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), St. Louis, MO, USA, 21–25 September 2020; pp. 1984–1989. [Google Scholar]
- Brum, D.; Veronez, M.R.; de Souza, E.M.; Koch, I.É.; Gonzaga, L.; Klein, I.; Matsuoka, M.T.; Rofatto, V.F.; Junior, A.M.; dos Reis Racolte, G.E.; et al. A Proposed Earthquake Warning System Based on Ionospheric Anomalies Derived From GNSS Measurements and Artificial Neural Networks. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9295–9298. [Google Scholar]
- Alshaye, M.; Alawwad, F.; Elshafiey, I. Hurricane tracking using Multi-GNSS-R and deep learning. In Proceedings of the 2020 3rd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 19–21 March 2020; pp. 1–4. [Google Scholar]
- Yan, Q.; Huang, W. Sea ice sensing from GNSS-R data using convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1510–1514. [Google Scholar] [CrossRef]
- Linty, N.; Farasin, A.; Favenza, A.; Dovis, F. Detection of GNSS ionospheric scintillations based on machine learning decision tree. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 303–317. [Google Scholar] [CrossRef]
- Liu, Y.; Morton, Y.; Jiao, Y. Application of Machine Learning to Characterization of GPS L1 Ionospheric Amplitude Scintillation. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1159–1166. [Google Scholar]
- Selbesoglu, M.O. Prediction of tropospheric wet delay by an artificial neural network model based on meteorological and GNSS data. Eng. Sci. Technol. Int. J. 2020, 23, 967–972. [Google Scholar] [CrossRef]
- Vilà-Valls, J.; Linty, N.; Closas, P.; Dovis, F.; Curran, J.T. Survey on signal processing for GNSS under ionospheric scintillation: Detection, monitoring, and mitigation. Navig. J. Inst. Navig. 2020, 67, 511–536. [Google Scholar] [CrossRef]
- Imbiriba, T.; Demirkaya, A.; Duník, J.; Straka, O.; Erdoğmuş, D.; Closas, P. Hybrid Neural Network Augmented Physics-based Models for Nonlinear Filtering. In Proceedings of the FUSION Conference, Linköping, Sweden, 4–7 July 2022. [Google Scholar]
- O’Shea, T.; Roy, T.; Clancy, T. Over-the-air deep learning based radio signal classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Moloney, C. Neural networks based sea ice detection and concentration retrieval from GNSS-R delay-Doppler maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3789–3798. [Google Scholar] [CrossRef]
- White, C.; Neiswanger, W.; Savani, Y. BANANAS: Bayesian Optimization with Neural Architectures for Neural Architecture Search. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 22 February–1 March 2021. [Google Scholar]
- Liu, S.; Deng, W. Very deep convolutional neural network based image classification using small training sample size. In Proceedings of the 2015 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, Malaysia, 3–6 November 2015; pp. 730–734. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Pastor, F.; García-González, J.; Gandarias, J.M.; Medina, D.; Closas, P.; García-Cerezo, A.J.; Gómez-de Gabriel, J.M. Bayesian and Neural Inference on LSTM-Based Object Recognition from Tactile and Kinesthetic Information. IEEE Robot. Autom. Lett. 2020, 6, 231–238. [Google Scholar] [CrossRef]
- Mathworks. Create Simple Deep Learning Network for Classification. Available online: https://www.mathworks.com/help/deeplearning/examples/create-simple-deep-learning-network-for-classification.html (accessed on 26 January 2023).




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borhani-Darian, P.; Li, H.; Wu, P.; Closas, P. Deep Learning of GNSS Acquisition. Sensors 2023, 23, 1566. https://doi.org/10.3390/s23031566
Borhani-Darian P, Li H, Wu P, Closas P. Deep Learning of GNSS Acquisition. Sensors. 2023; 23(3):1566. https://doi.org/10.3390/s23031566
Chicago/Turabian StyleBorhani-Darian, Parisa, Haoqing Li, Peng Wu, and Pau Closas. 2023. "Deep Learning of GNSS Acquisition" Sensors 23, no. 3: 1566. https://doi.org/10.3390/s23031566
APA StyleBorhani-Darian, P., Li, H., Wu, P., & Closas, P. (2023). Deep Learning of GNSS Acquisition. Sensors, 23(3), 1566. https://doi.org/10.3390/s23031566





