Application of Feedforward and Recurrent Neural Networks for Fusion of Data from Radar and Depth Sensors Applied for Healthcare-Oriented Characterisation of Persons’ Gait
Abstract
1. Introduction
- The localisation of a person walking around the monitored area according to various predefined movement scenarios.
- The estimation of several parameters, carrying information important for medical experts, on the basis of the estimated movement trajectories.
2. Compared Methods of Data Fusion
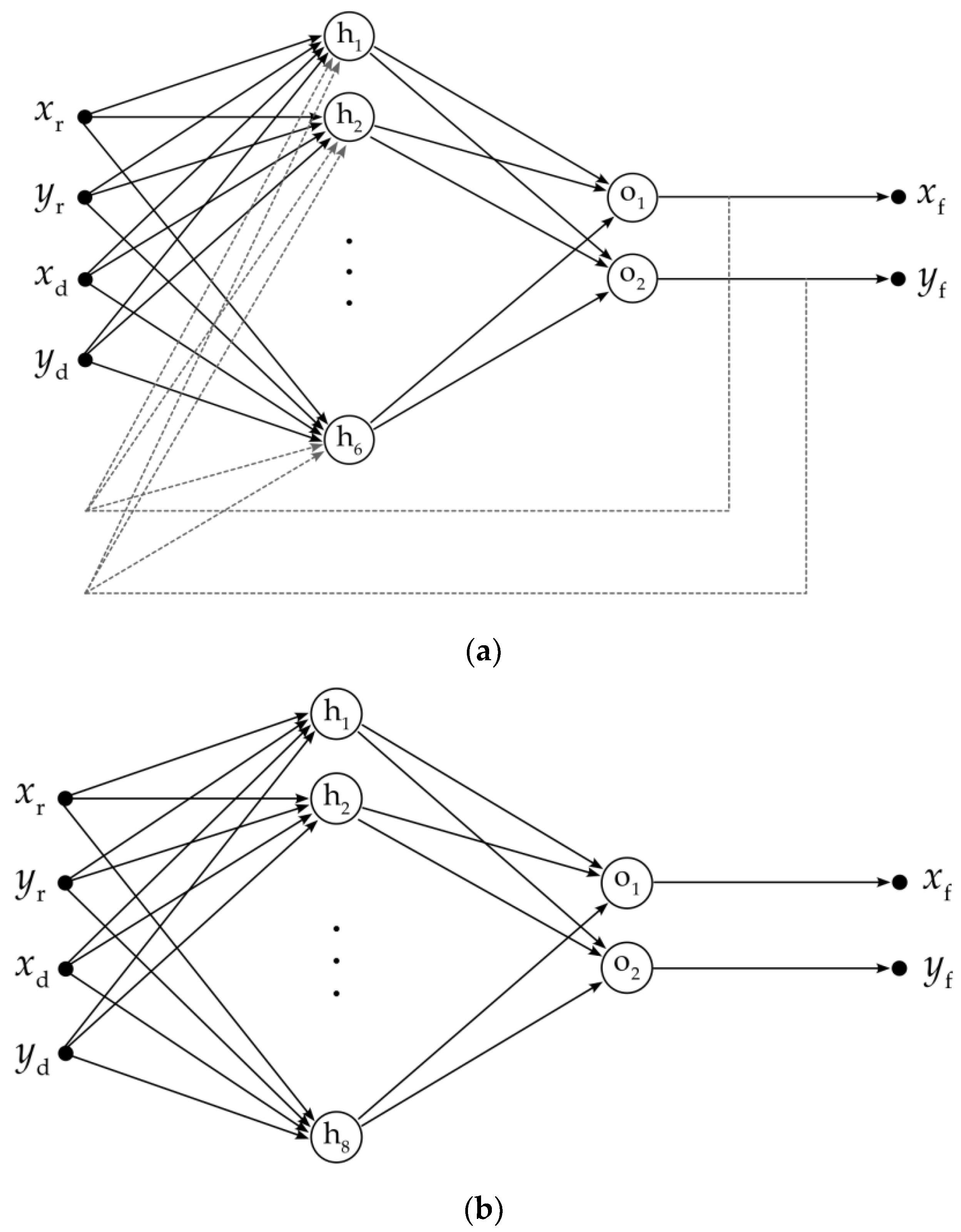
2.1. Method Based on Nonlinear Autoregressive Network with Exogenous Inputs
- Four input neurons—the input data represent two pairs of the x-y coordinates acquired by means of the impulse-radar sensor and depth sensor;
- Six neurons in a single hidden layer;
- Two output neurons—the output data represent one pair of fused x-y coordinates; the output values, delayed by two time instants, are fed back to the hidden layer;
2.2. Method Based on Multilayer Perceptron
2.3. Method Based on Kalman Filter
- is a state vector representative of the two-dimensional coordinates , corresponding to a time instant , and the velocities along these dimensions ;
- and are the matrices of the form:with being the time interval between the time instants and ;
- is a vector modelling the acceleration, whose elements are assumed to be the realisations of a zero-mean bivariate normal distribution with a known covariance matrix .
- is an observation matrix of the form:
- is a vector representative of the observation noise corrupting the data, whose elements are assumed to be realisations of a zero-mean bivariate normal distribution with a known covariance matrix .
- 1.
- Determination of the pre-estimate of the state vector and the pre-estimate of its covariance matrix:
- 2.
- Calculation of the estimate of the observation vector:
- 3.
- Calculation of the so-called innovation vector:and the estimate of its covariance matrix:for each vector of data ;
- 4.
- Calculation of the final estimate of the state vector:and the final estimate of its covariance matrix:
3. Extraction of Healthcare-Related Parameters
3.1. Detection of Motion
3.2. Estimation of Walking Direction and Moment of Turning
3.3. Estimation of Travelled Distance
3.4. Estimation of Walking Speed
4. Methodology of Experimentation
4.1. Acquisition of Measurement Data
- Two impulse-radar sensors based on Novelda NVA6201 (Novelda, Oslo, Norway) chip working in the frequency range 6.0–8.5 GHz [46], and having the data acquisition rate of 10 Hz;
- An infrared depth sensor being a part of the Microsoft Kinect V2 device (Microsoft, Redmond, WA, United States) [47], having the data acquisition rate of 30 Hz.
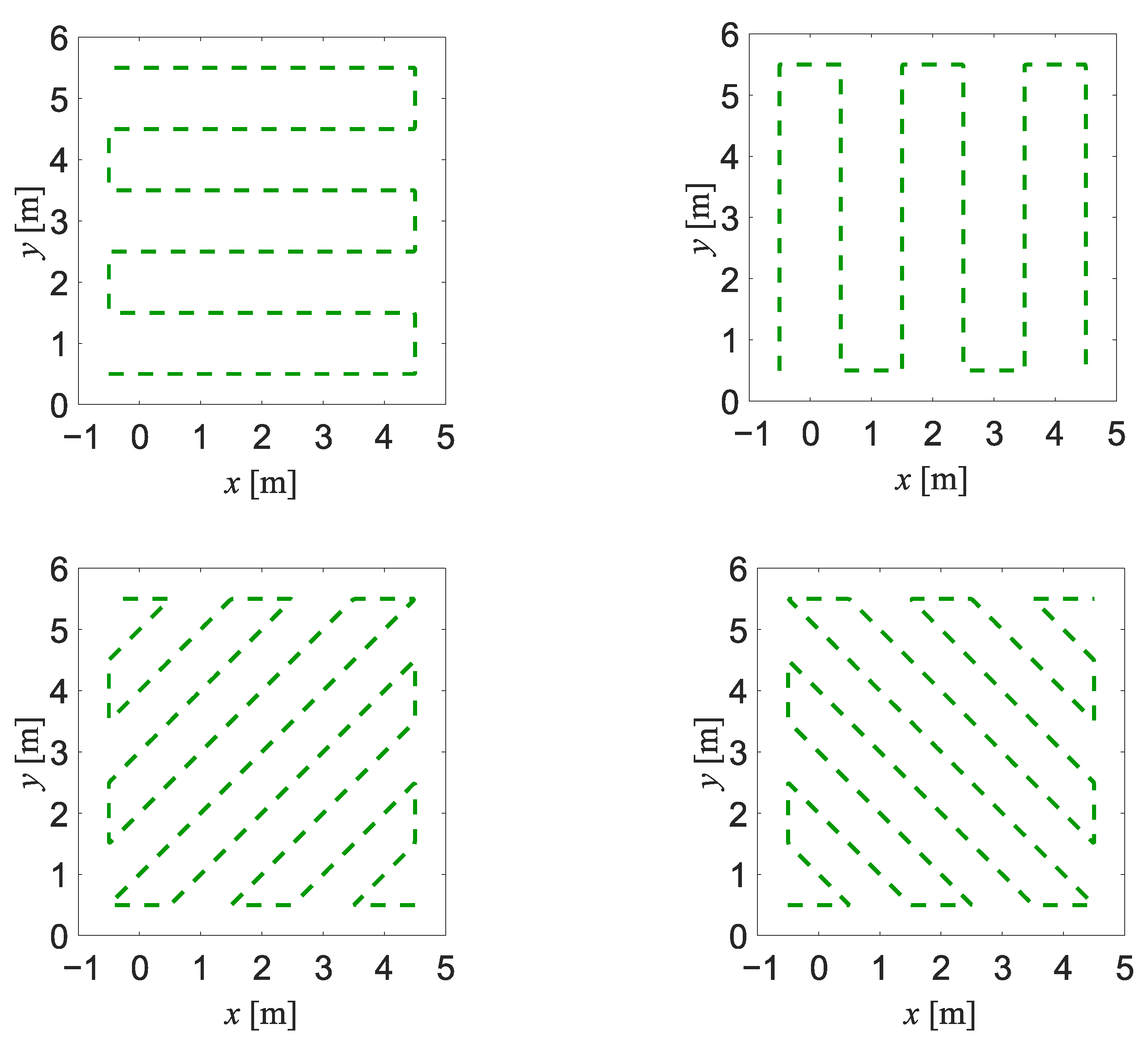
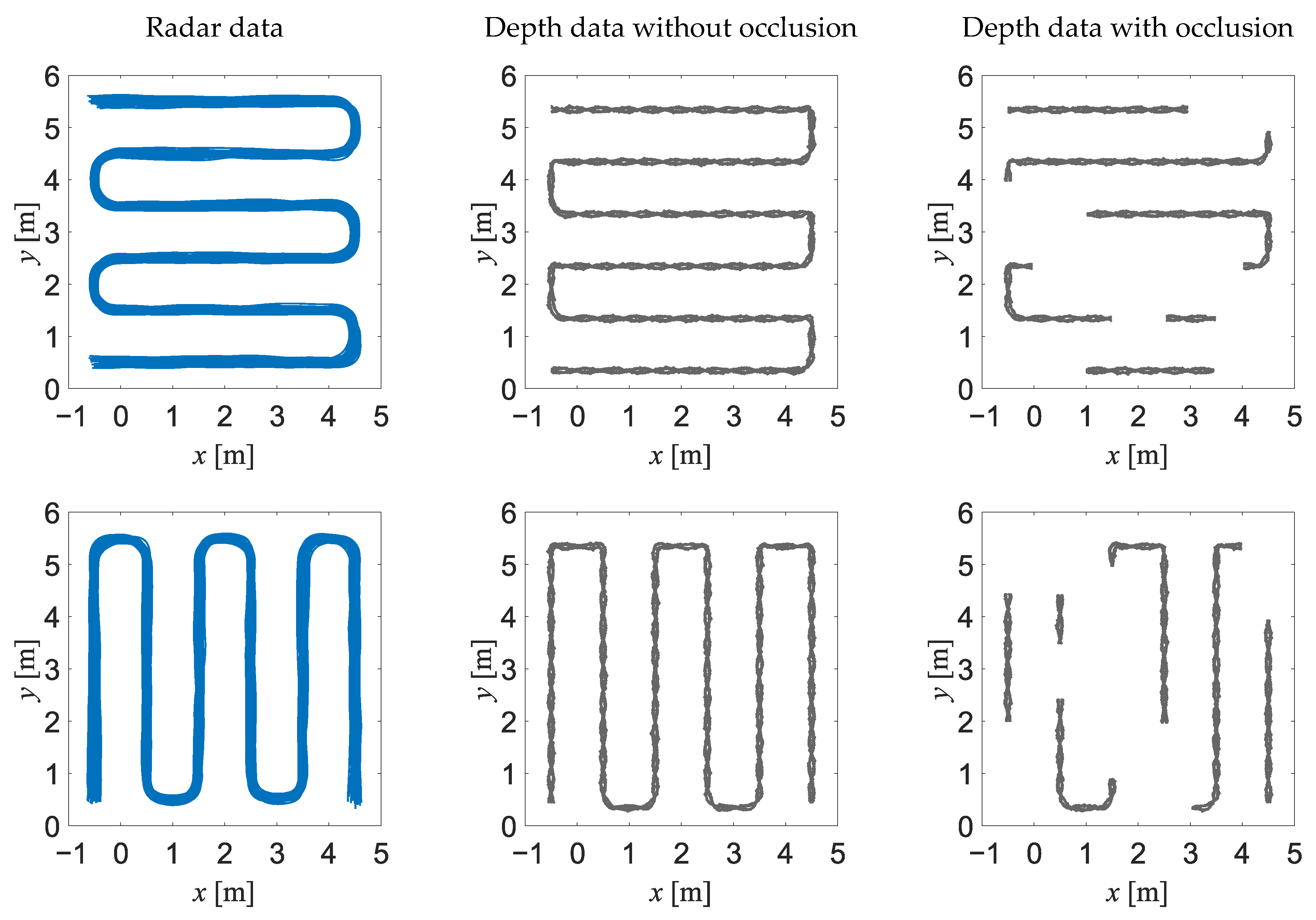
- In experiment EXP#1, a person walked forth and back along a serpentine trajectory, among the obstacles occluding that person (see Figure 4b); 30 walks were performed and the walking speed was kept constant at m/s.
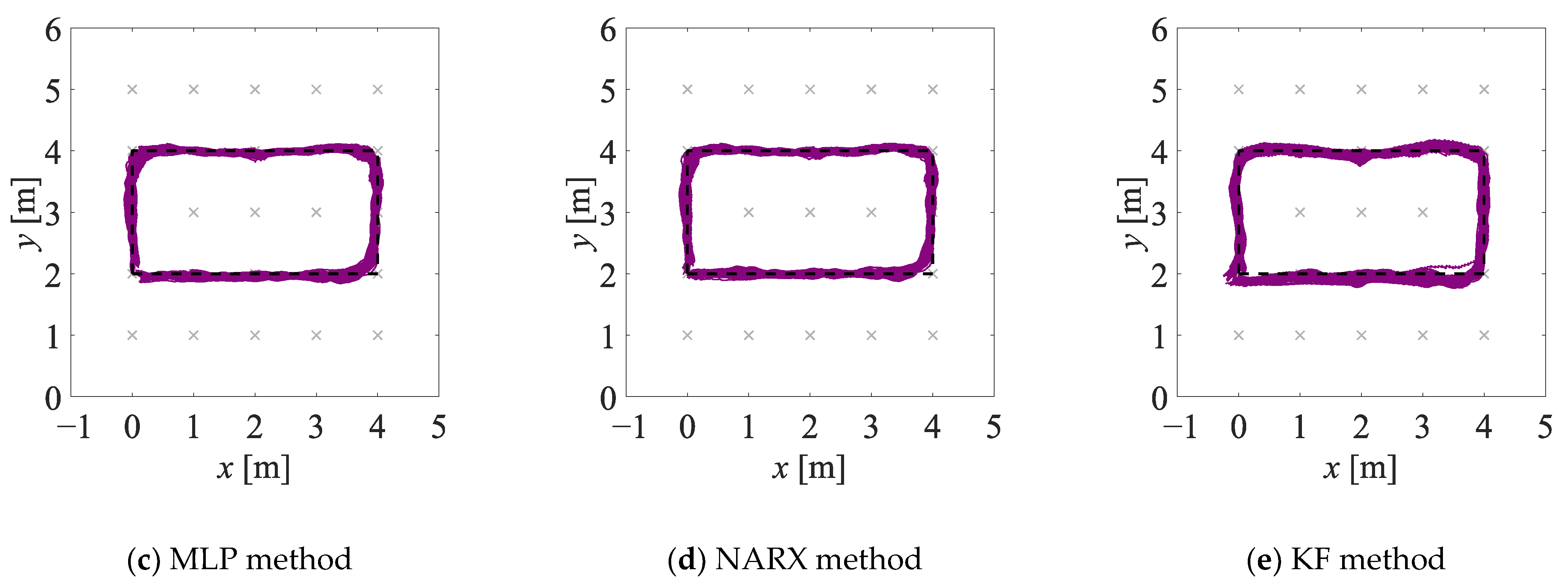
- In experiment EXP#2, a person walked clockwise and counter-clockwise along a rectangle-shaped trajectory (see Figure 4c), at six different values of the walking speed m/s. For each value of the walking speed, 20 walks were performed.
4.2. Criteria for Performance Evaluation
4.2.1. Indicators of Uncertainty of Estimation of Monitored Person’s Position
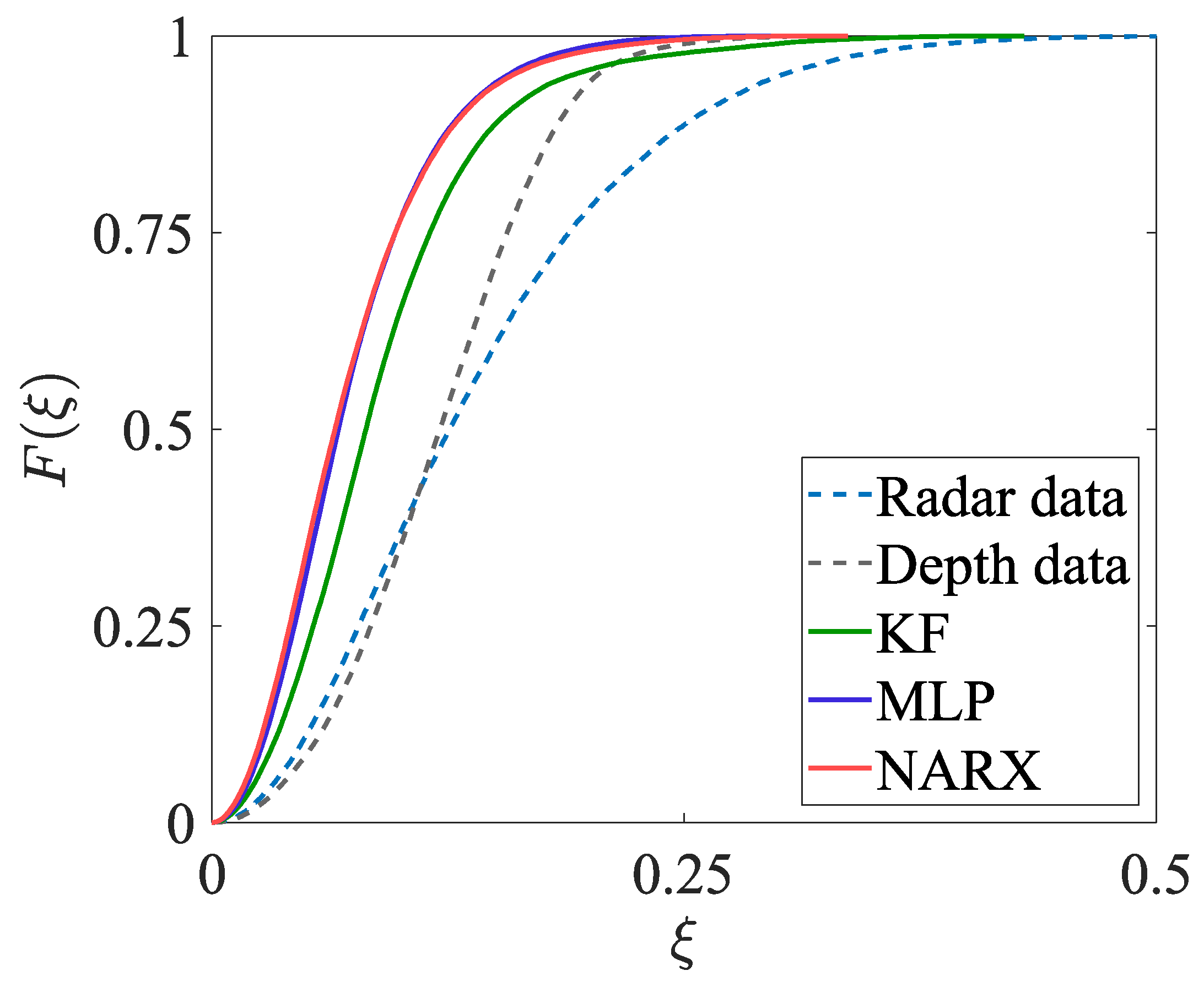
- The area under the empirical cumulative distribution function in the interval m, denoted with , taking the value from the interval ;
- The mean position error (MEAE);
- The maximum position error (MAXE);
- The standard deviation of the position errors (STDE).
4.2.2. Indicators of Uncertainty of Estimation of Healthcare-Related Parameters
- The mean error determined with respect to the corresponding reference value (ME);
- The standard deviation of that error (SE).
5. Results of Experimentation
5.1. Uncertainty of Estimation of Monitored Person’s Position
- The fused estimates of the person’s position are characterised by lower bias and dispersion when compared with the radar-data-based and depth-data-based estimates; moreover, the fused estimates are only slightly affected by the obstacles occluding a person. It should be stressed that in the case of the methods based on the artificial neural networks, the significant increase in the accuracy of the position estimation has been achieved despite the fact that the artificial neural networks were trained only on the synthetic data.
- In experiment EXP#1, where the monitored person was occluded by the obstacles, the more accurate estimates of the trajectories have been obtained by means of the NARX method than by means of the MLP method. This result can be explained by the fact that in the case of the recurrent neural network, the prediction of the person’s position at each time instant is based on the past position of that person. When the monitored person “disappears” behind the obstacle, larger measurement errors may corrupt the radar data and the depth data, but the recurrent neural network may react to such sudden changes and mitigate their influence on the result of the data fusion.
- If the values of the uncertainty indicators, calculated on the basis of the fused data, are concerned, the best overall results have been obtained for the NARX method: it is reflected in the lowest values of the mean error and the median error, as well as the indicator. Even though the values of the maximum error and the standard deviation of the errors are slightly greater when compared to the other methods, it does not affect the overall performance of the NARX method.
5.2. Uncertainty of Estimation of Healthcare-Related Parameters
5.2.1. Experiment EXP#1
- In the case of the radar data, the number of turns is significantly underestimated. This may be explained by the smoothing of the radar data during their preprocessing: as a result, two consecutive turns are often treated as one.
- In the case of the depth data, the travelled distance is significantly underestimated. This may be explained by the obstacles occluding the monitored person and making the tracking impossible.
- The radar-data-based and depth-data-based estimates of the mean walking speed are similarly accurate.
- The values of the uncertainty indicators are generally lower than the uncertainty indicators obtained for the radar data and for the depth data.
- The estimates of the number of turns, obtained for the MLP method and the NARX method, are considerably more accurate than those estimates obtained for the KF method—in the case of the last method, the number of turns for each realisation of the scenario has been overestimated by almost one. This may be explained by the corruption of the depth data related to “disappearing” of the monitored person behind the obstacles and the inability of the KF method to mitigate this phenomenon.
5.2.2. Experiment EXP#2
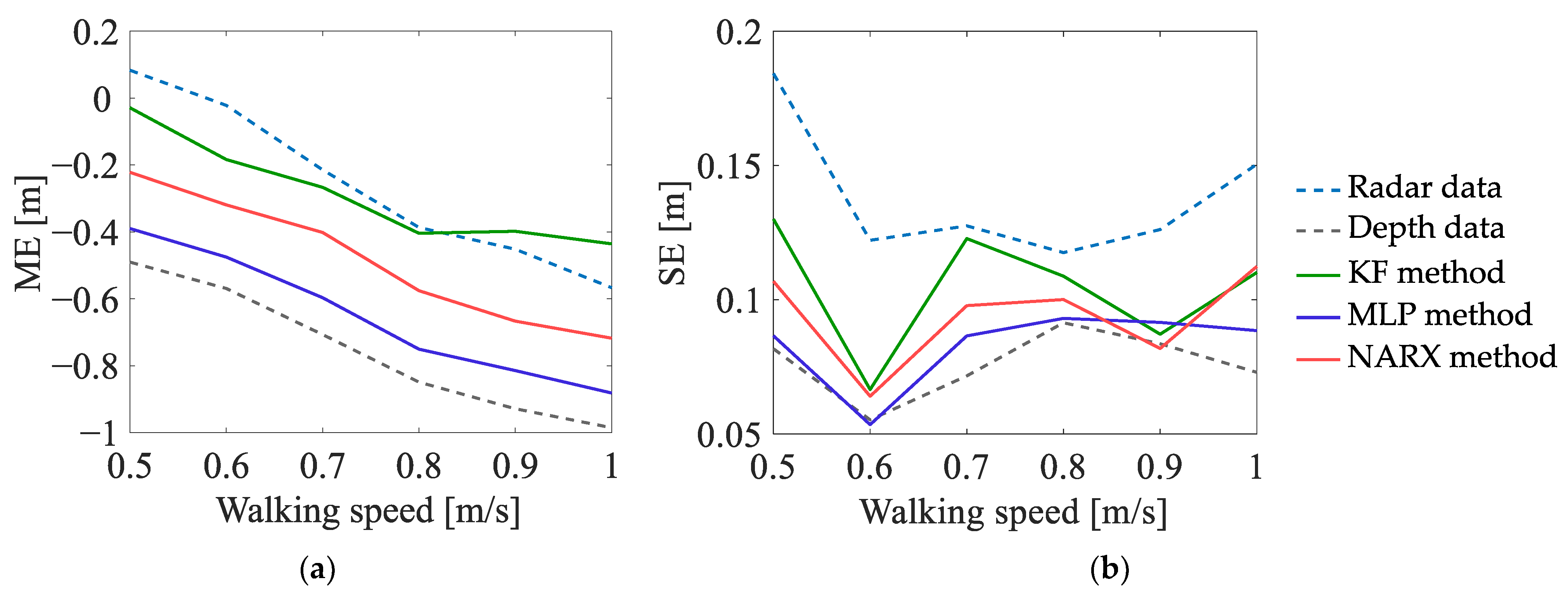
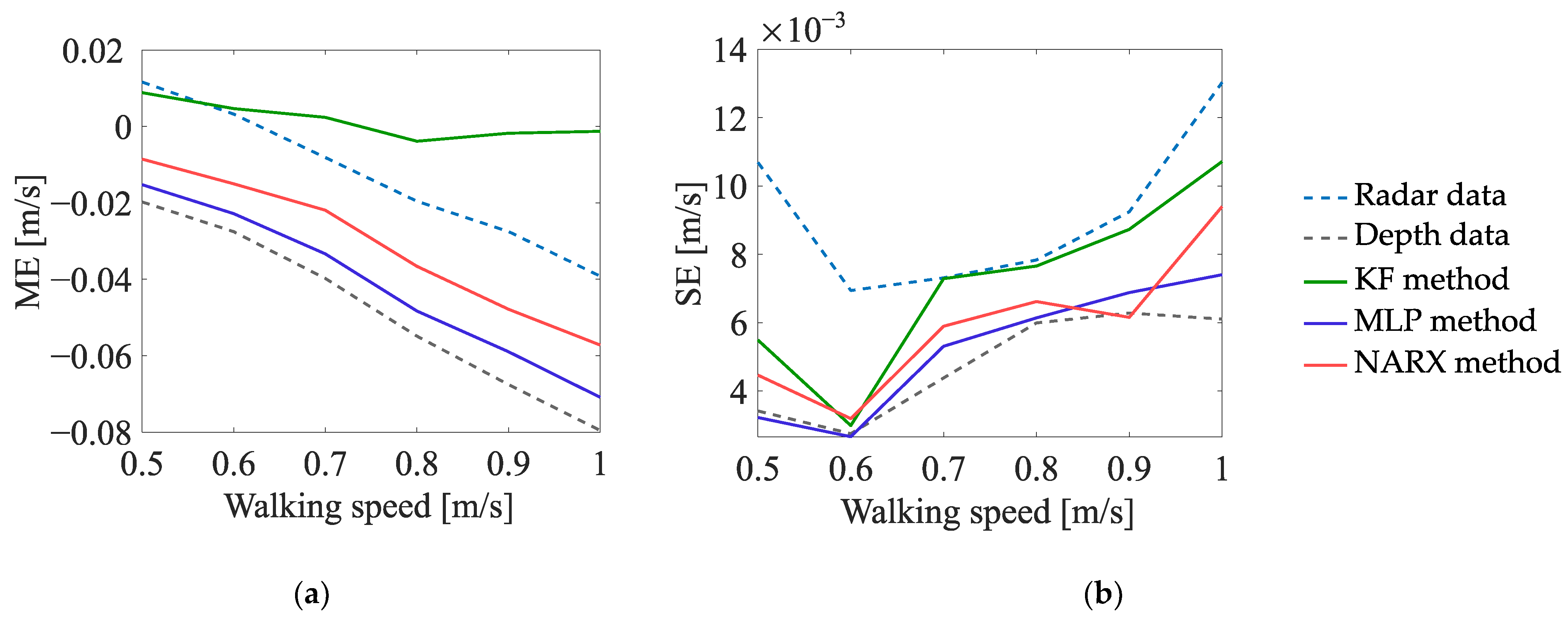
- In the case of the estimates of the number of turns, the values of the ME indicator, determined on the basis of the radar data, are generally lower than zero—meaning that, regardless of the walking speed, the number of turns is underestimated; on the other hand, the values of the ME indicator, determined on the basis of the data fused by the KF method, are greater than zero, which means that the number of turns is overestimated. The best results are obtained for the depth data and for the data fused by means of the MLP method and the NARX method—the values of the ME indicator, determined on the basis of those data, are not significantly affected by the walking speed of the person.
- In the case of the estimates of the travelled distance and the estimates of the walking speed, the values of the ME indicator, determined on the basis of the data fused by means of the KF method, are slightly better than the values of this indicator, determined on the basis of the data fused by means of the other methods. Moreover, for all the methods of data fusion, the values of the ME indicator decrease with the increase in the walking speed of the monitored person. This phenomenon is caused by the deviations of the estimates of the walking trajectory around the corners of that trajectory—the greater the walking speed, the smoother the trajectory becomes and the smaller the estimates of the distance and walking speed.
6. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- United Nations. World Population Prospects 2019: Highlights; ST/ESA/SER.A/423; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2019. [Google Scholar]
- Fuller, G.F. Falls in the elderly. Am. Fam. Physician 2000, 61, 2159–2168. [Google Scholar] [PubMed]
- Hamm, J.; Money, A.G.; Atwal, A.; Paraskevopoulos, I. Fall prevention intervention technologies: A conceptual framework and survey of the state of the art. J. Biomed. Inform. 2016, 59, 319–345. [Google Scholar] [CrossRef] [PubMed]
- Chaccour, K.; Darazi, R.; Hassani, A.H.E.; Andrès, E. From Fall Detection to Fall Prevention: A Generic Classification of Fall-Related Systems. IEEE Sens. J. 2017, 17, 812–822. [Google Scholar] [CrossRef]
- Baldewijns, G.; Luca, S.; Vanrumste, B.; Croonenborghs, T. Developing a system that can automatically detect health changes using transfer times of older adults. BMC Med. Res. Methodol. 2016, 16, 23. [Google Scholar] [CrossRef]
- Lusardi, M. Is Walking Speed a Vital Sign? Top. Geriatr. Rehabil. 2012, 28, 67–76. [Google Scholar] [CrossRef]
- Stone, E.; Skubic, M.; Rantz, M.; Abbott, C.; Miller, S. Average in-home gait speed: Investigation of a new metric for mobility and fall risk assessment of elders. Gait Posture 2015, 41, 57–62. [Google Scholar] [CrossRef]
- Thingstad, P.; Egerton, T.; Ihlen, E.F.; Taraldsen, K.; Moe-Nilssen, R.; Helbostad, J.L. Identification of gait domains and key gait variables following hip fracture. BMC Geriatr. 2015, 15, 150. [Google Scholar] [CrossRef]
- Berge, M. Telecare acceptance as sticky entrapment: A realist review. Gerontechnology 2016, 15, 98–108. [Google Scholar] [CrossRef][Green Version]
- Thilo, F.J.S.; Hahn, S.; Halfens, R.J.G.; Schols, J.M.G.A. Usability of a wearable fall detection prototype from the perspective of older people—A real field testing approach. J. Clin. Nurs. 2019, 28, 310–320. [Google Scholar] [CrossRef]
- Dubois, A.; Bihl, T.; Bresciani, J.-P. Identifying Fall Risk Predictors by Monitoring Daily Activities at Home Using a Depth Sensor Coupled to Machine Learning Algorithms. Sensors 2021, 21, 1957. [Google Scholar] [CrossRef]
- Liao, Y.Y.; Chen, I.H.; Wang, R.Y. Effects of Kinect-based exergaming on frailty status and physical performance in prefrail and frail elderly: A randomized controlled trial. Sci. Rep. 2019, 9, 9353. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.A.; Mentiplay, B.F.; Hough, E.; Pua, Y.H. Three-dimensional cameras and skeleton pose tracking for physical function assessment: A review of uses, validity, current developments and Kinect alternatives. Gait Posture 2019, 68, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Hynes, A.; Czarnuch, S.; Kirkland, M.C.; Ploughman, M. Spatiotemporal Gait Measurement With a Side-View Depth Sensor Using Human Joint Proposals. IEEE J. Biomed. Health Inform. 2021, 25, 1758–1769. [Google Scholar] [CrossRef] [PubMed]
- Vilas-Boas, M.D.C.; Rocha, A.P.; Cardoso, M.N.; Fernandes, J.M.; Coelho, T.; Cunha, J.P.S. Supporting the Assessment of Hereditary Transthyretin Amyloidosis Patients Based On 3-D Gait Analysis and Machine Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1350–1362. [Google Scholar] [CrossRef] [PubMed]
- Ferraris, C.; Cimolin, V.; Vismara, L.; Votta, V.; Amprimo, G.; Cremascoli, R.; Galli, M.; Nerino, R.; Mauro, A.; Priano, L. Monitoring of Gait Parameters in Post-Stroke Individuals: A Feasibility Study Using RGB-D Sensors. Sensors 2021, 21, 5945. [Google Scholar] [CrossRef] [PubMed]
- Castaño-Pino, Y.J.; González, M.C.; Quintana-Peña, V.; Valderrama, J.; Muñoz, B.; Orozco, J.; Navarro, A. Automatic Gait Phases Detection in Parkinson Disease: A Comparative Study. In Proceedings of the 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society, Montreal, QC, Canada, 20–24 July 2020; pp. 798–802. [Google Scholar]
- Oh, J.; Eltoukhy, M.; Kuenze, C.; Andersen, M.S.; Signorile, J.F. Comparison of predicted kinetic variables between Parkinson’s disease patients and healthy age-matched control using a depth sensor-driven full-body musculoskeletal model. Gait Posture 2020, 76, 151–156. [Google Scholar] [CrossRef]
- Albert, J.A.; Owolabi, V.; Gebel, A.; Brahms, C.M.; Granacher, U.; Arnrich, B. Evaluation of the Pose Tracking Performance of the Azure Kinect and Kinect v2 for Gait Analysis in Comparison with a Gold Standard: A Pilot Study. Sensors 2020, 20, 5104. [Google Scholar] [CrossRef]
- Guffanti, D.; Brunete, A.; Hernando, M. Non-Invasive Multi-Camera Gait Analysis System and its Application to Gender Classification. IEEE Access 2020, 8, 95734–95746. [Google Scholar] [CrossRef]
- Li, H.; Mehul, A.; Le Kernec, J.; Gurbuz, S.Z.; Fioranelli, F. Sequential Human Gait Classification With Distributed Radar Sensor Fusion. IEEE Sens. J. 2021, 21, 7590–7603. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Fioranelli, F.; Yang, S.; Romain, O.; Le Kernec, J. Hierarchical Radar Data Analysis for Activity and Personnel Recognition. Remote Sens. 2020, 12, 2237. [Google Scholar] [CrossRef]
- Niazi, U.; Hazra, S.; Santra, A.; Weigel, R. Radar-Based Efficient Gait Classification using Gaussian Prototypical Networks. Proceedings of IEEE Radar Conference, Online, 8–14 May 2021. [Google Scholar]
- Saho, K.; Sugano, K.; Uemura, K.; Matsumoto, M. Screening of apathetic elderly adults using kinematic information in gait and sit-to-stand/stand-to-sit movements measured with Doppler radar. Health Inform. J. 2021, 27. [Google Scholar] [CrossRef] [PubMed]
- Saho, K.; Uemura, K.; Matsumoto, M. Screening of mild cognitive impairment in elderly via Doppler radar gait measurement. IEICE Commun. Express 2020, 9, 19–24. [Google Scholar] [CrossRef]
- Seifert, A.-K.; Grimmer, M.; Zoubir, A.M. Doppler Radar for the Extraction Biomechanical Parameters in Gait Analysis. IEEE J. Biomed. Health Inform. 2021, 25, 547–558. [Google Scholar] [CrossRef] [PubMed]
- Fioranelli, F.; Kernec, J.L. Radar sensing for human healthcare: Challenges and results. In Proceedings of the IEEE Sensors, Sydney, Australia, 31 October–3 November 2021; pp. 1–4. [Google Scholar]
- Bhavanasi, G.; Werthen-Brabants, L.; Dhaene, T.; Couckuyt, I. Patient activity recognition using radar sensors and machine learning. Neural Comput. Appl. 2022, 34, 16033–16048. [Google Scholar] [CrossRef]
- Taylor, W.; Dashtipour, K.; Shah, S.A.; Hussain, A.; Abbasi, Q.H.; Imran, M.A. Radar Sensing for Activity Classification in Elderly People Exploiting Micro-Doppler Signatures Using Machine Learning. Sensors 2021, 21, 3881. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, L.; Chen, H.; Hong, H.; Zhu, X.; Li, C. Human Motion Recognition With Spatial-Temporal-ConvLSTM Network Using Dynamic Range-Doppler Frames Based on Portable FMCW Radar. IEEE Trans. Microw. Theory Tech. 2022, 70, 5029–5038. [Google Scholar] [CrossRef]
- Chen, M.; Yang, Z.; Lai, J.; Chu, P.; Lin, J. A Three-Stage Low-Complexity Human Fall Detection Method Using IR-UWB Radar. IEEE Sens. J. 2022, 22, 15154–15168. [Google Scholar] [CrossRef]
- Han, T.; Kang, W.; Choi, G. IR-UWB Sensor Based Fall Detection Method Using CNN Algorithm. Sensors 2020, 20, 5948. [Google Scholar] [CrossRef]
- Miękina, A.; Wagner, J.; Mazurek, P.; Morawski, R.Z.; Sudmann, T.T.; Børsheim, I.T.; Øvsthus, K.; Jacobsen, F.F.; Ciamulski, T.; Winiecki, W. Development of software application dedicated to impulse-radar-based system for monitoring of human movements. J. Phys. Conf. Ser. 2016, 772, 012028. [Google Scholar] [CrossRef]
- Wagner, J.; Mazurek, P.; Miękina, A.; Morawski, R.Z.; Jacobsen, F.F.; Sudmann, T.T.; Børsheim, I.T.; Øvsthus, K.; Ciamulski, T. Comparison of two techniques for monitoring of human movements. Measurement 2017, 111, 420–431. [Google Scholar] [CrossRef]
- Galambos, C.; Skubic, M.; Wang, S.; Rantz, M. Management of dementia and depression utilizing in-home passive sensor data. Gerontechnology 2013, 11, 457–468. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S.; Lusardi, M. Walking Speed: The Sixth Vital Sign. J. Geriatr. Phys. Ther. 2009, 32, 2–5. [Google Scholar] [CrossRef]
- Mazurek, P.; Wagner, J.; Miękina, A.; Morawski, R.Z. Comparison of sixteen methods for fusion of data from impulse-radar sensors and depth sensors applied for monitoring of elderly persons. Measurement 2020, 154, 107455. [Google Scholar] [CrossRef]
- Mazurek, P. Application of Artificial Neural Networks for Fusion of Data from Radar and Depth Sensors Applied for Persons’ Monitoring. J. Phys. Conf. Ser. 2019, 1379, 012051. [Google Scholar] [CrossRef]
- Mathworks. Matlab Documentation: Deep Learning Toolbox. Available online: https://www.mathworks.com/help/deeplearning/index.html (accessed on 9 November 2022).
- Bar-Shalom, Y.; Li, X.-R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001; p. 584. [Google Scholar]
- Durrant-Whyte, H. Multi-Sensor Data Fusion; Lecture notes; The University of Sydney: Sydney, Australia, 2001. [Google Scholar]
- Raol, J.R. Data Fusion Mathematics: Theory and Practice; CRC Press (Taylor & Francis Group): Boca Raton, FL, USA, 2016. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R. Multitarget-Multisensor Tracking: Principles and Techniques; YBS Publishing: Storrs, CT, USA, 1995. [Google Scholar]
- Simon, D. Optimal State Estimation; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Serra, J.; Vincent, L. An overview of morphological filtering. Circuits Syst. Signal Process. 1992, 11, 47–108. [Google Scholar] [CrossRef]
- Bajurko, P.; Yashchyshyn, Y. Study of Detection Capability of Novelda Impulse Transceiver with External RF Circuit. In Proceedings of the 8th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Warsaw, Poland, 24–26 September 2015; pp. 1–4. [Google Scholar]
- Lachat, E.; Macher, H.; Mittet, M.A.; Landes, T.; Grussenmeyer, P. First experiences with Kinect v2 sensor for close range 3d modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W4, 93–100. [Google Scholar] [CrossRef]
- van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]




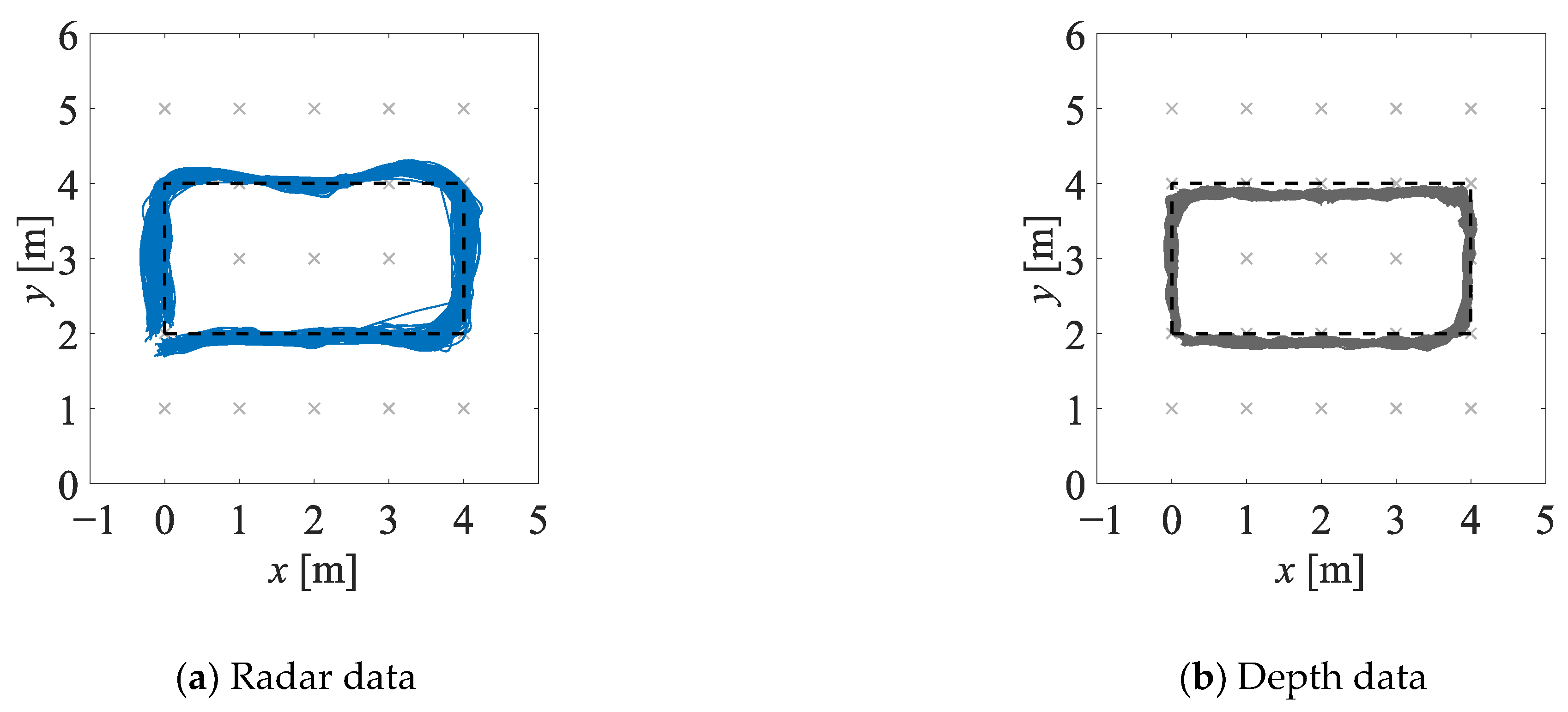


| Uncertainty Indicator | Radar Data | Depth Data | MLP | NARX | KF |
|---|---|---|---|---|---|
| MEAE [m] | 0.22 | 0.17 | 0.16 | 0.15 | 0.16 |
| MEDE [m] | 0.20 | 0.18 | 0.14 | 0.12 | 0.16 |
| MAXE [m] | 0.63 | 0.41 | 0.63 | 0.67 | 0.70 |
| STDE [m] | 0.12 | 0.07 | 0.11 | 0.10 | 0.08 |
| 0.78 | 0.83 | 0.84 | 0.85 | 0.84 |
| Uncertainty Indicator | Radar Data | Depth Data | MLP | NARX | KF |
|---|---|---|---|---|---|
| MEAE [m] | 0.14 | 0.12 | 0.07 | 0.07 | 0.09 |
| MEDE [m] | 0.13 | 0.12 | 0.07 | 0.07 | 0.08 |
| MAXE [m] | 0.60 | 0.33 | 0.32 | 0.34 | 0.43 |
| STDE [m] | 0.08 | 0.05 | 0.04 | 0.05 | 0.06 |
| 0.86 | 0.88 | 0.93 | 0.93 | 0.91 |
| Uncertainty Indicator | Radar Data | Depth Data | MLP | NARX | KF |
|---|---|---|---|---|---|
| Number of turns | |||||
| ME | –6.00 | –0.73 | –0.13 | 0.07 | 0.93 |
| SE | 1.08 | 0.91 | 1.36 | 1.34 | 1.20 |
| Travelled distance [m] | |||||
| ME | –1.43 | –6.86 | –0.74 | –0.79 | –0.53 |
| SE | 0.42 | 0.13 | 0.30 | 0.33 | 0.25 |
| Walking speed [m/s] | |||||
| ME | –0.03 | –0.04 | –0.02 | –0.02 | –0.01 |
| SE | 0.01 | 0.00 | 0.01 | 0.01 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazurek, P. Application of Feedforward and Recurrent Neural Networks for Fusion of Data from Radar and Depth Sensors Applied for Healthcare-Oriented Characterisation of Persons’ Gait. Sensors 2023, 23, 1457. https://doi.org/10.3390/s23031457
Mazurek P. Application of Feedforward and Recurrent Neural Networks for Fusion of Data from Radar and Depth Sensors Applied for Healthcare-Oriented Characterisation of Persons’ Gait. Sensors. 2023; 23(3):1457. https://doi.org/10.3390/s23031457
Chicago/Turabian StyleMazurek, Paweł. 2023. "Application of Feedforward and Recurrent Neural Networks for Fusion of Data from Radar and Depth Sensors Applied for Healthcare-Oriented Characterisation of Persons’ Gait" Sensors 23, no. 3: 1457. https://doi.org/10.3390/s23031457
APA StyleMazurek, P. (2023). Application of Feedforward and Recurrent Neural Networks for Fusion of Data from Radar and Depth Sensors Applied for Healthcare-Oriented Characterisation of Persons’ Gait. Sensors, 23(3), 1457. https://doi.org/10.3390/s23031457






