Identification of Vibration Frequencies of Railway Bridges from Train-Mounted Sensors Using Wavelet Transformation
Abstract
1. Introduction
2. Theoretical Background
2.1. Equation of Motion
2.2. Continuous Wavelet Transform
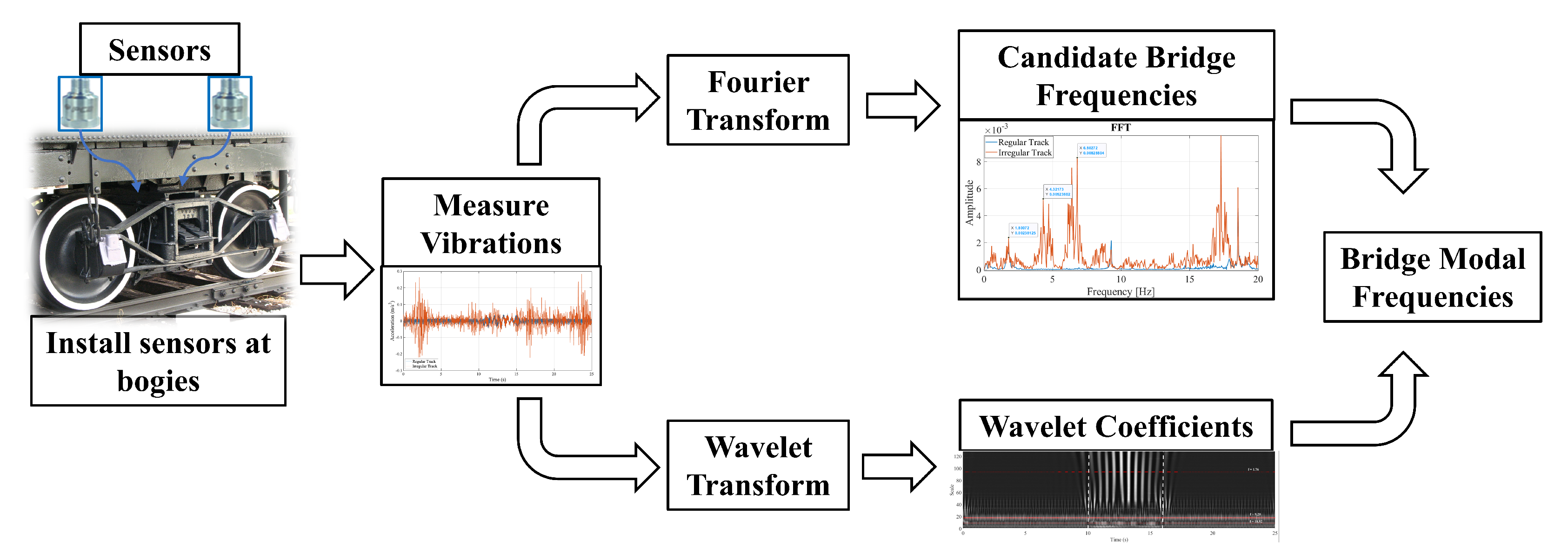
3. Proposed Methodology
- Mount accelerometers on the bogeys of a train and measure the vibrations that occur before, during, and after the train crosses a bridge.
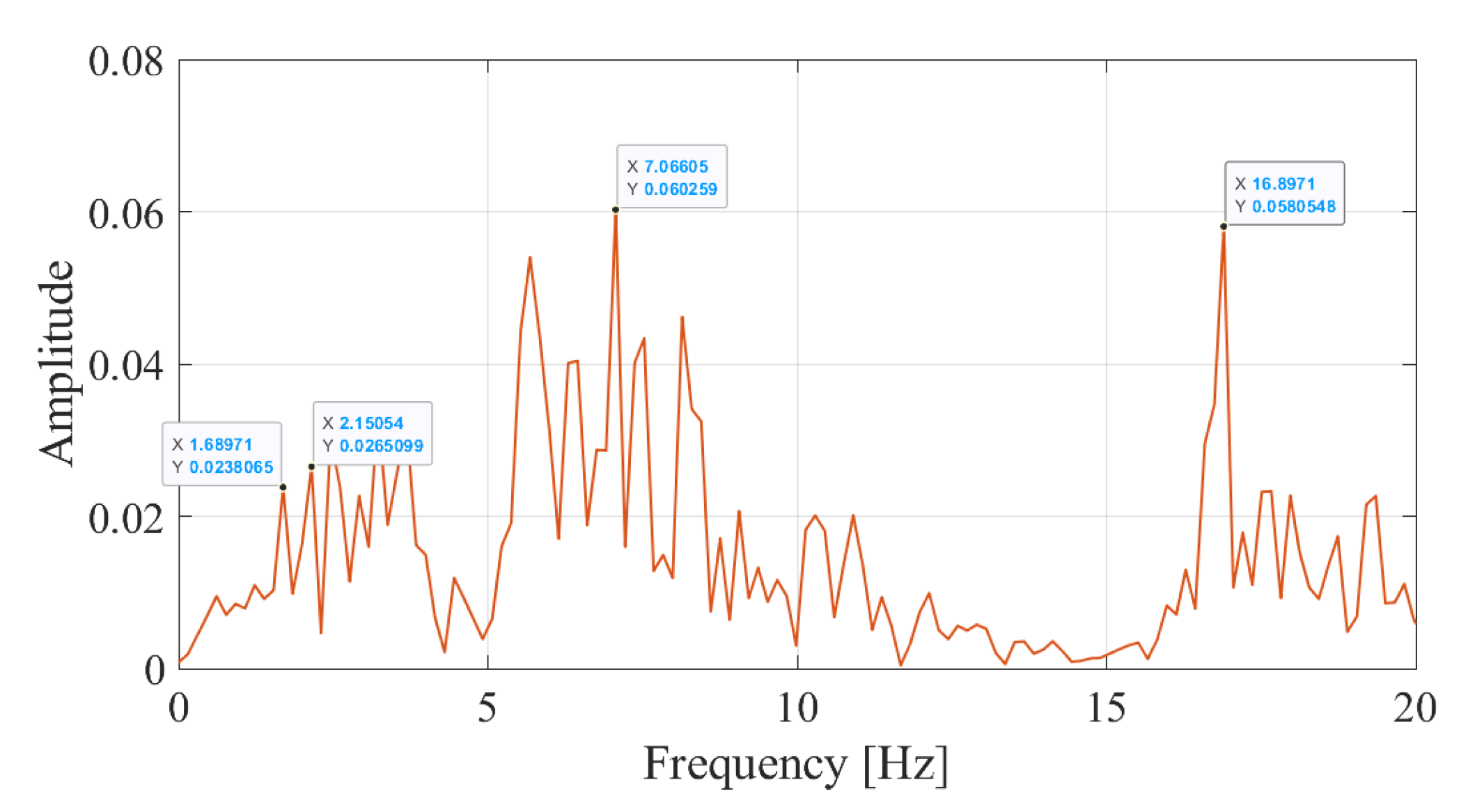
- Compute the Fourier Amplitude Spectrum (FAS) of the recorded vibrations and identify the candidate frequencies. The candidate frequencies are the peaks that are visible in the FAS that can be the bridge frequencies.
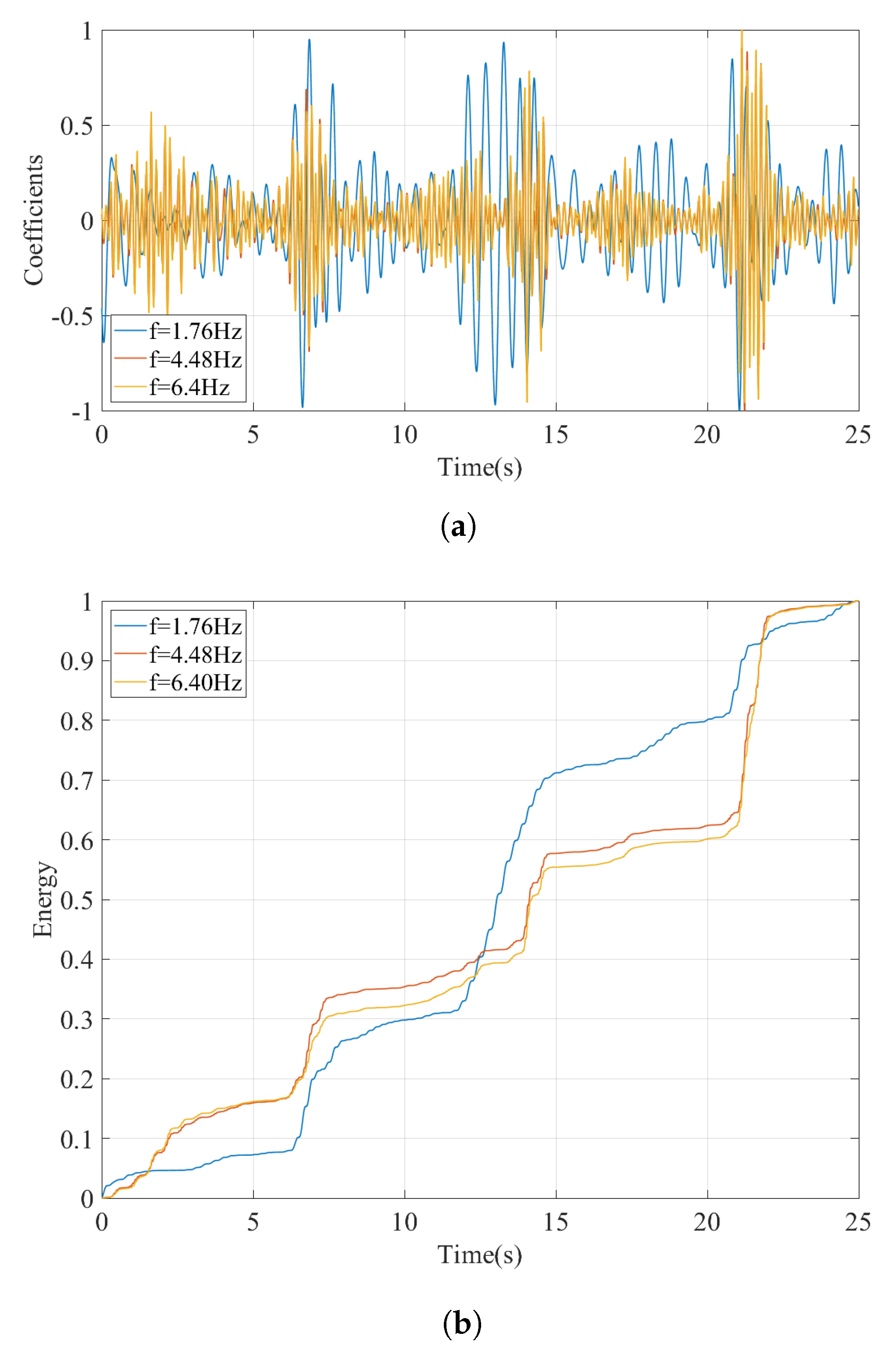
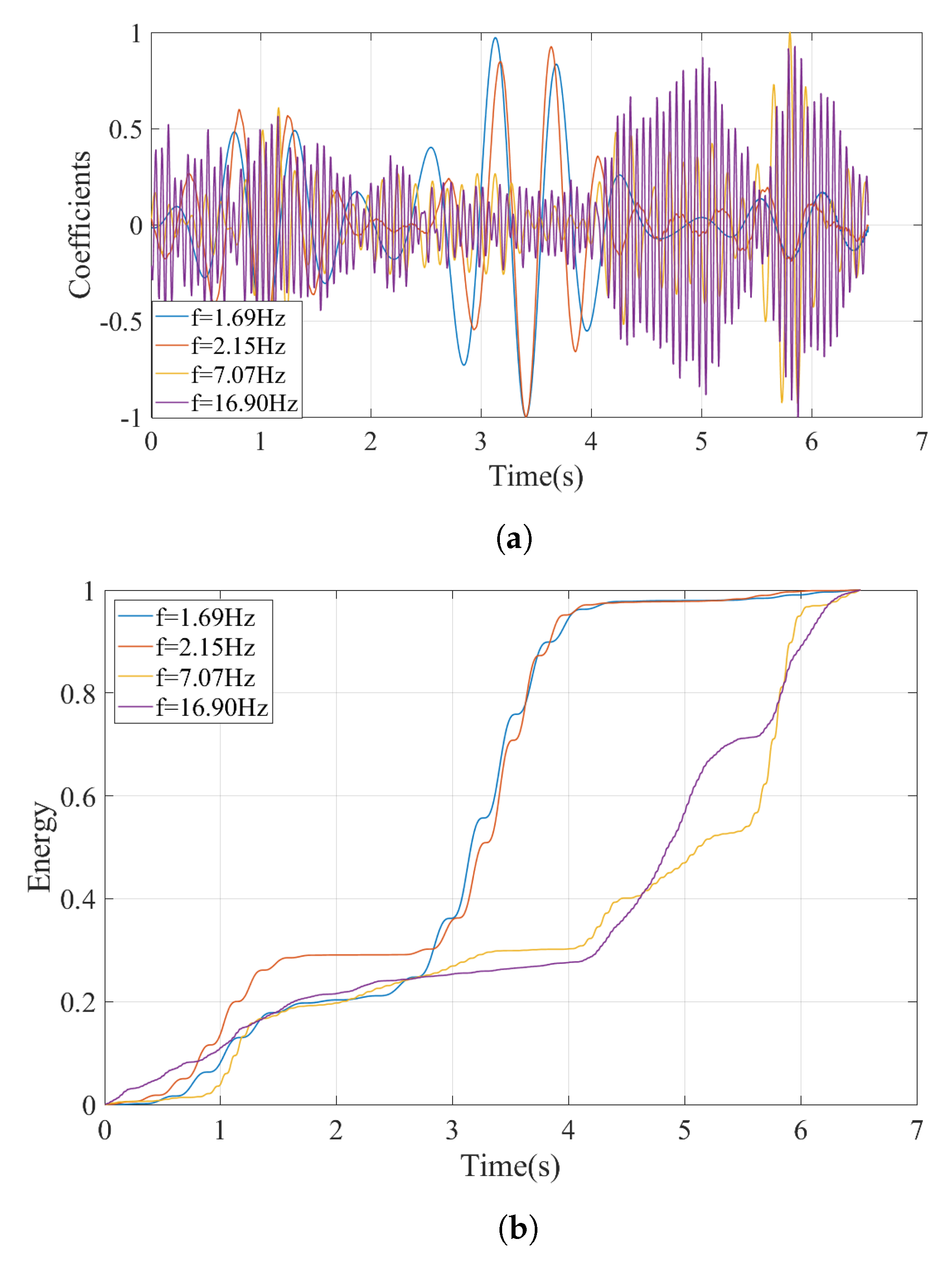
- Perform a continuous wavelet transform (CWT) of the acceleration signals recorded on the bogeys and create their wavelet coefficient maps.
- For each candidate frequency, isolate the coefficients of the CWT for that frequency by taking a horizontal section of the wavelet coefficient map at the scale corresponding to that candidate frequency.
- Compute the time variation of the energy of the coefficients at each candidate frequency and its development over time. The bridge frequency can then be identified as the frequency where the energy of the wavelet coefficients is concentrated at the time-frame where the bogey is crossing the bridge.
4. Finite Element Model
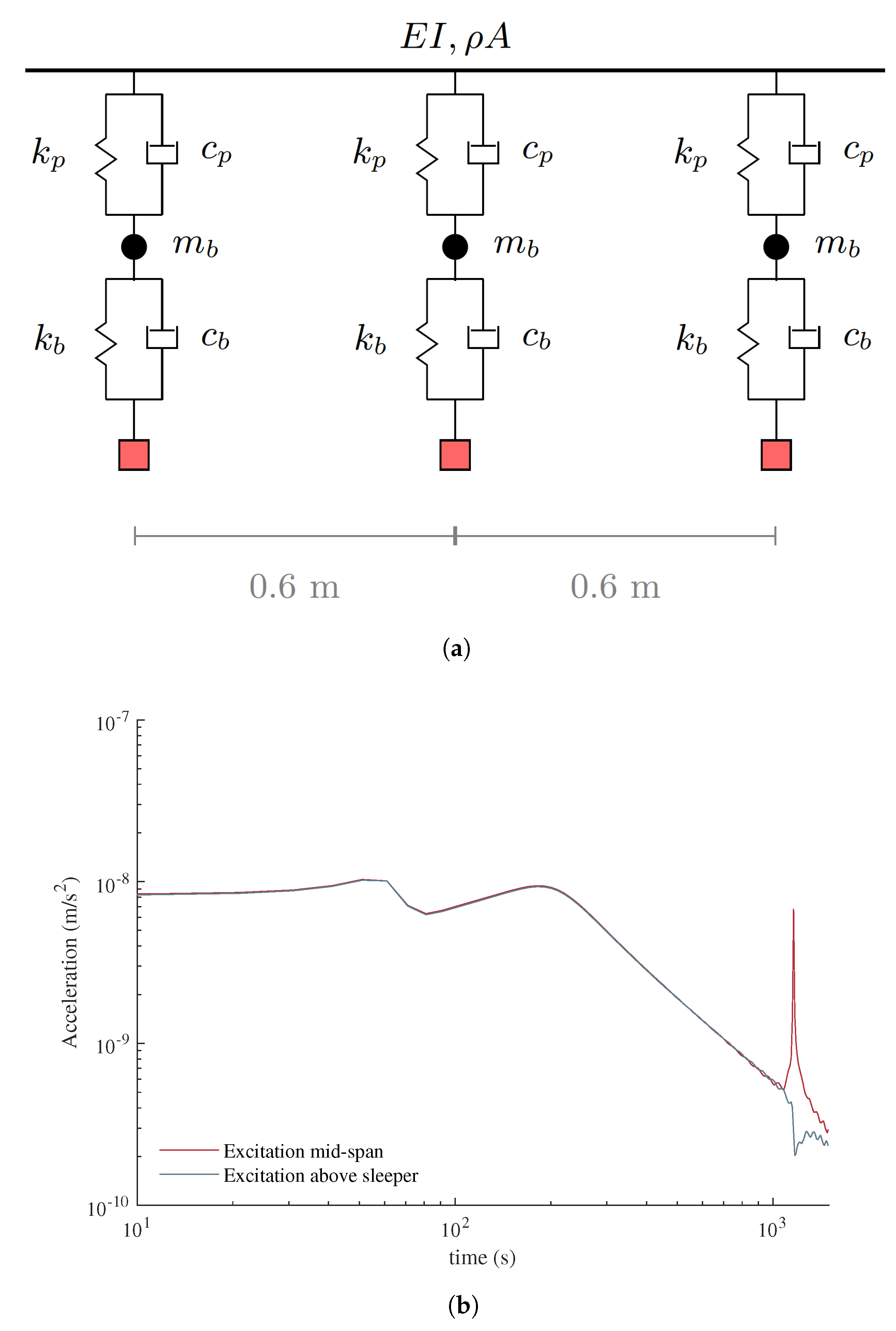
4.1. Train Model
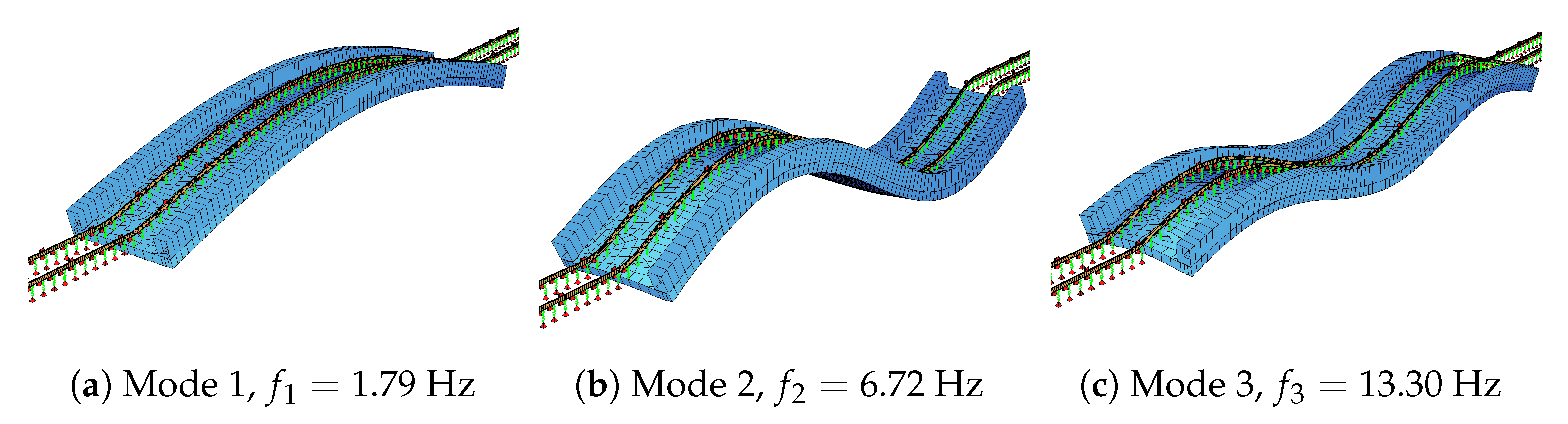
4.2. Bridge and Track Model
4.3. Track Irregularities
5. Case Studies
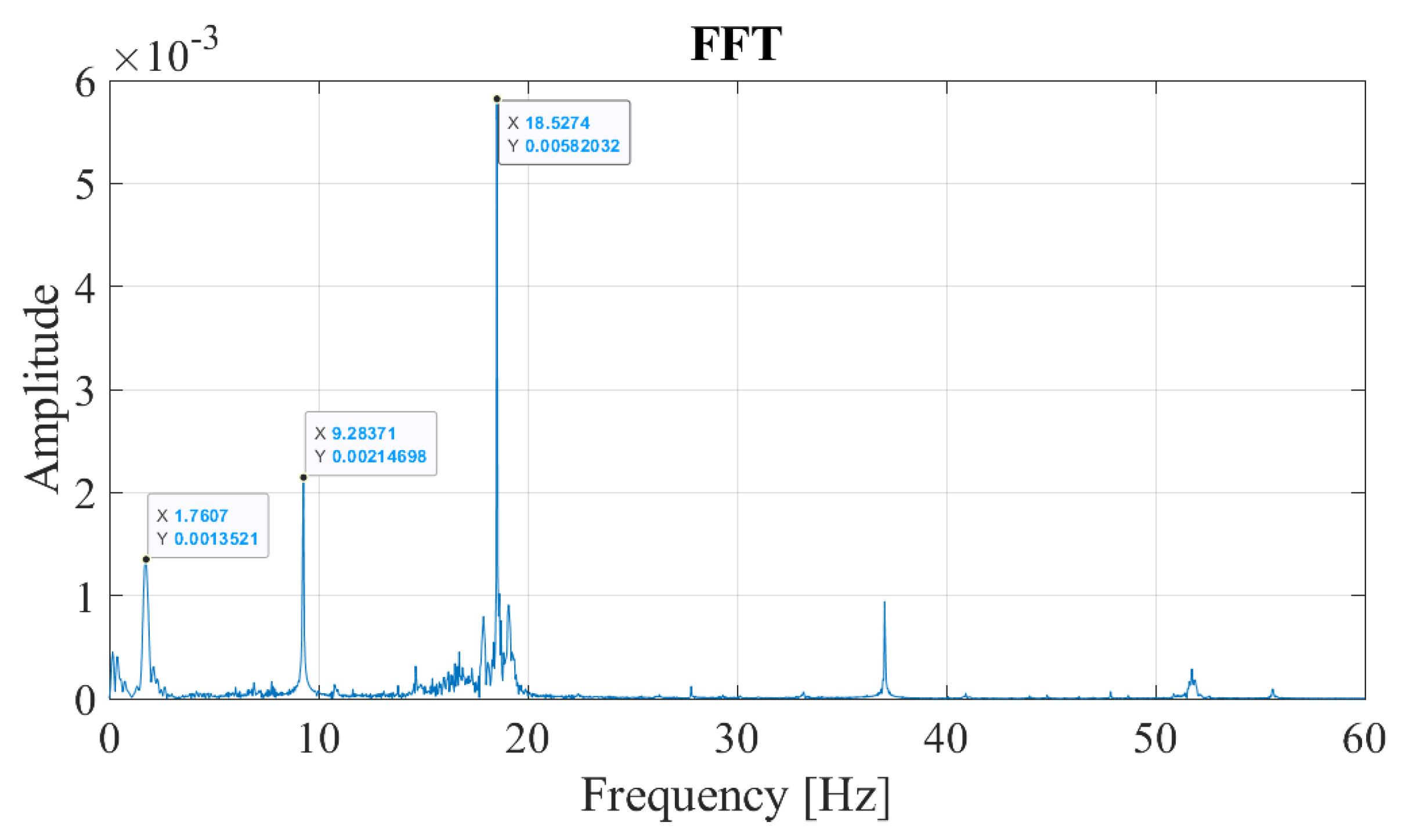
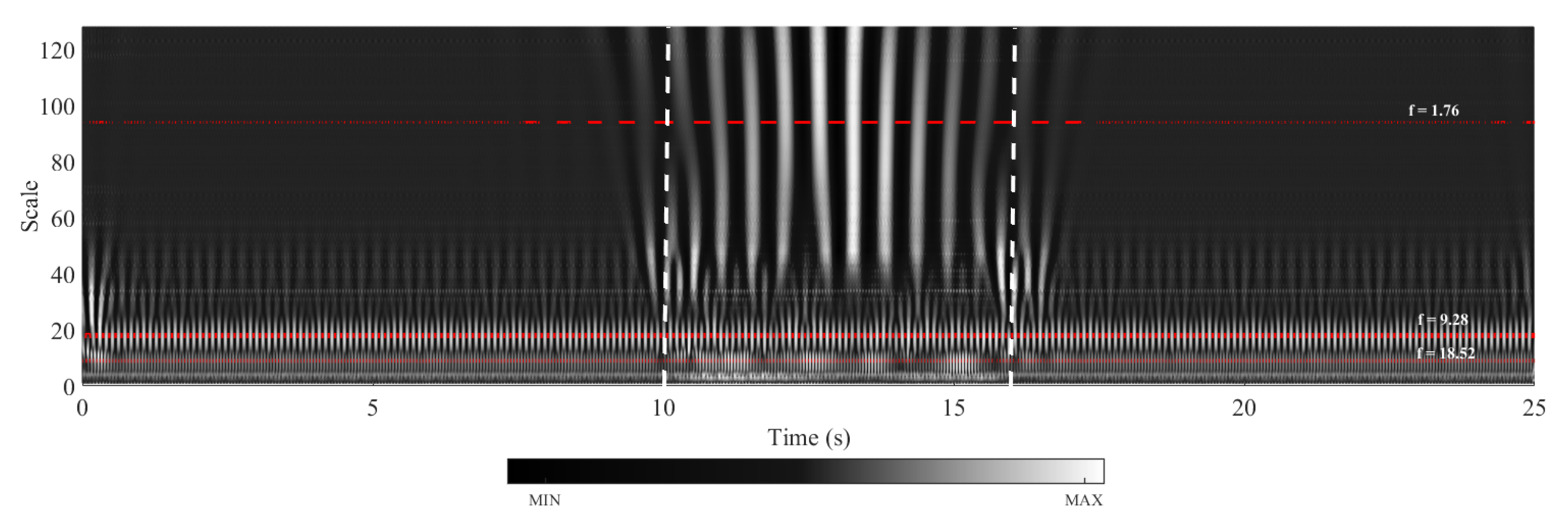
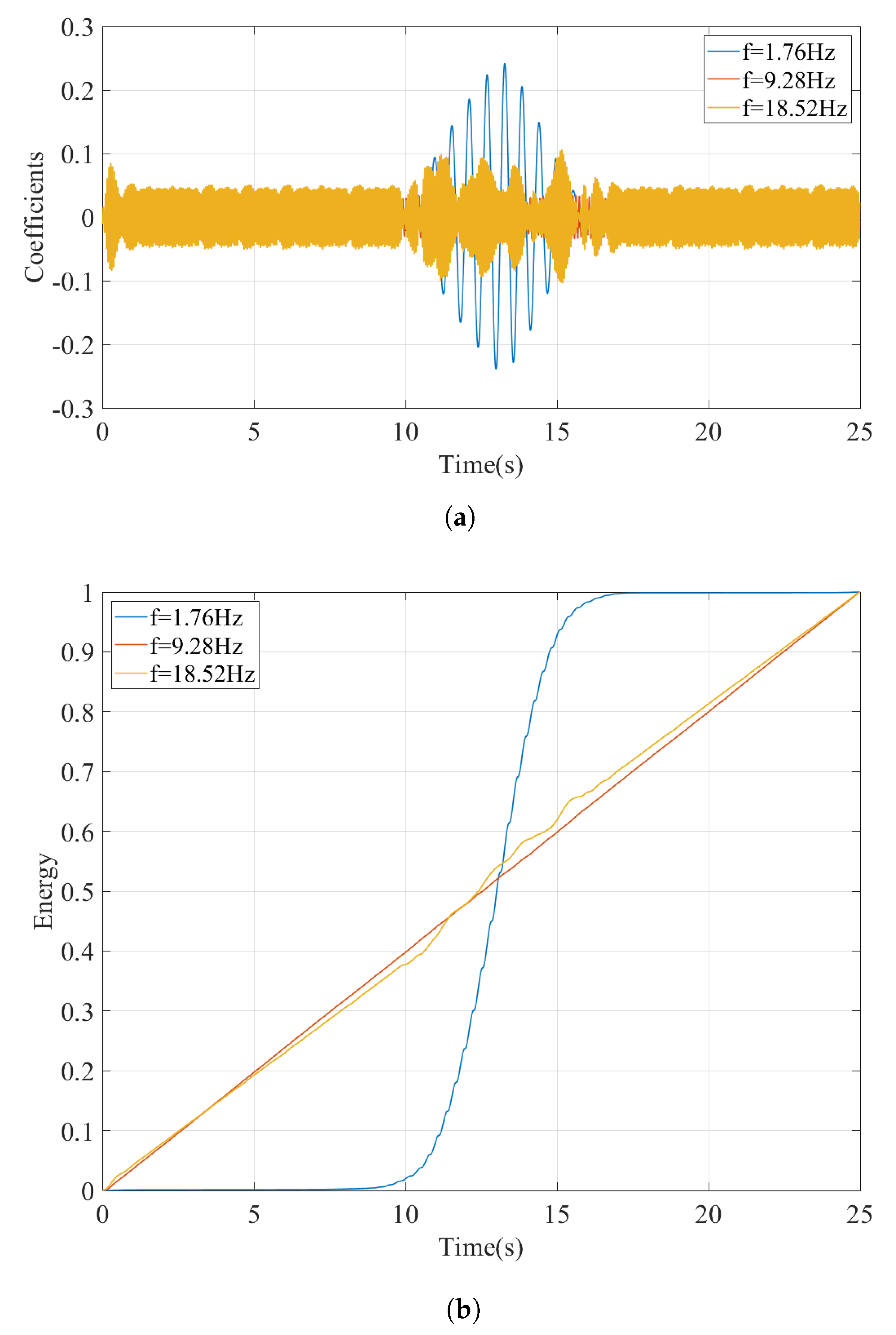
5.1. Case I: No Track Irregularities; Slow Train Speed
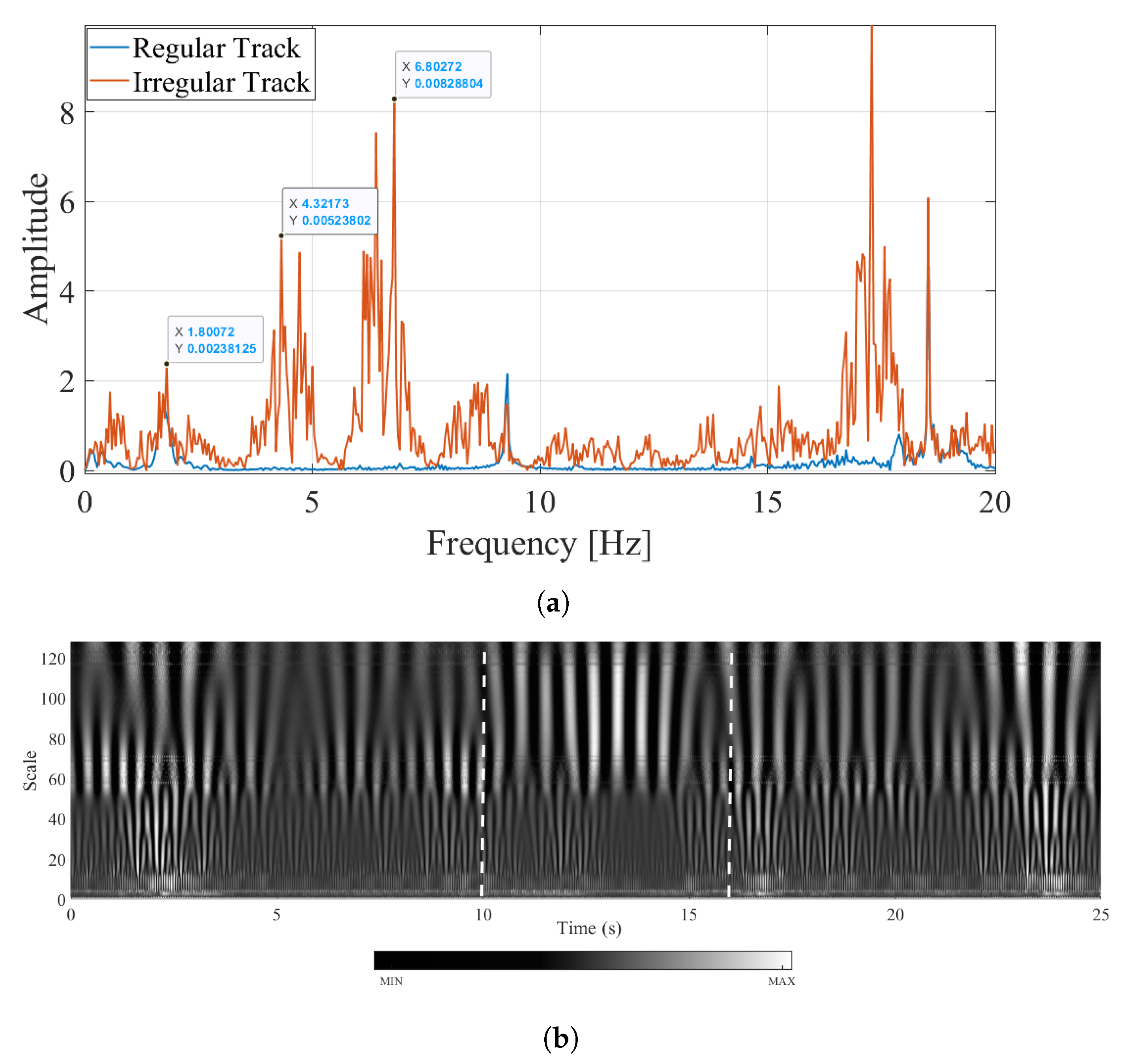
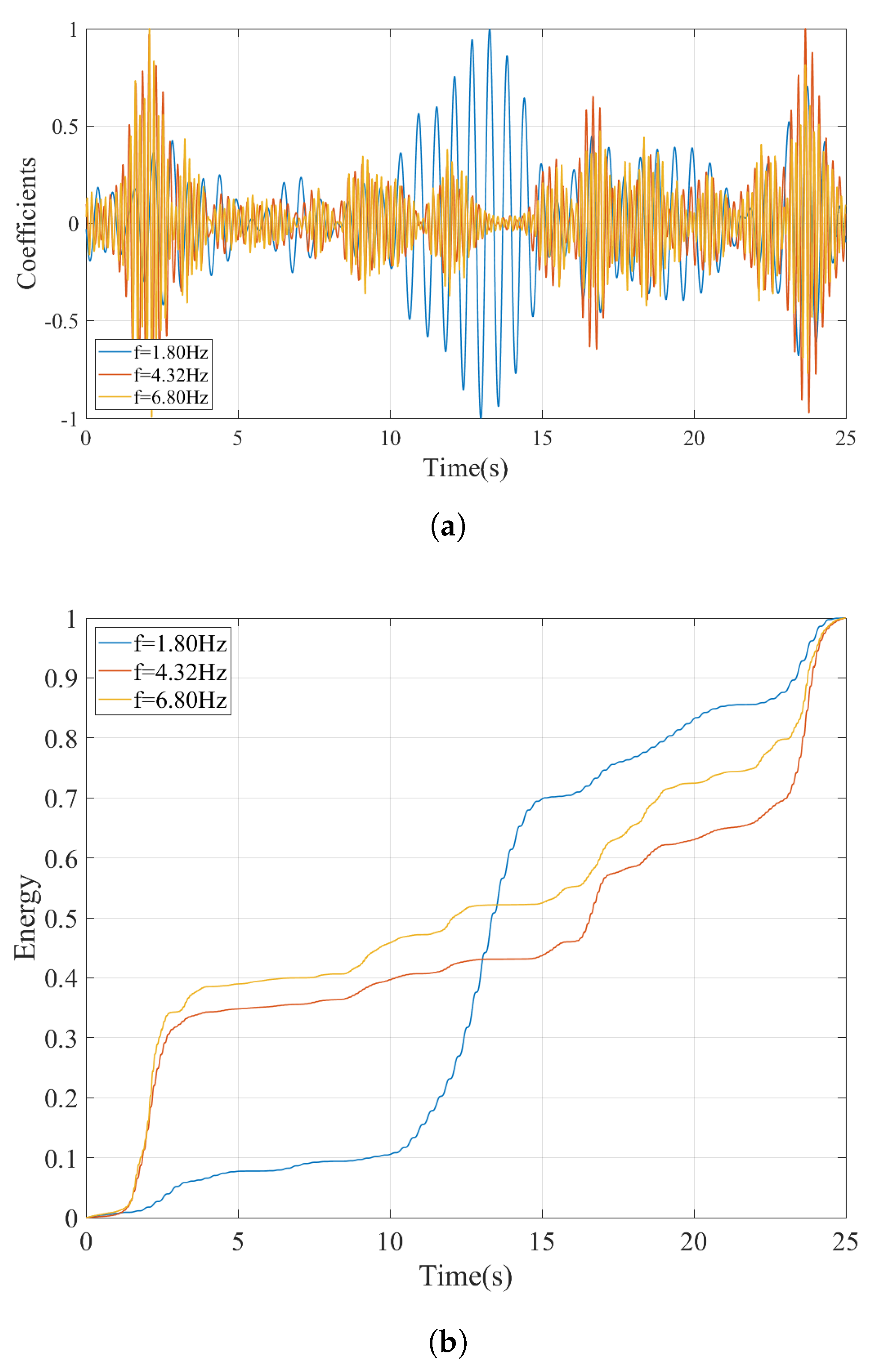
5.2. Case II: Considering Track Irregularities; Slow Train Speed
5.3. Case III: Considering Track Irregularities; Higher Train Speeds
6. Conclusions
- The numerical analysis indicate that the frequency content of the vibrations recorded on the bogie of a train is generally very complex with numerous peaks visible. This complexity is further amplified when the track irregularities are considered.
- Including the vibrations recorded on the front and back approaches in the data set collected from the bogie provides an opportunity to distinguish the bridge frequencies from the other peaks in the Fourier amplitude spectrum because the vibrations associated with the train-rail-track system are generally continuous through the entire route which includes the front approach, the bridge and the back approach. On the other hand, the vibrations on the bogie that are associated with the vibrations of the bridge occur only while the sensor is on the bridge.
- The continuous wavelet transform provides a powerful tool to distinguish the frequencies associated with the bridge vibrations from the other peaks visible in the Fourier amplitude spectrum. By taking a horizontal section on the wavelet coefficient map of the vibrations recorded on the bogie at the prominent frequencies visible on the FAS and computing the development of the energy at each frequency over time, the vibration frequencies associated with the vibrations of the bridge can be identified.
- The proposed method was shown to be able to pick out the bridge frequencies among other frequencies that have much higher energy than the bridge frequencies.
- Two different track irregularity profiles used in the numerical analysis showed that the proposed method can successfully detect the bridge frequencies even for very aggressive track irregularity profiles with sudden bumps located in the middle of the bridge.
- The proposed method was shown to work as effectively for high speeds as well as low speeds. As shown theoretically, the bridge frequencies that can be detected on the vehicle is shifted and this shift is linearly proportional to the speed of the vehicle. As long as this shift is considered, the bridge frequencies can be identified successfully for a speed of 90 km/h. The capability of identifying the bridge frequencies for relatively high train speeds distinguishes the proposed method from most of the work in the literature that is limited only to low vehicle speeds.
- The identified bridge frequencies are limited to the first vibration mode. This can be explained by the fact that the behavior of single-span bridges is generally dominated by the first mode. As such, only the first mode frequency is visible in the FAS of the accelerations recorded on the bogie. To evaluate the efficacy of the proposed method in identifying higher mode frequencies, further analysis on bridges whose behavior is significantly influenced by higher modes is needed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, C.; Liu, H.J.; Lam, H.F.; Adeagbo, M.O.; Peng, H.Y. Practical model updating of the Ting Kau Bridge through the MCMC-based Bayesian algorithm utilizing measured modal parameters. Eng. Struct. 2022, 254, 113839. [Google Scholar] [CrossRef]
- Salehi, M.; Erduran, E. Identification of boundary conditions of railway bridges using artificial neural networks. J. Civ. Struct. Health Monit. 2022, 12, 1223–1246. [Google Scholar] [CrossRef]
- Gönen, S.; Soyöz, S. Seismic analysis of a masonry arch bridge using multiple methodologies. Eng. Struct. 2021, 226, 111354. [Google Scholar] [CrossRef]
- Sangiorgio, V.; Nettis, A.; Uva, G.; Pellegrino, F.; Varum, H.; Adam, J.M. Analytical fault tree and diagnostic aids for the preservation of historical steel truss bridges. Eng. Fail. Anal. 2022, 133, 105996. [Google Scholar] [CrossRef]
- García-Macías, E.; Ruccolo, A.; Zanini, M.A.; Pellegrino, C.; Gentile, C.; Ubertini, F.; Mannella, P. P3P: A software suite for autonomous SHM of bridge networks. J. Civ. Struct. Health Monit. 2022, 1–18. [Google Scholar] [CrossRef]
- Erduran, E.; Gonen, S.; Alkanany, A. Parametric analysis of the dynamic response of railway bridges due to vibrations induced by heavy-haul trains. Struct. Infrastruct. Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Erduran, E.; Nordli, C.; Gonen, S. Effect of Elastomeric Bearing Stiffness on the Dynamic Response of Railway Bridges Considering Vehicle-Bridge Interaction. Appl. Sci. 2022, 12, 11952. [Google Scholar] [CrossRef]
- Gonen, S.; Erduran, E. A Hybrid Method for Vibration-Based Bridge Damage Detection. Remote Sens. 2022, 14, 6054. [Google Scholar] [CrossRef]
- Gonen, S.; Soyoz, S. Dynamic identification of masonry arch bridges using multiple methodologies. In Proceedings of the Conference Society for Experimental Mechanics Series; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Gonen, S.; Demirlioglu, K.; Erduran, E. Modal Identification of a Railway Bridge Under Train Crossings: A Comparative Study. In Dynamics of Civil Structures; Springer: Berlin/Heidelberg Germany, 2022; pp. 33–40. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yang, J.P. State-of-the-Art Review on Modal Identification and Damage Detection of Bridges by Moving Test Vehicles. Int. J. Struct. Stab. Dyn. 2018, 18, 1850025. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wang, Z.L.; Shi, K.; Xu, H.; Wu, Y.T. State-of-the-Art of Vehicle-Based Methods for Detecting Various Properties of Highway Bridges and Railway Tracks. Int. J. Struct. Stab. Dyn. 2020, 20, 2041004. [Google Scholar] [CrossRef]
- Yang, Y.B.; Lin, C.W.; Yau, J.D. Extracting bridge frequencies from the dynamic response of a passing vehicle. J. Sound Vib. 2004, 272, 471–493. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chang, K.C. Extraction of bridge frequencies from the dynamic response of a passing vehicle enhanced by the EMD technique. J. Sound Vib. 2009, 322, 718–739. [Google Scholar] [CrossRef]
- Zhu, L.; Malekjafarian, A. On the use of ensemble empirical mode decomposition for the identification of bridge frequency from the responses measured in a passing vehicle. Infrastructures 2019, 4, 32. [Google Scholar] [CrossRef]
- Li, W.M.; Jiang, Z.H.; Wang, T.L.; Zhu, H.P. Optimization method based on Generalized Pattern Search Algorithm to identify bridge parameters indirectly by a passing vehicle. J. Sound Vib. 2014, 333, 364–380. [Google Scholar] [CrossRef]
- Nagayama, T.; Reksowardojo, A.P.; Su, D.; Mizutani, T. Bridge natural frequency estimation by extracting the common vibration component from the responses of two vehicles. Eng. Struct. 2017, 150, 821–829. [Google Scholar] [CrossRef]
- Sitton, J.D.; Zeinali, Y.; Rajan, D.; Story, B.A. Frequency Estimation on Two-Span Continuous Bridges Using Dynamic Responses of Passing Vehicles. J. Eng. Mech. 2020, 146, 04019115. [Google Scholar] [CrossRef]
- Sadeghi Eshkevari, S.; Matarazzo, T.J.; Pakzad, S.N. Bridge modal identification using acceleration measurements within moving vehicles. Mech. Syst. Signal Process. 2020, 141, 106733. [Google Scholar] [CrossRef]
- Yang, Y.B.; Li, Y.C.; Chang, K.C. Constructing the mode shapes of a bridge from a passing vehicle: A theoretical study. Smart Struct. Syst. 2014, 13, 797–819. [Google Scholar] [CrossRef]
- Kong, X.; Cai, C.S.; Kong, B. Numerically Extracting Bridge Modal Properties from Dynamic Responses of Moving Vehicles. J. Eng. Mech. 2016, 142, 04016025. [Google Scholar] [CrossRef]
- Quqa, S.; Giordano, P.F.; Limongelli, M.P. Shared micromobility-driven modal identification of urban bridges. Autom. Constr. 2022, 134, 104048. [Google Scholar] [CrossRef]
- Oshima, Y.; Yamamoto, K.; Sugiura, K. Damage assessment of a bridge based on mode shapes estimated by responses of passing vehicles. Smart Struct. Syst. 2014, 13, 731–753. [Google Scholar] [CrossRef]
- Malekjafarian, A.; OBrien, E.J. Identification of bridge mode shapes using Short Time Frequency Domain Decomposition of the responses measured in a passing vehicle. Eng. Struct. 2014, 81, 386–397. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Lie, S.T. Estimation of mode shapes of beam-like structures by a moving lumped mass. Eng. Struct. 2019, 180, 654–668. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Khan, M.A.; OBrien, E.J.; Micu, E.A.; Bowe, C.; Ghiasi, R. Indirect Monitoring of Frequencies of a Multiple Span Bridge Using Data Collected from an Instrumented Train: A Field Case Study. Sensors 2022, 22, 7468. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, Y.; Chang, K. Effect of road surface roughness on the response of a moving vehicle for identification of bridge frequencies. Interact. Multiscale Mech. 2012, 5, 347–368. [Google Scholar] [CrossRef]
- González, A.; O’Brien, E.J.; Li, Y.Y.; Cashell, K. The use of vehicle acceleration measurements to estimate road roughness. Veh. Syst. Dyn. 2008, 46, 483–499. [Google Scholar] [CrossRef]
- Harris, N.K.; Gonzalez, A.; OBrien, E.J.; McGetrick, P. Characterisation of pavement profile heights using accelerometer readings and a combinatorial optimisation technique. J. Sound Vib. 2010, 329, 497–508. [Google Scholar] [CrossRef]
- Wang, H.; Nagayama, T.; Zhao, B.; Su, D. Identification of moving vehicle parameters using bridge responses and estimated bridge pavement roughness. Eng. Struct. 2017, 153, 57–70. [Google Scholar] [CrossRef]
- Zhan, Y.; Au, F.T. Bridge Surface Roughness Identification Based on Vehicle-Bridge Interaction. Int. J. Struct. Stab. Dyn. 2019, 19, 1–26. [Google Scholar] [CrossRef]
- Keenahan, J.C.; OBrien, E.J. Drive-by damage detection with a TSD and time-shifted curvature. J. Civ. Struct. Health Monit. 2018, 8, 383–394. [Google Scholar] [CrossRef]
- Bu, J.Q.; Law, S.S.; Zhu, X.Q. Innovative Bridge Condition Assessment from Dynamic Response of a Passing Vehicle. J. Eng. Mech. 2006, 132, 1372–1380. [Google Scholar] [CrossRef]
- OBrien, E.; Keenahan, J. Drive-by damage detection in bridges using the apparent profile.pdf. Struct. Control. Health Monit. 2015, 22, 813–825. [Google Scholar] [CrossRef]
- Kim, C.W.; Kawatani, M. Pseudo-static approach for damage identification of bridges based on coupling vibration with a moving vehicle. Struct. Infrastruct. Eng. 2008, 4, 371–379. [Google Scholar] [CrossRef]
- Hester, D.; González, A. A discussion on the merits and limitations of using drive-by monitoring to detect localised damage in a bridge. Mech. Syst. Signal Process. 2017, 90, 234–253. [Google Scholar] [CrossRef]
- Lin, C.W.; Yang, Y.B. Use of a passing vehicle to scan the fundamental bridge frequencies: An experimental verification. Eng. Struct. 2005, 27, 1865–1878. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y. Estimating bridge fundamental frequency from vibration response of instrumented passing vehicle: Analytical and experimental study. Adv. Struct. Eng. 2012, 15, 417–433. [Google Scholar] [CrossRef]
- McGetrick, P.J.; Kim, C.W.; González, A.; Brien, E.J. Experimental validation of a drive-by stiffness identification method for bridge monitoring. Struct. Health Monit. 2015, 14, 317–331. [Google Scholar] [CrossRef]
- Kim, J.; Lynch, J.P. Experimental analysis of vehiclebridge interaction using a wireless monitoring system and a two-stage system identification technique. Mech. Syst. Signal Process. 2012, 28, 3–19. [Google Scholar] [CrossRef]
- Miyamoto, A.; Yabe, A. Development of practical health monitoring system for short- and medium-span bridges based on vibration responses of city bus. J. Civ. Struct. Health Monit. 2012, 2, 47–63. [Google Scholar] [CrossRef]
- Chang, K.C.; Kim, C.W.; Kawatani, M. Feasibility investigation for a bridge damage identification method through moving vehicle laboratory experiment. Struct. Infrastruct. Eng. 2014, 10, 328–345. [Google Scholar] [CrossRef]
- Shirzad-Ghaleroudkhani, N.; Mei, Q.; Gül, M. Frequency Identification of Bridges Using Smartphones on Vehicles with Variable Features. J. Bridge Eng. 2020, 25, 04020041. [Google Scholar] [CrossRef]
- Yang, Y.B.; Shi, K.; Wang, Z.L.; Xu, H.; Wu, Y.T. Theoretical study on a dual-beam model for detection of track/bridge frequencies and track modulus by a moving vehicle. Eng. Struct. 2021, 244, 112726. [Google Scholar] [CrossRef]
- Zhan, J.; Wang, Z.; Kong, X.; Xia, H.; Wang, C.; Xiang, H. A Drive-By Frequency Identification Method for Simply Supported Railway Bridges Using Dynamic Responses of Passing Two-Axle Vehicles. J. Bridge Eng. 2021, 26, 04021078. [Google Scholar] [CrossRef]
- Zhan, J.; You, J.; Kong, X.; Zhang, N. An indirect bridge frequency identification method using dynamic responses of high-speed railway vehicles. Eng. Struct. 2021, 243, 112694. [Google Scholar] [CrossRef]
- Quirke, P.; Bowe, C.; OBrien, E.J.; Cantero, D.; Antolin, P.; Goicolea, J.M. Railway bridge damage detection using vehicle-based inertial measurements and apparent profile. Eng. Struct. 2017, 153, 421–442. [Google Scholar] [CrossRef]
- Fitzgerald, P.C.; Malekjafarian, A.; Cantero, D.; OBrien, E.J.; Prendergast, L.J. Drive-by scour monitoring of railway bridges using a wavelet-based approach. Eng. Struct. 2019, 191, 1–11. [Google Scholar] [CrossRef]
- Matsuoka, K.; Tanaka, H.; Kawasaki, K.; Somaschini, C.; Collina, A. Drive-by methodology to identify resonant bridges using track irregularity measured by high-speed trains. Mech. Syst. Signal Process. 2021, 158, 107667. [Google Scholar] [CrossRef]
- Morlet, J. Sampling theory and wave propagation. In Issues in Acoustic Signal/Image Processing and Recognition; Springer: Berlin/Heidelberg, Germany, 1983; pp. 233–261. [Google Scholar] [CrossRef]
- Reda Taha, M.M.; Noureldin, A.; Lucero, J.L.; Baca, T.J. Wavelet transform for structural health monitoring: A compendium of uses and features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Teolis, A. Computational Signal Processing with Wavelets; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Iwnick, S. Manchester benchmarks for rail vehicle simulation. Veh. Syst. Dyn. 1998, 30, 295–313. [Google Scholar] [CrossRef]
- Olsen, K.K. Numerical Study of Static and Dynamic Response from Introducing under Ballast Mat in a Ballasted Railway Track; Norwegian University of Science and Technology: Trondheim, Norway, 2021. [Google Scholar]
- Man, A. Dynatrack: A Survey of Dynamic Railway Track Properties and Their Quality. Ph.D. Thesis, University of Delft, Delft, The Netherlands, 2022. [Google Scholar]
- Receptance behaviour of railway track and subgrade. Arch. Appl. Mech. 1998, 68, 457–470. [CrossRef]
- Lau, A.; Hoff, I. Simulation of Train-Turnout Coupled Dynamics Using a Multibody Simulation Software. Model. Simul. Eng. 2018, 2018, 8578272. [Google Scholar] [CrossRef]
- Farkas, A. Measurement of Railway Track Geometry: A State-of-the-Art Review. Period. Polytech. Transp. Eng. 2020, 48, 76–88. [Google Scholar] [CrossRef]
- CEN/TC 256; Railway Application. European Committee for Standardization: Brussels, Belgium, 2007.
- Salehi, M.; Gonen, S.; Erduran, E. A Critical Look at the Use of Wavelets in Damage Detection. Lect. Notes Civ. Eng. 2023, 254 LNCE, 13–22. [Google Scholar] [CrossRef]








| Component | Property | Symbol | Value |
|---|---|---|---|
| Wheel | Stiffness | kN/m | |
| Mass | 906.5 kg | ||
| Height | 0.46 m | ||
| Boogie | Stiffness | 1120 kN/m | |
| Damping | 4 kNs/m | ||
| Mass inertia | 1610 kgm2 | ||
| Mass | 2615 kg | ||
| Height | 0.88 m | ||
| Length | 2.56 m | ||
| Density | 10,200 kg/m3 | ||
| Young’ Modulus | E | GPa | |
| Poison’s ratio | 0.2 | ||
| Cross section | 0.25 m, 0.15 m | ||
| Car | Stiffness | 430 kN/m | |
| Damping | 20 kNs/m | ||
| Mass inertia | kgm2 | ||
| Mass | 32,000 kg | ||
| Height | 1.8 m | ||
| Length | 19 m | ||
| Density | 7400 kg/m3 | ||
| Cross section | 0.65 m, 0.35 m |
| Component | Property | Symbol | Value |
|---|---|---|---|
| Rail-pad | Stiffness | 62 MN/m | |
| Damping | 32 kNs/m | ||
| ine Ballast | Stiffness | 230 MN/m | |
| Damping | 200 kNs/m | ||
| Mass | 1400 kg | ||
| Rail | Young’s modulus | 200 GPa | |
| Poisson’s ratio | 0.3 | ||
| Area | m2 | ||
| Moment of Inertia | m4 | ||
| Density | 7800 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erduran, E.; Pettersen, F.M.; Gonen, S.; Lau, A. Identification of Vibration Frequencies of Railway Bridges from Train-Mounted Sensors Using Wavelet Transformation. Sensors 2023, 23, 1191. https://doi.org/10.3390/s23031191
Erduran E, Pettersen FM, Gonen S, Lau A. Identification of Vibration Frequencies of Railway Bridges from Train-Mounted Sensors Using Wavelet Transformation. Sensors. 2023; 23(3):1191. https://doi.org/10.3390/s23031191
Chicago/Turabian StyleErduran, Emrah, Fredrik Marøy Pettersen, Semih Gonen, and Albert Lau. 2023. "Identification of Vibration Frequencies of Railway Bridges from Train-Mounted Sensors Using Wavelet Transformation" Sensors 23, no. 3: 1191. https://doi.org/10.3390/s23031191
APA StyleErduran, E., Pettersen, F. M., Gonen, S., & Lau, A. (2023). Identification of Vibration Frequencies of Railway Bridges from Train-Mounted Sensors Using Wavelet Transformation. Sensors, 23(3), 1191. https://doi.org/10.3390/s23031191








