A HOOI-Based Fast Parameter Estimation Algorithm in UCA-UCFO Framework
Abstract
:1. Introduction
- (1)
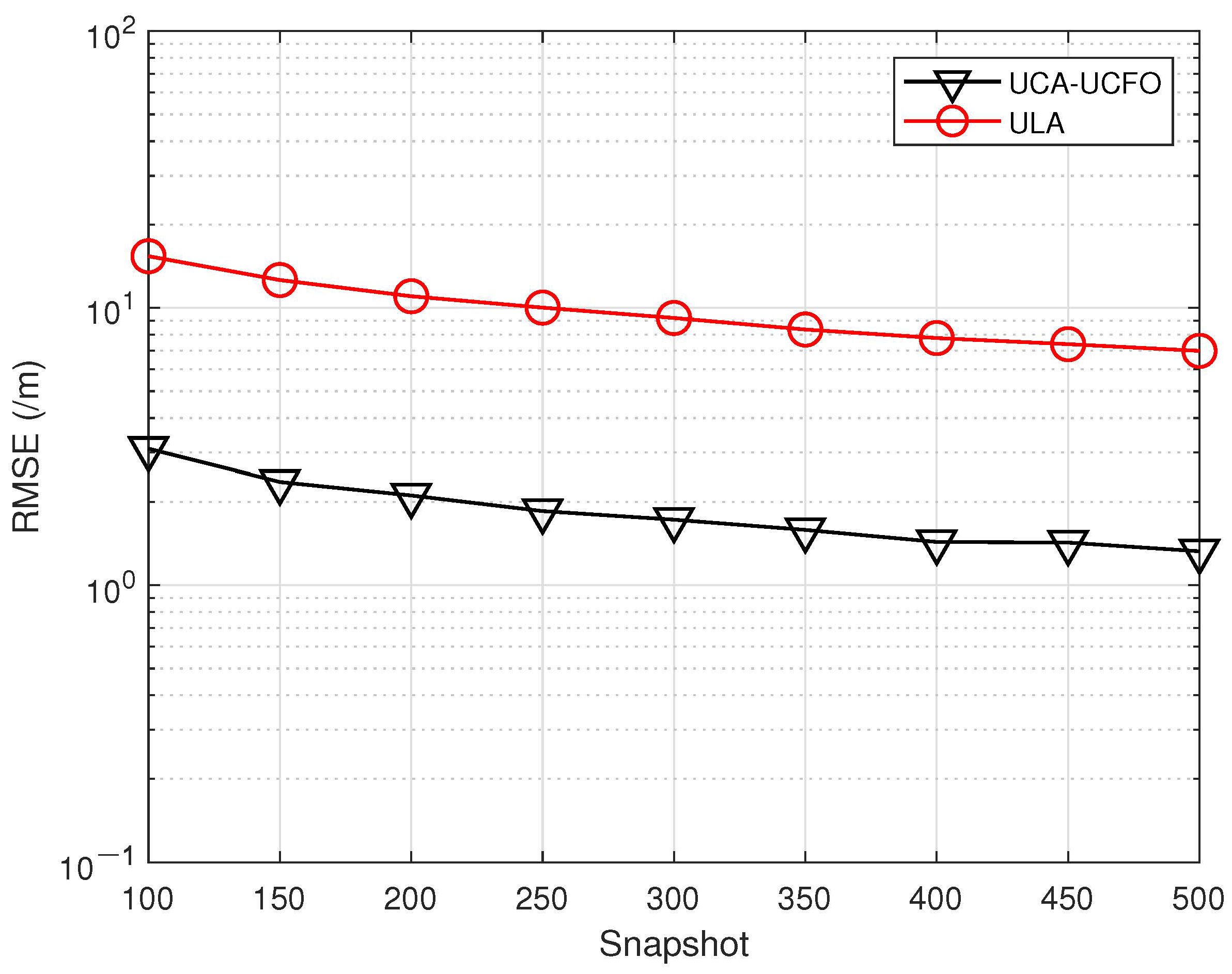
- The algorithm proposed in this paper is applied on the UCA-UCFO framework, where it is shown to be capable of parameter estimation accuracy improvement and has obvious advantages over ULA.
- (2)
- The method proposed in this paper solves the problem of angle and distance estimation in the tensor domain as the tensor stores the inherent multidimensional structure of the signal model, which improves the accuracy of target parameter estimation.
- (3)
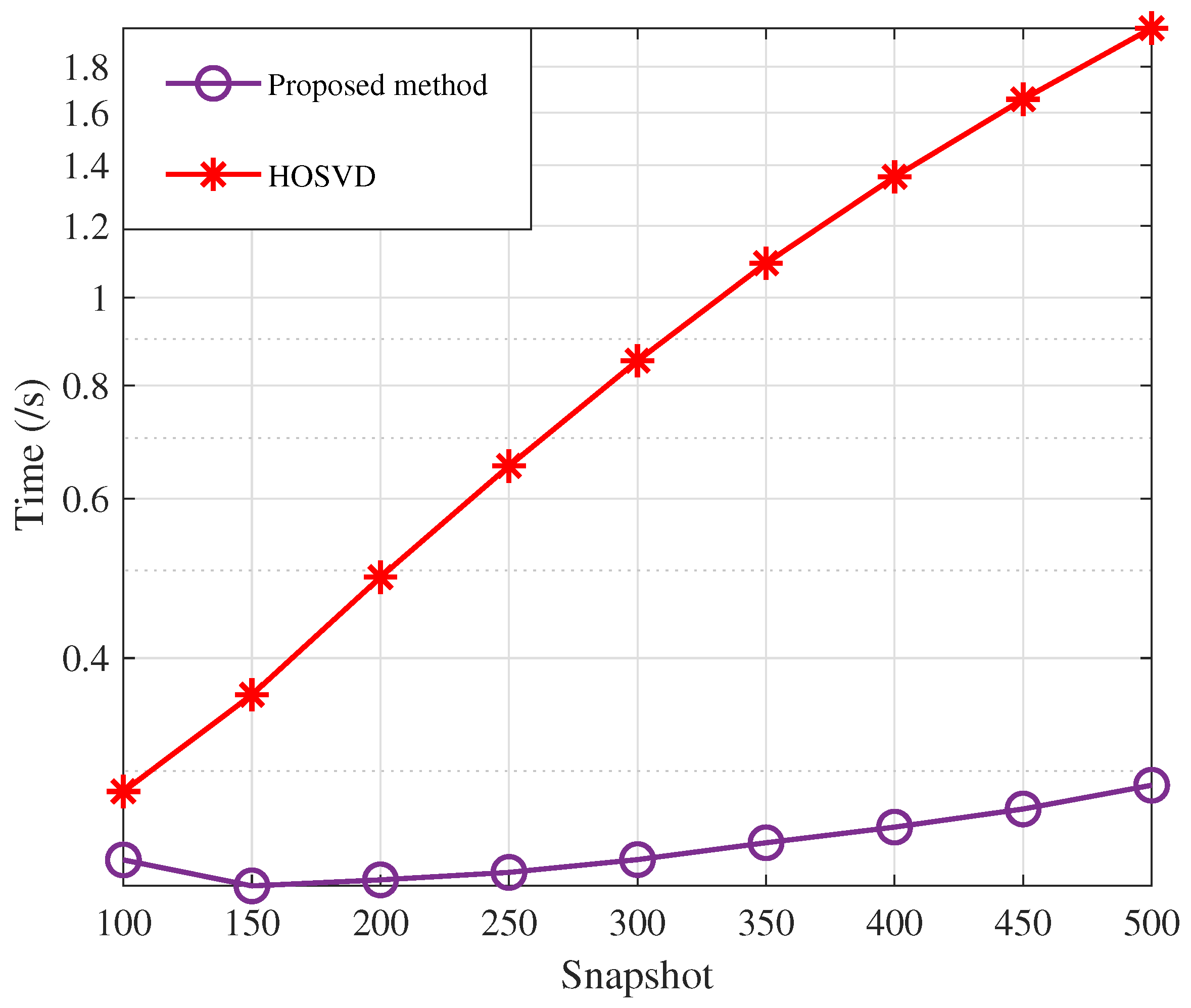
- The HOOI algorithm used in this paper ensures the same accuracy as HOSVD while significantly improving the running speed, making the parameter estimation algorithm more suitable for real-time scenarios.
2. The Basics of Tensor and Signal Representation Using Tensors
2.1. Essentials of Tensors
2.2. Signal Model Based on Tensors
3. A HOOI Method for Parameters Estimation
3.1. Factor Matrices and Core Tensor Construction Based on the HOOI Algorithm
- Step1:
- Suppose a Z-order tensor ; the factor matrix is ( is the size of the z-th tensor dimension). Let , initialize the core tensor as a zero tensor.
- Step2:
- Let , and for , perform the following operationsThen compute the SVD value of the mode-n extension of the tensor by determining the number of its principal singular values , and then let .
- Step3:
- Compute the core tensor for the k-th iterationJudge whether it converges or not: if the convergence condition is satisfied, then execute the next step; if the convergence criteria are not met or if the upper limit on the number of iterations has not been reached, go back to Step 2 and continue with the iterations.
- Step4:
- Outputs the factor matrix and the core tensor .
3.2. Angle of Arrival Estimation Using Reduced-Dimension MUSIC Algorithm via the Tensor-Based Method
3.3. Range Estimation
4. Proposed Algorithm Performance Evaluation
4.1. Computational Complexity Analysis
- (1)
- The HOSVD computation complexity of in Equation (17) is .
- (2)
- Constructing a signal subspace in Equation (21) requires .
- (3)
- Dimensionality reduction of a two-dimensional spectral Function (27) requires .
- (4)
- The search for one-dimensional spectral peaks in Equation (34) requires , where denotes the DOA search scope, and is the step size of the search.
- (5)
- Estimating range using rotational invariance requires .
4.2. Cramér–Rao Bound (CRB)
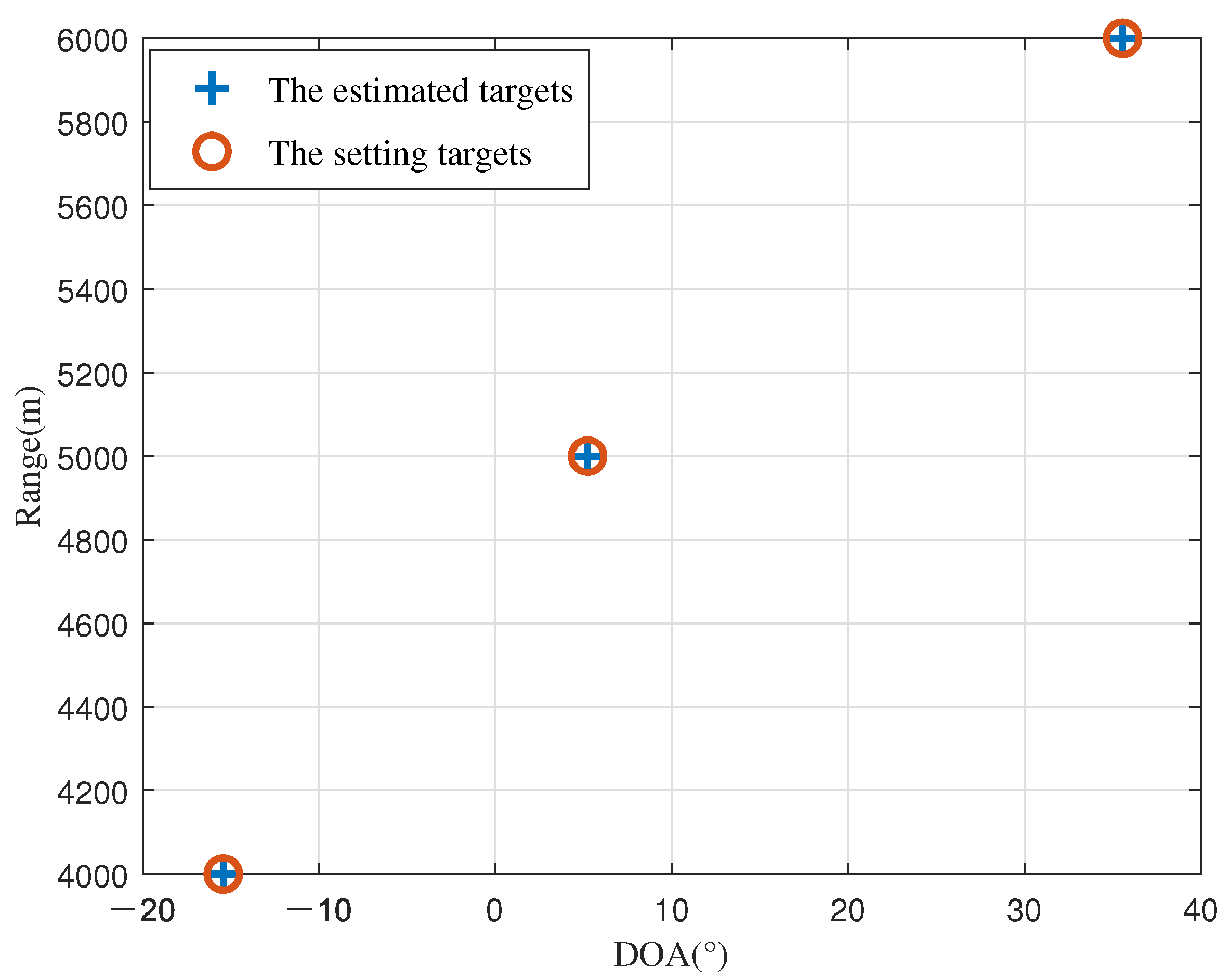
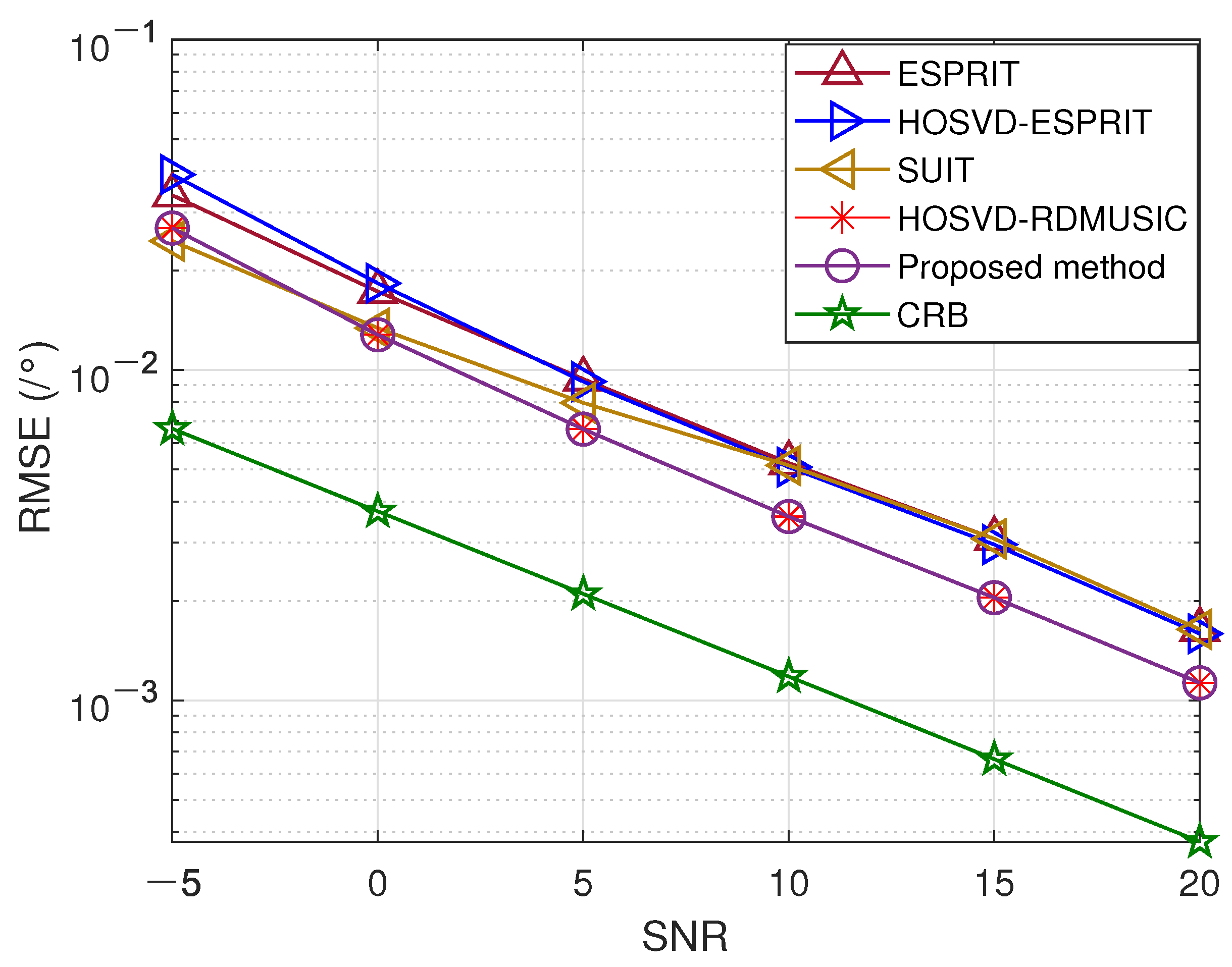
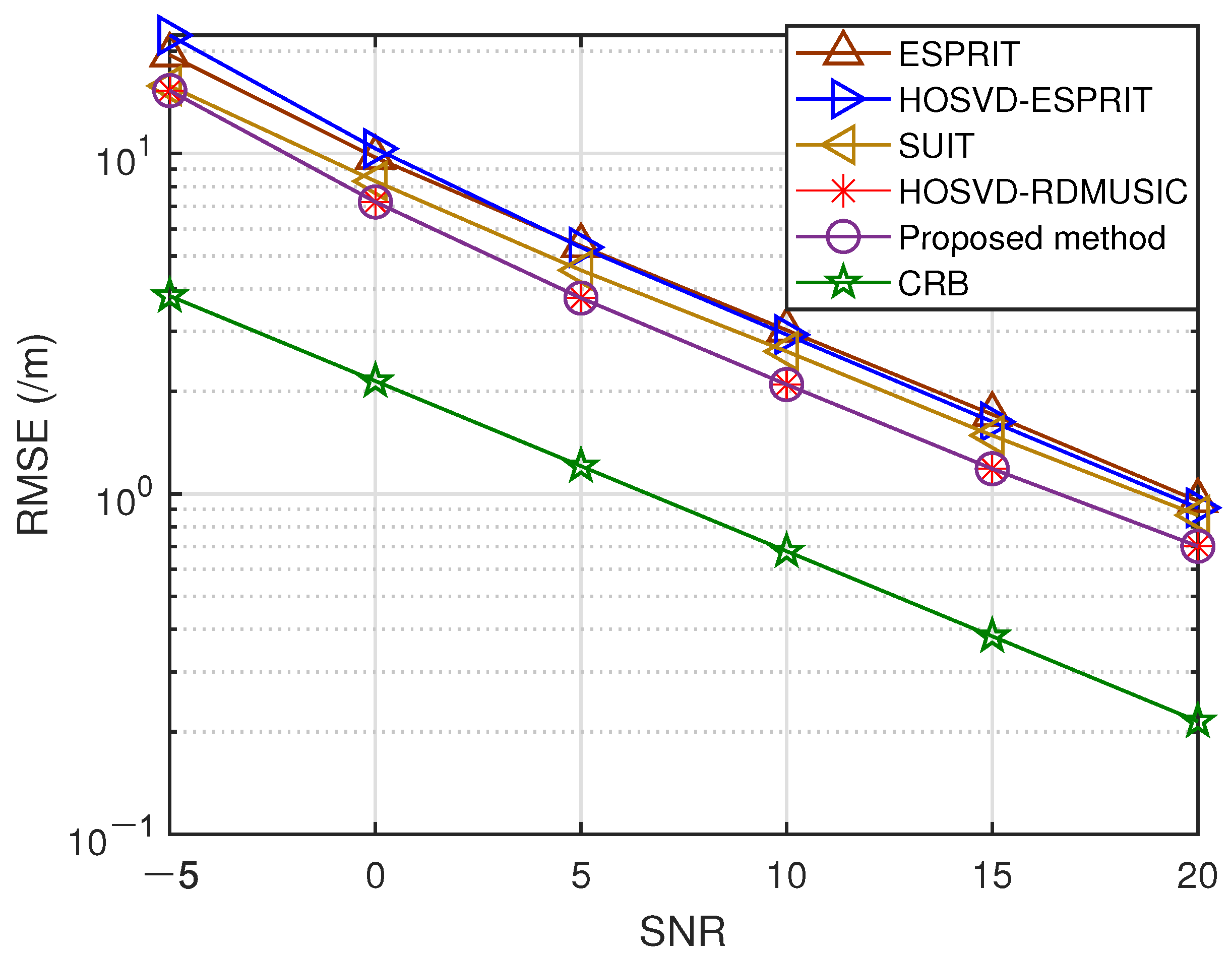
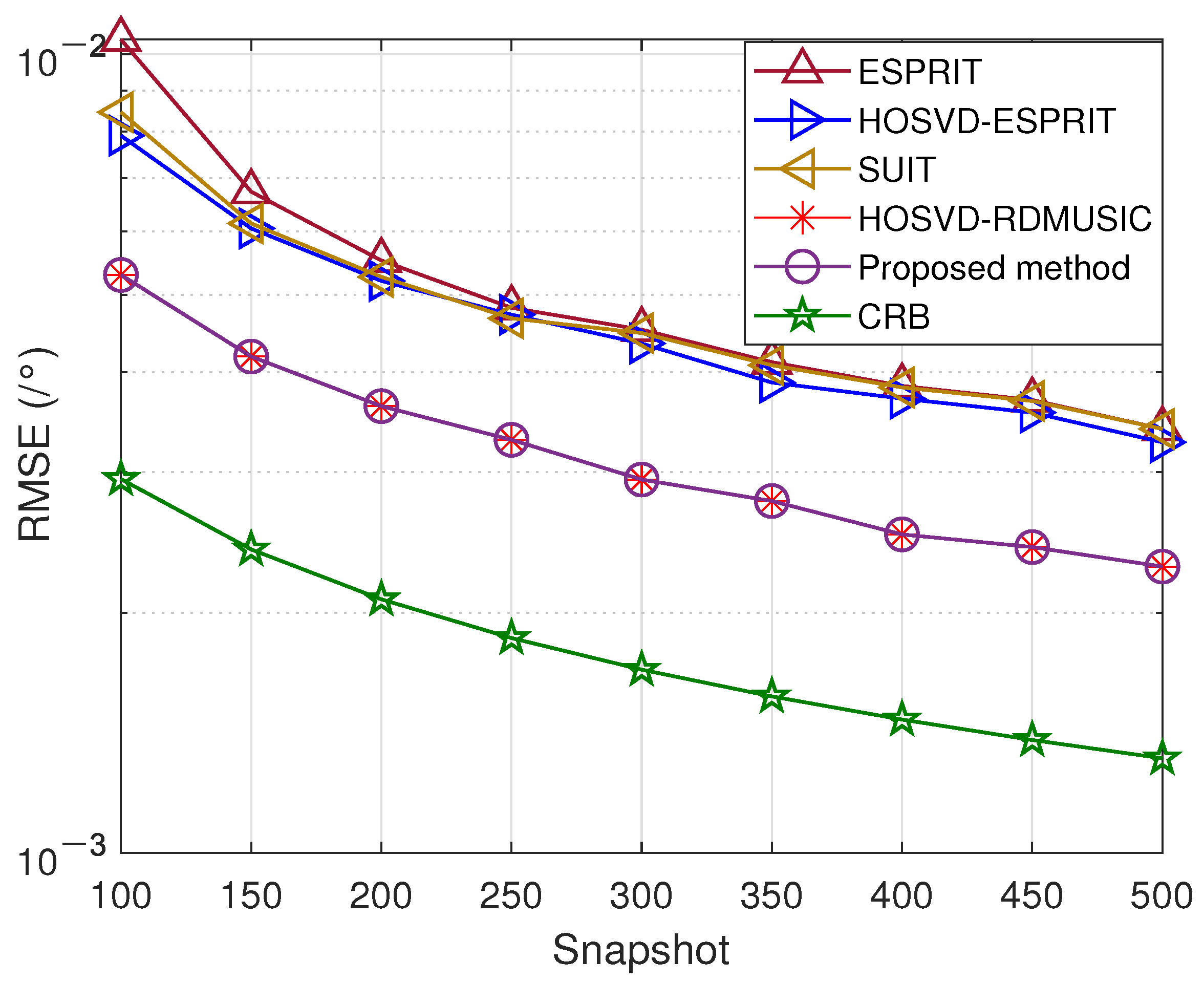
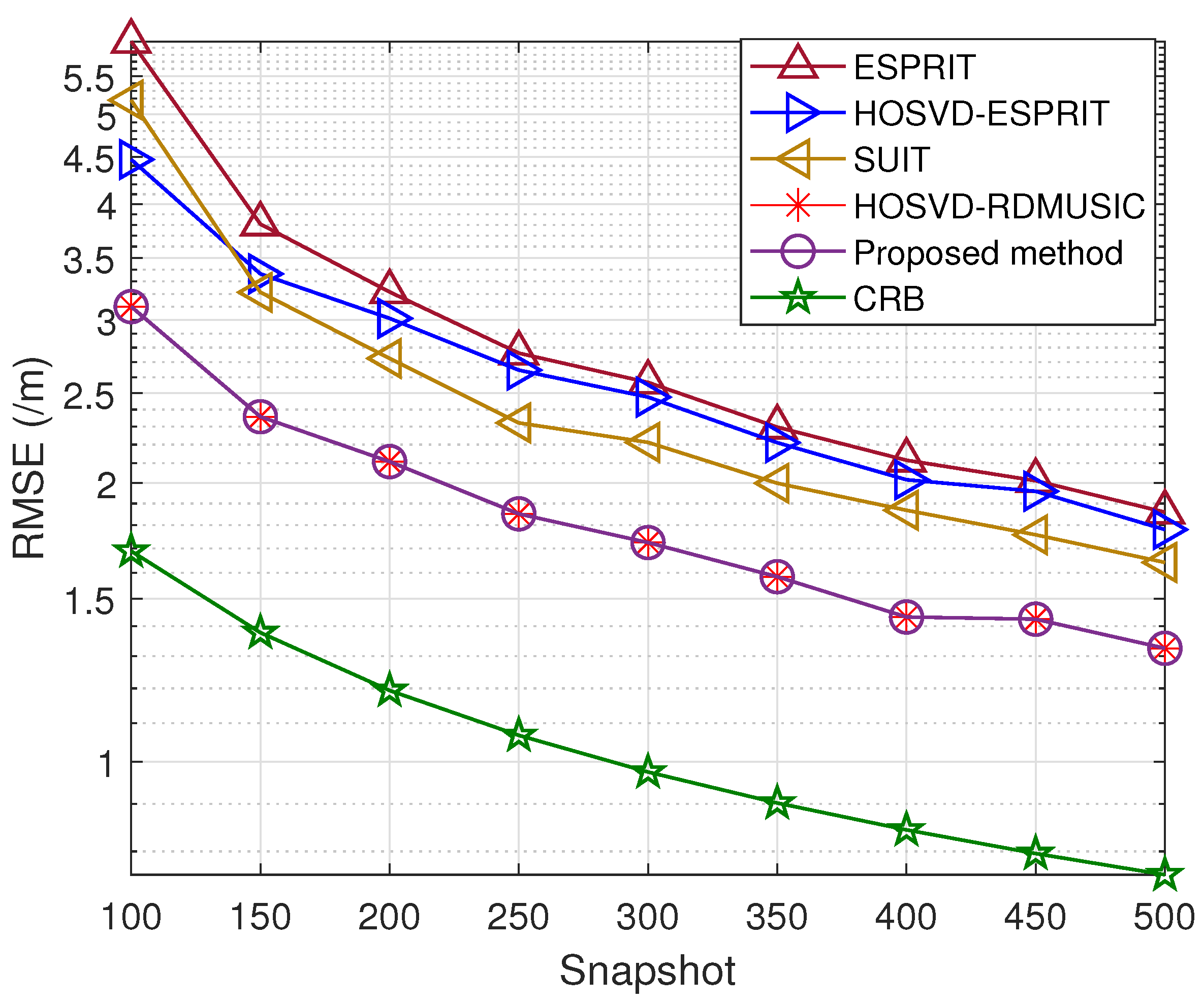
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| (bold Euler letters) | tensor |
| matrix set | |
| (bold capital letters) | matrix |
| (bold lowercase letter) | vector |
| conjugate | |
| transpose | |
| ⨂ | Kronecker product |
| ⊙ | Khatri-Rao product |
| conjugation-transpose | |
| elementary matrix | |
| inverse | |
| pseudo-inverse | |
| Extract the phase of the matrix | |
| diagonalization of matrix | |
| ∘ | Hadamard product |
| 0N | zero matrix |
References
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Frequency diverse array radars. In Proceedings of the 2006 IEEE Conference on Radar, Shanghai, China, 16–19 October 2006; p. 3. [Google Scholar]
- Mu, T.; Song, Y. Target range–angle estimation based on time reversal FDA-MIMO radar. Int. J. Microw. Wirel. Technol. 2020, 12, 267–275. [Google Scholar] [CrossRef]
- Wang, W. Applications of MIMO Technique for Aerospace Remote Sensing. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–10. [Google Scholar]
- Song, X.; Li, L.; Xue, W. Active disturbance rejection decoupling control for nonlinear MIMO uncertain systems with application to path following of self-driving bus. Control Eng. Pract. 2023, 133, 105432. [Google Scholar] [CrossRef]
- Ahmed, W. Accurate Detection for Self Driving Cars Using Multi-Resolution MIMO Radar. Ph.D. Dissertation, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2022. [Google Scholar]
- Bana, A.S.; De Carvalho, E.; Soret, B. Massive MIMO for internet of things (IoT) connectivity. Phys. Commun. 2019, 37, 100859. [Google Scholar] [CrossRef]
- Cetinkaya, O.; Balsamo, D.; Merrett, G.V. Internet of MIMO things: UAV-assisted wireless-powered networks for future smart cities. IEEE Internet Things Mag. 2020, 3, 8–13. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Zhang, X. FDA-MIMO for joint angle and range estimation: Unfolded coprime framework and parameter estimation algorithm. IET Radar Sonar Navig. 2020, 14, 917–926. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Direction of Arrival Estimation of Quasi-Stationary Signals Using Unfolded Coprime Array. IEEE Access 2017, 5, 6538–6545. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, X.; Lu, W. Joint frequency and DOA estimation of sub-Nyquist sampling multi-band sources with unfolded coprime arrays. Multidimens. Syst. Signal Process. 2022, 33, 1257–1272. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Sparse representation-based joint angle and Doppler frequency estimation for MIMO radar. Multidimens. Syst. Signal Process. 2015, 26, 179–192. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, M.Y.; Wu, S.J. Fast OMP algorithm for 2D angle estimation in MIMO radar. Electron. Lett. 2010, 46, 444–445. [Google Scholar] [CrossRef]
- Zahernia, A.; Dehghani, M.J.; Javidan, R. MUSIC algorithm for DOA estimation using MIMO arrays. In Proceedings of the 2011 6th International Conference on Telecommunication Systems, Services, and Applications (TSSA), Denpasar, Indonesia, 20–21 October 2011; pp. 149–153. [Google Scholar]
- Bencheikh, M.L.; Wang, Y. Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar. Electron. Lett. 2010, 46, 1. [Google Scholar] [CrossRef]
- Duofang, C.; Baixiao, C.; Guodong, Q. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 1. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Cao, R.; Zhou, M. Reduced-dimension MUSIC for angle and array gain-phase error estimation in bistatic MIMO radar. IEEE Commun. Lett. 2013, 17, 443–446. [Google Scholar] [CrossRef]
- Kong, Y.; Qin, Z.; Wang, T. An enhanced sparse representation-based intelligent recognition method for planet bearing fault diagnosis in wind turbines. Renew. Energy 2021, 173, 987–1004. [Google Scholar] [CrossRef]
- Jang, S.; Im, C.; Lee, H. A single-snapshot localization for monostatic FDA-MIMO radar. IEEE Commun. Lett. 2022, 26, 2899–29039. [Google Scholar] [CrossRef]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Ahmed, T.; Zhang, X.; Hassan, W.U. A higher-order propagator method for 2D-DOA estimation in massive MIMO systems. IEEE Commun. Lett. 2019, 24, 543–547. [Google Scholar] [CrossRef]
- Wen, F.; Xu, Y. HOSVD based multidimensional parameter estimation for massive MIMO system from incomplete channel measurements. Multidimens. Syst. Signal Process. 2018, 29, 1255–1267. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F.; He, J.; Truong, K.T. EMVS-MIMO radar with sparse Rx geometry: Tensor modeling and 2D direction finding. IEEE Trans. Aerosp. Electron. Syst. 2023; early access. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, F.; Shi, J.; Truong, T.K. 2D-DOA estimation for coherent signals via a polarized uniform rectangular array. IEEE Signal Process. Lett. 2023, 30, 893–897. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Lan, X.; Su, T. Traffic target location estimation based on tensor decomposition in intelligent transportation system. IEEE Trans. Intell. Transp. Syst. 2022; early access. [Google Scholar] [CrossRef]
- Wen, F.; Xiong, X.; Zhang, Z. Angle and mutual coupling estimation in bistatic MIMO radar based on PARAFAC decomposition. Digit. Signal Process. 2017, 65, 1–10. [Google Scholar] [CrossRef]
- Xiao, C.; Yang, C. A rank-adaptive higher-order orthogonal iteration algorithm for truncated Tucker decomposition. arXiv 2021, arXiv:2110.12564. [Google Scholar]
- Luo, D.; Ding, C.; Huang, H. Are tensor decomposition solutions unique? On the global convergence hosvd and parafac algorithms. arXiv 2021, arXiv:0902.4521. [Google Scholar]
- Tomioka, R.; Hayashi, K.; Kashima, H. Estimation of low-rank tensors via convex optimization. arXiv 2010, arXiv:1010.0789. [Google Scholar]
- Wang, X.; Wang, W.; Liu, J.; Liu, Q.; Wang, B. Tensor-based real-valued subspace approach for angle estimation in bistatic MIMO radar with unknown mutual coupling. Signal Process 2015, 116, 152–158. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, Y.; Cheng, Z.; Li, H. A novel unitary PARAFAC method for DOD and DOA estimation in bistatic MIMO radar. Signal Process. 2017, 138, 273–279. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X.; Su, T.; Guo, Y.; Lan, X. A HOOI-Based Fast Parameter Estimation Algorithm in UCA-UCFO Framework. Sensors 2023, 23, 9682. https://doi.org/10.3390/s23249682
Wang Y, Wang X, Su T, Guo Y, Lan X. A HOOI-Based Fast Parameter Estimation Algorithm in UCA-UCFO Framework. Sensors. 2023; 23(24):9682. https://doi.org/10.3390/s23249682
Chicago/Turabian StyleWang, Yuan, Xianpeng Wang, Ting Su, Yuehao Guo, and Xiang Lan. 2023. "A HOOI-Based Fast Parameter Estimation Algorithm in UCA-UCFO Framework" Sensors 23, no. 24: 9682. https://doi.org/10.3390/s23249682
APA StyleWang, Y., Wang, X., Su, T., Guo, Y., & Lan, X. (2023). A HOOI-Based Fast Parameter Estimation Algorithm in UCA-UCFO Framework. Sensors, 23(24), 9682. https://doi.org/10.3390/s23249682






