Fault Feature Extraction Method for Rolling Bearings Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Variational Mode Decomposition
Abstract
:1. Introduction
2. Theoretical Introduction
2.1. CEEMDAN
2.2. VMD
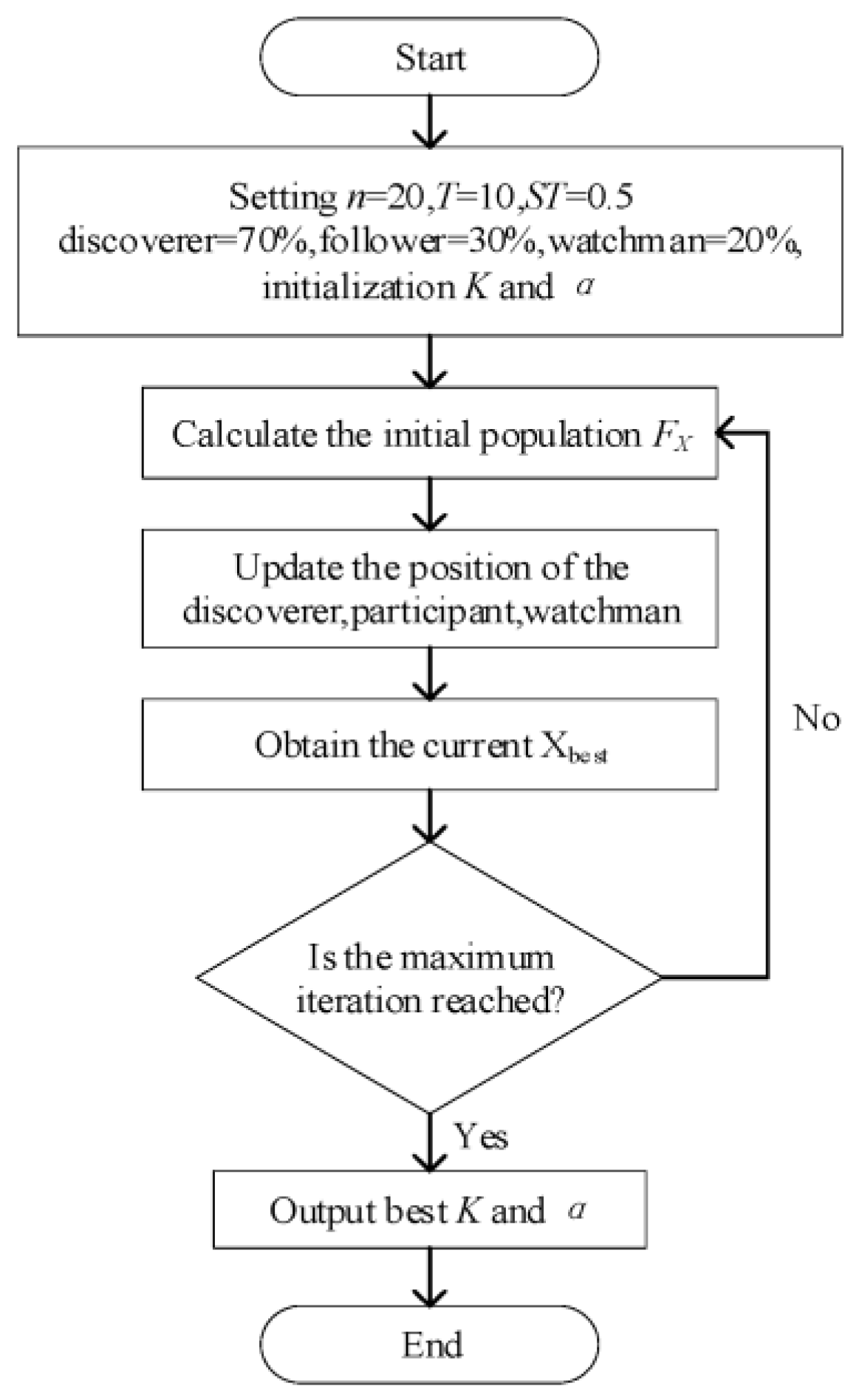
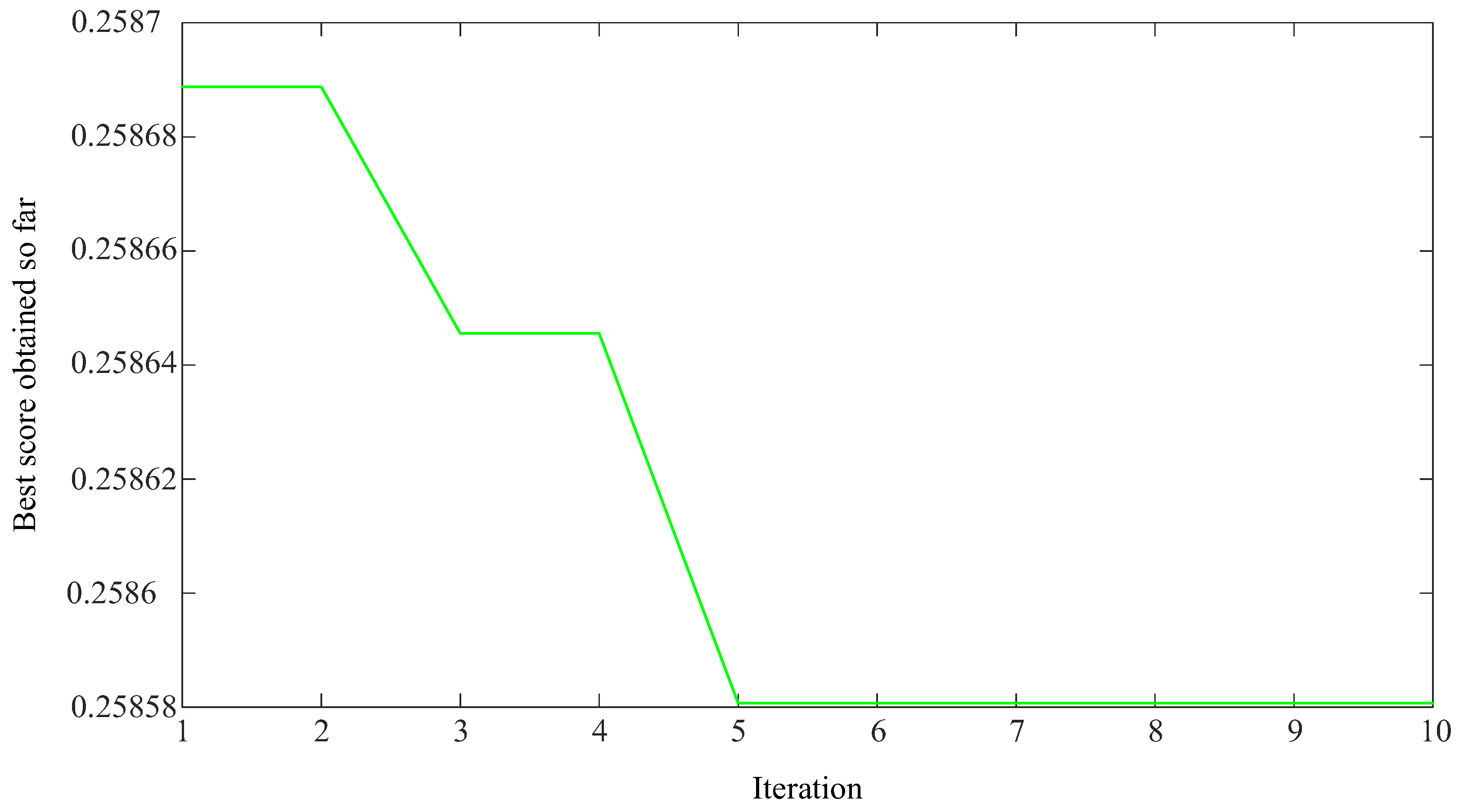
2.3. VMD Parameter Optimization Based on SSA
- (1)
- Initialization of SSA parameters: The sparrow number is set to n = 20, with maximum iterations T = 10 and the safety value ST = 0.5. The number of discoverers accounts for 70% of the sparrow population, the number of participants accounts for 30%, and 20% of the sparrows are selected from discoverers and followers as the watchmen.
- (2)
- The positions of sparrows in the population are set as X = , where d is the variable dimension of the optimization problem. Then, the fitness values of all sparrows can be expressed as FX = . Sparrows are divided into discoverers and followers by ranking the fitness value of each sparrow. The current position of the sparrow with the optimal fitness value is the optimal position Xbest.
- (3)
- Compared to followers, discoverers need to obtain food faster during foraging but also undertake the task of helping sparrow groups find food and provide food directions to followers. Thus, the discoverers have a more comprehensive range of searches than followers. The position of the discoverers is iteratively updated according to the following equation:where is the j-th dimensional position of the i-th sparrow in the t-th iteration, μ is a random number between 0 and 1, T is the maximum number of iterations, Q is a random number that obeys a normal distribution, L is a 1 × d matrix with all 1 elements, R2 is a warning value between 0 and 1, and ST is the safety value between 0.5 and 1.
- (4)
- During position iteration, the current optimal position Xbest is obtained by updating the fitness ranking of sparrow individuals.
- (5)
- Steps (3) and (4) are repeated until meeting the maximum number of iterations, T = 10. Then, the optimal location Xbest is determined and outputs the parameters K and α. Otherwise, the process returns to step (3).
3. Proposed Methods
3.1. Component Selection Index
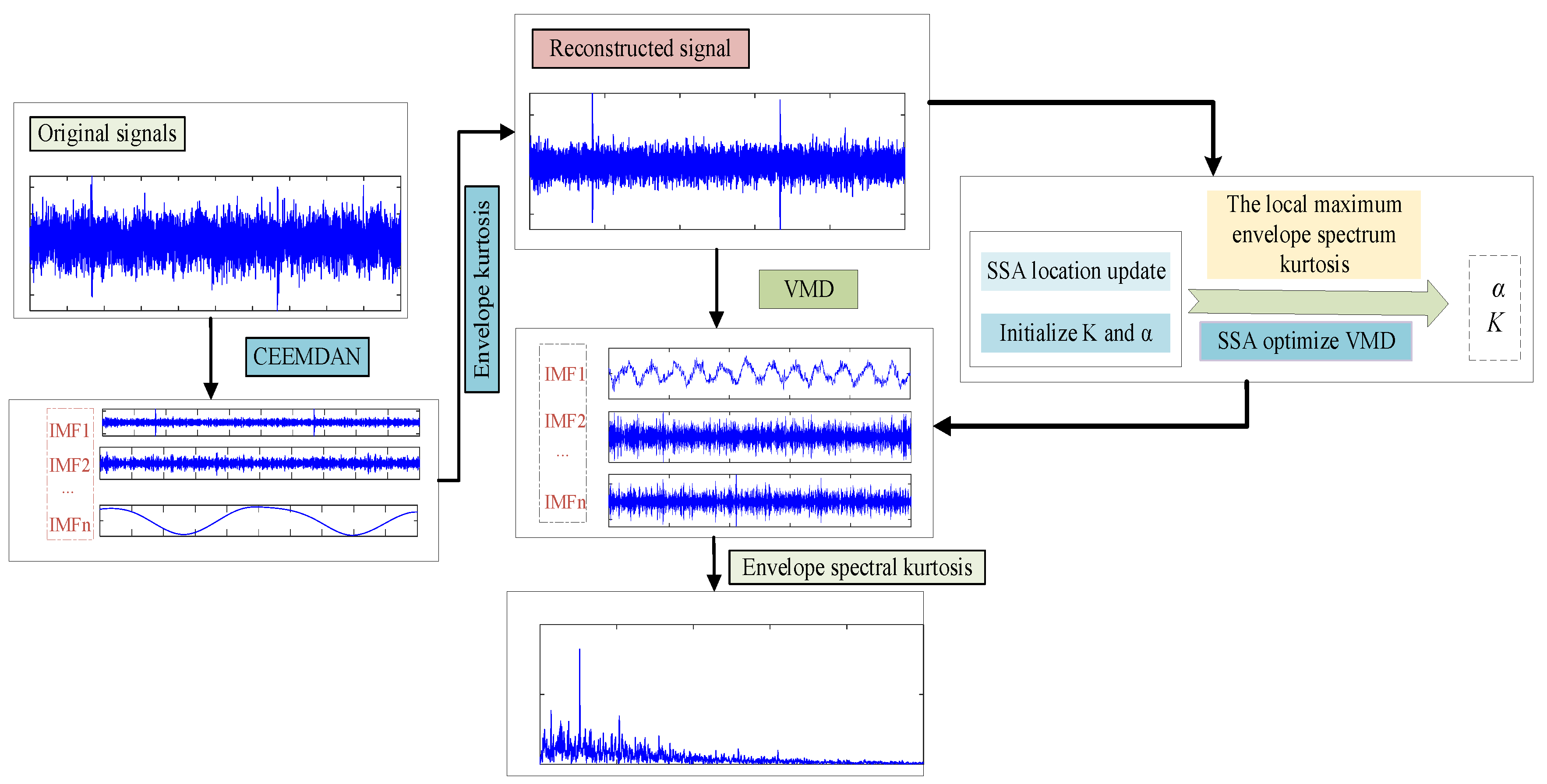
3.2. Feature Extraction Model Based on CEEMDAN and SSA-VMD
4. Experiment
4.1. Open Data Sets from Case Western Reserve University
4.1.1. Experimental Apparatus and Open Data Sets
4.1.2. Feature Extraction Based on CEEMDAN and SSA-VMD
4.1.3. Comparison with Other Methods
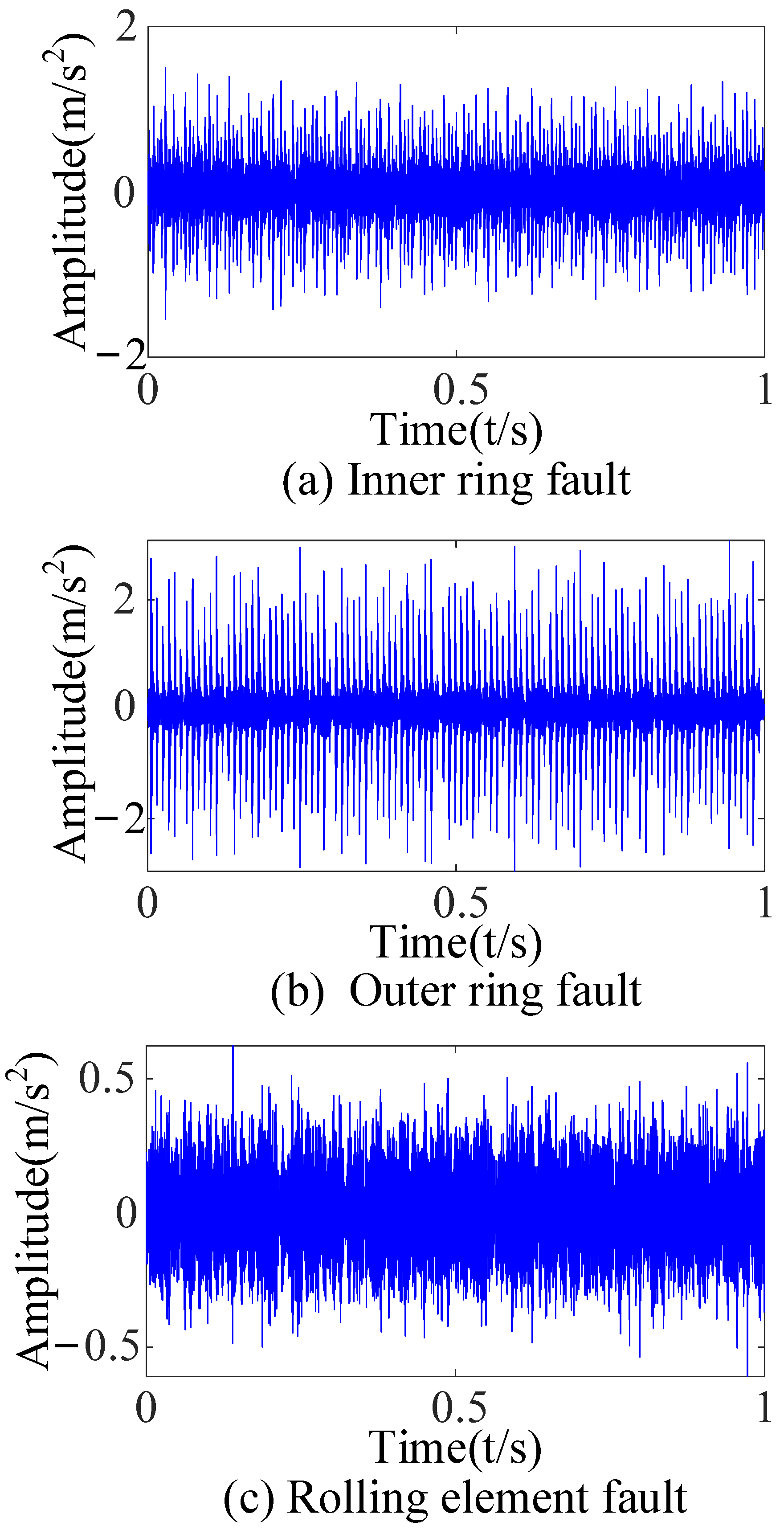
4.2. Data from Rolling Bearing Test Bed
4.2.1. Experimental Apparatus and Data Acquisition
4.2.2. Feature Extraction Based on CEEMDAN and SSA-VMD
4.2.3. Compared with Other Feature Extraction Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, C.; Li, H.; Zhao, X. Weak characteristic determination for blade crack of centrifugal compressors based on underdetermined blind source separation. Measurement 2018, 128, 545–557. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Liu, Z.; He, Z. An adaptive stochastic resonance method based on grey wolf optimizer algorithm and its application to machinery fault diagnosis. ISA Trans. 2017, 71, 206–214. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Qin-Xiao, C.; Cheng, Z.; Tao, X. Research on gearbox compound fault diagnosis method and system development based on entire gearbox health maintenance. Adv. Mech. Eng. 2023, 15, 16878132231197362. [Google Scholar] [CrossRef]
- Hailun, W.; Martinez, A. Application of modified culture Kalman filter in bearing fault diagnosis. Open Phys. 2018, 16, 757–765. [Google Scholar] [CrossRef]
- Wang, G.F.; Tai Yong, W.; Ren, C.Z.; Li, H.W. Application of complex shifted morlet wavelet in vibration monitoring of spindle bearing of crank shaft grinder. Key Eng. Mater. 2003, 259, 697–701. [Google Scholar] [CrossRef]
- Liang, C.; Chen, C.; Liu, Y.; Jia, X. A novel intelligent fault diagnosis method for rolling bearings based on compressed sensing and stacked multi-granularity convolution denoising auto-encoder. IEEE Access 2021, 9, 154777–154787. [Google Scholar] [CrossRef]
- Lin, T.; Chen, G.; Ouyang, W.; Zhang, Q.; Wang, H.; Chen, L. Hyper-spherical distance discrimination: A novel data description method for aero-engine rolling bearing fault detection. Mech. Syst. Signal Process. 2018, 109, 330–351. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Du, Z.; Li, X.; Yan, R. Nonlocal sparse model with adaptive structural clustering for feature extraction of aero-engine bearings. J. Sound. Vib. 2016, 368, 223–248. [Google Scholar] [CrossRef]
- Chen, X.; Qi, X.; Wang, Z.; Cui, C. Fault diagnosis of rolling bearing using marine predators algorithm-based support vector machine and topology learning and out-of-sample embedding. Measurement 2021, 176, 109116. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Chen, G.; Ding, J. Modified multiscale weighted permutation entropy and optimized support vector machine method for rolling bearing fault diagnosis with complex signals. ISA Trans. 2021, 114, 470–484. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.; Hu, B. Dictionary Learning via a Mixed Noise Model for Sparse Representation Classification of Rolling Bearings. IEEE Access 2020, 8, 213416–213425. [Google Scholar] [CrossRef]
- Jiang, Y.; Xie, J. VMD–RP–CSRN Based Fault Diagnosis Method for Rolling Bearings. Electronics 2022, 11, 4046. [Google Scholar] [CrossRef]
- Jiang, Q.; Chang, F.; Sheng, B. Bearing fault classification based on convolutional neural network in noise environment. IEEE Access 2019, 7, 69795–69807. [Google Scholar] [CrossRef]
- Li, W.; Qiu, M.; Zhu, Z.; Wu, B.; Zhou, G. Bearing fault diagnosis based on spectrum images of vibration signals. Meas. Sci. Technol. 2016, 27, 035005. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Zhou, X.; Jing, L. A deep learning-based method for machinery health monitoring with big data. J. Mech. Eng. 2015, 51, 49–56. [Google Scholar] [CrossRef]
- Miao, Y.; Shi, H.; Li, C.; Hua, J.; Lin, J. Period-refined CYCBD using time synchronous averaging for the feature extraction of bearing fault under heavy noise. Struct. Health Monit. 2023, 14759217231181514. [Google Scholar] [CrossRef]
- Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Pineda-Sanchez, M. Short-frequency Fourier transform for fault diagnosis of induction machines working in transient regime. IEEE Trans. Instrum. Meas. 2017, 66, 432–440. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, H.; Li, H. Multi-Mode Data Generation and Fault Diagnosis of Bearings Based on STFT-SACGAN. Electronics 2023, 12, 1910. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Hassan, M.A.M.; Albalawi, F.; Ghoneim, S.S.M.; Ali, Z.M.; Dardeer, M. Diagnostic modelling for induction motor faults via ANFIS algorithm and DWT-based feature extraction. Appl. Sci. 2021, 11, 9115. [Google Scholar] [CrossRef]
- Gu, K.; Zhang, Y.; Liu, X.; Li, H.; Ren, M. DWT-LSTM-based fault diagnosis of rolling bearings with multi-sensors. Electronics 2021, 10, 2076. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, X.; Zhou, Y. Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement. Machines 2023, 11, 475. [Google Scholar] [CrossRef]
- Chen, H.; Li, S.; Li, M. Multi-Channel High-Dimensional Data Analysis with PARAFAC-GA-BP for Nonstationary Mechanical Fault Diagnosis. Int. J. Turbomach. Propuls. Power 2022, 7, 19. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Du, W. Research on Fault Diagnosis of Gearbox with Improved Variational Mode Decomposition. Sensors 2018, 18, 3510. [Google Scholar] [CrossRef]
- Jiang, X.; Shen, C.; Shi, J.; Zhu, Z. Initial center frequency-guided VMD for fault diagnosis of rotating machines. J. Sound Vib. 2018, 435, 36–55. [Google Scholar] [CrossRef]
- Jiang, W.; Shan, Y.; Xue, X.; Ma, J.; Chen, Z.; Zhang, N. Fault Diagnosis for Rolling Bearing of Combine Harvester Based on Composite-Scale-Variable Dispersion Entropy and Self-Optimization Variational Mode Decomposition Algorithm. Entropy 2023, 25, 1111. [Google Scholar] [CrossRef]
- Ding, J.; Huang, L.; Xiao, D.; Li, X. GMPSO-VMD algorithm and its application to rolling bearing fault feature extraction. Sensors 2020, 20, 1946. [Google Scholar] [CrossRef]
- Zhou, Y.; He, F.; Qiu, Y. Dynamic strategy based parallel ant colony optimization on GPUs for TSPs. Sci. China Inf. Sci. 2017, 60, 1–3. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Lei, W. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Tan, C.; Yang, L.; Chen, H.; Xin, L. Fault diagnosis method for rolling bearing based on VMD and improved SVM optimized by METLBO. J. Mech. Sci. Technol. 2022, 36, 4979–4991. [Google Scholar] [CrossRef]
- Wei, D.; Jiang, H.; Shao, H.; Li, X. An optimal variational mode decomposition for rolling bearing fault feature extraction. Meas. Sci. Technol. 2019, 30, 055004. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- Kumar, A.; Vashishtha, G.; Gandhi, C.P.; Yuqing, Z. Novel convolutional neural network (NCNN) for the diagnosis of bearing defects in rotary machinery. IEEE Trans. Instrum. Meas. 2021, 70, 3510710. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 7 June 2023).
- Yang, S.; Gu, X.; Liu, Y.; Hao, R.; Li, S. A general multi-objective optimized wavelet filter and its applications in fault diagnosis of wheelset bearings. Mech. Syst. Signal Process. 2020, 145, 106914. [Google Scholar] [CrossRef]

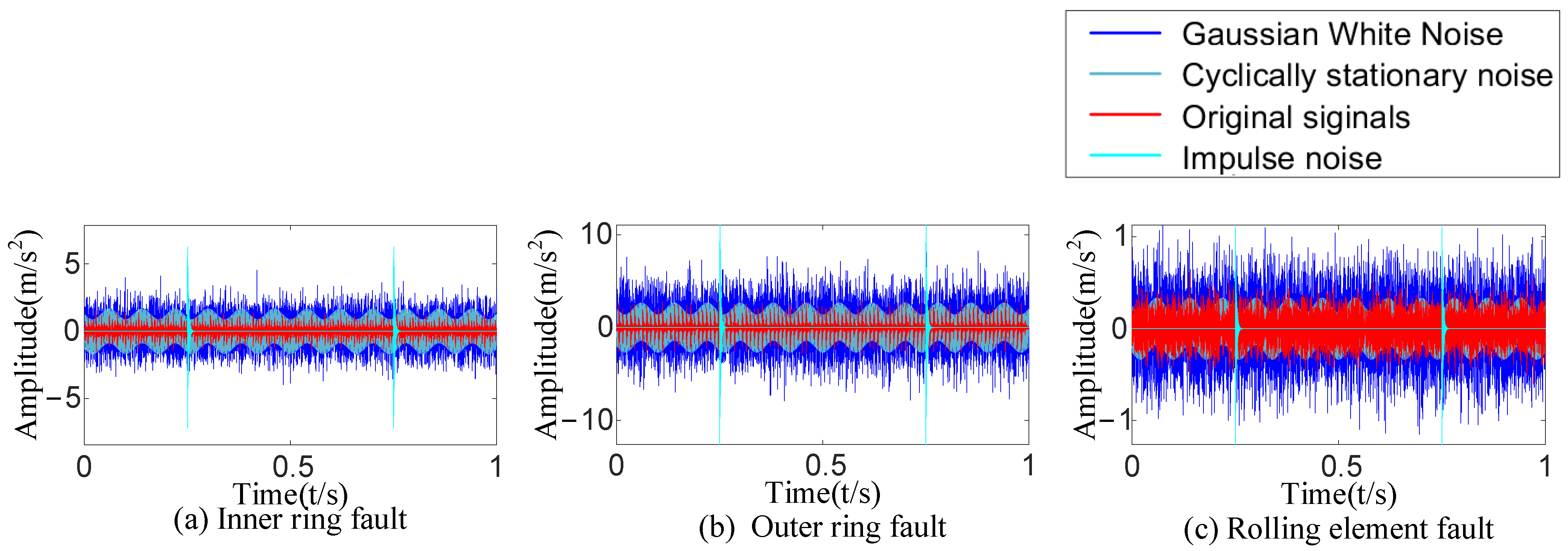
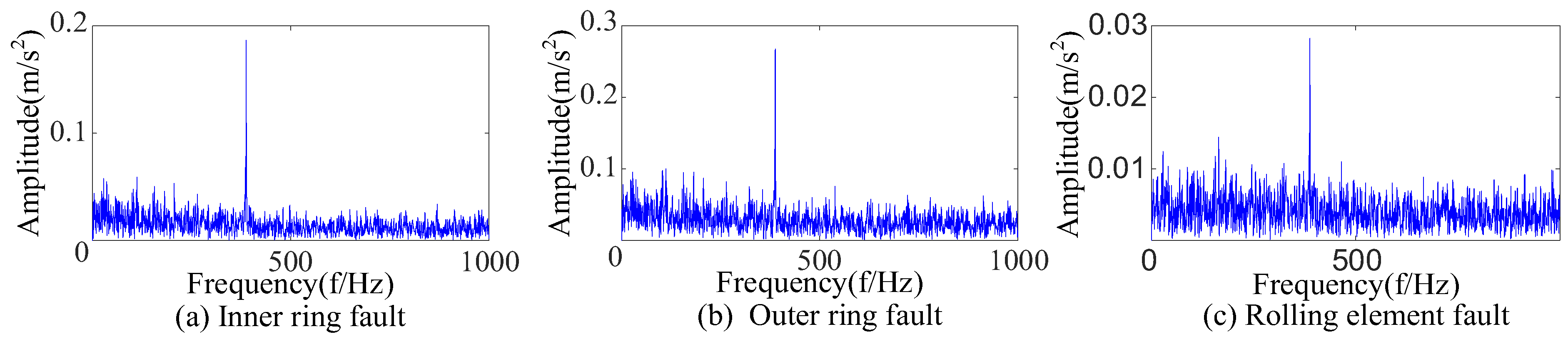
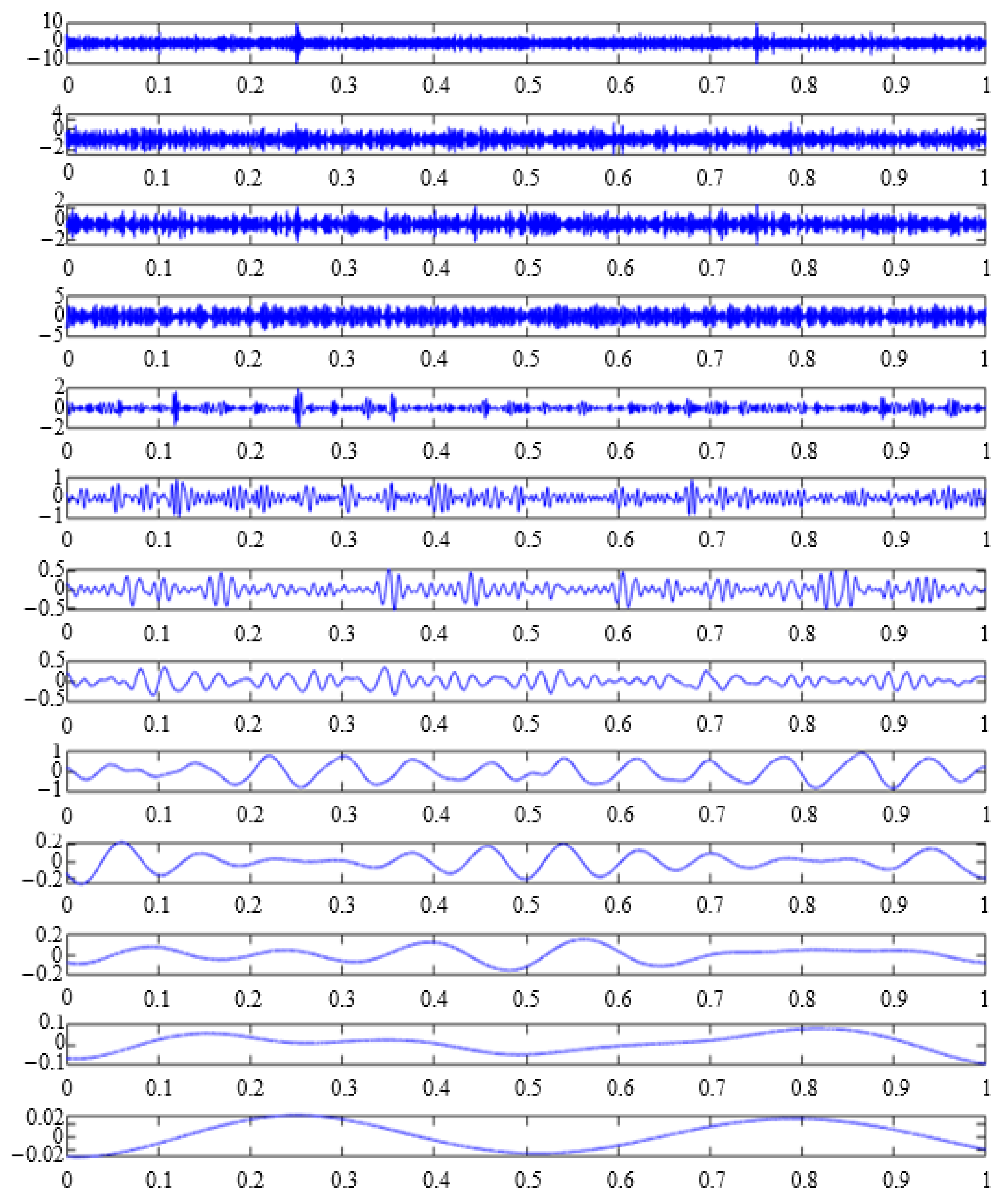

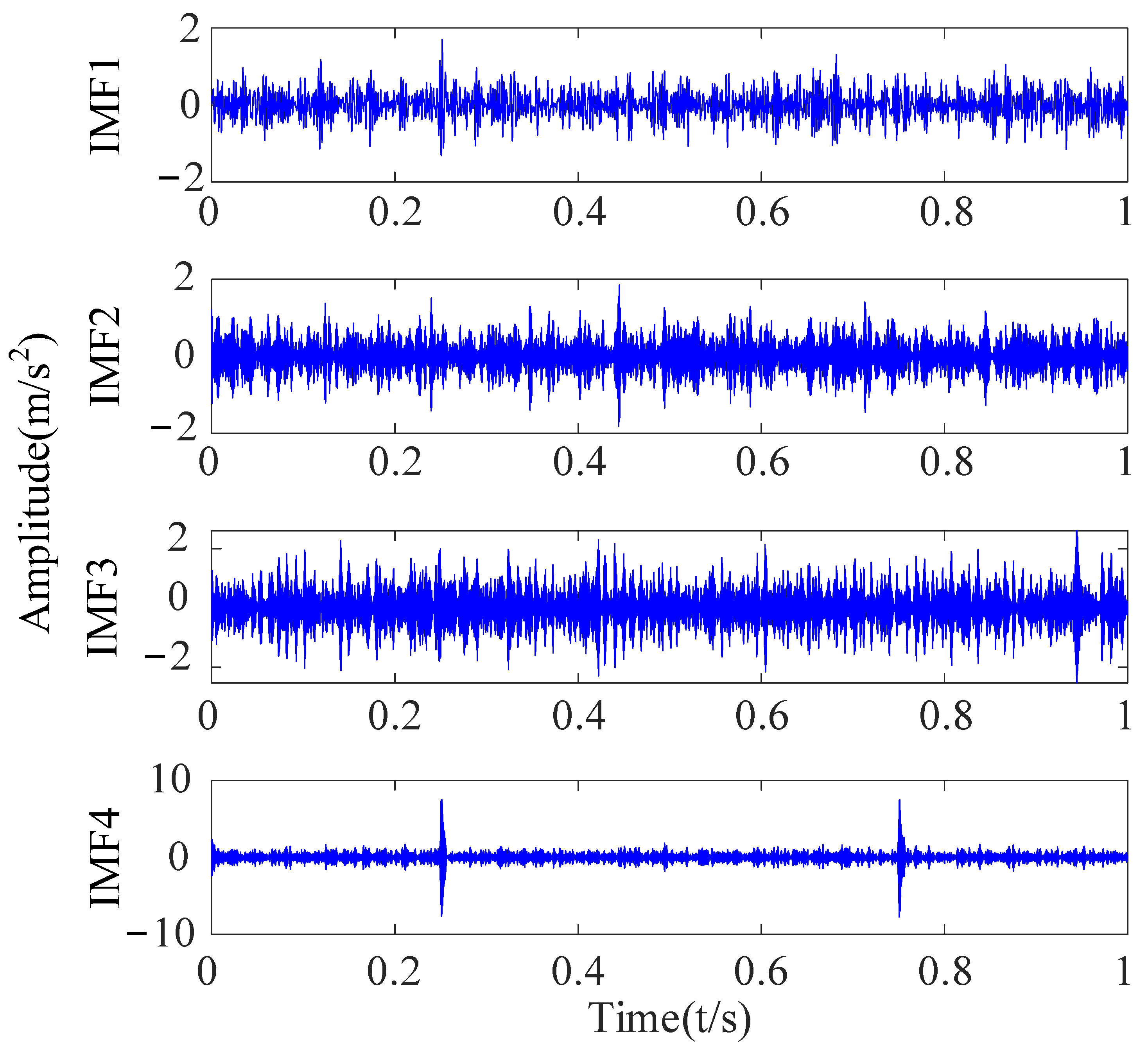
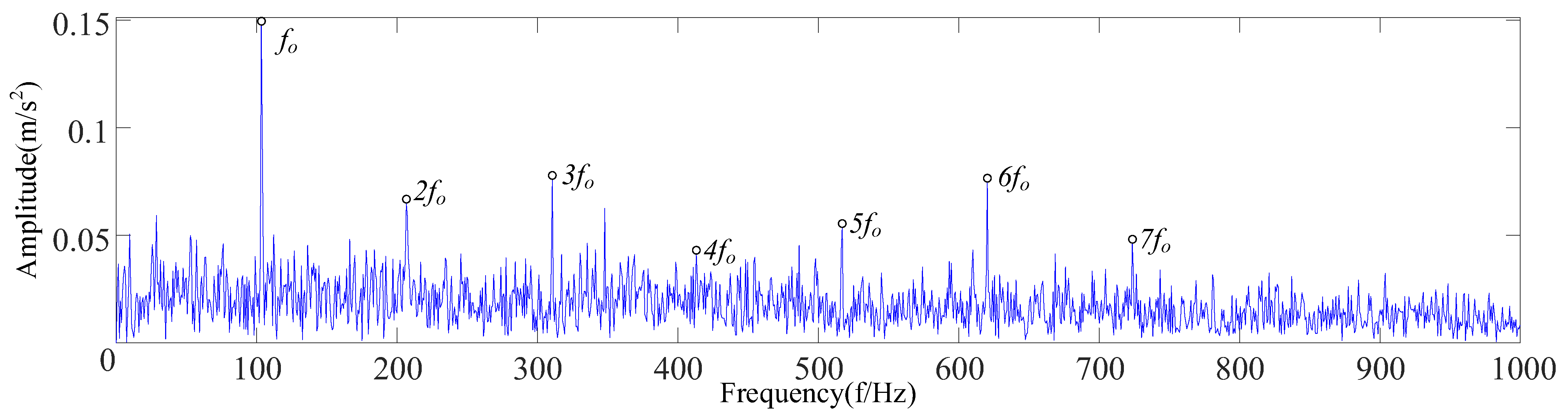
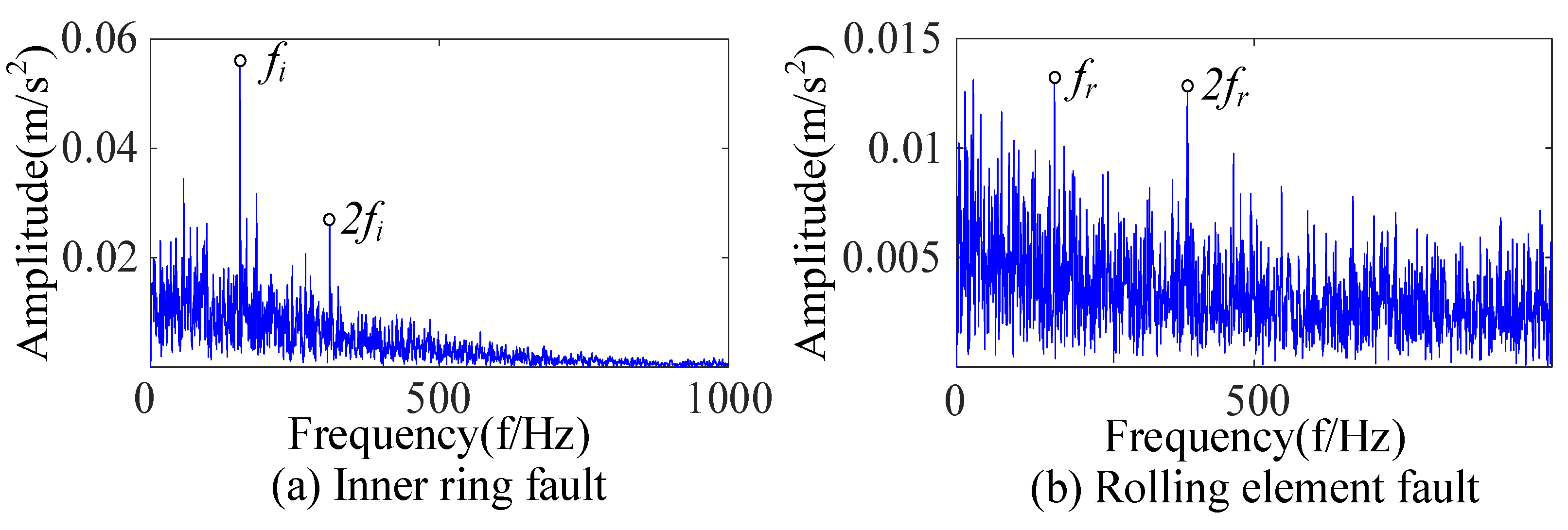
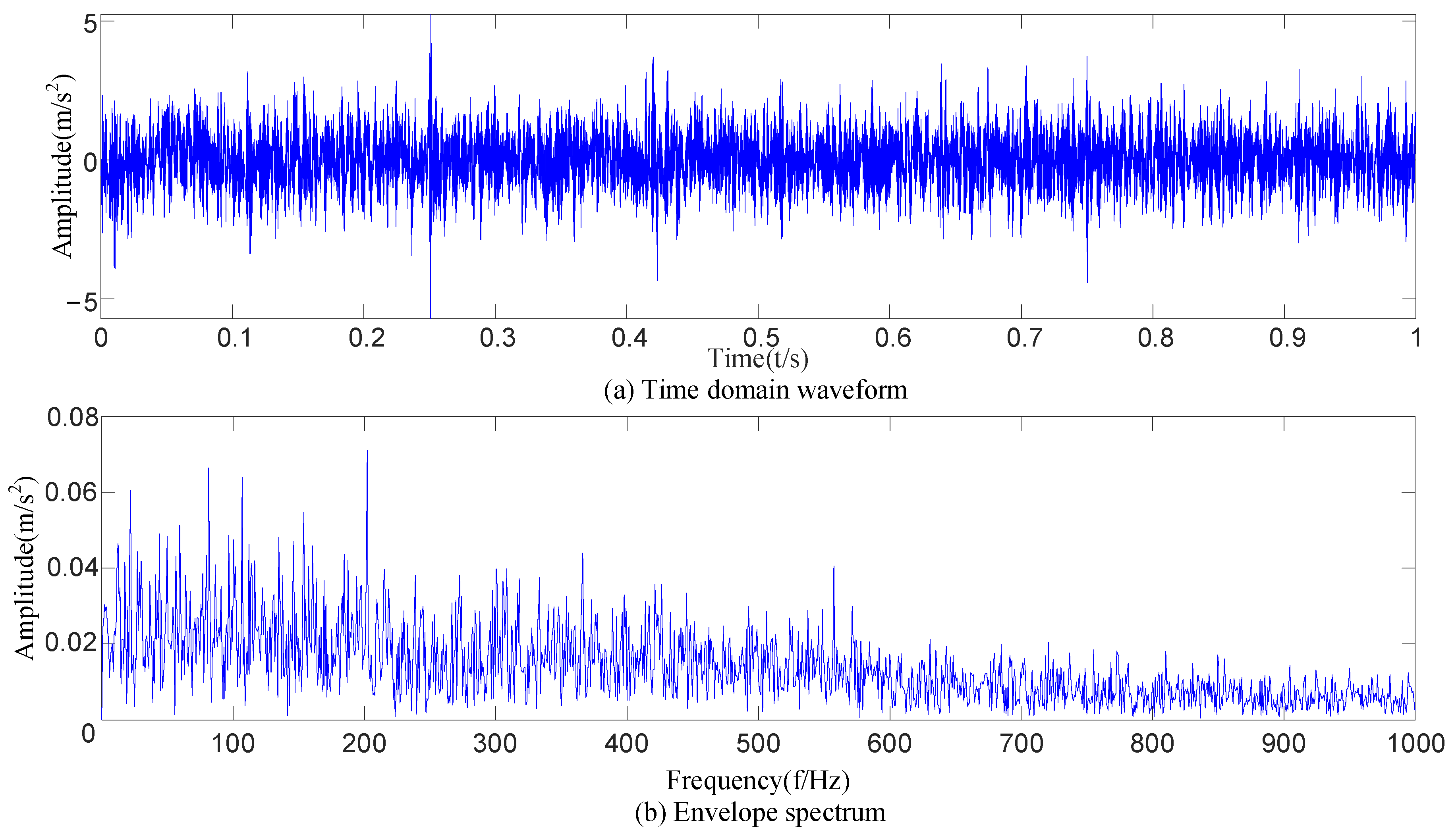
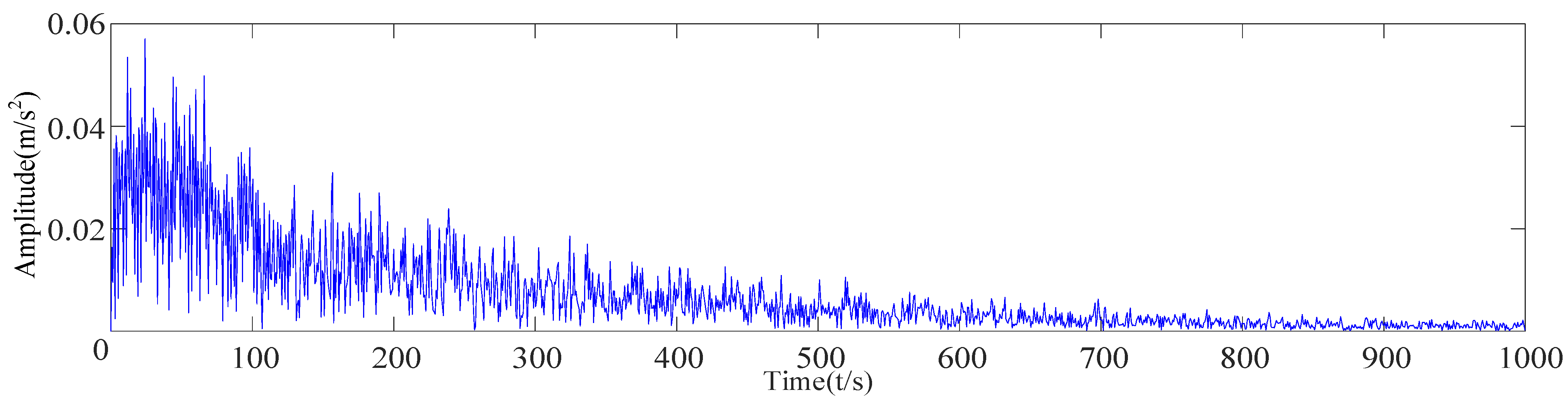
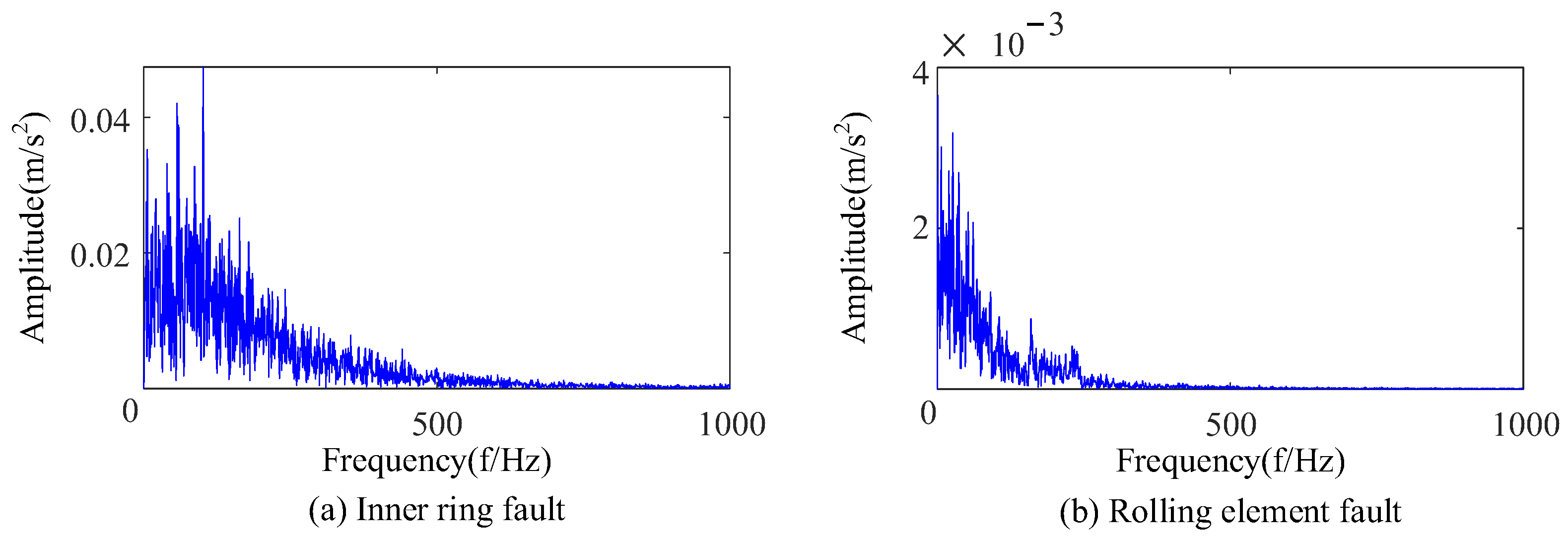
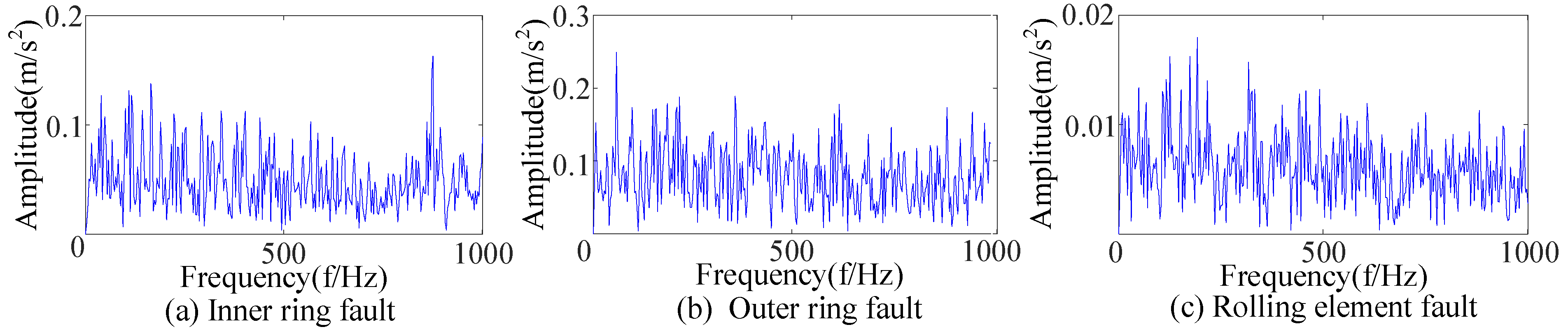


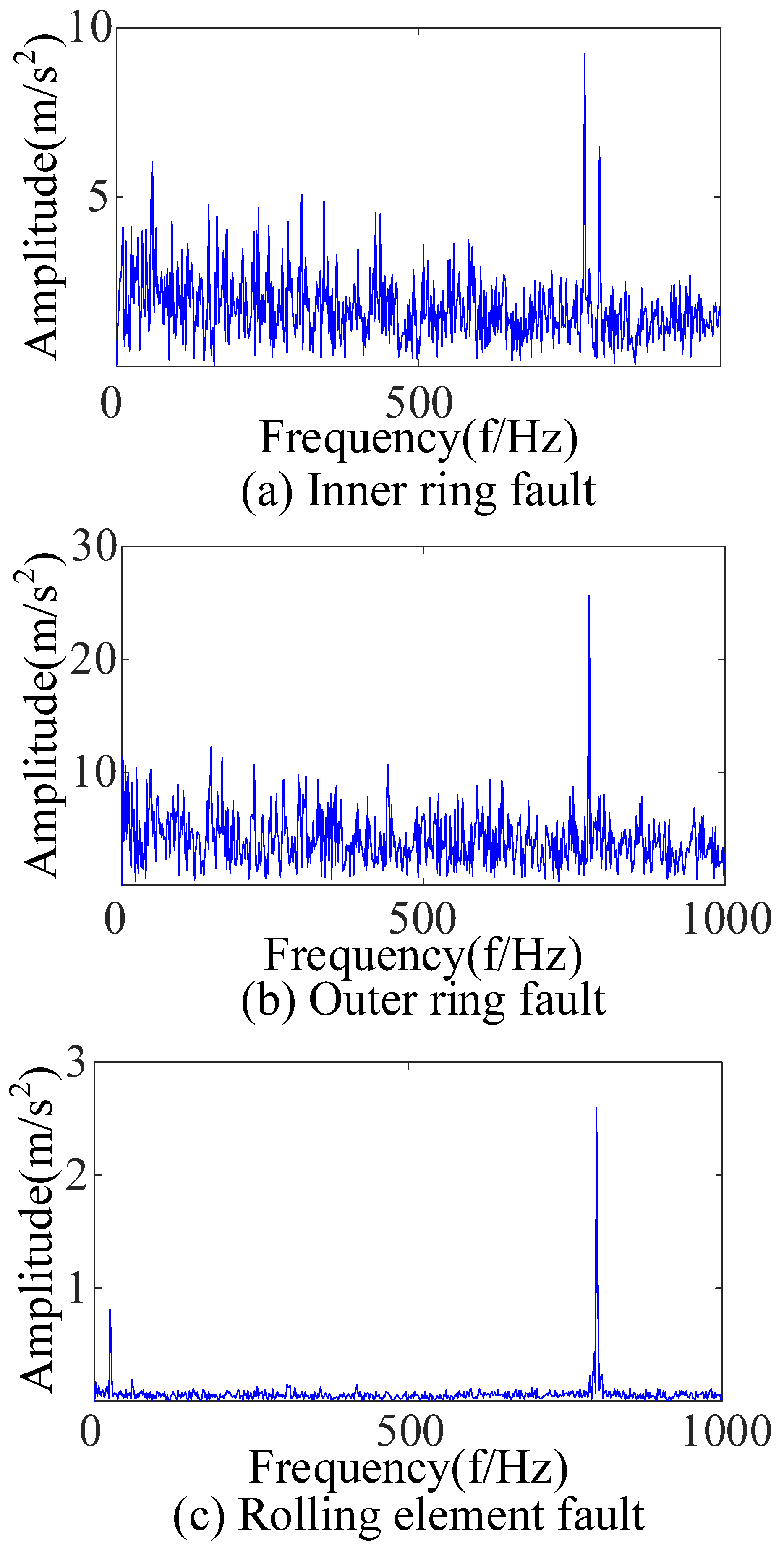

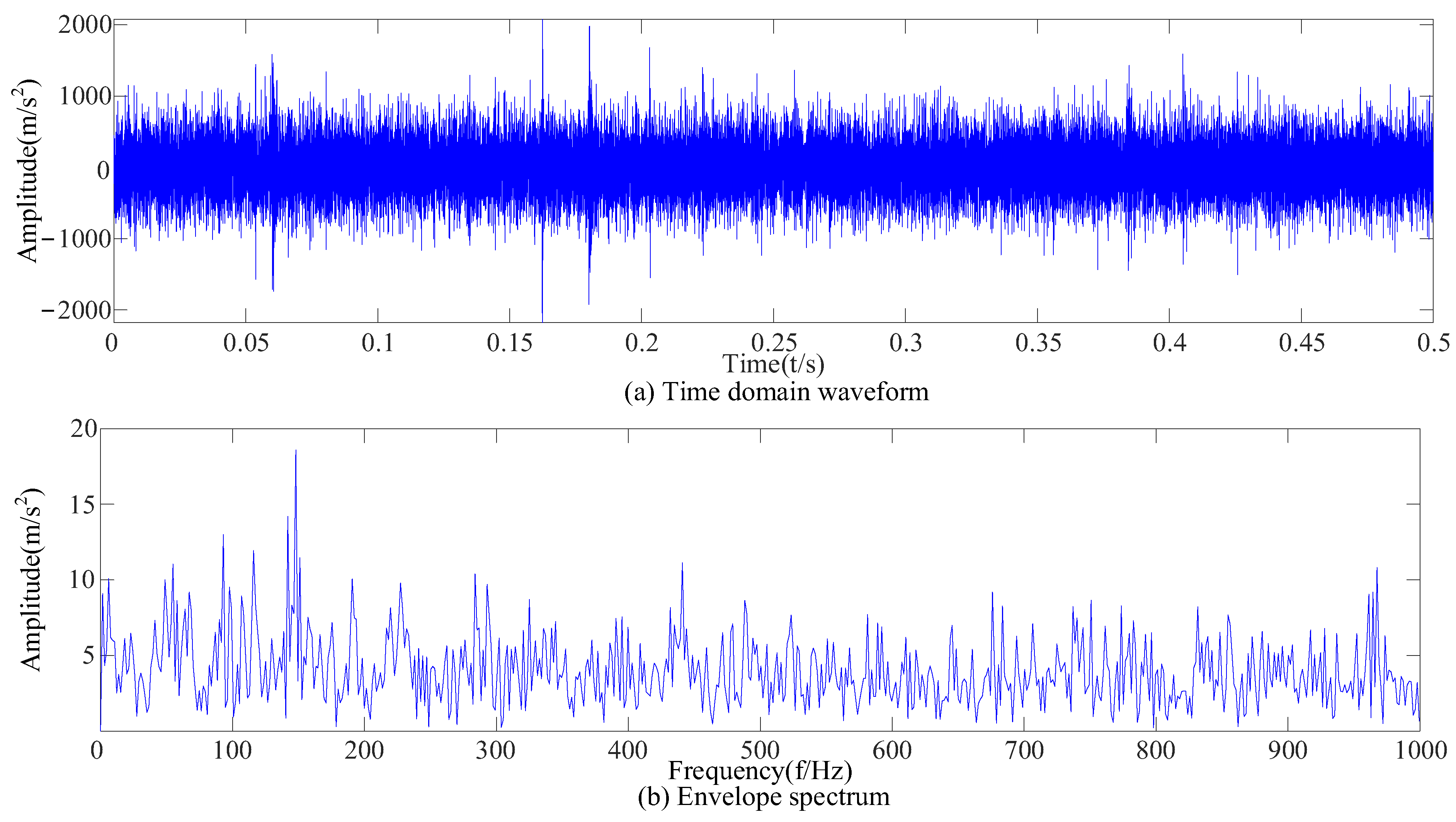
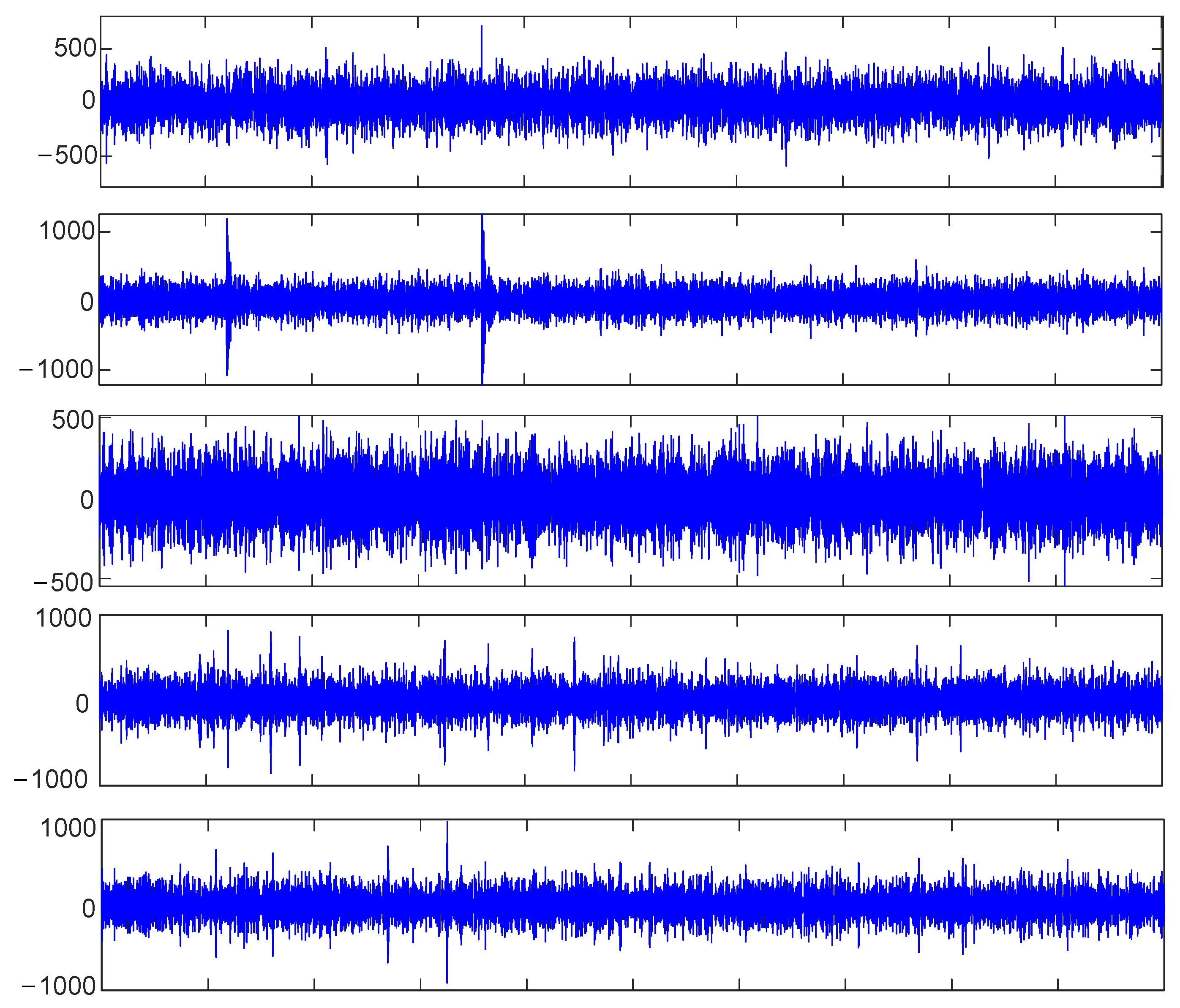



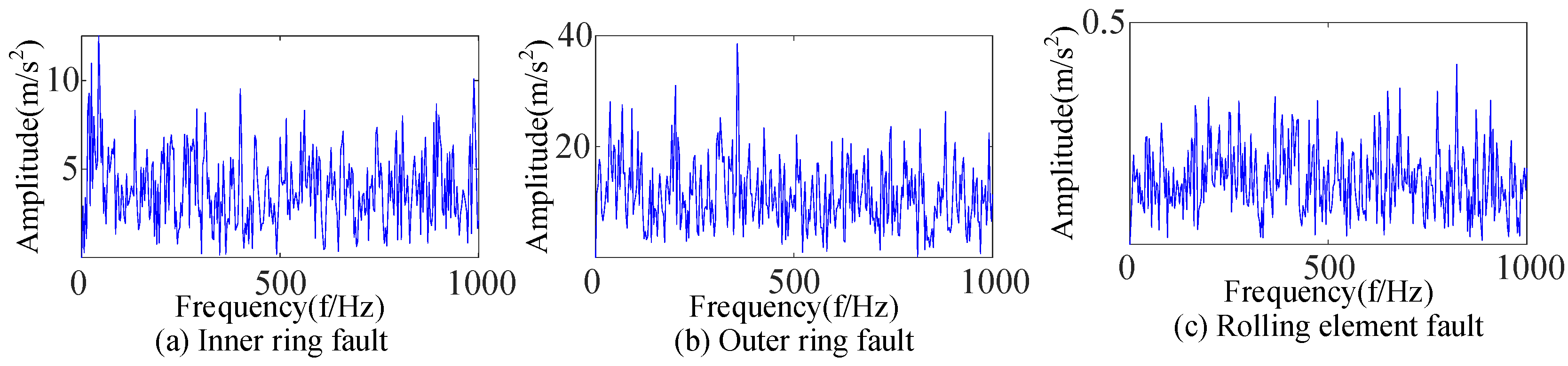
| R1 | r1 | λ | fo | A1 | fr | θ1 | B1 | R | θ2 |
|---|---|---|---|---|---|---|---|---|---|
| 1.5 | 0.12 | 400 | 4500 | 0.2 | 12.5 | π/2 | 0.64 | 16 | π/2 |
| X | IMF1 | IMF2 | IMF3 | IMF4 | MF5 | IMF6 | IMF7 | IMF8 | IMF9 | IMF10 | IMF11 | IMF12 | IMF13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KF | 3.29 | 16.05 | 3.53 | 3.81 | 2.98 | 8.35 | 3.14 | 3.14 | 2.73 | 2.52 | 2.31 | 1.99 | 2.10 | 3.66 |
| IMF1 | IMF2 | IMF3 | IMF4 | |
|---|---|---|---|---|
| KH | 4.46 | 3.44 | 19.42 | 5.04 |
| Inner 1 | Inner 2 | Inner 3 | Out 1 | Out 2 | Out 3 | Roll 1 | Roll 2 | Roll 3 | |
|---|---|---|---|---|---|---|---|---|---|
| Pc | 0.0304 | 0.0296 | 0.0325 | 0.0041 | 0.0256 | 0.0129 | 0.0021 | 0.0025 | 0.0147 |
| Inner 1 | Inner 2 | Inner 3 | Out 1 | Out 2 | Out 3 | Roll 1 | Roll 2 | Roll 3 | |
|---|---|---|---|---|---|---|---|---|---|
| Pc | 0.0350 | 0.0316 | 0.0332 | 0.0307 | 0.0363 | 0.0350 | 0.0181 | 0.0207 | 0.0193 |
| Inner 1 | Inner 2 | Inner 3 | Out 1 | Out 2 | Out 3 | Roll 1 | Roll 2 | Roll 3 | |
|---|---|---|---|---|---|---|---|---|---|
| Pc | 0.5128 | 0.5264 | 0.5083 | 0.4649 | 0.4502 | 0.4613 | 0.7201 | 0.6843 | 0.7014 |
| X’ | IMF1 | IMF2 | IMF3 | IMF4 | MF5 | IMF6 | IMF7 | IMF8 | IMF9 | IMF10 | IMF11 | IMF12 | IMF13 | IMF14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KH | 3.13 | 9.49 | 4.31 | 3.93 | 3.39 | 2.76 | 2.7 | 3.77 | 3 | 3.54 | 2.57 | 5.31 | 2.51 | 1.89 | 2.88 |
| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | |
|---|---|---|---|---|---|
| KF | 2.67 | 2.74 | 3.45 | 2.88 | 5.01 |
| Pc | Inner 1 | Inner 2 | Inner 3 | Out 1 | Out 2 | Out 3 | Roll 1 | Roll 2 | Roll 3 |
|---|---|---|---|---|---|---|---|---|---|
| CEEMDAN-VMD | 0.1993 | 0.1809 | 0.2103 | 0.2425 | 0.2637 | 0.2492 | 0.3821 | 0.3712 | 0.3697 |
| Envelope entropy | 0.0833 | 0.0895 | 0.0927 | 0.0819 | 0.0763 | 0.0771 | 0.0083 | 0.0132 | 0.0096 |
| EEMD-WTD | 0.0125 | 0.0296 | 0.0249 | 0.0317 | 0.0322 | 0.0284 | 0.0181 | 0.0329 | 0.0237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, H.; Xi, T.; Wei, S. Fault Feature Extraction Method for Rolling Bearings Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Variational Mode Decomposition. Sensors 2023, 23, 9441. https://doi.org/10.3390/s23239441
Wang L, Li H, Xi T, Wei S. Fault Feature Extraction Method for Rolling Bearings Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Variational Mode Decomposition. Sensors. 2023; 23(23):9441. https://doi.org/10.3390/s23239441
Chicago/Turabian StyleWang, Lijing, Hongjiang Li, Tao Xi, and Shichun Wei. 2023. "Fault Feature Extraction Method for Rolling Bearings Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Variational Mode Decomposition" Sensors 23, no. 23: 9441. https://doi.org/10.3390/s23239441
APA StyleWang, L., Li, H., Xi, T., & Wei, S. (2023). Fault Feature Extraction Method for Rolling Bearings Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Variational Mode Decomposition. Sensors, 23(23), 9441. https://doi.org/10.3390/s23239441






