Hybrid Control of the DC Microgrid Using Deep Neural Networks and Global Terminal Sliding Mode Control with the Exponential Reaching Law
Abstract
:1. Introduction
- A two-step low-level controller based on DNN and ERL-GTSMC is developed for the wind/PV/battery DC microgrid.
- A TensorFlow open-source Python library is utilized for DNN testing and training. A Pymgrid Python library is used to retrieve PV and load profiles.
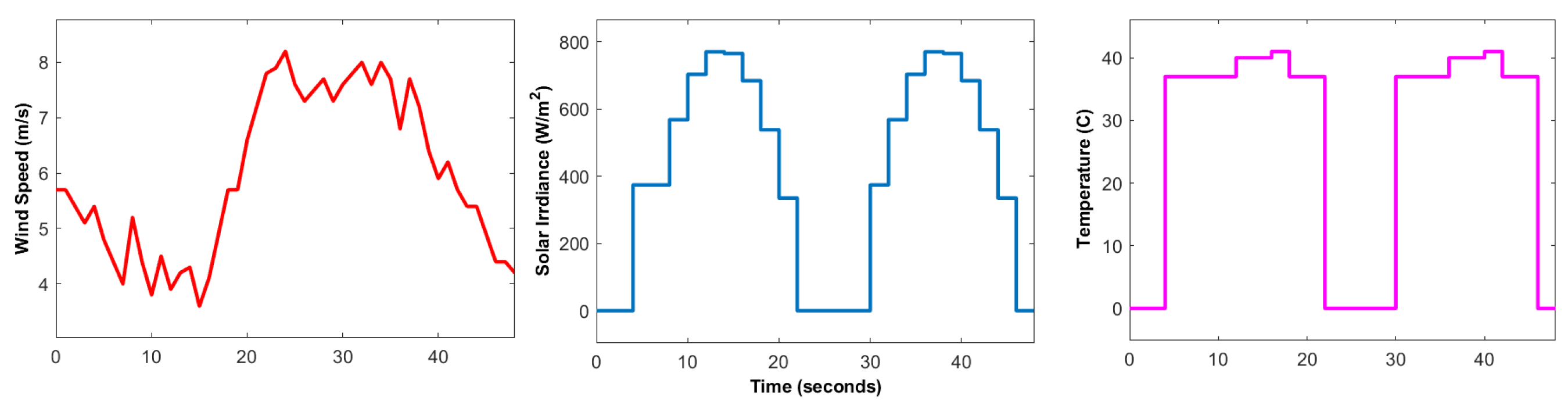
- Real-world weather profiles and residential building loads are used to test the performance of the controllers.
- Using TMS320F2837D microcontrollers (Texas Instruments, Dallas, TX, USA) hardware-in-the-loop experiments are conducted to analyze the behavior of a controller in industrial scenarios.
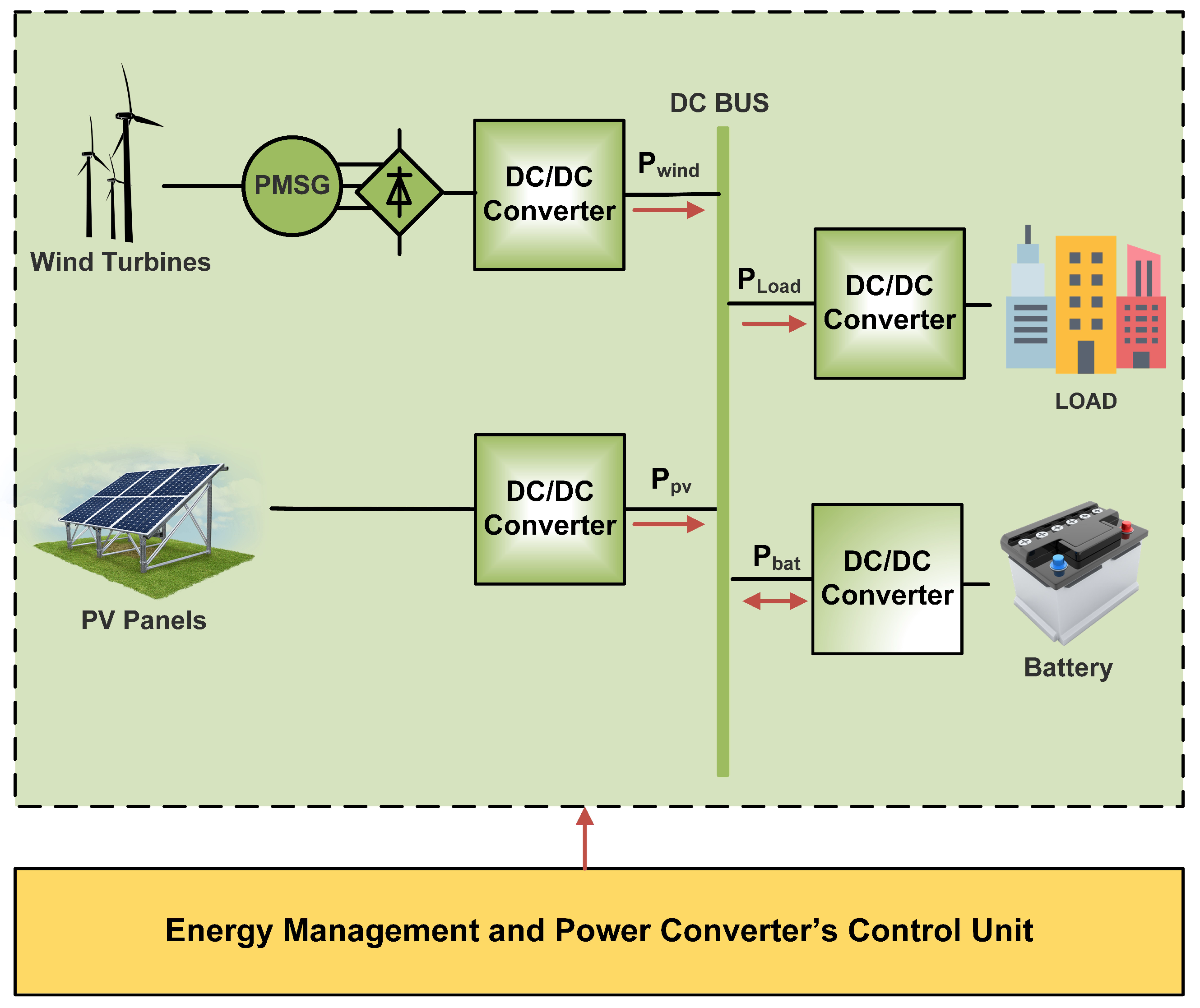
2. System Modeling and DNN Design
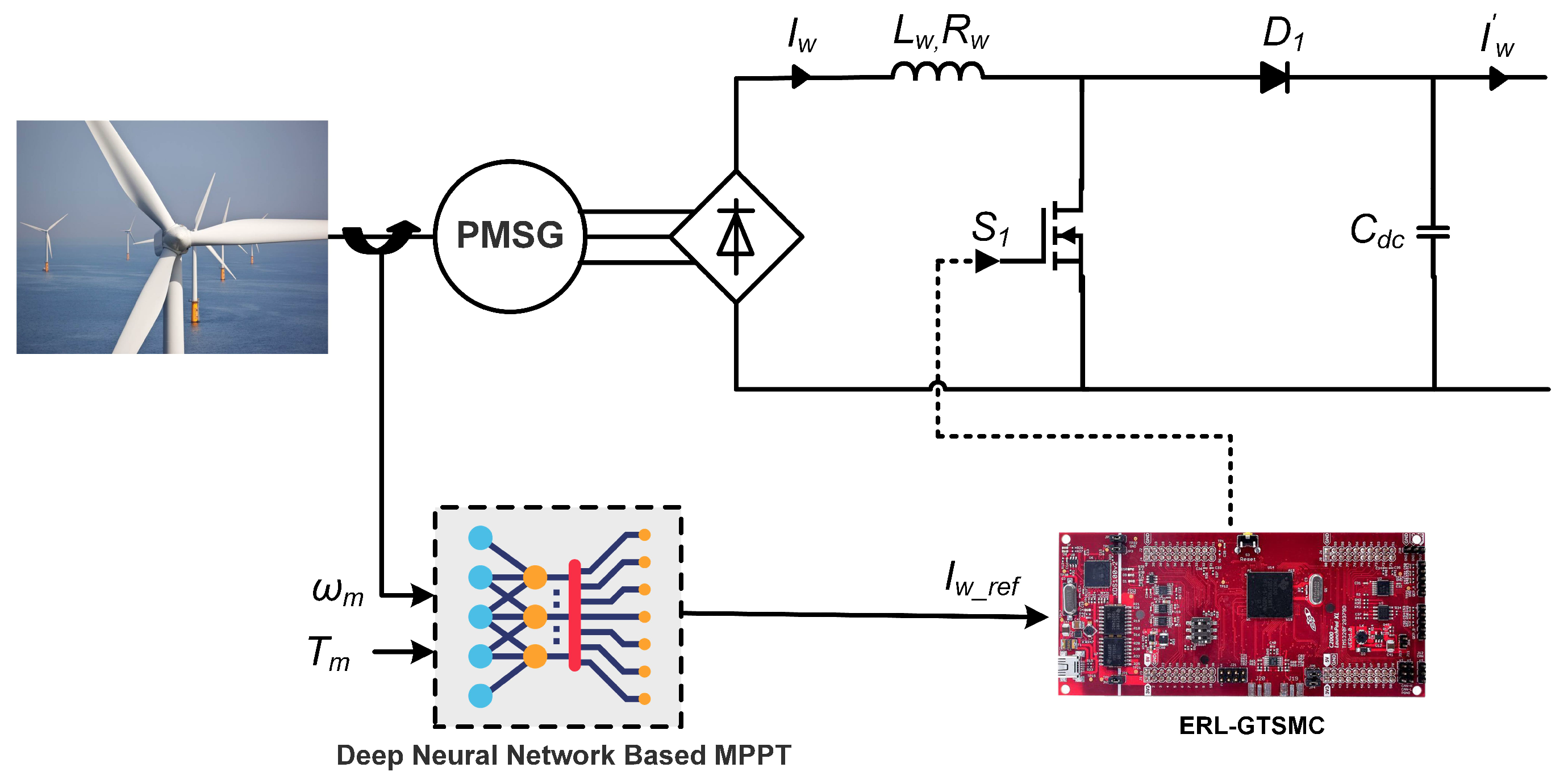
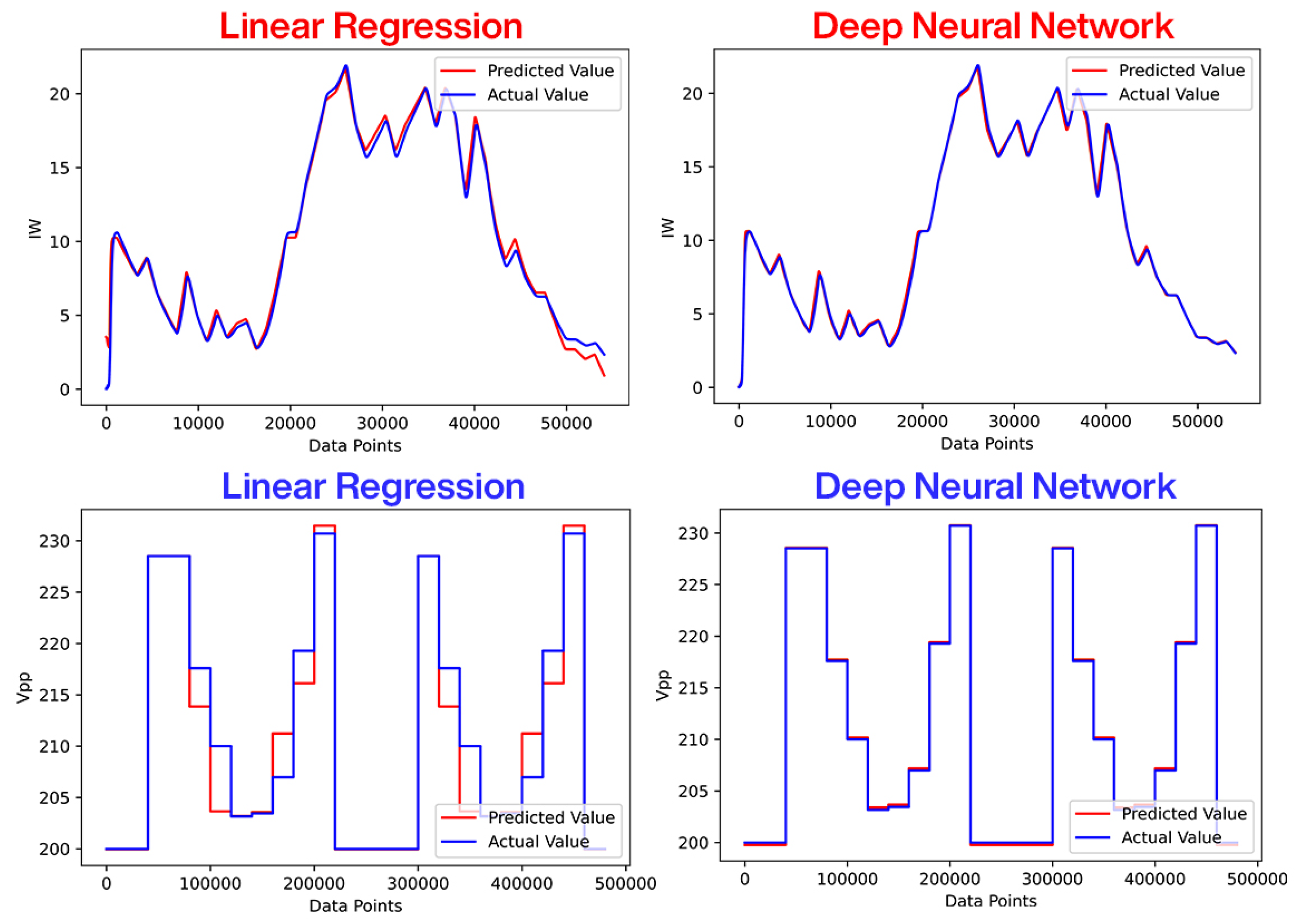
2.1. Modeling of WES and DNN Design
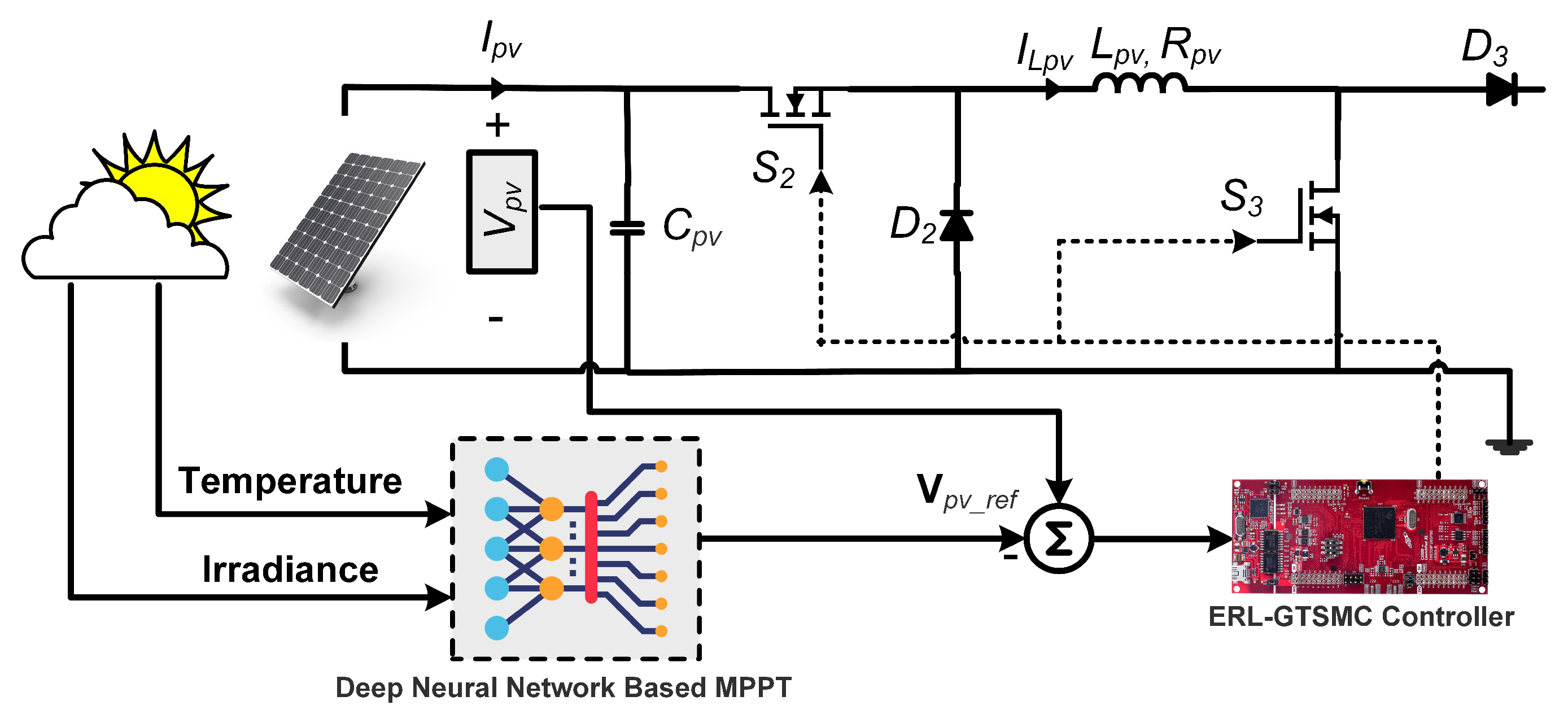
2.2. Modeling of PVS and DNN Design
2.3. Modeling of Battery
2.4. Microgrid Global Modeling
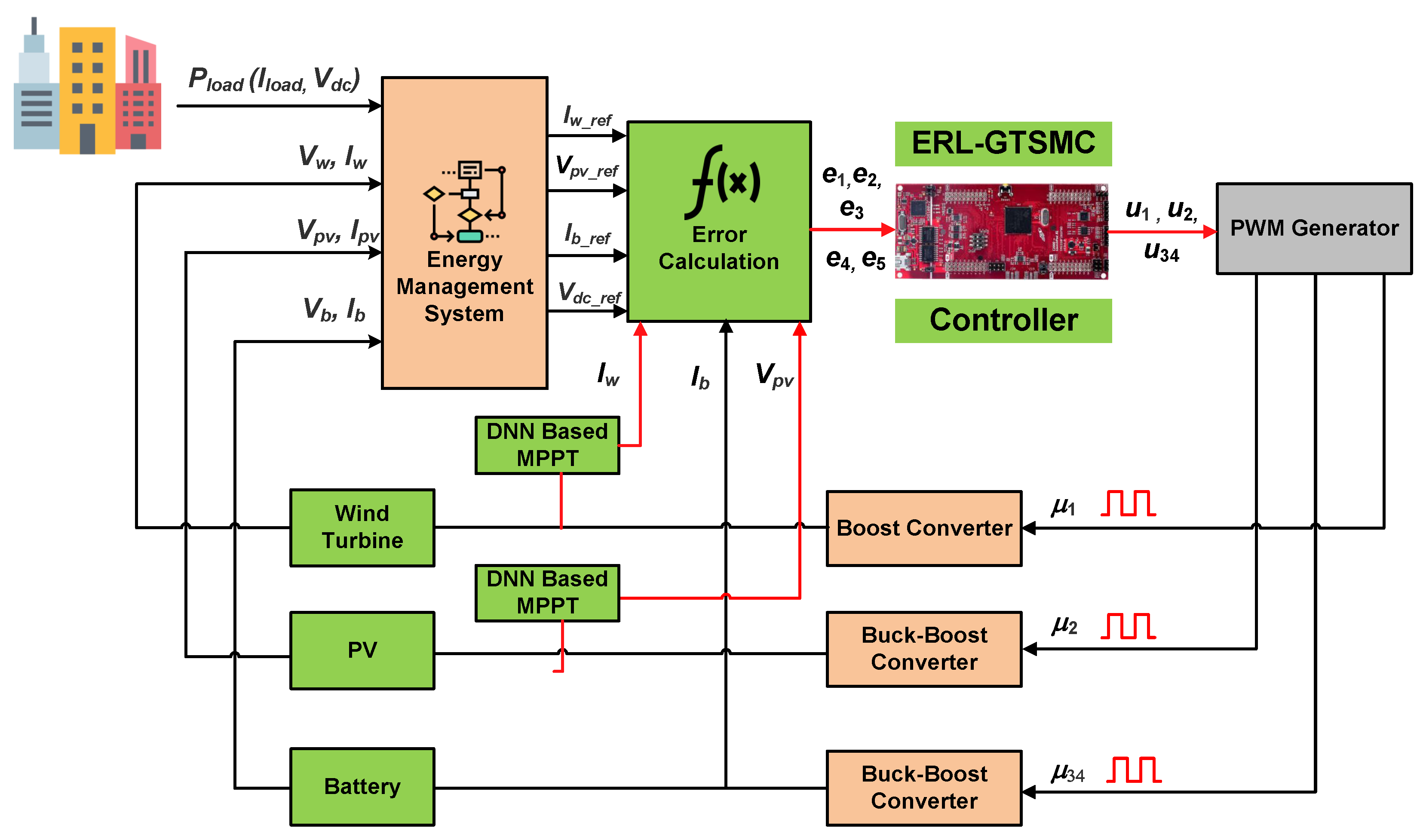
3. Design of ERL-GTSMC (Low-Level)
- MPPT for WES and PVS by tracking current and voltage references provided by DNN
- Tracking of Battery power to satisfy load demand
- Tracking of DC bus voltage under deviating load demand and weather conditions
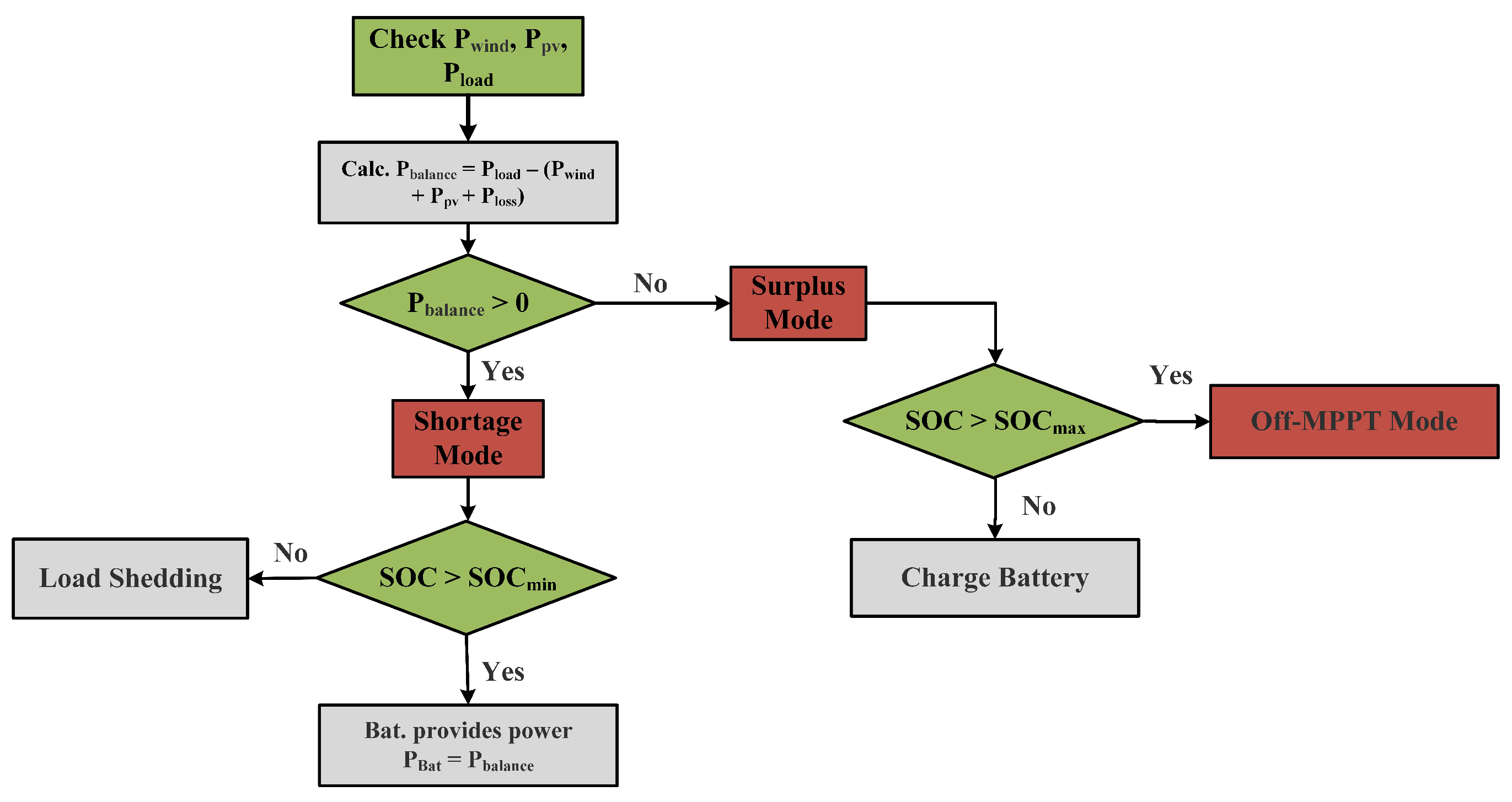
4. Energy Management System (High-Level)
5. Results and Discussion
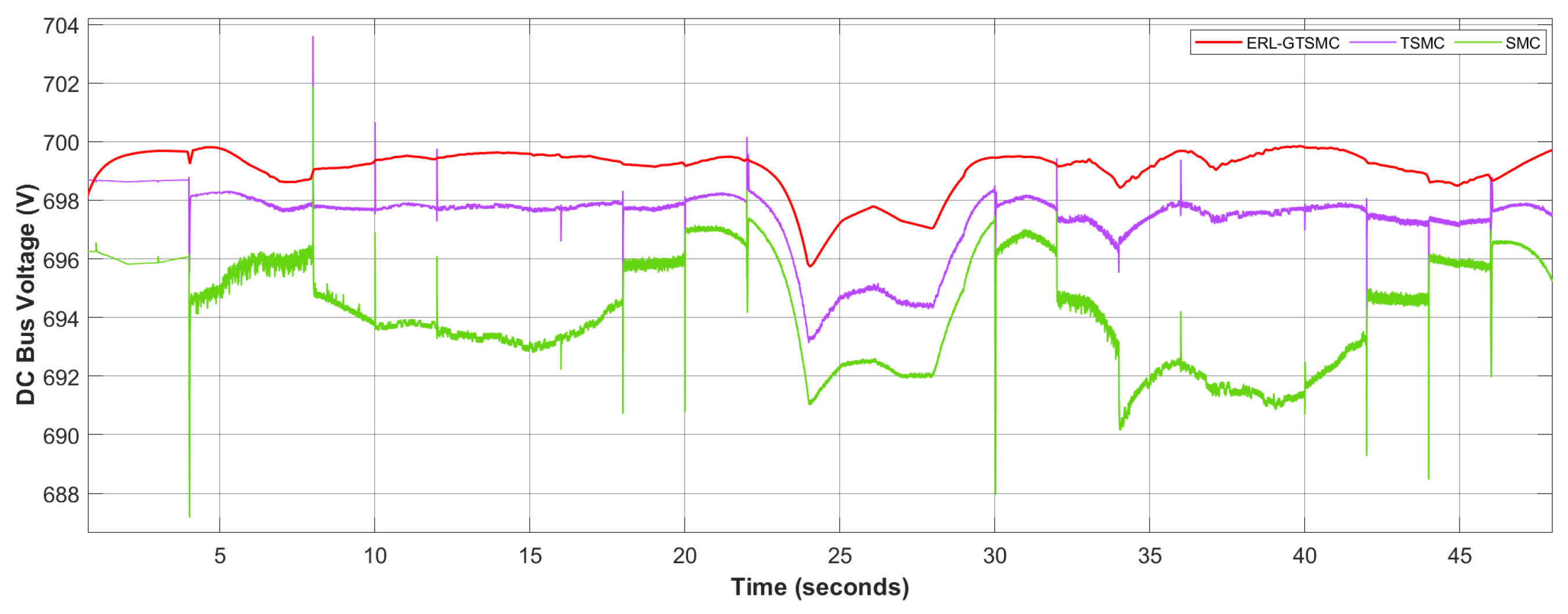
5.1. Comparative Analysis with Traditional Control Methods
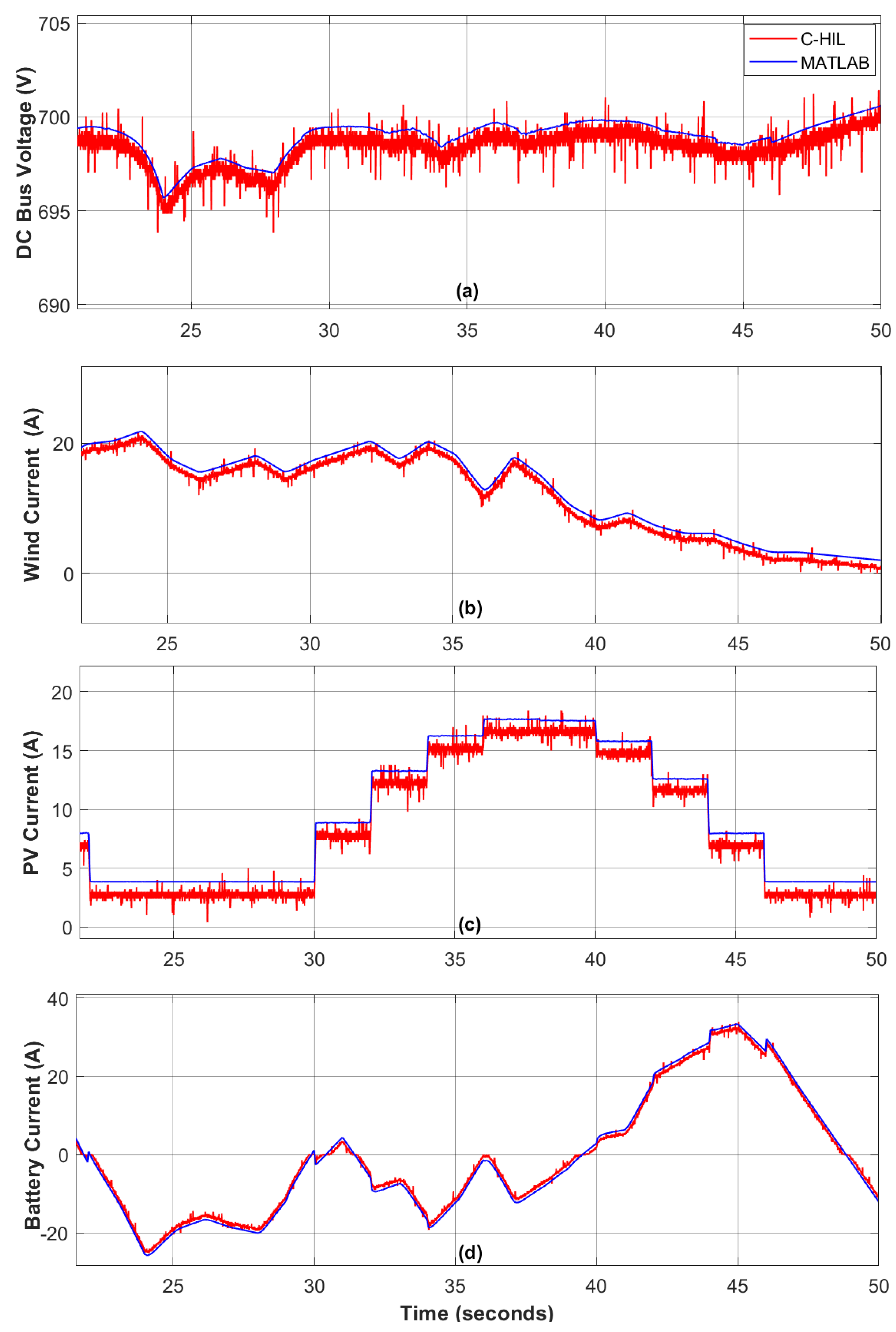
5.2. Experimental Testing Using Controller Hardware-in-the-Loop (C-HIL) Setup
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
| Wind Turbine/PMSG | |
| Density (air) | 1.2 kg/m |
| Wind speed | 5.5 m/s |
| 7 | |
| 0.43 | |
| Nominal RPM | 1000 |
| Line-line Voltage | 400 V |
| Rated Power | 20 kW |
| Battery | |
| Rated Voltage | 230 V |
| Rated Battery Capacity | 18 Ah |
| Batteries connected in series | 3 |
| Photovoltaic System | |
| Rated Voltage | 229 V |
| Rated Current | 14 A |
| Rated power of single module | 2 kW |
| Rated Maximum Power | 3.2 kW |
Appendix A.2
| DC Microgrid Configuration | |
| DC-link Voltage | 700 V |
| Frequency (MOSFETs Switching) | 25 kHz |
| Resistances | 7 m, 20 m, 20 m |
| Inductance | 3.3 mH, 3.8 mH, 3.1 mH |
| Capacitance | 68 F |
| Control Parameters | |
| ERL-GTSMC | , , , , |
| , , , | |
| , , | |
| TSMC | , , , , |
| , , , | |
| SMC | , , |
References
- Zolfaghari, M.; Gharehpetian, G.B.; Shafie-khah, M.; Catalão, J.P. Comprehensive review on the strategies for controlling the interconnection of AC and DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 136, 107742. [Google Scholar] [CrossRef]
- Nair, N.R.; Ebenezer, M. Operation and control of grid connected wind—PV hybrid system. In Proceedings of the 2014 International Conference on Advances in Green Energy (ICAGE), Thiruvananthapuram, India, 17–18 December 2014; Volume 11, pp. 197–203. [Google Scholar]
- Tamalouzt, S.; Benyahia, N.; Rekioua, T.; Rekioua, D.; Abdessemed, R. Performances analysis of WT-DFIG with PV and fuel cell hybrid power sources system associated with hydrogen storage hybrid energy system. Int. J. Hydrogen Energy 2016, 41, 21006–21021. [Google Scholar] [CrossRef]
- Hemeida, A.; El-Ahmar, M.; El-Sayed, A.; Hasanien, H.M.; Alkhalaf, S.; Esmail, M.; Senjyu, T. Optimum design of hybrid wind/PV energy system for remote area. Ain Shams Eng. J. 2020, 11, 11–23. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Wu, Y.; Wang, Q.; Liu, X.; Qi, L.; Lu, X.; Gao, L. How to make better use of intermittent and variable energy? A review of wind and photovoltaic power consumption in China. Renew. Sustain. Energy Rev. 2021, 137, 110626. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.R.I. Grid-connected wind-solar cogeneration using back-to-back voltage-source converters. IEEE Trans. Sustain. Energy 2019, 11, 315–325. [Google Scholar] [CrossRef]
- Akhbari, A.; Rahimi, M.; Khooban, M.H. Efficient and seamless power management of hybrid generation system based-on DFIG wind sources and microturbine in DC microgrid. Sustain. Energy Grids Netw. 2020, 23, 100367. [Google Scholar] [CrossRef]
- Chaurasia, G.S.; Singh, A.K.; Agrawal, S.; Sharma, N. A meta-heuristic firefly algorithm based smart control strategy and analysis of a grid connected hybrid photovoltaic/wind distributed generation system. Sol. Energy 2017, 150, 265–274. [Google Scholar] [CrossRef]
- Puchalapalli, S.; Tiwari, S.K.; Singh, B.; Goel, P.K. A Microgrid Based on Wind-Driven DFIG, DG, and Solar PV Array for Optimal Fuel Consumption. IEEE Trans. Ind. Appl. 2020, 56, 4689–4699. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chang, H.C.; Huang, C.Y. Design and implementation of the battery energy storage system in DC Micro-grid systems. Energies 2018, 11, 1566. [Google Scholar] [CrossRef]
- Kotra, S.; Mishra, M.K. Design and stability analysis of DC microgrid with hybrid energy storage system. IEEE Trans. Sustain. Energy 2019, 10, 1603–1612. [Google Scholar] [CrossRef]
- Kumar, K.; Bae, S. Dynamic power management based on model predictive control for hybrid-energy-storage-based grid-connected microgrids. Int. J. Electr. Power Energy Syst. 2022, 143, 108384. [Google Scholar] [CrossRef]
- Kumar, J.; Agarwal, A.; Agarwal, V. A review on overall control of DC microgrids. J. Energy Storage 2019, 21, 113–138. [Google Scholar] [CrossRef]
- Sinha, S.; Bajpai, P. Power management of hybrid energy storage system in a standalone DC microgrid. J. Energy Storage 2020, 30, 101523. [Google Scholar] [CrossRef]
- Naderipour, A.; Saboori, H.; Mehrjerdi, H.; Jadid, S.; Abdul-Malek, Z. Sustainable and reliable hybrid AC/DC microgrid planning considering technology choice of equipment. Sustain. Energy Grids Netw. 2020, 23, 100386. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N. Control techniques in AC, DC, and hybrid AC–DC microgrid: A review. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 738–759. [Google Scholar] [CrossRef]
- Armghan, H.; Yang, M.; Ali, N.; Armghan, A.; Alanazi, A. Quick reaching law based global terminal sliding mode control for wind/hydrogen/battery DC microgrid. Appl. Energy 2022, 316, 119050. [Google Scholar] [CrossRef]
- Iovine, A.; Siad, S.B.; Damm, G.; De Santis, E.; Di Benedetto, M.D. Nonlinear control of a dc microgrid for the integration of photovoltaic panels. IEEE Trans. Autom. Sci. Eng. 2017, 14, 524–535. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Xu, Y.; Guerrero, J.M. A coordinated control of hybrid ac/dc microgrids with PV-wind-battery under variable generation and load conditions. Int. J. Electr. Power Energy Syst. 2019, 104, 583–592. [Google Scholar] [CrossRef]
- Han, Y.; Chen, W.; Li, Q.; Yang, H.; Zare, F.; Zheng, Y. Two-level energy management strategy for PV-Fuel cell-battery-based DC microgrid. Int. J. Hydrogen Energy 2019, 44, 19395–19404. [Google Scholar] [CrossRef]
- Batiyah, S.; Sharma, R.; Abdelwahed, S.; Zohrabi, N. An MPC-based power management of standalone DC microgrid with energy storage. Int. J. Electr. Power Energy Syst. 2020, 120, 105949. [Google Scholar] [CrossRef]
- Nguyen, D.L.; Lee, H.H. Fuzzy PID controller for accurate power sharing in DC microgrid. In Proceedings of the International Conference on Intelligent Computing, Nanchang, China, 3–6 August 2019; Springer: Cham, Switzerland, 2019; Volume 9, pp. 71–80. [Google Scholar]
- Shotorbani, A.M.; Ghassem-Zadeh, S.; Mohammadi-Ivatloo, B.; Hosseini, S.H. A distributed secondary scheme with terminal sliding mode controller for energy storages in an islanded microgrid. Int. J. Electr. Power Energy Syst. 2017, 93, 352–364. [Google Scholar] [CrossRef]
- Roy, T.K.; Pramanik, M.A.H.; Ghosh, S.K. Design of an integral terminal-based sliding mode controller for PV and BESS-based DC microgrids. Energy Nexus 2022, 7, 100130. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Roy, T.K.; Saha, S.; Haque, M.E.; Pota, H.R. Robust nonlinear adaptive feedback linearizing decentralized controller design for islanded DC microgrids. IEEE Trans. Ind. Appl. 2019, 55, 5343–5352. [Google Scholar] [CrossRef]
- Mohammed, A.M.; Alalwan, S.N.H.; Taşcıkaraoğlu, A.; Catalão, J.P. Sliding mode-based control of an electric vehicle fast charging station in a DC microgrid. Sustain. Energy Grids Netw. 2022, 32, 100820. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Bhaskar, M.S.; Blaabjerg, F.; Holm-Nielsen, J.B.; Azam, F.; Sharma, A.K. A hybrid photovoltaic-fuel cell-based single-stage grid integration with Lyapunov control scheme. IEEE Syst. J. 2019, 14, 3334–3342. [Google Scholar] [CrossRef]
- Armghan, H.; Yang, M.; Wang, M.; Ali, N.; Armghan, A. Nonlinear integral backstepping based control of a DC microgrid with renewable generation and energy storage systems. Int. J. Electr. Power Energy Syst. 2020, 117, 105613. [Google Scholar] [CrossRef]
- Haque, T.; Roy, T.K.; Faria, F.; Khatun, M.M.; Sarkar, T.; Hore, A.K. Power flow control in dc microgrids using an integral sliding mode control approach. In Proceedings of the 2021 International Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), Rajshahi, Bangladesh, 8–9 July 2021; pp. 1–5. [Google Scholar]
- Jeyaraj, P.R.; Asokan, S.P.; Karthiresan, A.C. Optimum power flow in dc microgrid employing bayesian regularized deep neural network. Electr. Power Syst. Res. 2022, 205, 107730. [Google Scholar] [CrossRef]
- Napole, C.; Derbeli, M.; Barambones, O. A global integral terminal sliding mode control based on a novel reaching law for a proton exchange membrane fuel cell system. Appl. Energy 2021, 301, 117473. [Google Scholar] [CrossRef]
- Rahimi, M. Modeling, control and stability analysis of grid connected PMSG based wind turbine assisted with diode rectifier and boost converter. Int. J. Electr. Power Energy Syst. 2017, 93, 84–96. [Google Scholar] [CrossRef]
- Singaravel, M.R.; Daniel, S.A. MPPT with single DC–DC converter and inverter for grid-connected hybrid wind-driven PMSG–PV system. IEEE Trans. Ind. Electron. 2015, 62, 4849–4857. [Google Scholar] [CrossRef]
- Naghmash; Armghan, H.; Ahmad, I.; Armghan, A.; Khan, S.; Arsalan, M. Backstepping based non-linear control for maximum power point tracking in photovoltaic system. Sol. Energy 2018, 159, 134–141. [Google Scholar] [CrossRef]
- Bendary, A.F.; Ismail, M.M. Battery charge management for hybrid PV/wind/fuel cell with storage battery. Energy Procedia 2019, 162, 107–116. [Google Scholar] [CrossRef]








| Settling Time (s) | Chattering | Percent Overshoot (%) | Steady State Error (SSE) (%) | |
|---|---|---|---|---|
| SMC | 0.0317 | High | 1.82 | 0.971 |
| TSMC | 0.0445 | Mild | 0.714 | 0.314 |
| ERL-GTSMC | 0.05816 | Low | 0.00 | 0.0571 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharaf, M.A.; Armghan, H.; Ali, N.; Yousef, A.; Abdalla, Y.S.; Boudabbous, A.R.; Mehdi, H.; Armghan, A. Hybrid Control of the DC Microgrid Using Deep Neural Networks and Global Terminal Sliding Mode Control with the Exponential Reaching Law. Sensors 2023, 23, 9342. https://doi.org/10.3390/s23239342
Sharaf MA, Armghan H, Ali N, Yousef A, Abdalla YS, Boudabbous AR, Mehdi H, Armghan A. Hybrid Control of the DC Microgrid Using Deep Neural Networks and Global Terminal Sliding Mode Control with the Exponential Reaching Law. Sensors. 2023; 23(23):9342. https://doi.org/10.3390/s23239342
Chicago/Turabian StyleSharaf, Mohamed A., Hammad Armghan, Naghmash Ali, Amr Yousef, Yasser S. Abdalla, Anis R. Boudabbous, Hafiz Mehdi, and Ammar Armghan. 2023. "Hybrid Control of the DC Microgrid Using Deep Neural Networks and Global Terminal Sliding Mode Control with the Exponential Reaching Law" Sensors 23, no. 23: 9342. https://doi.org/10.3390/s23239342
APA StyleSharaf, M. A., Armghan, H., Ali, N., Yousef, A., Abdalla, Y. S., Boudabbous, A. R., Mehdi, H., & Armghan, A. (2023). Hybrid Control of the DC Microgrid Using Deep Neural Networks and Global Terminal Sliding Mode Control with the Exponential Reaching Law. Sensors, 23(23), 9342. https://doi.org/10.3390/s23239342








