Aberration Theory of a Flat, Aplanatic Metalens Doublet and the Design of a Meta-Microscope Objective Lens
Abstract
:1. Introduction
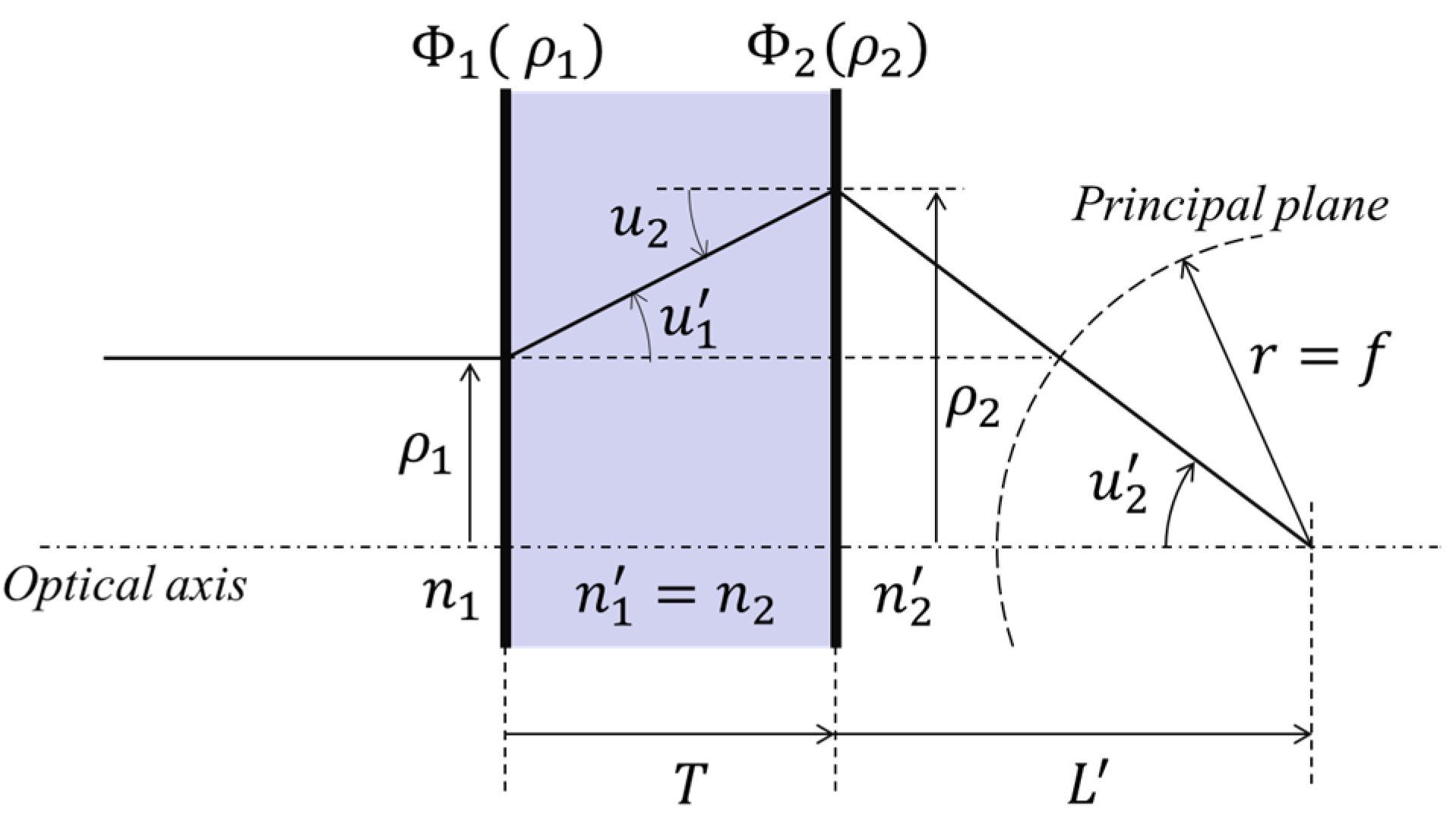
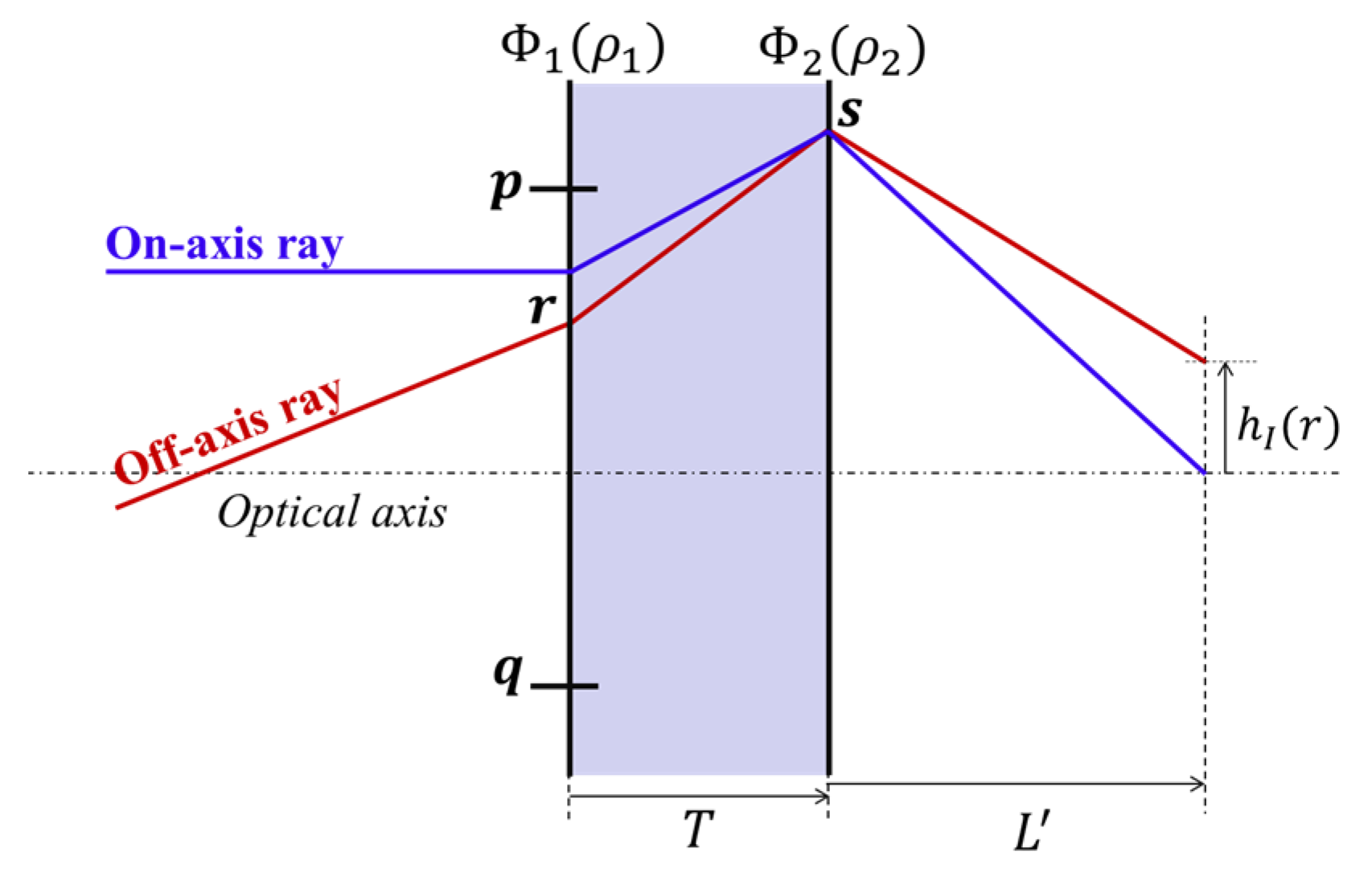
2. Theory of Aplanatic Metalens Doublet
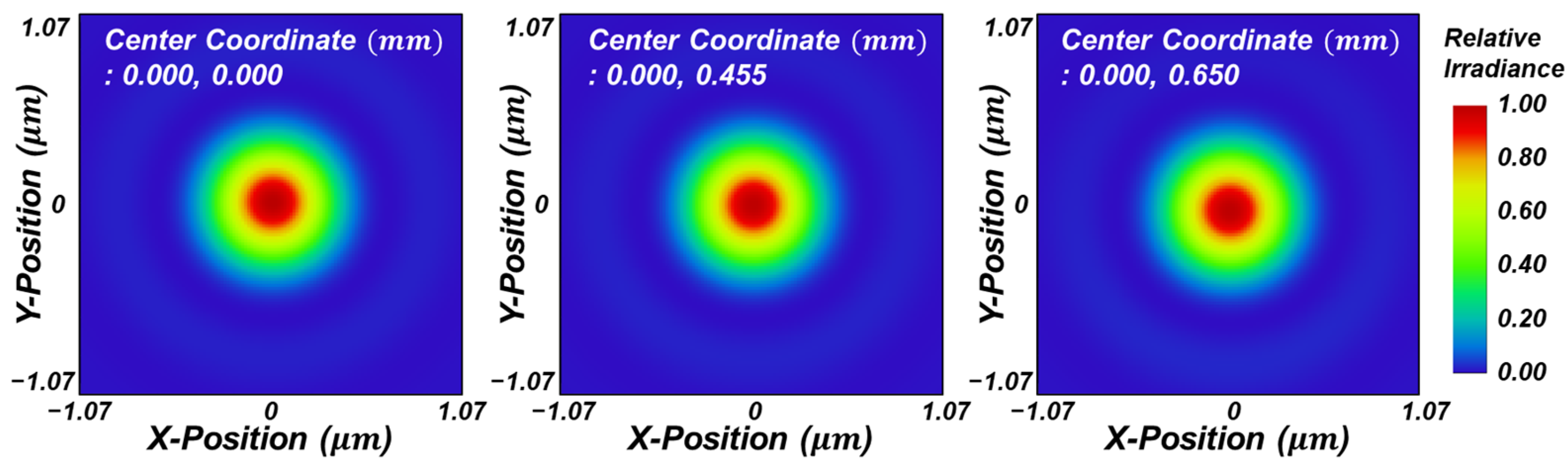
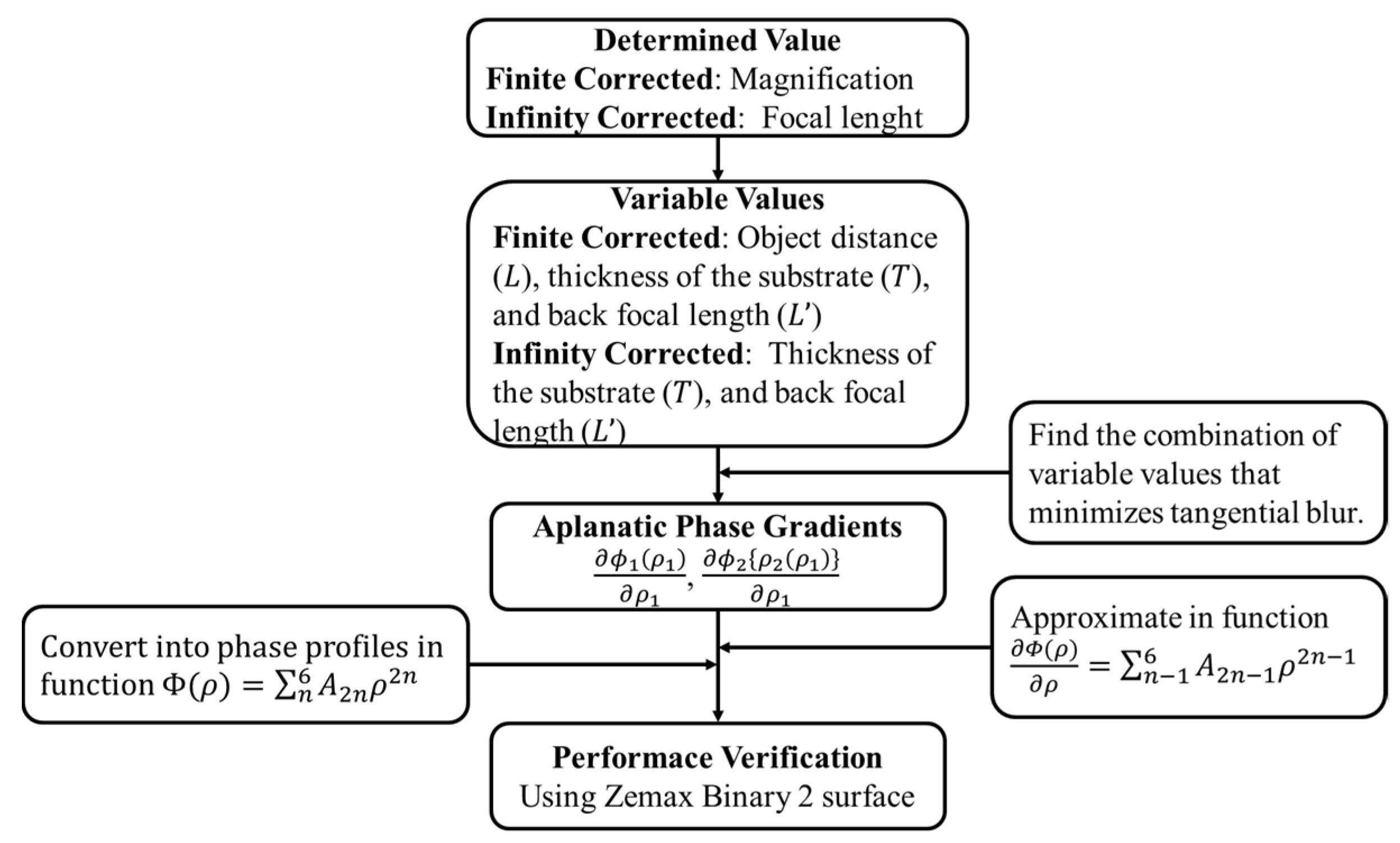
3. Optimization and Simulation of Doublet Metalenses
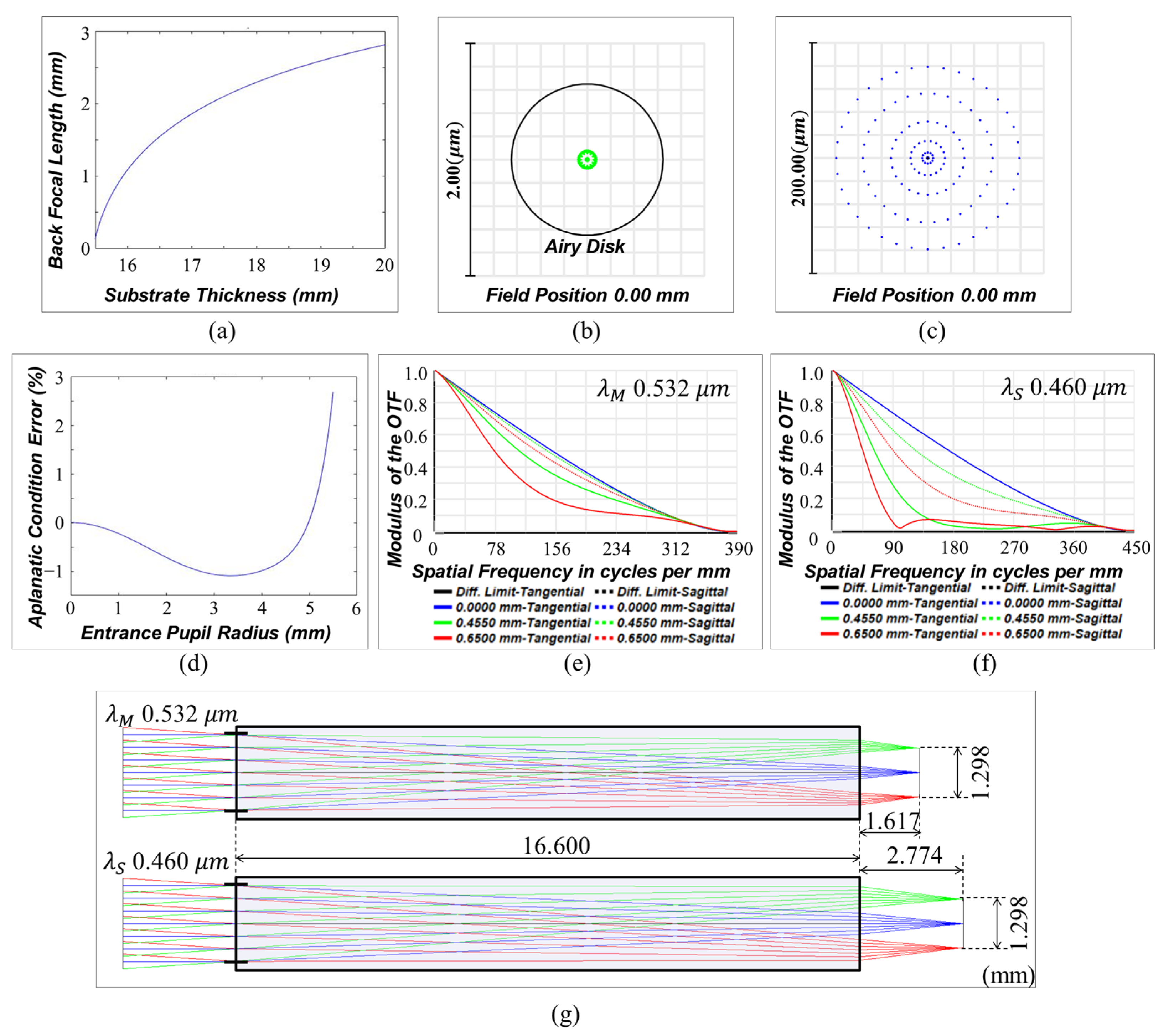
3.1. Compensation of Astigmatism and Field Curvature
3.2. Compensation of Lateral Achromatic Aberration
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, M.; Fu, Y.; Zheng, M.; Chen, H.; Zang, Y.; Duan, H.; Li, Q.; Qiu, M.; Hu, Y. Dielectric metalens for miniaturized imaging systems: Progress and challenges. Light Sci. Appl. 2022, 11, 195. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, C.; Kim, Y.; Jeong, J.; Choi, S.; Han, W.J.; Kim, J.; Lee, B. Dielectric Metalens: Properties and Three-Dimensional Imaging Applications. Sensors 2021, 21, 4584. [Google Scholar] [CrossRef]
- Lee, G.Y.; Hong, J.Y.; Hwang, S.; Moon, S.; Kang, H.; Jeon, S.; Kim, H.; Jeong, J.H.; Lee, B. Metasurface eyepiece for augmented reality. Nat. Commun. 2018, 9, 4562. [Google Scholar] [CrossRef]
- Colburn, S.; Zhan, A.; Majumdar, A. Metasurface optics for full-color computational imaging. Sci. Adv. 2018, 4, eaar2114. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lin, P.; Huang, Y.W.; Park, J.S.; Chen, W.T.; Shi, Z.; Qiu, C.W.; Cheng, J.X.; Capasso, F. Meta-optics achieves RGB-achromatic focusing for virtual reality. Sci. Adv. 2021, 7, eabe4458. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Sosler, J.; Bharwani, Z.; Capasso, F. A broadband achromatic polarization-insensitive metalens consisting of anisotropic nanostructures. Nat. Commun. 2019, 10, 355. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chen, M.K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.T.; Wang, J.H.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Guo, Y.; Ma, X.; Luo, X. Nanoapertures with ordered rotations: Symmetry transformation and wide-angle flat lensing. Opt. Express 2017, 25, 31471–31477. [Google Scholar] [CrossRef]
- Martins, A.; Li, K.; Li, J.; Liang, H.; Conteduca, D.; Borges, B.H.V.; Krauss, T.F.; Martins, E.R. On metalenses with arbitrarily wide field of view. ACS Photonics 2020, 7, 2073–2079. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, F.; Pu, M.; Guo, Y.; Li, X.; Ma, X. Recent advances of wide-angle metalenses: Principle, design, and applications. Nanophotonics 2022, 11, 1–20. [Google Scholar] [CrossRef]
- Arbabi, A.; Arbabi, E.; Kamali, S.M.; Horie, Y.; Han, S.; Faraon, A. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat. Commun. 2016, 7, 13682. [Google Scholar] [CrossRef] [PubMed]
- Groever, B.; Chen, W.T.; Capasso, F. Meta-lens doublet in the visible region. Nano Lett. 2017, 17, 4902–4907. [Google Scholar] [CrossRef]
- Martins, A.; Li, J.; Borges, B.H.V.; Krauss, T.F.; Martins, E.R. Fundamental limits and design principles of doublet metalenses. Nanophotonics 2022, 11, 1187–1194. [Google Scholar] [CrossRef]
- Kim, C.; Kim, S.J.; Lee, B. Doublet metalens design for high numerical aperture and simultaneous correction of chromatic and monochromatic aberrations. Opt. Express 2020, 28, 18059–18076. [Google Scholar] [CrossRef]
- Toba, H.; Takagi, H.; Ohashi, M.; Otaki, K.; Takigawa, Y. Influence on wide-angle doublet metalenses due to different types of all-dielectric metasurfaces. Appl. Opt. 2022, 61, 597–606. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.; Lee, G.-Y.; Kim, Y.; Kim, C.; Jeong, Y.; Lee, B. Dispersion-engineered Metasurface Doublet Design for Broadband and Wide-angle Operation in the Visible Range. IEEE Photon. J. 2023, 15, 2201209. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sisler, J.; Huang, Y.W.; Yousef, K.M.; Lee, E.; Qiu, C.W.; Capasso, F. Broadband achromatic metasurface-refractive optics. Nano Lett. 2018, 18, 7801–7808. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Genevet, P.; Kats, M.; Capasso, F. Aberrations of flat lenses and aplanatic metasurfaces. Opt. Express 2023, 21, 31530–31539. [Google Scholar] [CrossRef]
- Buralli, D.A.; Morris, G.M. Design of diffractive singlets for monochromatic imaging. Appl. Opt. 1991, 30, 2151–2158. [Google Scholar] [CrossRef] [PubMed]
- Kingslake, R.; Johnson, B. Lens Design Fundamentals, 2nd ed.; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Chen, C.; Song, W.; Chen, J.W.; Wang, J.H.; Chen, Y.H.; Xu, B.; Chen, M.K.; Li, H.; Fang, B.; Chen, J.; et al. Spectral tomographic imaging with aplanatic metalens. Light Sci. Appl. 2019, 8, 99. [Google Scholar] [CrossRef]
- Ghosh, G. Dispersion-equation coefficients for the refractive index and birefringence of calcite and quartz crystals. Opt. Commun. 1999, 163, 95–102. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]


| Specification | Commercial Microscope Objective Lens | Aplanatic Meta-Microscope Objective Lens |
|---|---|---|
| Magnification * | 20× | 20× |
| Focal length (mm) | 10 | 10 |
| NA | 0.42 | 0.5 |
| Resolving power (μm) | 0.760 | 0.650 |
| Diagonal FOV (mm) | 1/2″ sensor format: ±0.2 | ±0.65 |
| RMS wavefront error (mλ) | <0.06 | <0.011 |
| Distortion (%) | <|0.1| | −0.2 |
| Wavelength (μm) | 0.436 ~ 0.656 | 0.532 |
| Working distance (mm) | 20 | 8.681 |
| Parfocal length (mm) | 95 | 24.151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Jeong, J.; Kim, J.; Kim, S.-J. Aberration Theory of a Flat, Aplanatic Metalens Doublet and the Design of a Meta-Microscope Objective Lens. Sensors 2023, 23, 9273. https://doi.org/10.3390/s23229273
Han W, Jeong J, Kim J, Kim S-J. Aberration Theory of a Flat, Aplanatic Metalens Doublet and the Design of a Meta-Microscope Objective Lens. Sensors. 2023; 23(22):9273. https://doi.org/10.3390/s23229273
Chicago/Turabian StyleHan, Woojun, Jinsoo Jeong, Jaisoon Kim, and Sun-Je Kim. 2023. "Aberration Theory of a Flat, Aplanatic Metalens Doublet and the Design of a Meta-Microscope Objective Lens" Sensors 23, no. 22: 9273. https://doi.org/10.3390/s23229273
APA StyleHan, W., Jeong, J., Kim, J., & Kim, S.-J. (2023). Aberration Theory of a Flat, Aplanatic Metalens Doublet and the Design of a Meta-Microscope Objective Lens. Sensors, 23(22), 9273. https://doi.org/10.3390/s23229273





