Anomaly Detection in Time Series Data Using Reversible Instance Normalized Anomaly Transformer
Abstract
:1. Introduction
- the suggestion of the reversible instance normalized anomaly transformer to highlight anomalies better than normal datapoints;
- the achievement of comparable or better results in four actual datasets.
2. Related Works
2.1. Stochastic Models
2.2. Distance-Based Models
2.3. Information-Theoretic Models
2.4. Machine Learning and Deep Learning Models
2.5. Forecasting-Based Models
2.6. Reconstruction-Based Models
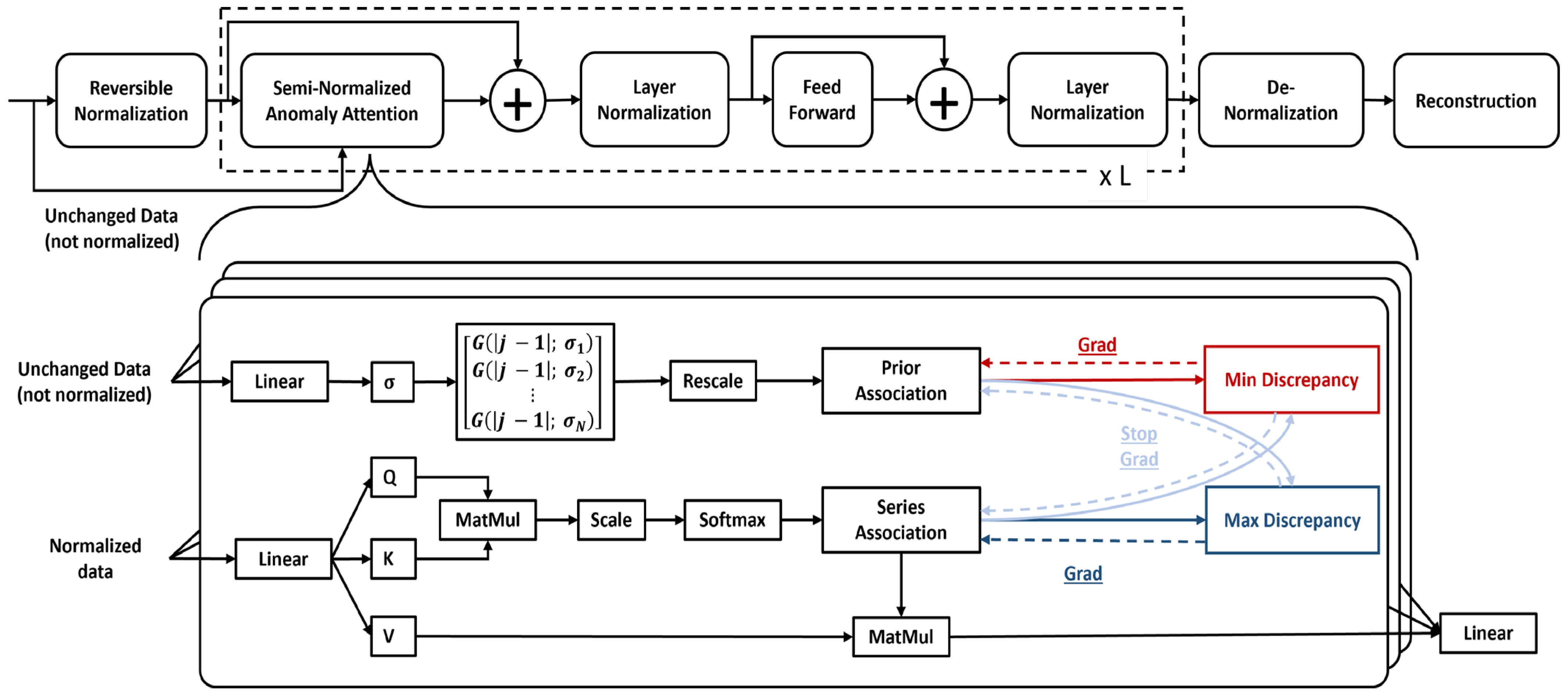
3. Proposed Method
3.1. Anomaly Transformer
3.2. Reversible Instance Normalization
3.3. Reversible Instance Normalized Anomaly Transformer (RINAT)
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Baselines
4.4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Homayouni, H.; Ray, I.; Ghosh, S.; Gondalia, S.; Kahn, M.G. Anomaly detection in COVID-19 time-series data. SN Comput. Sci. 2021, 2, 279. [Google Scholar] [CrossRef] [PubMed]
- Crépey, S.; Lehdili, N.; Madhar, N.; Thomas, M. Anomaly Detection in Financial Time Series by Principal Component Analysis and Neural Networks. Algorithms 2022, 15, 385. [Google Scholar] [CrossRef]
- Wang, Y.; Perry, M.; Whitlock, D.; Sutherland, J.W. Detecting anomalies in time series data from a manufacturing system using recurrent neural networks. J. Manuf. Syst. 2022, 62, 823–834. [Google Scholar] [CrossRef]
- Ayodeji, A.; Liu, Y.K.; Chao, N.; Yang, L.Q. A new perspective towards the development of robust data-driven intrusion detection for industrial control systems. Nucl. Eng. Technol. 2020, 52, 2687–2698. [Google Scholar] [CrossRef]
- Habeeb, R.A.A.; Nasaruddin, F.; Gani, A.; Hashem, I.A.T.; Ahmed, E.; Imran, M. Real-time big data processing for anomaly detection: A survey. Int. J. Inf. Manag. 2019, 45, 289–307. [Google Scholar] [CrossRef]
- Himeur, Y.; Ghanem, K.; Alsalemi, A.; Bensaali, F.; Amira, A. Artificial intelligence based anomaly detection of energy consumption in buildings: A review, current trends and new perspectives. Appl. Energy 2021, 287, 116601. [Google Scholar] [CrossRef]
- Barz, B.; Rodner, E.; Garcia, Y.G.; Denzler, J. Detecting regions of maximal divergence for spatio-temporal anomaly detection. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1088–1101. [Google Scholar] [CrossRef]
- Beeram, S.R.; Kuchibhotla, S. Time series analysis on univariate and multivariate variables: A comprehensive survey. Commun. Softw. Netw. Proc. INDIA 2020, 2019, 119–126. [Google Scholar]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Xu, J.; Wu, H.; Wang, J.; Long, M. Anomaly transformer: Time series anomaly detection with association discrepancy. arXiv 2021, arXiv:2110.02642. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Amodei, D. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Houlsby, N. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Kim, T.; Kim, J.; Tae, Y.; Park, C.; Choi, J.H.; Choo, J. Reversible instance normalization for accurate time-series forecasting against distribution shift. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary transformers: Exploring the stationarity in time series forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 9881–9893. [Google Scholar]
- Zhang, C.; Zhou, T.; Wen, Q.; Sun, L. TFAD: A decomposition time series anomaly detection architecture with time-frequency analysis. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta GA, USA, 17–21 October 2022; pp. 2497–2507. [Google Scholar]
- Kontopoulou, V.I.; Panagopoulos, A.D.; Kakkos, I.; Matsopoulos, G.K. A Review of ARIMA vs. Machine Learning Approaches for Time Series Forecasting in Data Driven Networks. Future Internet 2023, 15, 255. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Snyder, R.D.; Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. Int. J. Forecast. 2002, 18, 439–454. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Gu, X.; Akoglu, L.; Rinaldo, A. Statistical analysis of nearest neighbor methods for anomaly detection. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Fuhnwi, G.S.; Agbaje, J.O.; Oshinubi, K.; Peter, O.J. An Empirical Study on Anomaly Detection Using Density-Based and Representative-Based Clustering Algorithms. J. Niger. Soc. Phys. Sci. 2023, 5, 1364. [Google Scholar] [CrossRef]
- Benkabou, S.E.; Benabdeslem, K.; Canitia, B. Unsupervised outlier detection for time series by entropy and dynamic time warping. Knowl. Inf. Syst. 2018, 54, 463–486. [Google Scholar] [CrossRef]
- Filonov, P.; Lavrentyev, A.; Vorontsov, A. Multivariate industrial time series with cyber-attack simulation: Fault detection using an lstm-based predictive data model. arXiv 2016, arXiv:1612.06676. [Google Scholar]
- Chauhan, S.; Vig, L. Anomaly detection in ECG time signals via deep long short-term memory networks. In Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA), IEEE, Paris, France, 19–21 October 2015; pp. 1–7. [Google Scholar]
- Ren, H.; Xu, B.; Wang, Y.; Yi, C.; Huang, C.; Kou, X.; Zhang, Q. Time-series anomaly detection service at microsoft. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 July 2019; pp. 3009–3017. [Google Scholar]
- Song, H.; Rajan, D.; Thiagarajan, J.; Spanias, A. Attend and diagnose: Clinical time series analysis using attention models. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Deng, A.; Hooi, B. Graph neural network-based anomaly detection in multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 4027–4035. [Google Scholar]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv 2016, arXiv:1607.00148. [Google Scholar]
- Park, D.; Hoshi, Y.; Kemp, C.C. A multimodal anomaly detector for robot-assisted feeding using an lstm-based variational autoencoder. IEEE Robot. Autom. Lett. 2018, 3, 1544–1551. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, K.; Wu, X. LSTM-based VAE-GAN for time-series anomaly detection. Sensors 2020, 20, 3738. [Google Scholar] [CrossRef]
- Tuli, S.; Casale, G.; Jennings, N.R. Tranad: Deep transformer networks for anomaly detection in multivariate time series data. arXiv 2022, arXiv:2201.07284. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar]
- Abdulaal, A.; Liu, Z.; Lancewicki, T. Practical approach to asynchronous multivariate time series anomaly detection and localization. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 2485–2494. [Google Scholar]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Shen, L.; Li, Z.; Kwok, J. Timeseries anomaly detection using temporal hierarchical one-class network. Adv. Neural Inf. Process. Syst. 2020, 33, 13016–13026. [Google Scholar]
- Xu, H.; Chen, W.; Zhao, N.; Li, Z.; Bu, J.; Li, Z.; Qiao, H. Unsupervised anomaly detection via variational auto-encoder for seasonal kpis in web applications. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 187–196. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Li, Z.; Zhao, Y.; Han, J.; Su, Y.; Jiao, R.; Wen, X.; Pei, D. Multivariate time series anomaly detection and interpretation using hierarchical inter-metric and temporal embedding. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 3220–3230. [Google Scholar]
- Zhou, B.; Liu, S.; Hooi, B.; Cheng, X.; Ye, J. Beatgan: Anomalous rhythm detection using adversarially generated time series. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI-19), Macao, China, 10–16 August 2019; Volume 2019, pp. 4433–4439. [Google Scholar]
- Zong, B.; Song, Q.; Min, M.R.; Cheng, W.; Lumezanu, C.; Cho, D.; Chen, H. Deep autoencoding gaussian mixture model for unsupervised anomaly detection. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yairi, T.; Takeishi, N.; Oda, T.; Nakajima, Y.; Nishimura, N.; Takata, N. A data-driven health monitoring method for satellite housekeeping data based on probabilistic clustering and dimensionality reduction. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1384–1401. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Shin, Y.; Lee, S.; Tariq, S.; Lee, M.S.; Jung, O.; Chung, D.; Woo, S.S. Itad: Integrative tensor-based anomaly detection system for reducing false positives of satellite systems. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Virtual, 19–23 October 2020; pp. 2733–2740. [Google Scholar]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Kloft, M. Deep one-class classification. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4393–4402. [Google Scholar]
- Tariq, S.; Lee, S.; Shin, Y.; Lee, M.S.; Jung, O.; Chung, D.; Woo, S.S. Detecting anomalies in space using multivariate convolutional LSTM with mixtures of probabilistic PCA. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2123–2133. [Google Scholar]
- Anderson, O.; Kendall, M. Time-Series. J. R. Stat. Soc. Ser. D 1976. [Google Scholar]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, IEEE, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
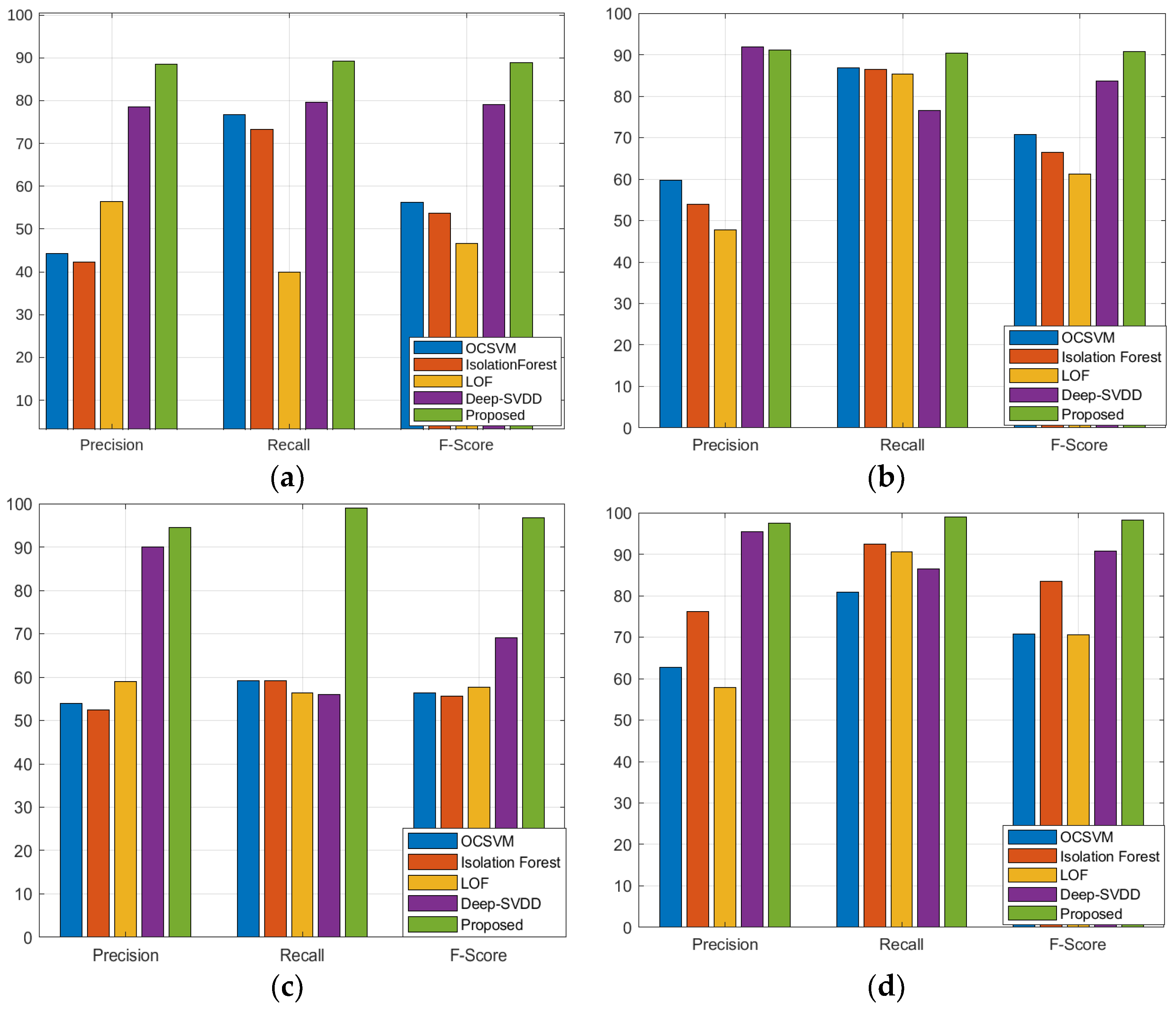
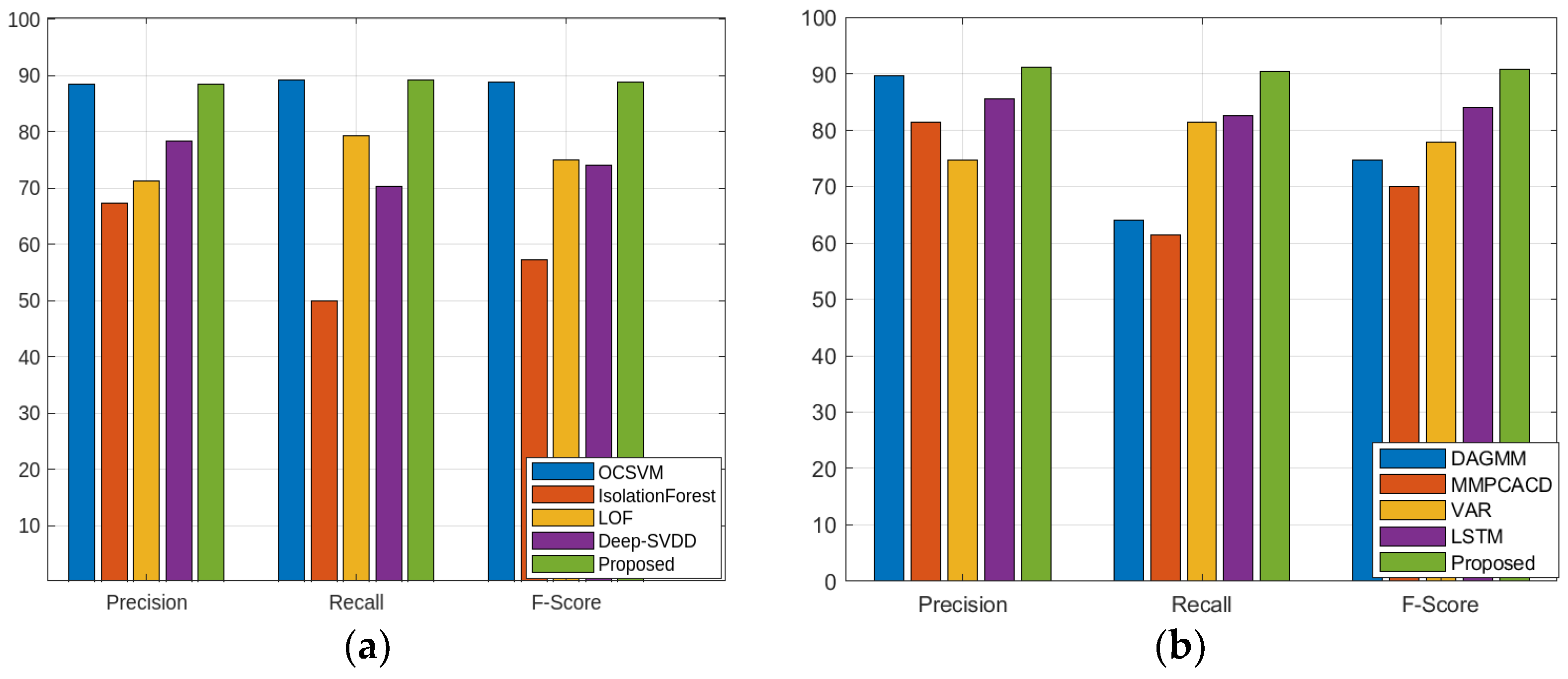
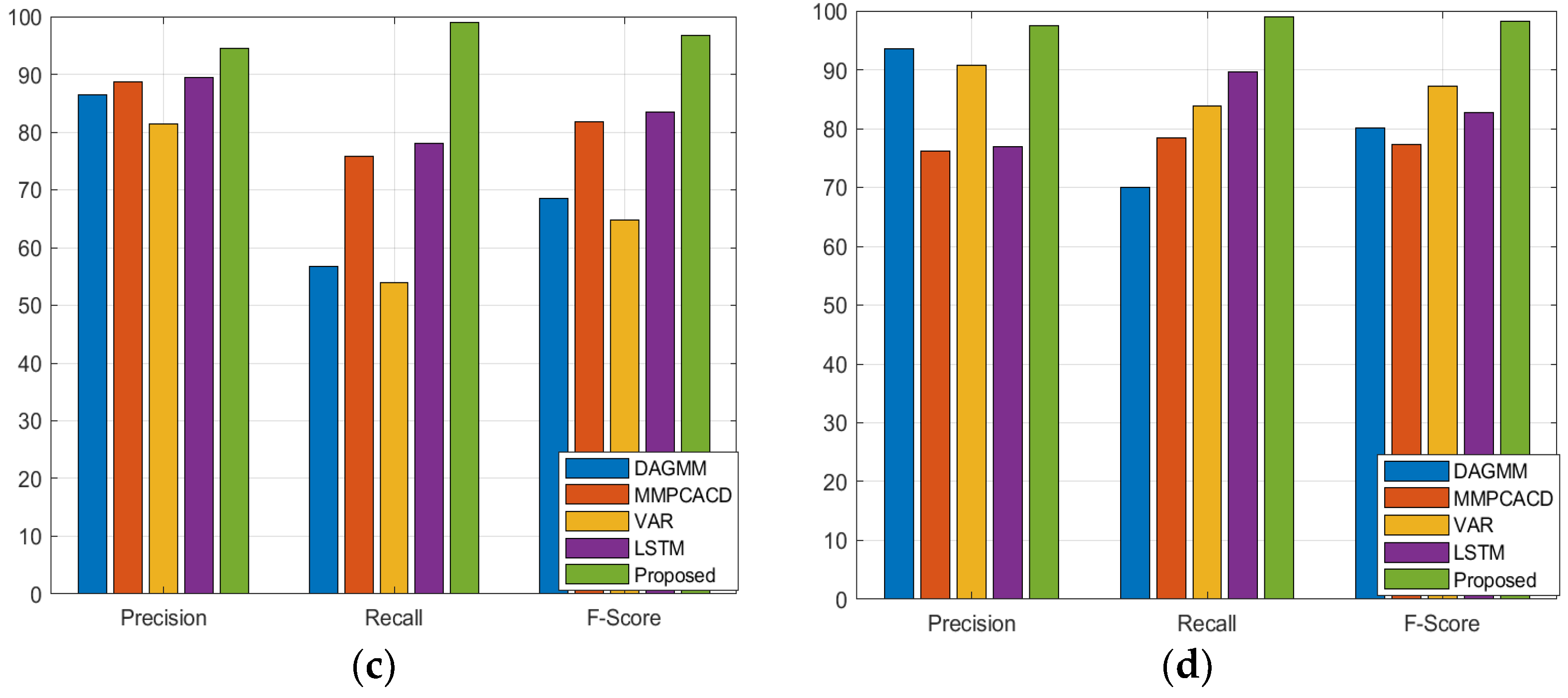
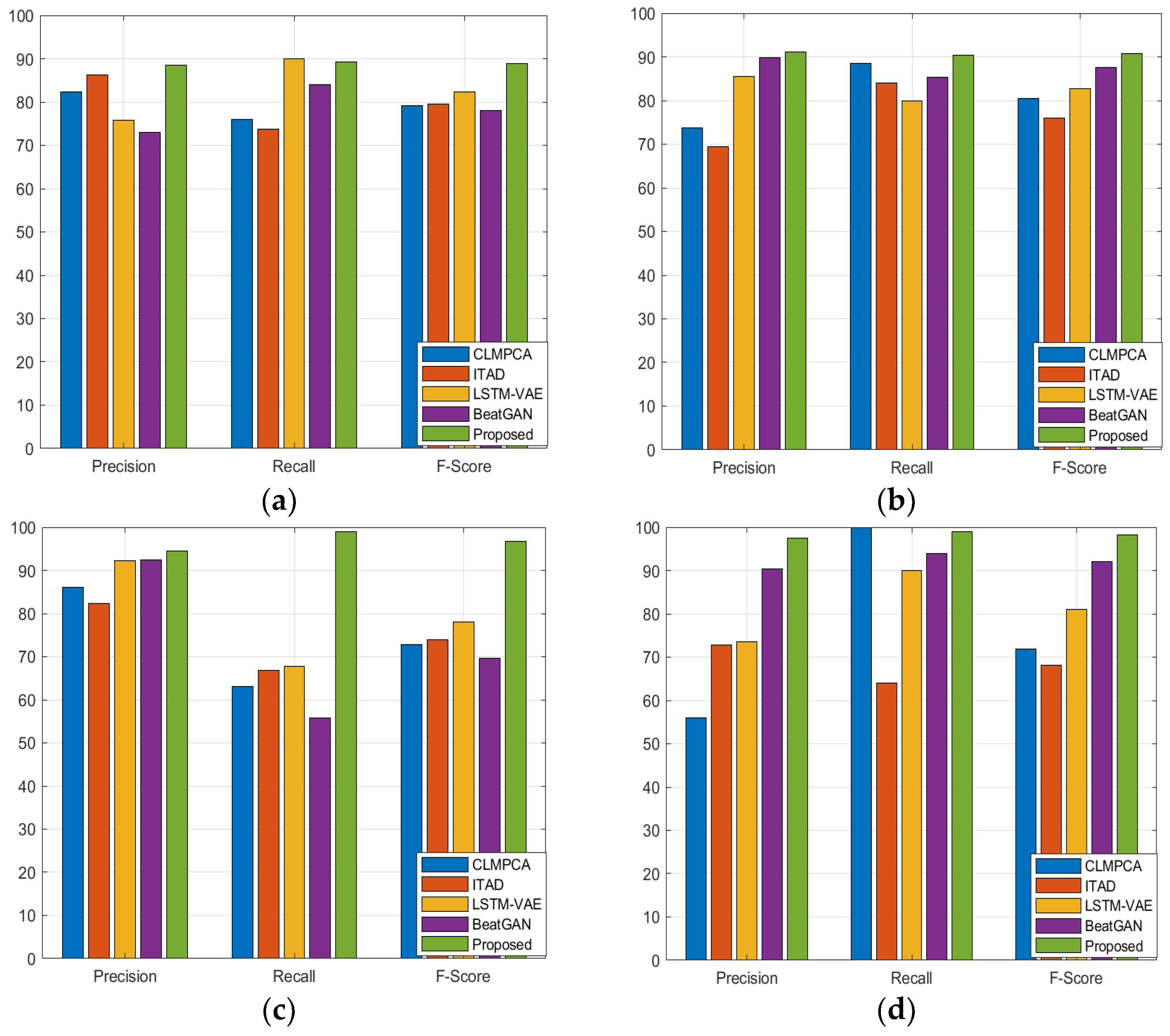
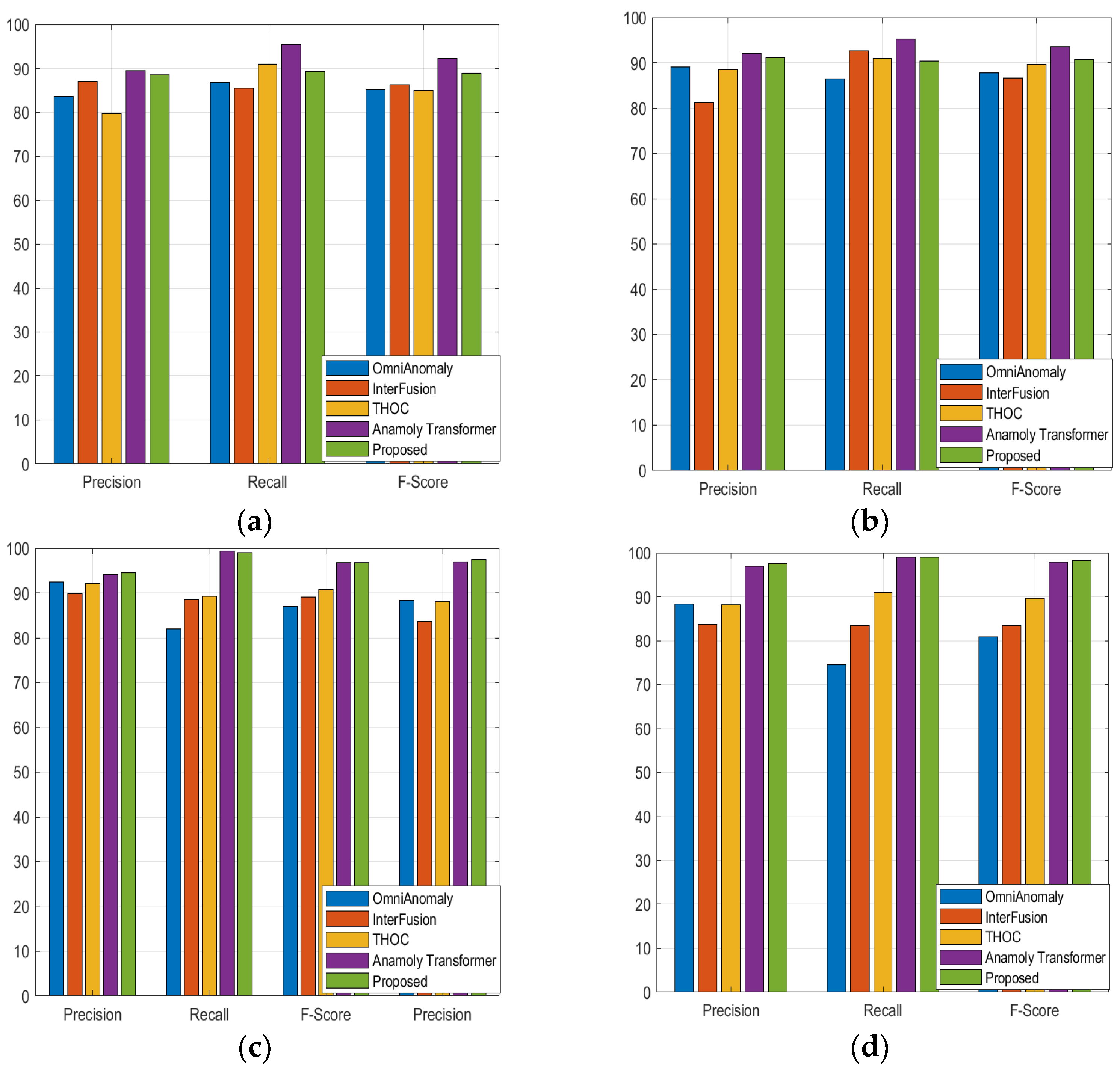

| Dataset | SMD | MSL | SMAP | PSM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | P | R | F1 | P | R | F1 | P | R | F1 | P | R | F1 |
| OCSVM | 44.34 | 76.72 | 56.19 | 59.78 | 86.87 | 70.82 | 53.85 | 59.07 | 56.34 | 62.75 | 80.89 | 70.67 |
| IsolationForest | 42.31 | 73.29 | 53.64 | 53.94 | 86.54 | 66.45 | 52.39 | 59.07 | 55.53 | 76.09 | 92.45 | 83.48 |
| LOF | 56.34 | 39.86 | 46.68 | 47.72 | 85.25 | 61.18 | 58.93 | 56.33 | 57.60 | 57.89 | 90.49 | 70.61 |
| Deep-SVDD | 78.54 | 79.67 | 79.10 | 91.92 | 76.63 | 83.58 | 89.93 | 56.02 | 69.04 | 95.41 | 86.49 | 90.73 |
| DAGMM | 67.30 | 49.89 | 57.30 | 89.60 | 63.93 | 74.62 | 86.45 | 56.73 | 68.51 | 93.49 | 70.03 | 80.08 |
| MMPCACD | 71.20 | 79.28 | 75.02 | 81.42 | 61.31 | 69.95 | 88.61 | 75.84 | 81.73 | 76.26 | 78.35 | 77.29 |
| VAR | 78.35 | 70.26 | 74.08 | 74.68 | 81.42 | 77.9 | 81.38 | 53.88 | 64.83 | 90.71 | 83.82 | 87.13 |
| LSTM | 78.55 | 85.28 | 81.78 | 85.45 | 82.50 | 83.95 | 89.41 | 78.13 | 83.39 | 76.93 | 89.64 | 82.80 |
| CL-MPPCA | 82.36 | 76.07 | 79.09 | 73.71 | 88.54 | 80.44 | 86.13 | 63.16 | 72.88 | 56.02 | 99.93 | 71.80 |
| ITAD | 86.22 | 73.71 | 79.48 | 69.44 | 84.09 | 76.07 | 82.42 | 66.89 | 73.85 | 72.80 | 64.02 | 68.13 |
| LSTM-VAE | 75.76 | 90.08 | 82.30 | 85.49 | 79.94 | 82.62 | 92.20 | 67.75 | 78.10 | 73.62 | 89.92 | 80.96 |
| BeatGAN | 72.90 | 84.09 | 78.10 | 89.75 | 85.42 | 87.53 | 92.38 | 55.85 | 69.61 | 90.30 | 93.84 | 92.04 |
| OmniAnomaly | 83.68 | 86.82 | 85.22 | 83.02 | 86.37 | 87.67 | 92.49 | 81.99 | 86.92 | 88.39 | 74.46 | 80.83 |
| InterFusion | 87.02 | 85.43 | 86.22 | 81.28 | 92.70 | 86.62 | 89.77 | 88.52 | 89.14 | 83.61 | 83.45 | 83.52 |
| THOC | 79.76 | 90.95 | 84.99 | 88.45 | 90.97 | 89.69 | 92.06 | 89.34 | 90.68 | 88.14 | 90.99 | 89.54 |
| Anomaly Transformer | 89.40 | 95.45 | 92.33 | 92.09 | 95.15 | 93.59 | 94.13 | 99.40 | 96.69 | 96.91 | 98.90 | 97.89 |
| Our Model | 88.56 | 89.29 | 88.92 | 91.06 | 90.29 | 90.68 | 94.40 | 99.04 | 96.67 | 97.52 | 99.06 | 98.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baidya, R.; Jeong, H. Anomaly Detection in Time Series Data Using Reversible Instance Normalized Anomaly Transformer. Sensors 2023, 23, 9272. https://doi.org/10.3390/s23229272
Baidya R, Jeong H. Anomaly Detection in Time Series Data Using Reversible Instance Normalized Anomaly Transformer. Sensors. 2023; 23(22):9272. https://doi.org/10.3390/s23229272
Chicago/Turabian StyleBaidya, Ranjai, and Heon Jeong. 2023. "Anomaly Detection in Time Series Data Using Reversible Instance Normalized Anomaly Transformer" Sensors 23, no. 22: 9272. https://doi.org/10.3390/s23229272
APA StyleBaidya, R., & Jeong, H. (2023). Anomaly Detection in Time Series Data Using Reversible Instance Normalized Anomaly Transformer. Sensors, 23(22), 9272. https://doi.org/10.3390/s23229272







