A Novel, Efficient Algorithm for Subsurface Radar Imaging below a Non-Planar Surface
Abstract
:1. Introduction
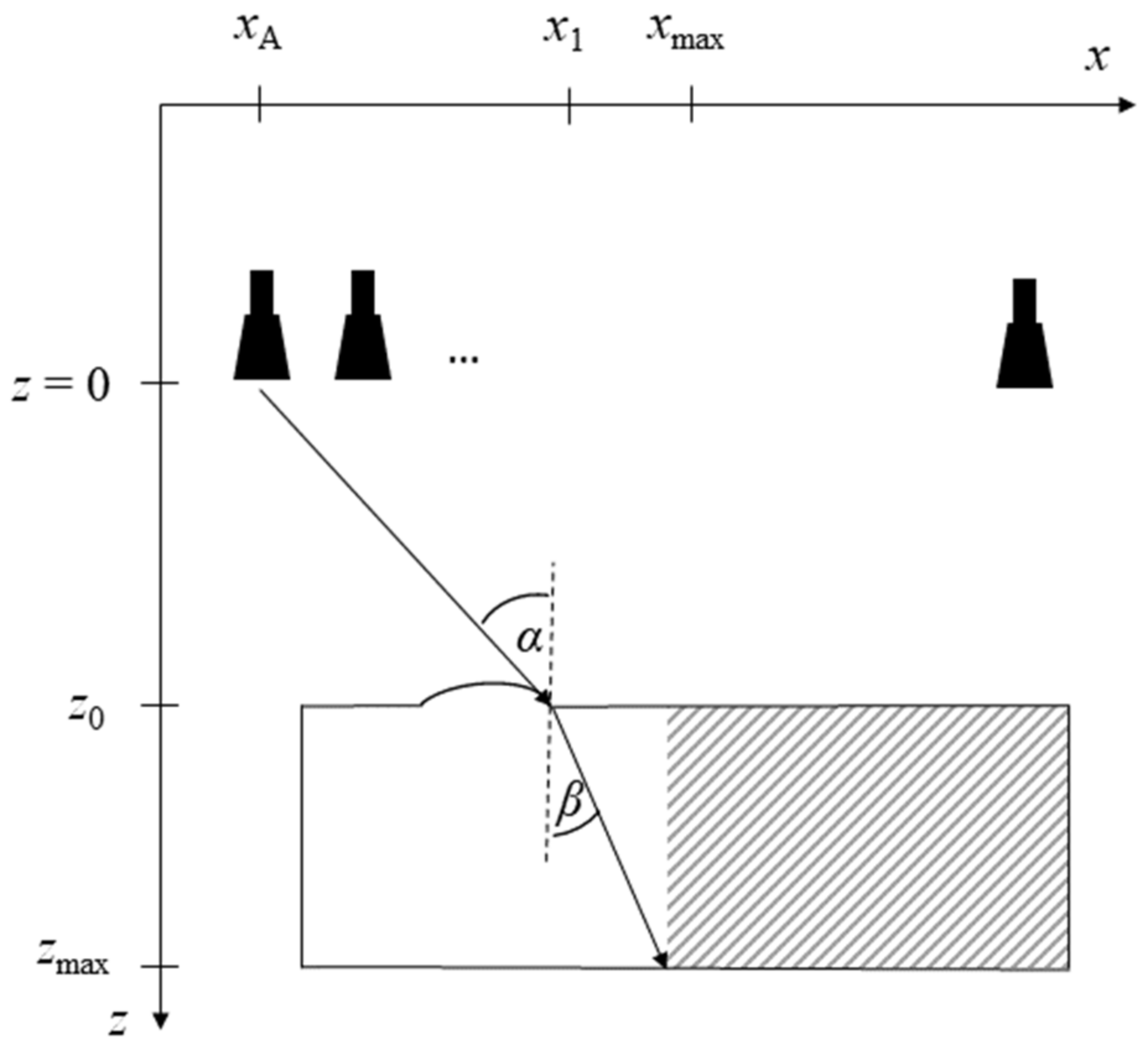
2. Novel Reconstruction Concept
2.1. Imaging Formalism
- 2D Fourier transform the receive signal over aperture dimensions (x, y);
- Shift the spectrum obtained in step 1 iteratively to target planes via phase shift proportional to depth (Equation (9));
- Focusing: 2D inverse Fourier transform over kx and ky and sum over frequency.
2.2. Proposed Approach
- Divide reconstruction domains according to Section 2.2;
- Sub-image 1: Reconstruct whole image in k-space;
- Sub-image 2: Reconstruct necessary image part in spatial domain;
- Adjust amplitudes by means of boundary reflection;
- Overwrite necessary image part of sub-image 1 by sub-image 2.
2.3. Discussion
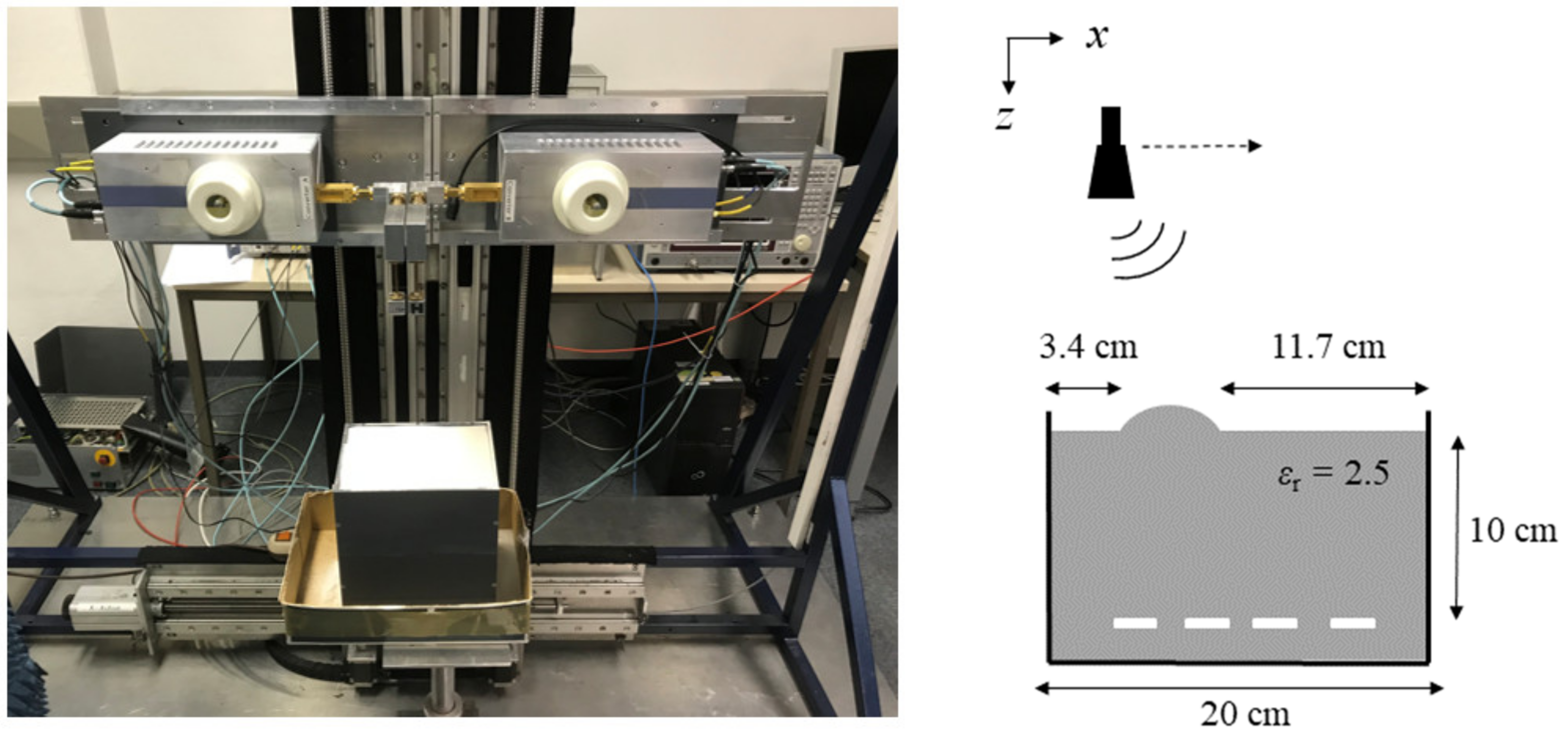
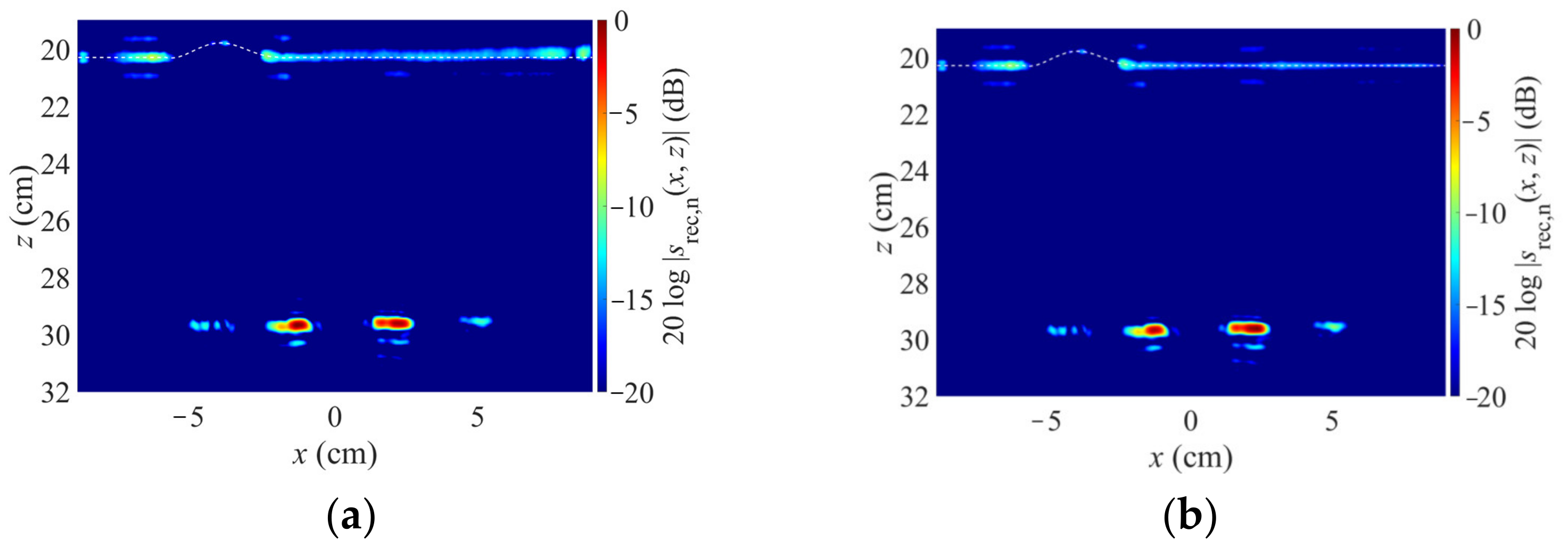
2.4. Experimental Verification
3. Extension to MIMO Radar
3.1. Adaption of Proposed Concept
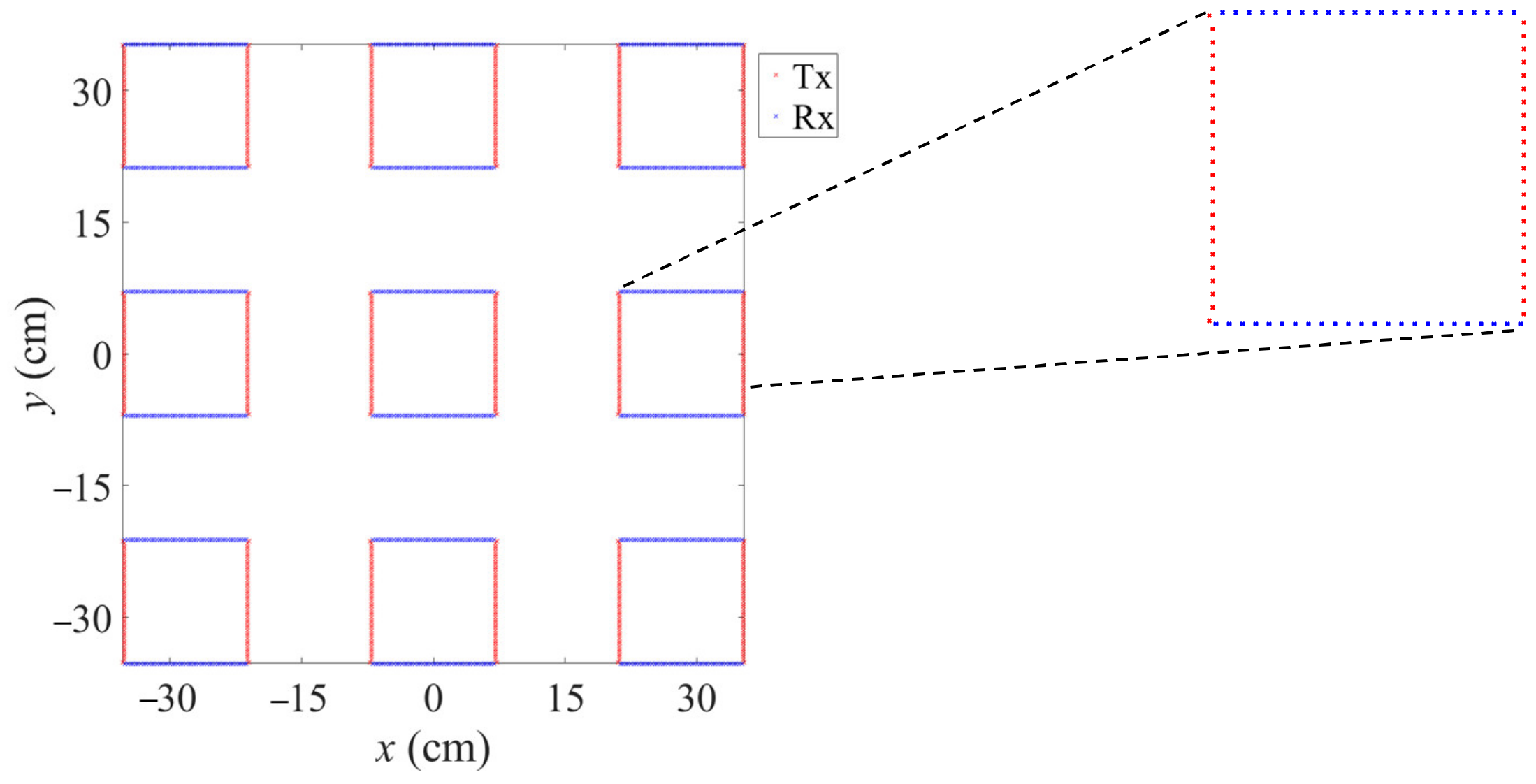
3.2. Demonstration Setup
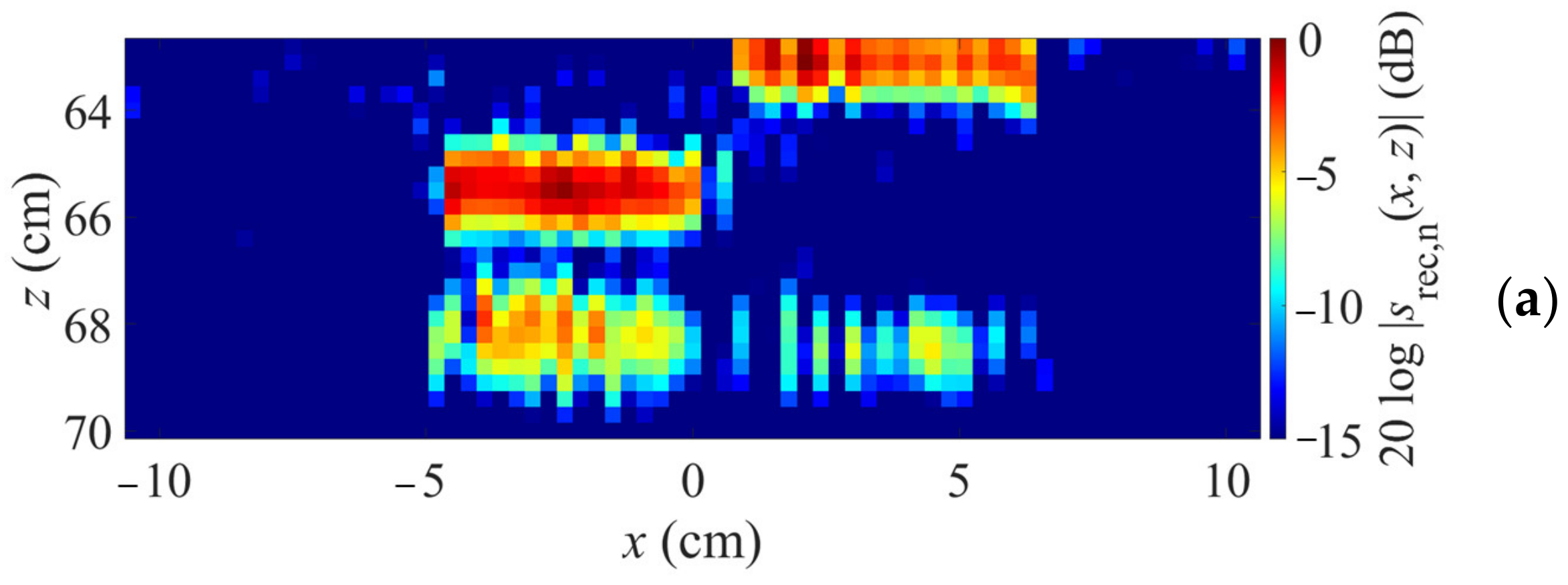
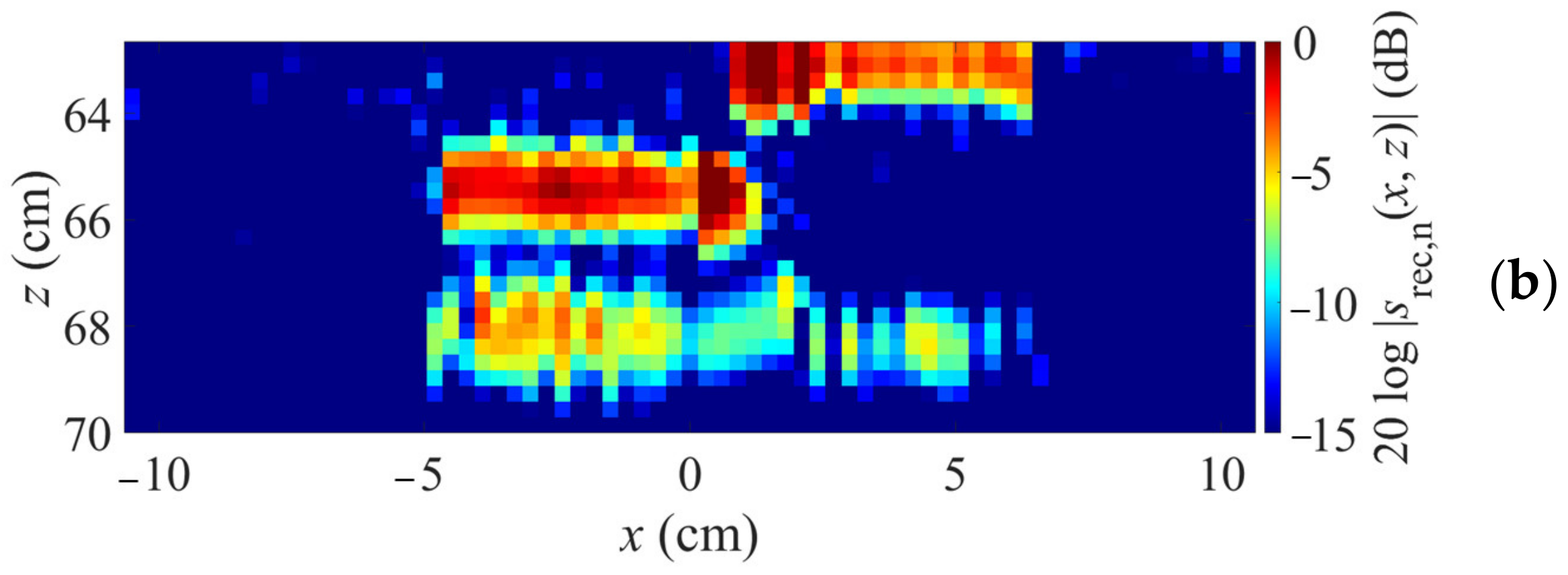
3.3. Imaging Results
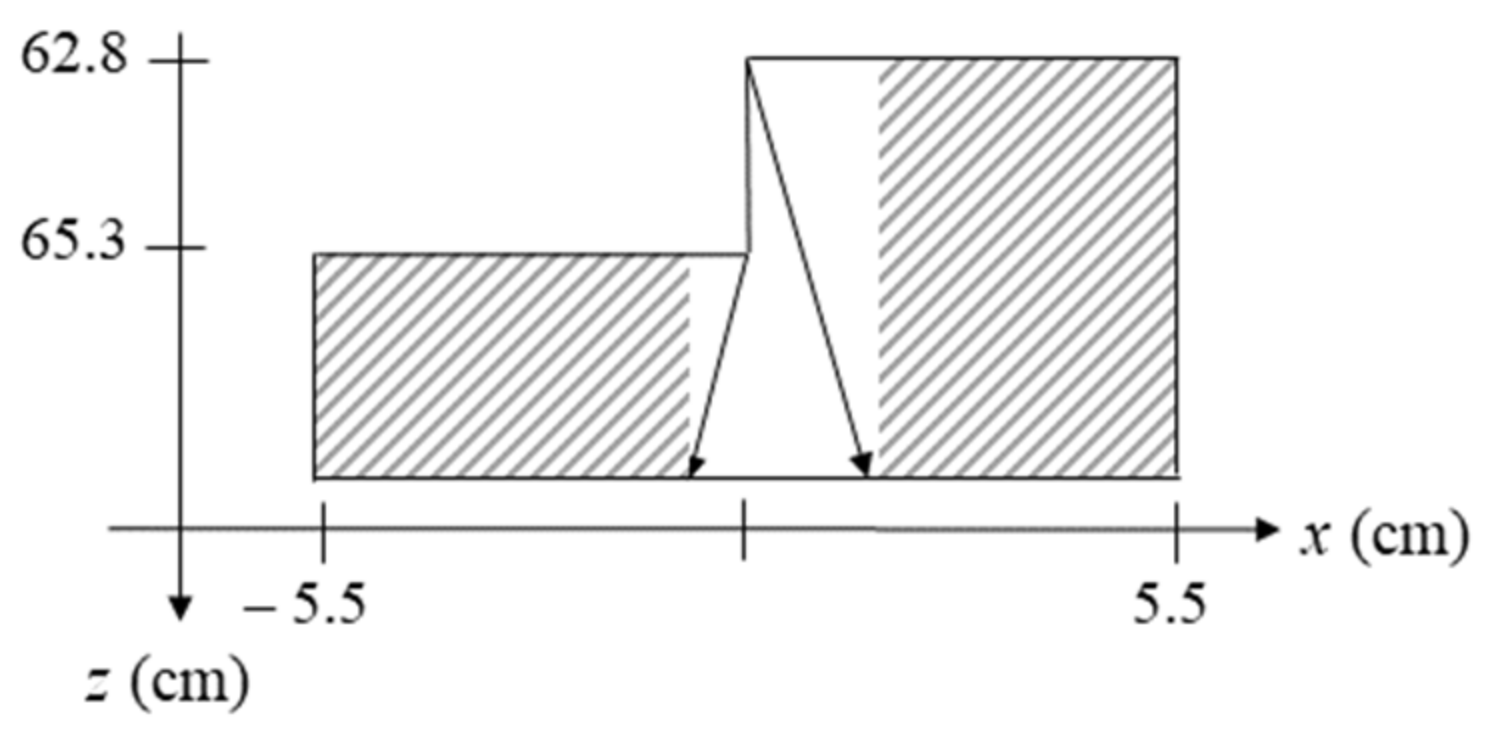
- k-space reconstruction through planar material boundary part at z = 65.3 cm in the field x < −0.84 cm;
- k-space reconstruction through planar material boundary part at z = 62.8 cm in the field x > 1.56 cm;
- spatial domain reconstruction in the field −0.84 cm < x < 1.56 cm.
3.4. Computational Complexity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cumming, I.G.; Wong, F.H. SAR Processing Algorithms. In Digital Processing of Synthetic Aperture Radar Data; Artech House: Boston, MA, USA, 2005; pp. 223–362. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; John Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- Ahmed, S.S.; Schiessl, A.; Gumbmann, F.; Tiebout, M.; Methfessel, S.; Schmidt, L.-P. Advanced microwave imaging. IEEE Microw. Mag. 2012, 13, 26–43. [Google Scholar] [CrossRef]
- Ahmed, S.S. Microwave Imaging in Security—Two Decades of Innovation. IEEE J. Microw. 2021, 1, 191–201. [Google Scholar] [CrossRef]
- Laribi, A.; Hahn, M.; Dickmann, J.; Waldschmidt, C. Performance Investigation of Automotive SAR Imaging. In Proceedings of the 2018 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Munich, Germany, 15–17 April 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Waldschmidt, C.; Hasch, J.; Menzel, W. Automotive Radar—From First Efforts to Future Systems. IEEE J. Microw. 2021, 1, 135–148. [Google Scholar] [CrossRef]
- Johansson, E.M.; Mast, J.E. Three-dimensional ground-penetrating radar imaging using synthetic aperture time-domain focusing. In Proceedings of the SPIE 2275, Advanced Microwave and Millimeter-Wave Detectors, San Diego, CA, USA, 14 September 1994. [Google Scholar] [CrossRef]
- Ullmann, I.; Egerer, P.; Schür, J.; Vossiek, M. Automated Defect Detection for Non-Destructive Evaluation by Radar Imaging and Machine Learning. In Proceedings of the 2020 German Microwave Conference (GeMiC), Cottbus, Germany, 9–11 March 2020; pp. 25–28. [Google Scholar]
- Ahmad, F.; Zhang, Y.; Amin, M.G. Three-Dimensional Wideband Beamforming for Imaging Through a Single Wall. IEEE Geosci. Remote Sens. Lett. 2008, 5, 176–179. [Google Scholar] [CrossRef]
- Mensa, D. High Resolution Radar Cross-Section Imaging; Artech House: Norwood, MA, USA, 1991. [Google Scholar]
- Heinzel, A.; Peichl, M.; Schreiber, E.; Bischeltsrieder, F.; Dill, S.; Anger, S.; Kempf, T.; Jirousek, M. Focusing method for ground penetrating MIMO SAR imaging within half-spaces of different permittivity. In Proceedings of the 11th EUSAR, Hamburg, Germany, 6–9 June 2016; pp. 842–846. [Google Scholar]
- Gazdag, J. Wave-equation migration with the phase-shift method. Geophysics 1978, 43, 1342–1351. [Google Scholar] [CrossRef]
- Stolt, R.H. Migration by Fourier-transform. Geophysics 1978, 43, 23–48. [Google Scholar] [CrossRef]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Gao, H.; Li, C.; Wu, S.; Geng, H.; Zheng, S.; Qu, X.; Fang, G. Study of the extended phase shift migration for three-dimensional MIMO-SAR imaging in terahertz band. IEEE Access 2020, 8, 24773–24783. [Google Scholar] [CrossRef]
- Zhu, R.; Zhou, J.; Jiang, G.; Fu, Q. Range migration algorithm for near-field MIMO-SAR imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2280–2284. [Google Scholar] [CrossRef]
- Stoffa, P.L.; Fokkemat, J.T.; de Luna Freire, R.M.; Kessinger, W.P. Split-step Fourier migration. Geophysics 1990, 55, 410–421. [Google Scholar] [CrossRef]
- Gazdag, J.; Sguazzero, P. Migration of seismic data by phase shift plus interpolation. Geophysics 1984, 49, 124–131. [Google Scholar] [CrossRef]
- Bonomi, E.; Brieger, L.; Nardone, C.; Pieroni, E. Phase shift plus interpolation: A scheme for high-performance echo-reconstructive imaging. Comput. Phys. 1998, 12, 126–132. [Google Scholar] [CrossRef]
- Gazdag, J. Wave equation migration with the accurate space derivative method. Geophys. Prsospect. 1980, 28, 60–70. [Google Scholar] [CrossRef]
- Qin, K.; Yang, C.; Sun, F. Generalized frequency-domain synthetic aperture focusing technique for ultrasonic imaging of irregularly layered objects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 133–146. [Google Scholar] [CrossRef] [PubMed]
- Ullmann, I.; Adametz, J.; Oppelt, D.; Benedikter, A.; Vossiek, M. Non-destructive testing of arbitrarily shaped objects with millimetre-wave synthetic aperture imaging. J. Sens. Sens. Syst. 2018, 7, 309–317. [Google Scholar] [CrossRef]
- Grathwohl, A.; Stelzig, M.; Kanz, J.; Fenske, P.; Benedikter, A.; Knill, C.; Ullmann, I.; Hajnsek, I.; Moreira, A.; Krieger, G.; et al. Taking a Look Beneath the Surface: Multicopter UAV-Based Ground-Penetrating Imaging Radars. IEEE Microw. Mag. 2022, 23, 32–46. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Liu, Q.H. Three-Dimensional GPR Ray Tracing Based on Wavefront Expansion with Irregular Cells. IEEE Trans. Geosc. Remote Sens. 2011, 49, 679–687. [Google Scholar] [CrossRef]
- Skjelvareid, M.H.; Olofsson, T.; Birkelund, Y.; Larsen, Y. Synthetic aperture focusing of ultrasonic data from multilayered media using an omega-K algorithm. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1037–1048. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Pergamon Press: London, UK, 1970. [Google Scholar]
- Shao, W.; Mc Collough, T.R.; Mc Collough, W.J. A Phase Shift and Sum Method for UWB Radar Imaging in Dispersive Media. IEEE Trans. Microw. Theory Techn. 2019, 67, 2018–2027. [Google Scholar] [CrossRef]
- Ullmann, I.; Vossiek, M. A Computationally Efficient Reconstruction Approach for Imaging Layered Dielectrics with Sparse MIMO Arrays. IEEE J. Microw. 2021, 1, 659–665. [Google Scholar] [CrossRef]
- Álvarez, Y.; Rodriguez-Vaqueiro, Y.; Gonzalez-Valdes, B.; Mantzavinos, S.; Rappaport, C.M.; Las-Heras, F.; Martinez-Lorenzo, J.A. Fourier-based imaging for multistatic radar systems. IEEE Trans. Microw. Theory Techn. 2014, 62, 1798–1810. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A.G. A sparse aperture MIMO-SAR-based UWB imaging system for concealed weapon detection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 509–518. [Google Scholar] [CrossRef]



| Step | Computational Complexity |
|---|---|
| 2D FFT | Nx · Ny· log2(Nx·Ny) |
| Backpropagation to boundary | Nx · Ny · Nω |
| Backpropagation inside material | Nx · Ny · Nω· (Nz − 1) |
| 2D IFFT | Nx · Ny· log2(Nx·Ny) · Nz |
| Tx phase correction | NTx · Nx · Ny · Nz· Nω |
| Summation ω | Nω · Nx · Ny · Nz |
| Summation Tx | NTx · Nx · Ny · Nz |
| Calculation of optical paths | NTx · Nx’· Ny · Nz + NRx · Nx’ · Ny · Nz |
| Spatial domain reconstruction | NTx · NRx · Nx’ · Ny · Nz· Nω |
| Total (NTx = NRx= 846, Nω = 64, Nx = Ny = 235, Nz = 35, Nx′ = 7) | 2.74 · 1012 |
| Step | Computational Complexity |
|---|---|
| Calculation of optical paths | NTx · Nx · Ny · Nz + NRx · Nx · Ny · Nz |
| Spatial domain reconstruction | NTx · NRx · Nx · Ny · Nz · Nω |
| Total (NTx = NRx = 846, Nω = 64, Nx = Ny = 235, Nz = 35, Nx′ = 7) | 8.85 · 1013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullmann, I.; Vossiek, M. A Novel, Efficient Algorithm for Subsurface Radar Imaging below a Non-Planar Surface. Sensors 2023, 23, 9021. https://doi.org/10.3390/s23229021
Ullmann I, Vossiek M. A Novel, Efficient Algorithm for Subsurface Radar Imaging below a Non-Planar Surface. Sensors. 2023; 23(22):9021. https://doi.org/10.3390/s23229021
Chicago/Turabian StyleUllmann, Ingrid, and Martin Vossiek. 2023. "A Novel, Efficient Algorithm for Subsurface Radar Imaging below a Non-Planar Surface" Sensors 23, no. 22: 9021. https://doi.org/10.3390/s23229021
APA StyleUllmann, I., & Vossiek, M. (2023). A Novel, Efficient Algorithm for Subsurface Radar Imaging below a Non-Planar Surface. Sensors, 23(22), 9021. https://doi.org/10.3390/s23229021






