AI-Assisted Cotton Grading: Active and Semi-Supervised Learning to Reduce the Image-Labelling Burden
Abstract
1. Introduction
2. Materials and Methods
2.1. Cotton Lint Samples
2.2. Colour Vision System
2.3. Image-Processing Method
2.4. Machine Learning Methods
3. Results and Discussion
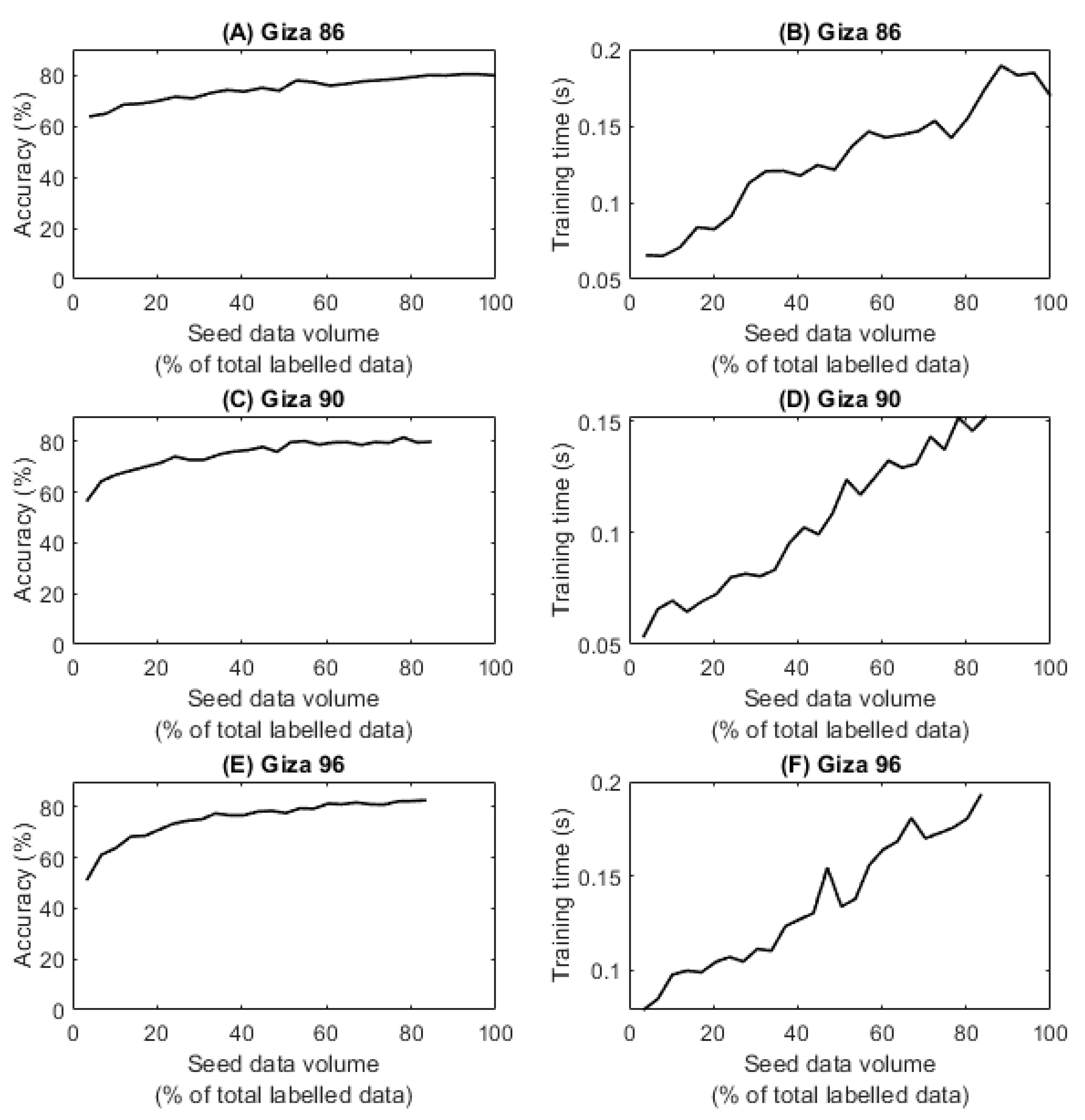
3.1. Supervised Learning Results
- Limited model capacity: In some cases, the model’s capacity may not be enough to handle the increased amount of data. When the model’s complexity is insufficient to capture the patterns in the data, adding more data may not improve the accuracy [50]. It may be that the random forest models developed within this study are not complex enough to process more data and future work should explore other models, such as deep learning that achieved an accuracy of 98.9% when classifying Chinese upland cotton grade [11].
- Data quality: The quality of the new data added to the training set can affect the model’s accuracy. If the new data are noisy, inconsistent, or biased, they may not contribute much to the model’s accuracy and may even degrade it. Previous work highlighted the presence of human error within the labelling of Egyptian cotton data used to train the models [32], implying that data quality may be causing the models’ accuracy to plateau.
- Data redundancy: As the amount of training data increases, some of the data may become redundant or provide little new information to the model. This can lead to a plateau in accuracy as the model is not gaining any new insights from the additional data.
- Bias and variance trade-off: As more data are added, the model’s variance may decrease, but its bias may increase, resulting in a trade-off between the two that limits the improvement in accuracy [51].
- Saturation of the underlying distribution: Similar to data redundancy, the model’s accuracy can plateau if the additional data do not introduce new patterns or relationships that the model has not already learned from the existing data. The model may have already learned all the useful information from the existing data, and further data points do not contribute much to its accuracy.
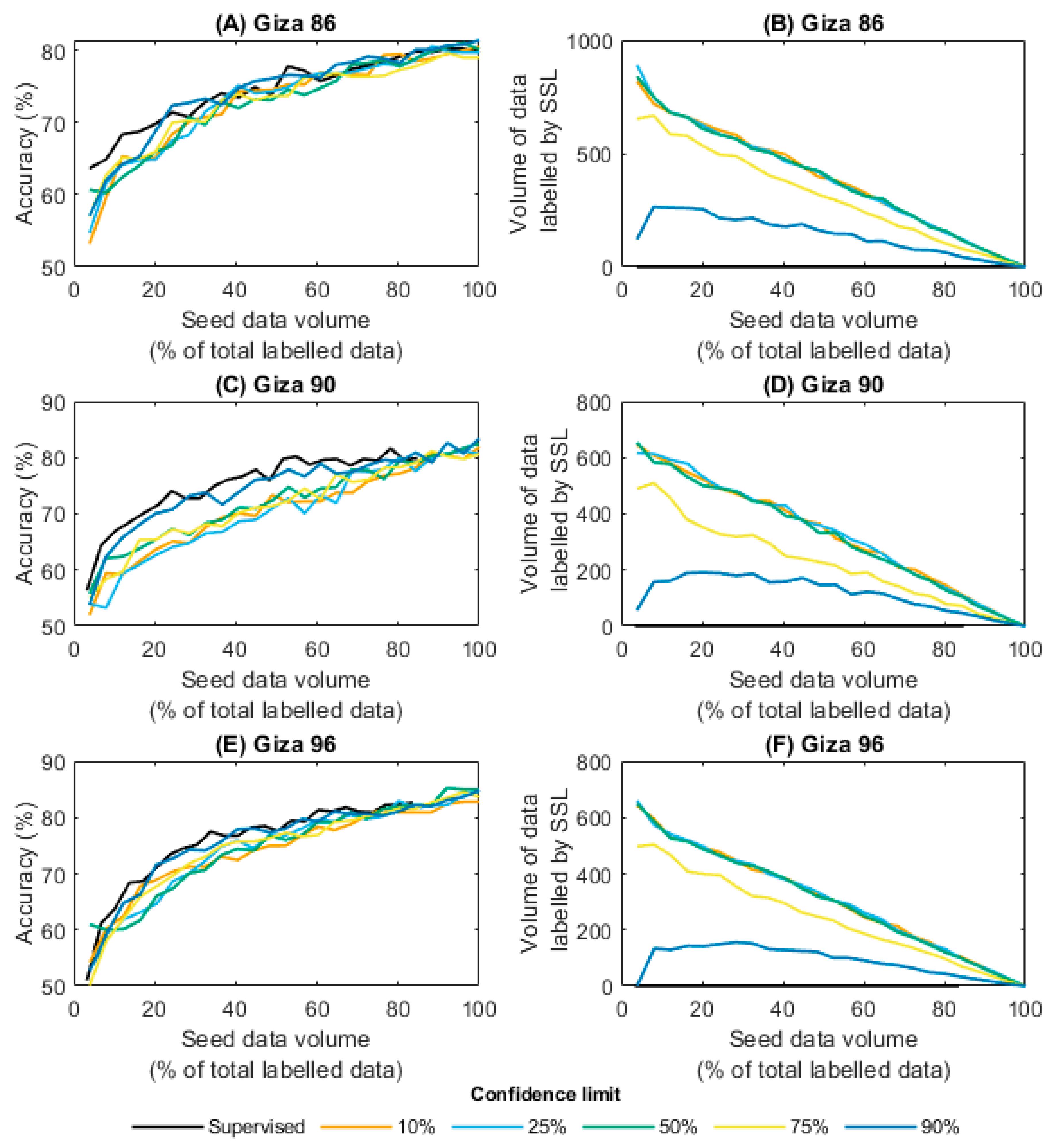
3.2. Semi-Supervised Learning Results
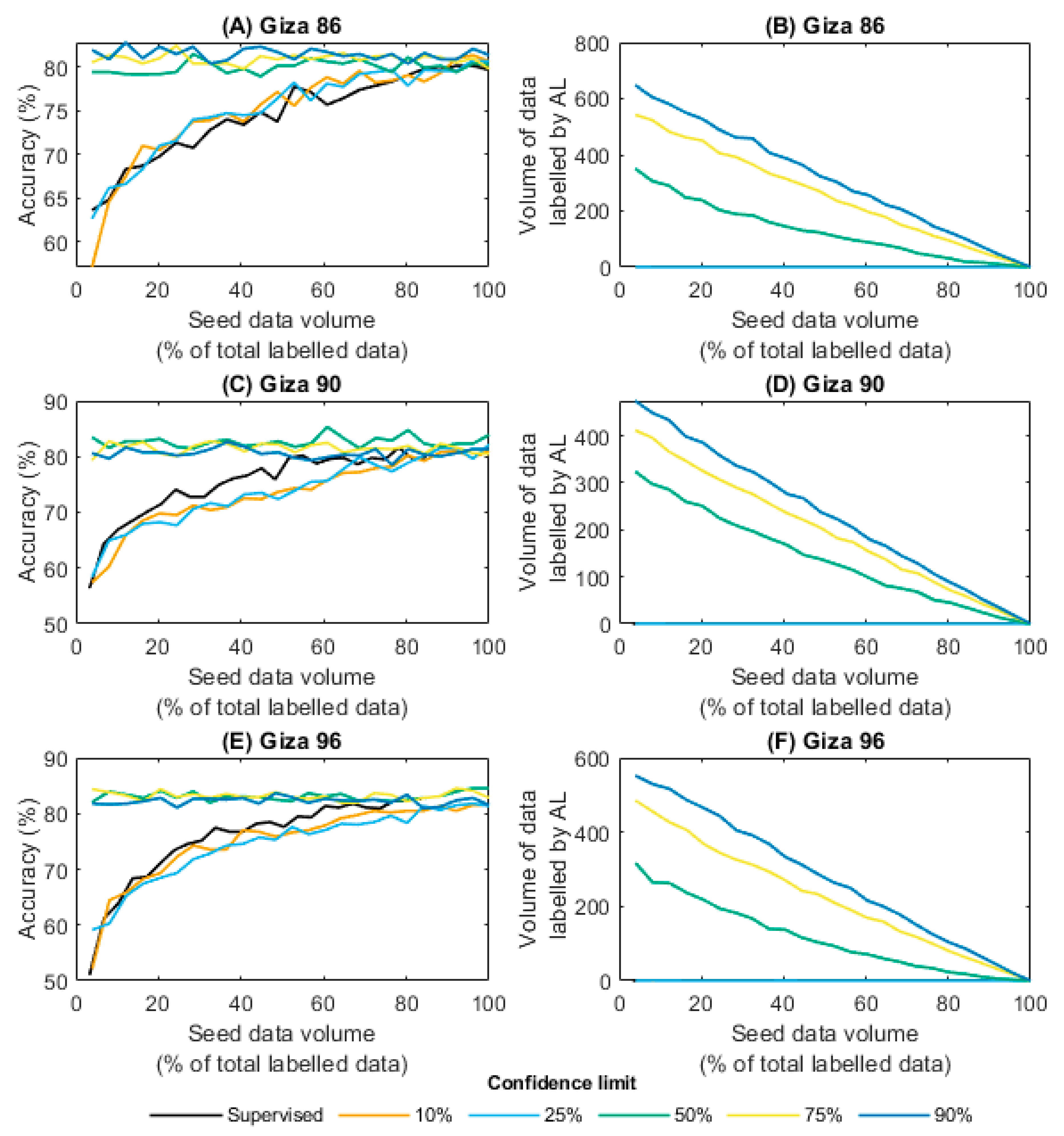
3.3. Active Learning Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Houben, C.; Lapkin, A.A. Automatic discovery and optimization of chemical processes. Curr. Opin. Chem. Eng. 2015, 9, 1–7. [Google Scholar] [CrossRef][Green Version]
- Samuelsson, O.; Björk, A.; Zambrano, J.; Carlsson, B. Gaussian process regression for monitoring and fault detection of wastewater treatment processes. Water Sci. Technol. 2017, 75, 2952–2963. [Google Scholar] [CrossRef] [PubMed]
- Mowbray, M.; del Rio-Chanona, E.; Harun, I.; Hellgardt, K.; Zhang, D. Ensemble Learning for bioprocess dynamic modelling and prediction. Authorea Prepr. 2020. [Google Scholar] [CrossRef]
- Rady, A.; Adedeji, A. Assessing different processed meats for adulterants using visible-near-infrared spectroscopy. Meat Sci. 2018, 136, 59–67. [Google Scholar] [CrossRef]
- Watson, N.J.; Bowler, A.L.; Rady, A.; Fisher, O.J.; Simeone, A.; Escrig, J.; Woolley, E.; Adedeji, A.A. Intelligent sensors for sustainable food and drink manufacturing. Front. Sustain. Food Syst. 2021, 5, 642786. [Google Scholar] [CrossRef]
- Rady, A.M.; Guyer, D.E.; Watson, N.J. Near-infrared spectroscopy and hyperspectral imaging for sugar content evaluation in potatoes over multiple growing seasons. Food Anal. Methods 2021, 14, 581–595. [Google Scholar] [CrossRef]
- Yu, C. Chapter 2—Natural Textile Fibres: Vegetable Fibres. In Woodhead Publishing Series in Textiles; Sinclair, R., Ed.; Woodhead Publishing: Sawston, UK, 2015; pp. 29–56. ISBN 978-1-84569-931-4. [Google Scholar]
- Abdullah, K.; Khan, Z. Breeding Cotton for International Trade. In Cotton Breeding and Biotechnology; Khan, Z., Ali, Z., Khan, A.A., Eds.; Taylor & Francis Group: Boca Raton, FL, USA, 2022; ISBN 9781003096856. [Google Scholar]
- Delhom, C.D.; Martin, V.B.; Schreiner, M.K.; Martin, V.B.; Schreiner, M.K. Engineering and ginning textile industry needs. J. Cotton Sci. 2017, 21, 210–219. [Google Scholar] [CrossRef]
- Eder, Z.P.; Morgan, G.; Agrilife, A.; Eder, Z.P.; Singh, S.; Fromme, D.; Collins, G.; Bourland, F.; Morgan, G. Impact of cotton leaf and bract characteristics on cotton leaf grade. Crop. Forage Turfgrass Manag. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Lv, Y.; Gao, Y.; Rigall, E.; Qi, L.; Gao, F.; Dong, J. Cotton appearance grade classification based on machine learning. Procedia Comput. Sci. 2020, 174, 729–734. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, C.; Deng, D. Content estimation of foreign fibers in cotton based on deep learning. Electronics 2020, 9, 1795. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Patil, R.B. Clustering and neural networks to categorize cotton trash. Opt. Eng. 1994, 33, 1642–1653. [Google Scholar] [CrossRef]
- Matusiak, M.; Walawska, A. Important aspects of cotton colour measurement. Fibres Text. East. Eur. 2010, 18, 17–23. [Google Scholar]
- Liu, Y.; Gamble, G.; Thibodeaux, D. UV/Visible/Near-Infrared reflectance models for the rapid and non-destructive prediction and classification of cotton color and physical indices. Trans. ASABE 2010, 53, 1341–1348. [Google Scholar] [CrossRef]
- Hussein, M.G.; El-Marakby, A.M.; Tolb, A.M.; Amal, Z.A.M.; Ebaido, I. Relationship between fiber cotton grade and some related characteristics of long and extra-long staple Egyptian cotton varieties (Gossypium barbadense. L). Arab Univ. J. Agric. Sci. 2020, 28, 191–205. [Google Scholar] [CrossRef]
- Ahmed, Y.N.; Delin, H. Current situation of Egyptian cotton: Econometrics study using ARDL model. J. Agric. Sci. 2019, 11, 88–97. [Google Scholar] [CrossRef]
- Xu, B.; Fang, C.; Huang, R.; Watson, M.D. Cotton color measurements by an imaging colorimeter. Text. Res. J. 1998, 68, 351–358. [Google Scholar] [CrossRef]
- Xu, B.; Fang, C.; Watson, M.D. Investigating new factors in cotton color grading. Text. Res. J. 2016, 68, 779–787. [Google Scholar] [CrossRef]
- Cheng, L.; Ghorashi, H.; Duckett, K.; Zapletalova, T.; Watson, M. Color grading of cotton part II: Color grading with an expert system and neural networks. Text. Res. J. 1999, 69, 893–903. [Google Scholar] [CrossRef]
- Cui, X.; Cai, Y.; Rodgers, J.; Martin, V.; Watson, M. An investigation into the intra-sample variation in the color of cotton using image analysis. Text. Res. J. 2014, 84, 214–222. [Google Scholar] [CrossRef]
- Wang, X.; Yang, W.; Li, Z. A fast image segmentation algorithm for detection of pseudo-foreign fibers in lint cotton. Comput. Electr. Eng. 2015, 46, 500–510. [Google Scholar] [CrossRef]
- Thomasson, J.A.; Shearer, S.A.; Byler, R.K. Image-processing solution to cotton color meaurement problems: Part I. instrument design and construction. Trans. ASAE 2005, 48, 421–438. [Google Scholar] [CrossRef]
- Heng, C.; Chen, L.; Shen, H.; Wang, F. Study on the measurement and evaluation of cotton color using image analysis. Mater. Res. Express 2020, 7, 75101. [Google Scholar] [CrossRef]
- Kang, T.J.; Kim, S.C. Objective evaluation of the trash and color of raw cotton by image processing and neural network. Text. Res. J. 2016, 72, 776–782. [Google Scholar] [CrossRef]
- Chen, S.; Ling, L.N.; Yuan, R.C.; Sun, L.Q. Classification model of seed cotton grade based on least square support vector machine regression method. In Proceedings of the Proceedings: 2012 IEEE 6th International Conference on Information and Automation for Sustainability, Beijing, China, 27–29 September 2012; pp. 198–202. [Google Scholar]
- Mustafic, A.; Li, C.; Haidekker, M. Blue and UV LED-induced fluorescence in cotton foreign matter. J. Biol. Eng. 2014, 8, 29. [Google Scholar] [CrossRef] [PubMed]
- Kuzy, J.; Li, C. A pulsed thermographic imaging system for detection and identification of cotton foreign matter. Sensors 2017, 17, 518. [Google Scholar] [CrossRef]
- Liu, Y.; Foulk, J. Potential of visible and near infrared spectroscopy in the determination of instrumental leaf grade in lint cottons. Text. Res. J. 2013, 83, 928–936. [Google Scholar] [CrossRef]
- Liu, Y.; He, Z.; Shankle, M.; Tewolde, H. Compositional features of cotton plant biomass fractions characterized by attenuated total reflection Fourier transform infrared spectroscopy. Ind. Crops Prod. 2016, 79, 283–286. [Google Scholar] [CrossRef]
- He, D.; Wang, Q.; Arandjelovi’c, O.A. Edge detecting method for microscopic image of cotton fiber cross-section using RCF deep neural network. Information 2021, 12, 196. [Google Scholar] [CrossRef]
- Fisher, O.J.; Rady, A.; El-Banna, A.A.A.; Watson, N.J.; Emaish, H.H. An image processing and machine learning solution to automate Egyptian cotton lint grading. Text. Res. J. 2022, 93, 2558–2575. [Google Scholar] [CrossRef]
- Egyptian Agricultural Channel. Cotton the Stages of Trading and Ginning and the Factors Affecting the Determination of Grades. 2023. Available online: https://misrelzraea.com/43153-2/ (accessed on 15 August 2023).
- Cotton Arbitration and Testing General Organization. Available online: https://www.egyptcotton-catgo.org/HomePageEN.aspx (accessed on 15 August 2023).
- Gourlot, J.-P.; Drieling, A.; Qaud, M.; Gordon, S.; Knowlton, J.; Matusiak, M.; van der Sluijs, R.; Martin, V.; Froese, K.; Delhom, C. Interpretation and Use of Instrument Measured Cotto Characteristics; International Cotton Advisory Committee (ICAC): Washington, DC, USA, 2020; Available online: https://ica-bremen.org/cotton-information/cotton-quality-information/the-cotton-testing-guideline/ (accessed on 23 October 2023).
- Li, Y.; Yang, J. Few-shot cotton pest recognition and terminal realization. Comput. Electron. Agric. 2020, 169, 105240. [Google Scholar] [CrossRef]
- Yang, J.; Guo, X.; Li, Y.; Marinello, F.; Ercisli, S.; Zhang, Z. A survey of few-shot learning in smart agriculture: Developments, applications, and challenges. Plant Methods 2022, 18, 28. [Google Scholar] [CrossRef]
- Li, Y.F.; Liang, D.M. Safe semi-supervised learning: A brief introduction. Front. Comput. Sci. 2019, 13, 669–676. [Google Scholar] [CrossRef]
- Bao, X.M.; Peng, X.; Wang, Y.M.; Cao, Z.B. Textile image segmentation based on semi-supervised clustering and Bayes decision. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 3, pp. 559–562. [Google Scholar] [CrossRef]
- Zhou, Q.; Mei, J.; Zhang, Q.; Wang, S.; Chen, G. Semi-supervised fabric defect detection based on image reconstruction and density estimation. Text. Res. J. 2020, 91, 962–972. [Google Scholar] [CrossRef]
- Seeger, M. A Taxonomy for Semi-Supervised Learning Methods. In Semi-Supervised Learning; Chapelle, O., Schölkopf, B., Zien, A., Eds.; The MIT Press: Cambridge, MA, USA, 2010; pp. 15–31. ISBN 9780262514125. [Google Scholar]
- Cohncohn, D.A.; Ghahramani, Z.; Jordan, M.I. Active learning with statistical models. J. Articial Intell. Res. 1996, 4, 129–145. [Google Scholar] [CrossRef]
- Thakur, G.S.; Daigle, B.J.; Qian, M.; Dean, K.R.; Zhang, Y.; Yang, R.; Kim, T.-K.; Wu, X.; Li, M.; Lee, I.; et al. A Multimetric Evaluation of Stratified Random Sampling for Classification: A Case Study. IEEE Life Sci. Lett. 2016, 2, 43–46. [Google Scholar] [CrossRef]
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform. 2014, 6, 10. [Google Scholar] [CrossRef]
- Charte, F.; Romero, I.; Pérez-Godoy, M.D.; Rivera, A.J.; Castro, E. Comparative analysis of data mining and response surface methodology predictive models for enzymatic hydrolysis of pretreated olive tree biomass. Comput. Chem. Eng. 2017, 11, 23–30. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Zeng, X.; Luo, G. Progressive sampling-based Bayesian optimization for efficient and automatic machine learning model selection. Health Inf. Sci. Syst. 2017, 5, 2. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef]
- Hussein, K.M.; Ebaido, I.A.; Kamal, M.M. Exploration of the validity of utilizing different aspects of color attributes to signalize and signify the lint grade of Egyptian cottons. Indian J. Fibre Text. Res. 2013, 3, 52–56. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Gu, Y.; Zydek, D.; Jin, Z. Active Learning based on Random Forest and Its Application to Terrain Classification BT—Progress in Systems Engineering; Selvaraj, H., Zydek, D., Chmaj, G., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 273–278. [Google Scholar]


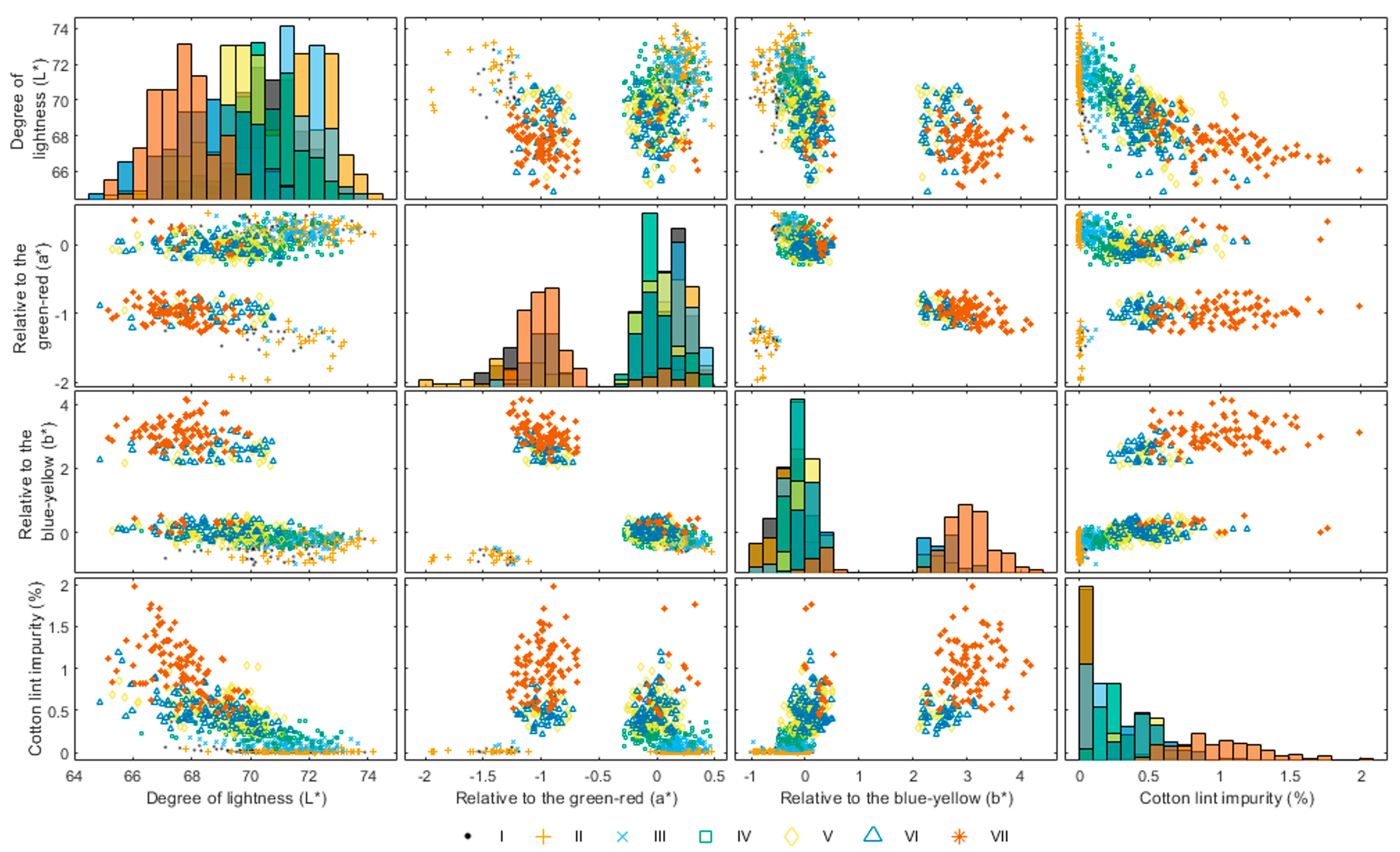
| Egyptian Cotton Grade | Giza 86 | Giza 90 | Giza 96 |
|---|---|---|---|
| I—Fully good | 115 | 0 | 103 |
| II—Good to fully good | 118 | 100 | 0 |
| III—Good | 113 | 131 | 109 |
| IV—Fully good fair to good | 119 | 116 | 118 |
| V—Fully good fair | 150 | 124 | 97 |
| VI—Good fair to fully good fair | 115 | 131 | 102 |
| VII—Good fair | 115 | 101 | 120 |
| VIII—Fully fair to good fair | 0 | 0 | 0 |
| IX—Fully fair | 0 | 0 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fisher, O.J.; Rady, A.; El-Banna, A.A.A.; Emaish, H.H.; Watson, N.J. AI-Assisted Cotton Grading: Active and Semi-Supervised Learning to Reduce the Image-Labelling Burden. Sensors 2023, 23, 8671. https://doi.org/10.3390/s23218671
Fisher OJ, Rady A, El-Banna AAA, Emaish HH, Watson NJ. AI-Assisted Cotton Grading: Active and Semi-Supervised Learning to Reduce the Image-Labelling Burden. Sensors. 2023; 23(21):8671. https://doi.org/10.3390/s23218671
Chicago/Turabian StyleFisher, Oliver J., Ahmed Rady, Aly A. A. El-Banna, Haitham H. Emaish, and Nicholas J. Watson. 2023. "AI-Assisted Cotton Grading: Active and Semi-Supervised Learning to Reduce the Image-Labelling Burden" Sensors 23, no. 21: 8671. https://doi.org/10.3390/s23218671
APA StyleFisher, O. J., Rady, A., El-Banna, A. A. A., Emaish, H. H., & Watson, N. J. (2023). AI-Assisted Cotton Grading: Active and Semi-Supervised Learning to Reduce the Image-Labelling Burden. Sensors, 23(21), 8671. https://doi.org/10.3390/s23218671









